Доклады Академии наук СССР. 1952. Том LХХХIII, № математика

Вид материала

Доклад

Содержание Для того, чтобы уравнение (5) имело недискретный спектр, необходимо и достаточно, чтобы область Если уравнение (5) задано в двумерной области Для того, чтобы разностное уравнение

Подобный материал:

• Доклады Академии Наук ссср, 1946, Том L, стр. 143-146, 98.11kb.
• Древняя российская история от начала российского народа до кончины великого князя ярослава, 1396.58kb.
• СНиП 11-4-79. Естественное и искусственное освещение, 2183.39kb.
• С. Н. Собрание сочинений. М.: 1952 Т. С. 105-106. Бернштейн С. Н. Собрание сочинений., 8.17kb.
• Сорокина) с участием Госхимпроекта Госстроя СССР (Л. М. Волкова), ниижб госстроя СССР, 1136.27kb.
• Неона Александровича Арманда. Чтения-конференции включают, 361.86kb.
• Организационная социальная психология, 4868.96kb.
• Разработаны цниипромзданий Госстроя СССР канд техн наук Н. А. Ушаков руководитель темы;, 1998.39kb.
• Дво ран статьи и доклады, опубликованные в 2007, 475.79kb.
• С. В. Тимофеев- руководитель темы, канд геол минер наук, 1112.63kb.

Доклады Академии наук СССР.

1952.Том LХХХIII, № 1.


МАТЕМАТИКА

А.М. Молчанов

КРИТЕРИЙ ДИСКРЕТНОСТИ СПЕКТРА ДИФФЕРЕНЦИАЛЬНОГО

УРАВНЕНИЯ ВТОРОГО ПОРЯДКА.

(представлено академиком М.В.Келдышем 31 ХII 1951).

В работе рассматриваются уравнения вида

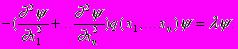(1)

Уравнение задано во всем пространстве, а функция 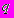предполагается ограниченной снизу. Для таких уравнений найдены необходимые и достаточные условия дискретности спектра.

Это условие формулируется особенно просто для обыкновенного дифференциального уравнения второго порядка:

Уравнение

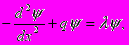(2)

заданное на всей прямой 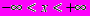, имеет дискретный спектр в том и только в том случае, если

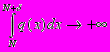(3)

пр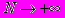и или 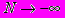и для любого фиксированного 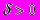;функция 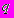предполагается ограниченной снизу.

Уравнения в частных производных существенно отличаются, с точки зрения условий дискретности спектра, от обыкновенных дифференциальных уравнений. Так же как и в одномерном случае, для недискретности спектра достаточно существование счетной последовательности одинаковых непересекающихся кубов 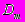, таких, что 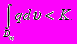Но, в отличие от одномерного, в n-мерном случае можно на каждом 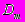выделить такое множество 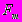, что при произвольном изменении 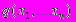на этих множествах спектр остается недискретным, а изменяя 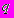надлежащим образом можно добиться выполнения условия, аналогичного условию (3).

Множества 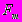должны быть несущественными вырезами кубов 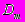в следующем смысле. Множество 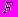, расположенное в кубе 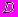, называется несущественным вырезом этого куба, если емкость 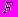достаточно мала по сравнению с емкостью 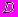, 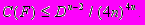Введение этого понятия позволяет сформулировать критерий дискретности спектра.

Для того чтобы уравнение (1) имело дискретный спектр, необходимо и достаточно, чтобы интеграл функции 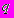по кубу 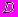с любым несущественным вырезом F неограниченно возрастал, когда куб 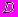, сохраняя размер уходит на бесконечность, а вырез F как угодно изменяется:

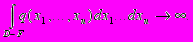(4)

Методика исследования, развитая для уравнения (1), непосредственно переносится на уравнения типа

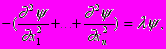(5)

заданные в области 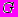, с граничными условиями на границе области 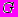. В работе найдены необходимые и достаточные условия дискретности спектра уравнения (5).

Так как, однако, формулировка сильно выигрывает в наглядности , если говорить об условиях недискретности спектра, то здесь будут приведены именно эти условия.

Для того, чтобы уравнение (5) имело недискретный спектр, необходимо и достаточно, чтобы область 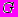, в котором оно задано, содержало счетную последовательность одинаковых кубов с несущественными вырезами.

В двух важных частных случаях теорему можно усилить.

Если граница области 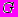имеет ограниченную кривизну, то спектр уравнения (5) недискретен тогда и только тогда, когда область 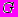содержит счетное число одинаковых непересекающихся кубов.

Эта теорема справедлива для пространства любого числа измерений. Для плоскости возможно усиление основной теоремы в несколько ином направлении.

Если уравнение (5) задано в двумерной области , дополнение к которой односвязно, то для недискретности спектра необходимо и достаточно, чтобы область 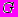содержала счетное число одинаковых непересекающихся квадратов.

В заключении в работе доказывается критерий дискретности спектра для разностного аналога дифференциального уравнения. В то время, как обычно теоремы для разностных уравнений оказываются значительно сложнее соответствующих теорем для дифференциальных уравнений, критерий дискретности спектра разностного уравнения формулируется неожиданно просто:

Для того, чтобы разностное уравнение:

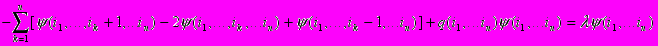имело дискретный спектр, необходимо и достаточно, чтобы 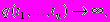когда



Этот результат наиболее отчетливо вскрывает основную причину дискретности спектра - причину, которая в дифференциальных уравнениях маскируется тонкостями поведения коэффициента 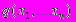на несущественных множествах.

Автор считает своим долгом принести глубокую благодарность проф. И.М. Гельфанду за руководство работой.

Поступило

23 ХII 1951