Физические основы строения и эволюции звезд
| Вид материала | Учебник |
- Ю. А. Головин, инженер, 97.95kb.
- Концепция эволюции в биологии, 91.47kb.
- Алюминий, его физические и химические свойства, 54.07kb.
- Законы эволюции вселенной часть постановка задачи об эволюции вселенной, 370.32kb.
- Возможность обнаружения «гравитационного линзирования» в системах двойных звезд, 188.55kb.
- Задачи: а Обучающие: Рассмотреть положение элементов-неметаллов в Периодической системе, 208.56kb.
- В основу программы положены основные дисциплины федерального компонента Государственного, 121.94kb.
- Фундаментальные физические константы кузовков Виктор Степанович, 28.5kb.
- Фундаментальные физические константы кузовков Виктор Степанович, 28.27kb.
- Лектор: д ф. м н., с н. с. Самусь Николай Николаевич, 55.12kb.
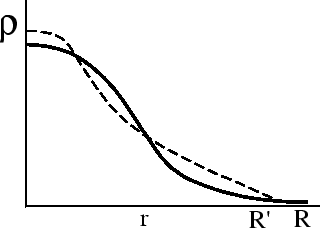 |
| Рис. 10. |
В химически однородной звезде необязательно переносить вещество: к тем же результатам относительно устойчивости можно прийти, просто изменяя распределение вещества
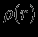 , не меняя при этом взаимного расположения слоев (рис. 10). Можно утверждать, что если равновесие звезды слегка нарушить, то энергия при этом не изменится. Точная формулировка этого утверждения: условие экстремума полной энергии звезды
, не меняя при этом взаимного расположения слоев (рис. 10). Можно утверждать, что если равновесие звезды слегка нарушить, то энергия при этом не изменится. Точная формулировка этого утверждения: условие экстремума полной энергии звезды 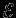 совпадает с условием равновесия.
совпадает с условием равновесия. Рассматриваем звезду с произвольным распределением энтропии
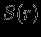 . Полная энергия звезды
. Полная энергия звезды 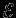 складывается из тепловой энергии
складывается из тепловой энергии 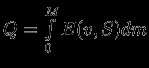 и гравитационной энергии1.2
и гравитационной энергии1.2 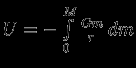 :
: 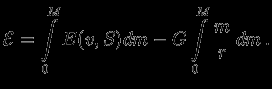
Найдем условие экстремума
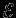 , используя
, используя 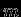 в качестве лагранжевой координаты. Распределение плотности полностью определено, если задана функция
в качестве лагранжевой координаты. Распределение плотности полностью определено, если задана функция 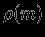 . Будем варьировать
. Будем варьировать 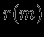 , т.е. смещать отдельные слои, считая энтропию
, т.е. смещать отдельные слои, считая энтропию 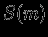 фиксированной, при этом у нас будут определены вариации и всех остальных величин. Имеем:
фиксированной, при этом у нас будут определены вариации и всех остальных величин. Имеем: 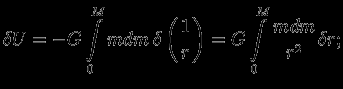
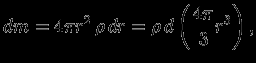 поэтому
поэтому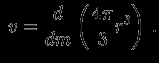
Тогда
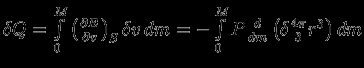 . Интегрируя по частям с учетом того, что
. Интегрируя по частям с учетом того, что 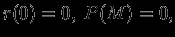 получим
получим 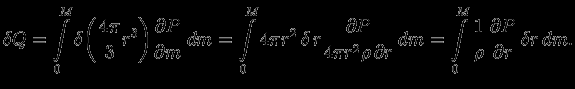
В результате
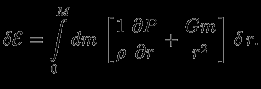
Если
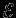 экстремально, то
экстремально, то 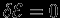 при любых
при любых 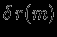 , следовательно, из экстремальности
, следовательно, из экстремальности 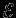 следует уравнение равновесия
следует уравнение равновесия 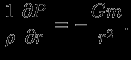
Чем полезен вариационный принцип? Оказывается, что с помощью этого принципа исследовать устойчивость много проще, чем используя уравнение равновесия. В этом можно убедиться следующим образом. Запишем выражение для полной энергии звезды, не предполагая равенства нулю скоростей движения вещества звезды:
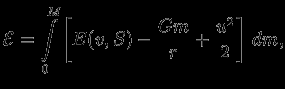
где
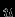 -- скорость элемента массы. Очевидно, что равновесное расстояние (которое всегда соответствует экстремуму энергии) будет устойчивым, если экстремум является минимумом. Действительно, тогда из него не может возникнуть никакое другое состояние, ни с
-- скорость элемента массы. Очевидно, что равновесное расстояние (которое всегда соответствует экстремуму энергии) будет устойчивым, если экстремум является минимумом. Действительно, тогда из него не может возникнуть никакое другое состояние, ни с 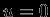 (но другим
(но другим 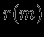 ), ни тем более с
), ни тем более с 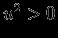 . Следовательно, исследование устойчивости сводится к нахождению условий, при которых вторая вариация энергии
. Следовательно, исследование устойчивости сводится к нахождению условий, при которых вторая вариация энергии 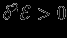 .
. Помимо исследования устойчивости вариационный принцип позволяет находить приближенные решения для структуры звезды.
1.8 Теорема вириала
Предположим, что уравнение состояния степенное:
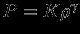 . Тогда удельная тепловая энергия
. Тогда удельная тепловая энергия 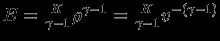 . Мы знаем, что в равновесии
. Мы знаем, что в равновесии 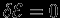 при произвольной
при произвольной 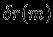 . Пусть
. Пусть 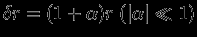 . Такое возмущение описывает подобное (гомологическое) расширение или сжатие звезды. Тогда
. Такое возмущение описывает подобное (гомологическое) расширение или сжатие звезды. Тогда 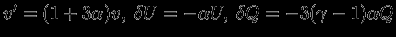 . Следовательно,
. Следовательно, 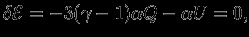
откуда
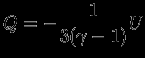
(это соотношение и называют теоремой вириала). Для одноатомного газа с
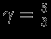 имеем
имеем 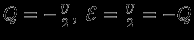 .
.  |
| Рис. 11. |
Теперь положим
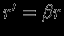 , причем не будем считать
, причем не будем считать 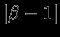 малой величиной, а исходное состояние -- равновесным. Обозначим через
малой величиной, а исходное состояние -- равновесным. Обозначим через 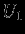 и
и 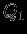 соответствующие величины энергий исходной модели. Тогда после преобразования
соответствующие величины энергий исходной модели. Тогда после преобразования 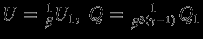 (для степенного уравнения состояния). Если
(для степенного уравнения состояния). Если 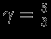 , то
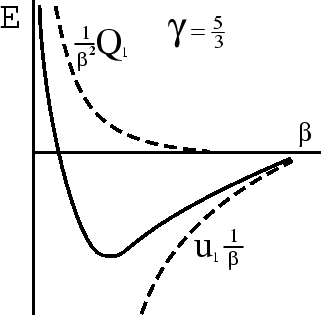
, то 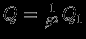 . Как выглядит в этом случае кривая
. Как выглядит в этом случае кривая 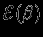 ? При
? При 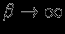 асимптотика определяется величиной
асимптотика определяется величиной 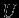 , при
, при 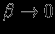 -- величиной
-- величиной 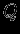 (рис. 11). Получаем, что при
(рис. 11). Получаем, что при 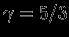 кривая имеет один и только один минимум, т.е. равновесие устойчиво.
кривая имеет один и только один минимум, т.е. равновесие устойчиво. Получим теорему вириала другим способом из уравнения равновесия, причем зависимость
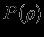 может быть произвольной. (Выше при выводе теоремы вириала из вариационного принципа зависимость
может быть произвольной. (Выше при выводе теоремы вириала из вариационного принципа зависимость 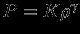 была существенна). Умножим уравнение равновесия (1.6) на
была существенна). Умножим уравнение равновесия (1.6) на 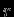 :
: 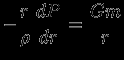
и проинтегрируем по
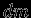 :
: 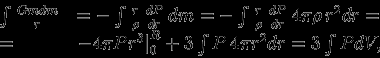
т.е.
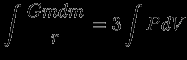
теорема вириала при произвольном
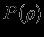 .
. При степенном уравнении состояния, используя
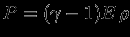 , имеем уже известное соотношение
, имеем уже известное соотношение 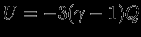 .
. В действительности уравнение состояния не степенное, но для многих оценок полезно знать свойства звезд с таким уравнением состояния. Для степенного уравнения состояния имеется подобие, т.е. достаточно решить задачу при данном
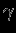 для одного значения
для одного значения 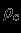 , чтобы найти функциональную зависимость
, чтобы найти функциональную зависимость 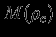 и
и 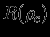 . В систему уравнений
. В систему уравнений 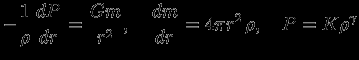
входят размерные константы
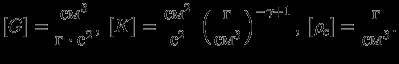
Поэтому, комбинируя
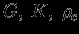 в различных степенях, можно получить массу, радиус и другие характеристики звезды. Эту задачу можно решить формально, составляя систему уравнений типа
в различных степенях, можно получить массу, радиус и другие характеристики звезды. Эту задачу можно решить формально, составляя систему уравнений типа 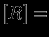 см
см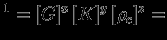 см
см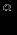 г
г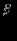 с
с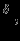
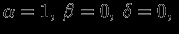 т.е.
т.е.
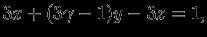
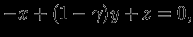
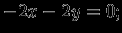
откуда
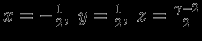 , т.е.
, т.е. 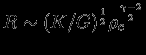 .
. Более наглядно эта связь получается с помощью порядковых оценок:
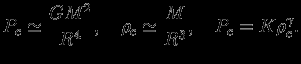
Смысл первого соотношения легко понять, если вспомнить, что сила притяжения между двумя половинками звезды
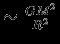 , а давление (сила на единицу площади, пропорциональной
, а давление (сила на единицу площади, пропорциональной 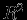 )
) 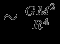 . Исключая из этих выражений
. Исключая из этих выражений 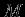 , имеем выражение для
, имеем выражение для 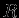 , а исключая
, а исключая 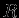 , находим
, находим 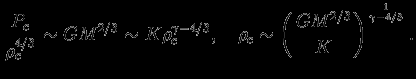
Подчеркнем, что вид кривых
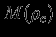 и
и 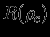 зависит от безразмерной величины
зависит от безразмерной величины 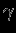 , т.е. кривые для разных
, т.е. кривые для разных 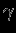 не подобны.
не подобны.
