Качественный анализ электромагнитных полей систем простых антенн

Вид материала

Автореферат

Содержание ПЕРМЯКОВ Валерий Александрович Институт Радиотехники и Электроники Российской Академии Наук Общая характеристика работы Краткое содержание работы D=const), т.е. соответствует синхронному изменению компонент E А представление (4) соответствует плоской гармонической волне круговой поляризации. При произвольной зависимости амплитуды A Анализ особенностей электрического поля ОЭГ в негармоническом режиме возбуждения. Список публикаций по теме диссертации

Подобный материал:

• Учебная программа по дисциплине теория и техника антенн толмачев А. И. Врезультате, 52.61kb.
• Научно-образовательный материал компьютерное моделирование электромагнитных полей, 22.61kb.
• Новые методы защиты населения крупных городов от электромагнитных полей, шума и радоновыделения, 102.38kb.
• «влияние электромагнитных волн на здоровье человека», 452.98kb.
• Применение электромагнитных волн миллиметрового диапазона в ортопедии и травматологии, 15.01kb.
• Аннотация отчет, 50.53kb.
• Е. М. Глушкова Качественный анализ Методические указания, 2541.02kb.
• Моделирование электростатических и электромагнитных полей приминительно к процессам, 91.97kb.
• Факторов влияющих на жизнедеятельность, 1625.04kb.
• Применение Аппарат «Рикта -01», 11.92kb.

На правах рукописи


КОРЮКИН Александр Николаевич


КАЧЕСТВЕННЫЙ АНАЛИЗ ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ СИСТЕМ ПРОСТЫХ АНТЕНН


Специальность 05.12.07 – Антенны, СВЧ устройства и их технологии


АВТОРЕФЕРАТ

диссертации на соискание ученой степени кандидата

технических наук


Москва – 2008г.


Работа выполнена на кафедре Антенных устройств и распространения радиоволн Московского энергетического института (Технического университета)


Научный руководитель: доктор физико-математических наук, профессор

ПЕРМЯКОВ Валерий Александрович


Официальные оппоненты: доктор физико – математических наук

КРЮКОВСКИЙ Андрей Сергеевич


кандидат технических наук

ОМАРОВ Геннадий Сайфуллаевич


Ведущая организация Институт Радиотехники и Электроники Российской Академии Наук


Защита состоится 27 ноября 2008г. в 15.30 в аудитории А 402 на заседании диссертационного совета при Московском энергетическом институте (Техническом университете) по адресу: 111250, г. Москва, ул. Красноказарменная, д. 17.


Отзывы в двух экземплярах, заверенные печатью, присылать по адресу: 111250, Москва, ул. Красноказарменная, д.14, Ученый совет МЭИ (ТУ)


С диссертацией можно ознакомиться в библиотеке МЭИ (ТУ)


Автореферат разослан 21 октября 2008г.


Ученый секретарь

диссертационного совета

кандидат технических наук, доцент Т.И. Курочкина.


ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность темы. Среди различных классов антенн особую роль играют элементарные излучатели. К ним относятся элементарные электрический и магнитный вибраторы, рамки, щелевые излучатели и т.д. Из элементарных излучателей, в свою очередь, можно составить такие антенны, как турникетная антенна (скрещенные электрические диполи) и элемент Гюйгенса (скрещенные магнитный и электрический диполи), а также формировать антенные решетки.

Теория излучения элементарных антенн, начатая работой Г. Герца, подробно разработана для гармонического режима излучения. Однако до сих пор недостаточно исследована структура ближних полей систем элементарных антенн при произвольном соотношении амплитуд и фаз токов.

Во второй половине ХХ века появились новые направления исследований, связанных со сверхширокополосными (СШП) и сверхкороткими импульсными (СКИ) сигналами. Первое из этих направлений возникло в связи с изучением процессов воздействия мощных электромагнитных (ЭМ) импульсов, возникающих при ядерном взрыве, на работу радиосистем, и моделирования этих процессов (работы К.Баума и др.). Появились работы по применению СШП и СКИ сигналов в радиолокации, что потребовало развития соответствующих методов измерений и расчета (работы Х. Хармута и др., Ю.Л.Астанина и А.А.Костылева, И.Я. Иммореева, В.В.Крымского, В.Б.Авдеева и др.) Определение поляризации СШП сигналов было предложено в монографии А.И. Козлова, А.И.Логвина, В.А.Сарычева. Большое внимание было уделено экспериментальному исследованию излучения антеннами СШП сигналов (работы А.Ф.Кардо-Сысоева, В.И.Кошелева и др.). Вопросы подповерхностной радиолокации, в том числе использование для этой цели СШП и СКИ сигналов, рассматривались в работах Д. Даниэлса, А.Ю.Гринева и др. Применение СШП и СКИ сигналов стимулировало развитие теории антенн, поскольку подходы, развитые ранее для квазимонохроматического режима, либо не годились, либо были недостаточно эффективными при анализе излучения СШП и СКИ сигналов.

Традиционный для квазимонохроматических сигналов метод анализа излучения антенн, основанный на частотном преобразовании Фурье, может быть использован для расчета характеристик антенн и в случае СШП сигналов. Однако при этом возникают две трудности. Первая – вычислительная - даже на современных персональных компьютерах время расчета характеристик реальных антенн для СШП сигналов может достигнуть недопустимо больших значений. Вторая трудность – принципиальная. Заключается она в том, что трудно получить понимание процессов нестационарного излучения антенн, используя частотный метод и суммируя большое число частотных гармоник полей.

Чтобы обойти упомянутые трудности, потребовалась разработка прямых пространственно – временных методов расчета полей антенн, возбуждаемых импульсными токами. Прямые пространственно – временные методы можно разделить на две группы: аналитические и численные. Основным аналитическим методом является метод запаздывающих потенциалов, позволяющий найти выражения для полей антенн в свободном пространстве в виде интегралов по объему сторонних токов, а в случае простых антенн – замкнутые выражения для полей в элементарных функциях.

С методической точки зрения обратим внимание на применение теории катастроф в задачах электродинамики. Согласно В.И.Арнольду теория катастроф представляет собой совокупность приложений теории особенностей дифференцируемых отображений (Х.Уитни) и теории бифуркаций динамических систем (А.Пуанкаре, А.А.Андронов). Теория особенностей дифференцируемых отображений в приложении к электродинамике получила развитие в работах Д.С.Лукина, А.С.Крюковского, Е.А.Палкина с соавторами. Основное направление этих исследований – изучение высокочастотных асимптотик ЭМ полей численно-аналитическими методами. В работах Д.С.Лукина с сотрудниками были введены специальные функции волновых катастроф, дана их классификация, изучены различные приложения этих функций в задачах излучения антенн и распространения сигналов, в том числе СШП, в неоднородных диспергирующих и поглощающих средах.

Другая ветвь теории катастроф базируется на анализе физических процессов в различных системах, описываемых обыкновенными дифференциальными уравнениями (ОДУ) и в этом смысле относится к качественной теории динамических систем, развивавшейся А. Пуанкаре и А.А.Андроновым. С помощью этой теории в электродинамике исследовались процессы распространения волн в линейных и нелинейных средах.

В настоящей работе поставлена задача теоретического исследования методами качественной теории ОДУ ЭМ полей, создаваемых системами элементарных излучателей (элемент Гюйгенса, турникетная антенна). ЭМ поле комбинации диполей определяется замкнутыми выражениями через известные функции их дипольных моментов. Через известные поля записываются ОДУ силовых линий, которые и являются исходными для качественного анализа. Ранее качественные методы были использованы для изучения полей диполя Герца при произвольном его возбуждении в работах Пермякова В.А. c соавторами и показали свою эффективность. Качественные методы позволяют с единых позиций рассматривать процессы излучения в гармоническом, периодическом негармоническом и импульсном режимах излучения. Это единство методики, с одной стороны, позволяет установить сходство и различия гармонического и негармонического процессов, и с другой стороны - выявить аспекты формирования полей в гармоническом режиме возбуждения, которые до сих пор не были установлены. Помимо методической новизны анализ простейших излучателей актуален и потому, что такие излучатели используются в СШП системах радиолокации и радиосвязи.

Цели работы. Развитие методики качественного анализа силовых линий нестационарного ЭМ поля, излучаемого простыми антеннами, состоящими из комбинации элементарных излучателей.

Анализ ЭМ полей простых систем элементарных излучателей (турникетная антенна, элемент Гюйгенса) на основе качественных методов для произвольных (гармонического, негармонического периодического и импульсного) режимов возбуждения.

Выявление закономерностей формирования полей таких антенн с позиций их применения в практических приложениях.

Основные задачи. Определение эволюции особенностей – нулей электрического (магнитного) поля и условий их структурной перестройки для обобщенного элемента Гюйгенса (ОЭГ) - системы скрещенных электрического и магнитного диполей, возбуждаемых произвольными сторонними токами.

Определение эволюции особенностей электрического и магнитного полей и условий их структурной перестройки для системы двух скрещенных электрических диполей – элементарной турникетной антенны (ТА) при произвольном режиме возбуждения.

Научная новизна результатов. Разработана методика качественного анализа нестационарных ЭМ полей элементарных антенн, основанная на изучении особенностей ОДУ силовых линий электрического и магнитного полей в пространстве с учетом зависимости полей от времени.

Для ОЭГ проведено исследование траекторий особенностей электрического поля в пространстве-времени в гармоническом и импульсном режимах возбуждения, дана классификация типов траекторий в зависимости от их поведения в пространстве-времени (подвижные, неподвижные, пульсирующие особенности поля). Впервые показано, что, используя антенну типа ОЭГ, при определенных временных зависимостях возбуждающих дипольных моментов можно сформировать два неподвижных нуля электрического поля на конечном расстоянии от излучателя.

Для элементарной турникетной антенны дана классификация режимов излучения в зависимости от характеристик возбуждающих дипольных моментов: синхронный - структура силовых линий турникетной антенны совпадает со структурой силовых линий эквивалентного электрического диполя, несинхронный – особенности располагаются только в плоскости расположения диполей, специальный режим – имеются неподвижные особенности электрического поля только в точке расположения диполей и на бесконечности.

Предложено новое, отличное от известного, определение поляризации плоских импульсных ЭМ волн, основанное на понятии частоты вращения вектора электрического поля.

Достоверность результатов. Подтверждается использованием хорошо известных и апробированных методов качественной теории ОДУ в сочетании с численными методами интегрирования уравнений силовых линий. В частных случаях результаты проведенного анализа совпадают с известными из литературы.

Основные положения, выносимые на защиту.

1. Методика качественного анализа ЭМ полей системы элементарных излучателей, основанная на исследовании траекторий особенностей - нулей электрического и магнитного полей в пространстве - времени, определения условий их бифуркации, качественном анализе силовых линий электрического и магнитного полей, позволила выявить закономерности формирования ЭМ полей простейших систем элементарных излучателей (элемент Гюйгенса, турникетная антенна) при произвольном возбуждении диполей и может быть применена к более сложным системам элементарных излучателей.

2. Путем выбора параметров дипольных моментов элемента Гюйгенса в гармоническом и негармоническом режимах возбуждения можно сформировать один или два неподвижных нуля электрического поля и, соответственно, область с минимальной интенсивностью поля на конечном расстоянии от антенны, что может быть использовано при реализации антенн сотовых телефонов и других мобильных средств связи с уменьшенным влиянием электромагнитного поля на пользователя.

3. Структура электромагнитных полей элементарной турникетной антенны в зависимости от временных зависимостей возбуждающих дипольных моментов относится к одному из трех режимов: синхронный - структура силовых линий турникетной антенны совпадает со структурой силовых линий эквивалентного электрического диполя, несинхронный – подвижные особенности полей располагаются только в плоскости расположения диполей, специальный режим – имеются только неподвижные особенности электрического поля в точке расположения диполей и на бесконечности.

4. Предложенное определение поляризации плоских импульсных электромагнитных волн, основанное на частоте вращения вектора электрического поля, позволяет дать наглядную классификацию поляризации плоских импульсных волн.

Практическая значимость.

Обнаруженная в работе возможность формирования двух неподвижных нулей электрического поля элемента Гюйгенса представляет практический интерес для создания антенн сотовых телефонов и других систем связи с наименьшим воздействием на пользователя. Эффект формирования нулей поля на конечных расстояниях от антенны может быть использован также в системах ближней (в том числе подповерхностной) радиолокации.

Предложенное в работе определение поляризации нестационарных ЭМ волн по частоте вращения вектора электрического поля отличается простотой и может найти применение в практических измерениях поляризации нестационарных сигналов.

Реализация основных результатов. Результаты диссертационной работы использованы в учебном процессе кафедры Антенных устройств и распространения радиоволн МЭИ(ТУ), а также вошли в отчеты по г/б НИР № 01200605946 «Исследования принципов и процессов генерации, излучения, распространения и обработки опто-, акусто и радиосигналов для совершенствования современных информационно – телекоммуникационных комплексов, выполняемой по плану Минобрнауки РФ.

Апробация. Основные результаты докладывались на ежегодных конференциях студентов и аспирантов МЭИ(ТУ) в 2004 - 2007 г.г., на XX1 всероссийской научной конференции «Распространение радиоволн», Йошкар-Ола, 25-27 мая 2005 г., второй всероссийской конференции «Сверхширокополосные сигналы в радиолокации, связи и акустике». Муром, 4-7 июля 2006 г., на Московском электродинамическом семинаре, ИРЭ РАН, 2008 г., на семинаре по математическому моделированию волновых процессов, РОСНОУ, 2008 г.

Публикации. Результаты диссертации опубликованы в 14 печатных работах, из них 9 научных статей и текстов докладов в соавторстве (3 статьи в изданиях из перечня ВАК), а также 5 тезисов докладов.

Объем и структура работы. Диссертация состоит из трех глав, введения, заключения, списка литературы из 64 источников, списка публикаций автора и Приложений.

Текст занимает 170 страницы, содержит 2 таблицы и 37 рисунков.


КРАТКОЕ СОДЕРЖАНИЕ РАБОТЫ

Во введении дано краткое описание проблемы, приведен обзор работ по теме диссертации, обоснована актуальность темы, сформулированы цели и задачи работы, основные положения, выносимые на защиту. Указаны методы решения поставленных задач. Дана краткая характеристика работы. Определены практическая ценность результатов и область их применения.

В первой главе приведены исходные нестационарные уравнения Максвелла для однородной среды без потерь и основные соотношения, необходимые для расчета электромагнитных полей элементарных излучателей в нестационарном режиме возбуждения. Рассмотрены известные определения поляризации гармонических электромагнитных волн и СШП сигналов, а также предложено новое определение поляризации плоских нестационарных электромагнитных волн.

Исходными для анализа нестационарных процессов в однородной изотропной среде являются нестационарные уравнения Максвелла в дифференциальной форме со сторонними электрическими и магнитными зарядами и токами. Аналитическое решение уравнений Максвелла в случае точечных электрических диполей представляется соотношениями

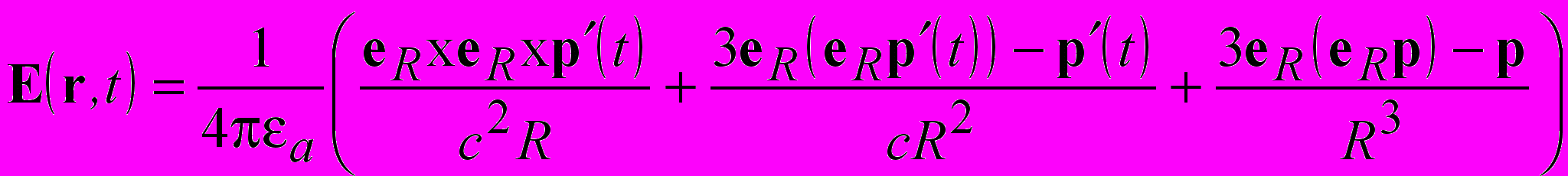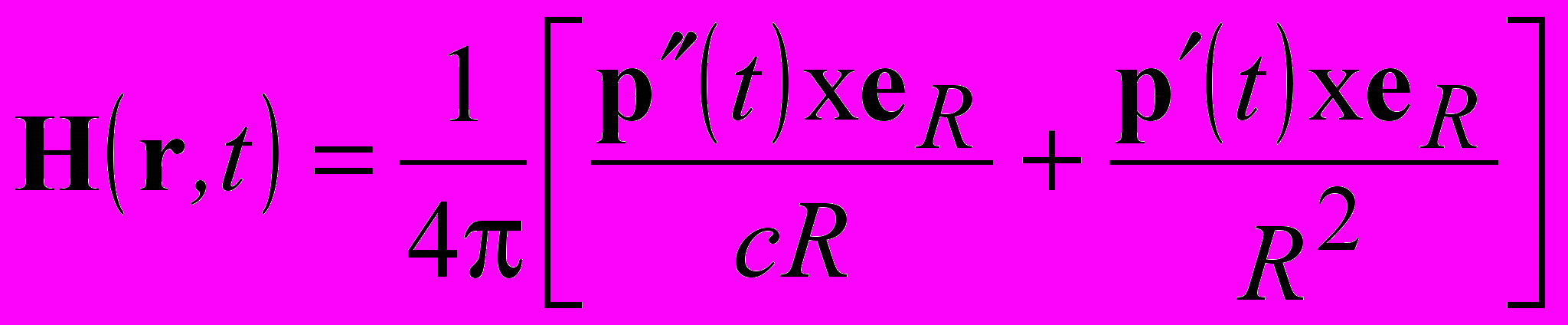, (1) , (2)

эквивалентными приведенным в Фейнмановских лекциях по физике, т.6. В (1),(2) p(t-R/c) – дипольный момент с учетом запаздывания на время распространения от диполя до точки наблюдения, штрихи означают производные по времени, e_R – единичный вектор. Представление электрического поля (1) удобно для анализа тем, что первое слагаемое в скобках убывает, как R^-1, и определяет поле излучения, следующее по порядку слагаемое убывает, как R^-2, и дает поле индукции, последнее слагаемое дает квазистатическое электрическое поле диполя, убывающее, как R^-3. Из (1), (2) с использованием принципа перестановочной двойственности находятся поля магнитного диполя.

Далее обсуждаются известные определения поляризации плоских гармонических волн и плоских СШП сигналов, приведенные в монографии А.И. Козлова, А.И.Логвина, В.А.Сарычева «Поляризация радиоволн». Предложенная в этой монографии классификация поляризации плоских СШП сигналов основана на выделении классов сигналов, частотные Фурье – гармоники которых являются сигналами круговой или эллиптической поляризации, причем пространственные компоненты электрического поля в декартовой системе координат связаны преобразованием Гильберта. В отличие от этого определения в главе 1 предложено иное определение поляризации нестационарных плоских волн, в основу которого положена такая характеристика волны, как угловая частота вращения вектора Е, определяемая через отношение компонент электрического поля:

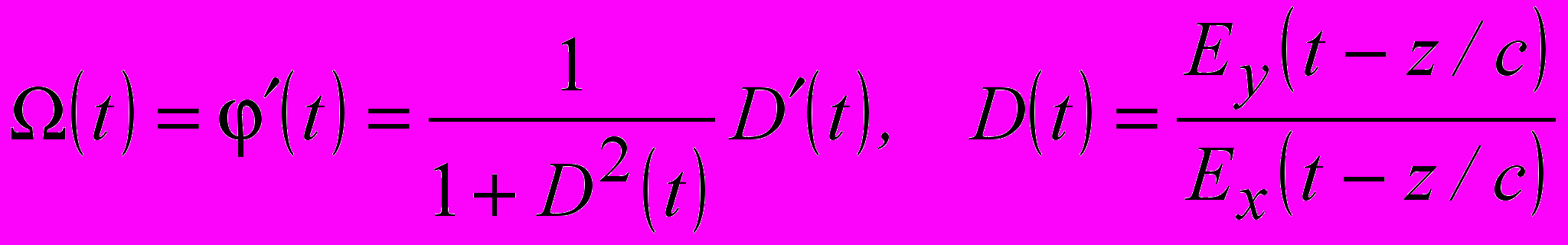(3)

здесь компоненты электрического поля E_y и E_x - в общем случае негармонические функции, плоская волна распространяется в направлении оси z. По аналогии с гармоническим режимом предложены следующие определения поляризации плоской нестационарной волны.

1. Линейная поляризация реализуется в отсутствие вращения вектора Е ( D=const), т.е. соответствует синхронному изменению компонент E_y и E_x .

2. Поле с постоянной частотой вращения вектора Е реализуется при условии

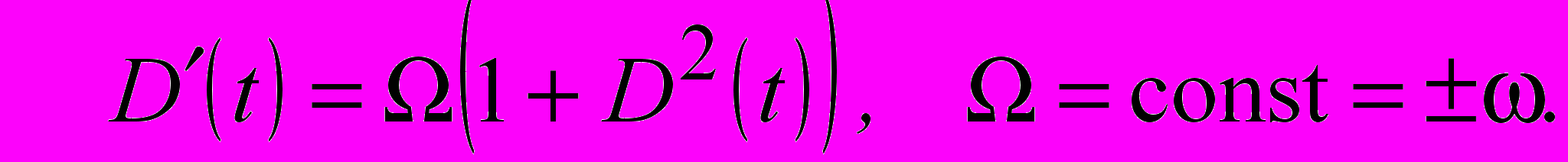Этому условию удовлетворяют компоненты E_y и E_x, имеющие следующий вид

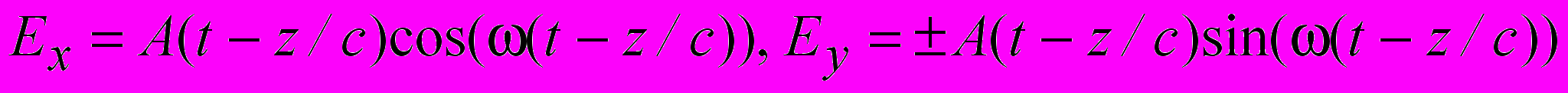. (4)

В частном случае постоянной амплитуды А представление (4) соответствует плоской гармонической волне круговой поляризации. При произвольной зависимости амплитуды A от времени годограф вектора Е во времени на плоскости (x,y) будет не окружностью, а кривой переменного радиуса, но скорость вращения вектора Е будет постоянной.

В качестве примера сигнала, удовлетворяющего соотношению (4), рассмотрим импульс, определяемый выражениями A_x=A_y=sin²(ω(t-z/c)), 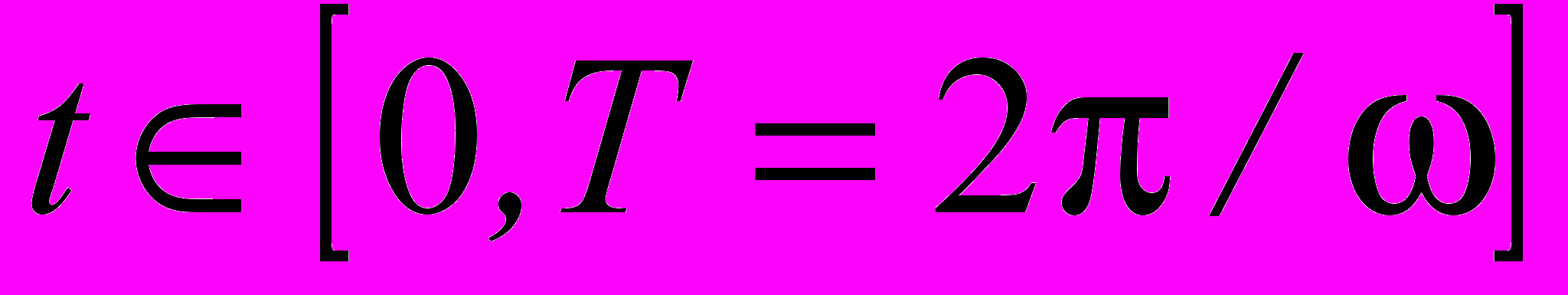. Зависимости компонент E_x (t), E_y(t) для этого примера при z=0 приведены на рис. 1 а), годограф вектора электрического поля во времени на плоскости (x,y) – на рис. 1 б),






б)
Рис.1 a)

3. Поле с переменной частотой вращения вектора Е при сохранении направления вращения реализуется при или 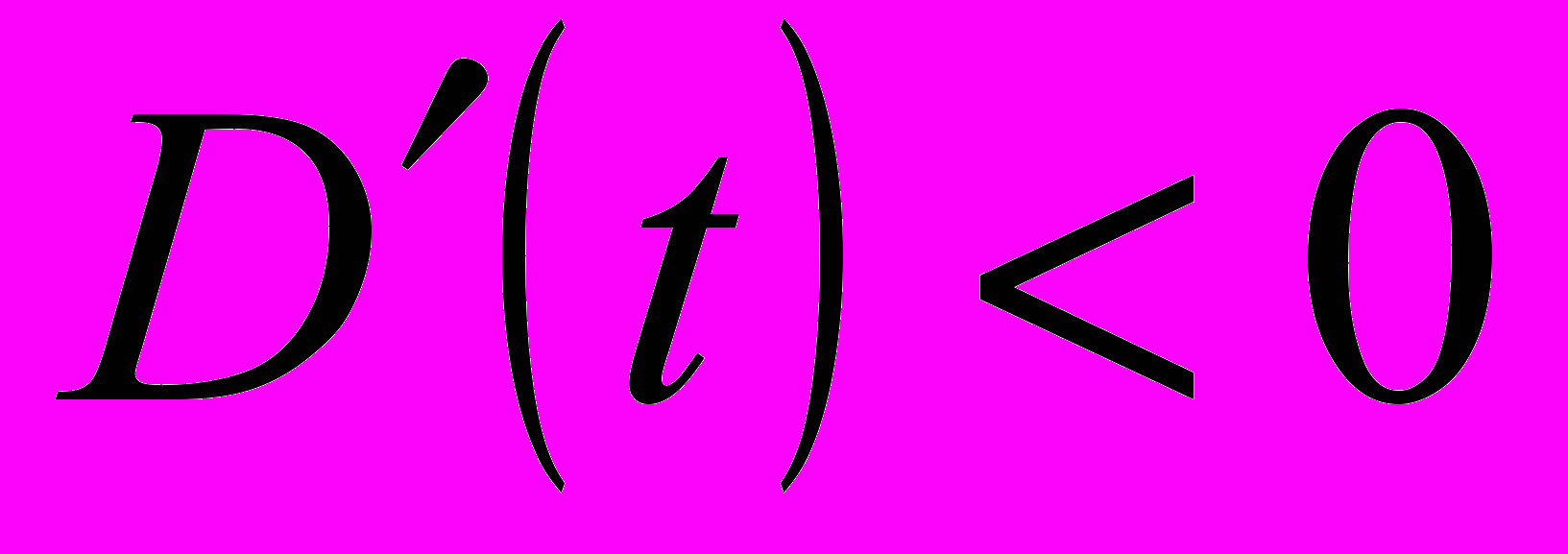. Частным случаем данного определения является эллиптическая поляризация гармонической волны.

4. Общий случай поляризации имеет место при произвольных зависимостях E_x и E_y от времени. При этом скорость вращения вектора Е может изменяться произвольным образом, в том числе может меняться направление вращения вектора Е.

Во второй главе изложен общий подход к анализу структуры силовых линий электрического и магнитного полей источников поля в гармоническом и негармоническом режимах излучения на основе качественной теории ОДУ. Система ОДУ силовых линий электрического поля в сферических координатах имеет вид

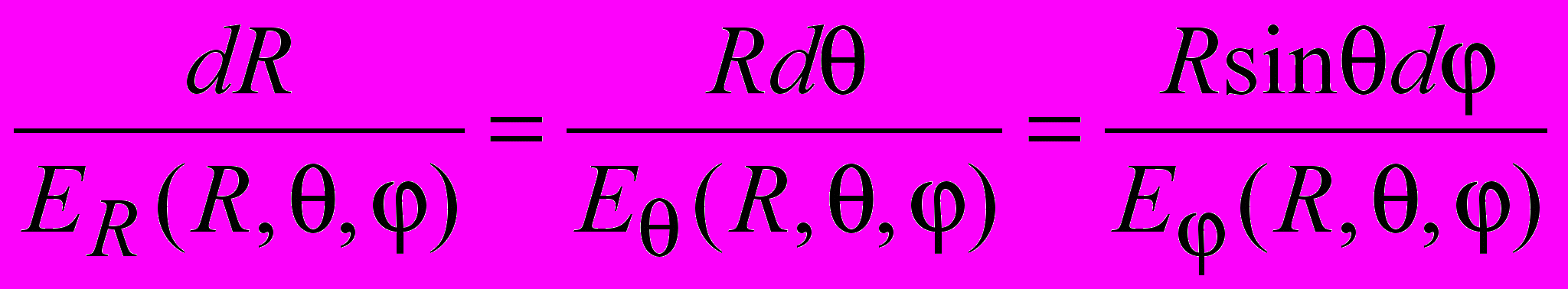(5)

Аналогично записываются уравнения для силовых линий магнитного поля и вектора Пойнтинга. Выражения для компонент полей в случае элементарных источников известны. Программа качественного анализа электромагнитных полей в полном объеме включает в себя следующие пункты: определение типа (точки, линии, поверхности) особенностей полей и их траекторий в пространстве – времени, а также их бифуркаций; локальный качественный анализ структуры силовых линий в окрестности особенностей; качественный анализ в целом структуры силовых линий. Основное внимание в работе уделено весьма нетривиальному в данном случае анализу особенностей уравнений.

Основное содержание второй главы составляет качественный анализ электрического поля ОЭГ, под которым понимается система ортогональных магнитного и электрического диполей при произвольной зависимости дипольных моментов от времени. Вдоль оси х декартовой системы координат расположен электрический, вдоль оси у – магнитный диполь и заданы дипольные моменты электрического и магнитного диполей . Компоненты электрического поля ОЭГ записаны в сферической системе координат (угол  отсчитывается от оси z, угол  - от оси x в плоскости (x,y))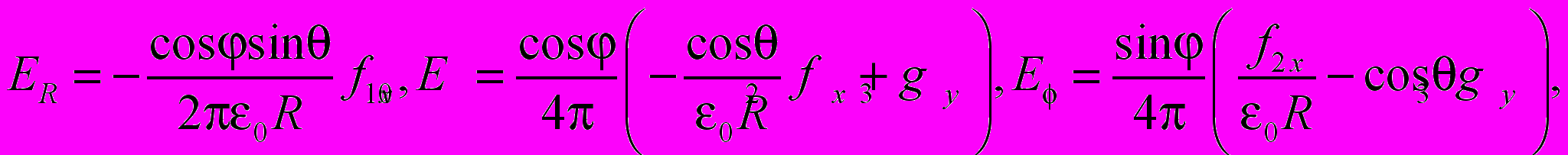

(6)

где 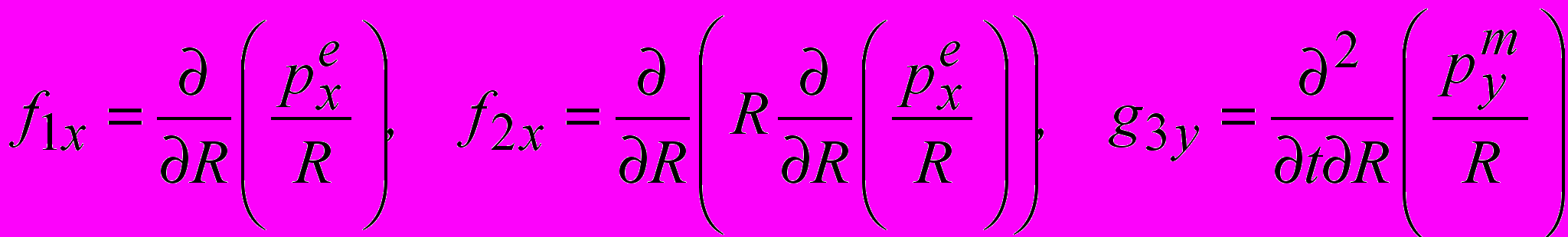. (7) Принципиальным моментом анализа является то, что компоненты (6) зависят не только от пространственных координат, но и от времени. Пространственная и временная переменные в функциях дипольных моментов 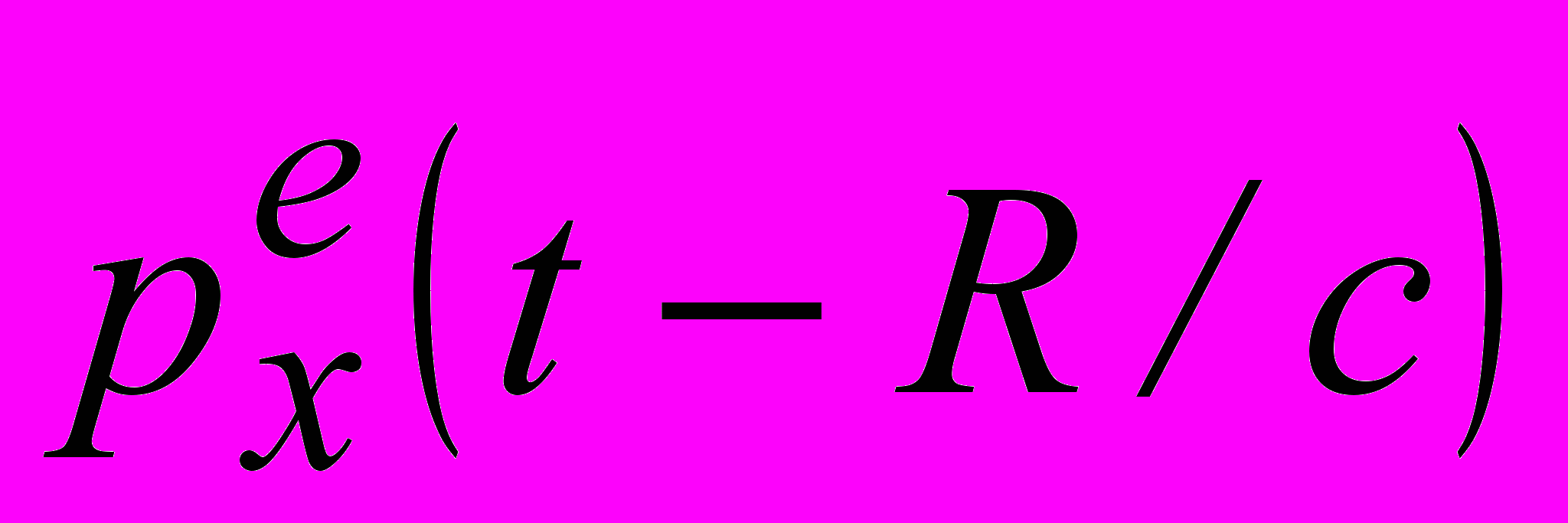и 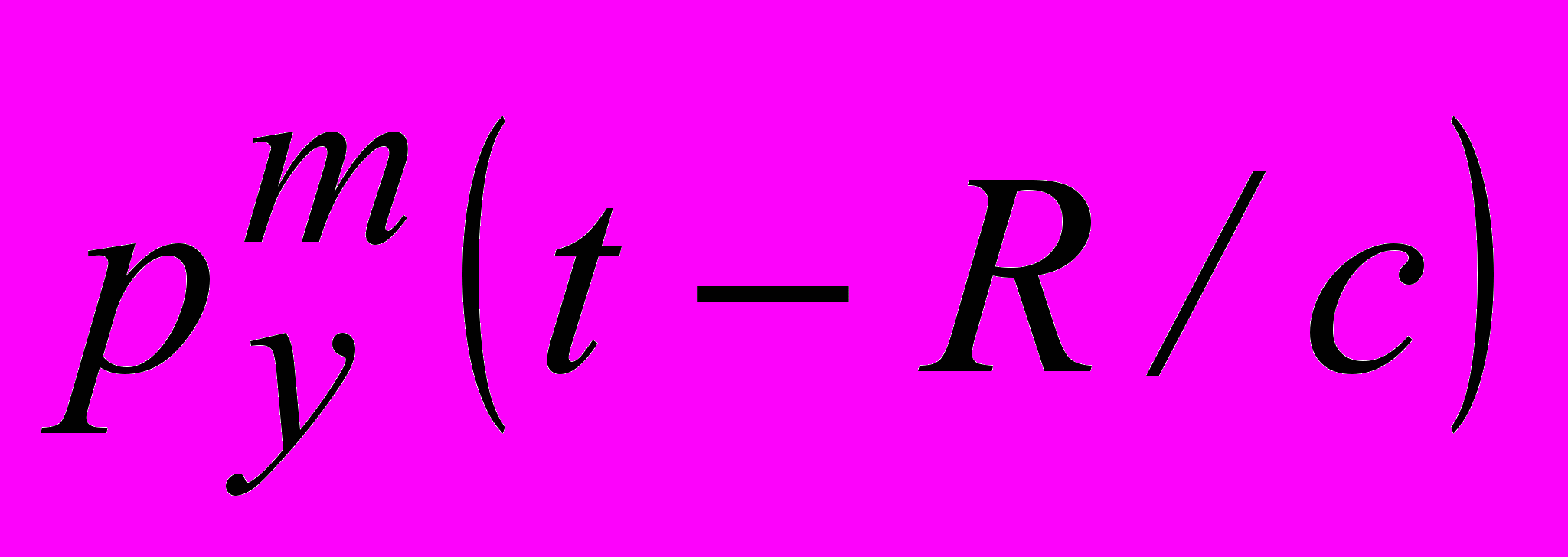связаны линейно. Поэтому можно ограничиться изучением структуры полей в трехмерном пространстве, рассматривая время, как параметр. Поскольку рассматриваются силовые линии в трехмерном пространстве, особенности ОДУ могут иметь место не только в точках, но и на особых линиях либо поверхностях в пространстве. Параметрическая зависимость компонент (6) от времени приводит к новому качеству - особенности поля в пространстве могут быть как неподвижными, так и подвижными. Условия определения положений особенностей электрического поля на конечных расстояниях антенны имеют вид

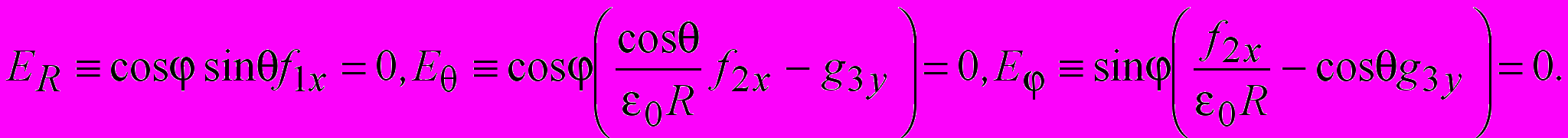(8)

Из совместности требований (8) следуют три условия.

Условие I – особенности в плоскости (0,y,z) при

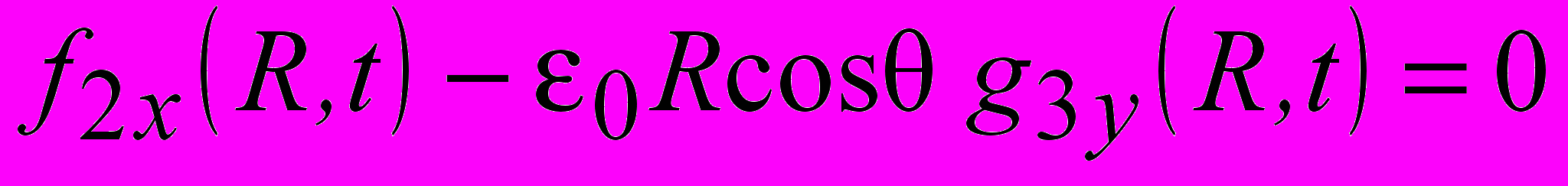, (9)

Условие II – особенности в плоскости (x,0, z) при

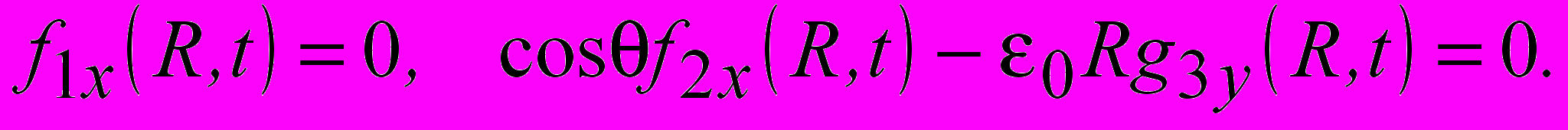(10)

Условие III – особенности в пространстве (x,y,z)

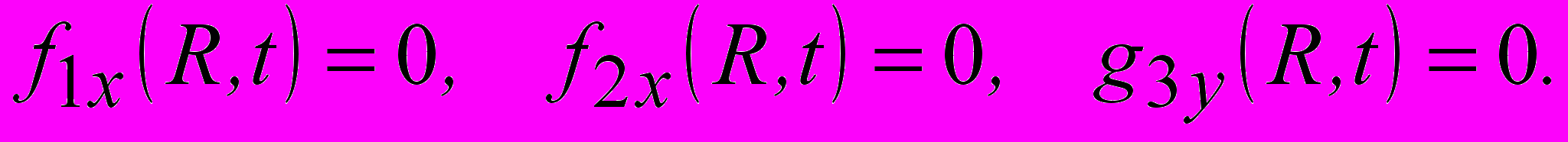(11)

Условие (9) – это уравнение движущихся в пространстве поверхностей вращения, пересечение этих поверхностей с плоскостью (0,y,z) дает семейство движущихся особых линий ОДУ в этой плоскости. Первое уравнение (10) определяет семейство движущихся в пространстве сферических поверхностей, второе - семейство движущихся в пространстве поверхностей вращения. Их пересечение в некоторые моменты времени t_n дает кривые в плоскостях (x,y,z)), сечение кривых плоскостью (x,0,z) - положения особых точек в эти моменты времени. Последнее условие (11) означает совпадение сферических поверхностей, на которых обращаются в нуль три компоненты электрического поля, в какой-то момент времени. Это условие носит исключительный характер. Как известно из качественного анализа полей электрического диполя, одновременное обращение в нуль компонент электрического поля электрического диполя на сфере невозможно в гармоническом режиме и реализуется только при определенных временных зависимостях дипольного момента в негармоническом режиме возбуждения (В.А.Пермяков, Д.В.Сороковик, Нелинейный мир, №4, 2008 г). В случае ОЭГ эта ситуация еще менее вероятна, поскольку одновременно должны быть выполнены три соотношения (10). Поэтому далее условие (11) рассматриваться не будет. Анализ особенностей электрического поля ОЭГ в гармоническом режиме возбуждения.

Дипольные моменты ОЭГ задаются следующими соотношениями

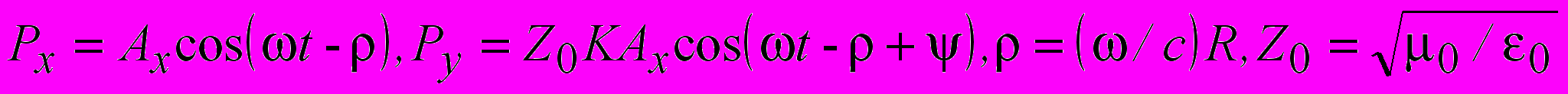(12)

При выполнении условия (9) в плоскости (0,y,z) существуют подвижные особые линии и неподвижные особые точки. Траектории подвижных особых линий в плоскости (0,y,z) имеют вид

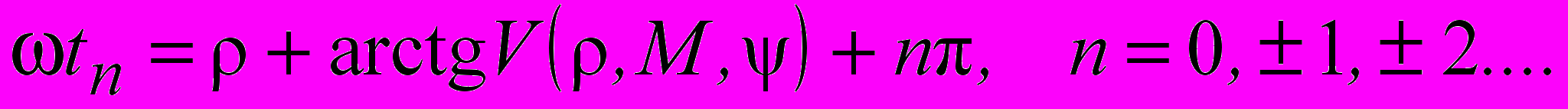, (13)

где

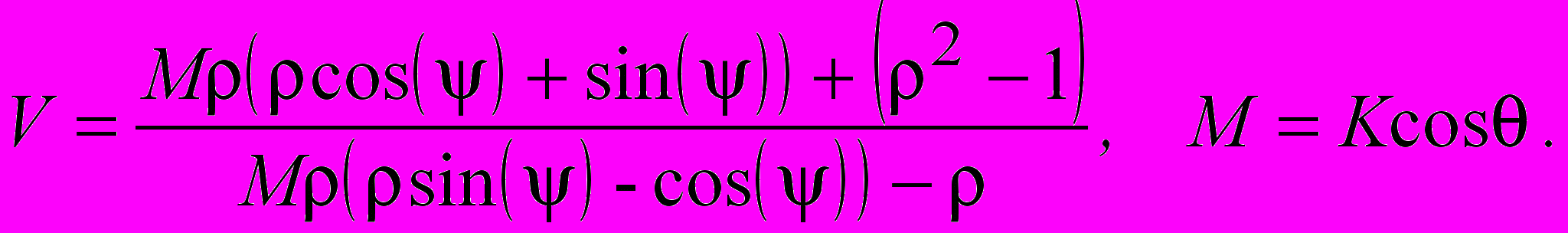(14)

В фиксированный момент времени решение (13) определяет особые линии на плоскости (0,y,z) , заданные в неявной форме, как функции переменных ρ и θ. Эволюция особенностей, как траекторий (ωt_n), анализируется на множестве параметров М=Kcos, . Зависимости ρ(t) - неоднозначные функции времени t. Изменению числа корней функции ρ(t) соответствуют точки бифуркации, которые определяются условием 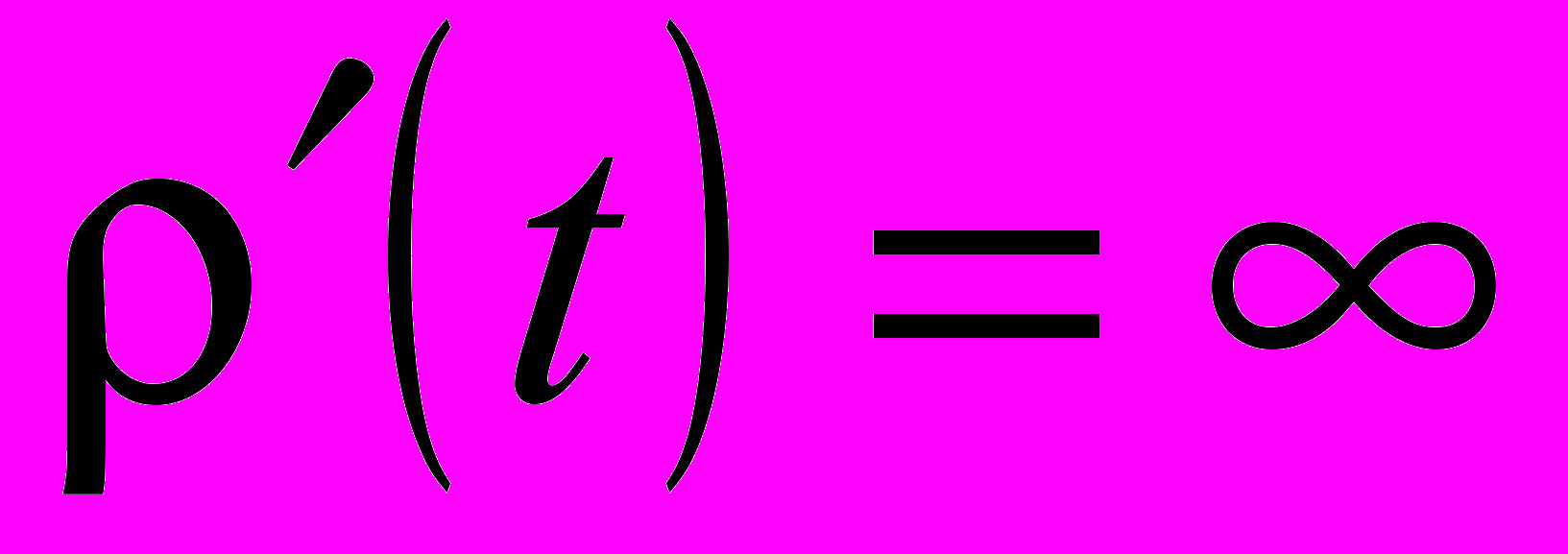. Анализ этого условия приводит к разбиению пространства параметров М, ψ на три области с качественно различным поведением траекторий (13): без точек бифуркации, с одной и двумя точками. На подвижных особых линиях могут располагаться неподвижные особые точки. Положения последних находятся из (13) наложением условия 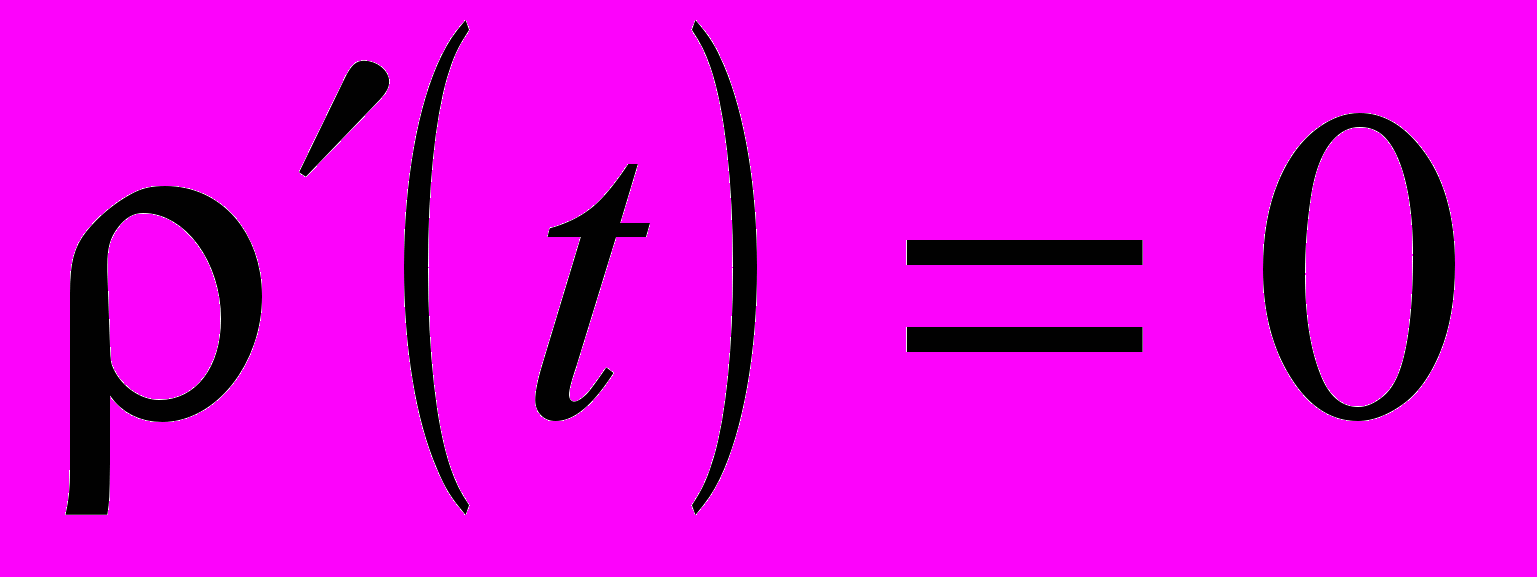и определяются выражениями

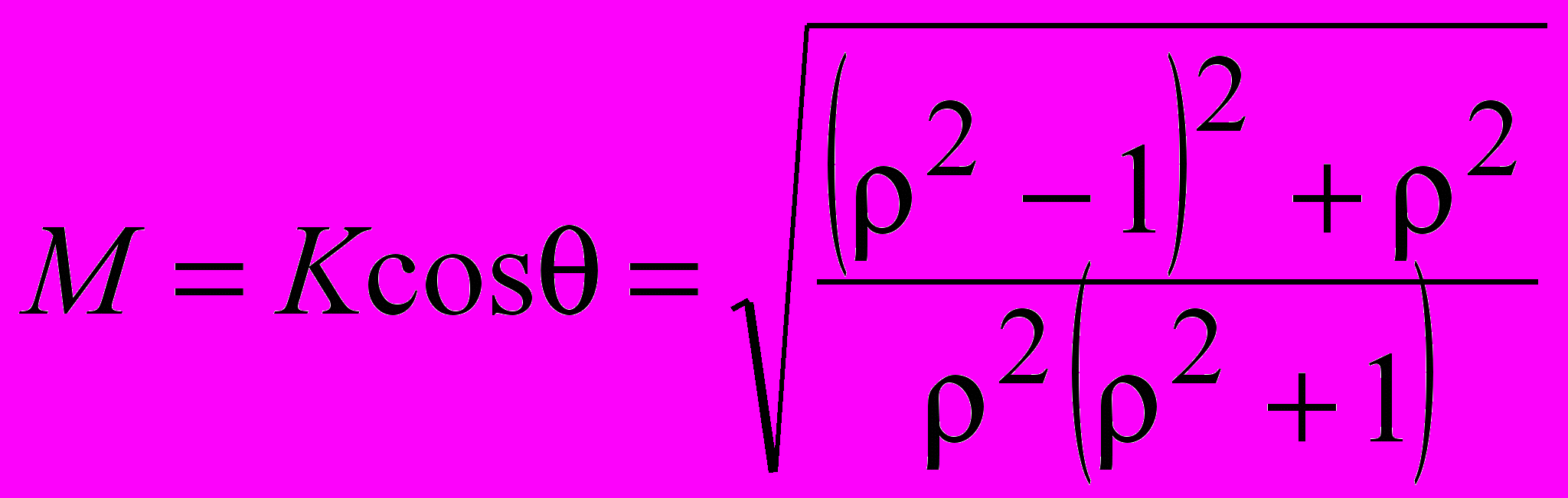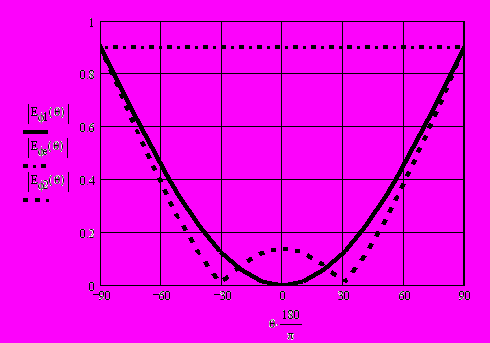
, . (15)

Паре значений  и  соответствуют две неподвижные особые точки на плоскости (0,y,z), симметрично расположенные относительно оси z. В предельном случае 0 особые точки смещаются на ось z и сливаются. Неподвижные особые точки ОЭГ на оси z были ранее обнаружены В.А.Пермяковым и А.С.Голобородько (Вестник МЭИ, 1999, № 5); результат (15) согласуется с этой работой при =0. В качестве примера на рис. 2 показаны зависимости модуля комплексной амплитуды электрического поля ОЭГ на окружности радиуса ₀ = 2 при значениях K и , определяющих неподвижные нули электрического поля на лучах θ₀=0 (сплошная линия) и θ₀=π/6 (штриховая). Штрих – пунктиром нанесена амплитуда поля одиночного электрического диполя Е_φe , принятая равной 0,9; остальные кривые нормированы относительно этой величины.

Рис.2.

Проведены расчеты структуры электрического поля ОЭГ в плоскости расположения неподвижных особых точек для ряда моментов времени и конкретных параметров дипольных моментов; показано, что структура поля определяется положением неподвижных особых точек и подвижных особых линий, при этом формируется динамическая область с минимальным значением поля, содержащая неподвижные особые точки. На рисунках 3а)-3г) в левом верхнем углу каждого рисунка показаны линии уровня напряженности электрического поля в окрестности неподвижных ОТ, располагающихся на луче θ₀=π/6 для четырех различных значений времени. Справа вверху от графиков линий уровня приведены графики распределения поля в сечении х=0, слева внизу – в сечении y=0, справа внизу – траектории подвижных особых линий. Из рисунков видно, что в сечении х=0 реализуются две неподвижные особые точки и подвижные особые линии электрического поля; напряженность электрического поля остается равной нулю в неподвижных особых точках во все моменты времени и достаточно малой в промежутке между неподвижными нулями, заметно меняясь во времени вне этого промежутка.

Из картины эволюции подвижных особых линий следует, что они со временем они сдвигаются в сторону больших расстояний. С течением времени подвижные особые линии, прилегающие к оси z, сближаются (рис. 3 в), и далее сливаются (рис. 3 г), что соответствует переходу через точку бифуркации. Меняя отношение амплитуд и разность фаз дипольных моментов 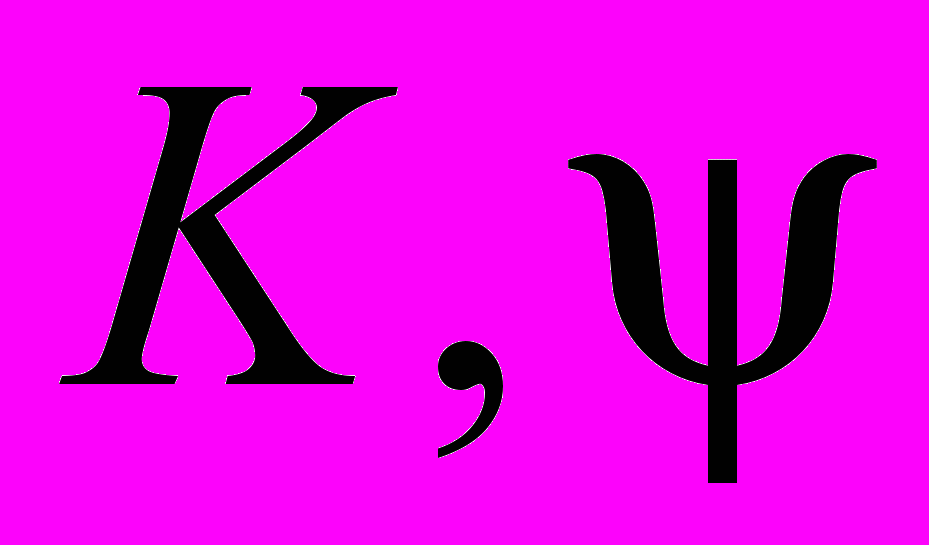, можно управлять положением неподвижных нулей, что может найти практическое применение. На основе этого явления могут быть созданы антенны сотовых телефонов и других устройств связи с минимальным воздействием на пользователя.

Эффект формирования подвижных нулей электрического поля может быть использован для создания антенных решеток систем ближней и подповерхностной радиолокации с целью минимизации отраженных сигналов от мешающих предметов.

Было проведено также исследование особенностей электрического поля в плоскости (x,0,z); найдены аналитические выражения для положения подвижных особых точек, а также условия возникновения в определенные моменты и в определенных точках плоскости (x,0,z) неподвижных особых точек, которые названы пульсирующими.

Анализ особенностей электрического поля ОЭГ в негармоническом режиме возбуждения.

Расположение особых точек в плоскости (0,y,z) определяется условием (8), которое сводится к

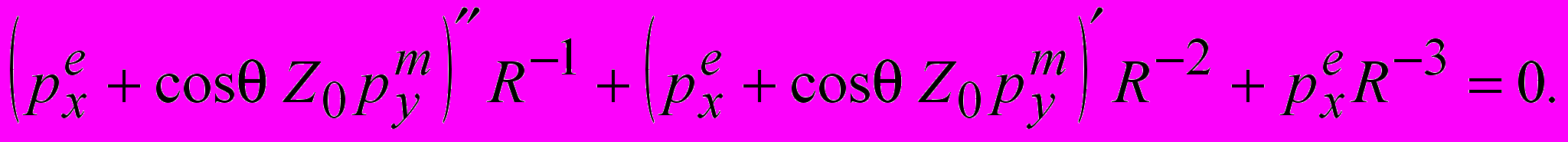(16)


Здесь производные берутся по аргументу τ =ct-R. Первое слагаемое соответствует вкладу в компоненту E_φ поля излучения, второе – поля







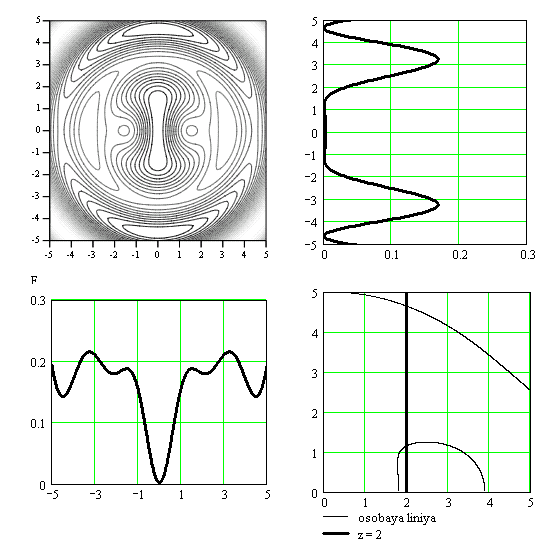
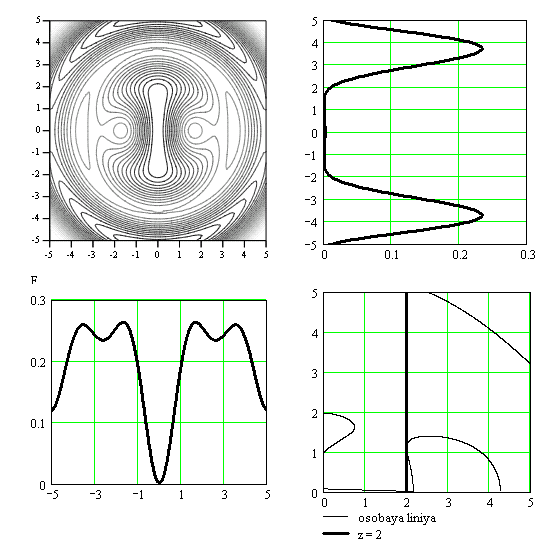
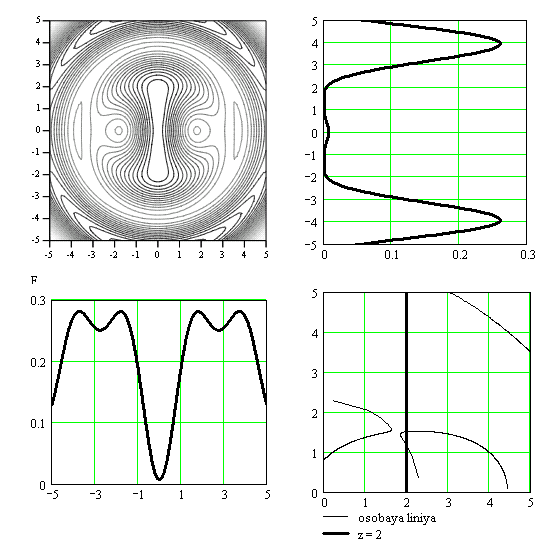
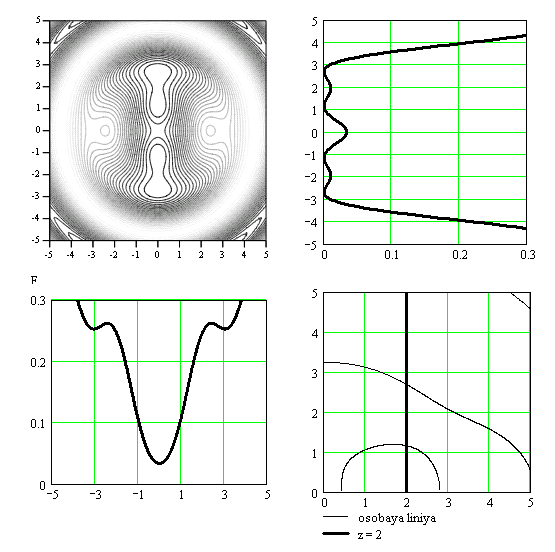
Рис.3.

индукции, третье - квазистатической составляющей электрического поля.

Выбрав связь между дипольными моментами 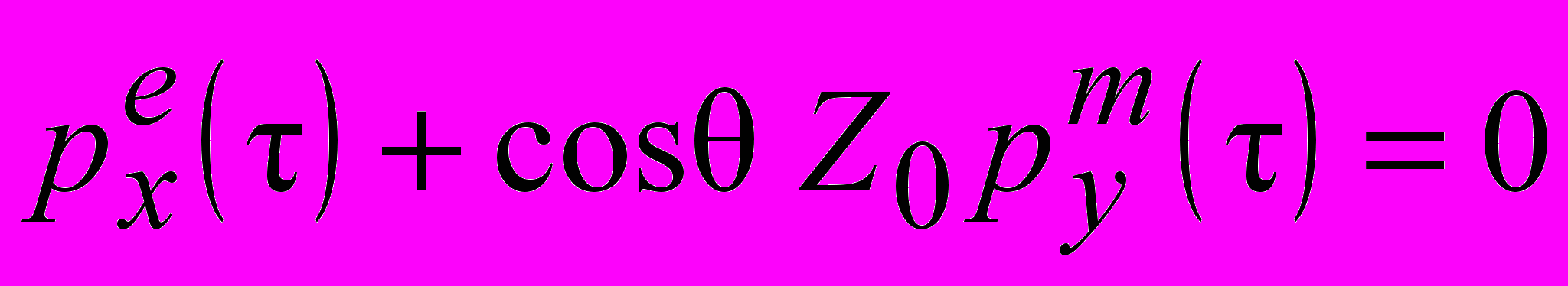, можно скомпенсировать в данном направлении θ компоненты поля, убывающие, как 1/R и 1/R², но не компоненту порядка 1/R³. То - есть, используя связь (16), можно получить частичную компенсацию компонент электрического поля (за исключением компоненты порядка 1/R³) не только в дальней, но и в промежуточной зоне.

Представляется интересной и практически важной возможность формирования неподвижных нулей электрического поля в негармоническом режиме возбуждения ОЭГ. Для этой цели предложен способ определения импульсных дипольных моментов, обеспечивающих обращение в нуль электрического поля во все моменты времени на заданном расстоянии от ОЭГ. Следует задаться временной зависимостью функции 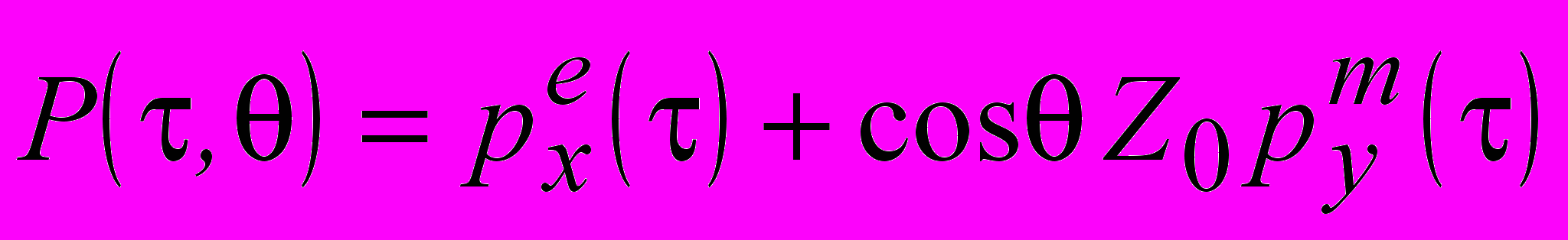при фиксированном угле , определить из (16) функцию дипольного момента 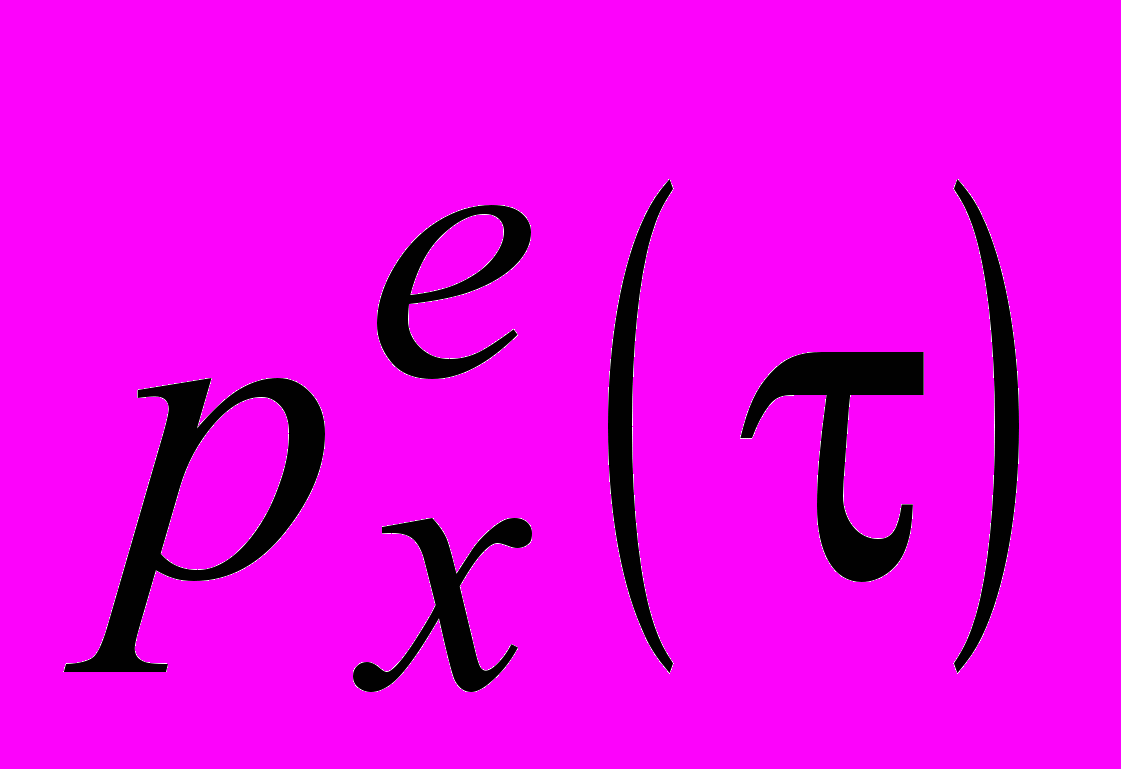, а из функции - дипольный момент 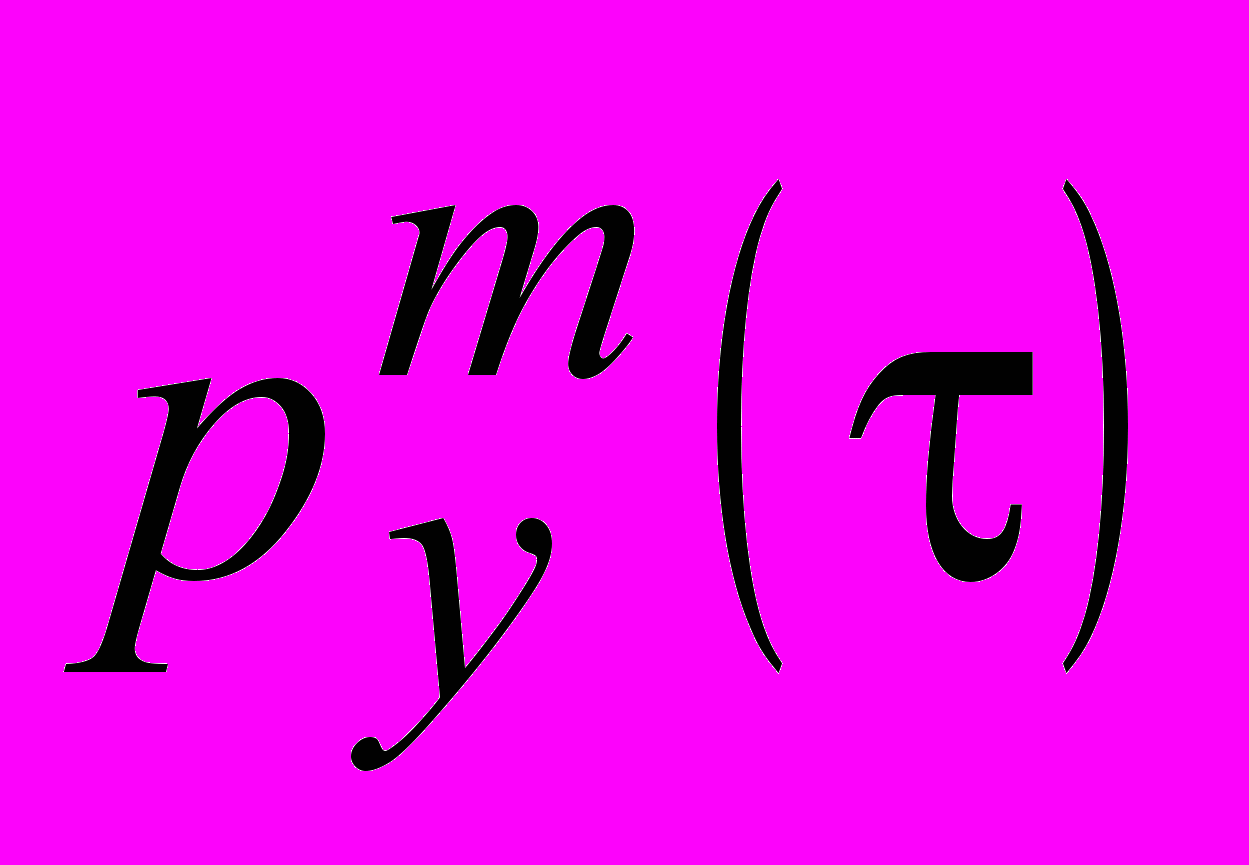. Таким образом, в случае нестационарного излучения ОЭГ можно сформировать неподвижные во времени нули электрического поля на конечном расстоянии от антенны. Приведен конкретный пример определения возбуждающих нестационарных дипольных моментов, порождаемых функцией в виде суммы гауссовых импульсов.

Во второй главе рассмотрена также классификация энергетических диаграмм направленности ОЭГ в гармоническом режиме излучения в зависимости от значений параметров .

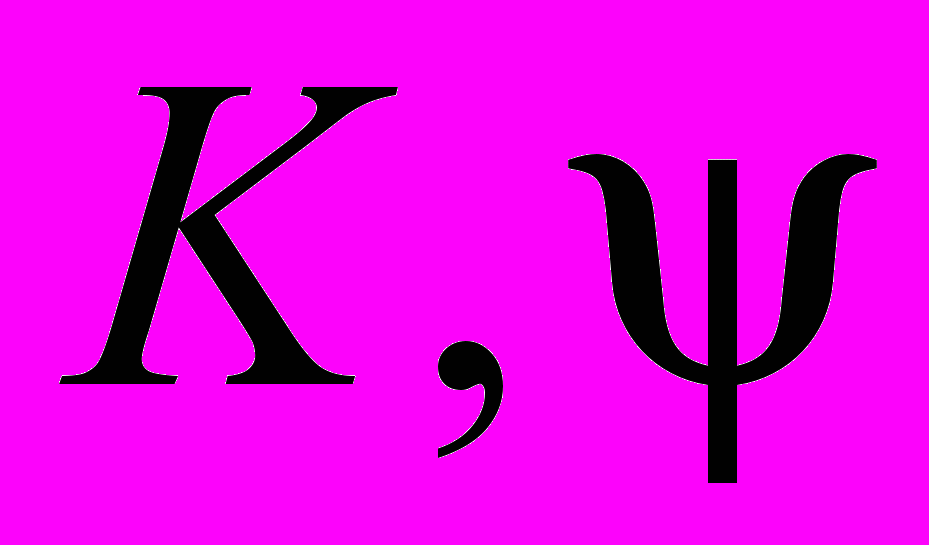В конце главы проведен локальный анализ силовых линий электрического поля ОЭГ в окрестности особой линии на плоскости (0,y,z);

показано, что в плоскости, перпендикулярной особой линии, структура силовых линий соответствует особой точке типа центра либо типа седла.

Полученные результаты по формированию особых точек и линий электрического поля переносятся на магнитное поле ОЭГ с помощью принципа перестановочной двойственности.

В третьей главе выполнен качественный анализ электромагнитного поля элементарной турникетной антенны (ТА) в гармоническом и негармоническом режимах возбуждения. Элементарная ТА представляет собой систему двух скрещенных электрических диполей, расположенных вдоль осей х и у декартовой системы координат. Система уравнений для компонент электрического поля ТА имеет вид

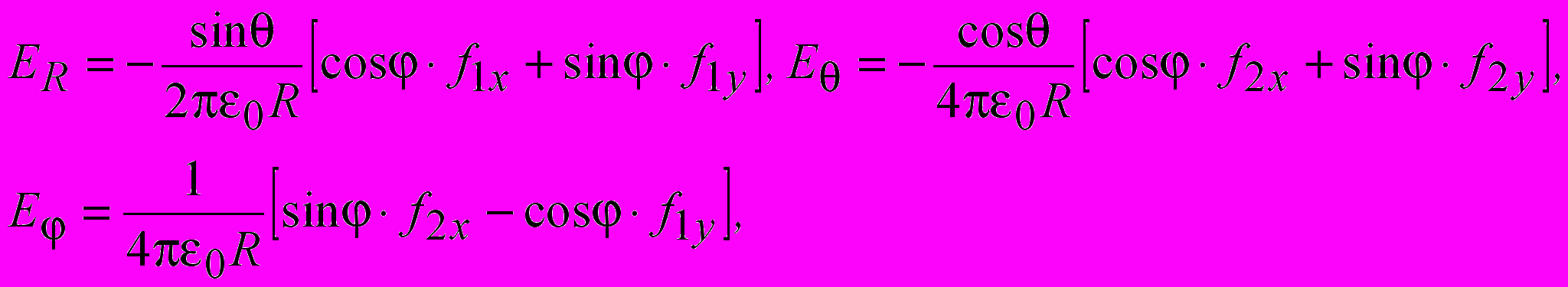(17)

где функции определены в (7) для запаздывающего дипольного момента 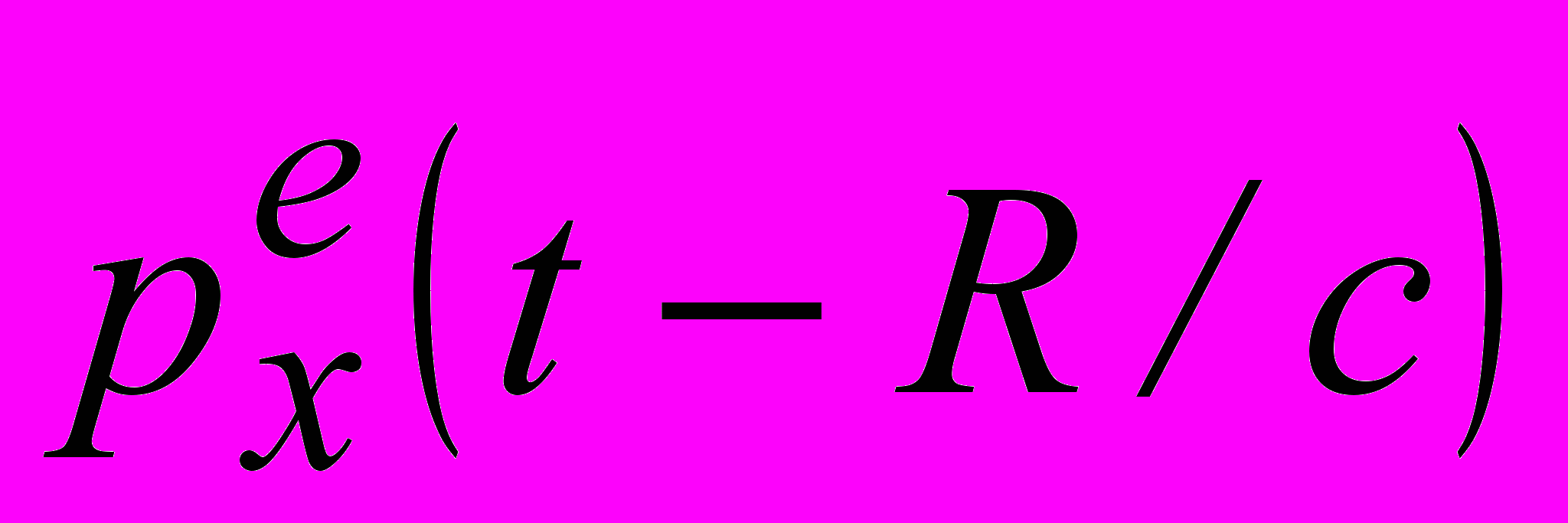, функции 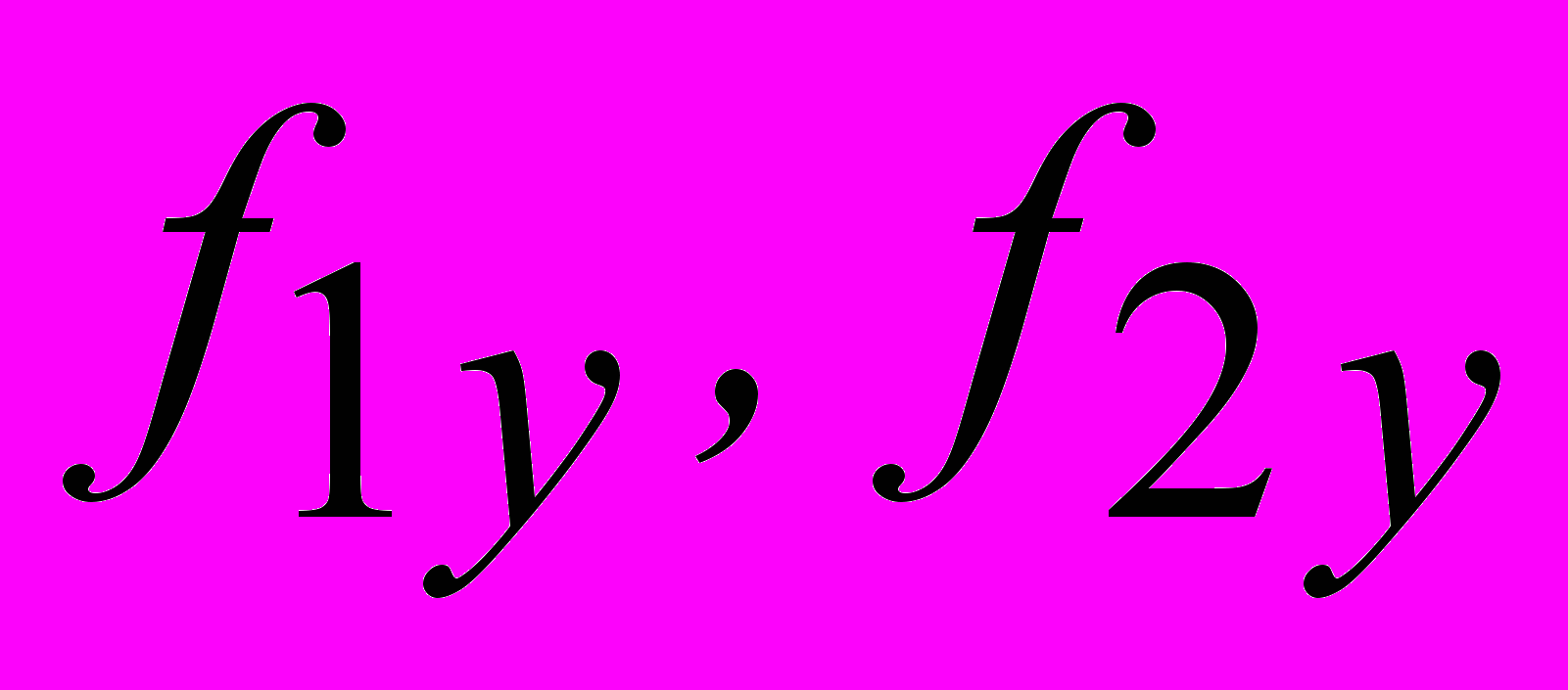задаются аналогично для запаздывающего дипольного момента .

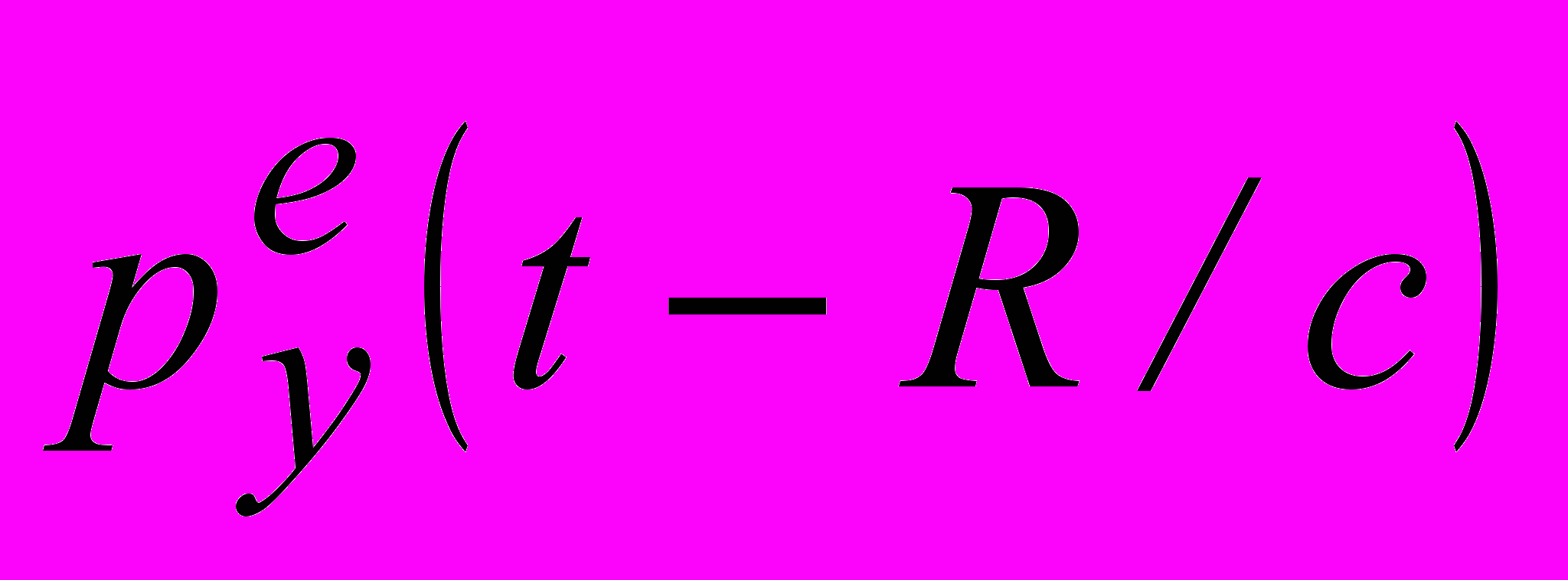Получены условия существования особенностей электрического поля ТА:

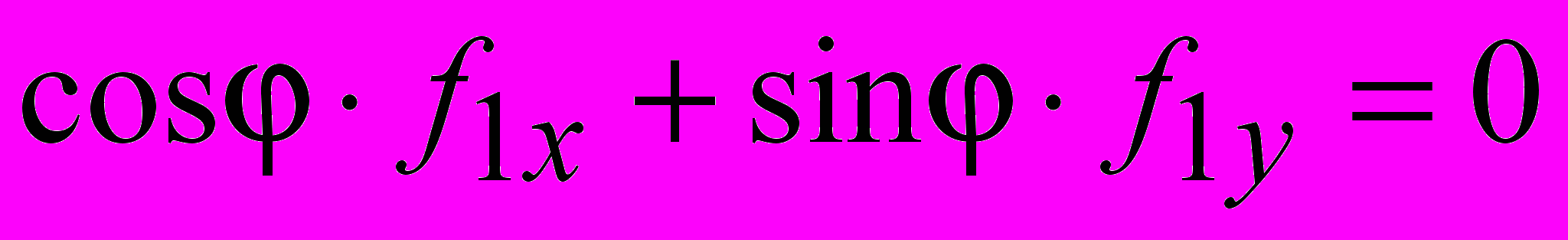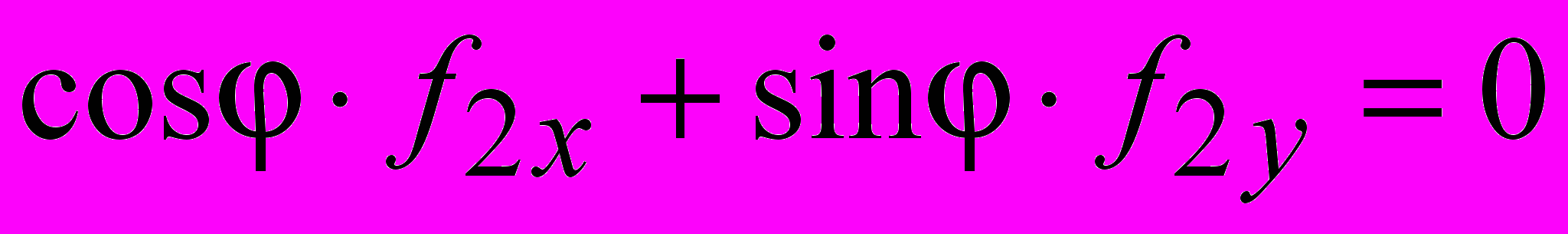(а), (б), 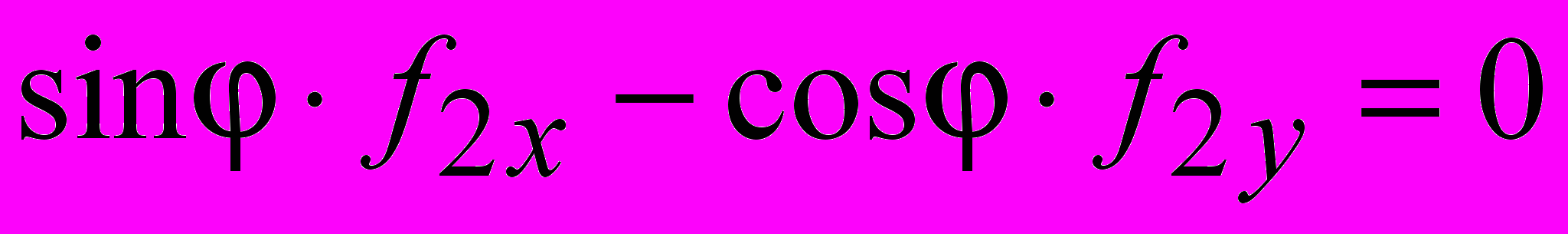(в), (18)

а) 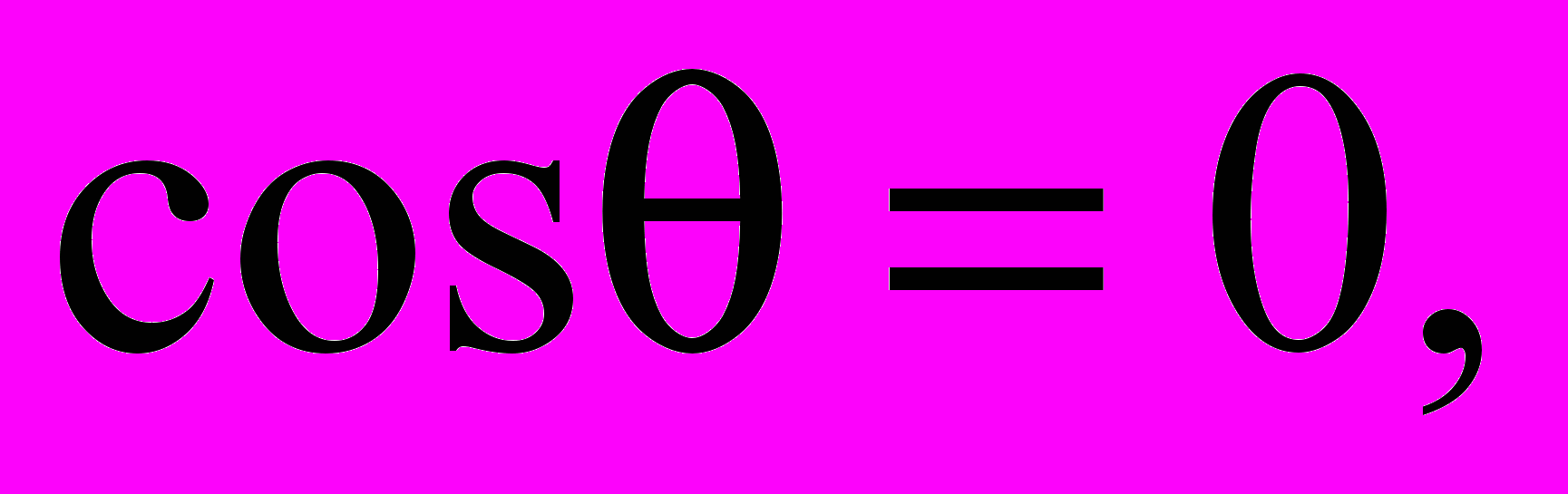б) уравнения (18а) и (18в). (19)

Анализ условий (18) и (19) позволил дать классификацию особенностей электрического поля по связи с временными зависимостями дипольных моментов ТА. Обнаружены три характерных ситуации, соответствующих принципиально различному поведению особых точек, и, следовательно, качественно отличающимся структурам поля.

1) Условие (18) выполняется в особом случае синфазного (противофазного) возбуждения диполей в гармоническом режиме или синхронного возбуждения – в негармоническом. Этот случай реализуется, когда отношение дипольных моментов – постоянная величина

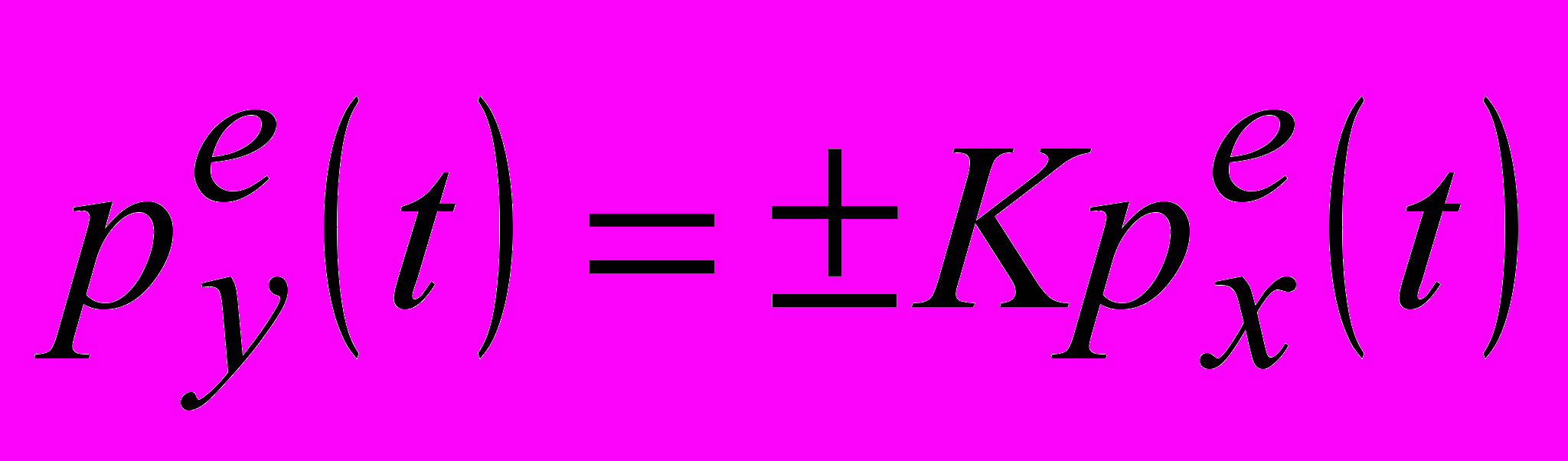(20)

и система диполей может быть заменена эквивалентным диполем с дипольным моментом 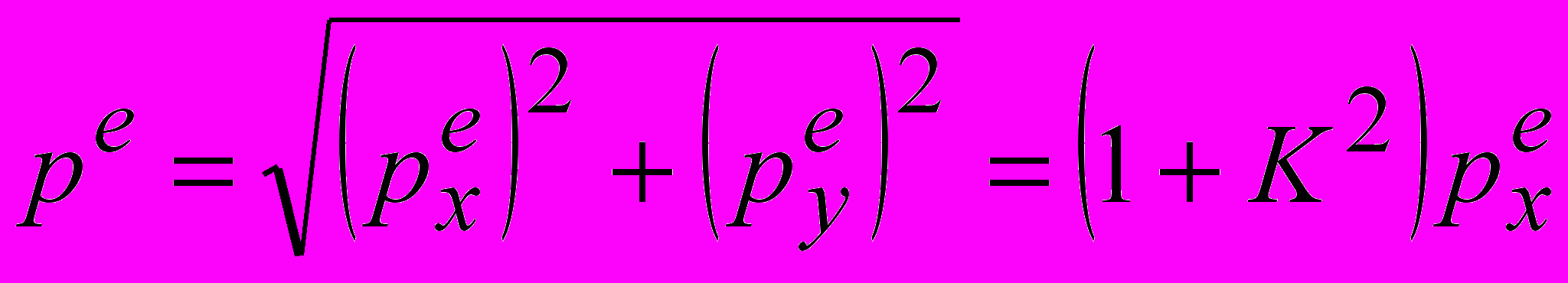, ось которого направлена под углом 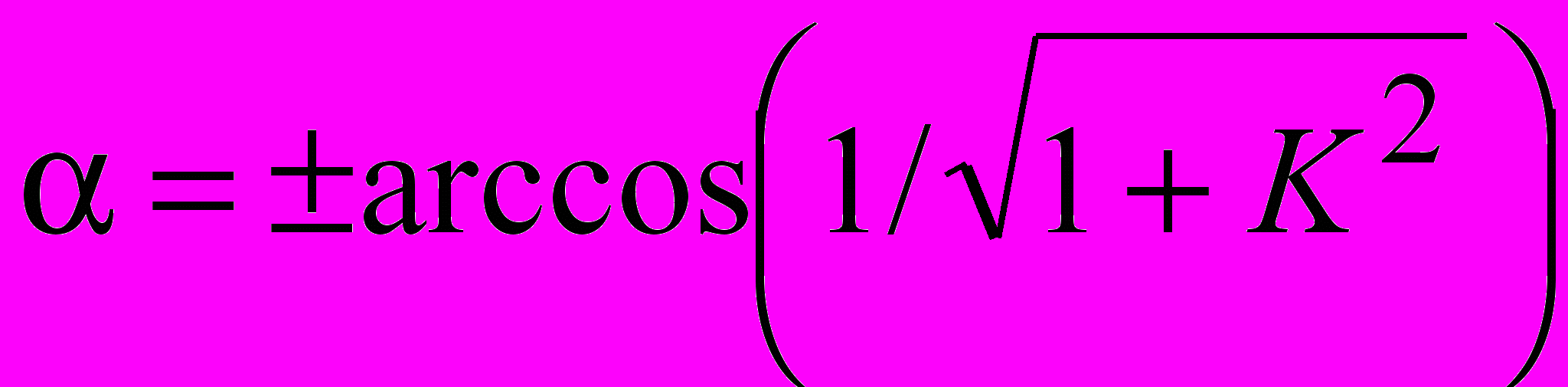к оси x в плоскости ( x,y). При этом наряду с неподвижными особыми точками в месте расположения диполей и на бесконечности имеют место движущиеся особенности (нули) электрического поля на оси эквивалентного диполя и в его экваториальной плоскости (см. цитированную выше работу В.А.Пермякова, Д.В.Сороковика).

2) Другим особым является случай отсутствия подвижных особых точек электрического поля во всем пространстве. Ему соответствует следующее из (19) условие

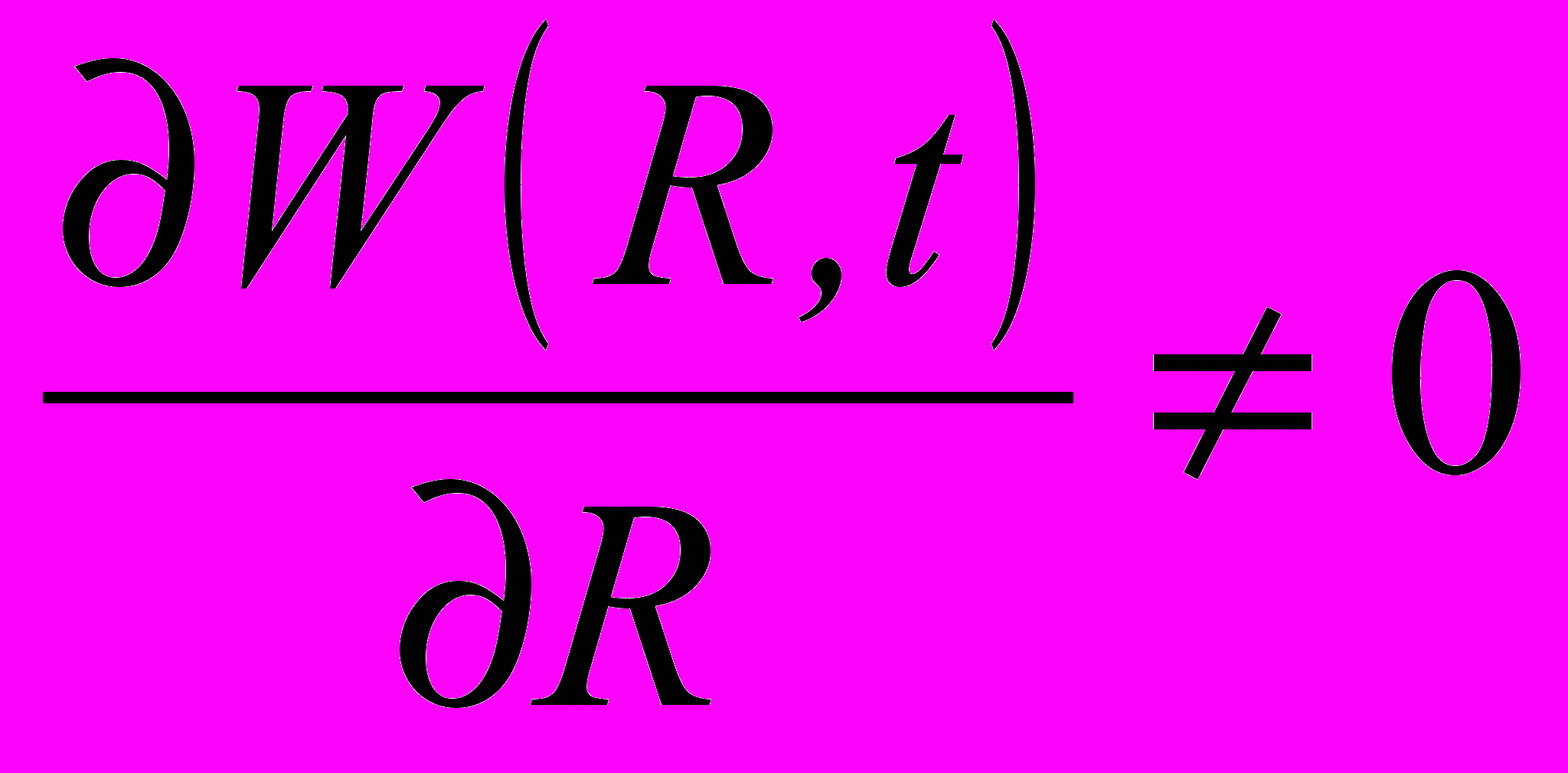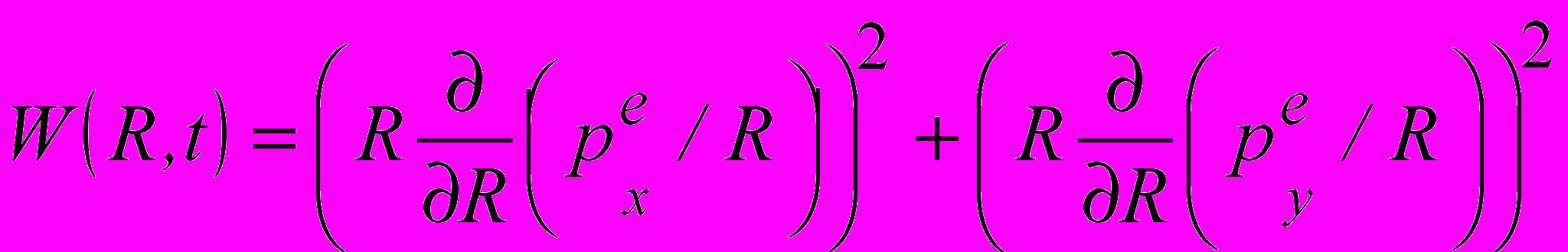, (21)

которое должно выполняться при любых конечных радиусах на всем временном интервале. Если это условие выполнено, можно однозначно и непрерывно соединить центр диполей вдоль любой траектории силовой линии, из него выходящей, с полем в окрестности бесконечно удаленной точки, т.е. в дальней зоне. Условие (21) выполняется в частном случае гармонического возбуждения ТА при равенстве амплитуд и равной ±π2 разности фаз дипольных моментов; при этом оно имеет вид 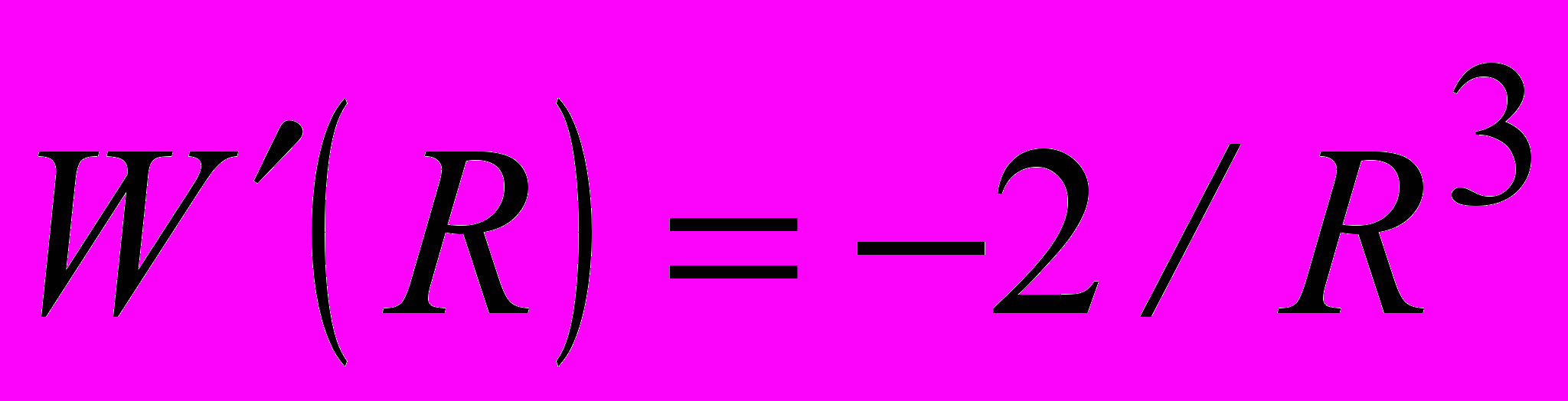. В нестационарном случае отсутствие подвижных особенностей можно проверить, задаваясь конкретными зависимостями дипольных моментов от времени.

3) Общим является случай возбуждения диполей дипольными моментами, когда выполняется условие (19), но не удовлетворяются условия (20) и (21); при этом, помимо неподвижных ОТ, имеют место подвижные ОТ электрического поля только в плоскости расположения диполей.

В общем случае возбуждения ТА рассмотрена эволюция траекторий особых точек электрического поля в плоскости расположения диполей. При гармонической зависимости дипольных моментов от времени получены аналитические зависимости траекторий подвижных особых точек от радиальной и угловой координат в плоскости расположения диполей. Особые точки электрического поля движутся по спиралям, раскручивающимся вокруг центра расположения диполей, причем существуют только вне некоторой окружности; определено положение этой окружности и условия бифуркации траекторий при изменении параметров ТА. Проанализированы особенности магнитного поля в гармоническом режиме. Показано, что как в общем случае возбуждения, так и для классической турникетной антенны (амплитуды дипольных моментов равны, а разность фаз равна ±π2) магнитное поле равно нулю на особых линиях в плоскости расположения диполей; получены аналитические выражения для особых линий и рассмотрена их эволюция во времени. Показано, что особые линии магнитного поля в каждый момент времени имеют вид спиралей, выходящих из начала координат и вращающихся вокруг центра ТА. На основе анализа эволюции особенностей электрического и магнитного полей установлены качественные особенности поведения вектора Пойнтинга ТА.

В нестационарном режиме на конкретных зависимостях дипольных моментов ТА от времени показано, что траектории подвижных особых точек электрического поля в плоскости расположения диполей имеют вид спиралей, однако, в отличие от гармонического режима, они не монотонно раскручиваются вокруг центра ТА, а имеют точки поворота.

Для магнитного поля в нестационарном режиме показано, что при несинхронном возбуждении существуют особые линии спиральной формы в плоскости расположения диполей, выходящие из центра ТА и вращающиеся вокруг него; в синхронном режиме возбуждения эти особые линии вырождаются в прямые, совпадающие с осью эквивалентного диполя.

Проведен локальный анализ особых точек электрического поля в гармоническом режиме возбуждения. Показано, что особые точки относятся либо к типу узел, либо к типу седло-узел. Отмечено, что при сохранении параметров дипольных моментов 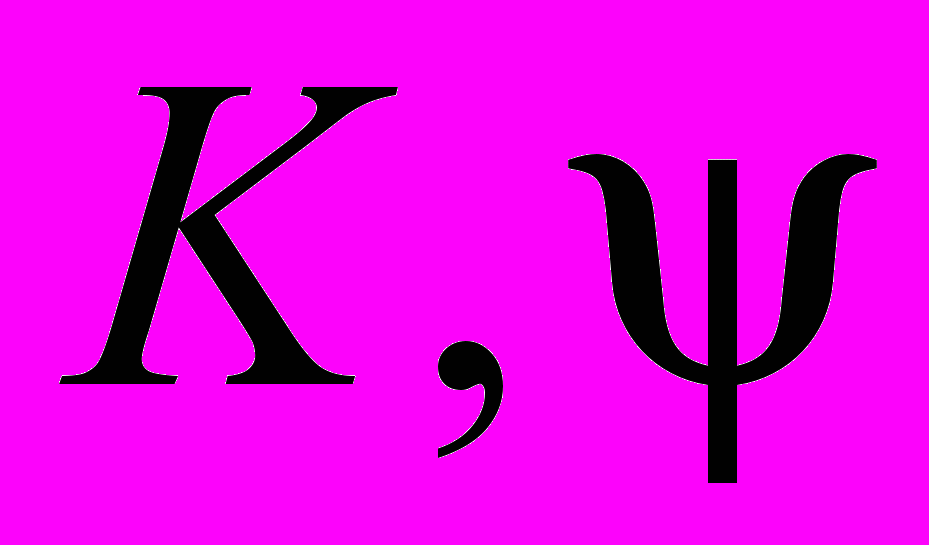тип особой точки может меняться с течением времени.

Приведены результаты численного интегрирования методом Рунге-Кутты уравнений силовых линий электрического и магнитного полей для различных значений параметров возбуждающих дипольных моментов в гармоническом режиме, подтверждающие качественно различное поведение силовых линий электрического поля в согласии с приведенной выше классификацией особенностей электрического поля ТА.

В особом случае параметров диполей 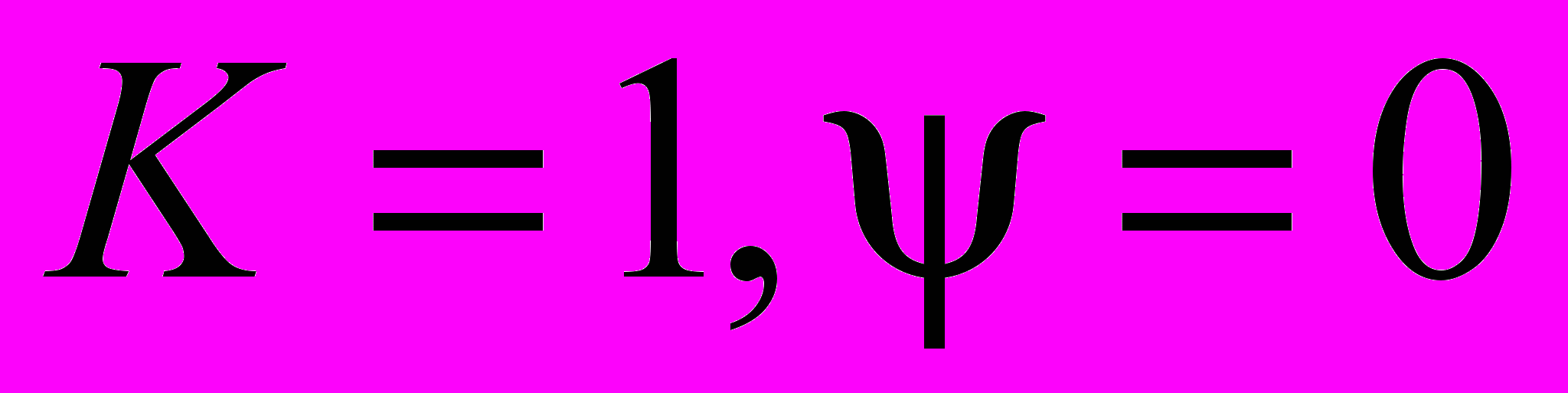турникетная антенна заменяется эквивалентным электрическим диполем; результаты интегрирования силовых линий при этом согласуются со случаем одиночного диполя. В особом случае параметров диполей 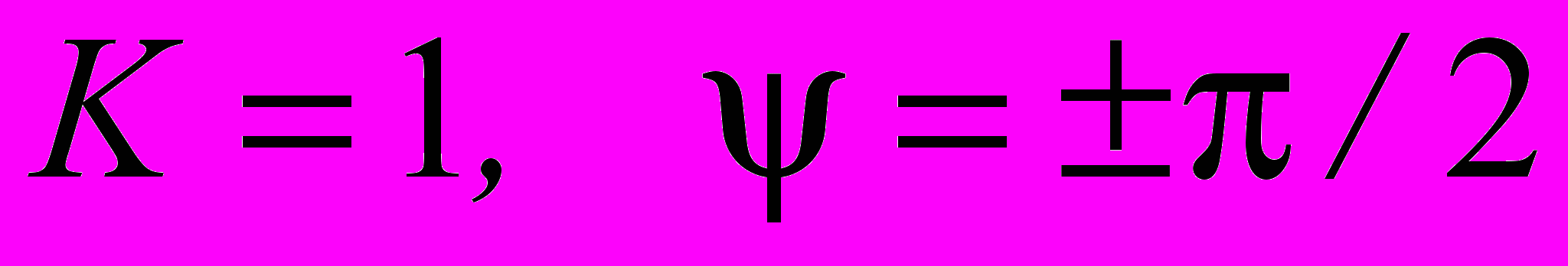(классическая ТА) силовые линии электрического поля имеют вид регулярных спиралей, выходящих из центра турникетной антенны и раскручивающихся в пространстве в направлении больших радиусов. В общем случае возбуждения ТА силовые линии электрического поля имеют существенно более сложную структуру. В зависимости от параметров диполей и расположения начальных точек на сфере малого радиуса силовые линии могут иметь вид спиралей, монотонно удаляющихся от центра ТА, либо кривых, которые вначале удаляются, а затем возвращаются в область вблизи центра ТА – этот процесс может повторяться несколько раз.

В предпоследнем параграфе рассмотрен вопрос о формировании неподвижных нулей электрического поля на конечных расстояниях от системы электрических диполей. Для системы N+1 параллельных диполей, центры которых находятся в одной плоскости, показано, что при заданном моменте одного диполя моменты остальных могут быть выбраны так, чтобы обеспечить формирование N неподвижных нулей в плоскости центров диполей. Приведен конкретный пример расчета электрического поля в окрестности нуля поля, сформированного системой из двух диполей.

В последнем параграфе главы проведено обсуждение вопроса о сопоставлении мгновенных и средних по времени энергетических диаграмм направленности (ДН) турникетной антенны в гармоническом и негармоническом режимах возбуждения. Отмечено, что известная теорема о структуре векторного поля на сфере (см, например, В.И.Арнольд, Обыкновенные дифференциальные уравнения), в соответствии с которой векторное поле на сфере в физическом пространстве имеет не менее одного нуля, может быть применена только ко мгновенным ДН антенн, поскольку при ее выводе векторное поле полагается не зависящим от времени. Формирование нулей средней по времени ДН антенны определяется при этом тем, как ведут себя нули мгновенной ДН: если нули мгновенной ДН неподвижны, средняя по времени ДН также имеет неподвижные нули; если нули мгновенной ДН движутся на интервале интегрирования по времени средней ДН, нули последней отсутствуют.

В заключении диссертации сформулированы основные выводы по работе, обсуждена ценность полученных результатов с точки зрения практического применения, намечены направления дальнейшего развития данной работы.

СПИСОК ПУБЛИКАЦИЙ ПО ТЕМЕ ДИССЕРТАЦИИ

1. Корюкин А.Н., Пермяков В.А. Качественный анализ электромагнитных полей обобщенного элемента Гюйгенса. /Нелинейный мир, 2008, т.6, № 4, с. 296-299.

2. Пермяков В.А., Корюкин А.Н. О прямом пространственно – временном описании плоских электромагнитных импульсных волн произвольной поляризации. /Вестник МЭИ, 2008, № 2, с. 68-73.

3. Пермяков В.А., Корюкин А.Н. Можно ли причесать электромагнитного ежа? О мгновенных и средних по времени диаграммах направленности антенн. /Антенны, 2008, № 4, с.3-5.

4. Корюкин А.Н., Сороковик Д.В., научный руководитель Пермяков В.А. ЭВМ программа для изучения нестационарных процессов излучения простых антенн. / Конф. МЭИ, 2004, стр. 86.

5. Корюкин А.Н., научный руководитель Пермяков В.А. Качественное и численное исследование структуры электромагнитного поля системы диполей. /Конф. МЭИ, 2005, с. 93

6. Корюкин А.Н., научный руководитель Пермяков В.А. Качественный анализ структуры поля элементарной турникетной антенны, /Конф. МЭИ, 2006, с. 120-121

7. Корюкин А.Н., научный руководитель Пермяков В.А. Качественный анализ структуры поля элемента Гюйгенса. /Конф. МЭИ, 2007, с.88-89.

8. Пермяков В.А., Сороковик Д.В., Корюкин А.Н. Применение методов качественной теории дифференциальных уравнений к анализу процессов нестационарного излучения простых антенн./ Конф. ИРЭМВ – 2005, с. 31-33.

9. Пермяков В.А., Корюкин А.Н. О прямом пространственно – временном описании сверхширокополосных электромагнитных сигналов произвольной поляризации. / Распространение радиоволн. Сборник докладов. XXI Всероссийская научная конференция , 25-27 мая 2005 г., Йошкар-Ола, 2005, том 2, с. 418-422.

10. Пермяков В.А., Сороковик Д.В., Корюкин А.Н. Анализ процессов излучения простых антенн методами качественной теории дифференциальных уравнений./ Сверхширокополосные сигналы в радиолокации, связи и акустике. Сборник докладов. Вторая всероссийская конференция-семинар. Муром, 4-7 июля 2006, Муром, изд. Муромского института Владимирского госуниверситета. 2006, с.67-70

11. Permyakov V.A., Sorokovik D.V., Korykin A.N. Qualitative Analysis of Elementary Antennas Impuls Radiation. / The Third International Conference. Ultrawideband and Ultrashort Impulse Signals. UWBUSIS-2006. September 18-22, 2006. Sevastopol, Ukraine. Pp. 308-310.

(Пермяков В.А., Сороковик Д.В., Корюкин А.Н. Качественный анализ импульсного излучения элементарных антенн. /Третья Международная конференция «Сверхширокополосные и сверхкороткие импульсные сигналы». 18-22 сентября 2006 г. Севастополь, Украина. с 308-310.)

12. Пермяков В.А., Корюкин А.Н. Качественный анализ особенностей электромагнитного поля элементарной турникетной антенны в гармоническом режиме излучения. /Радиотехнические тетради, 2008, №36, с. 95-99.

13. Корюкин А.Н. Качественный анализ структуры поля системы элементарных излучателей. /Конф. МЭИ, 2008, с.89-90.

14. Пермяков В.А., Сороковик Д.В., Корюкин А.Н. Качественный анализ полей простых антенн. /Международная научная конф., посвященная 100-летию со дня рождения академика В.А. Котельникова. Тезисы докладов. – М.: 2008, с. 59-61.