Игра «Математическое поле чудес» (Приложение 4) 4 день: Проведение школьных олимпиад по математике среди 5 9 классов. (Приложение 5)
| Вид материала | Документы |
СодержаниеСколькими способами можно уплатить 78 рублей, имея деньги трех- и пятирублевого достоинства! Игра со зрителями Игра со зрителями Олимпиадные задания по математике. 9 класс 2007 год. |
- Приказ «18» ноября 2010 г. №2931 Опроведении областных олимпиад среди обучающихся, 160.18kb.
- Внеклассное мероприятие по окружающему миру в начальной школе. Игра «Поле чудес», 69.02kb.
- О. Н. Пупышева з адания школьных олимпиад, 7957.4kb.
- Разработаны программы элективных курсов. Программа элективного курса по математике, 98.58kb.
- Методические рекомендации о проведении школьного этапа олимпиад (приложение 1). График, 149.9kb.
- Положение о районных турнирах по математике учащихся 5-7 классов и по физике учащихся, 15.76kb.
- Положение об открытом слете (приложение №1); смету расходов на проведение открытого, 86.53kb.
- Правила внутреннего трудового распорядка Приложение, 3806.48kb.
- Задачи, которые я ставлю перед собой в работе: выяснить, насколько проблема актуальна, 187.81kb.
- Методические материалы по математике для средних школ. Задачи математических олимпиад, 14.49kb.

МОУ «Задоринская основная общеобразовательная школа»
Куликова Л.В. –учитель математики.
2007 -2008 учебный год.
Цели проведения недели: расширение знаний и умений по математике;
выявление более одаренных учащихся в области
математики;
развитие интереса к предмету;
развитие творческих способностей и активности
учащихся;
сплочение классных коллективов.
Участники недели математики: 5 – 9 классы.
Распорядок недели:
1 день: Беседа «Юные математики»
(Приложение 1)
2 день: 1.Игра между 5 – 7 классами «Математический поезд»
(Приложение 2)
2. «Играй, смекай, отгадывай» -кто больше и правильнее отгадает ребусов, шарад, логогрифов, задач, загадок и многое другое.
(Приложение 3)
3 день: 1. Конкурс математических газет.
2. Игра «Математическое поле чудес»
(Приложение 4)
4 день: Проведение школьных олимпиад по математике среди 5 – 9 классов.
(Приложение 5)
5 день: Игра «Математический КВН» между сборными командами 5 – 9
классов.
(Приложение 6)
Приложение 1.
Беседа «Юные математики»
Истории математики известны случаи очень раннего проявления математических способностей. Расскажем о них.
Французский ученый XVII века Блэз Паскаль стал интересоваться математикой в столь раннем возрасте, что отец ему запретил ею заниматься. Однако, зайдя через некоторое время в детскую комнату, он обнаружил, что мальчик углубился в рассмотрение какого-то рисунка из прямых линий и окружностей.
Выяснилось, что маленький Блэз самостоятельно нашел доказательства первых теорем геометрии Евклида и думал о том, как доказать следующую теорему. В шестнадцатилетнем возрасте он доказал утверждение, которое до сих пор изучается в высших учебных заведениях под именем теоремы Паскаля.
Паскаль сконструировал первую вычислительную машину, написал несколько работ по арифметике, алгебре и вообще внес большой вклад в математическую науку.
Очень рано раскрылись дарования и у Карла Гаусса, позднее ставшего одним из крупнейших математиков XIX века (его даже называли «царем математиков»),
Рассказывают, что в возрасте трех лет он заметил ошибку, сделанную его отцом в расчетах. А семи лет мальчик пошел в школу. В то время в одной классной комнате занимались ученики разных классов. Чтобы занять первоклассников, пока он будет заниматься с третьим классом, учитель велел им сложить все числа от 1 до 100. Но не успел он закончить чтение условия задачи, как маленький Карл написал на своей грифельной доске ответ и положил на учительский стол.
С сожалением смотрел преподаватель на мальчика: ясно было, что за такой короткий срок он не мог сделать 99 сложений. Остальные ученики терпеливо складывали числа, сбиваясь, стирая написанное и снова складывали. Когда учитель закончил занятия с третьеклассниками, он взял со своего стола грифельные доски. Ни у кого не было правильного результата. И только на доске Карла стоял ответ: 5050, причем никаких вычислений не было.
«Как же ты это сосчитал?» — спросил учитель.
«Очень просто,— ответил мальчик.— Я сложил 1 и 100, получил 101. Потом сложил 2 и 99, тоже получилось 101; 3 и 98— снова 101, и так до 50+51 = 101. Значит, надо сложить 50 слагаемых по 101 каждое, то есть умножить 101 на 50. А это и равно 5050».
Изумленный учитель понял, что встретил самого способного ученика в своей жизни. В дальнейшем Гаусс сделал много замечательных открытий в математике.
Французский математик Алексис Клеро, живший в XVIII веке, написал первую научную работу на тринадцатом году жизни, а в 18 лет был уже утвержден научным сотрудником Парижской Академии наук. А венгерский математик Л. Поша в возрасте 12 лет удивил известного ученого Эрдеша. Эрдешу удалось доказать с помощью сложных рассуждений, что если взять несколько идущих подряд натуральных чисел и отобрать из них больше половины, то среди отобранных чисел обязательно встретятся два взаимно простых числа. Например, если мы выберем из чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 семь чисел 2, 4, 5, 6, 8, 9, 12, то числа 4 и 9 окажутся взаимно простыми.
И какие бы семь чисел мы ни выбирали из идущих подряд двенадцати натуральных чисел, все равно хоть два из них будут взаимно просты.
Эрдеш предложил мальчику доказать это утверждение. Тот подумал полминуты и ответил: но ведь из этих чисел два обязательно будут соседними, а соседние числа не могут иметь общих делителей, кроме 1. Многоопытный ученый был потрясен остроумным решением. И ведь, действительно, так как мы берем больше половины всех чисел, то не может случиться, что между любыми двумя из них есть невзятое нами число. Значит, обязательно найдутся два соседних числа!
Очень рано раскрылись математические способности у французского математика и революционера Эвариста Галуа. Он прожил только 21 год и погиб на дуэли, подстроенной полицией. В ночь перед дуэлью он написал письмо своему другу, в котором изложил полученные им результаты. Долгое время ученые не понимали идей погибшего юноши: настолько они опережали свое время. Но когда разобрались в его неопубликованных работах, имя Галуа стало одним из наиболее почитаемых в математике. И хотя со дня его гибели прошло более 150 лет, до сих пор в науке говорят о «полях Галуа» и «группах Галуа».
Идеи Галуа и по сей день, открывают новые пути в развитии науки.
Французский математик Бертран выучился в девять лет алгебре и геометрии весьма оригинальным образом. Его дядя руководил курсами по подготовке юношей в одно из самых известных высших учебных заведений Франции — Политехническую школу. Юный Бертран посещал занятия на этих курсах, хотя самый молодой из слушателей был, по крайней мере, вдвое старше него. И хотя преподаватели не обращали внимания на мальчика, он понимал все, что происходило в классе. Десяти лет Бертран после серьезного испытания был зачислен на эти курсы. Бертран получил ряд интересных результатов в математике.
Необыкновенные дарования проявил в детстве один из виднейших английских математиков XIX века Гамильтон. Десяти лет он изучил геометрию, прочтя латинское издание очень трудной книги Евклида «Начала». Когда в его родной город приехал изумительный счетчик Кольбурн и выступал на эстраде, юный Гамильтон вступил с ним в соревнование и ни в чем ему не уступил. А в тринадцать лет Гамильтон прочел написанную одним из величайших английских ученых Ньютоном «Всеобщую арифметику» и поступил в университет. Уже в 22 года он был назначен профессором этого университета. Но способности Гамильтона проявлялись не только в математике. К двенадцати годам он изучил двенадцать языков, хорошо знал географию.
Условия жизни в царской России препятствовали развитию народных талантов. И все же некоторым юным крестьянам удавалось проявить свой талант. В 1834 году одиннадцатилетний крестьянский мальчик Иван Петров из деревни Рагозине Кологривского уезда Костромской губернии проявил выдающиеся способности к арифметике. Во время испытания ему дали 12 задач, которые не умевший ни читать, ни писать Ваня решил в уме за 1 час 17 минут.
Вот некоторые из них:
Между двумя селениями посажено по дороге 1658 деревьев на равных расстояниях. Как велико расстояние между селениями, если одно дерево от другого отстоит на 8 аршин! (В одной сажени 3 аршина, в одной версте 500 саженей.)
Сколькими способами можно уплатить 78 рублей, имея деньги трех- и пятирублевого достоинства!
Последнюю из этих задач мальчик решил всеми шестью возможными способами.
При повторном испытании он решил в уме задачу: Сколько в году секунд, если считать, что в году 365 суток по 24 часа, каждый час — 60 минут, минута — 60 секунд? Сбившись сначала в подсчетах, он попросил позволения отвечать по порядку и, почти не задумываясь, сказал: число часов 8 760, минут 525 600, секунд 31 536 000.
Проверьте его ответ!
К сожалению, неизвестно, как потом сложилась судьба этого самородка.
Удивительный случай произошел в детстве с одной из самых знаменитых женщин-математиков Софьей Васильевной Ковалевской. Когда в доме ее отца шел ремонт, на детскую комнату не хватило обоев. Эта комната простояла несколько лет, оклеенная лишь простой бумагой. Но по счастливой случайности на эту предварительную оклейку пошли записи лекций по высшей математике, которые читал один из крупнейших русских ученых XIX века Михаил Васильевич Остроградский в Петербургской Академии наук.
Листы, испещренные странными, непонятными формулами, обратили на себя внимание маленькой Сони. Целые часы проводила она около стен детской комнаты, пытаясь понять порядок, в котором шли листы, и прочесть написанный на них текст. От этого внешний вид многих формул врезался в ее память, да и сопровождавшие их слова запомнились ей, хотя она и не могла тогда понять их смысл. Но когда через несколько лет пятнадцатилетняя Соня брала первые уроки высшей математики, ее преподаватель удивился, как скоро она усвоила сложнейшие понятия этой науки. А дело было в том, что в ту минуту, когда он объяснял ей эти понятия, девочка вдруг вспомнила слова из лекций Остроградского, которые она когда-то заучивала, глядя на стены своей комнаты.
Впоследствии Софья Васильевна стала членом-корреспондентом Петербургской Академии наук. Она написала ряд замечательных научных работ. Одна из них была удостоена премии Парижской Академии наук. И сейчас студенты-математики изучают теорему Ковалевской, знакомятся с ее исследованиями о вращении волчка. И если в XIX веке женщина-математик была редкостью, то сейчас среди действительных членов и членов-корреспондентов Академии наук СССР есть такие замечательные ученые, как математики Полина Яковлевна Кочина и Ольга Александровна Ладыженская.
Совсем юными начали свою научную деятельность многие советские академики-математики. В начале двадцатых годов к известному киевскому профессору математики Николаю Митрофановичу Крылову привели четырнадцатилетнего подростка Колю Боголюбова, Пораженный его талантом, Крылов начал занятия с ним, и уже через три года появилась их совместная научная работа. Ко дню совершеннолетия Боголюбов опубликовал несколько работ совместно с Крыловым. Академик Николай Николаевич Боголюбов несколько лет возглавлял Математический институт имени В. А. Стеклова Академии наук СССР, сейчас является одним из виднейших советских ученых.
На первом курсе университета началась научная деятельность академика Андрея Николаевича Колмогорова, одного из крупнейших ученых XX века. Столь же рано проявились математические дарования академика Льва Семеновича Понтрягина, который смог преодолеть обрушившееся на него несчастье: в четырнадцатилетнем возрасте он ослеп в результате взрыва. Несмотря на это, Лев Семенович стал виднейшим математиком.
Но не всегда математические способности раскрываются уже на школьной скамье. Выдающийся московский математик академик Николай Николаевич Лузин отнюдь не отличался в школе успехами по математике. Его отцу даже пришлось пригласить репетитора. Но потом, когда Лузин познакомился с высшими областями математики, он настолько увлекся наукой, что вскоре стал одним из самых крупных ученых нашей страны. Немецкий математик Якоб Штейнер до 18 лет был пастухом и почти не знал грамоты. Но потом он быстро окончил школу и университет, а в 29 лет уже преподавал математику, вскоре стал членом Берлинской Академии наук.
Приложение 2.
Игра «Математический поезд».
Станция 1. «Сообразительная»
Какая из команд решит больше правильно задач.
Задачи.
1. На грядке сидели 4 воробья. Прилетели еще 2 воробья. Кот Васька подкрался и схватил одного воробья. Сколько воробьев осталось на грядке
2. Четверо играли в домино 4 часа. Сколько асов играл каждый?
3. Горело пять свечей. Две из них потушили. Сколько свечей останется?
4.Тройка лошадей пробежала 30 км. Сколько километров пробежала каждая лошадь?
5. По дороге шли 2 мальчика и нашли 2 рубля За ними еще четверо идут, сколько они найдут?
6. Сколько грецких орехов в пустом стакане?
7. Петух, стоя на одной ноге, весит 3 кг. Сколько он весит, стоя на двух ногах?
8.У отца 6 сыновей. Каждый сын имеет одну сестру. Сколько детей у отца?
9.Найдите два таких числа, произведение которых 24 и частное тоже 24.
10. Сколько получится десятков, если два десятка умножить на 3 десятка?
11. Имеется кусок сукна длиной 16 м, от которого каждый день отрезают по 2 метра. По истечении скольких дней отрежут последний кусок?
12.Какие часы показывают точное время только два раза в сутки?
Станция 2 «Смекалистых»
Решить шарады.
1.Предлогом стоит в начале моем,
В конце же – загородный дом.
А целое мы все решали
И у доски, и за столом.
2. Игра - в ней лошади нужны,
К игре проступок пристегни.
И называй, дружочек, смело
То, что давно уже не цело.
3. Первый можно завязать,
Если галстук папин взять.
А второй, словарь листая. –
Мера скорости морская.
4. Две ноты - два слога,
А слово - одно,
И меру длины
Означает оно.
Станция 3 «Волшебные спички»
Задание
- Положите 12 спичек так, чтобы получилось 5 квадратов.
- В фигуре построенной в 1 задании, уберите 4 спички так, чтобы осталось два одинаковых квадрата.
Станция 4 «Геограмм»
Найди ошибки:
Атрезок, многугольник, точька, примая,
лучь, акружность,
кводрад, триугольник, обьем, площать.
Станция 5 «Ребусная»
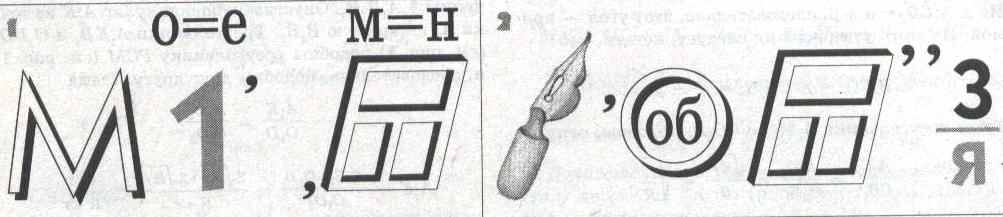
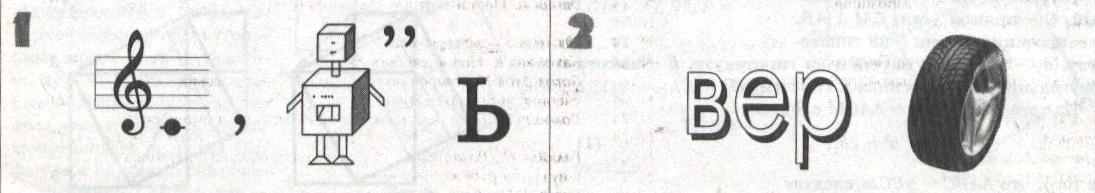
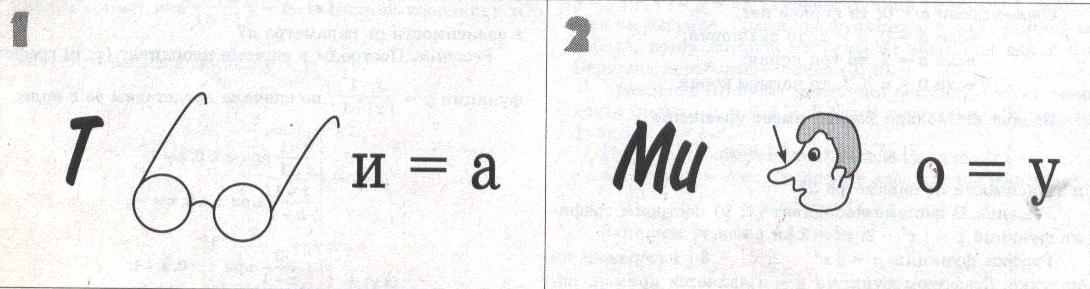
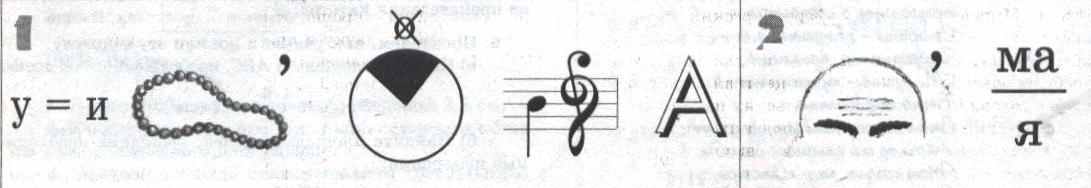

Станция 6 «Фантазеры»
Составить из фигур «Танграма», «Колумбова яйца» и «Волшебного круга» фигуры.



Станция 7 «Попробуй, сосчитай».
На листке в разброс написаны числа от 1 до 30. Кто сосчитает, указывая на число быстрее, тот и выигрывает.
Приложение 4
8 и 9 классы
Тема: Все о математике – ученые, открытия, понятия – по программе и далеко за ее пределами.
Ход игры:
I.Выбор участников игры.
На доске записаны два уравнения:
1) 4,7у-(2,5у + 12,4) =1,9;
2) 3,5х-(2,3х - 3,8) = 4,28.
Первые девять учеников, правильно решившие уравнения,
приглашаются для участия в игре "Поле чудес".
II. Из 9 участников определяется первая "тройка".
Предлагается устно ответить на один из следующих вопросов:
- На что похожа половина яблока? ( на его вторую половину).
- Сын моего отца, а мне не брат . (Я сам).
- Назовите ближайшую к земле звезду. (Солнце)
По результатам ответов определяется первая "тройка" участников.
Задание 1.
Это слово известно не только в математике, но и в металлообработке, в печатном деле, только имеет разный смысл. Это форма для отливок литер в типографии, в металлообработке – инструмент для штамповки. В математике – это таблица чисел, состоящая из нескольких строк и столбцов. (матрица)
ИГРА СО ЗРИТЕЛЯМИ
Кто из древних математиков был первым олимпийским чемпионом по кулачному бою? (Пифагор)
III. Вторая "тройка" определяется жеребьевкой: оставшиеся 6 участников вытаскивают жетоны. Те, кому выпали жетоны с цифрами 1,2,
3, включаются во вторую "тройку".
Задание 2.
Здесь зашифровано имя сподвижника, друга и любимца Петра 1., прадеда Пушкина. Этот человек – автор двухтомного учебника по геометрии. (Ганнибал)
Игра со зрителями
Слово на доске – составная часть компьютера. (Клавиатура)
IV. Третью "тройку" составляют последние 3 ученика из 9.
Задание 3. Здесь зашифрован раздел математики. Эта часть математики была признана наукой в 18 веке, когда возникла теория вероятностей. Теперь эта наука применяется при решении шахматных и шашечных задач, магических квадратов, домино, игры в карты, кости, при отгадывании шифров. Что это за раздел математики? (Комбинаторика)
ИГРА СО ЗРИТЕЛЯМИ
Что есть общего у равнобедренного треугольника и степени? (Основание)
ФИНАЛЬНАЯ ИГРА
Играют победители в "тройках". Если определились только два победителя или один, то в финальной игре принимают участие победители игры со зрителями.
Задание.
Здесь зашифровано имя автора этой красивой теоремы. «Если на сторонах треугольника во внешнюю сторону построить равносторонние треугольники, то их центры будут вершинами равностороннего треугольника». Этот треугольник носит имя автора. Это имя известно каждому, но не на стезе математики. Математикой этот человек занимался удовольтвия ради. В ней он чувствовал красоту, объект, достойный приложения. Он – автор нескольких теорем и известных занимательных геометрических задач. А свое имя он прославил на весь мир совсем по другому поводу. Как имя автора этой теоремы? (Наполеон Бонапарт)
СУПЕРИГРА
На доске зашифровано имя, Верн ее псевдоним, всемирно известного писателя, автора не менее известной повести – сказки. Но не всем известно настоящее имя этого писателя – Чарлз Доджсон, священник и известный профессор математики. (Льюис Кэролл)
Приложение 5.
Олимпиадные задания по математике. 5 класс. 2007 год.
1.Вычеркните в числе 4000538 пять цифр так, чтобы оставшееся
число было наибольшим. 3 балла
2.Для того чтобы разрезать металлическую балку на две части нужно
уплатить 5 рублей. Сколько будет стоить работа, если балку нужно
разрезать на 10 частей? 3 балла
3.Парусник отправляется в плавание в понедельник в полдень.
Плавание будет продолжаться 100 часов. Назовите день и час его
возвращения в порт. 4 балла
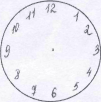
4.Разбей циферблат часов с помощью отрезков на три части так,
чтобы сумма чисел в каждой из этих частей была одной и той же.
5 баллов
5.На улице, став в кружок, беседуют четыре девочки: Аня, Валя,
Галя, Надя. Девочка в зеленом платье (не Аня и не Валя) стоит между
девочкой в голубом платье и Надей. Девочка в белом платье стоит
между девочкой в розовом платье и Валей.
Какое платье носит каждая девочка? 5 баллов
6.Расставьте скобки в записи 7 9 + 12: 3 - 2 так, чтобы значение
полученного выражения было равно
а) 23; б) 75 4 балла
Олимпиадные задания по математике. 6 класс 2007 год.
1.Поставьте вместо звездочек цифры: 59,27
+ **,45
78,3*
181,*
2.Выразите число 16 с помощью четырех пятерок, соединяя их
знаками арифметических действий. 3 балла
3.Разместите 8 козлят и 9 гусей в пяти хлевах так, чтобы в каждом
хлеве были и козлята и гуси, а число их ног равнялось 10. 4 балла
4.Некоторый товар стоил 500 рублей. Затем цену на него увеличили
на 10%, а затем уменьшили на 10%. Какой стала цена в итоге?
5 баллов
5.Три подруги вышли в белом, синем, зеленом платьях и туфлях
таких же цветов. Известно, что только у Ани цвет платья и туфель
совпадает. Ни платье, ни туфли Вали не были белыми. Наташа была в
зеленых туфлях. Определите цвет платья и туфель каждой подруги.
4 балла
6.В классе 35 учеников. Из них: 20 школьников занимаются в
математическом кружке, 11 _ в экологическом, 10 ребят не посещают
эти кружки. Сколько экологов увлекается математикой? 5 баллов.
Олимпиадные задания по математике. 7 класс. 2007 год.
1.При каких значениях с уравнение сх = 9:
а) имеет корень, равный -9; 0; 1\5.
б) не имеет корней.
в) имеет положительный корень. 3 балла
4 балла
2. Число 56 разложите на два слагаемых так, чтобы 1/3 первого слагаемого была равна 1/4 второго. 4 балла.
3.Насколько процентов увеличиться площадь прямоугольника, если
его длину увеличить на20%, а ширину - на 10%? 5 баллов
4.Найдите все значения х и у , для которых ху + 1 = х + у 5 баллов
5. Бочка наполнена бензином. Как перелить, из нее в мотоцикл 6 литров бензина с помощью 9-литрового ведра и 5-литрового бидона? 4 балла
6. Поезд проходит мимо светофора за 5 секунд, а мимо платформы длиной 150 метров за 15 секунд. Найдите длину поезда и его скорость. .7 баллов
Олимпиадные задания по математике. 8 класс 2007 год.
1.Поставьте знаки модуля так, чтобы равенство 1 – 2 – 4 – 8 – 16 =19 стало верным.
3 балла
2.Одну овцу волк съедает за 2 дня, волк – за 3 дня, а собака – за 6 дней. За сколько дней они вместе съедят овцу? 4 балла.
3.Пассажир едет в поезде, который идет со скорость 60 км/ч, и видит, что
мимо окна проходит встречный поезд в течение 4 с. Какова скорость
встречного поезда, если его длина 120 м? 5 баллов
4.Постройте график функции: у = !х - 3| 5 баллов
5.Восстановите математическую запись примера:
АННА
+ ВАЛЯ
4809
Разные буквы обозначают разные цифры, а одинаковые буквы - одинаковые
цифры. 6 баллов
б.Докажите, что биссектрисы внешних углов прямоугольника
пересекаясь, образуют квадрат. 8 баллов
Олимпиадные задания по математике. 9 класс 2007 год.
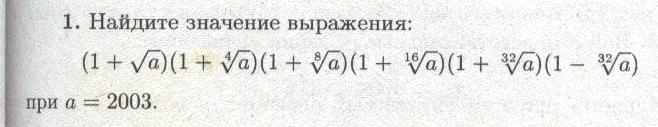

Приложение 6.
«Математический КВН»
Соревнуются две команды, составленные из учеников 5 – 9 классов.
Команды дают название и выбирают капитанов.
1 конкурс: «Разминка»
Команды по очереди отвечают на 5 вопросов.
Вопросы 1 команде.
1. Единица скорости на море. (Узел)
2. Наименьшее натуральное число. (1)
3. Как найти неизвестное делимое?
4. Периметр квадрата равен – 20 см. Чему равна его площадь? ( 25 кв. см.)
5. Можно ли при умножении чисел получить ноль? (Да)
Вопросы 2 команде.
- Чему равен 1 пуд? (16 кг)
- Назовите наибольшее отрицательное число. (-1)
- Как найти неизвестный делитель?
- Площадь квадрата 49 кв.см.. Чему равен его периметр? ( 28 см)
- Назовите единицу массы драгоценных камней. (Карат)
2 конкурс: «Конкурс капитанов».
- Анкета капитанов.
По примерному плану ( возраст, рост, цвет глаз, походка, характер, цвет волос, костюм, вес) капитаны должны охарактеризовать своего противника.
- Отмерить на глаз 50 см.
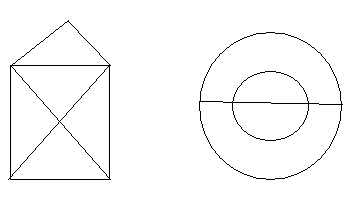
3 конкурс: «Конкурс художников».
Нарисовать фигуры, не отрывая карандаш от бумаги и не проводя дважды по одной и той же линии.
4 конкурс: «Не собьюсь»
Нужно сосчитать до 30. Вместо числа, оканчивающегося на 3 и делящегося на 3, надо говорить «Не собьюсь».
5 конкурс: «Математический хоккей».
Участники команд по очереди выполняют действия в числовом выражении.
(43 19 – 26928 : 33) ( 16112 :53 – 304)
Подведение итогов.
