Geum.ru

Материалы Международной научно- технической конференции «Вторые ержановские чтения». Актобе. 2007. С. 473-477

Вид материалаДокументы

Содержание


Регистр сдвига
Вектор сообщения
Логическая схема для реализации деления многочленов
Подобный материал:
// Материалы Международной научно- технической конференции «Вторые ержановские чтения». – Актобе. – 2007. – С.473-477


УДК 681.3.07

А.А. Садыков, Н.Н. Ташатов


кодирование в систематической форме линейных

циклических кодов


Евразийский национальный университет им. Л.Н. Гумилева, г. Астана


Кодирование в систематической форме.

Используем некоторые алгебраические свойства циклического кода для разви­тия процедуры систематического кодирования, которая была рассмотрена в [4]. В этой статье было введено понятие систематическая форма и рассмотрено уменьшение сложности, которое делает эту форму кодирования более привлекательной.

Запишем вектор сообщения в форме многочлена степени k – 1 следующим образом:


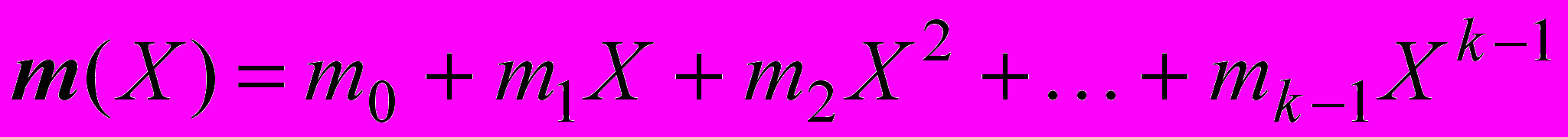. (1)


Символы сообщения в систематической форме используются как часть кодового сло­ва. Сдвинем символы сообщения в k крайних правых разряда кодового слова, а затем прибавим биты четности, разместив их в крайние левые п – k разряды. Такой сдвиг не вызывает переполнения п–разрядного регистра сдвига. Таким образом, осуществляем алгебраическую манипуляцию многочлена сообщения, и он оказывается сдвинутым вправо на п - k позиций. Умножив m(X) на 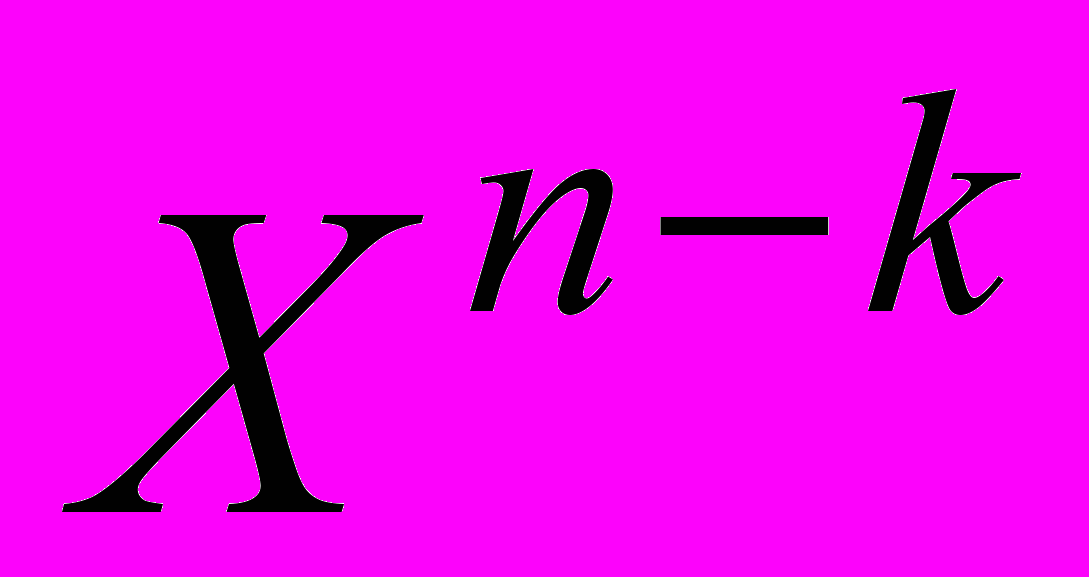, получаем сдвинутый вправо многочлен сообщения:


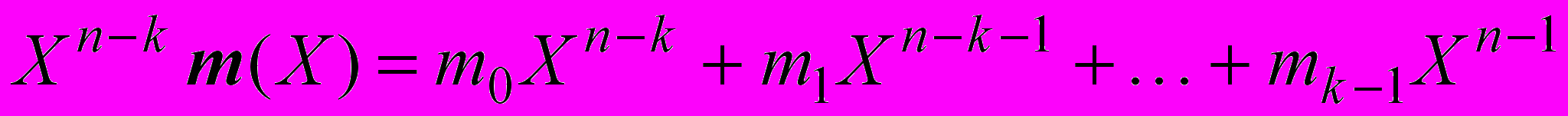. (2)


Регистр сдвига

0 n-1

0
…
0
0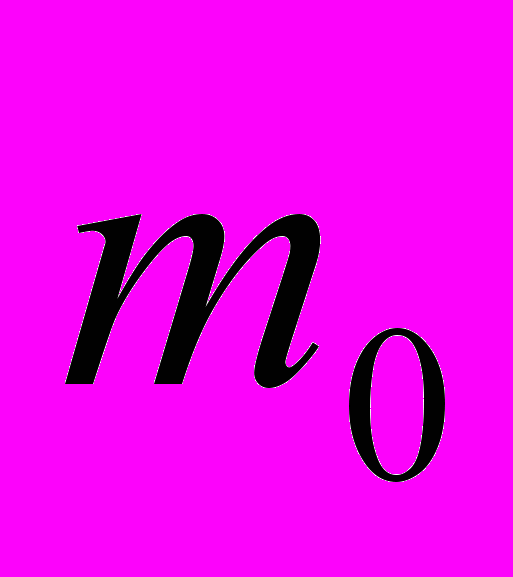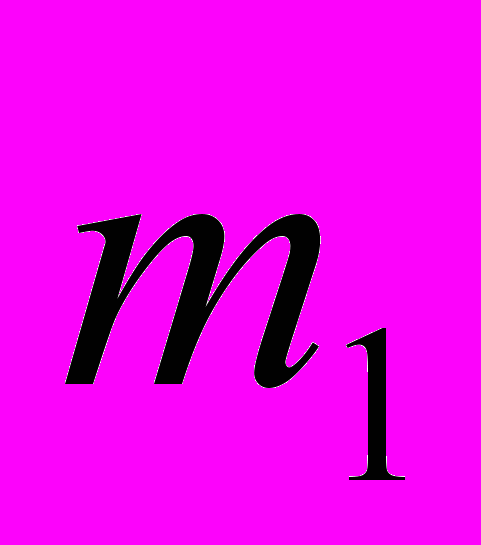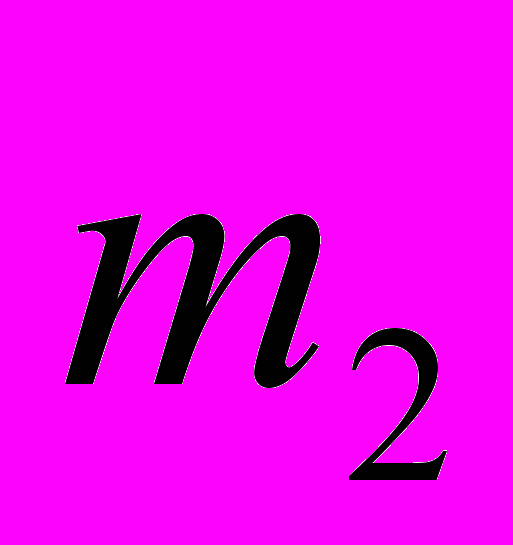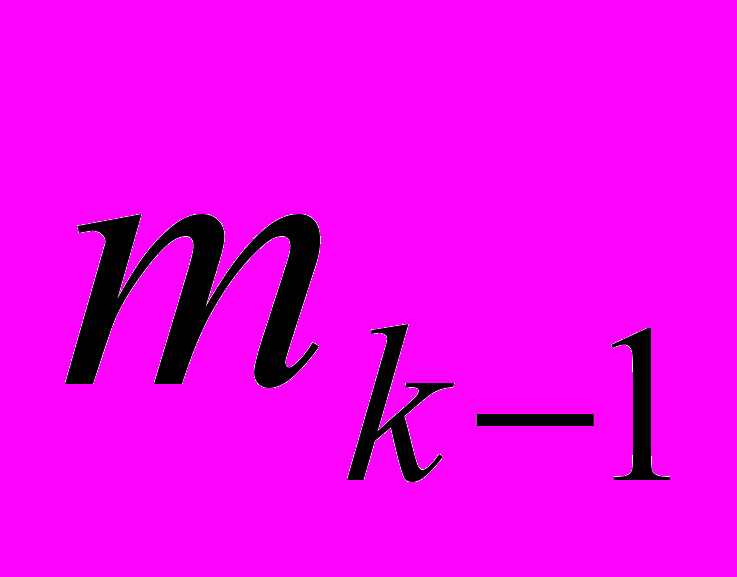






…







Вектор сообщения


Рисунок 1 – Сдвиг многочлена в регистре сдвига с обратными

связями длины п на p = п – k позиций


Разделив уравнение (2) на g(X), получим:


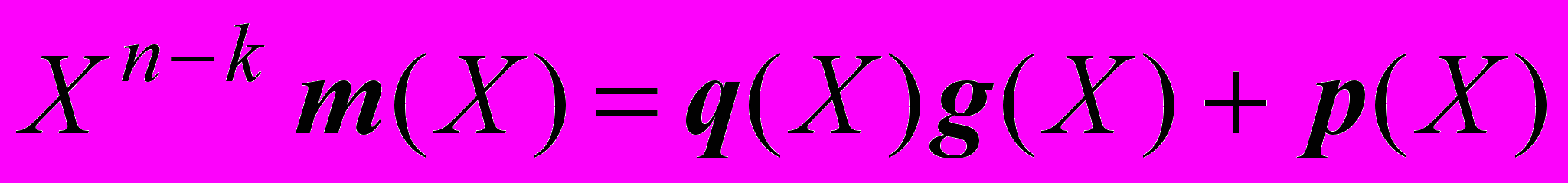. (3)


Остаток р(Х) записывается следующим образом:


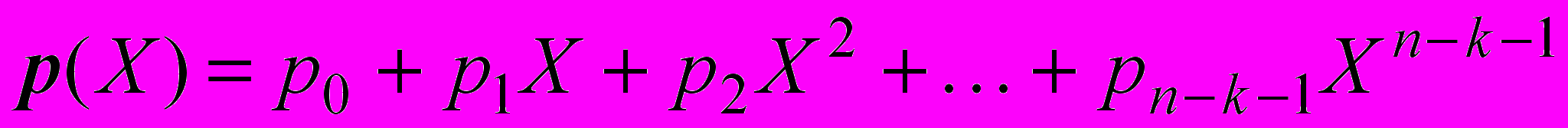, (4)


или


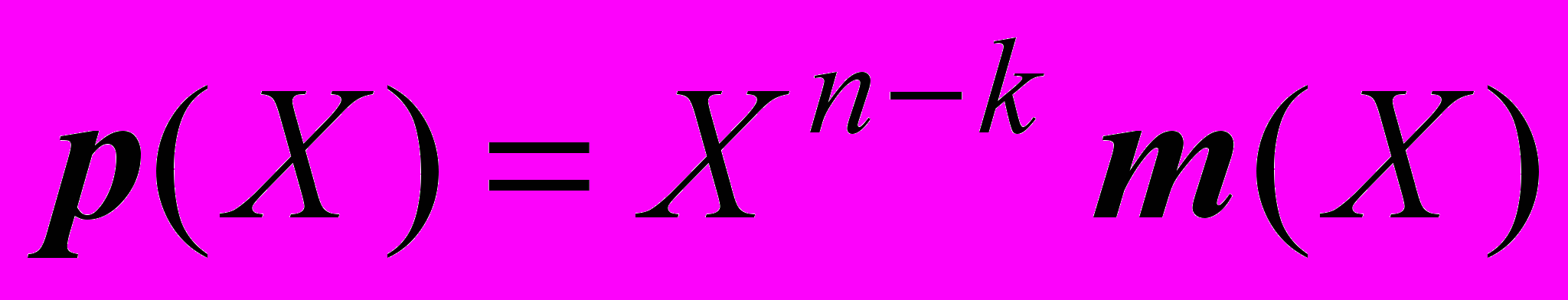по модулю 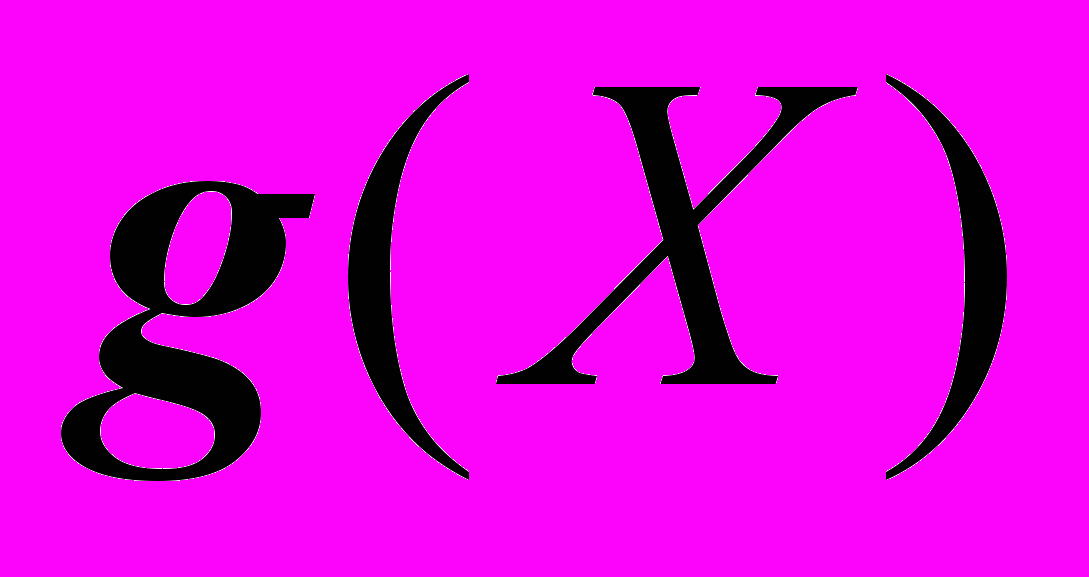. (5)

Прибавим р(Х) к обеим частям уравнения (3) и используя сложение по модулю 2, получим:


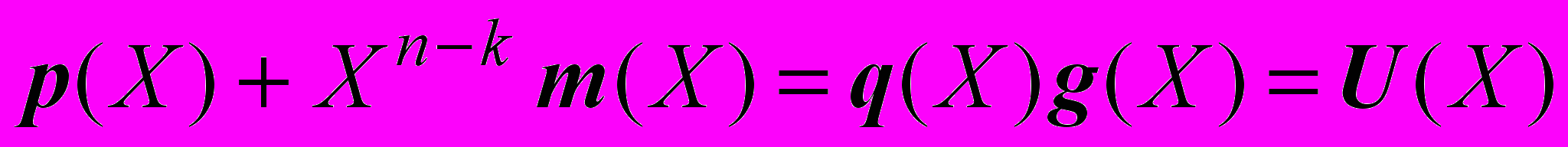. (6)


Из (6) вытекает алгоритм кодирования систематического циклического (n, k) – кода:
  1. Вектор сообщения в форме многочлена m(X), степени k – 1, умножается на ;
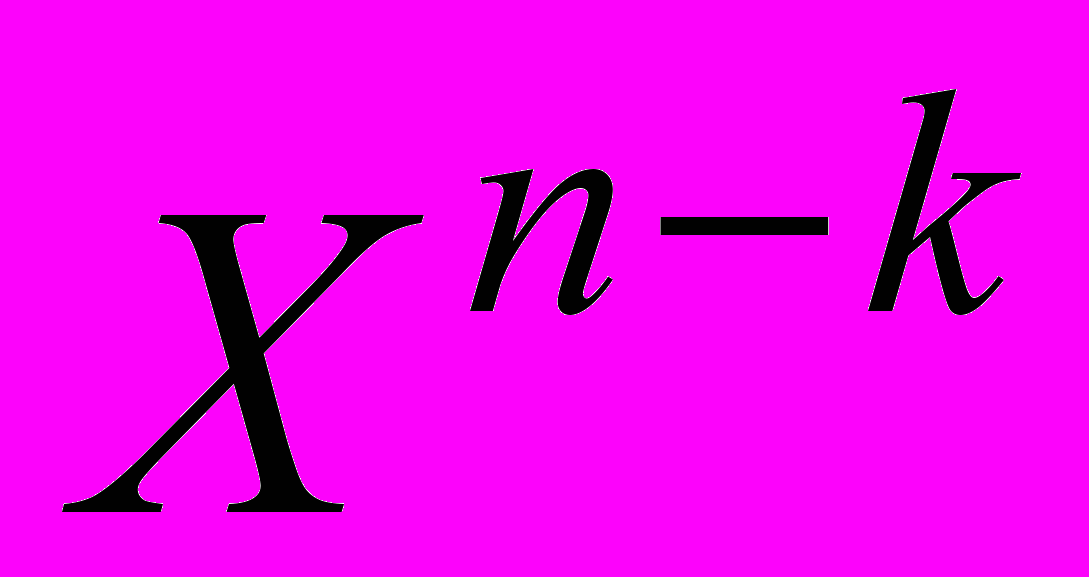  2. Находится остаток р(Х) от деления 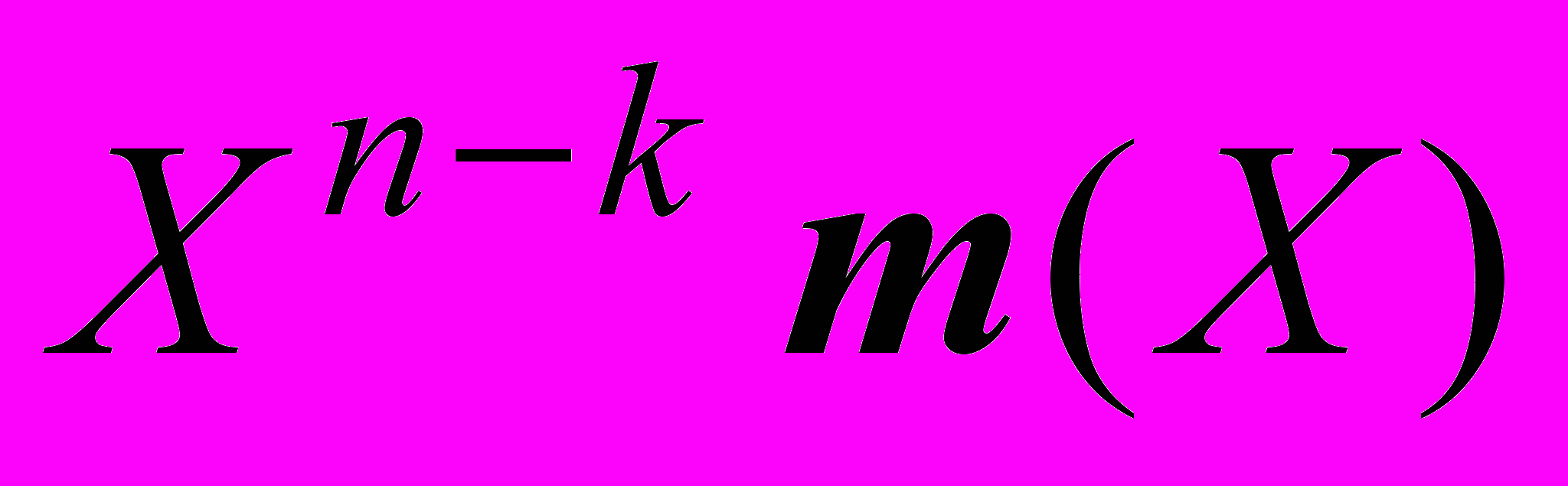на g(X);
  3. Многочлен р(Х) заносится в п – k левых разрядов регистра сдвигов (см. рис. 1)


Левая часть уравнения (6) является действительным многочленом кодового слова, так как это многочлен степени не превышающая п - 1, который при делении на g(X) дает нулевой остаток. Это кодовое слово будет выглядеть следующим образом:





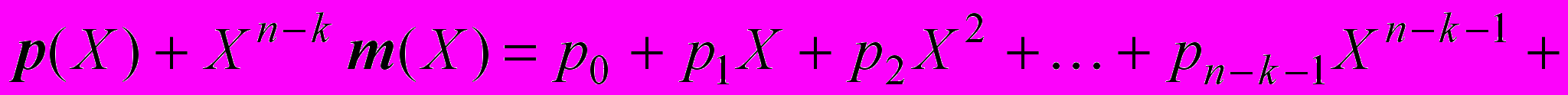
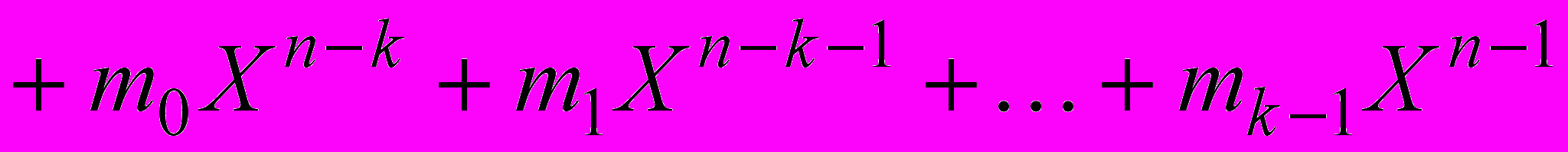. (7)


Многочлен кодового слова соответствует вектору кода


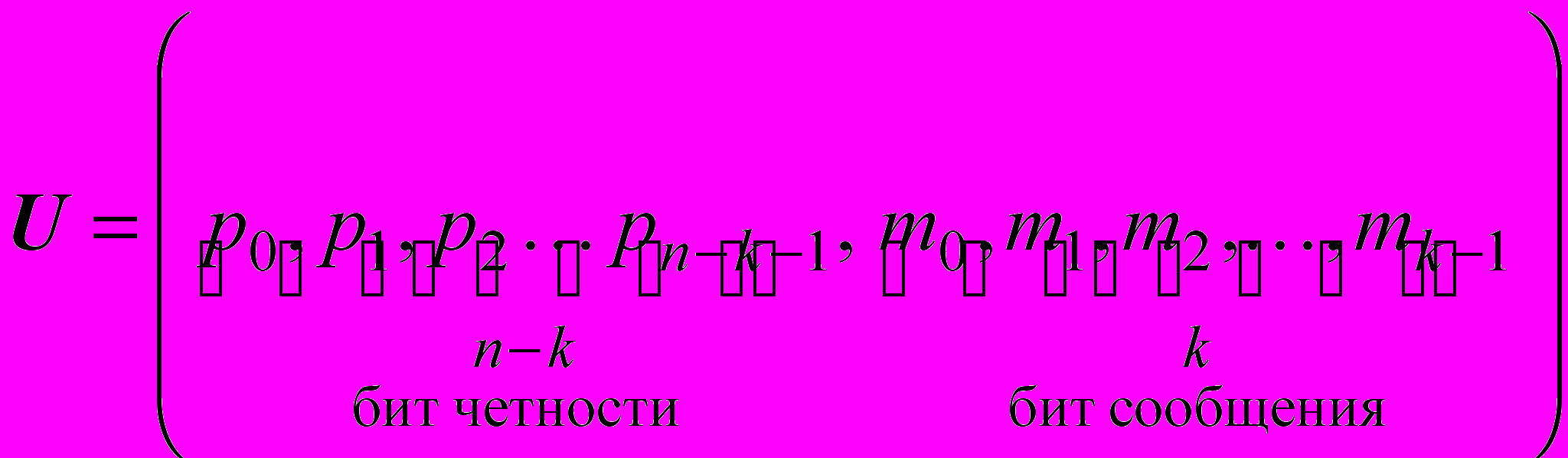. (8)


Циклический код в систематической форме.

Пусть дан вектор сообщения m = 1 0 0 1 1. Из набора кодовых слов (7, 4) с помощью порождающего многочлена g(X) = 1 + X + X3 надо получить систематическое кодо­вое слово.


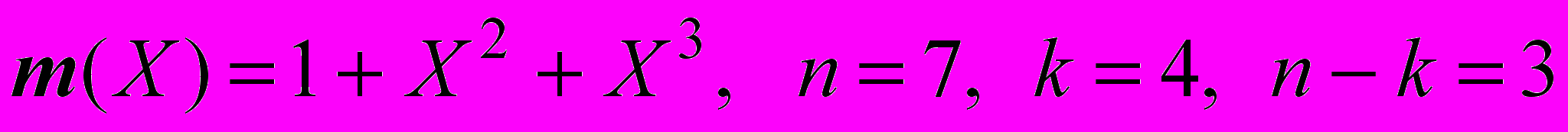. (9)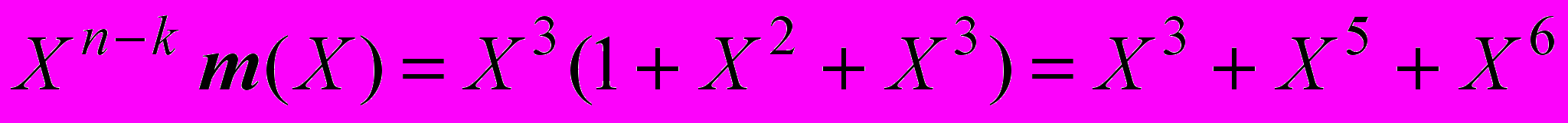


. (10)


Разделим 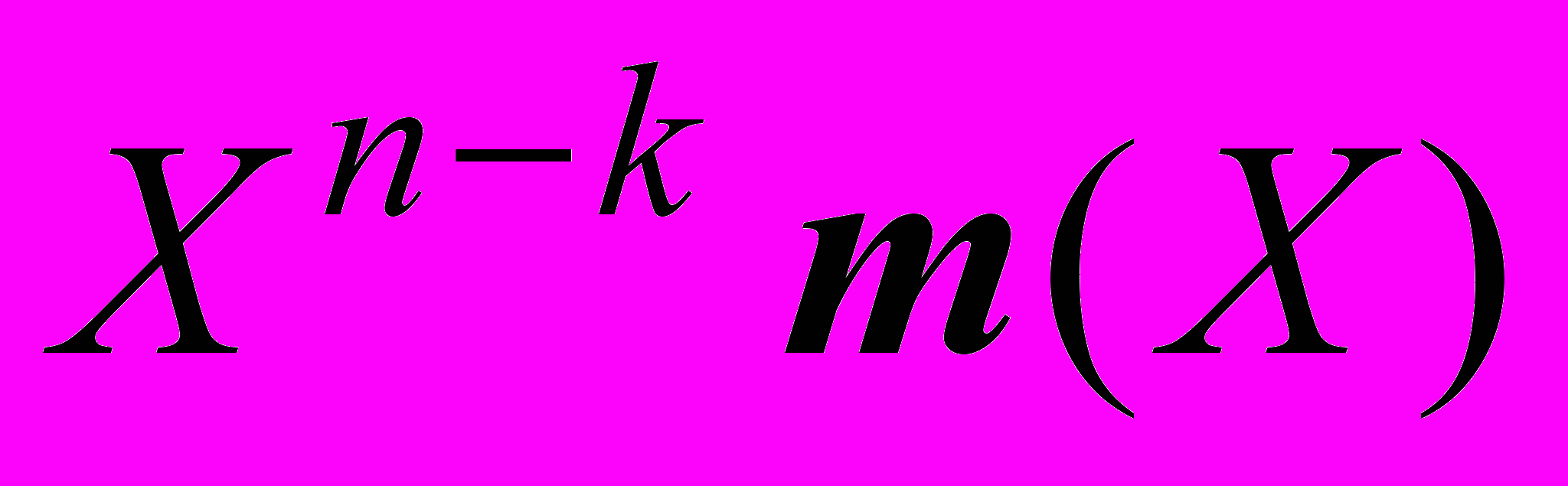на g(X), получим:


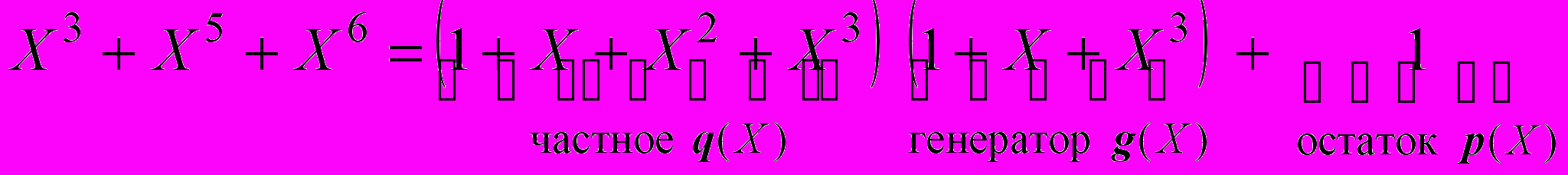. (11)


Используя уравнение (6), получаем следующее:


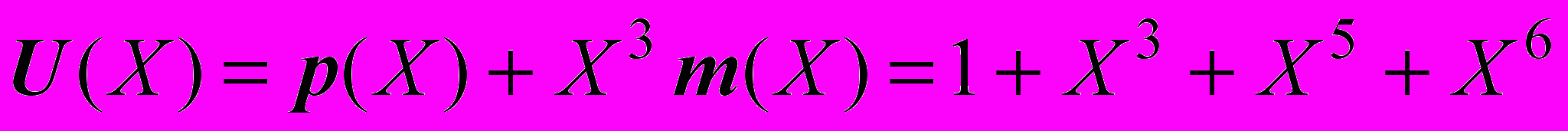. (12)


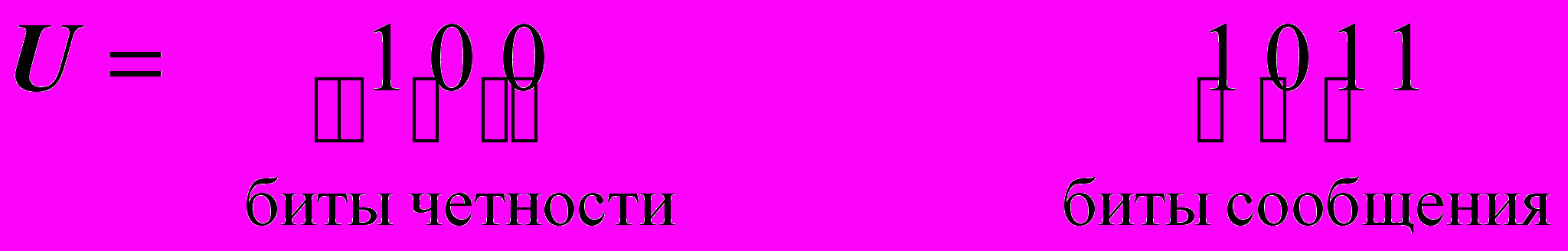. (13)


Логическая схема для реализации деления многочленов.

Важнейшее преимущество циклических кодов по сравнению с другими методами кодирования заключается в простоте их технической реализации. Использование в схемах кодеров и декодеров регистров сдвига с обратными связями, позволяет просто и достаточно эффективно защищать от ошибок информационные массивы большой длины. Процедура деления многочленов является основной в кодерах и декодерах циклических кодов. Пусть даны два многочлена V(X) и g(X), где


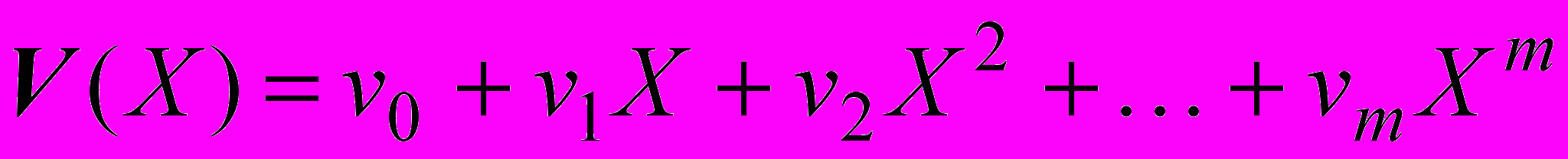. (14)


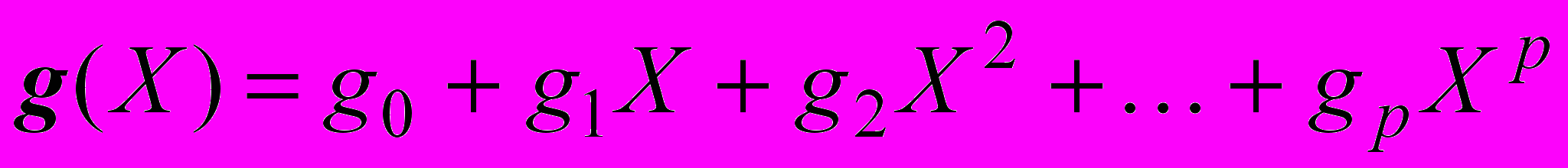. (15)


причем т > р. Схема деления, приведенная на рисунке 2, выполняет деление многочлена V(X) на g(X), определяя частное и остаток от деления


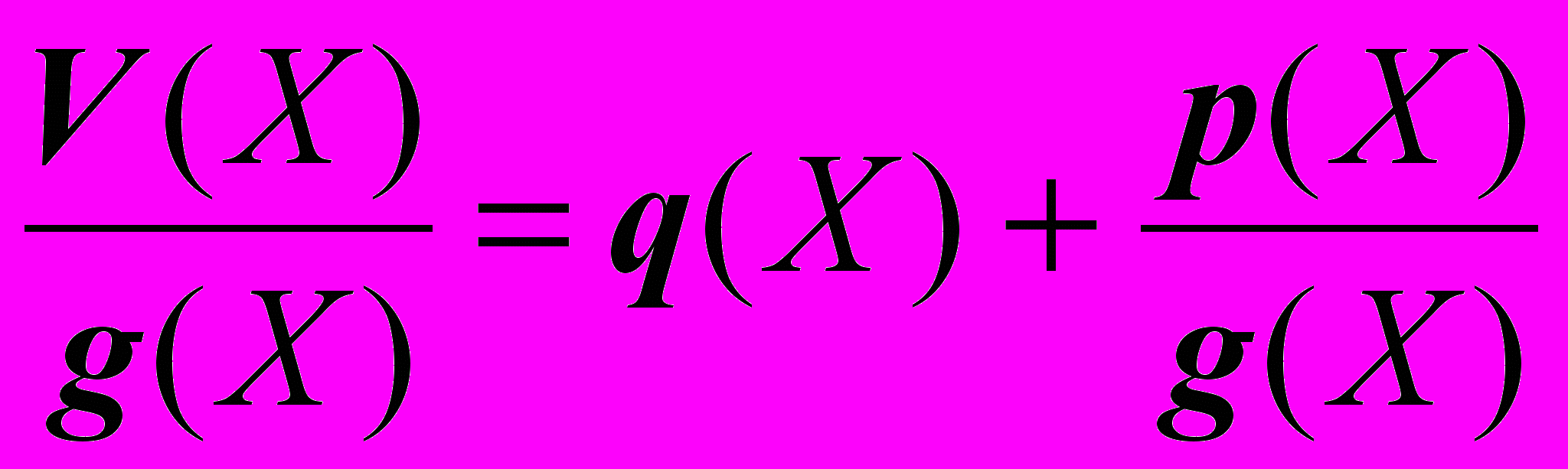. (16)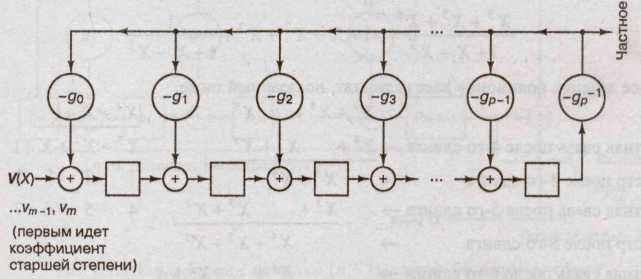






Рисунок 2 – Логическая схема для реализации деления многочленов


Разряды регистра в исходном состоянии содержат нули. Коэффициенты V(X) посту­пают и продвигаются по регистру сдвига по одному за такт, начиная с коэффициентов более высокого порядка. Частное после р-го сдвига на выходе равно 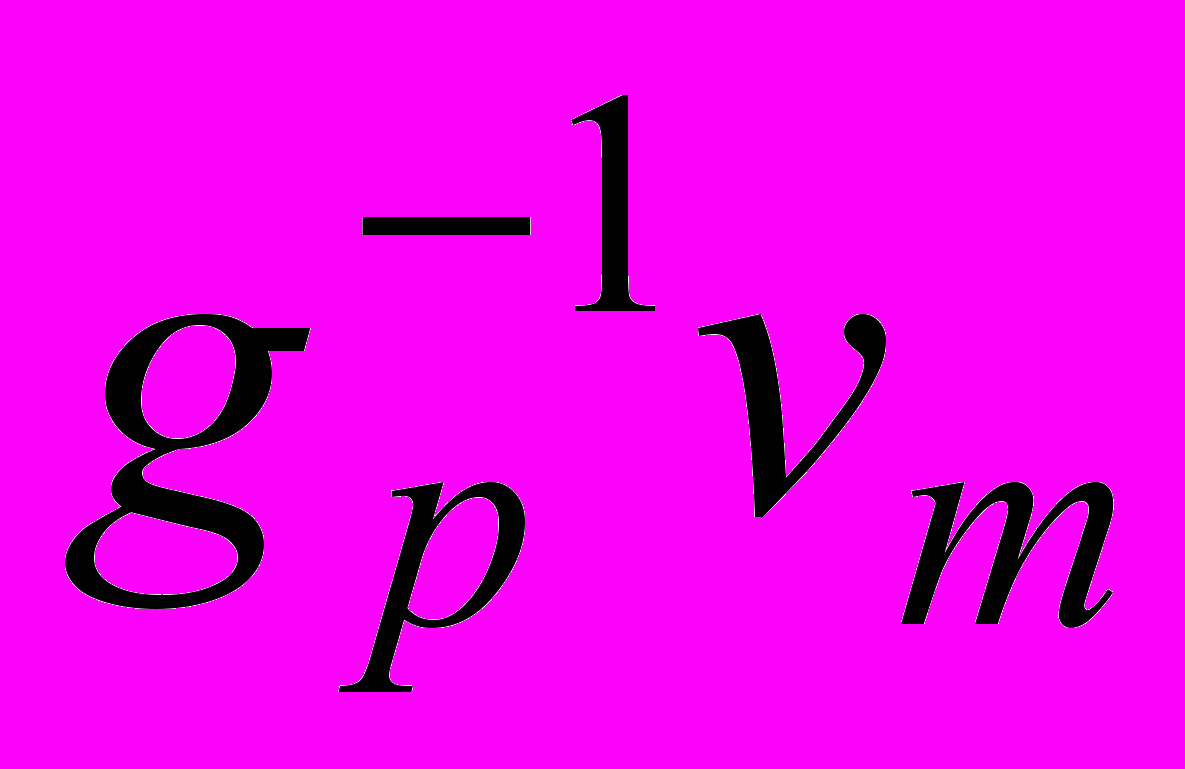. Получаем слагаемое наивысшего порядка в частном. Затем из делимого для каждого коэффициента частного qi вычитаем многочлен 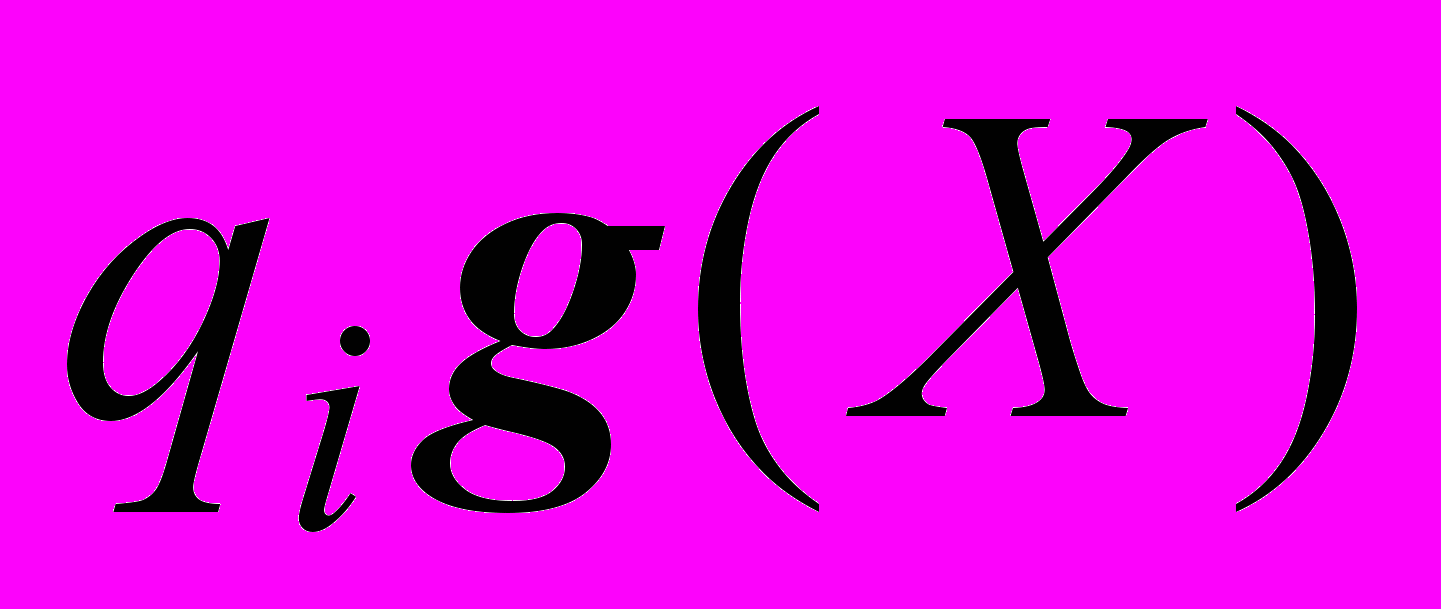. Это вычитание обеспечивает обратная связь, показанная на рисунке 2. Разность крайних слева р слагаемых остается в де­лимом, а слагаемое обратной связи 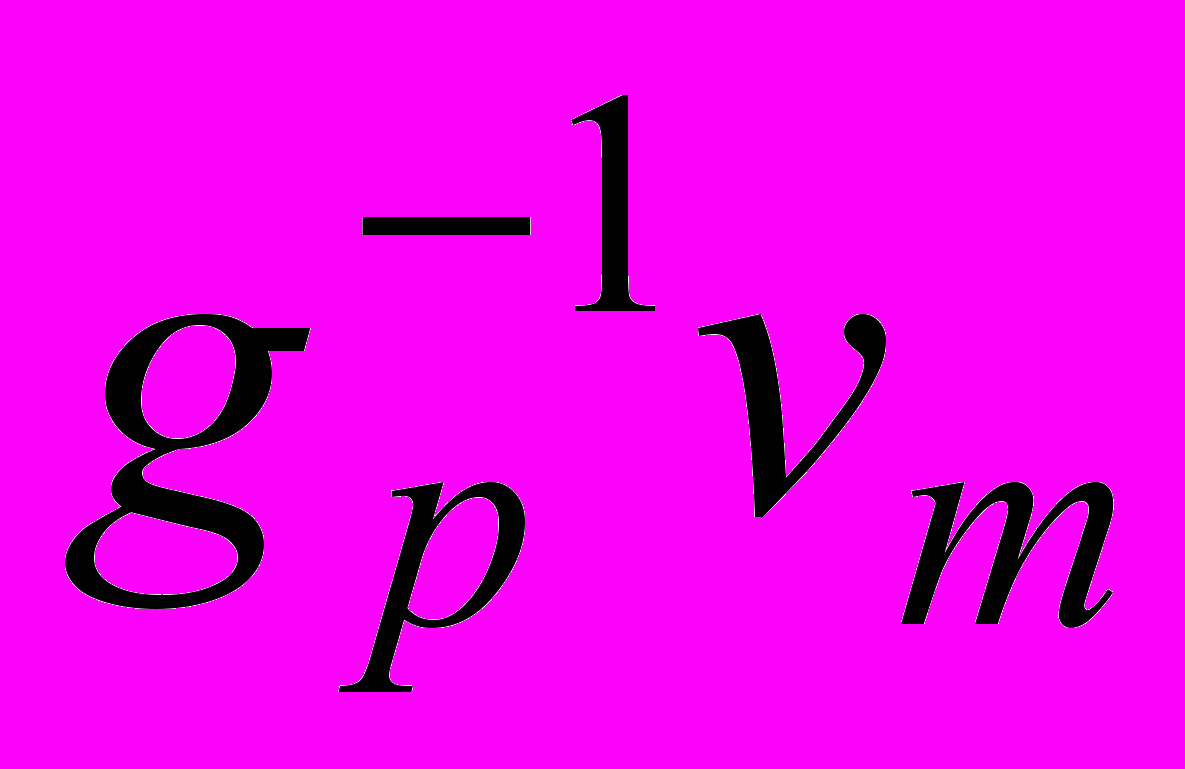формируется при каждом сдвиге схемы и отображается в виде содержимого регистра. При каждом сдвиге регистра разность смещается на один разряд. Слагаемое наивысшего порядка, которое по построению схемы равно нулю, удаляется, в то время как следующий значащий коэффициент в V(X) перемещается на его место. После всех m + 1 сдвигов регистра, на выход последовательно выдается частное, а остаток остается в регистре.

Рассмотрим схему деления многочленов, используя рисунок 2. Пусть 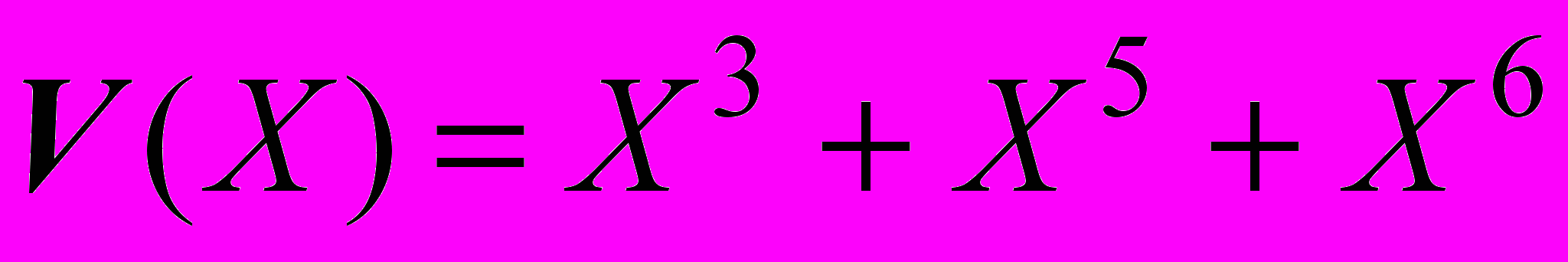, т.е. V = 0001011, и 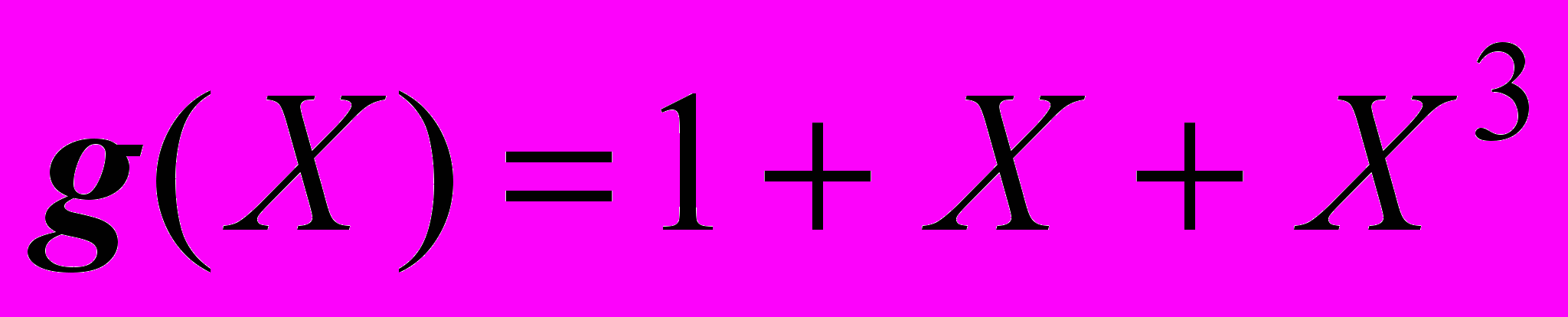. Разделим V(X) на g(X). Схема деления должна выполнить следующее действие


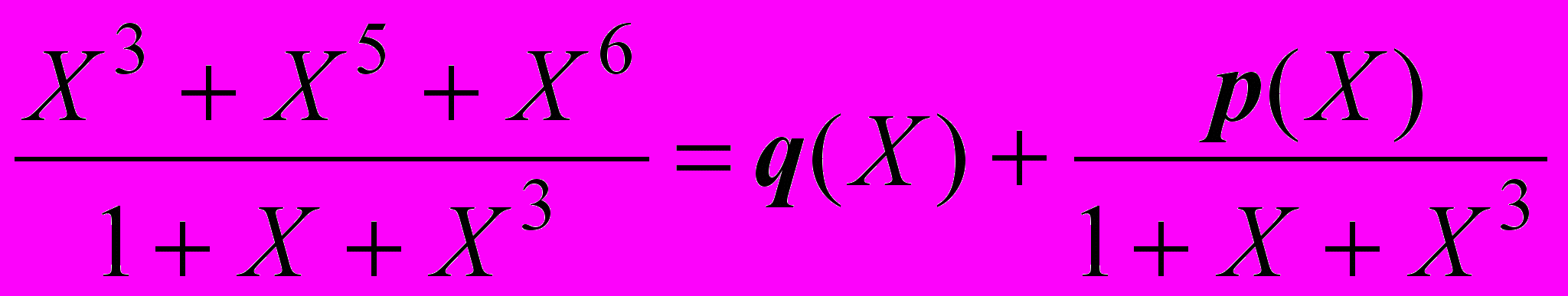. (17)


Необходимый регистр сдвига с обратной связью показан на рисунке 3.



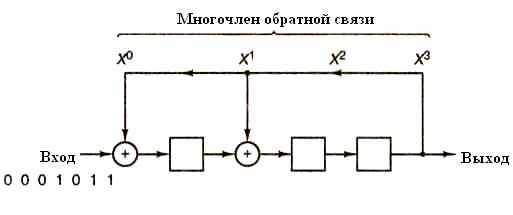
Рисунок 3 – Схема деления для примера


Пусть первоначально регистр содержит нули. Схема выполнит следующие шаги.


Входная очередь
Номер сдвига
Содержимое регистра
Выход и обратная связь

0001011
0
000
-

000101
1
100
0

00010
2
110
0

0001
3
011
0

000
4
011
1

00
5
111
1

0
6
101
1

-
7
100
1


После четвертого сдвига коэффициенты частного 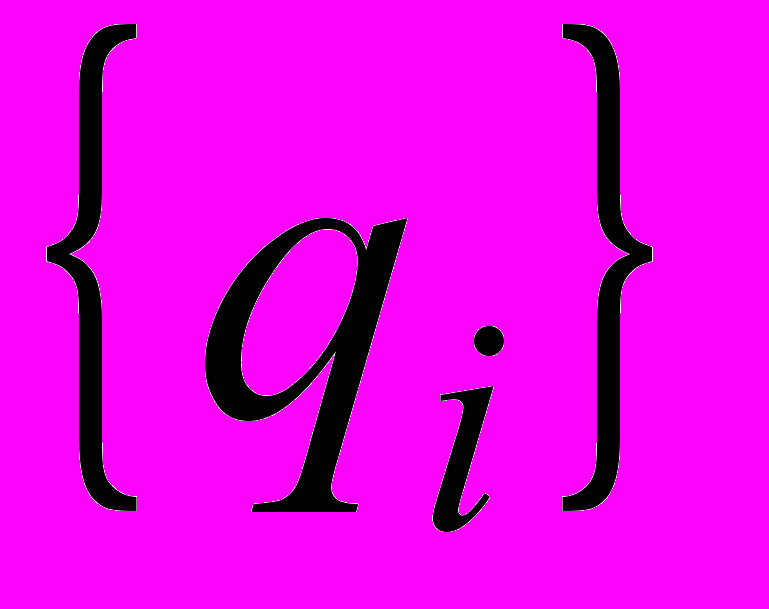, которые последовательно поступали с выхода, равны 1111. Тогда многочлен частного имеет следующий вид 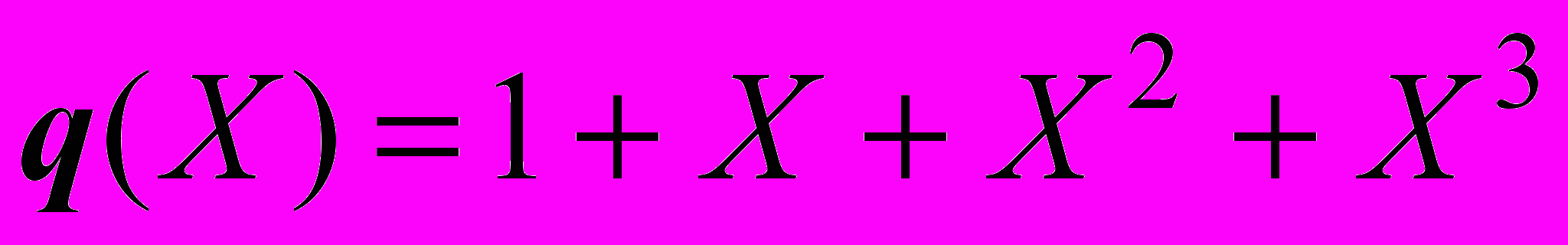. Коэффициенты остатка 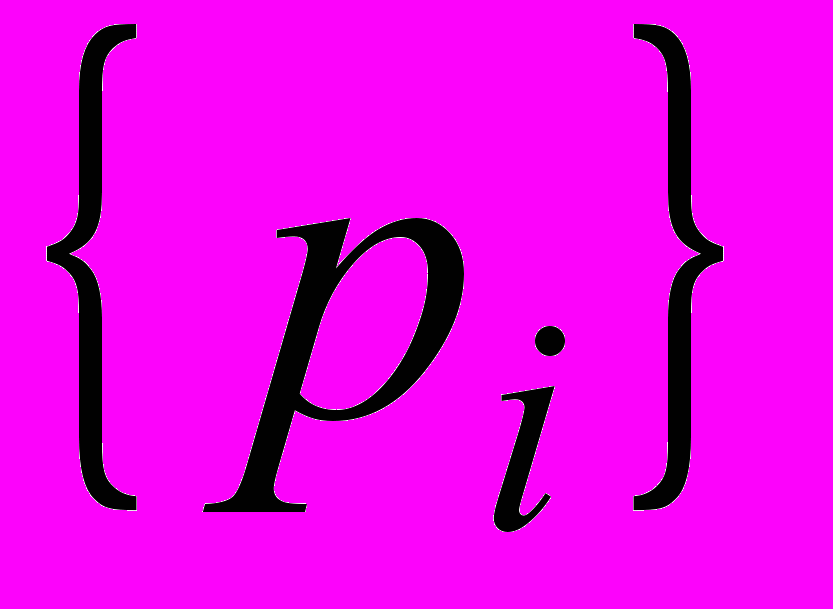имеют вид 100, т.е. многочлен остатка имеет вид p(X) = 1. Схема выполнила следующее вычисления


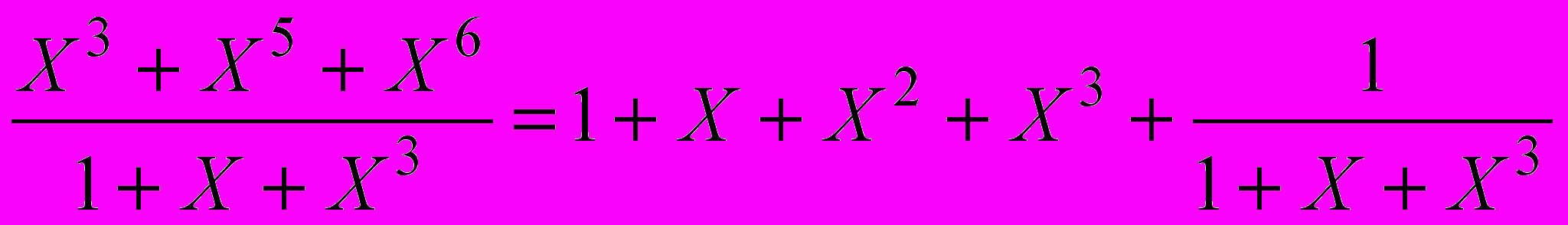. (18)


Прямое деление многочленов дает тот же результат.


СПИСОК ЛИТЕРАТУРЫ

  1. Скляр Б. Цифровая связь. Теоретические основы и практическое применение. Изд. 2-е, испр.: Пер. с англ. – Издательский дом «Вильямс», 2004. – 1104 с. ил.
  2. Вернер М. Основы кодирования. Москва: Техносфера, 2004. – 288 с.
  3. Березюк Н.Т., Андрущенко А.Г., Мощицкий С.С. Кодирование информации (двоичные коды). Харьков, издательское объединение «Вища школа», 1978, 252 с.
  4. Ташатов Н.Н. Систематические линейные блочные коды с контролем четности. // Вестник ПГУ им. С.М. Торайгырова. – 2007. – № (в печати).