О спектральных свойствах дискретного преобразования фурье

Вид материала

Документы

Подобный материал:

• Методические указания по выполнению лабораторной работы №4 по курсу "Цифровая обработка, 155.95kb.
• Лекция №5 «Боровская теория водородоподобного атома», 181.56kb.
• В. Е. Логинов, П. А. Ишин, 111.9kb.
• Шарль Фурье. Шарль Фурье (1772-1832гг.), 813.94kb.
• «упаковать», 279.17kb.
• Возможности применения вейвлет-преобразования в скважинной сейсморазведке, 37.66kb.
• Учебно-методический комплекс для специальности, 359.2kb.
• Методические рекомендации разработаны: Т. Б. Киметач, К. В. Понкратов (экц мвд рф)., 191.52kb.
• Задачи и организация курса. Литература. Понятия сигнала и системы Лекция №2 Классификация, 22.9kb.
• Калужский Филиал Московского Государственного Технического Университета им. Н. Э. Баумана, 66.73kb.

О СПЕКТРАЛЬНЫХ СВОЙСТВАХ ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ .


Р.И Каримов.


(Воронежский институт МВД России, Воронеж.)


Дискретное преобразование Фурье (ДПФ) является одним из самых известных и полезных на практике математических инструментов. Это преобразование широко применяется в электродинамике и оптике, теории кодирования и криптографии, при анализе систем связи и фильтрации сигналов, в алгоритмах сжатия информации и вычислительной томографии.

Важность ДПФ для приложений определяется в том числе и тем, что задачи о вычислении ДПФ, циклической свертки последовательностей, произведения больших чисел или многочленов по существу эквивалентны. Важное значение имеют быстрые алгоритмы ДПФ, в которых число необходимых операций уменьшено по сравнению с обычным бесхитростным вычислением за счёт изощрённой оптимизации порядка выполнения действий. Наиболее известны быстрые алгоритмы Гуда, Кули и Тьюки, Винограда, Рейдера [1-3]. Фундаментальную роль ДПФ играет в современной криптографии [4].

ДПФ определяется матрицей n х n с элементами



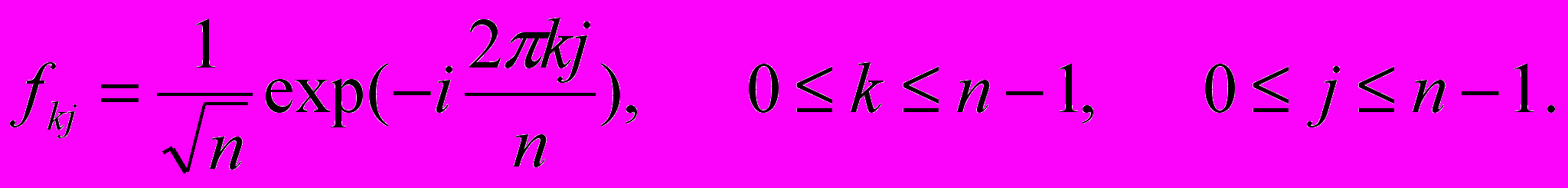
Таким образом, матрица ДПФ без учёта нормирующего множителя устроена так: первые строка и столбец состоят из единиц, во второй строке стоят корни из единицы порядка n в естественном порядке, следующие строки являются последовательными степенями второй строки. С точностью до множителя это матрица Вандермонда.

Так, например, пр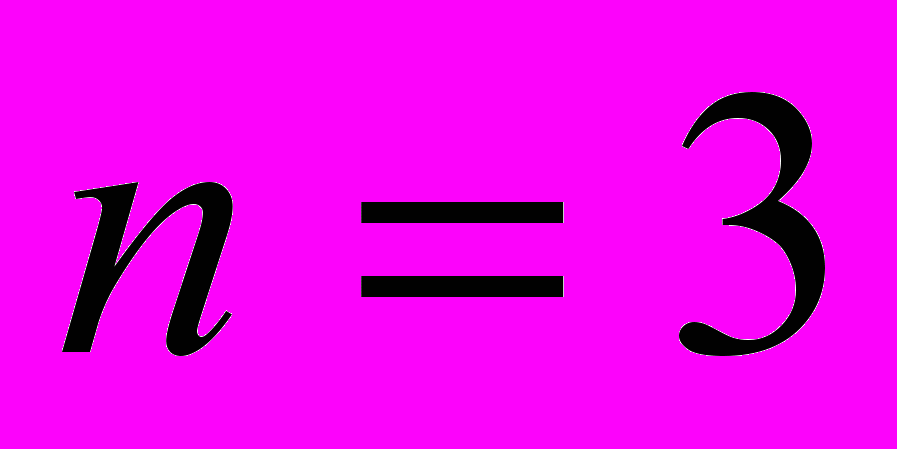и и 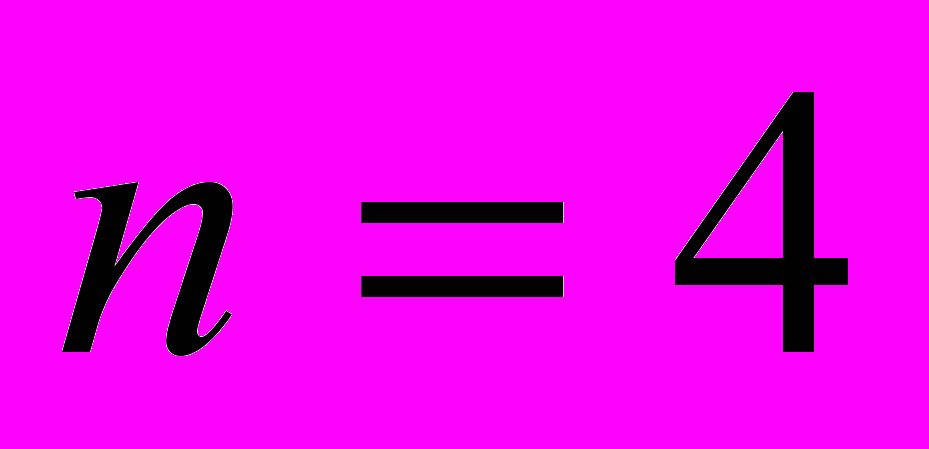матрицы ДПФ имеют вид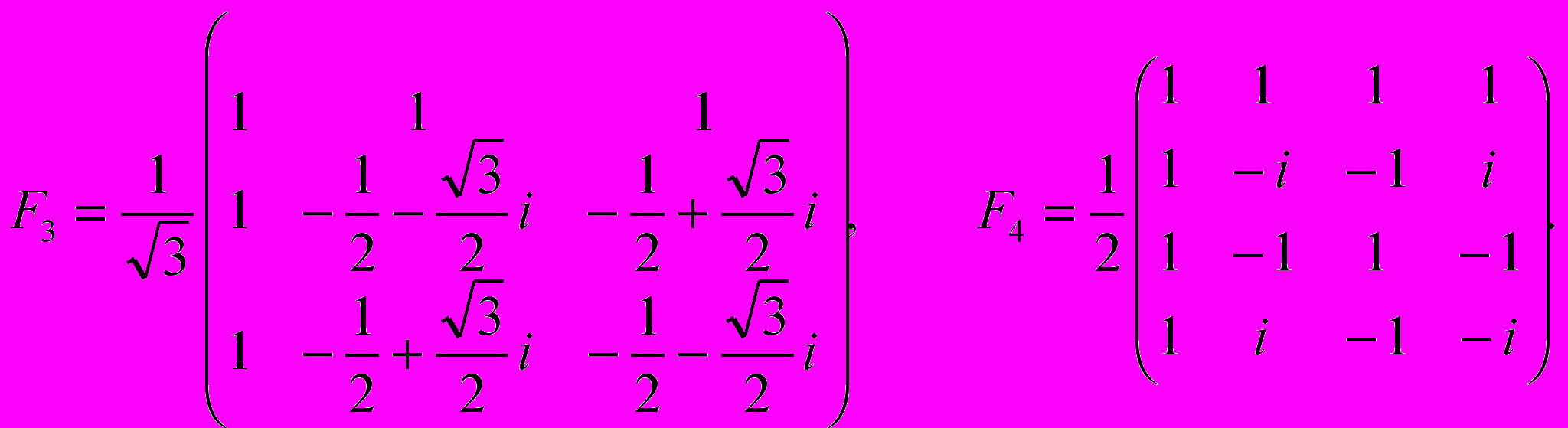



Несмотря на общеизвестность преобразования ДПФ, некоторые стандартные задачи для него имеют незнакомые широкому кругу специалистов свойства. Рассмотрим в качестве примера естественную задачу о нахождении спектра ДПФ при любом 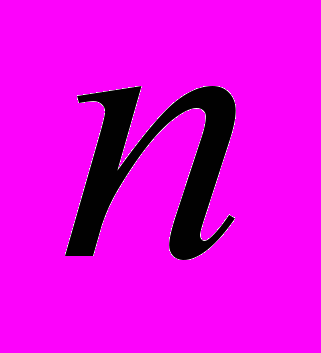. Решение этой задачи отсутствует в основной литературе по преобразованиям Фурье и нетривиально. Известно, что четвертая степень ДПФ есть тождественное преобразование, поэтому собственными значениями могут быть лишь числа 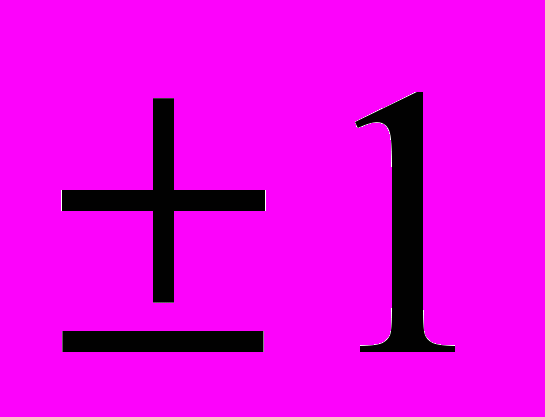, 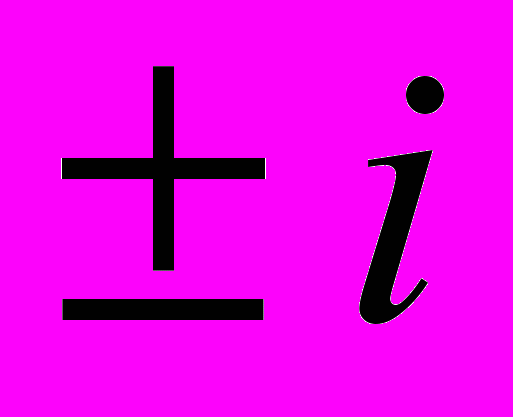. Основная сложность состоит в вычислении кратностей данных чисел. Аналогия с непрерывным преобразованием Фурье, для которого четыре этих значения совершенно равноправны, приводит к весьма правдоподобному предположению, что хотя бы в случае размерности 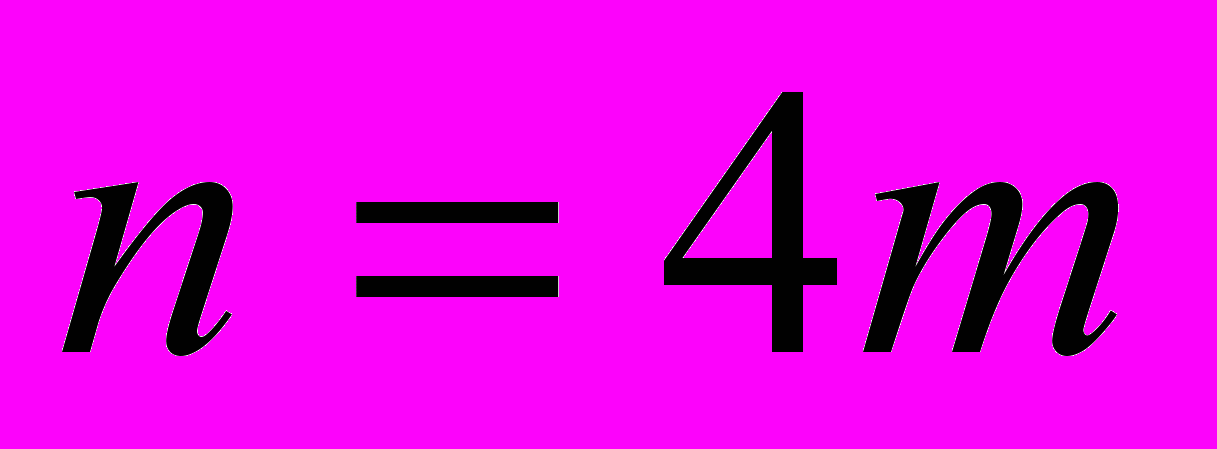собственные значения ДПФ также равноправны, и, следовательно, все имеют кратность m.

Однако вычисления уже при 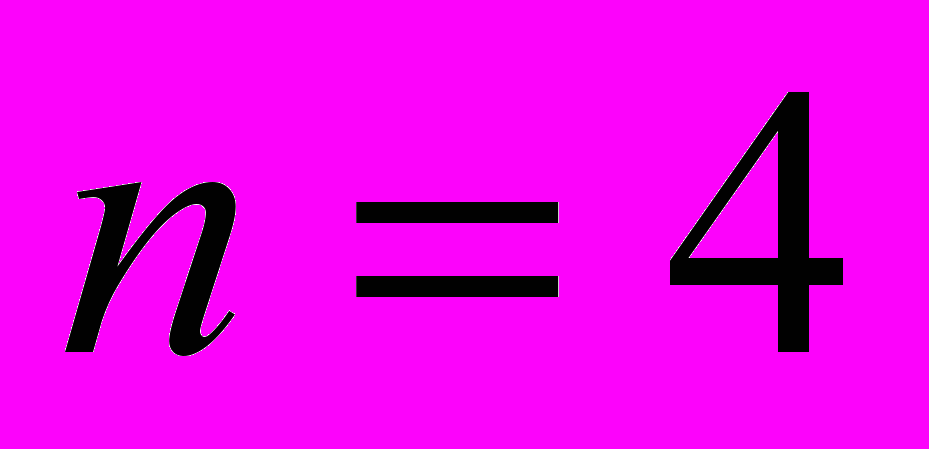опровергают это предположение. В этом случае значения 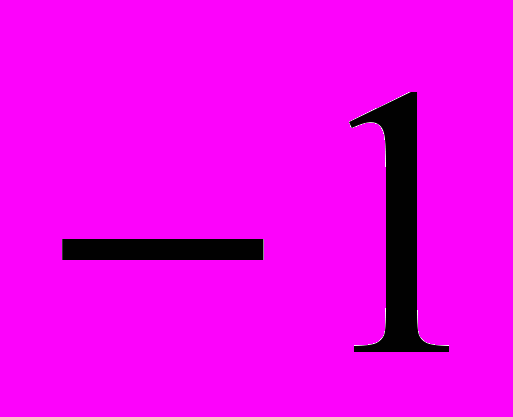, 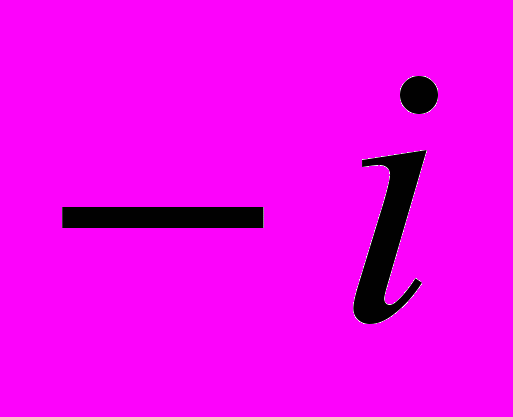являются простыми, значение 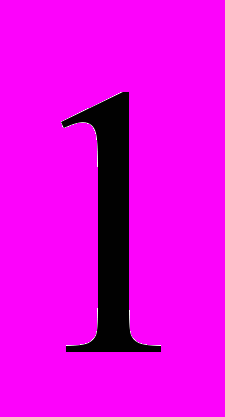имеет кратность 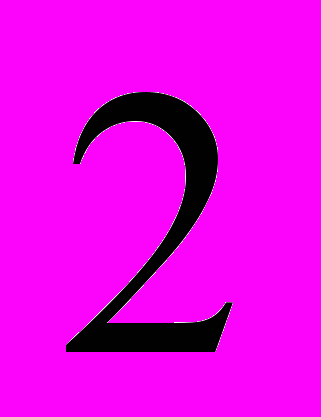, а значение 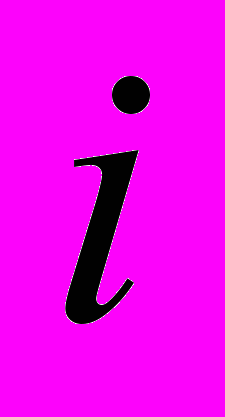вообще отсутствует в спектре! Всё это нарушает симметрию спектра, присущую непрерывному случаю.

Определение. Рассмотрим множество корней степени n из единицы, упорядоченное произвольным способом 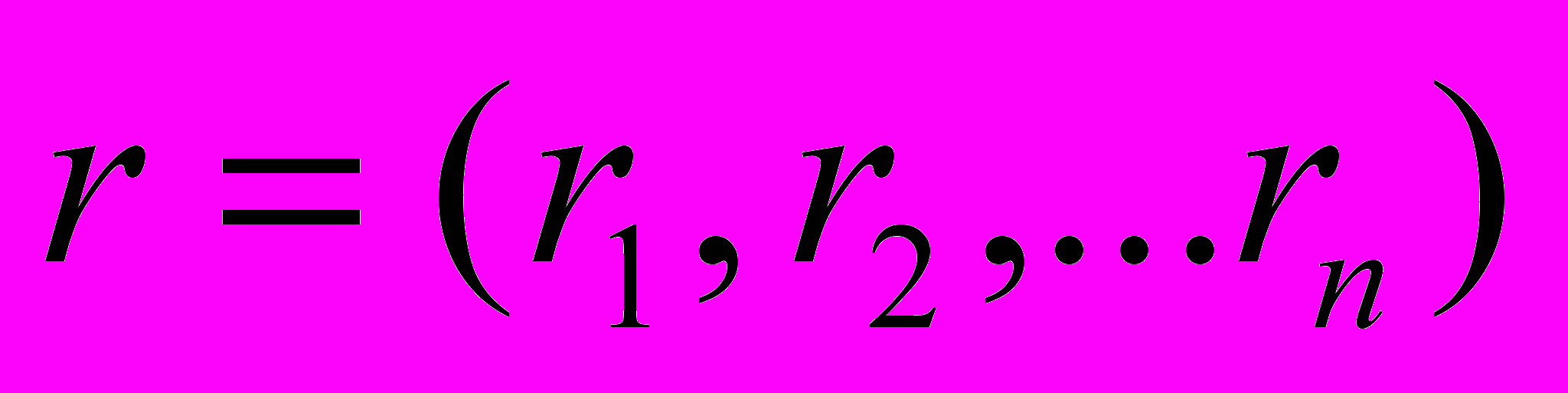. Назовём модифицированным дискретным преобразованием Фурье (МДПФ), построенным по данной перестановке r множества корней из единицы, оператор с матрицей размеров n x n следующего вида


.


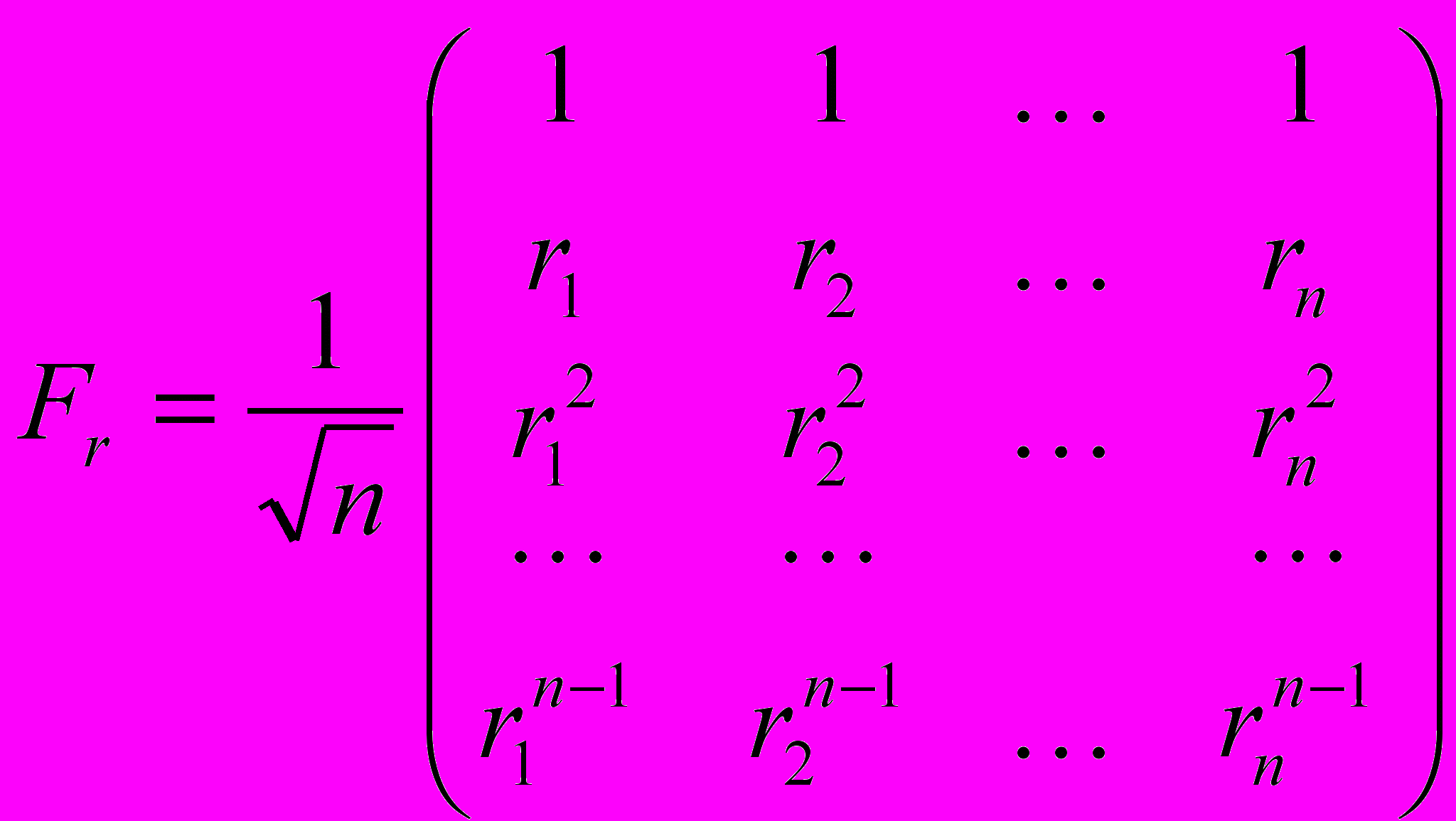Ясно, что в результате получается с точностью до множителя некоторая матрица Вандермонда. Всего при данном n получится n! различных модифицированных преобразований. Обычное классическое ДПФ также входит в этот набор, остальные являются новыми. Так при n=4 получаются 24 различных МДПФ, при n=5 получаются 120 преобразований.

Целью работы является изучение спектральных свойств указанных новых модифицированных преобразований Фурье. В частности, представляют особый интерес преобразования при n=4m с симметричным спектром (а при n=4 с простым), в котором все собственные значения имеют одинаковые кратности. Это не выполняется для обычных ДПФ ни при каких размерностях. Такие преобразования с симметричным спектром являются в определённом смысле более естественными, чем обычное ДПФ, так как они ближе к своему непрерывному аналогу в плане равноправности точек спектра. Не исключено, что такие МДПФ за счёт более простых спектральных свойств могут оказаться полезнее в различных вычислительных приложениях.

ЛИТЕРАТУРА.

1. Блэйхут Р. Быстрые алгоритмы цифровой обработки сигналов. М, Мир, 1989.
   

2. Нуссбаумер Г. Быстрое преобразование Фурье и алгоритмы вычисления свёрток. М., Радио и связь, 1985.

3. Ноден П., Китте К. Алгебраическая алгоритмика. М., Мир, 1999.

4. Черемушкин А.В. Лекции по арифметическим алгоритмам в криптографии. М., МЦНМО, 2002.

5. Schur I. Uber die Gaussschen Summen// Nach. Gessel. Gottingen, Math-Phys Klasse, 1921, P. 147 – 153.

6. Berndt B.C., Evans R.J., Williams K.S. Gauss and Jacobi sums. John Wiley& Sons, 1998.

7. Ситник С.М. Перестановочные аналоги дискретного преобразования Фурье// Труды Международной школы-семинара по геометрии и анализу памяти Н.В.Ефимова, Абрау-Дюрсо, Лиманчик, 2006, С. 156 – 158.

8. Ситник С.М. Модифицированное дискретное преобразование Фурье// Вестник Воронежского института МВД России, 2006, № 7, С. 196 – 201.

9. Ситник С.М., Телкова С.А. Об одном варианте дискретного преобразования Фурье// Чернозёмный альманах научных исследований. Серия «Прикладная математика и информатика», 2006, № 1(2), С. 154 – 159.

10. Ситник С.М. Компьютерный анализ спектральных свойств модифицированных дискретных преобразований Фурье.// Доклады Адыгской (Черкесской) Международной академии наук. -2007, Т. 9, №1, с. 98--103.