Ов государственной власти, органов местного самоуправления, организаций, общественных объединений на основе формирования и использования информационных ресурсов

Вид материала

Документы

Содержание Система кодирования Порядковую систему (последовательая нумерация объектов числами натурального ряда) Фасетная система классификации Естественная форма числа. Отрицание (инверсия). Логическое умножение (конъюнкция) Логическое сложение (дизъюнкция). Логическая функция

Подобный материал:

• Утверждён, 299.54kb.
• Законопроект, 181.46kb.
• Отчёт о деятельности Комитета по делам национальностей и казачества Администрации Волгоградской, 400.7kb.
• Правительство российской федерации распоряжение от 31 августа 2002 г. N 1225-р, 264.28kb.
• Администрация мурманской области постановление от 27 ноября 1996 г. N 428 о порядке, 62.02kb.
• Постановление от 20 марта 2003 г. N 198 о государственной (областной) поддержке молодежных, 90.15kb.
• Задачи и направления работ по созданию единой системы межведомственного взаимодействия, 133.23kb.
• Ставрополь, 2226.38kb.
• Порядок обжалования нормативно-правовых актов и иных решений, принятых органами местного, 25.62kb.
• Согласно ст. 46 Конституции РФ решения и действия (или бездействие) органов государственной, 240.97kb.

Прагматическая мера информации (Харкевича).

Эта мера определяет полезность информации (ценность) для достижения пользователем поставленной цели. Эта мера также величина относительная, обусловленная особенностями использования этой информации в той или иной системе. Ценность информации целесообразно измерять в тех же самых единицах (или близких к ним), в которых измеряется целевая функция.

В экономической системе прагматические свойства (ценность) информации можно определить приростом экономического эффекта функционирования, достигнутым благодаря использованию этой информации для управления системой:

Inb(g)=П(g /b)-П(g),

где Inb(g) -ценность информационного сообщения b для системы управления g,

П(g) -априорный ожидаемый экономический эффект функционирования системы управления g,

П(g /b) - ожидаемый эффект функционирования системы g при условии, что для управления будет использована информация, содержащаяся в сообщении b.


Вопрос №12.

Показатели качества информации.

Возможность и эффективность использования информации обусловливаются такими основными ее потребительскими показателями качества, как:

Репрезентативность информации связана с правильностью ее отбора и формирования в целях адекватного отражения свойств объекта.

Содержательность информации отражает семантическую емкость, равную отношению количества семантической информации в сообщении к объему обрабатываемых данных, т.е. C=Ic/Vд.

Достаточность (полнота) информации отражает полноту информации, т. е. информация содержит минимальный, но устойчивый для принятия правильного решения набор показателей.

Доступность информации обеспечивается выполнением соответствующих процедур ее получения и преобразования.

Актуальность информации определяется степенью сохранения ценности информации для управления в момент ее использования и зависит от динамики изменения ее характеристик и от интервала времени, прошедшего с момента возникновения данной информации.

Своевременность информации означает ее поступление не позже заранее назначенного момента времени, согласованного с временем решения поставленной задачи.

Точность информации определяется степенью близости получаемой информации к реальному состоянию объекта, процесса, явления и т.п.

Достоверность информации определяется ее свойством отражать реально существующие объекты с необходимой точностью.

Устойчивость информации отражает ее способность реагировать на изменения исходных данных без нарушения необходимой точности.


Вопрос №13.

Классификация и кодирование информации.

Классификация - система распределения объектов (предметов, явлений, процессов, понятий) по классам в соответствии с определенным признаком. Классификация объектов - это процедура группировки на качественном уровне, направленная на выделение однородных свойств. Применительно к информации как к объекту классификации выделенные классы называют информационными объектами. Свойства информационных объектов определяются информационными параметрами (реквизитами).

Реквизит – логически неделимый информационный элемент, описывающий свойства объекта.

Для полноты охвата объектов и однозначности реквизитов разрабатываются классификатор.

Классификатор – систематизированный свод наименований и кодов классификационных группировок.

Методы классификации объекта:

1. 
   Иерархический (Windows)
   
2. Фасетный (штрих-коды)
   
3. Дескрипторный (Интернет)
   

Система кодирования применяется для замены названия объекта на условное обозначение (код) в целях обеспечения удобной и более эффективной обработки информации.

Система кодирования - совокупность правил кодового обозначения объектов.

Процедура присвоения объекту кодового обозначения называется кодированием. Можно выделить две группы методов, используемых в системе кодирования, которые образуют:

• классификационную систему кодирования, ориентированную на проведение предварительной классификации объектов либо на основе иерархической системы, либо на основе фасетной системы;
  
• регистрационную систему кодирования, не требующую предварительной классификации объектов.
  

Классификационное кодирование применяется после проведения классификации объектов. Различают последовательное (для иерархической системы) и параллельное ( для фасетной классификации) кодирование.

Регистрационное кодирование используется для однозначной идентификации объектов и не требует предварительной классификации объектов и подразделяется на:

• Порядковую систему (последовательая нумерация объектов числами натурального ряда)
  
• Серийно-порядковую систему ( предварительное выделение групп объектов в серии)
  

Признаки классификации информации:

Место возникновения информации: входная, выходная, внутренняя, внешняя;

1. 
   Стадия обработки: первичная, вторичная, промежуточная, результативная;
   
2. Способ отображения: текстовый, графический;
   
3. Стабильность: постоянная, переменная;
   
4. Функции управления: плановые, нормативно-справочные, учетные, оперативные.
   

Вопрос №14.

Иерархическая и фасетная системы классификации

Иерархическая система классификации строится следующим образом:

• исходное множество элементов составляет 0-й уровень и делится в зависимости от выбранного классификационного признака на классы (группировки), которые образуют 1-й уровень;
  
• каждый класс 1-го уровня в соответствии со своим, характерным для него классификационным признаком делится на подклассы, которые образуют 2-й уровень;
  
• каждый класс 2-го уровня аналогично делится на группы, которые образуют 3-й уровень и т.д.
  

Достоинства иерархической системы классификации:

• простота построения;
  
• использование независимых классификационных признаков в различных ветвях иерархической структуры. Недостатки иерархической системы классификации;
  
• жесткая структура, которая приводит к сложности внесения изменений, так как приходится перераспределять все классификационные группировки;
  
• невозможность группировать объекты по заранее не предусмотренным сочетаниям признаков.
  

Фасетная система классификации в отличие от иерархической позволяет выбирать признаки классификации независимо друг от друга. Признаки классификации называются фасетами(facet - рамка). Каждый фасет содержит совокупность однородных значений данного классификационного признака. Причем значения в фасете могут располагаться в произвольном порядке хотя предпочтительнее их упорядочение.



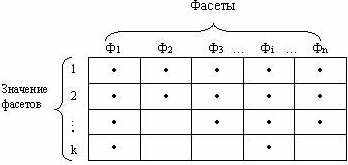
Достоинства фасетной системы классификации:

• возможность создания большой емкости классификации, т.е. использования большого числа признаков классификации и их значений для создания группировок;
  
• возможность простой модификации всей системы классификации без изменения структуры существующих группировок.
  

Недостатком фасетной системы классификации является сложность ее построения, так как необходимо учитывать все многообразие классификационных признаков.


Вопрос №15.

Позиционные системы счисления

Система счисления - это способ наименования и изображения чисел с помощью символов, имеющих определенные количественные значения. В зависимости от способа изображения чисел системы счисления делятся на позиционные и непозиционные.

В позиционной системе счисления количественное значение каждой цифры зависит от ее места (позиции) в числе (15¹51).

Число единиц какого-либо разряда, объединяемых в единицу более старшего разряда, называют основанием позиционной системы счисления. Если количество таких цифр равно P, то система счисления называется P-ичной. Основание системы счисления совпадает с количеством цифр, используемых для записи чисел в этой системе счисления.

Запись произвольного числа Х в P-ичной позиционной системе счисления основывается на представлении этого числа в виде многочлена



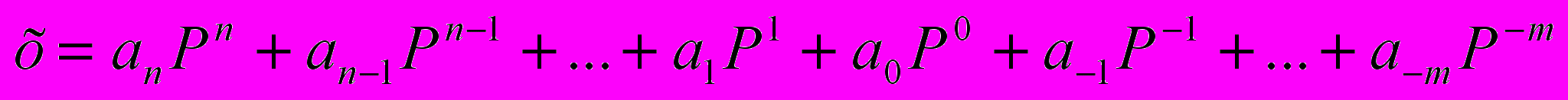
В современных компьютерах используются позиционные системы счисления с основаниями 2, 8, 10 и 16, которые соответственно называются двоичная, восьмеричная, десятичная и шестнадцатеричная системы счисления.

Число в позиционной системе счисления представляется в виде разрядов. Крайняя слева цифра называется цифрой старшего разряда, крайняя справа – цифрой младшего разряда.

Число в позиционной системе счисления представляется степенным рядом

,

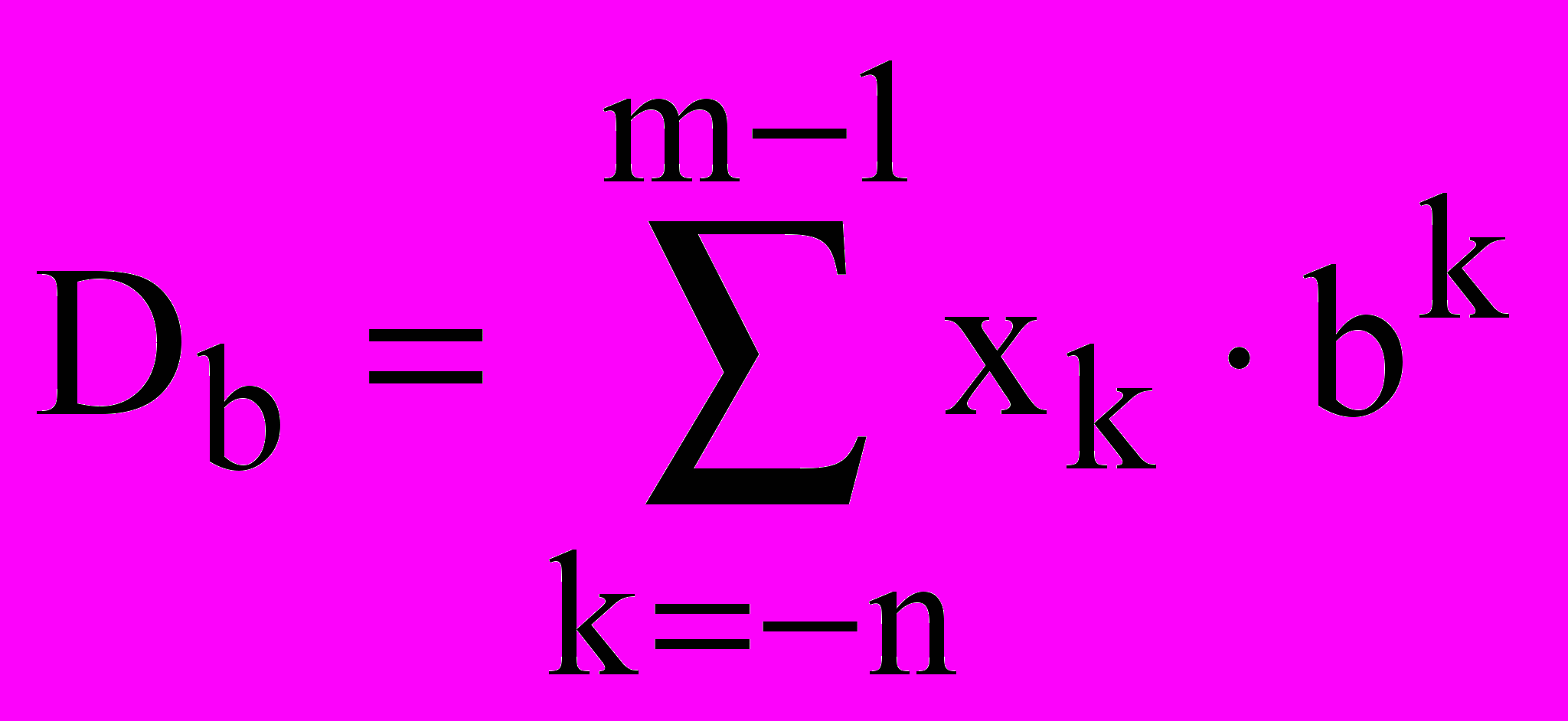где xk – любое число из алфавита системы (набор символов) с основанием b; m и n –число разрядов соответственно для целой и дробной части числа.


Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими многочленами. При этом нужно только пользоваться теми таблицами сложения и умножения, которые соответствуют данному основанию P системы счисления.


Вопрос №16.

Перевод чисел из одной системы счисления в другую.

С помощью него осуществляются арифметические действия в компьютере, адресация файлов и другие операции.

Перевод чисел из восьмеричной системы счисления в двоичную и наоборот переводится по триадам. При переводе из восьмеричной системы в двоичную каждая цифра заменяется триадой. При переводе из двоичной системы в восьмеричную число разбивается на триады справа налево, недостающие цифры слева дополняются нулями. После этого, каждую триаду заменяют восьмеричной цифрой.

Перевод чисел из шестнадцатеричной системы счисления в двоичную и наоборот переводится по тетрадам. При переводе из шестнадцатеричной системы в двоичную каждая цифра заменяется тетрадой. При переводе из двоичной системы в шестнадцатеричную число разбивается на тетрады справа налево, недостающие цифры слева дополняются нулями. После этого, каждую тетраду заменяют шестнадцатеричной цифрой

Перевод чисел из восьмеричной системы счисления в шестнадцатиричную и обратно осуществляется с помощью вспомогательного двоичного кода числа.

Преобразования из десятичной системы счисления в двоичную, восьмеричную и шестнадцатиричную выполняются на основе перевода целого и дробного числа из десятичной системы путем:

1. 
   метод умножения
   

Последовательно делить число и получаемые целые части на основание системы счисления до тех пор, пока целая часть не станет меньше основания счисления. Полученные остатки от деления, представленные цифрами из нового счисления, образуют код.

2. Метод умножения
   

При переводе дробного числа из десятичной системы счисления в другие нужно последовательно умножать исходное число и получаемые дробные части произведения на основании новой системы счисления до тех пор, пока дробная часть произведения не станет равна нулю или не будет получено требуемое по условию количество разрядов. Полученные целые части являются разрядами числа в новой системе и их необходимо представить цифрами алфавита новой системы счисления.

Пример: 0,37510→ O,Y2 0, 375*2= 0, 750


0, 75*2= 1, 50 => 0,37510=0,0112


Вопрос №17.

Формы представления двоичных чисел в персональном компьютере

Двоичные коды чисел в ПК могут представляться в двух формах: с плавающей или фиксированной запятой.

Представление чисел в формате с фиксированной запятой называется естественной формой числа, а с плавающей запятой – нормальной формой числа. под эти форматы отводится определенное количество разрядов: 16, 32 и т. д.

Естественная форма числа. Для представления чисел в этом формате следующие правила: запятая в строгоопределенном месте, отделяющем целую часть от дробной. Наиболее часто такая форма используется для представления целых чисел.

Во всех форматах знак числа помещается в старший разряд, кодируется как 0 для положительного числа либо как 1 для отрицательного.

Достатком таких форматов является ограничение кодированного числа, т. к. число разрядов в числе ограниченно.

Нормальная форма чисел – представление чисел в формате с плавающей запятой. Этот формат используется для расширения диапазона координируемых чисел. Любое число в этом формате можно представить виде

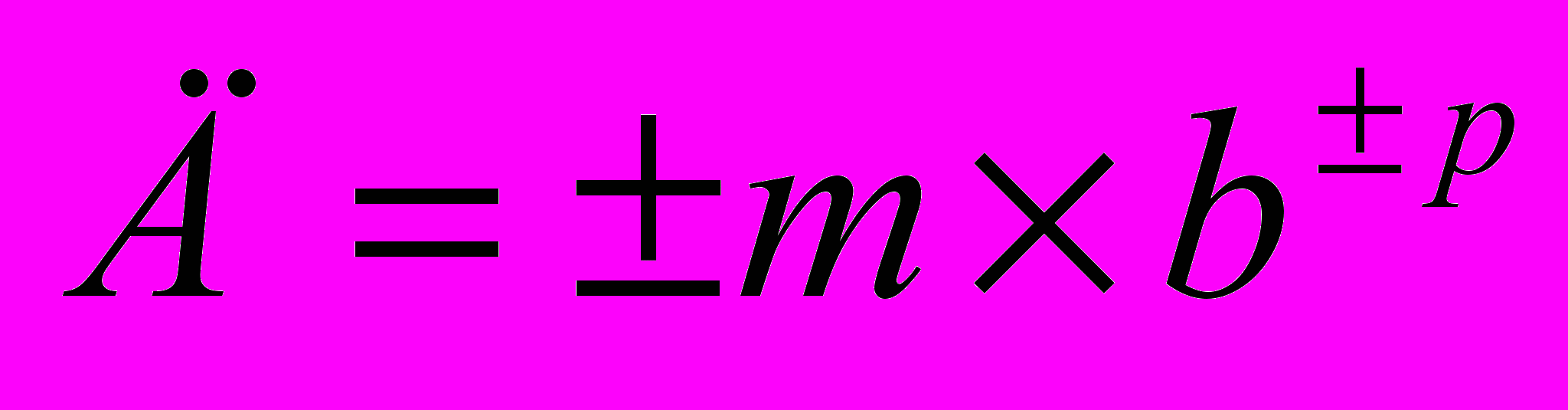, где m – мантисса

b – основание системы счисления

p – порядок

Все эти величины кодируются двоичными числами без увеличения значения. Для кодирования знака мантиссы и знака порядка отводится 2 старших разряда в формате числа. Старший разряд сожержит знак мантиссы.

Для представления отрицательных чисел используется прямой код числа. Обратный и дополнительный коды используются для замены операции вычитания операцией сложения. Сущность этих кодов: вычитаемое число x как отрицательное число представляется виде дополнения до некоторой константы с такой, что (с-х)=0. Обратный и допольнительный коды отличаются выбором этой константы. Для дополнительного кода отрицательное число z=-x=(10n-x)-10n представим как z=-x=(10n-1-x)-10n+1, где x>; n – величина разрядной сетки, 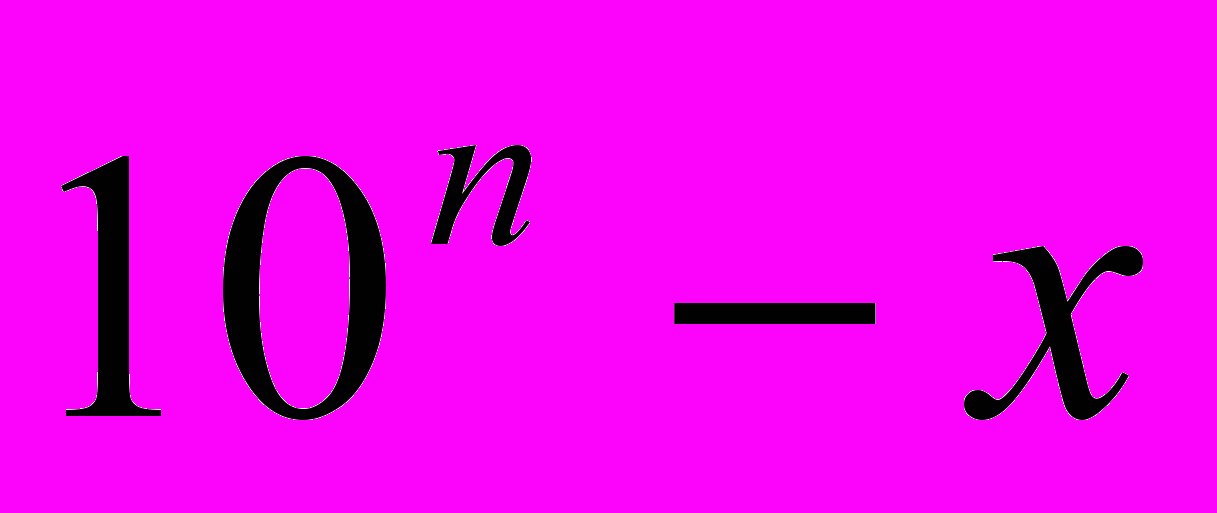- дополнительный код числа. Для обратного кода отрицательное число z представим как равенство, где z<0, x>, n – обратный код числа.


Вопрос №18.

Машинные коды чисел.

Положительное число в прямом, обратном, дополнительном кодах одинаково.

Прямой код отрицательных и положительных чисел имеет различие только в знаковом разряде. Модуль числа не меняется.

Обратный код отрицательного числа получается путем инверсии прямого кода, т. е. замены 1 на 0 и всех 0 на 1.

Дополнительный код получается из обратного прибавлением 1 к младшему разряду. Перенос 1 в знаковый разряд не учитывается.

Дополнительный код отрицательного числа получается из прямого кода заменой всех 1 на 0 и всех 0 на 1, кроме единицы самого младшего разряда и следующих за ней нулей.

В компьютере числа в естественной записи хранятся ввиде дополнительного кода, а числа в нормальной форме – в прямом коде.

Обратный код применяется для получения дополнительного кода.


Вопрос № 19

Варианты представления информации в персональном компьютере

В настоящее время большая часть персональных компьютеров в мире занята обработкой текстовой информации. При вводе текстовой информации происходит её двоичное кодирование, символ преобразуется в двоичный код. В процессе вывода на экран производится обратный процесс – декодирование.

В традиционных кодировках для кодировки одного символа используется 8 бит, что позволяет закодировать 256 различных символов.

В качестве международного стандарта присвоения символу определенного числового кода принята кодовая таблица ASCII.

Существует несколько различных кодировок кириллицы (КОИ-8, Windows, MS-DOS, Macintosh, ISO).

В концу 90-ых появился международный стандарт Unicode, который использует 2 байта для размещения кода символа, с его помощью можно закодировать 65 536 различных символов.

Графические изображения, хранящиеся в аналоговой (непрервывной) форме на бумаге, фото- и кинопленке, могут быть преобразованы в цифровой компьютерный формат путем пространственной дискретизации. Это реализуется путем сканирования, результатом которого является растровое изображение. Оно состоит из отдельных точек (пикселей). Качество растрового изображения определяется его разрешением и используемой палитрой цветов.

В аналоговой форме звук представляет собой волну с непрерывно меняющейся амплитудой и частотой. При преобразовании звука в цифровую дискретную форму производится временная дискретизация, при которой в определенные моменты времени амплитуда звуковой волны измеряется и квантируется, т. е. ей присваивается значение из некоторого фиксированного набора. Это происходит с помощью аналого-цифрового преобразователя, размещенного на звуковой плате.


Вопрос №20

Понятие кодов ASCII

В качестве международного стандарта принята кодовая таблица ASCII (American Standard Code for Information Interchange - Американский стандартный код для обмена информацией).

ASCII – кодировка, используемая для представления в компьютере текстовых данных. 7-ми или 8-битная таблица ASCII позволяет закодировать 128 или 256 разных знаков.

Коды в таблице распределяются следующим образом.

От 0 до 32 - определенные операции – управляющие коды, соответствуют функциональным клавишам.

Коды с 33 по 127 являются интернациональными и соответствуют символам латинского алфавита, цифрам, знакам арифметических операций и знакам препинания.

Коды 128-255 являются национальными, т. е. в национальных кодировках одному и тому же коду соответствуют разные символы.


Вопрос №21.

Понятие математической логики

Математическая логика изучает вопросы применения математических методов для решения логических задач и построения логических схем, которые лежат в основе работы любого компьютера. Суждения в математической логике называют высказываниями или логическими выражениями. Подобно тому, как для описания действий над переменными был разработан раздел математики алгебра, так и для обработки логических выражений в математической логике была создана алгебра высказываний, или алгебра логики.

Алгебра логики - это раздел математической логики, значениявсех элементов (функций и аргументов) которой определены в двухэлементном множестве: 0 и 1. Алгебра логики оперирует с логическими высказываниями.

Высказывание - это любое предложение, в отношении которого имеет смысл утверждение о его истинности или ложности. При этом считается, что высказывание удовлетворяет закону исключенного третьего, т.е. каждое высказывание или истинно, или ложно и не может быть одновременно и истинным, и ложным.

В алгебре логики все высказывания обозначают буквами а, b, с и т.д., и в дальнейшем над ними можно производить любые действия, предусмотренные данной алгеброй.

Основные законы:

1. Закон идемпотентности:

а+а=а;

а*а=а

2. Закон коммутативности

a+b=b+a

a*b=b*a

3. Закон ассоциативности

a+(b+c)=(a+b)+c

4. Закон дистрибутивности

a*(b+c)=ab+ac

a+b*c=(a+c)*(a+c)

5. Закон двойного обращения



6. Закон де Моргана



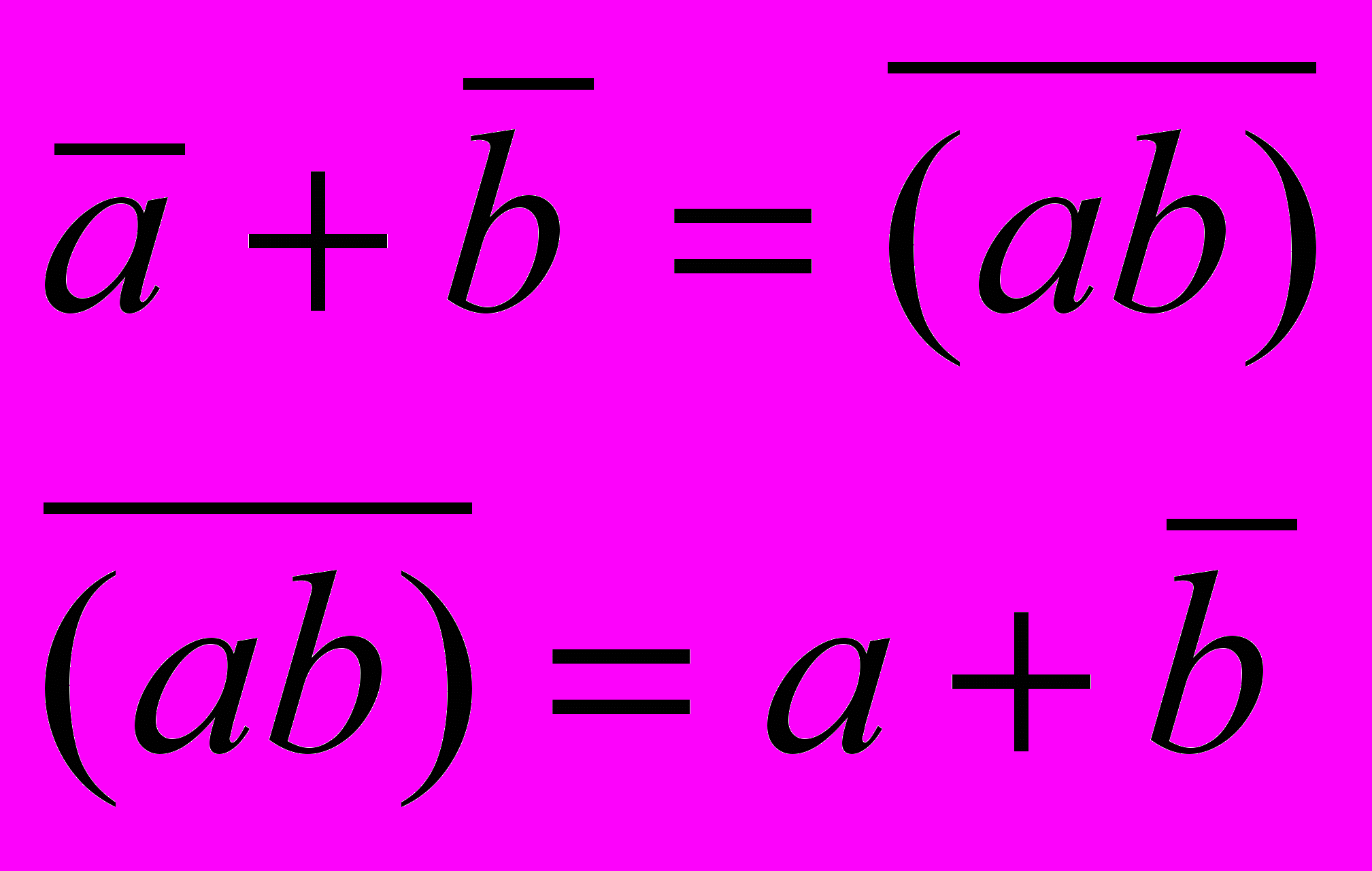
7. Закон для констант




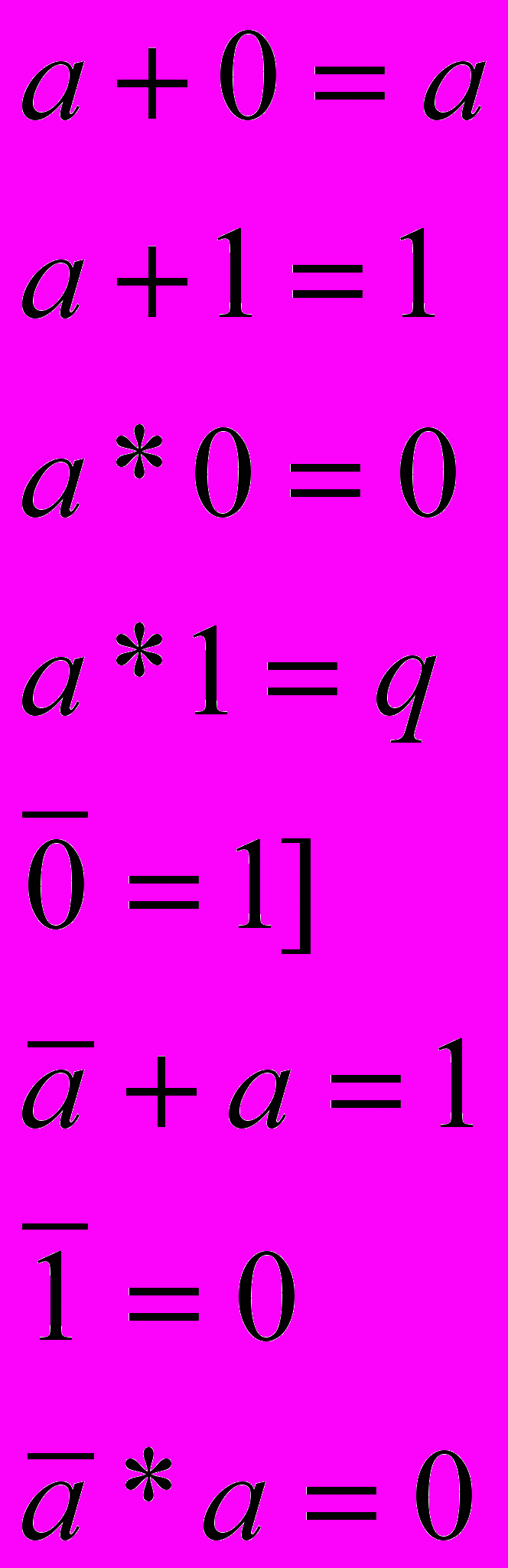
Вопрос №22.

Особенности операций и функций в алгебре логики.

Логическая операция – способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний. Правила выполнения операций в алгебре логики определяются рядом аксиом, теорем и следствий. Основные операции алгебры высказываний:

1. 
   Отрицание (инверсия). Применяется к одному высказыванию и меняет его на противоположное. Отрицание логического высказывания А обозначается как .
   

А
0	1
1	0

Отрицая верное высказывание, мы говорим ложь; отрицая неверное высказывание, мы говорим истину.

2. Логическое умножение (конъюнкция) – ставит в соотетствие двум простым высказываниям составное, являющееся истинным тогда и только тогда, когда оба исходных высказываний истинны.
   

   A	B	AÙB
   0	0	0
   0	1	0
   1	0	0
   1	1	1

3. Логическое сложение (дизъюнкция). Ставит в соответствие двум простым высказываниям составное, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.
   

A	B	AÚB
0	0	0
0	1	1
1	0	1
1	1	1

Логическая функция – это функция, в которой переменные принимают только два значения: логическая единица или логический ноль. Любая логическая функция может быть задана с помощью таблицы истинности, в левой части которой записывается набор аргументов, а в правой части – соответствующие значения логической функции. При построении таблицы истинности необходимо учитывать порядок выполнения логических операций. Операции в логическом выражении выполняются слева направо с учетом скобок в следующем порядке:

1. инверсия;

2. конъюнкция;

3. дизъюнкция;

4. импликация и эквивалентность.


Вопрос №23.