Курсовая работа по дисциплине «Теория вычислительных процессов»

Вид материала

Курсовая

Содержание Краткая теория по теме курсовой работы Заключение. Список используемой литературы. Краткая теория по теме курсовой работы

Подобный материал:

• Курсовая работа по дисциплине «Экономическая теория», 226.61kb.
• Рабочая программа дисциплины теория вычислительных процессов и структур для студентов, 164.28kb.
• Методические рекомендации по выполнению курсовых работ по дисциплине «Экономическая, 193.84kb.
• Методические рекомендации по написанию курсовой работы по дисциплине «экономическая, 170.15kb.
• Курсовая работа по дисциплине Экономическая теория на тему: Теория стоимости в экономической, 400.97kb.
• Методические рекомендации для выполнения курсовой работы по дисциплине «Экономическая, 546.07kb.
• Курсовая работа по дисциплине «Экономическая теория», 274kb.
• Курсовая работа по дисциплине "Теория автоматизированного управления", 106.5kb.
• Курсовая работа по дисциплине «Экономическая теория» на тему: Антимонопольное регулирование:, 499.27kb.
• Курсовая работа По дисциплине «Экономическая теория» Тема: «Налоги. Их функции и роль, 11.07kb.

Государственный комитет Российской Федерации по телекоммуникациям

Сибирский государственный университет

телекоммуникаций и информатики


КУРСОВАЯ РАБОТА


По дисциплине « Теория вычислительных процессов»


Вариант №4


Работу выполнил

студент группы ПДВ-01

Карецкая Ольга Павловна


Работу проверил

Моренкова Ольга Ильинична


Новосибирск 2012

Задание к курсовой работе

1. Написать программу решения задачи, номер которой совпадает с Вашими двумя последними цифрами пароля (использовать язык СИ или Паскаль).
   
2. Составить и исследовать ССП в линейной и графовой формах.
   
3. Построить и исследовать инварианты и ограничения цикла(ов).
   
4. Составить схему программы в виде сети Петри и осуществить анализ ее свойств на основе дерева достижимости.
   

Содержание

Краткая теория по теме курсовой работы

1. Программная реализация.
   
2. ССП и результаты ее исследования:
   
   1. Линейная форма стандартной схемы.
      
   2. Графовая форма стандартной схемы
      
   3. Исследование ССП.
      
3. Построение и исследование инвариантов и ограничений циклов.
   
   1. Построение цикла с помощью инварианта.
      
   2. Исследование инвариантов и ограничений цикла.
      
4. Схема программы в виде сети Петри. Анализ ее свойств на основе дерева достижимости.
   
   1. Схема программы в виде сети Петри.
      
   2. Дерево достижимости.
      
   3. Анализ свойств сетей Петри на основе дерева достижимости.
      

Заключение.

Список используемой литературы.

Краткая теория по теме курсовой работы

1. Программная реализация.
   

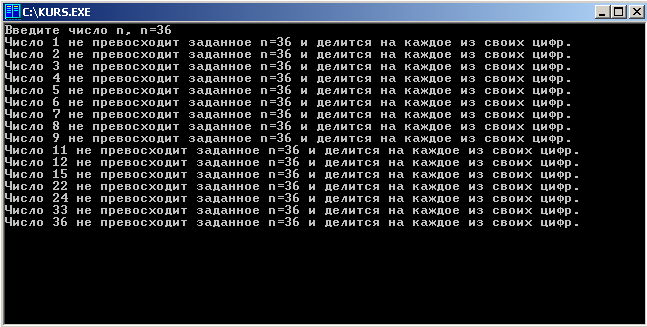
Найти все натуральные числа, не превосходящие заданного N и делящиеся на каждую из своих цифр.

Задание 1.

Написать программу решения задачи, номер которой совпадает с Вашими двумя последними цифрами пароля (использован язык Паскаль).

program kurs_v04;

uses crt;

Label 1;

var i,j,n,n1,d:integer;

s: string;

Begin

ClrScr;

Write('Введите число n, n=');

Read(n);

for i:=1 to n do

begin

str(i,s);

For j:=1 to length(s) do

begin

val(s[j],n1,d);

if n1=0 then goto 1;

If i mod n1<>0 then goto 1;

end;

Writeln('Число ',i,' не превосходит заданное n=',n,' и делится на каждое из своих цифр.' );

1: end;

Readkey;

end.

Результат работы программы:




2. ССП и результаты ее исследования:

1. Линейная форма стандартной схемы.
   

Составить и исследовать ССП в линейной и графовой формах.

ССП в линейной форме:

0: start(y, n) goto 1

1: if P(i,n)=0 goto 2 else goto 9

2: s=i goto 3

3: if P(j, F(s))=0 goto 4 else 7

4: n1=s[j] goto5

5: if F(i, n1)=0 goto 6 else 8

6: j=j+1 goto 3

7: r=i goto 8

8: i=i+1 goto 1

9: stop(i)

2. Графовая форма стандартной схемы
   

ССП в графовой форме


start(y, n)

0.





1.





s=i

2.





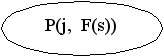
3.

r=i

7.

n1=s[j]

i=i+1

4.



8.





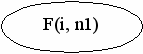
5.

j=j+1



6.

stop(i)

9.

3. Исследование ССП.
   

2. Построение и исследование инвариантов и ограничений циклов.
   
   1. Построение цикла с помощью инварианта.
      
   2. Исследование инвариантов и ограничений цикла.
      
3. Схема программы в виде сети Петри. Анализ ее свойств на основе дерева достижимости.
   
   1. Схема программы в виде сети Петри.
      
   2. Дерево достижимости.
      
   3. Анализ свойств сетей Петри на основе дерева достижимости.
      

Заключение.

Список используемой литературы.