Geum.ru

Рекомендации по составлению заданий для олимпиады по математике

Вид материалаДокументы

Содержание


Рекомендации по составлению заданий для олимпиады по математике
Требования к выполнению и оформлению работы
Критерии оценки олимпиадных задач
Возможная шкала оценивания заданий.
Максимальное число баллов за задание
Примерные задачи для школьных олимпиад
5. Задача Безу.
Подобный материал:

ШКОЛЬНАЯ МАТЕМАТИЧЕСКАЯ ОЛИМПИАДА


Подбор заданий для олимпиады по математике является важным организационным моментом.

Для школьной олимпиады следует подбирать задачи в рамках государственного образовательного стандарта, делая акцент на интересные, разнообразные задания творческого характера, которые были бы одновременно и поучительны, и имели бы практическое применение. Кроме того, задания должны способствовать раскрытию творческого потенциала участника олимпиады, расширять его кругозор, развивать интерес к изучению предмета, выявлять одаренных, творчески мыслящих школьников и учащихся, имеющих нестандартное мышление.


Рекомендации по составлению заданий для олимпиады по математике

  1. Задания школьной олимпиады должны быть разного уровня сложности (уровень трудности первых двух задач составляет 10%-30%, последних – 80%-95%). Это позволит, с одной стороны, провести отбор учащихся для участия в городской олимпиаде, а с другой, - соблюсти принцип дифференциации обучения. Кроме того, в «олимпиадный вариант» следует включить и утешительную задачу для слабого участника, и трудную – для сильного.
  2. Задачи, в том числе и невысокого уровня трудности, должны содержать "изюминку", благодаря которой более сильный ученик решит ее быстрее и рациональнее.
  3. Включаемые задания должны быть из разных разделов курса математики, но, как правило, из тех, которые изучались в данном и предыдущем учебном году.
  4. Следует включать также логические задачи, задачи на применение принципа Дирихле, инвариантов, графов, задачи на раскраски, переливания, взвешивания, уравнения в целых числах и т.д. Это способствует и обогащению знаниевого запаса школьников, и развитию познавательного интереса и логического мышления учащихся, а также выявлению учащихся, мыслящих нестандартно.
  5. Предпочтительнее предлагать практико-ориентированые задания. Кроме того, задачи должны быть лишены официозной "сухости", и нести, к примеру, элемент занимательности.
  6. Количество заданий должно быть достаточно большим и значительно превышать то количество, которое может решить даже самый сильный ученик за отведенные часы (в 8-ых классах – 1,5-2 ч; 9 – 11-ых – 2-3ч). Такая организация заданий позволит развивать тактические умения учащихся для того, чтобы, оценив сложность заданий, правильно распределить акценты при выборе очередности их решения.
  7. Следует избегать заданий с длительными выкладками, на использование трудно запоминающихся формул, справочных таблиц. Решение задач не должно быть громоздким, а реализация его – поглощать много времени.


Требования к выполнению и оформлению работы


Требования к выполнению и оформлению работы излагаются в Положении о проведении школьной математической олимпиады и соответствуют требованиям к оформлению письменной работы по математике.


Критерии оценки олимпиадных задач


Критерии оценки олимпиадных задач вырабатываются членами жюри. «Вес» задачи определяется в зависимости от уровня ее трудности для данного состава участников. Более трудные задачи оцениваются большим количеством баллов.

Обычно правильное и полное решение задачи оценивается указанными в условии баллами. За погрешности и ошибки, допущенные при выполнении задания, с каждой задачи снимается определенное количество баллов, зависящее от характера допущенных ошибок.

К недочетам следует отнести описки, негрубые вычислительные ошибки, не влияющие на правильность дальнейшего хода рассуждений.

Некоторые ошибки, которые можно отнести к существенным:
  • нет обоснования отдельных логических шагов при решении задачи;
  • в записях математических выражений отсутствует математическая культура;
  • наличие недвусмысленности в ходе записи решений;
  • нет анализа правильности полученного результата;
  • грубые вычислительные ошибки;
  • ошибки, допущенные при преобразованиях.

Верным можно считать решение, содержащее
  • правильную последовательность его шагов,
  • верное обоснование всех ключевых моментов,
  • безошибочные чертежи, рисунки, схемы,
  • правильно выполненные вычисления и преобразования и т.д.

Решение считается неполным, если оно:
  • содержит основные идеи, но не доведено до конца;
  • при верной общей схеме рассуждений содержит пробелы, т.е. явно или скрыто опирается на недоказанные утверждения, которые нельзя счесть известными или очевидными.


Возможная шкала оценивания заданий.


Качество

выполнения

задания
Максимально возможное число баллов за задание

10
7
5
3

Верное решение

10
7
5
3

Верное решение с недочетами
9
6
4
2,5

Решение верное в основных чертах, но неполное или содержит непринципиальные ошибки
6 – 8
4 – 5
3
2

Решение в целом неверное, но содержит более или менее существенное продвижение в верном направлении
1 – 5
1 – 3
1 – 2
1

Решение неверно или отсутствует
0
0
0
0


Другой подход к оценке заданий заключается в том, что каждое задание оценивается значками +, 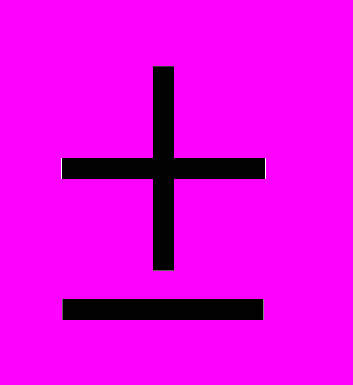, , 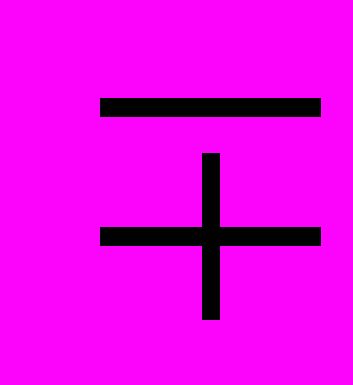-, 0.


Качество выполнения задания
Оценка за задание
Максимальное число баллов за задание

10
7
5
3

Верное решение
+
10
7
5
3

Верное решение с недочетом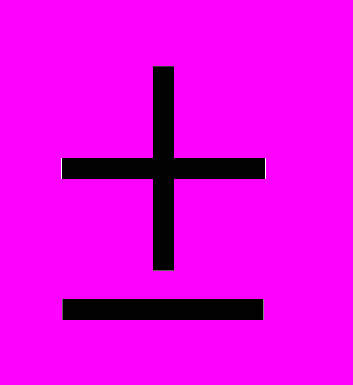


9
6
4
2 – 2,5

Найдена идея решения, но оно не доведено до конца или выполнена лишь часть задания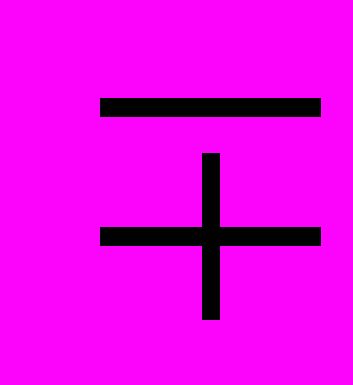


3 – 8
3 – 5
2 – 3
1,5 – 2

Решение неверное, но ученик искал его, хотя и не нашел
-
1 – 2

1 – 2
1
1

Отсутствие решения
0
0
0
0
0


Возможны и другие подходы к оцениванию заданий.


Примерные задачи для школьных олимпиад


8 класс
  1. Вычислите:

.
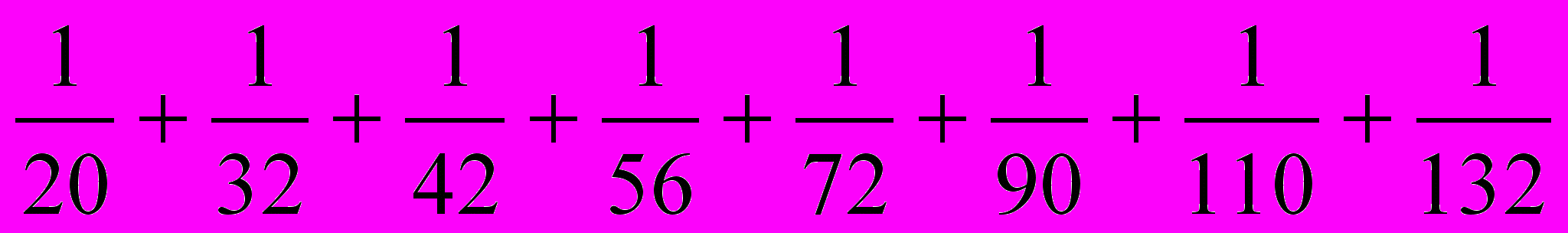  1. Решите уравнение, содержащее 2004 пары скобок:

х-(х-(х-…-(х-(х-1001))..))=1003.
  1. Постройте график функции:

у = .
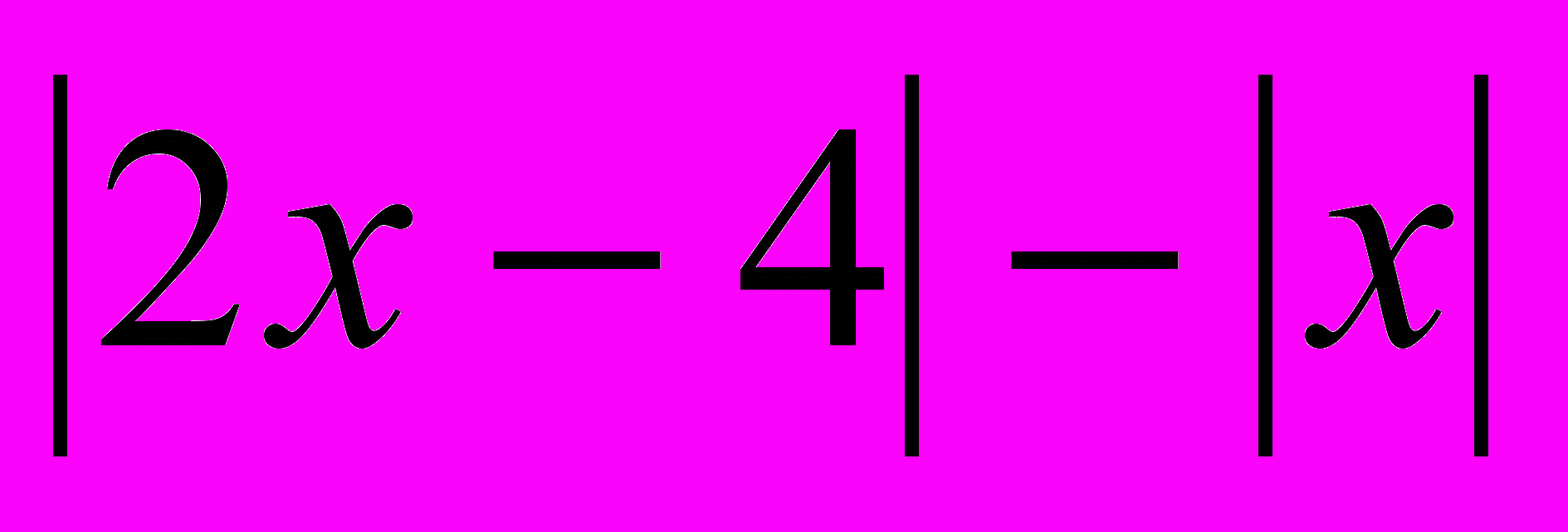  1. Л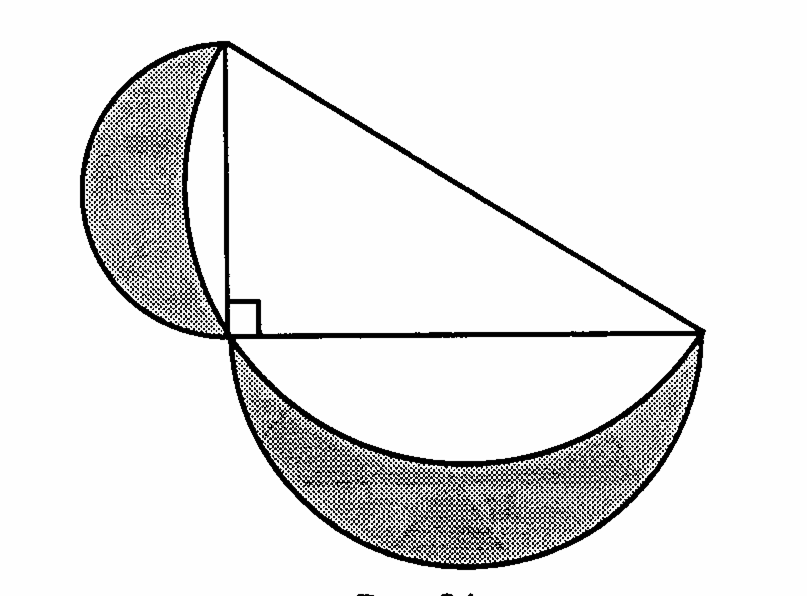уночки Гиппократа. На катетах и гипотенузе прямоугольного треугольника построили полуокружности. Докажите, что сумма площадей заштрихованных луночек равна площади данного треугольника.



5. Задача Безу. Некто купил лошадь и спустя некоторое время продал ее за 24 пистоля. При этой продаже он теряет столько процентов, сколько стоила его лошадь. За какую цену он ее купил?

6. Остап Бендер купил 4 новых колеса для «Антилопы Гну». Известно, что передние колеса этого автомобиля изнашиваются через 30 тыс. км, а задние – через 20 тыс. км. Какое наибольшее расстояние можно проехать на этом автомобиле, если Адам Козлевич догадается вовремя поменять передние колеса с задними?

7. Пять школьников приехали из пяти различных городов на областную математическую олимпиаду. «Откуда вы, ребята?» - спросили их хозяева. Вот что ответил каждый их них.

Андреев: «Я приехал из Грязи, а Григорьев живет в Лебедяни».

Борисов: «В Лебедяни живет Васильев. Я же прибыл из Усмани».

Васильев: «Я прибыл из Грязи, а Борисов – из Ельца».

Григорьев: «Я прибыл из Лебедяни, а Данилов из Чаплыгина».

Данилов: «Да, я действительно из Чаплыгина, Андреев же живет в Усмани».

Хозяева очень удивились противоречивости ответов приехавших гостей. Ребята объяснили им, что каждый из них высказал одно утверждение правильное, а другое ложное. Но по их ответам вполне можно установить, кто и откуда приехал. Откуда же приехал каждый школьник?

9 класс

  1. Вычислите: .



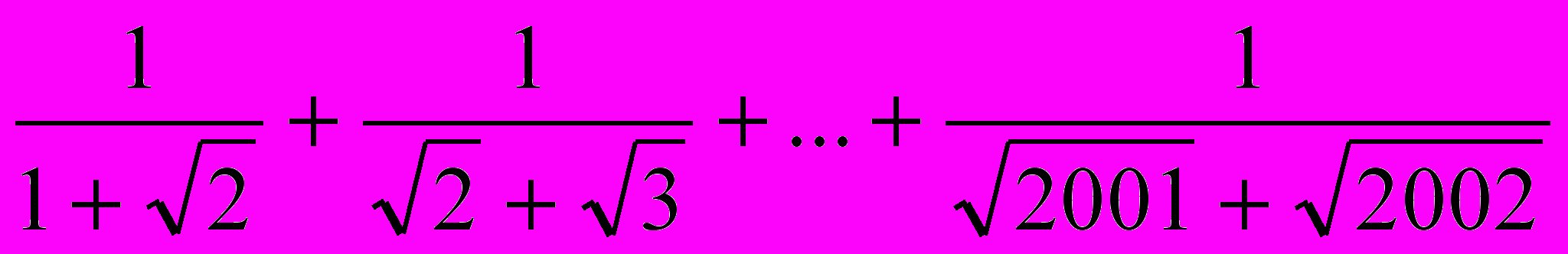  1. Постройте график функции: у = .
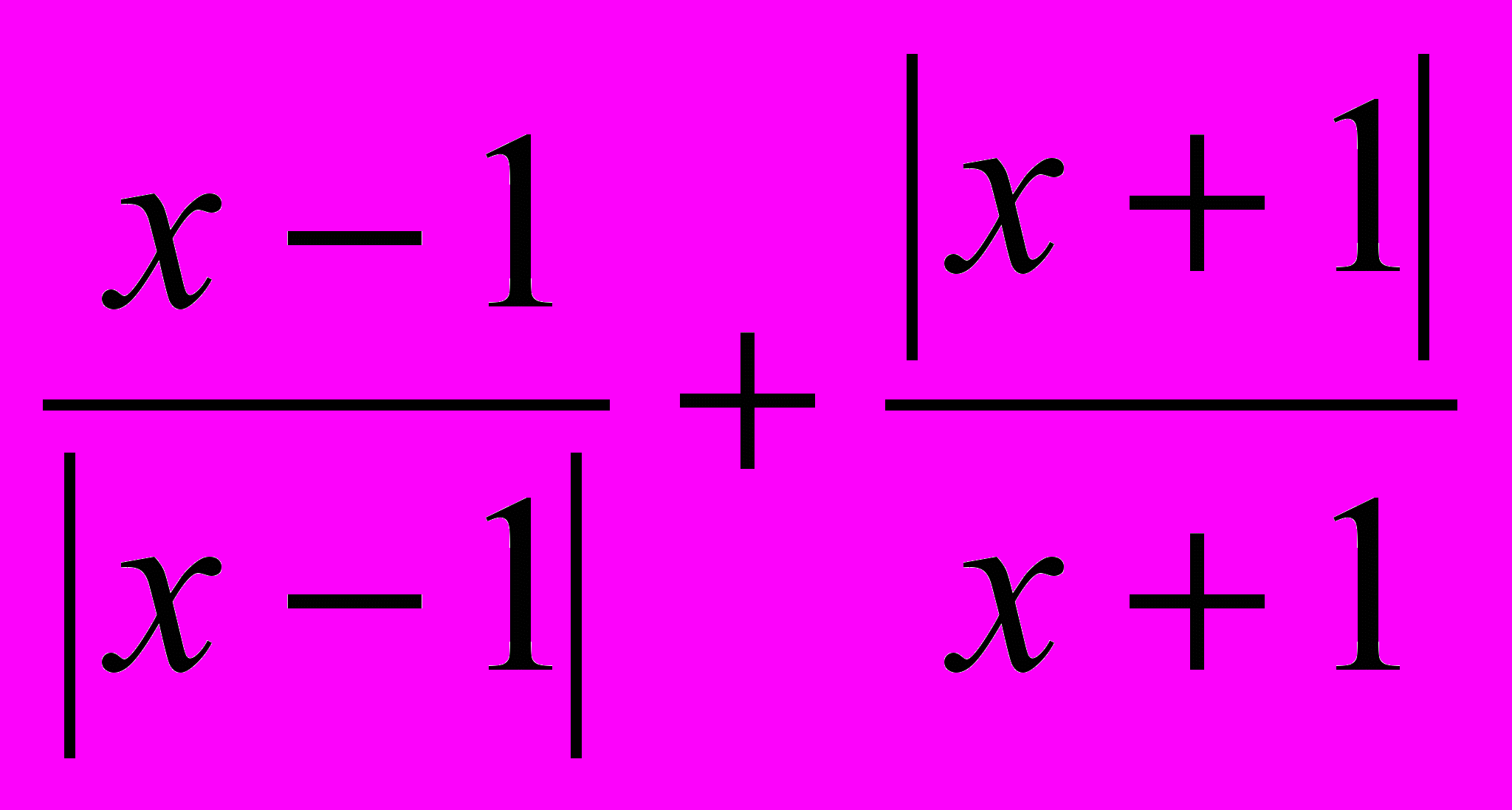  2. Решите неравенство:

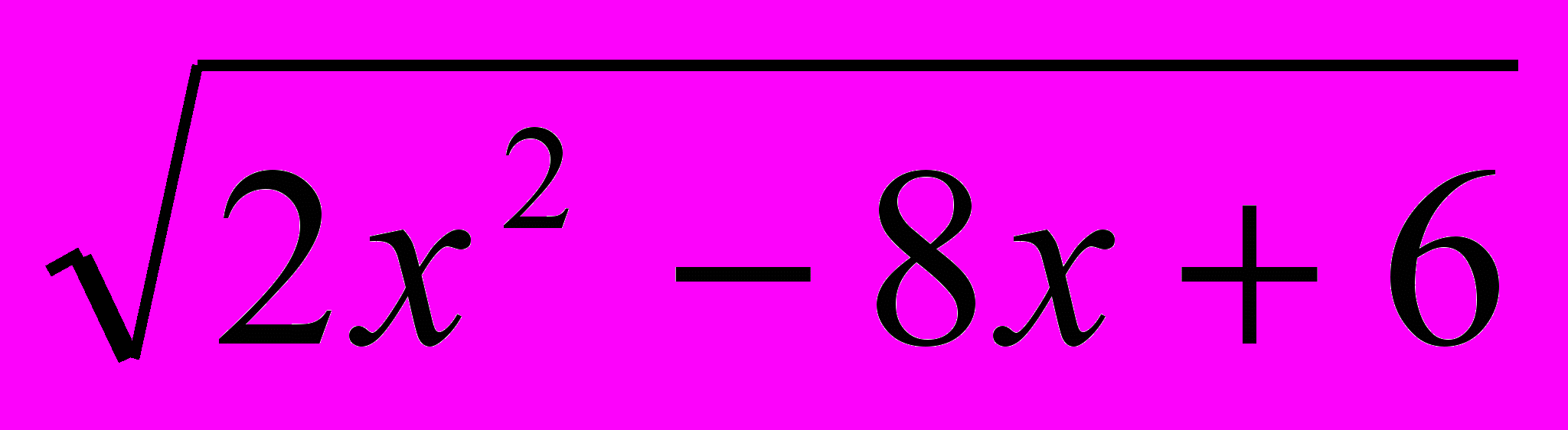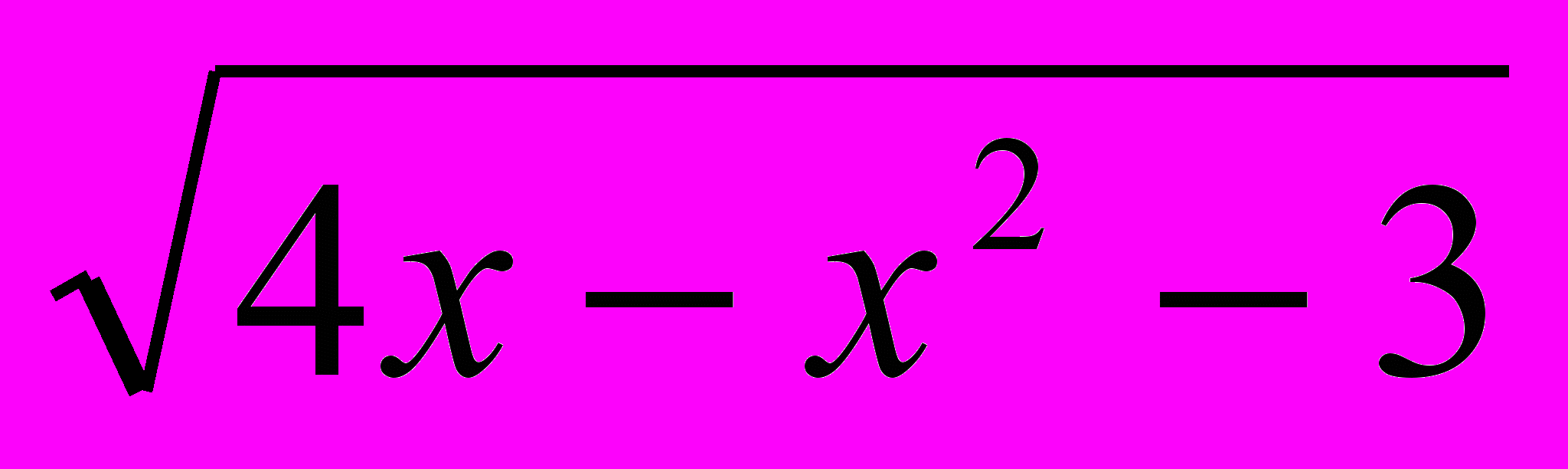
+ < х – 1.
  1. Имеется 9 пустых больших коробок. В некоторые из них положили по 10 пустых средних коробок, а в некоторые средние – по 10 пустых маленьких. Всего оказалось 109 коробок. Сколько среди них было пустых коробок?
  2. От двух кусков сплава в 6 кг и 12 кг с различным содержанием меди отрезано по куску равной массы. Каждый из отрезанных кусков сплавлен с остатком другого куска, после чего процентное содержание меди в обоих кусках стало одинаковым. Какова масса отрезанного куска?
  3. Длины сторон ВС, АС, АВ треугольника АВС равны а, в, с соответственно. Выразите через а, в и с длины медиан та, тв, тс треугольника АВС.
  4. Четверо ребят – Алексей, Борис, Владимир и Григорий участвовали в лыжных гонках. На следующий день, на вопрос кто какое место занял, они ответили так:

Алексей: «Я не был ни первым и ни последним»;

Борис: «Я не был последним»;

Владимир: «Я был первым»;

Григорий: «Я был последним».

Известно, что три из этих ответов были правдивыми, а один – ложью. Кто сказал правду? Кто был первым?


10 класс

  1. Вычислите:

.

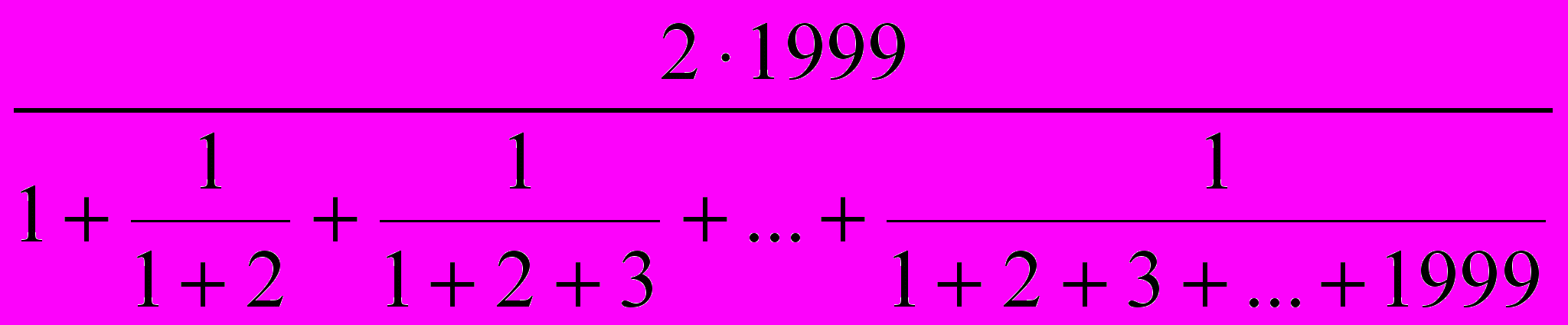  1. Решите уравнение:

(х-2)(х-3)(х+4)(х+5)=1320.
  1. При каком целом к неравенство х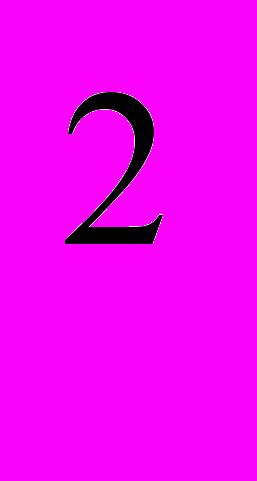+2(4к-1)х+15к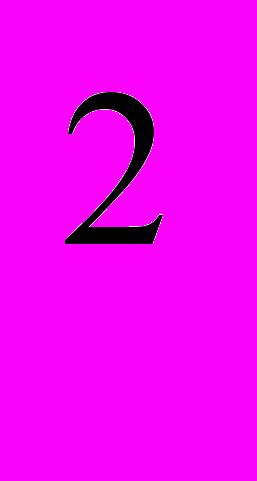-2к-7>0 верно при любом действительном х?
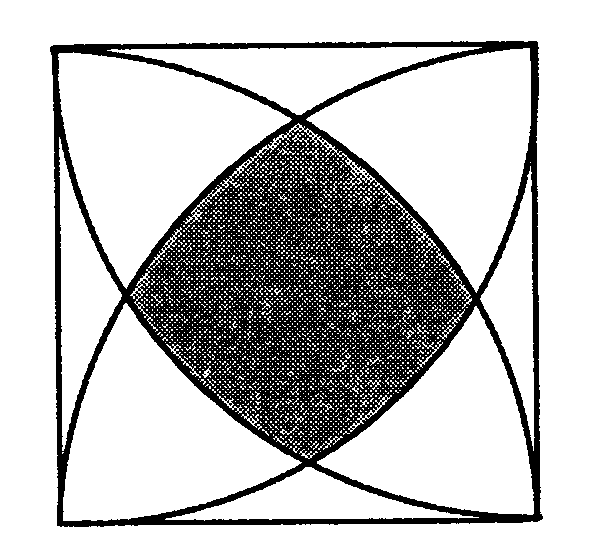
  2. Дан квадрат, сторона которого равна а. Вычислите площадь заштрихованной фигуры, образованной дугами окружностей радиуса а с центрами в вершинах квадрата.




  1. В некотором царстве, некотором государстве стоимость алмаза пропорциональна квадрату его массы. При огранке алмаза откололась некоторая его часть. Какая часть алмаза откололась, если его стоимость уменьшилась на 36%?
  2. Какое время между 6 и 7 часами показывают часы в тот момент, когда положения их часовой и минутной стрелок совпадают?
  3. Директор школы беседует с 4 учениками школы, подозреваемыми в хищении классного журнала из учительской. Александр сказал, что журнал похитил Борис. Борис утверждал, что виноват Григорий. Григорий заверил директора, что Борис врет. Виктор настаивал на том, что журнал взял не он. Директору школы удалось установить, что один из учащихся сказал все же правду. Кто похитил журнал?



11 класс

  1. Решите уравнение:

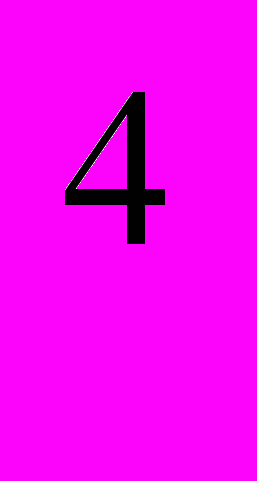х- 8х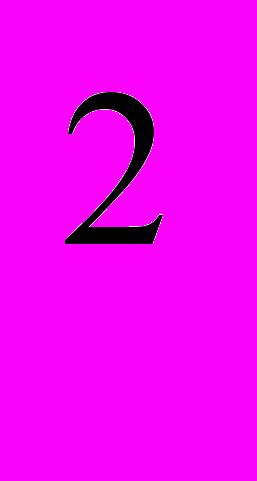+ 17 = sin.
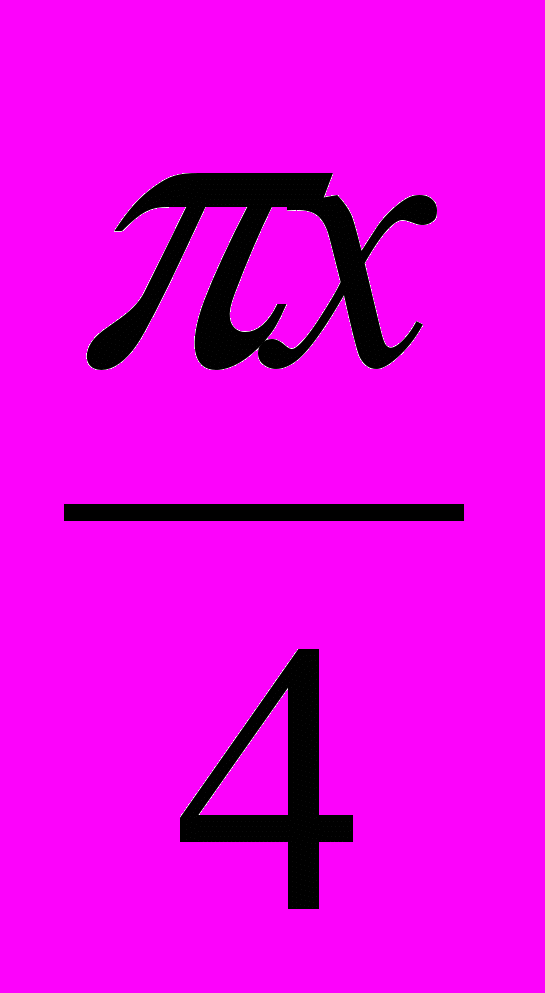  1. Напишите уравнение общей касательной к графикам функций:

f(х)= х2-6х+12 и g(х)= - х2+10х-22.
  1. Постройте график функции:

у = .
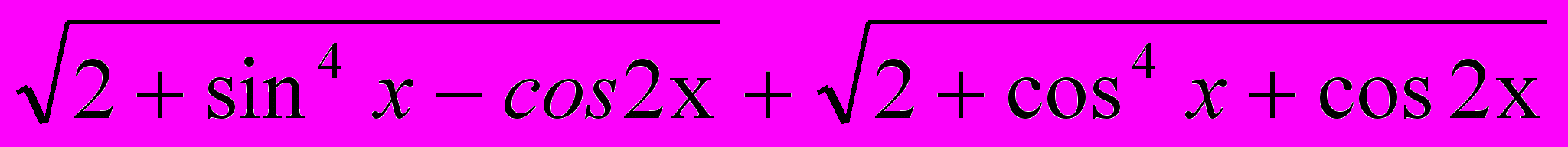  1. У торговца имеются два бочонка вина: емкостью 40 л ценою 7 руб. за литр и емкостью 10 л ценою 5 руб. за литр. По какому одинаковому количеству вина нужно взять из каждого бочонка и перелить в другой, чтобы цены вина за литр в двух бочонках сравнялись?
  2. Существует ли пирамида DАВС, у которой сумма плоских углов при каждой вершине основания АВС равна 180º, 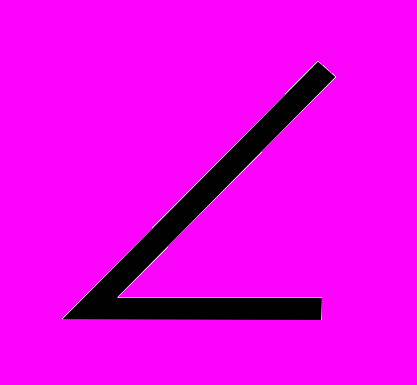АDС=30º,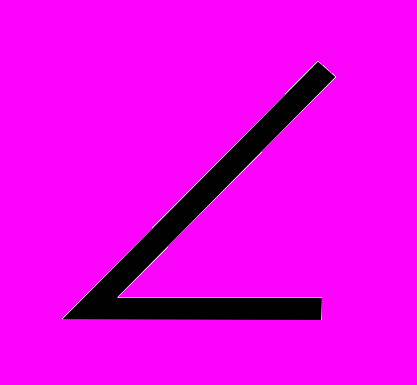АDВ=60º
  3. Найти сумму 6+66+666+…+666…6 (последнее слагаемое содержит п шестерок).
  4. В школьном драмкружке решили ставить «Ревизора», и тут разгорелся спор.
  • Ляпкиным-Тяпкиным буду я, - заявил Гена.
  • Нет, я! Я всю жизнь мечтал воплотить этот образ, - возразил Дима.
  • Хорошо, я уступлю, если мне дадут роль Хлестакова, - проявил

великодушие Гена.
  • А мне Осипа, - не уступал в великодушии Дима.
  • Хочу быть Земляникой или Городничим, - сказал Володя.
  • Нет, Городничим буду я, - хором закричали Алик и Боря, - или

Хлестаковым, - добавили они одновременно.

Удастся ли ребятам распределить роли так, чтобы все были довольны?