5. Специальная теория относительности

Вид материала

Документы

Содержание Длительность событий в разных системах отсчета Длина тел в разных системах отсчета Релятивистский закон сложения скоростей Масса в релятивистской механике 5.3. Четырехмерное пространство-время. Интервал между событиями. 5.5. Закон взаимосвязи массы и энергии

Подобный материал:

• Специальная теория относительности и эксперимент, 634.58kb.
• Урок-повторения и обобщения темы "сто специальная теория относительности", 114.09kb.
• Реферат по физике, 72.71kb.
• Учебная программа Дисциплины р7 «Специальная теория относительности» по направлению, 98.91kb.
• Фиговые листики теории относительности, 819.43kb.
• Атом и вещество часть 3 опыт физо и теория относительности, 455.51kb.
• Лекция Электромагнитная картина мира Специальная и общая теории относительности, 167.51kb.
• "Теория относительности мистификации века" написана на основе "Очерка о теории относительности",, 807.08kb.
• Подготовка Великой Хартии справедливости и перспективы гражданского общества в России, 22.31kb.
• Модульные программы к теме «Теория относительности» (6 ч, 10 кл.)*, 135.43kb.

5. Специальная теория относительности

5.1. Преобразования Галилея. Механический принцип относительности.

Рассмотрим две системы отсчета k (с координатными осями х,y,z) и K (с координатными осями X,Y,Z) (рис.14).





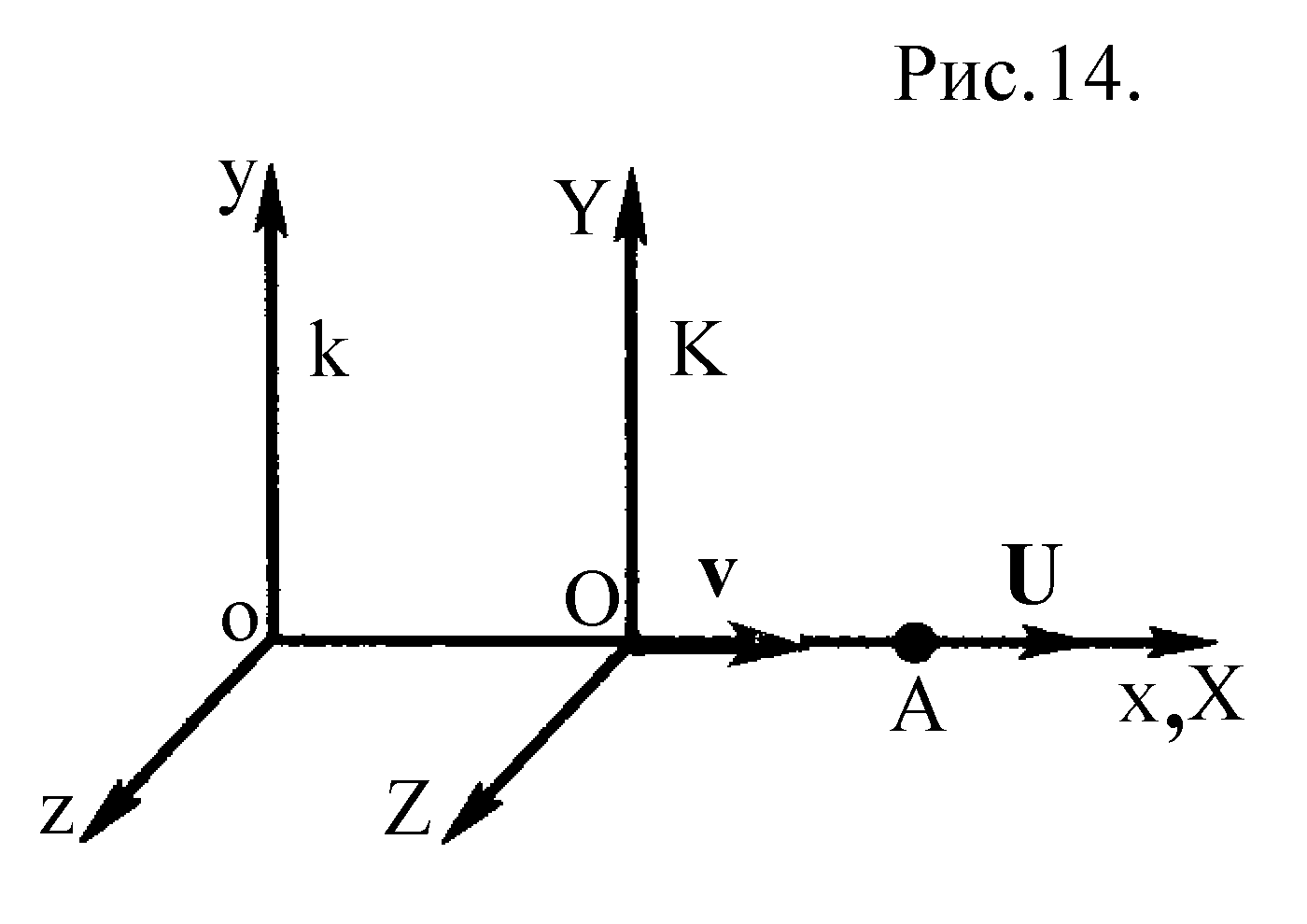
Будем условно считать систему k неподвижной, а система К будет двигаться относительно системы k равномерно и прямолинейно со скоростью 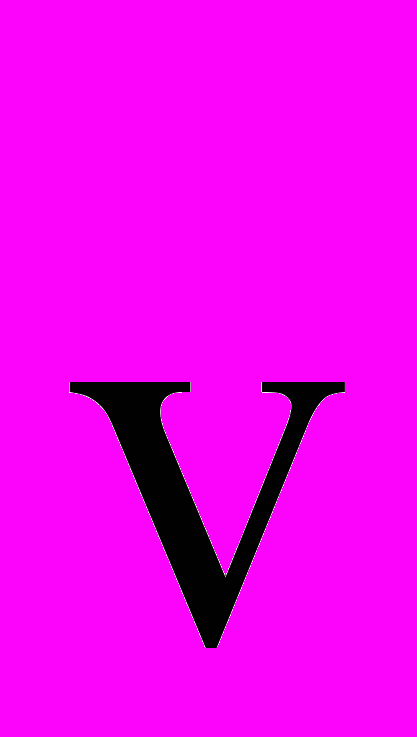вдоль положительного направления оси Х.

Отсчет времени начинается с момента, когда начала координат обоих систем совпадают.

Связь между координатами произвольной точки А в обеих системах:

x = X + vt (5.1)

Уравнение (5.1) следует дополнить уравнением

t = T, (5.2)

что означает, что промежуток времени между двумя событиями одинаков во всех инерциальных системах.

Уравнения (5.1-5.2) называются преобразованиями Галилея.


Переход от одной инерциальной системы к другой может быть записан в виде

k K: X= x - vt, Y= y, Z= z

K k: x = X + vt, y = Y, z = Z (5.3)

Кроме того, в классической механики считается, что ход времени не зависит от относительного движения систем отсчета, т.е. преобразования (5.3) следует дополнить уравнением

t = T. (5.4)


Пусть точка А движется в системе К вдоль оси Х со скоростью . Тогда из преобразований Галилея следует, что скорость 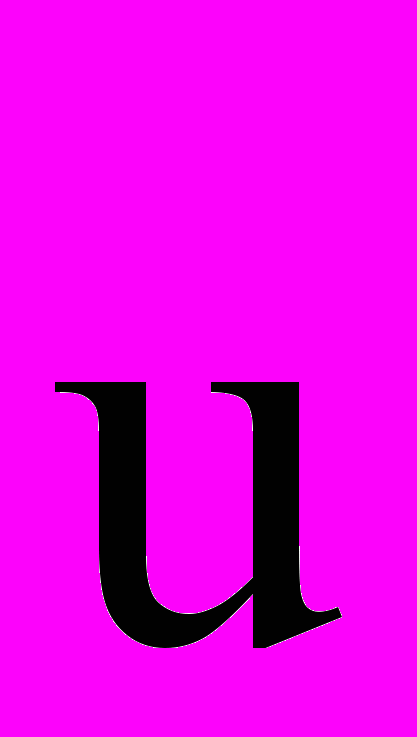точки А в системе k равна

(5.5)

правило сложения скоростей в классической механике

откуда можно получить правило преобразований ускорения

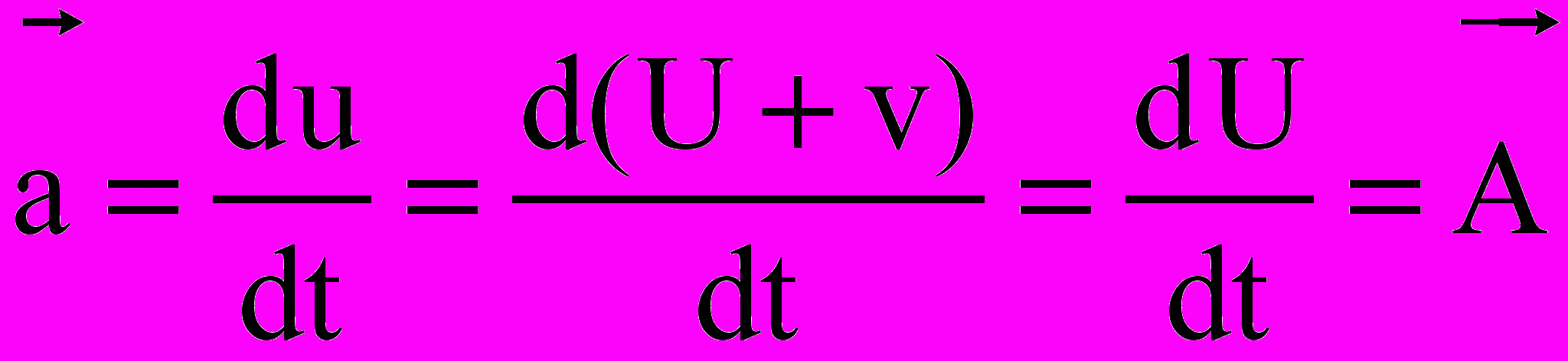(5.6)

(здесь учтено, что v=const, тогда как U≠const),

т.е. ускорение точки A в системах k и K, движущихся друг относительно друга равномерно и прямолинейно, одинаково.


Преобразования Галилея не изменяют расстояния между двумя точками (x₁,y₁,z₁) и (x₂,y₂,z₂) трехмерного пространства



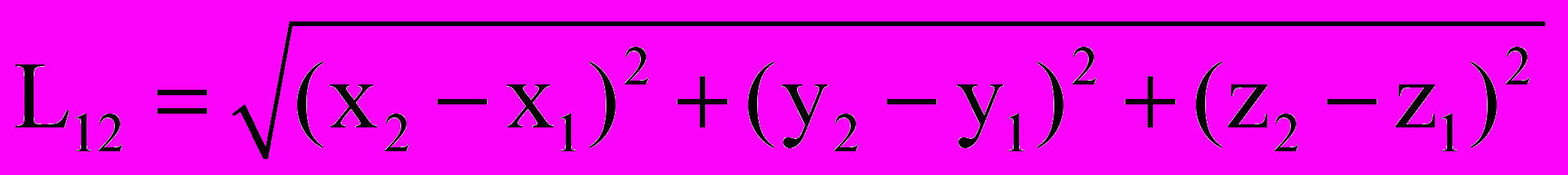
и промежутки времени между двумя событиями

t₁₂ = t₂ - t₁.

Иными словами, величины L₁₂ и t₁₂ являются инвариантами относительно преобразований Галилея.


Кроме того, пространственные и временные преобразования являются независимыми (время является единым для всех инерциальных системы отсчета).


5.2. Принцип относительности и принцип инвариантности скорости света. Преобразования Лоренца.

Основываясь на экспериментальном факте, Эйнштейн сформулировал второй принцип: скорость света в вакууме c не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета.


При учете постулатов Эйнштейна преобразования Галилея (5.1), описывающие переход от одной инерциальной системы отсчета к другой, следует заменить более общими преобразованиями Лоренца



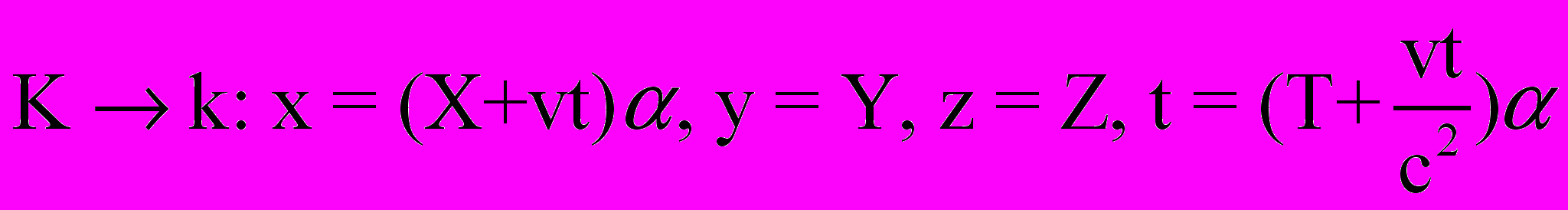(5.7)

где


Преобразования Лоренца симметричны для систем k и K, и отличаются только знаком при скорости v (если система К движется относительно системы k со скоростью +v, то система k движется относительно системы К со скоростью -v).


Постулаты Эйнштейна и теория, построенная на них, получили название специальной (частной) теории относительности.


Механика, построенная на основе постулатов Эйнштейна и преобразований Лоренц, получила название релятивистской механики.


Нетрудно видеть, что при малых скоростях (v<

Иными словами, специальная теория относительности описывает механику тел, движущихся со скоростями, близкими к скорости света.

Из преобразований Лоренца следует, что движение материальных тел со скоростями v  c невозможно, т.к. величины координат и времени становятся мнимыми (т.е. теряют физический смысл).

Длительность событий в разных системах отсчета

Пусть в некоторой точке X, покоящейся относительно системы K, происходит событие длительности

t_o=T₁-T₂

T₁,T₂ - моменты начала и конца события).

Тогда из преобразований Лоренца (5.7) можно получить, что длительность этого события в системе отсчета k

t = t₁ - t₂ = t_o, (5.8)

и поскольку  > 1, то длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе отсчета, относительно которой эта точка неподвижна.

Иными словами, часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоящихся часов.

Таким образом, промежуток времени между двумя событиями не является инвариантом относительно преобразований Лоренца.


Длина тел в разных системах отсчета

Пусть в системе K имеется покоящийся стержень, расположенный вдоль оси X, имеющий длину

L= X₂ - X₁

X₁, X₂ - координаты начала и конца стержня, индекс “о” означает, что стержень в системе K покоится.

Применяя к X₁ и X₂ преобразования Лоренца (5.7), получим, что длина стержня, измеренная в системе k, относительно которой он движется (L=x₂-x₁), равна

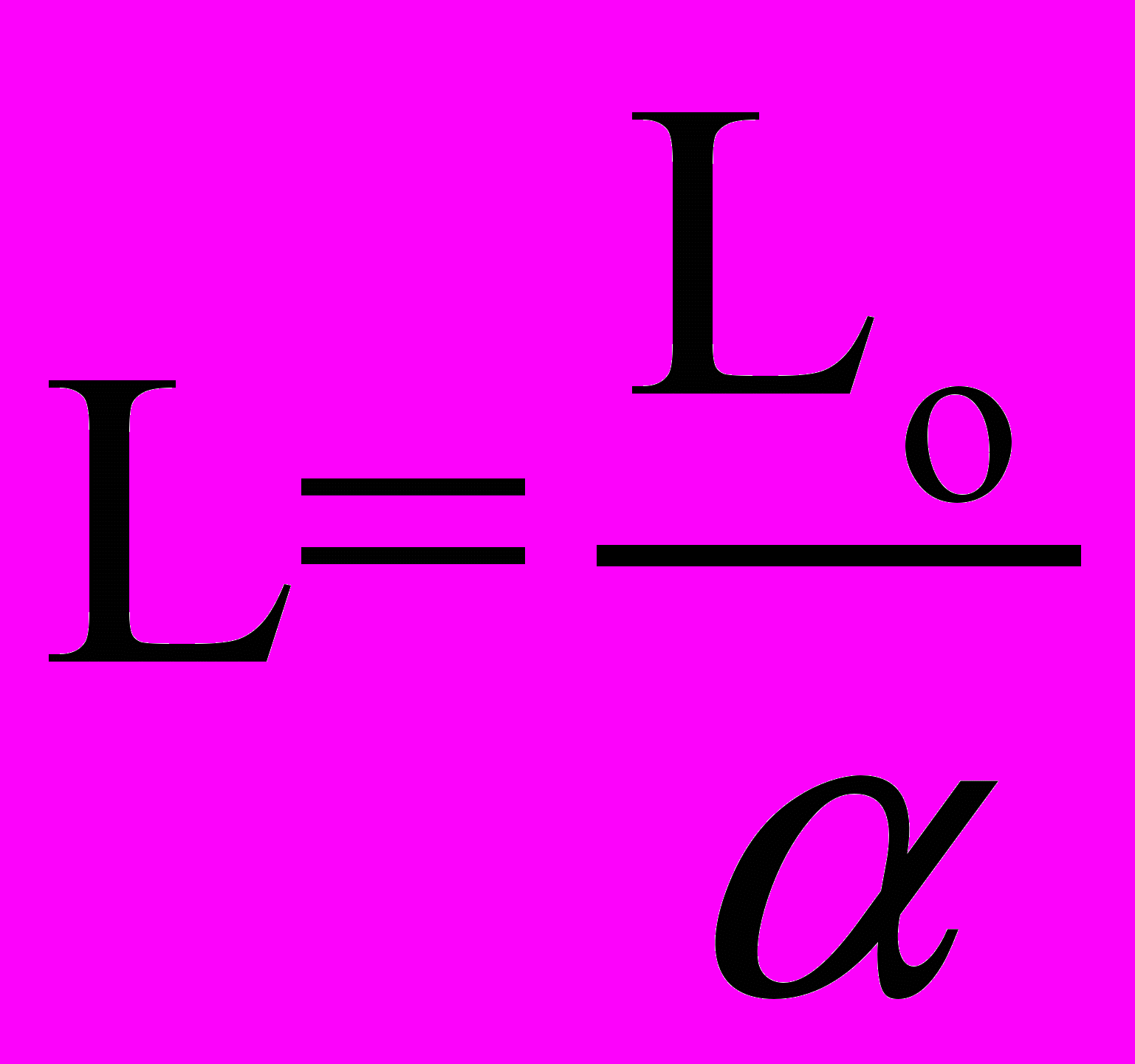, (5.9)

и поскольку  > 1, то линейный размер тела, движущегося относительно инерциальной системы отсчета, уменьшается в направлении движения в ^-1 раз (лоренцово сокращение длины): линейные размеры тела наибольшие в той системе отсчета, относительно которой тело покоится.

Иными словами, расстояние между двумя точками трехмерного пространства не является инвариантной величиной относительно преобразований Лоренца.

Из соотношения (5.9) следует, что поперечные размеры тела не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчета.


Релятивистский закон сложения скоростей

Пусть точка A в системе K движется по направлению оси X со скоростью U, причем система K движется относительно системы k по направлению оси X со скоростью v.

Поскольку 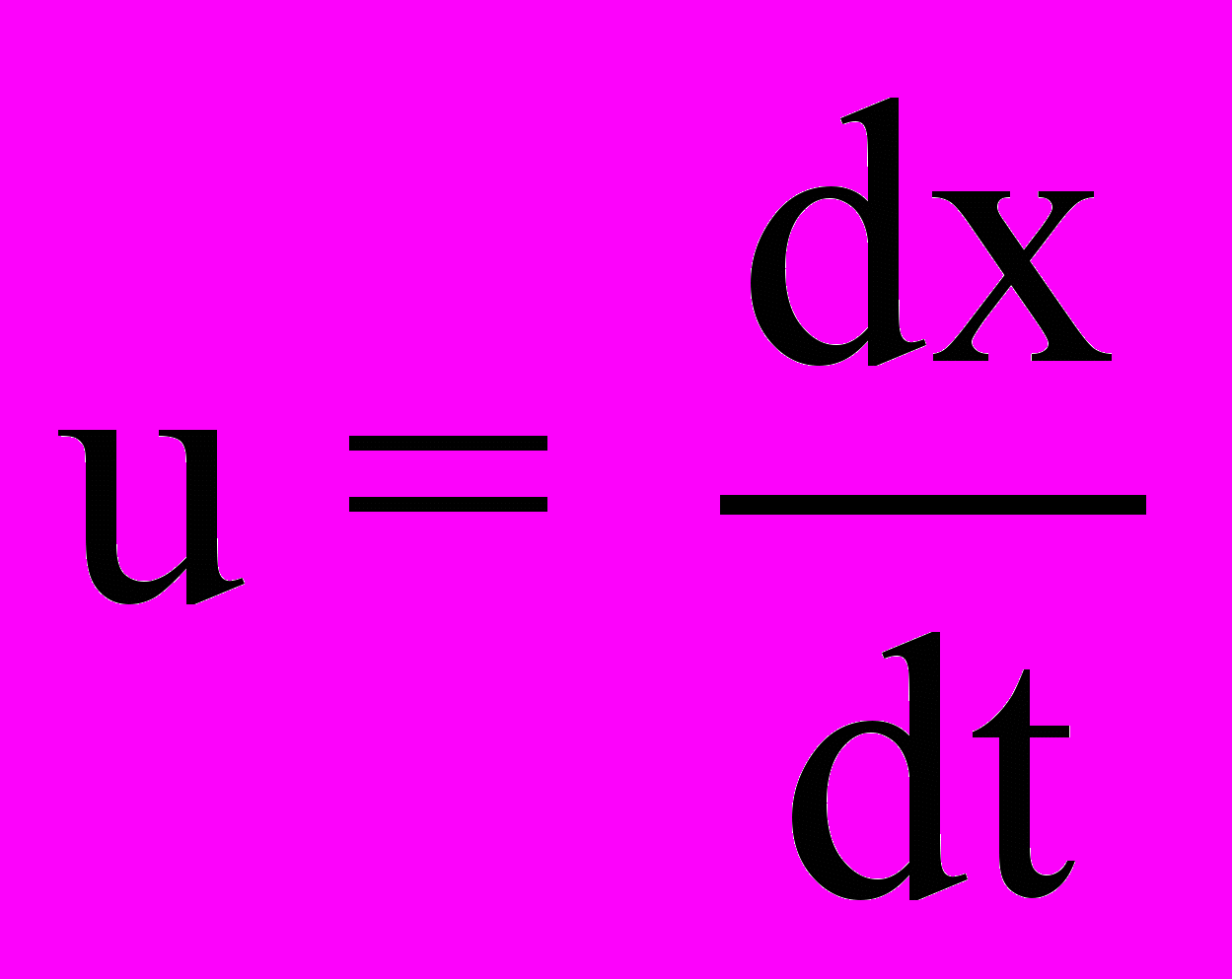и 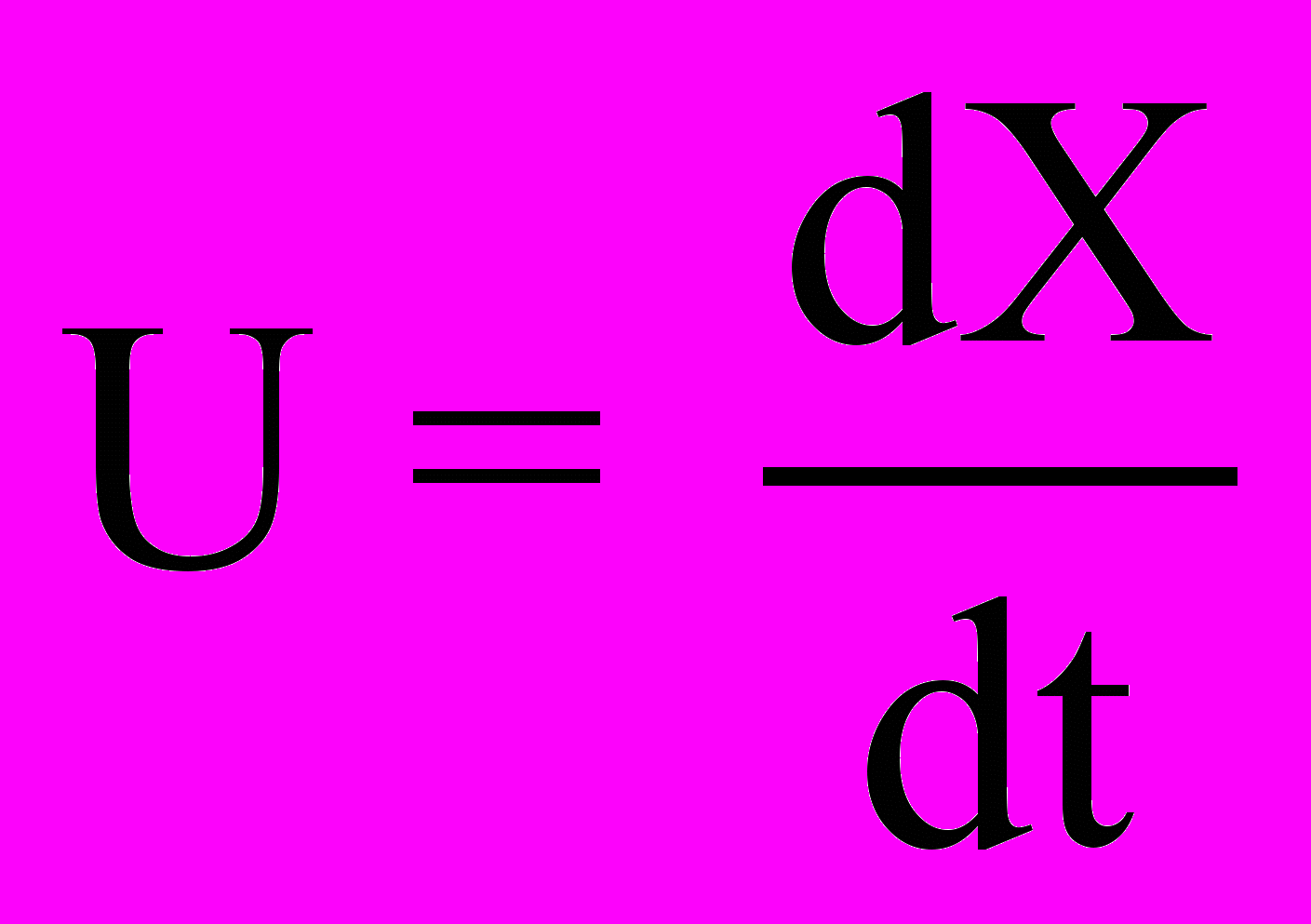, то преобразуя согласно (5.7) величины dx и dt, получим релятивистский закон сложения скоростей

(5.10)

Видно, что если скорости v, U и u малы по сравнению со скоростью света с, то последние преобразования переходят в закон сложения скоростей классической механики.

Таким образом, законы релятивистской механики в предельном случае малых скоростей (по сравнению со скоростью света) переходят в законы классической механики.

Релятивистский закон сложения скоростей подчиняется второму постулату Эйнштейна: при сложении любых скоростей результирующая скорость не может превысить скорость света в вакууме (скорость света в вакууме есть предельная скорость, которую невозможно превысить ).


Масса в релятивистской механике

Масса движущихся частиц зависит от их скорости

m = m_o, (5.11)

где m_o - масса покоя частицы (т.е. масса, измеренная в той инерциальной системе отсчета, относительно которой частица находится в покое), m - релятивистская масса.

Следовательно, релятивистская масса одной и той же частицы различна в разных инерциальных системах отсчета.


5.3. Четырехмерное пространство-время. Интервал между событиями.

В классической механике каждое событие характеризовалось тремя пространственными координатами (x,y,z) и параметром - временем t, причем расстояние между двумя точками трехмерного пространства и время t являются инвариантами по отношению к галилеевым преобразованиям координат - эти величины не зависят от выбора инерциальной системы отсчета.

В релятивистской механике величины L₁₂ и t не являются инвариантами относительно преобразований Лоренца.

Таким инвариантом оказывается интервал между двумя событиями

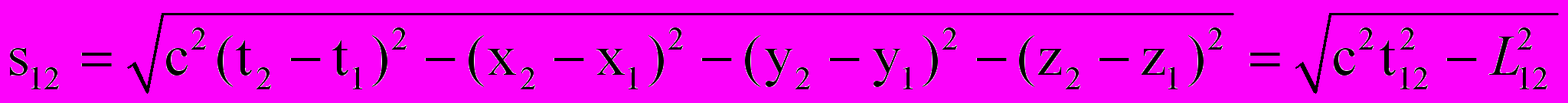(5.12)

где



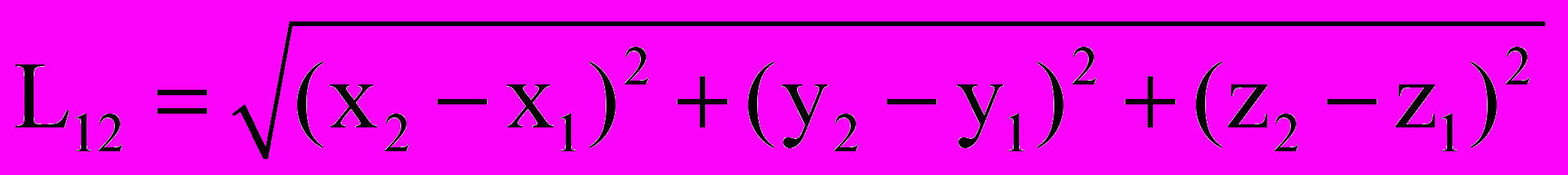
расстояние между двумя точками трехмерного пространства, в которых в моменты времени t₁ и t₂ произошли события,

t₁₂=t₂-t₁.

Инвариантность интервала означает, что пространство и время органически связаны между собой, образуя четырехмерный мир пространство-время.


5.5. Закон взаимосвязи массы и энергии

Эйнштейн получил

E = mc² = m_oc² (5.14)

Последнее уравнение выражает фундаментальный закон природы - закон взаимосвязи (пропорциональности) массы и энергии (в полную энергию не входит потенциальная энергия тела во внешнем силовом поле).

Покоящееся тело также обладает энергией

E_o = m_oc², (5.15)

которая называется энергией покоя.


Чтобы охарактеризовать прочность связей системы частиц (например, атомного ядра как системы, состоящей из нуклонов) вводят понятие энергии связи.

Энергия связи равна работе, которую необходимо затратить, чтобы разложить систему на составные части (например, атомное ядро на нуклоны):



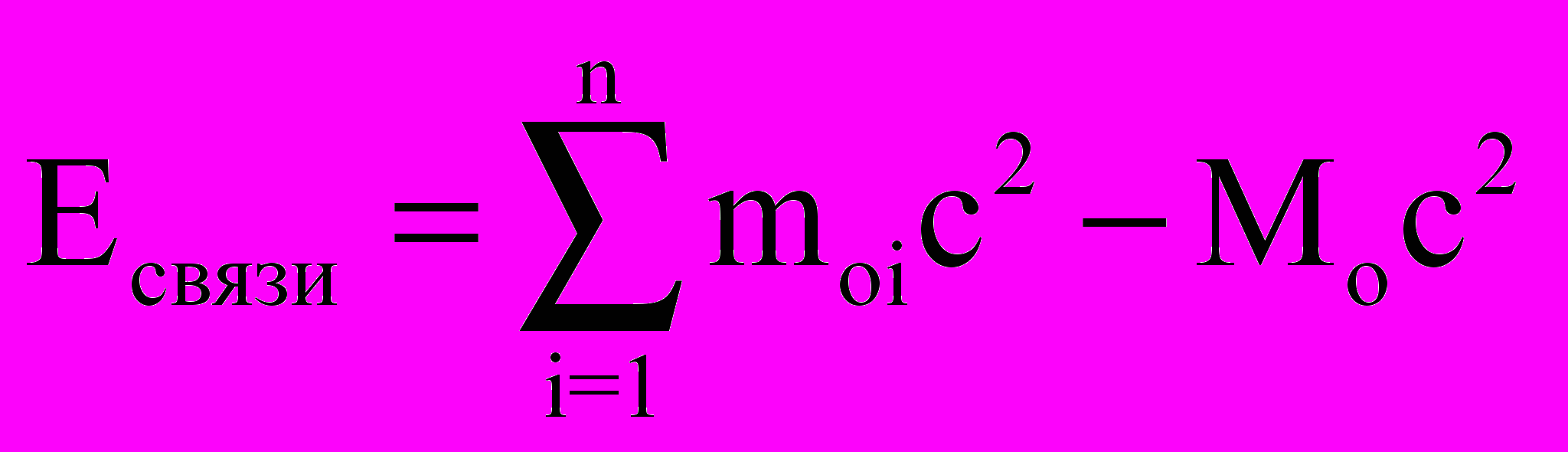
где m_oi - масса покоя i-частицы в свободном состоянии, M_o-масса покоя системы, состоящей из n-частиц.