Тематический план изучения дисциплины «Информационные технологии управления» по специальности: «Бухгалтерский учёт и аудит» I. Распределение учебного времени по семестрам и видам учебных занятий

Содержание

ТЕМАТИЧЕСКИЙ ПЛАН

В том числе по видам учебных занятий

Виды учебных занятий

Раздел, тема и учебные вопросы занятия

Задание на самостоятельную работу

1. Семестр
   

Тема №1. Введение. Становление современной математики. Множества. Элементы высшей алгебры (комплексные числа).

1. Роль и место математики в решении интеллектуальных задач в различных сферах человеческой деятельности.
   
2. Геометрия Евклида как первая естественно-научная теория.
   
3. Основные этапы развития и структура современной математики.
   

Лекция №2

1. Множества. Операции над множествами.
   
2. Выпуклые множества и их свойства.
   
3. Комплексные числа. Арифметические операции над комплексными числами.
   
4. Комплексная плоскость. Тригонометрическая и показательная формы комплексного числа.
   
5. Многочлен в комплексной области. Теорема Безу. Основная теорема алгебры.
   

Практическое занятие №1

Множества и операции с ними.

1. Операции над множествами.
   
2. Числовые множества.
   
3. Модуль действительного числа.
   

Практическое занятие №2

Комплексные числа.

1. Комплексные числа. Геометрический смысл комплексного числа.
   
2. Тригонометрическая и показательная форма комплексного числа.
   
3. Операции над комплексными числами. Формула Муавра. Извлечение корня.
   

Лекция №3

1. Основные сведения о матрицах. Операции над матрицами.
   
2. Определители квадратных матриц. Свойства определителей. Определители n-го порядка.
   
3. Обратная матрица.
   
4. Ранг матрицы. Способы вычисления ранга.
   

Лекция №4

1. Системы линейных уравнений. Матричная запись системы. Решение системы n линейных уравнений с n независимыми переменными методом обратной матрицы.
   
2. Правило Крамера. Система m линейных уравнений с n неизвестными. Метод Гаусса. Общее, частное, базисное решения системы. Фундаментальная система решений.
   
3. Модель Леонтьева (балансовый анализ).
   

Лекция №5

1. Системы координат на плоскости и в пространстве. Декартовы прямоугольные координаты. Преобразование координат. Трехмерное пространство.
   
2. Векторы на плоскости и в пространстве. Линейные операции над векторами. Скалярное произведение векторов и его свойства.
   

Лекция №6

Линейная зависимость векторов. Квадратичные формы.

1. Линейно независимые системы векторов. Базис. Разложение вектора по базису. Линейные операторы и действия над ними. Собственные векторы и собственные значения.
   
2. Квадратичные формы. Линейная модель обмена (модель международной торговли)
   

Лекция №7

Понятие и примеры пространств.

1. Понятие евклидова пространства, метрического, нормированного пространств.
   
2. Примеры экономических пространств.
   

Практическое занятие №3

1. Действия над матрицами.

2. Вычисление определений n-го порядка («обнуление», разложение по строке (столбцу).
   

Практическое занятие №4

1. Нахождение обратной матрицы. Нахождение ранга матрицы.
   
2. Решение экономических задач с использованием матриц
   

Практическое занятие №5

Решение систем линейных уравнений.

1. Решение систем линейных уравнений тремя методами (Метод Крамера, метод обратной матрицы, метод Гаусса)
   

Практическое занятие №6

Векторная алгебра.

1. Векторы. Линейные операции над векторами. Разложение вектора по базису.
   
2. Вычисление скалярного, векторного, смешанного производства.
   
3. Нахождение собственных векторов и собственных значений матрицы
   

Практическое занятие №7

Применение линейной алгебры в задачах экономики.

1. Модель Леонтьева межотраслевого баланса. Линейная модель обмена (модуль международной торговли)
   

Лекция №8

Прямая на плоскости.

1. 
   Уравнение линии на плоскости. Общее уравнение прямой.
   
2. Взаимное расположение 2-х прямых. Различные формы задания уравнения прямой.
   
3. Расстояние от точки до прямой. Условия параллельности и перпендикулярности двух прямых
   

Лекция №9

Прямая и плоскость в пространстве.

1. Уравнение плоскости в пространстве. Взаимное расположение плоскостей.
   
2. Уравнение прямой в пространстве. Способы задания прямой в пространстве.
   

Лекция №10

Кривые и поверхности второго порядка.

1. Кривые второго порядка, их геометрические свойства и уравнения. Основные поверхности второго порядка
   

Практическое занятие №8

Прямая на плоскости.

1. Уравнение прямой на плоскости, пересечение прямых. Расстояние от точки до прямой.
   

Практическое занятие №9

Прямая на плоскости.

1. Взаимное расположение прямых на плоскости (параллельность, перпендикулярность).
   
2. Угол между двумя прямыми.
   

Практическое занятие №10

Кривые 2-го порядка

1. Кривые 2-го порядка на плоскости и их основные характеристики.
   

Лекция №11

Функции и их свойства.

1. Понятие функции. Основные свойства функций. Основные элементарные функции и их свойства.
   
2. Понятие сложной и обратной функций. Неявные функции. Классификация функций.
   
3. Применение функций в экономике. Интерполирование функций
   

Лекция №12

Предел фунции и последовательности.

1. Числовые последовательности. Предел числовой последовательности и его свойства.
   
2. Предел функции на бесконечности и в точке. Односторонние пределы.
   
3. Бесконечно малые и бесконечно большие функции. Сравнение бесконечно малых.
   
4. Свойства функций, имеющих предел (основные теоремы о пределах)
   

Лекция №13

Замечательные пределы. Непрерывность функции. Точки

разрыва.

1. 1-й и 2-й замечательные пределы.
   
2. Непрерывность функции в точке. Свойства функций, непрерывных в точке. Точки разрыва и их классификация.
   
3. Свойства функций, непрерывных на отрезке. Непрерывность основных элементарных функций.
   
4. Экономическое приложение – задача о непрерывном начислении процентов.
   

Практическое занятие №11

Пределы последовательностей.

1. Вычисление пределов числовых последовательностей.
   

Практическое занятие №12

Раскрытие неопределённостей.

1. Вычисление пределов функций. 1-й и 2-й замечательные пределы.
   

Практическое занятие №13

Непрерывность функции

1. Исследование функций на непрерывность. Определение точек разрыва.
   

Лекция №14

Производная функции одной переменной.

1. Определение производной, ее геометрический и экономический смысл.
   
2. Производная суммы, произведения и частного. Производная сложной функции. Производная обратной функции.
   
3. Основные правила дифференцирования. Производные основных элементарных функций.
   
4. Понятие производных высших порядков.
   

Лекция №15

Приложения производной.

1. Основные теоремы дифференциального исчисления. Правило Лопиталя.
   
2. Условия возрастания и убывания функции. Точки экстремума. Необходимое условие экстремума. Достаточные признаки существования экстремума.
   

Лекция №16

Приложения производной.

1. Исследование функции на выпуклость и вогнутость. Точки перегиба. Асимптоты функции. Общая схема исследования функции и построение ее графика.
   

Лекция №17

Понятие дифференциала. Применение производной в эко-

номике.

1. Дифференциал функции. Применение дифференциала в приближенных вычислениях.
   
2. Дифференциалы высших порядков.
   
3. Использование понятия производной в экономике. Приложение производной в экономической теории.
   

Практическое занятие №14

Вычисление производных.

1. Нахождение производных сумм разности произведения, частного, сложных функций
   

Практическое занятие №15

Правило Лопиталя.

1. Вычисление пределов с помощью правила Лопиталя
   

Практическое занятие №16

Построение эскиза графика функции.

1. Построение графиков функций, используя общую схему исследования функций
   

Практическое занятие №17

Дифференциал. Производная в экономике.

1. Приближённое вычисление дифференциалов.
   
2. Решение экономических задач, используя понятие производной
   

Зачет

Тема №6. Неопределенный интеграл.

Всего часов учебных занятий – 12 , из них: лекции – 6 часов, практические занятия – 6 часов.

1. Первообразная функции. Неопределенный интеграл и его основные свойства.
   

1. Интегралы от основных элементарных функций. Замена переменной в неопределенном интеграле.
   
2. Метод интегрирования по частям.
   

1. Интегрирование рациональных и простейших иррациональных функций.
   
2. Интегрирование тригонометрических функций.
   

1. Неопределенный интеграл и его свойства.
   
2. Интегрирование методом разложения.
   
3. Замена переменной в неопределенном интеграле.
   

1. Метод интегрирования по частям.
   
2. Интегрирование рациональных функций.
   

1. Интегрирование иррациональных функций.
   
2. Интегрирование тригонометрических функций.
   

Тема №7. Определенный интеграл.

Всего часов учебных занятий – 12 , из них: лекции – 6 часов, практические занятия – 6 часов.

1. Определенный интеграл, его геометрический и экономический смысл.
   
2. Основные свойства определенного интеграла.
   
3. Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
   
4. Интегрирование по частям и замена переменной в определенном интеграле
   

1. Приближенные методы интегрирования.
   
2. Приложения определенного интеграла.
   
3. Использование понятия определенного интеграла в экономике.
   

1. Формула Ньютона-Лейбница.
   
2. Замена переменной в определенном интеграле. Интегрирование по частям в определённом интеграле.
   

1. Приближенные методы интегрирования.
   

1. Приложение определенного интеграла.
   
2. Использование определенного интеграла.
   
3. Использование определенного интеграла в экономике.
   

Тема №8. Несобственные интегралы.

Всего часов учебных занятий – 4 , из них: лекции – 2 часов, практические занятия – 2 часа.

1. Несобственные интегралы 1-го и 2-го рода. Признаки сходимости несобственных интегралов.
   

1. Несобственный интеграл 1-го и 2-го рода.
   
2. Признаки сходимости.
   

Тема №8. Функции многих переменных.

Всего часов учебных занятий – 10 , из них: лекции – 4 часов, практические занятия – 6 часов.

2. Функции многих переменных. Предел и непрерывность.
   
3. Основные свойства непрерывных функций.
   
4. Частные и полное приращения функции многих переменных.
   
5. Понятие производной по направлению и градиента.
   

3. Дифференцирование неявной и сложной функции. Частные производные и дифференциалы высших порядков функции многих переменных.
   
4. Использование функций многих переменных в экономической теории. Экономические приложения: изокванты ПФ, кривые безразличия.
   
5. Коэффициенты эластичности, предельная производительность труда..
   

1. Экстремумы функции многих переменных. Необходимое условие локального экстремума. Достаточное условие локального экстремума.
   
2. Условный экстремум функции многих переменных: теорема о разрешимости системы функциональных уравнений, метод множителей Лагранжа.
   
3. Понятие о методе наименьших квадратов. Примеры решения экономических задач.
   

1. Область определения ФНП.
   
2. График. Линии уровня.
   

1. Частные производные. Производные по направлению.
   
2. Градиент. Частные производные высших порядков.
   

1. Экстремумы функции дву4х переменных. Необходимое условие экстремума.
   
2. Достаточное условие экстремума. Наибольшее и наименьшее значение функции.
   

Тема №10. Ряды. Числовые ряды. Степенные ряды.

Всего часов учебных занятий – 10 , из них: лекции – 4 часов,

практические занятия – 6 часов.

1. Определение числового ряда и его суммы.
   
2. Необходимый признак сходимости числовых рядов.
   
3. Гармонический ряд. Ряд с положительными членами.
   
4. Достаточные признаки сходимости числового ряда (признак сравнения, признак Даламбера, интегральный признак Коши).
   

1. Знакопеременные ряды. Абсолютная и условная сходимость.
   

1. Понятие о функциональных рядах. Интервал и радиус сходимости степенного ряда.
   
2. Разложение функции в степенные ряды (ряды Тейлора и Маклорена).
   
3. Применение рядов в приближенных вычислениях.
   

1. Признаки сходимости рядов с положительными членами.
   

Практическое занятие №29

1. Знакопеременные ряды. Теорема Лейбница.
   

Практическое занятие №30

1. Разложение функций в степенные ряды. Применение рядов в приближенных вычислениях.
   

Тема №10. Дифференциальные уравнения.

Всего часов учебных занятий – 14 , из них: лекции – 8 часов, практические занятия – 6 часов.

1. Уравнения с разделяющимися переменными.
   
2. Однородные и линейные уравнения 1-го порядка.
   
3. Уравнения в полных дифференциалах.
   
4. Задача Коши. Дифференциальные уравнения высших порядков.
   

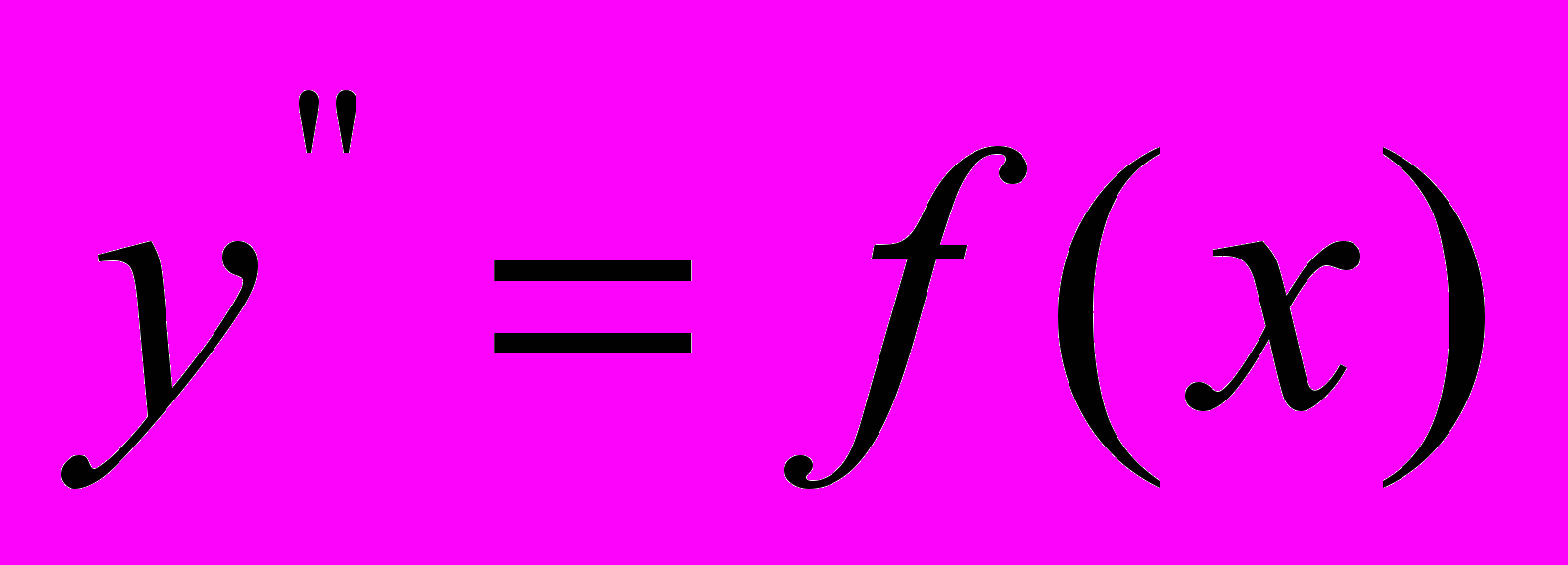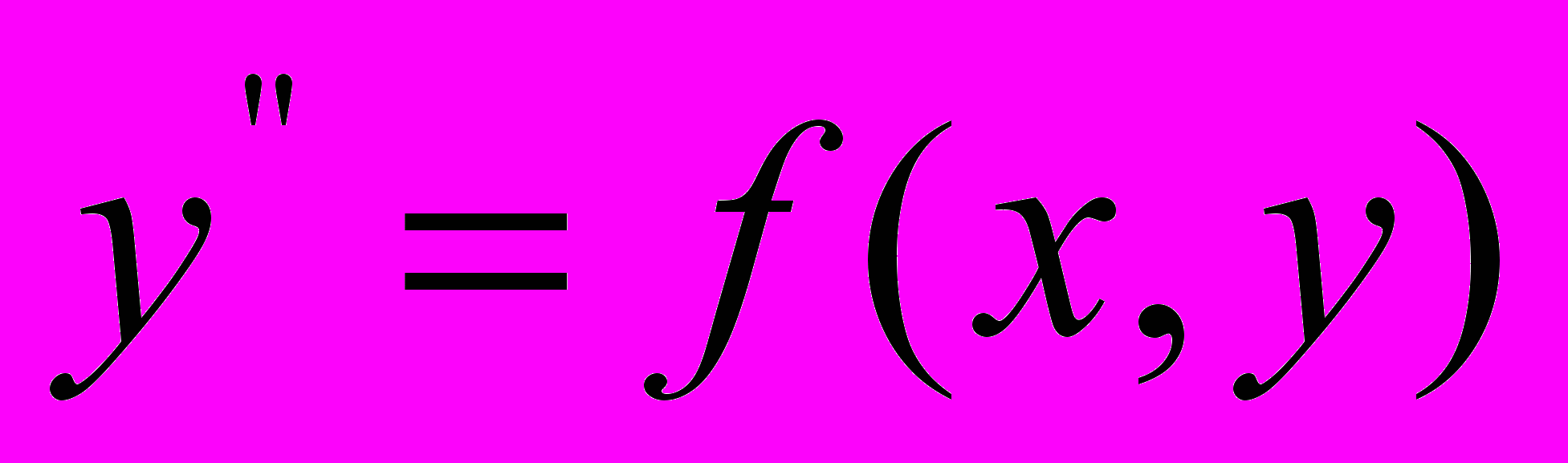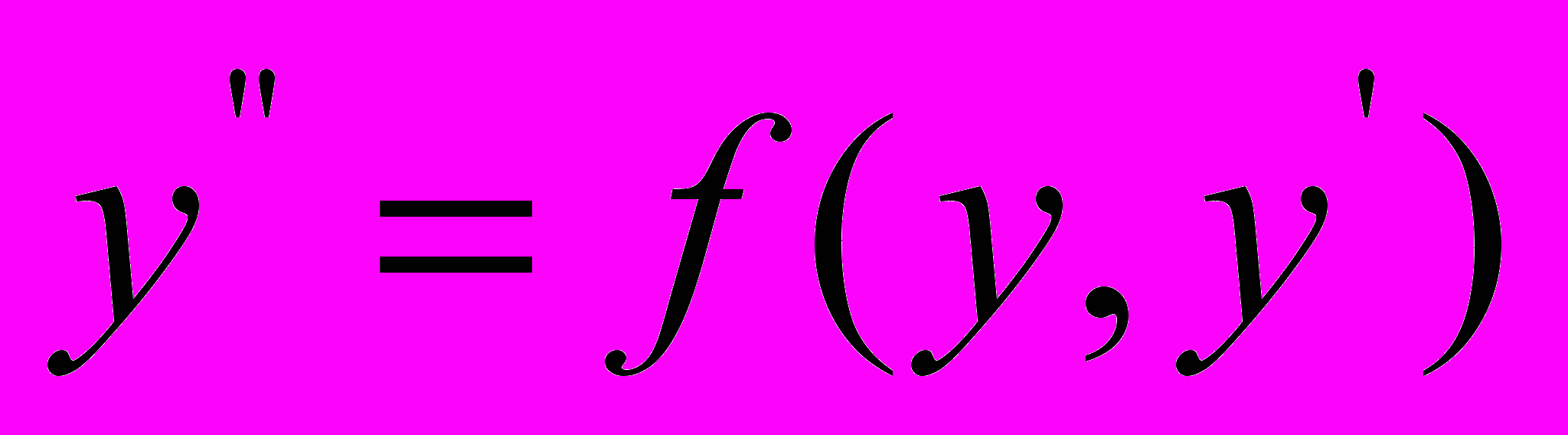1. Дифференциальные уравнения 2-го порядка: , , , методы их решения.
   
2. Линейные дифференциальные уравнения (однородные, неоднородные, с постоянными коэффициентами).
   

1. Уравнение с разделяющими переменными. Однородные уравнения