Geum.ru

Информационное сообщение о Четвертой международной конференции по проблемам управления

Вид материалаДокументы

Содержание


Программный комитет мкпу-iv
Организационный комитет мкпу-iv
Направления и секции
Организационное управление и менеджмент
Управление в промышленности, энергетике и транспортных системах
Россия, Москва Moscow
Правила оформления текстов докладов
Шрифт: Times New Roman; ЗАГОЛОВОК
Формат абзацев и порядок материала
Исследование одного вида однородных дифференциальных уравнений
E-mail: Ivanov@mail.ru
1. Решение ОДУ дробного порядка с помощью преобразования Лапласа
2. Постановка задачи
Подобный материал:

ИНФОРМАЦИОННОЕ СООБЩЕНИЕ

о Четвертой международной конференции по проблемам управления

(Россия, Москва, Институт проблем управления

имени В.А. Трапезникова РАН, 2009 год)


Четвертая международная конференция по проблемам управления (МКПУ-IV) проводится в рамках Мультиконференции “Теория и системы управления” в январе 2009 года в Институте проблем управления имени В.А. Трапезникова РАН (г. Москва, Россия).

Конференция организуется ИПУ РАН и Российским Национальным комитетом по автоматическому управлению.


ПРОГРАММНЫЙ КОМИТЕТ МКПУ-IV

Васильев С.Н. (председатель), Куржанский А.Б. (сопредседатель), Алескеров Ф.Т., Амбарцумян А.А., Ашимов А.А. (Казахстан), Бубницкий З. (Польша), Бурков В.Н., Бутковский А.Г., Верыньски А. (Польша), Вишневский В.М., Городецкий В.И., Грумпас П. (Греция), Гуковский Д.Э. (Израиль), Деметрович Я. (Сербия), Дорофеюк А.А., Емельянов С.В., Кириллова Ф.М. (Белоруссия), Коган Б.Я. (США), Койво Х. (Финляндия), Коровин С.К., Кротов В.Ф., Кузнецов Н.А., Кузнецов О.П., Куликовский Р. (Польша), Кульба В.В., Кунцевич В.М. (Украина), Курдюков А.П., Льюнг Л. (Швеция), Малинецкий Г.Г., Мандель А.С., Меерков С.М. (США), Налэч М. (Польша), Ниеми А. (Финляндия), Новиков Д.А., Новосельцев В.Н., Пархоменко П.П., Плотт Ч. (США), Поляк Б.Т., Попков Ю.С., Похиолайнен С. (Финляндия), Рутковский В.Ю., Салуквадзе М.Е. (Грузия), Сизых Н.В., Сун Цзян (Китай), Телькснис Л.А. (Литва), Теряев Е.Д., Федосов Е.А., Фрадков А.Л., Фукуда Т. (Япония), Хенчеи Г. (Венгрия), Чжан Шэн (Китай), Шершеналиев Ж. (Киргизия), Юсупов Р.А., Якубович В.А.


ОРГАНИЗАЦИОННЫЙ КОМИТЕТ МКПУ-IV

Павлов Б.В. (председатель), Мандель А.С. (зам. председателя), Бодякин В.И. (ученый секретарь), Венец В.И., Грязина Е.Н., Дургарян И.С., Курдюков А.П., Пятницкая М.В.


Конференция проводится с 26 по 30 января 2009 года.

26 января  открытие конференции, пленарное заседание.

27-30 января  пленарные и секционные заседания, круглые столы


МКПУ-IV направлена на то, чтобы
  • предоставить возможность ее участникам в свободной форме, в том числе и в процессе дискуссий, обсудить (на пленарных и секционных заседаниях и за круглым столом) современное состояние науки об управлении;
  • выявить основные тенденции и связи между различными направлениями науки об управлении;
  • выявить в процессе дискуссий наиболее перспективные направления теории управления;
  • обсудить задачи, которые ставит перед теорией управления современная практика.



Направления и секции




  1. Общие вопросы современной теории управления

  1. Анализ и синтез систем управления.
  2. Оптимальное управление.
  3. Распределенные системы.
  4. Стохастические системы управления.
  5. Вопросы обработки сложноорганизованной информации.
  1. Устойчивость, робастность, инвариантность, адаптация в управляемых динамических системах
  1. Устойчивость систем управления.
  2. Робастность и инвариантность систем управления.
  3. Адаптация в управляемых динамических системах.
  1. Проблемно-ориентированные системы управления
  1. Управление в междисциплинарных социально-экономических моделях.
  2. Управление в междисциплинарных медико-биологических моделях.
  3. Политическое управление.
  4. Теория выбора и теория принятия решений.
  5. Управление безопасностью сложных систем.

  1. Организационное управление и менеджмент

  1. Управление в организационных системах.
  2. Активные системы.
  3. Управление в логистике.
  4. Рефлексивное управление.

  1. Управление в промышленности, энергетике и транспортных системах

  1. Управление технологическими процессами и предприятиями.
  2. Технические средства управления.
  3. Управление транспортными потоками.
  4. Системы логического управления.
  5. Надежность и техническая диагностика.
  1. Управление в гибридных и других сложных моделях динамических и интеллектуальных систем
  1. Искусственный интеллект в управлении.
  2. Групповое управление и мультиагентные системы.
  3. Управление знаниями.
  4. Нейронные сети.
  1. Информационные технологии в управлении, управление в вычислительных и телекоммуникационных системах
  1. Вычислительные системы и сетевые технологии в управлении.
  2. Управление в вычислительных и телекоммуникационных сетях.
  3. Автоматизированное проектирование.
  1. Управление подвижными объектами
  1. Управление авиационными летательными объектами.
  2. Управление аэрокосмическими объектами.
  3. Управление подводными и надводными судами.
  1. Профессиональная подготовка специалистов в области управления
  1. Анализ направлений, методик и программ профессиональной подготовки специалистов в области управления, особенности внедрения Болонской системы.
  2. Инновационные и информационные технологии подготовки специалистов в области управления.
  3. Анализ форм подготовки, качества и рейтингов высших учебных заведений.


Если Вы желаете принять участие в работе МКПУ-IV, то сообщите об этом нам, указав свое имя, место работы, почтовый и электронный адреса, а также интересующие вас разделы. Просим тезисы докладов высылать на имя Оргкомитета

по электронному адресу: iccpripu@ipu.ru

или (на электронных носителях) по почтовому адресу:


117997 Profsoyuznaya 65


Россия, Москва Moscow

Профсоюзная 65 Russia 117997

Тел. (495) 334-8969 Tel. (495) 334-8969


Дополнительную информацию можно получить в сети Internet по адресу:


ssi.ru


Официальные языки конференции: русский и английский. Во время работы конференции будет организован синхронный перевод.

Если Вы предполагаете выступить на конференции с докладом, просим прислать по электронной почте на имя Оргкомитета тезисы доклада (в формате редакторов Word под Windows или TeX, лист A4, через один интервал, не более 2 стр.) не позднее 30 апреля 2008 г.

На основании полученных тезисов Программный комитет осуществит отбор работ для включения в программу МКПУ-IV с объявлением результатов отбора и уведомлением авторов, включенных в программу докладов, не позднее 20 мая 2008 г.

Полный текст включенных в программу докладов (в формате редакторов Word под Windows или TeX, лист A4, через один интервал, не более 8 стр.) должен быть представлен в Оргкомитет не позднее 30 июня 2008 года. К началу конференции тексты всех докладов, принятых к участию в конференции, будут опубликованы.

О размерах оргвзноса и сроках его отправки будет сообщено дополнительно.

Правила оформления текстов докладов

Формат листа: А4, поля: верхнее – 2,1 см, нижнее – 2,4 см, левое и правое – 2,5 см, расстояние до колонтитула (верхнего, нижнего) – 1,27 см. Номера страниц располагаются внизу с равнением по центру, шрифт Times New Roman; размер – 12.

Шрифт: Times New Roman; ЗАГОЛОВОК – прямые полужирные прописные, размер – 14; Подзаголовки – прямые полужирные, размер – 13, Фамилии И.О. (авторы) – прямые полужирные, размер – 12; координаты (место работы и E-mail авторов) – курсивные, размер – 12; текст доклада и его аннотация – прямые, размер – 11; слова Аннотация: (первое слово аннотации доклада, размер – 11) и Литература (подзаголовок списка литературы, размер – 13) – прямые полужирные.

Интервалы: весь материал набирается через один интервал.

Формат абзацев и порядок материала:

Первые строки: Заголовок (выравнивание по центру).

Следующие строки: Фамилии И.О. авторов – через запятые: выравнивание по центру, без отступа в абзаце, интервал перед абзацем – 6 пт.

Следующие строки: координаты авторов (организация, почтовый адрес, E-mail) – выравнивание по центру, без отступа в абзаце, интервал перед абзацем – 6 пт.

Пропуск одной строки.

Следующие строки: аннотация, которая начинается со слова Аннотация: (последующий текст – обычный шрифт размера 11, с выравниванием в абзаце по ширине и отступом в абзаце слева и справа по 1 см).

Пропуск одной строки.

Следующие строки: текст доклада до списка литературы (выравнивание по ширине, отступ в абзаце 1,27 см, ссылки на литературу в квадратных скобках).

Комментарии. Все подзаголовки в тексте доклада (включая слова Введение, Заключение и Литература) с выравниванием по центру, без отступа в абзаце и с интервалом до подзаголовка – 12 пт, и после подзаголовка – 6 пт. Все формулы с интервалом (до и после) 6 пт. Формулы без номеров с выравниванием по центру. Формулы с номерами (справа) с выравниванием номера по правому краю и размещением текста формулы по центру. Рисунки и подписи к рисункам – с выравниванием по центру (без отступа в абзаце) и интервалом для формулы и подписи к ней (до и после) – 6 пт. Шрифт подписи: размер – 11, прямой полужирный (точка в конце подписи обязательна). Тексты теорем, следствий, утверждений и т.п. фрагментов набираются отдельным абзацем с равнением по ширине, отступом – 1,27 см, интервалом (до и после) – 6 пт; начинаются со слов Теорема 1, Следствие 2, Утверждение 3, и т.п., с порядковым номером (шрифт: размер 11, курсивный полужирный); последующий текст теоремы, следствия, утверждения и т.п. фрагментов, включая точку после номера, набирается обычным шрифтом.

Пропуск одной строки.

Следующая строка: слово Литература (выравнивание по центру, без отступа в абзаце).

Следующие строки: список литературы с нумерацией (списком в форме нумерации ссылок арабскими цифрами с точкой, равнение по левому краю, цифры номеров с отступом от края – 0,0 см, а текст каждой ссылки с отступом от левого края – 0,8 см). В списке литературы Фамилии И.О. авторов набираются курсивом, остальной текст каждой ссылки обычным прямым шрифтом, всё выравнивается по левому краю.

Тезисы оформляются по тем же правилам (за исключением аннотации, которая в тезисах не нужна, при этом в тезисах не обязательно вводить рубрикацию разделов), но их объем, как указано выше, не должен превышать 2 страниц.

ИССЛЕДОВАНИЕ ОДНОГО ВИДА ОДНОРОДНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

А.В. Иванов1), В.В. Степанов2)

1)Самарская государственная академия

Россия, 443041, г. Самара, ул. Свободы, 4

E-mail: Ivanov@mail.ru

2) Самарский проектно-технологический институт

Россия, 443052, г. Самара, ул. Новая, 7

E-mail: Stepanov@mail.ru


Аннотация: В настоящее время в области естественных наук для исследования динамических процессов применяются дифференциальные уравнения дробного порядка, использование которых позволяет с высокой математической точностью описать проходящие процессы в различных областях науки.


Введение

В настоящее время в области естественных наук [1-4] для исследования динамических процессов применяются дифференциальные уравнения дробного порядка [5], использование которых сформировать точное математическое описание.

В теории автоматического управления задача, связанная с исследованием дифференциальных уравнений дробного порядка возникла из предположения о возможности использовать в устройствах управления законов регулирования описываемых дробными интегро-дифференциальными уравнениями. Для проверки данной гипотезы были выбраны широко распространенные универсальные ПИД законы регулирования, в которых интегральное и дифференциальное звено были заменены аналогичными, только с дробным порядком. Временные и частотные свойства полученных дробных ПИД законов регулирования изучены, и результаты опубликованы в работах [1, 4]. В результате применения указанных законов регулирования для целей управления и проводимых изысканий возникли новые трудности.

В работе приведены исследования на основе преобразования Лапласа, применительно к одному виду однородных дифференциальных уравнений (ОДУ) и определение его устойчивости в зависимости от действительных корней характеристического уравнения.

1. Решение ОДУ дробного порядка с помощью преобразования Лапласа

Сделаем предположение о возможности описания некоторых динамических звеньев систем с помощью дифференциальных уравнений дробного порядка вида

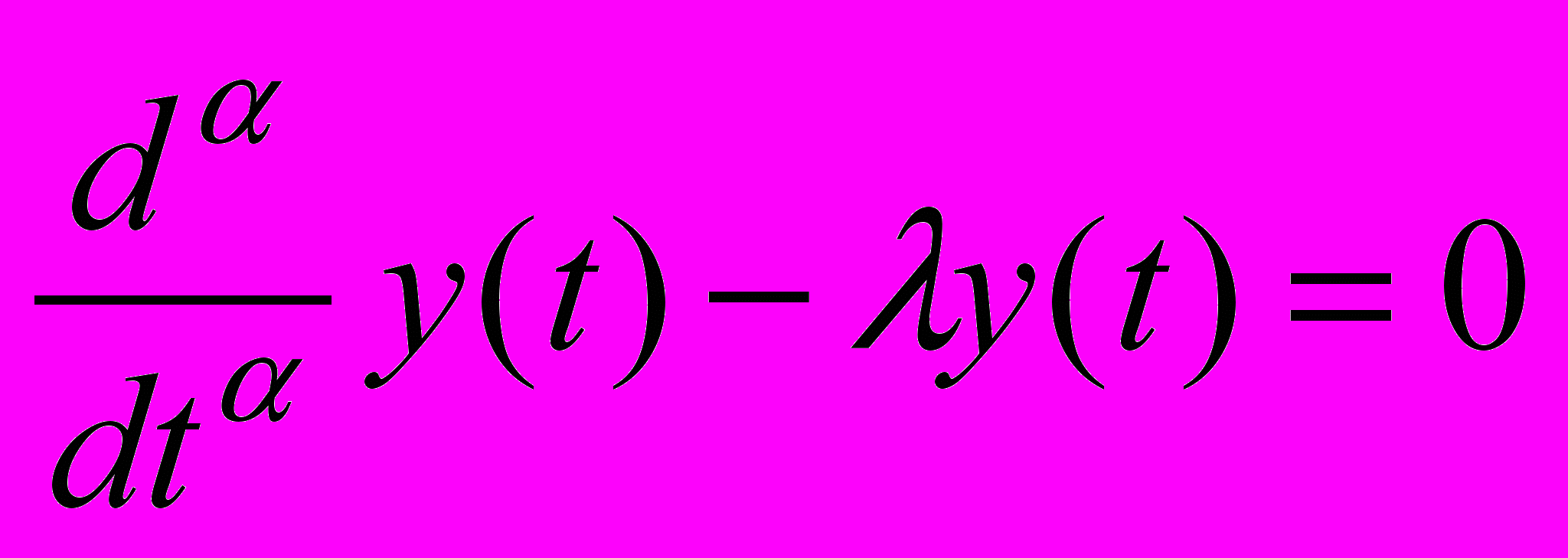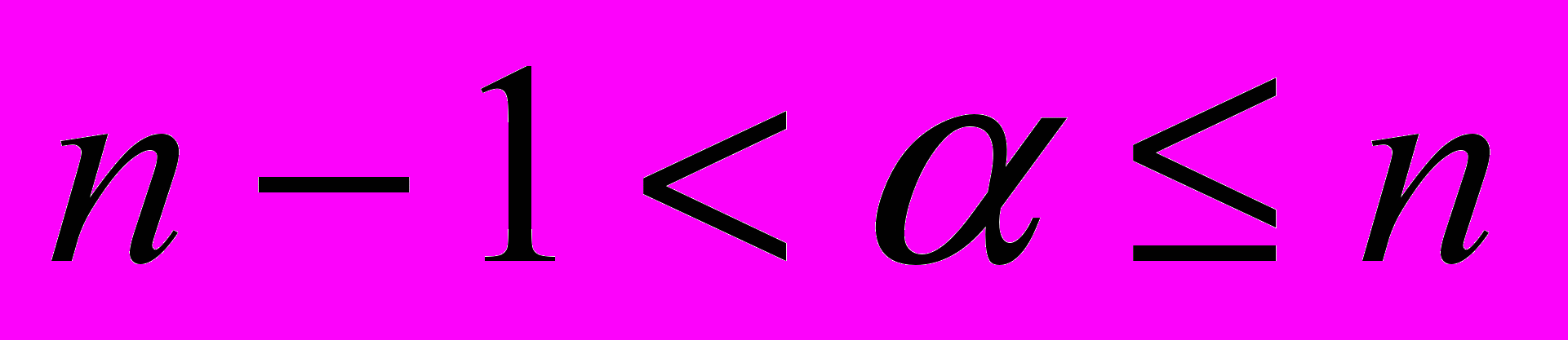, где , (1)

существование решения, которых с ненулевыми начальными условиями приведено в монографии [5] и включает в себя функции Миттаг-Леффлера [5]

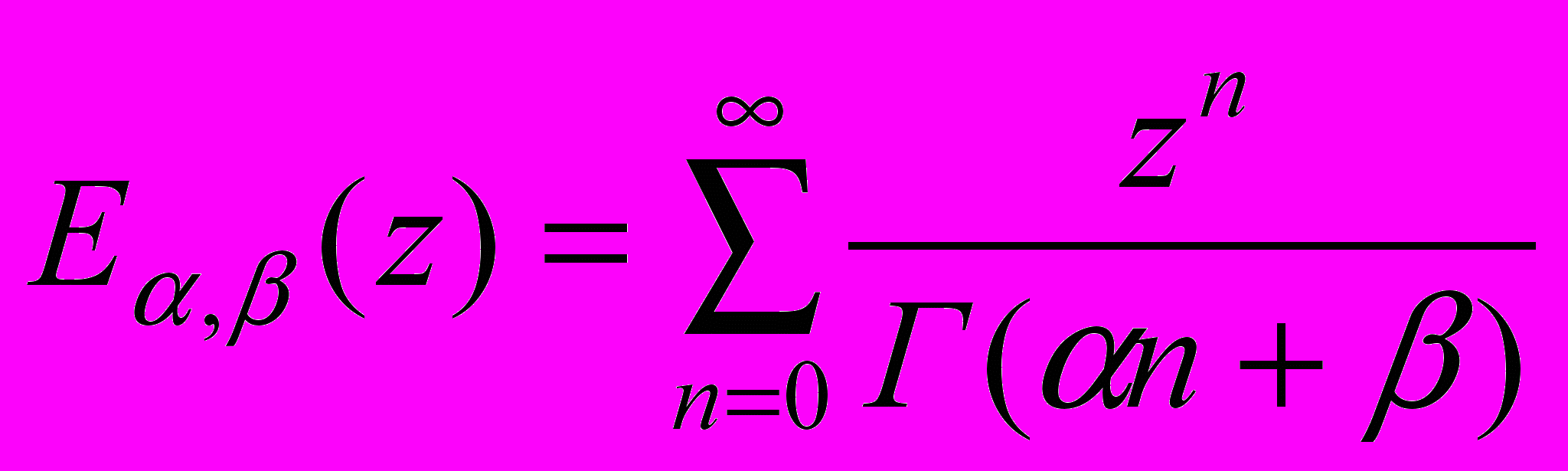, где, .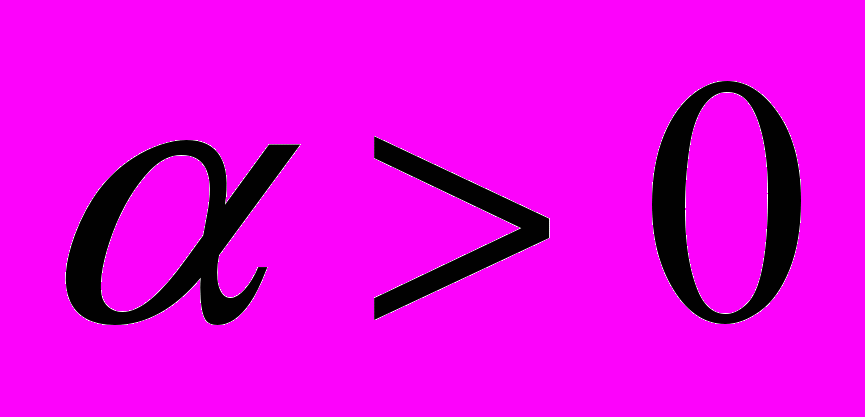

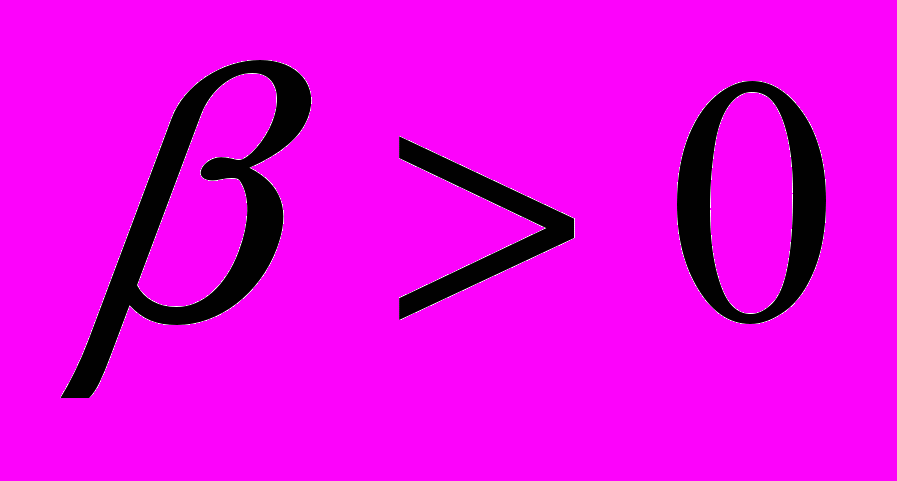2. Постановка задачи

Рассматриваются нелинейные системы вида

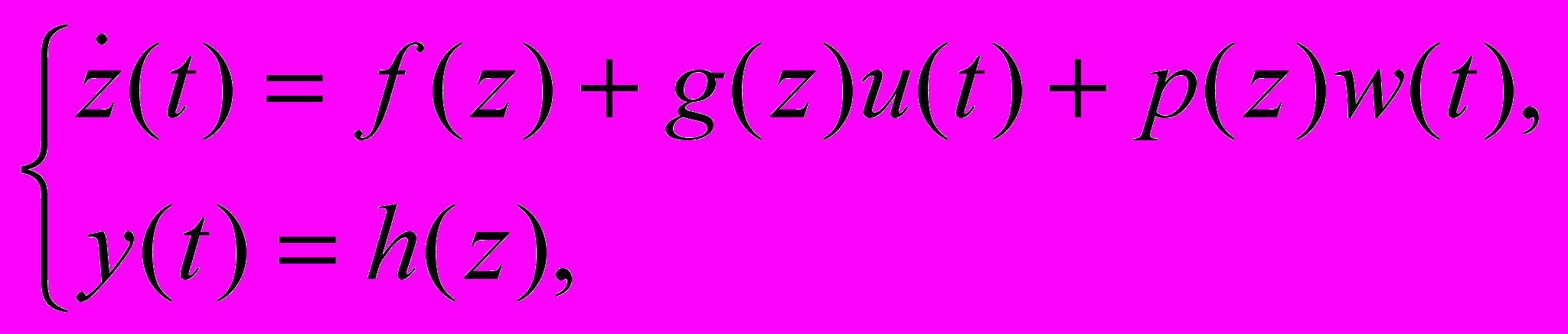(2)

где 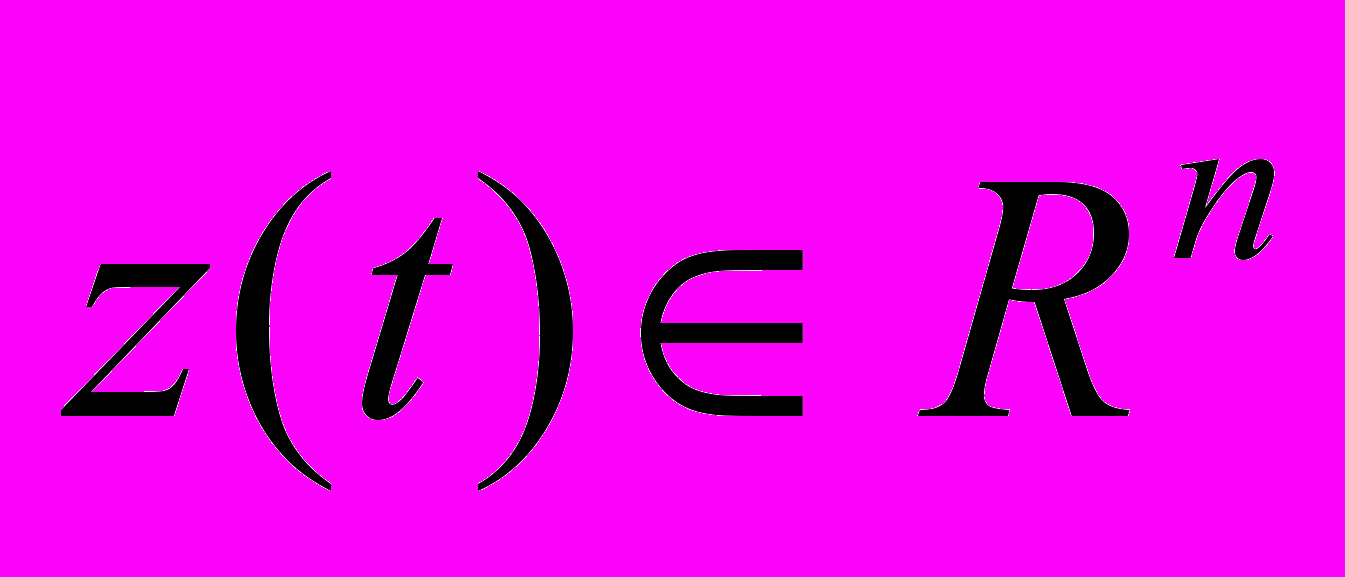– вектор состояния, 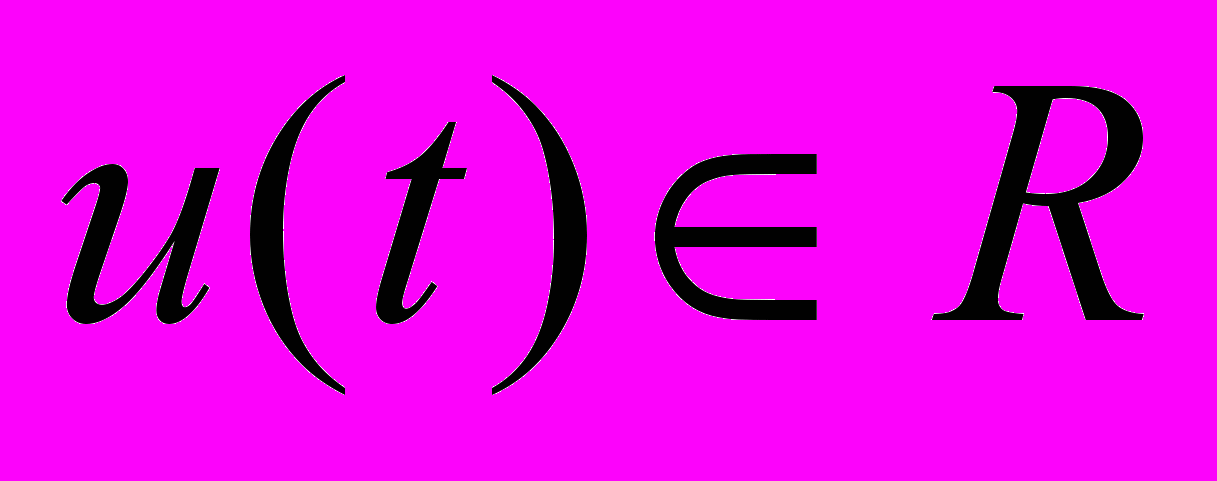– сигнал управления, 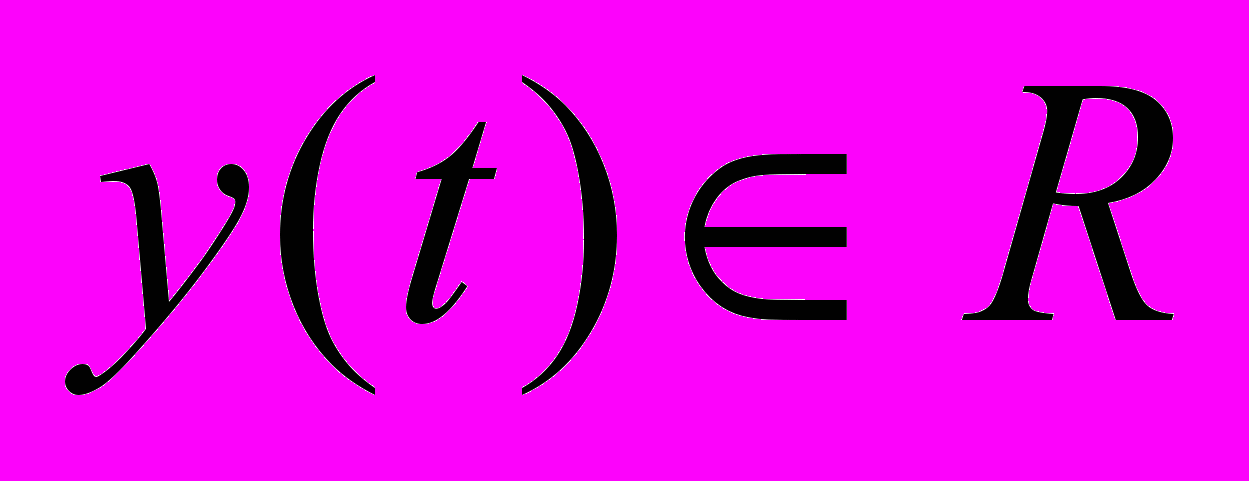– выходная (регулируемая) переменная, 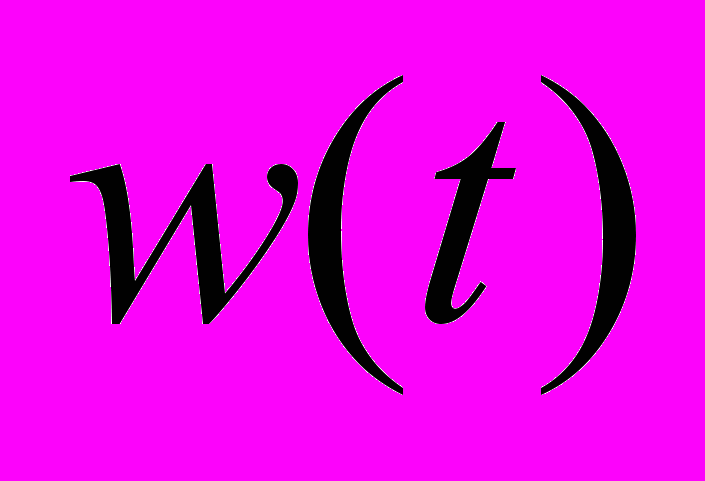– неизвестное ограниченное возмущение, 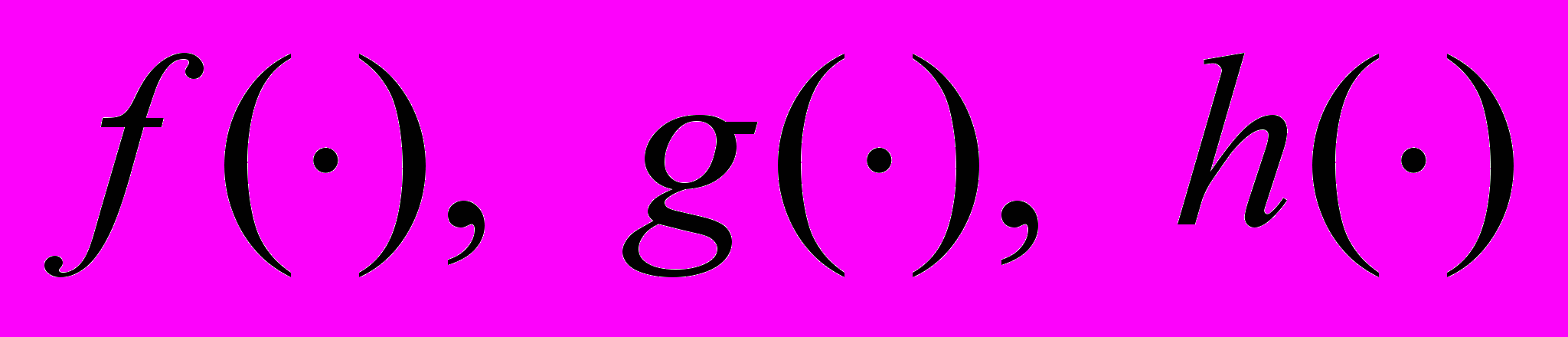, 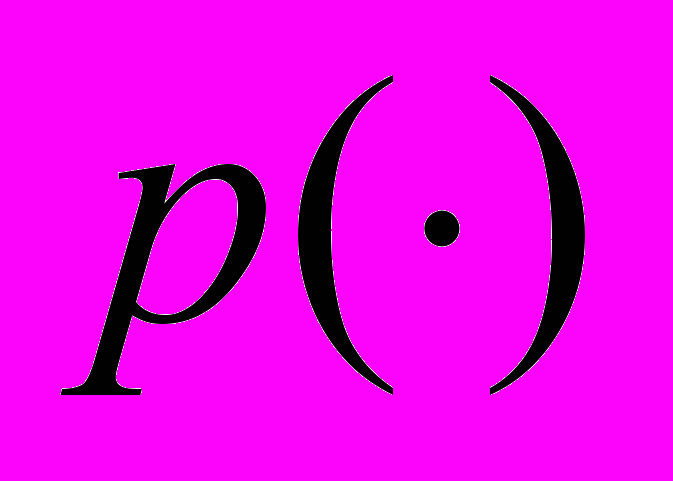– гладкие функции своих аргументов.

Допущение 1. Пусть 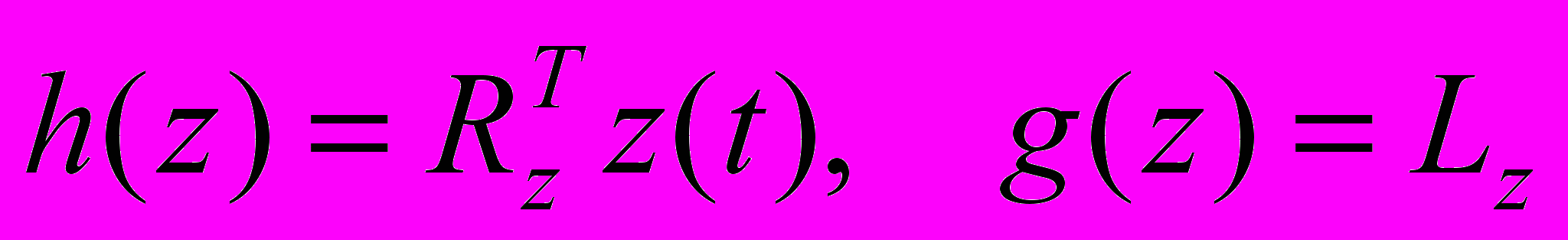, , 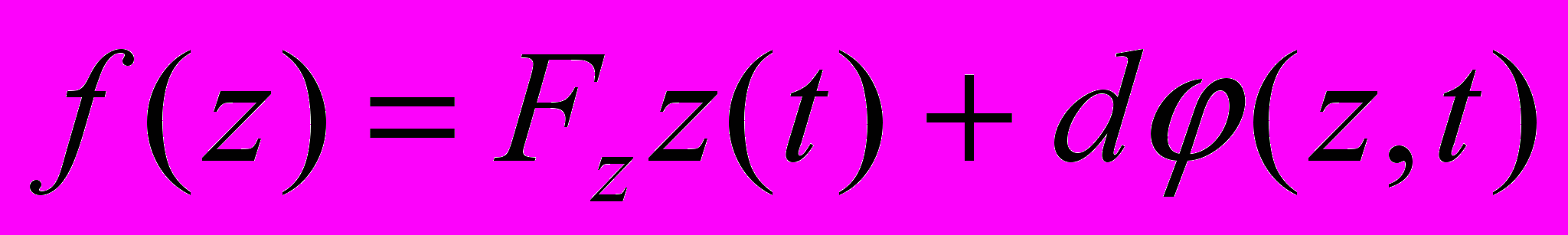где 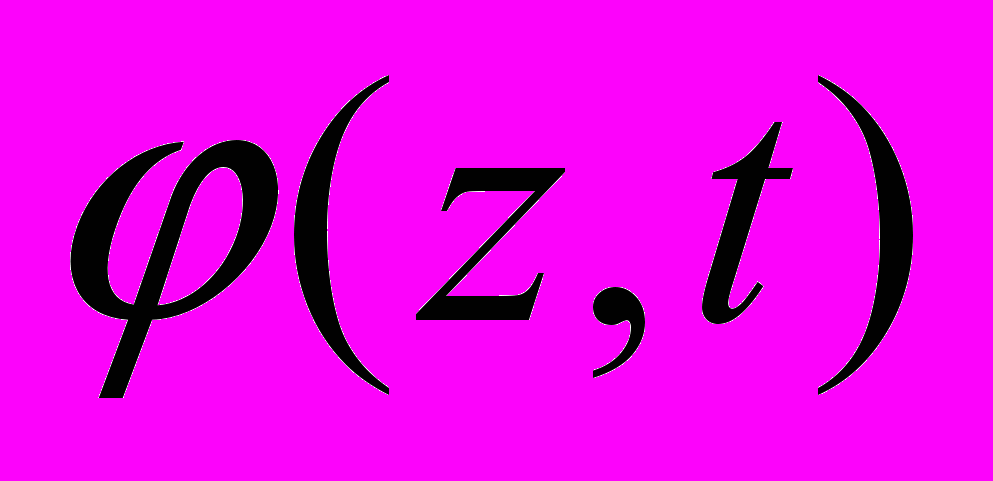– неизвестная функция и .

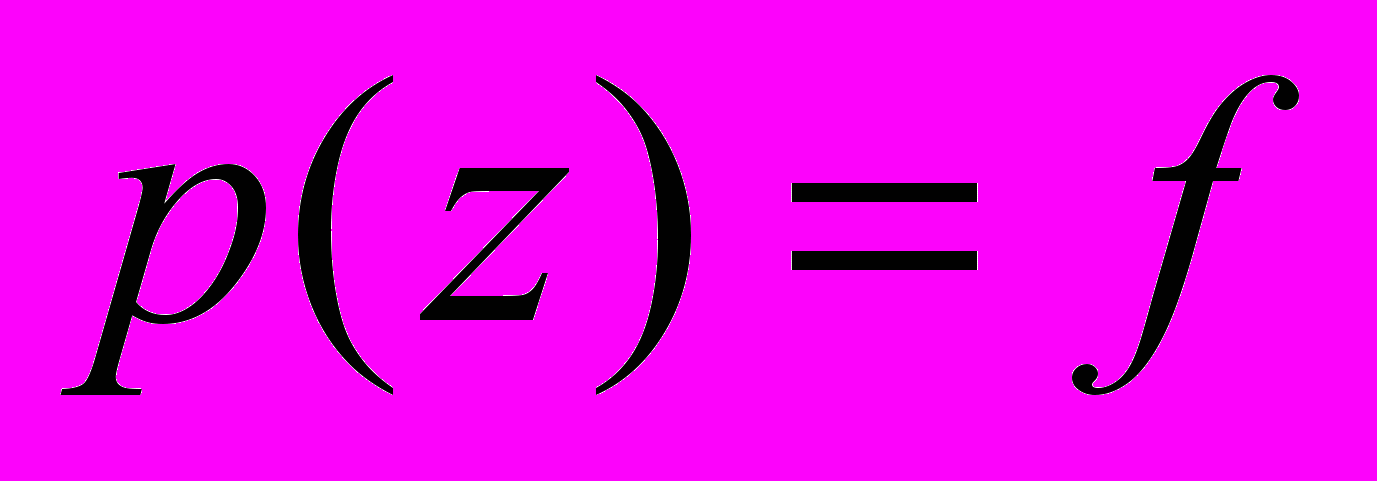Тогда модель (2) примет вид

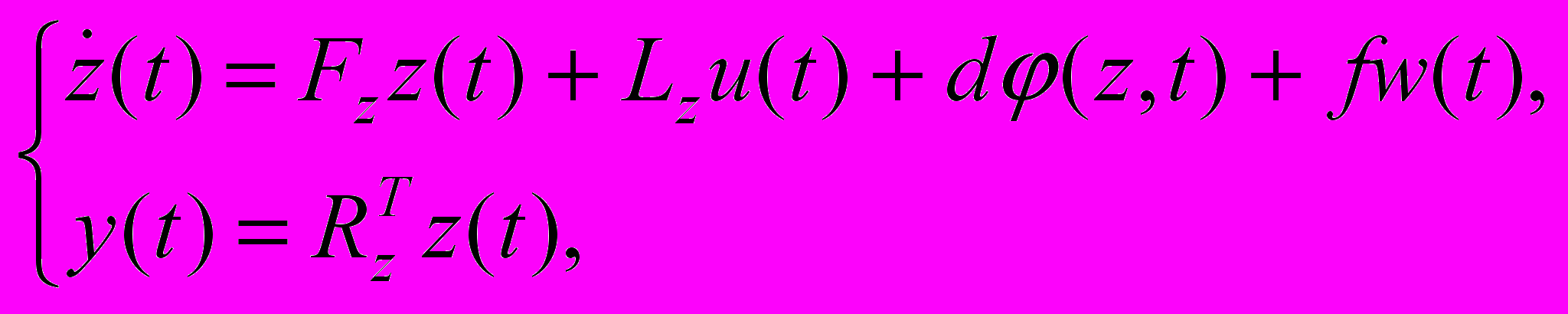(3)

где 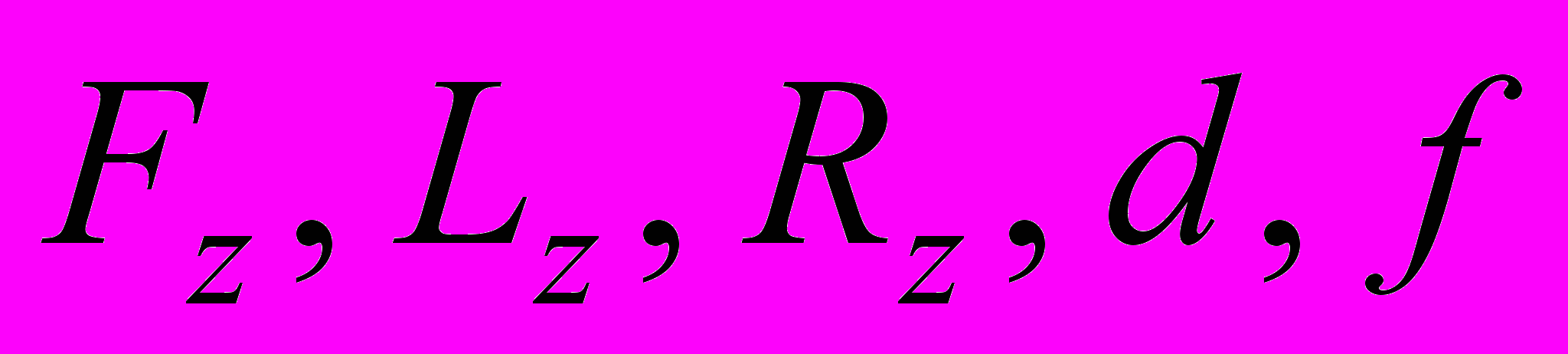– матрицы с неизвестными коэффициентами, пара 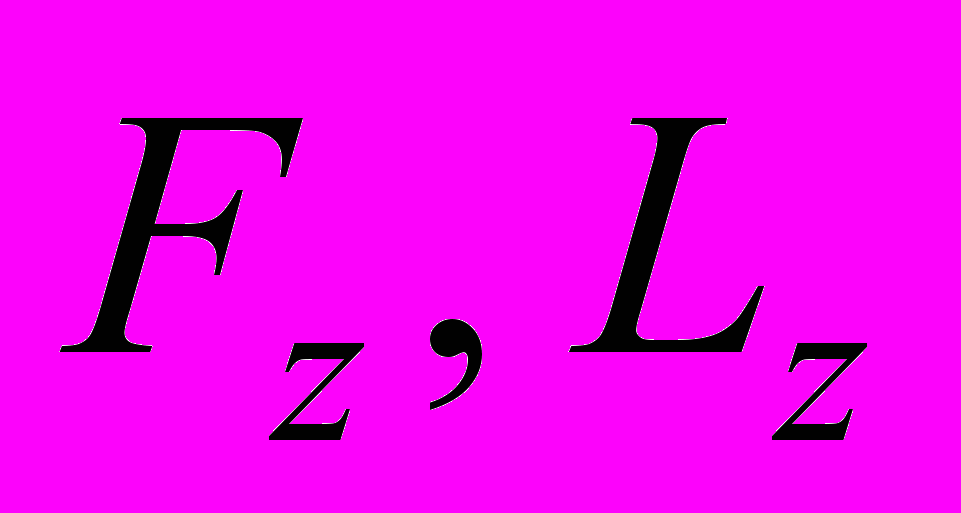– полностью управляемая, пара 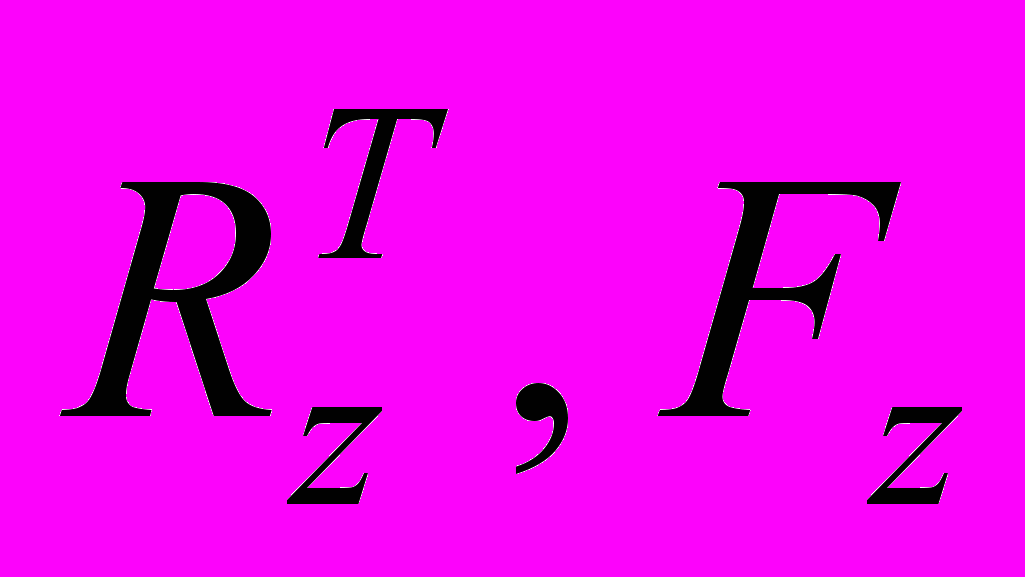– полностью наблюдаемая. Структурная схема нелинейной системы (3) приведена на рис. 1.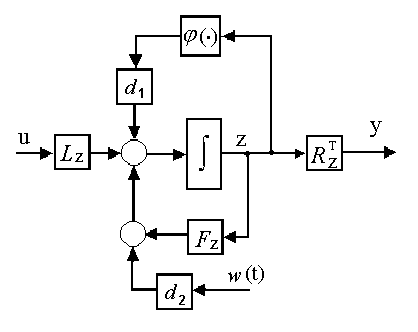



Рис. 1. Нелинейная система.

Заключение

Из всего перечисленного можно сделать вывод, что при всех отрицательных действительных корнях уравнение (1) сходится, то есть решение однородного дифференциального уравнения устойчиво в том случае, если все корни характеристического уравнения отрицательны.


Литература
    1. Сербина Л.И. Математическое моделирование движения влаги в средах с фрактальной структурой // Материалы VIII региональной конференции “Вузовская наука – Северо-Кавказскому региону”. Том первый. Естественные и точные науки. Технические и прикладные науки. Ставрополь: СевКав ГТУ, 2004. С. 212.
    2. Саичев А.И., Уткин С.Г. Асимптотические законы супердиффузии / Журнал технической физики. 2003. Том 73. Вып. 7. С. 1-6.
    3. Хоменко А.В., Ляшенко Я.А. Стохастическая теория непрерывного режима плавления ультратонкой пленки смазки / Журнал технической физики. 2005. Том 75. Вып. 11. С. 17-25.
    4. Самко С.Г., Килбас А.А., Марычев О.И. Интегралы и производные дробного порядка и некоторые их приложения. – Минск: Наука и техника, 1987. 688 с.
    5. Иващенко Н.Н. Автоматическое регулирование. Теория и элементы систем. – М.: Машиностроение, 1973, 606 с.