#G0 гост 12248-96 Группа Ж39 #G1 #G0межгосударственный стандарт грунты методы лабораторного определения характеристик прочности и деформируемости
| Вид материала | Документы |
СодержаниеG0образец графического оформления результатов Приложение х Приложение ц Приложение ш G0приложение щ |
- Государственный стандарт СССР гост 5180-84 "Грунты. Методы лабораторного определения, 566.97kb.
- Гост 310. 4-81. Цементы. Методы определения предела прочности при изгибе и сжатии, 164.5kb.
- Государственный стандарт союза сср бетоны определение прочности механическими методами, 393.25kb.
- Гост 24846-81 "Грунты. Методы измерения деформаций оснований зданий и сооружений", 380.07kb.
- Гост 5686-94 межгосударственный стандарт грунты методы полевых испытаний сваями, 555.3kb.
- Государственный стандарт СССР гост 26824-86 "Здания и сооружения. Методы измерения, 205.34kb.
- Государственный стандарт РФ гост р 51871-2002 "Устройства водоочистные. Общие требования, 1080.58kb.
- Гост р проект национальный стандарт российской федерации, 300.94kb.
- 01. 344. 02-80, 89.44kb.
- Государственный стандарт союза сср испытания на пожароопасность. Методы испытаний., 109.54kb.
#G0ОБРАЗЕЦ ГРАФИЧЕСКОГО ОФОРМЛЕНИЯ РЕЗУЛЬТАТОВ
ИСПЫТАНИЯ ГРУНТА МЕТОДОМ ОДНОПЛОСКОСТНОГО СРЕЗА
ПО ПОВЕРХНОСТИ СМЕРЗАНИЯ
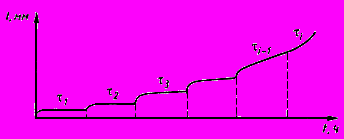
Рисунок Ф.1
ПРИЛОЖЕНИЕ Х
(рекомендуемое)
#G1
#G0ПРИНЦИПИАЛЬНАЯ СХЕМА УСТАНОВКИ ДЛЯ ИСПЫТАНИЯ
МЕРЗЛОГО ГРУНТА МЕТОДОМ ОДНООСНОГО СЖАТИЯ
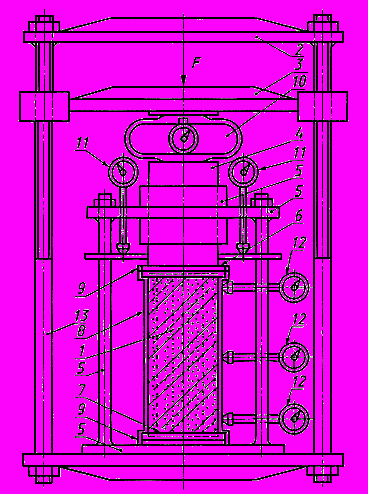
1 - образец грунта; 2 - неподвижная платформа; 3 - подвижная платформа; 4 - шток; 5 - направляющее устройство; 6 - верхний штамп; 7 - нижний штамп; 8 - паровлагонепроницаемая оболочка; 9 - резиновое прижимное кольцо; 10 - динамометр;
11 - измеритель продольных деформаций; 12 - измеритель поперечных деформаций; 13 - продольная тяга
Рисунок Х.1
ПРИЛОЖЕНИЕ Ц
(рекомендуемое)
#G1
#G0ОБРАЗЕЦ ГРАФИЧЕСКОГО ОФОРМЛЕНИЯ РЕЗУЛЬТАТОВ ИСПЫТАНИЯ
МЕРЗЛОГО ГРУНТА МЕТОДОМ ОДНООСНОГО СЖАТИЯ
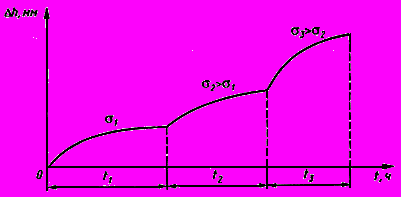
#G1
#G0Рисунок Ц.1
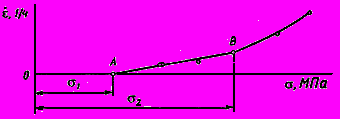
Рисунок Ц.2
ПРИЛОЖЕНИЕ Ш
(рекомендуемое)
#G1
#G0ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК ДЕФОРМИРУЕМОСТИ
МЕРЗЛОГО ГРУНТА ПО РЕЗУЛЬТАТАМ ИСПЫТАНИЯ
МЕТОДОМ ОДНООСНОГО СЖАТИЯ
1 Модуль линейной деформации
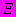 и коэффициент нелинейной деформации
и коэффициент нелинейной деформации 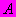 определяют по зависимости, устанавливающей связь между относительными продольными деформациями
определяют по зависимости, устанавливающей связь между относительными продольными деформациями 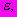 напряжениями
напряжениями 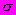 и временем действия нагрузки
и временем действия нагрузки 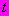
#G1

#G0
где
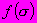 - функция напряжений
- функция напряжений 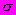 для времени
для времени 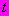 их действия, равного 1 ч, которую принимают в виде:
их действия, равного 1 ч, которую принимают в виде: 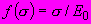 - для модели линейно деформируемого основания,
- для модели линейно деформируемого основания,#G1
#G0
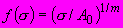 - для модели нелинейно деформируемого основания,
- для модели нелинейно деформируемого основания,где
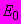 и
и 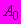 - параметры функции
- параметры функции 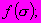
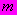 - коэффициент нелинейности по напряжениям.
- коэффициент нелинейности по напряжениям.2 Предельно длительные значения
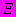 и
и 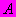 вычисляют по формулам:
вычисляют по формулам:

где
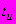 - время, равное сроку службы здания или сооружения и принимаемое
- время, равное сроку службы здания или сооружения и принимаемое 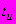 = 50 лет = 4,38·10
= 50 лет = 4,38·10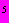 ч;
ч; 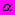 - коэффициент нелинейности во времени.
- коэффициент нелинейности во времени.3 Для установления зависимости (Ш.1) исходные данные испытаний (6.3.5) обрабатывают в соответствии с теорией наследственной ползучести. Используя кривую ползучести (6.3.5.7), последовательно вычисляют ряд значений
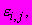 имеющих смысл деформаций, которые развились бы под действием постоянного напряжения (
имеющих смысл деформаций, которые развились бы под действием постоянного напряжения (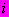 = 1, 2, ...), соответствующего напряжению
= 1, 2, ...), соответствующего напряжению 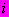 -й ступени нагружения, за время
-й ступени нагружения, за время 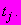 Вычисления производят по формуле
Вычисления производят по формуле 
где
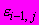 - полная относительная продольная деформация предшествующей ступени нагружения в момент времени
- полная относительная продольная деформация предшествующей ступени нагружения в момент времени 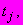 вычисленная по этой формуле ранее при
вычисленная по этой формуле ранее при 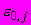 = 0;
= 0;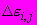 - приращение относительной деформации, определяемое по кривой ползучести (6.3.5.7) и представляющее собой разность между деформацией, накопленной к моменту, когда
- приращение относительной деформации, определяемое по кривой ползучести (6.3.5.7) и представляющее собой разность между деформацией, накопленной к моменту, когда 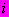 -я ступень нагрузки действовала в течение времени
-я ступень нагрузки действовала в течение времени 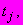 и деформацией, накопленной к началу действия
и деформацией, накопленной к началу действия 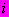 -й ступени нагрузки.
-й ступени нагрузки.Моменты времени
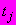 назначают одинаковыми для каждой ступени нагружения с учетом указаний 6.1.4.3.
назначают одинаковыми для каждой ступени нагружения с учетом указаний 6.1.4.3.Результаты представляют в виде семейства кривых ползучести при постоянных напряжениях
 (рисунок Ш.1).
(рисунок Ш.1).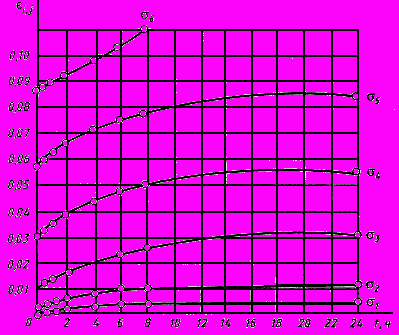
Рисунок Ш.1
4 Для определения параметра
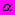 и набора значений
и набора значений 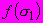 полученные значения
полученные значения 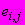 представляют в виде семейства параллельных прямых в координатах
представляют в виде семейства параллельных прямых в координатах 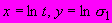 (рисунок Ш.2). Далее
(рисунок Ш.2). Далее 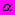 и
и 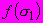 вычисляют по формулам:
вычисляют по формулам:

где
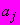 и
и 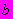 - параметры, определяемые графически или способом наименьших квадратов (пункт 8).
- параметры, определяемые графически или способом наименьших квадратов (пункт 8).5 Для модели линейно деформируемого основания набор значений
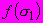 аппроксимируют прямой в координатах
аппроксимируют прямой в координатах 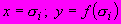 (рисунок Ш.3) и вычисляют значение
(рисунок Ш.3) и вычисляют значение 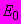 по формуле
по формуле 
где
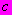 - параметр, определяемый графически или способом наименьших квадратов (пункт 9).
- параметр, определяемый графически или способом наименьших квадратов (пункт 9).6 Для модели нелинейно деформируемого основания набор значений
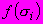 аппроксимируют прямой в координатах
аппроксимируют прямой в координатах 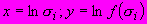 (рисунок Ш.4) и вычисляют значение
(рисунок Ш.4) и вычисляют значение 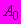 и
и 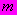 по формулам:
по формулам:
#G1

#G0
где
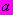 и
и 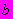 - параметры, определяемые графически или способом наименьших квадратов (пункт 10).
- параметры, определяемые графически или способом наименьших квадратов (пункт 10).-
#G0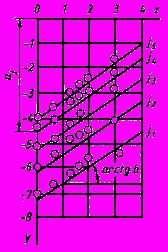
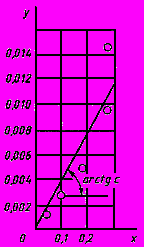
Рисунок Ш.2.
Рисунок Ш.3.
7 Коэффициент поперечного расширения
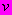 определяют из зависимости, устанавливающей связь между относительными продольными
определяют из зависимости, устанавливающей связь между относительными продольными 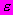 и поперечными деформациями
и поперечными деформациями 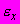
#G1

#G0
Для определения
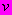 экспериментальные данные (относительные продольные и поперечные деформации) в конце каждой ступени нагружения, определяемые по пункту 3, представляют в координатах
экспериментальные данные (относительные продольные и поперечные деформации) в конце каждой ступени нагружения, определяемые по пункту 3, представляют в координатах 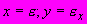 (рисунок Ш.3). Далее значения
(рисунок Ш.3). Далее значения 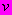 вычисляют по формуле
вычисляют по формуле 
где
 - параметр, определяемый графически или способом наименьших квадратов (пункт 9).
- параметр, определяемый графически или способом наименьших квадратов (пункт 9).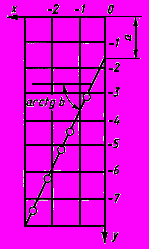
Рисунок Ш.4.
8 Параметры
 и
и  уравнения семейства параллельных прямых
уравнения семейства параллельных прямых 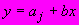 определяют графически (рисунок Ш.2), при этом:
определяют графически (рисунок Ш.2), при этом: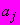 - в масштабе чертежа равен отрезку, отсекаемому на оси ординат
- в масштабе чертежа равен отрезку, отсекаемому на оси ординат 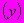
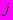 -й из семейства параллельных прямых наилучшего приближения к экспериментальным точкам;
-й из семейства параллельных прямых наилучшего приближения к экспериментальным точкам;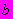 - в масштабе чертежа равен тангенсу угла наклона семейства параллельных прямых к оси абсцисс
- в масштабе чертежа равен тангенсу угла наклона семейства параллельных прямых к оси абсцисс 
Способом наименьших квадратов параметры
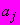 и
и 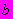 определяют по формулам:
определяют по формулам:
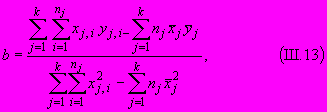
где
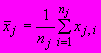 и
и 
- средние значения координат экспериментальных точек соответственно
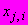 и
и 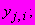
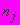 - число точек в
- число точек в 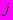 -й выборке;
-й выборке;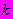 - число
- число 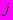 -х выборок.
-х выборок.9 Параметр
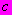 уравнения прямой, проходящей через начало координат
уравнения прямой, проходящей через начало координат 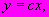 определяют графически (рисунок Ш.3), при этом
определяют графически (рисунок Ш.3), при этом 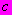 в масштабе чертежа равен тангенсу угла наклона к оси абсцисс
в масштабе чертежа равен тангенсу угла наклона к оси абсцисс 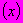 прямой наилучшего приближения к экспериментальным точкам, проходящей через начало координат.
прямой наилучшего приближения к экспериментальным точкам, проходящей через начало координат.Способом наименьших квадратов параметр
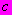 определяют по формуле
определяют по формуле 
#G1
| #G0где 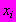 и и 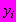 | - координаты экспериментальных точек; |
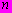 | - число точек. |
10 Параметры
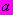 и
и 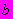 уравнения прямой
уравнения прямой 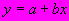 определяют графически (рисунок Ш.4), при этом:
определяют графически (рисунок Ш.4), при этом: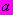 в масштабе чертежа равен отрезку, отсекаемому на оси ординат
в масштабе чертежа равен отрезку, отсекаемому на оси ординат 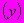 прямой наилучшего приближения к экспериментальным точкам;
прямой наилучшего приближения к экспериментальным точкам;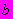 в масштабе чертежа равен тангенсу угла наклона прямой к оси абсцисс
в масштабе чертежа равен тангенсу угла наклона прямой к оси абсцисс 
Способом наименьших квадратов параметры
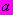 и
и 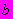 определяют по формулам:
определяют по формулам: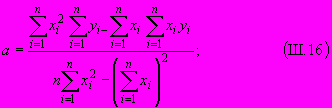
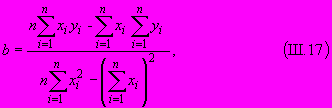
где
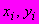 и
и 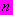 - то же, что и в пункте 9.
- то же, что и в пункте 9. 11. Исходные данные и результаты расчета записывают в таблицу Ш.1.
#G1
#G0 Таблица Ш.1
(левая часть)
| #G0Но- мер сту- пени наг- ру- же- ния  | Нап- ря- же- ние 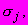 МПа | Вре- мя отс- чета де- фор- ма- ций 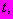 ч ч | Отно- сите- льные про- доль- ные дефо- рма- ции 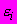 | При- раще- ние отно- сите- льных про- доль- ных дефо- рма- ций 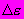 | Отно- сите- льные про- доль- ные дефо- рма- ции 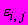 от пос- то- янных нап- ряже- ний | Отно- сите- льные попе- реч- ные дефо- рма- ции 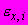 | При- раще- ние отно- сите- льных попе- реч- ных дефо- рма- ций 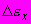 | Отно- сите- льные попе- реч- ные дефо- рма- ции 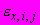 от пос- то- янных нап- ряже- ний | Функ- ции нап- ряже- ний 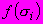 | Коэф- фици- ент нели- ней- нос- ти во вре- мени 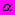 | Пара- метр 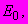 МПа·ч | Пара- метр 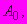 МПа·ч |
| | | | | | | | | | | | | |
#G1
#G0 Таблица Ш.1
(правая часть)
| #G0Мо- дуль лине- йной дефо- рма- ции 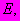 МПа | Коэффициент нелинейной деформации 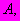 МПа | Показатель нелиней- ности по напряже- ниям 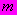 | Коэф- фици- ент попе- реч- ного рас- шире- ния 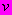 | Условно- мгновен- ное сопроти- вление 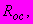 МПа | Пре- дел дли- тель- ной проч- нос- ти 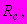 МПа | При- меча- ние |
| | | | | | | |
#G1
#G0ПРИЛОЖЕНИЕ Щ
(рекомендуемое)
#G1
#G0ОБРАЗЕЦ ГРАФИЧЕСКОГО ОФОРМЛЕНИЯ РЕЗУЛЬТАТОВ
ИСПЫТАНИЯ МЕРЗЛОГО ГРУНТА МЕТОДОМ
КОМПРЕССИОННОГО СЖАТИЯ
| #G0 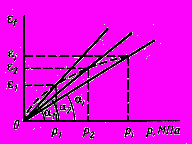 | 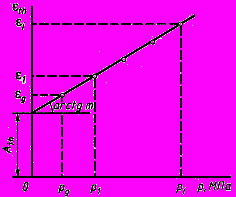 |
| Рисунок Щ.1 | Рисунок Щ.2 |
#G1
Текст документа сверен по:
официальное издание
МНТКС - М.: ИПК Издательство
стандартов, 1997
