Длинные конечно, но выбрать нужное можно!!!

Вид материала

Программа

Содержание Инварианты в программировании 2) Кольцевой связный список 3) Список с пропусками 4) Развёрнутый связный список Рекурсивным называется объект Алгоритм называется рекурсивным Бинарное дерево

Подобный материал:

• Межрегионального Маркетингового Центра «Владимир-Москва» было проведено исследование, 69.27kb.
• 9. Православное учение о человеке, 3218.12kb.
• 9. Православное учение о человеке, 6232.66kb.
• Коммерческий акт №, 22.66kb.
• Как выбрать санки.                                                                                                               , 126.61kb.
• Самостоятельная работа Философская концепция мыслителя (2004) Самостоятельная работа, 784.22kb.
• Самостоятельная работа 10. Философская концепция мыслителя Эта самостоятельная работа, 807.98kb.
• Цели и задачи логистики, 43.75kb.
• Игра по литературе «Эрудит» (11 класс), 137.84kb.
• 9. Упрощенная система налогообложения, 98.06kb.

Инварианты в программировании

Пока мы представили инварианты как мощный инструмент для решения задач по математике. Однако, инварианты встречаются в программировании гораздо чаще, чем можно себе представить. Фактически, любая повторяющаяся операция в алгоритме содержит инвариант!

Утверждение - это предложение, которое можно проверить (оно может оказаться истинным или ложным).

27. Какие инварианты имеет смысл выбрать при доказательстве корректности алгоритмов поиска? Почему?///////////////(см вопрос 23)

28. Что такое связный список? Какие виды связных списков Вы знаете?

Связный список — структура данных, состоящая из узлов, каждый из которых содержит как собственные данные, так и одну или две ссылки («связки») на следующее и/или предыдущее поле. Принципиальным преимуществом перед массивом является структурная гибкость: порядок элементов связного списка может не совпадать с порядком расположения элементов данных в памяти компьютера, а порядок обхода списка всегда явно задаётся его внутренними связями.

Виды связных списков

1) Линейный связный список

1.1 Односвязный список. В односвязном списке можно передвигаться только в сторону конца списка. Узнать адрес предыдущего элемента невозможно.



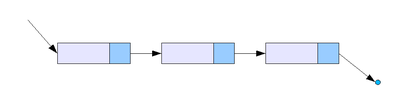
1.2 Двусвязный список. По двусвязному списку можно передвигаться в любом направлении — как к началу, так и к концу. В этом списке проще производить удаление и перестановку элементов, т.к. всегда известны адреса тех элементов списка, указатели которых направлены на изменяемый элемент.



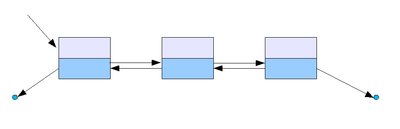
1.3 XOR-связный список

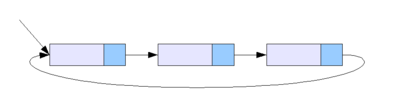
2) Кольцевой связный список

Разновидностью связных списков является кольцевой (циклический, замкнутый) список. Он тоже может быть односвязным или двусвязным. Последний элемент кольцевого списка содержит указатель на первый, а первый (в случае двусвязного списка) — на последний.



3) Список с пропусками

Список с пропусками - это несколько слоев. Нижний слой - это обычный упорядоченный связный список.




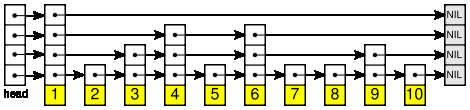
4) Развёрнутый связный список — список, каждый физический элемент которого содержит несколько логических (обычно в виде массива, что позволяет ускорить доступ к отдельным элементам).


29. Какие операции доступны над связными списками? Какую временную сложность они имеют?

Р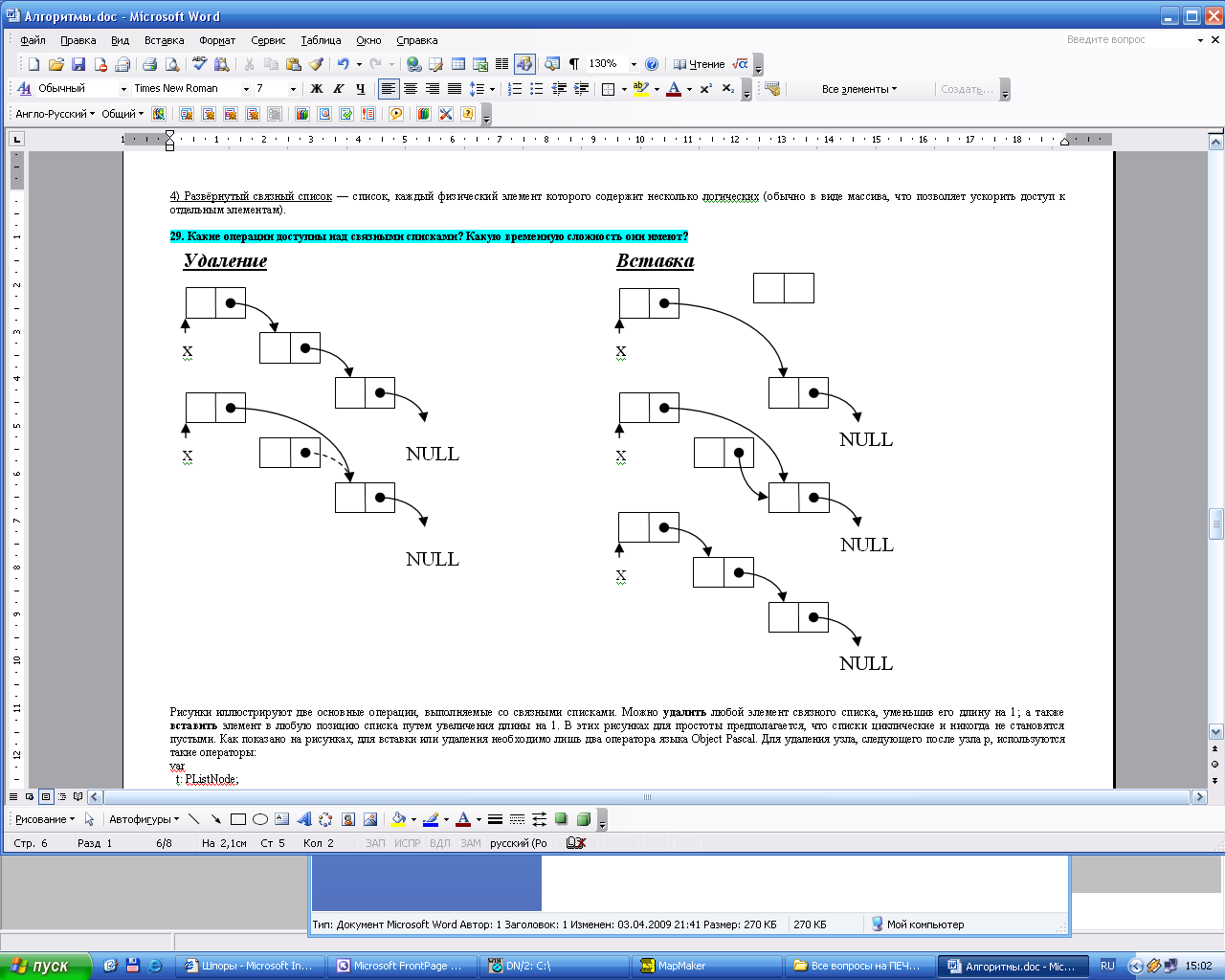исунки иллюстрируют две основные операции, выполняемые со связны­ми списками. Можно удалить любой элемент связного списка, уменьшив его длину на 1; а также вставить элемент в любую позицию списка путем увеличения длины на 1. В этих ри­сунках для простоты предполагается, что списки циклические и никогда не становятся пустыми. Как показано на рисун­ках, для вставки или удаления необходимо лишь два оператора языка Object Pascal. Для удаления узла, следующего пос­ле узла p, используются такие операторы:

var

t: PListNode;

...

t:= p.Next;

p.Next:= t.Next;

Dispose (t);

Для вставки в список узла t в позицию, следу­ющую за узлом p используется такие операторы:

t.Next:= p.Next;

p.Next:= t;

Простота вставки и удаления оправдывает су­ществование связных списков. Соответствующие операции неестественны и неудобны для масси­вов, поскольку требуют перемещения всего со­держимого массива, которое следует после затра­гиваемого элемента.

Связные списки плохо приспособлены для по­иска k-того элемента (по индексу) – операции, которая характеризует эффективность доступа к данным массивов. В массиве для доступа к k-тому элементу используется простая запись a[k], а в списке для этого необходимо отследить k ссылок.

Для удаления из связного списка узла, следующего за узлом p, значение t устанавливается таким образом, чтобы указатель ссылался на удаляемый узел, а затем изменяется указатель p: p.Next. Указатель t может использоваться для ссылки на удаляемый узел. Хотя его ссылка по-прежнему указывает на список, обычно подобная ссылка не используется после удаления узла из списка, за исключением, возможно, информирования системы через вызов Dispose () о том, что задействованная память может быть вновь востребована.

Другая операция, неестественная для списков с единичными ссылками, – "поиск элемента, пред­шествующего данному".

После удаления узла из связного списка по­средством операции p.Next:= p.Next.Next, повторное обращение к нему окажется невоз­можным.


30. Какую временную сложность имеет алгоритм сортировки слиянием для односвязного списка? Для двухсвязного списка?

Односвязный список: Узнать адрес предыдущего элемента невозможно.

Для сортировки связных списков обычно используют алгоритм сортировки слиянием. Сортировка слиянием (merge sort) – алгоритм сортировки, который упорядочивает списки (или другие структуры данных, доступ к элементам которых можно получать только последовательно, например – потоки) в определённом порядке. Эта сортировка – хороший пример использования принципа «разделяй и властвуй».

Предположим, что имеется односвязный список с одним фиктивным начальным узлом. Таким образом, каждый сортируемый узел будет иметь родительский узел. Рассмотрим процесс слияния. Пусть имеются два списка, описываемых родительскими узлами первых узлов. Будем считать, что оба списка отсортированы. Можно легко разработать алгоритм слияния двух таких списков в один. При этом, процесс будет заключаться только в выполнении удалений и вставок.

31. Какое пространство занимает односвязный список размером 10, элементами данных в котором служат целые числа? Проведите расчет.////////////////

---*----32. Какое пространство занимает двухсвязный список размером 10, элементами данных в котором служат целые числа? Проведите расчет.

Двусвязным списком называется связанное хранение линейного списка, если каждый элемент хранения имеет два компонента указателя (ссылки на предыдущий и последующий элементы линейного списка).

33. Что такое дерево? Какие виды деревьев Вы знаете?

Деревья – это математические абстракции, играющие главную роль при разработ­ке и анализе алгоритмов, поскольку

• мы используем деревья для описания динамических свойств алгоритмов;
  
• мы строим и используем явные структуры данных, которые являются конкрет­ными реализациями деревьев.
  

Мы часто встречаемся с деревьями в повседневной жизни – это основное поня­тие очень хорошо знакомо. Например, многие люди отслеживают предков и наслед­ников с помощью генеалогического дерева; как будет показано, значительная часть терминов заимствована именно из этой области применения. Еще один пример – организация спортивных турниров; среди прочих, в исследовании этого применения принял участие и Льюис Кэрролл. В качестве третьего примера мож­но привести организационную диаграмму большой корпорации; это применение от­личается иерархическим разделением, характерным для алгоритмов типа "разделяй и властвуй". Четвертым примером служит дерево синтаксического разложения предложения английского (или любого другого языка) на составляющие его части; такое дерево близко связано с обработкой компьютерных языков.

Применительно к компьютерам, одно из наиболее известных применений струк­тур деревьев – для организации файловых систем. Файлы хранятся в каталогах (иног­да называемых также папками), которые рекурсивно определяются как последова­тельности каталогов и файлов. Это рекурсивное определение снова отражает естественное рекурсивное разбиение на составляющие и идентично определению определенного типа дерева.

Существует множество различных типов деревьев, и важно понимать различие между абстракцией и конкретным представлением, с которым выполняется работа для данного приложения. Соответственно, мы подробно рассмотрим различные типы деревьев и их представления. Рассмотрение начнется с определения деревьев как аб­страктных объектов и с ознакомления с большинством основных связанных с ними терминов. Мы неформально рассмотрим различные типы деревьев, которые следу­ет рассматривать в порядке сужения самого этого понятия:

• деревья;
  
• деревья с корнем;
  
• упорядоченные деревья;
  
• n-арные и бинарные деревья.
  

После этого неформального рассмотрения мы перейдем к формальным опреде­лениям и рассмотрим представления и приложения. На рисунке приведена иллюст­рация многих из этих базовых концепций, которые будут сначала рассматриваться, а затем и определяться.

Дерево – это непустая коллекция вершин и ребер, удовлетворяющих опре­деленным требованиям. Вершина – это простой объект (называемый также уз­лом), который может иметь имя и содержать другую связанную с ним инфор­мацию; ребро – это связь между двумя вершинами. Путь в дереве – это список отдельных вершин, в котором следующие друг за другом вершины соединя­ются ребрами дерева. Определяющее свойство дерева – существование только одно пути, соединяющего любые два узла. Если между какой-либо парой узлов существу­ет более одного пути или если между какой-либо парой узлов путь отсутствует, мы имеем граф, а не дерево. Несвязанный набор деревьев называется лесом .

Дерево с корнем – это дерево, в котором один узел назна­чен корнем дерева. В области компьютеров термин дерево обычно применяется к деревьям с корнем, а термин свободное дерево – к более общим структу­рам, описанным в предыдущем абзаце. В дереве с корнем любой узел является кор­нем поддерева, состоящего из него и расположенных под ним узлов.

С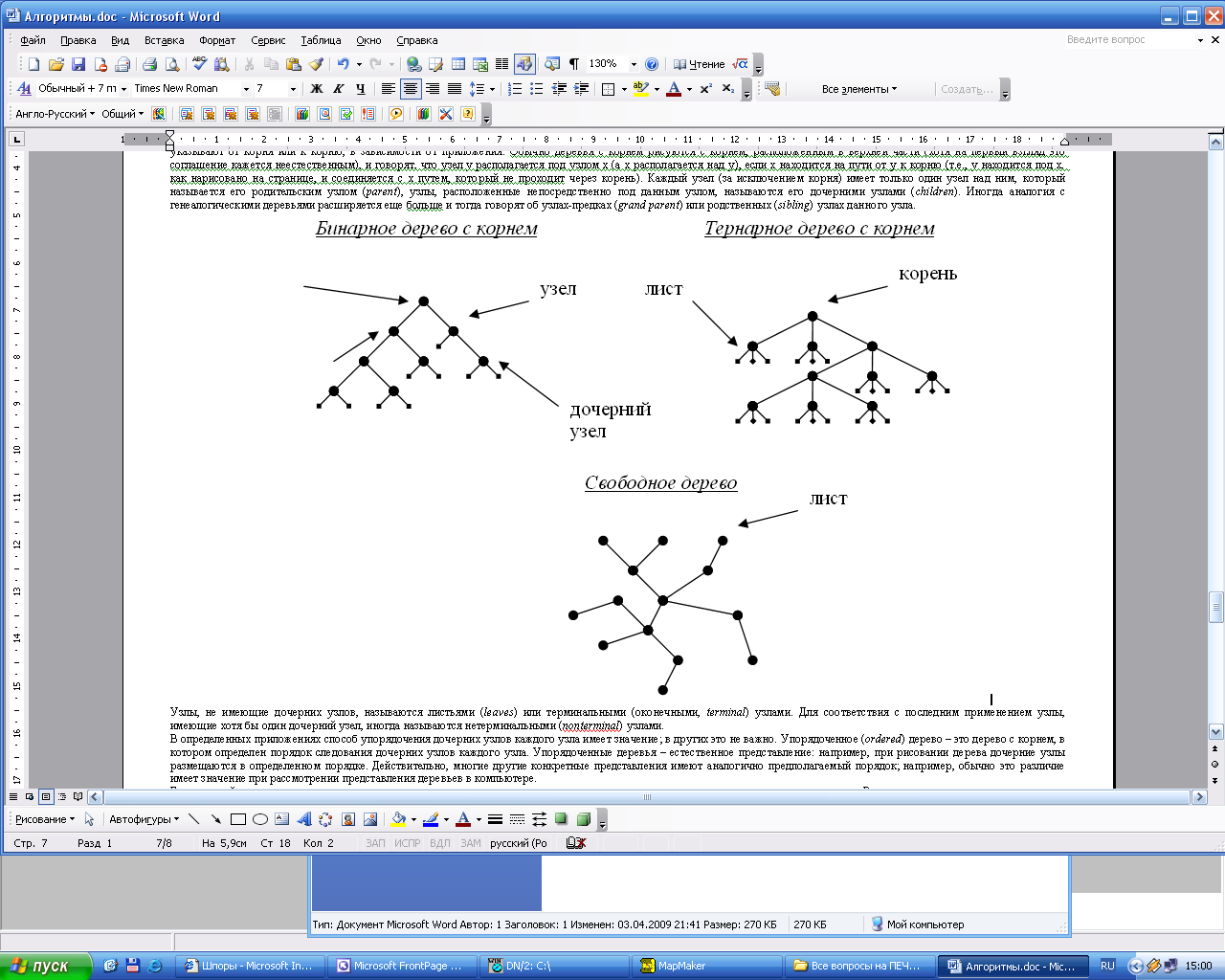уществует только один путь между корнем и каждым из других узлов дерева. Данное определение никак не определяет направление ребер; обычно считается, что все ребра указывают от корня или к корню, в зависимости от приложения. Обычно деревья с корнем рисуются с корнем, расположенным в верхней части (хотя на пер­вый взгляд это соглашение кажется неестественным), и говорят, что узел y распола­гается под узлом x (а x располагается над y), если x находится на пути от y к корню (т.е., у находится под x, как нарисовано на странице, и соединяется с x путем, кото­рый не проходит через корень). Каждый узел (за исключением корня) имеет только один узел над ним, который называется его родительским узлом (parent), узлы, распо­ложенные непосредственно под данным узлом, называются его дочерними узлами. Иногда аналогия с генеалогическими деревьями расширяется еще больше и тогда говорят об узлах-предках или родственных узлах данно­го узла.

Узлы, не имеющие дочерних узлов, называются листьями или терминаль­ными узлами. Для соответствия с последним применением узлы, имеющие хотя бы один дочерний узел, иногда называются нетерминальными узлами.

В определенных приложениях способ упорядочения дочерних узлов каждого узла имеет значение; в других это не важно. Упорядоченное дерево – это дерево с корнем, в котором определен порядок следования дочерних узлов каждого узла. Упорядоченные деревья – естественное представление: например, при рисовании де­рева дочерние узлы размещаются в определенном порядке. Действительно, многие другие конкретные представления имеют аналогично предполагаемый порядок; например, обычно это различие имеет значение при рассмотрении представления дере­вьев в компьютере.

Если каждый узел должен иметь конкретное количество дочерних узлов, появля­ющихся в конкретном порядке, мы имеем n-арное дерево. В таком дереве часто можно определить специальные внешние узлы, которые не имеют дочерних узлов. Тогда внешние узлы могут действовать в качестве фиктивных, на которые ссылаются узлы, не имеющие указанного количества дочерних узлов. В частности, простейшим типом n-арного дерева является бинарное дерево. Бинарное дерево – это упоря­доченное дерево, состоящее из узлов двух типов: внешних узлов без дочерних узлов и внутренних узлов, каждый из которых имеет ровно два дочерних узла. Поскольку два дочерних узла каждого внутреннего узла упорядочены, говорят о левом дочернем и правом дочернем узлах внутренних узлов. Каждый внутрен­ний узел должен иметь и левый, и правый дочерние узлы, хотя один из них или оба могут быть внешними узлами. Лист в n-арном дереве – это внутренний узел, все дочерние узлы которого являются внешними.


34. Что такое бинарное дерево поиска? В чем отличие бинарного дерева поиска от простого бинарного дерева?

Метод бинарного поиска

На практике довольно часто производится поиск в массиве, элементы которого упорядочены по некоторому критерию (такие массивы называются упорядоченными). Например, массив фамилий, как правило, упорядочен по алфавиту, массив данных о погоде — по датам наблюдений. В случае, если массив упорядочен, то применяют другие, более эффективные по сравнению с методом простого перебора алгоритмы, один из которых — метод бинарного поиска.

Пусть есть упорядоченный по возрастанию массив целых чисел. Нужно определить, содержит ли этот массив некоторое число (образец).

Метод (алгоритм) бинарного поиска реализуется следующим образом:

1. Сначала образец сравнивается со средним (по номеру) элементом массива (рис. 5.10, а).

• Если образец равен среднему элементу, то задача решена.
  
• Если образец больше среднего элемента, то это значит, что искомый элемент расположен ниже среднего элемента (между элементами с номерами sred+1 и niz), и за новое значение verb принимается sred+i, а значение niz не меняется
  
• Если образец меньше среднего элемента, то это значит, что искомый элемент расположен выше среднего элемента (между элементами с номерами verh и sred-1), и за новое значение niz принимается sred-1, а значение verh не меняется
  
• 2. После того как определена часть массива, в которой может находиться искомый элемент, по формуле (niz-verh) /2+verh вычисляется новое значение sred и поиск продолжается.
  

Алгоритм бинарного поиска, блок-схема которого представлена на рис. 5.11, заканчивает свою работу, если искомый элемент найден или если перед выполнением очередного цикла поиска обнаруживается, что значение verh больше, чем niz.

Вид диалогового окна программы Бинарный поиск в массиве приведен на рис. 5.12. Поле метки Label3 используется для вывода результатов поиска и протокола поиска. Протокол поиска выводится, если установлен флажок выводить протокол. Протокол содержит значения переменных verh, niz, sred. Эта информация, выводимая во время поиска, полезна для понимания сути алгоритма.


35. Что такое рекурсия? Почему рекурсивные алгоритмы удобно применять при обработке деревьев?

Рекурсивным называется объект, частично состоящий или определяемый с помощью самого себя. Факториал — это классический пример рекурсивного объекта. Факториал числа п — это произведение целых чисел от 1 до п. Обозначается факториал числа п так: n!.

Таким образом, если вычисление факториала п реализовать как функцию, то в теле этой функции будет инструкция вызова функции вычисления факториала числа (п - 1), т. е. функция будет вызывать сама себя. Такой способ вызова называется рекурсией, а функция, которая обращается сама к себе, называется рекурсивной функцией

Алгоритм называется рекурсивным, если он прямо или косвенно обращается к самому себе. Часто в основе такого алгоритма лежит рекурсивное определение какого-то понятия. Например, о факториале числа N можно сказать, что N! = N*(N – 1)!, если N > 0 и N! = 1 если N = 0. Это – рекурсивное определение.

Деревья – это математические абстракции, играющие главную роль при разработ­ке и анализе алгоритмов, поскольку мы используем деревья для описания динамических свойств алгоритмов;мы строим и используем явные структуры данных, которые являются конкрет­ными реализациями деревьев.

Бинарное дерево (binary tree) – это упоря­доченное дерево, состоящее из узлов двух типов: внешних узлов без дочерних узлов и внутренних узлов, каждый из которых имеет ровно два дочерних узла. Поскольку два дочерних узла каждого внутреннего узла упорядочены, говорят о левом дочернем (left child) и правом дочернем узлах (right child) внутренних узлов.

Математические свойства бинарных деревьев. Свойства бинарных деревьев:

• Бинарное дерево с N внутренними узлами имеет N + 1 внешних узлов.
  
• Бинарное дерево с N внутренними узлами имеет 2N связей: N-1 связей с внутренними узлами и N+1 связей с внешними узлами.
  

Из этих соотношений следуют также простые рекурсивные определения, вытека­ющие непосредственно из рекурсивных определений деревьев и бинарных деревьев. Например, высота дерева на 1 больше максимальной высоты поддеревьев его кор­ня, а длина пути дерева, имеющего N узлов равна сумме длин путей поддеревьев его корня плюс N-1. Приведенные соотношения также непосредственно связаны с ана­лизом рекурсивных алгоритмов. Например, для многих рекурсивных вычислений вы­сота соответствующего дерева в точности равна максимальной глубине рекурсии, или размеру стека, необходимого для поддержки вычисления.

• Длина внешнего пути любого бинарного дерева, имеющего N внутренних уз­лов, на 2N больше длины внутреннего пути.
  
• Высота бинарного дерева с N внутренни­ми узлами не меньше lg N и не больше N-1.
  

При работе с бинарными деревьями существуют две связи и, сле­довательно, три основных порядка возможного по­сещения узлов:

• прямой обход (сверху вниз), при котором мы посещаем узел, а затем левое и пра­вое поддеревья
  
• поперечный обход (слева направо), при котором мы посещаем левое поддерево, затем узел, а затем правое поддерево
  
• обратный обход (снизу вверх), при котором мы посещаем левое и правое подде­ревья, а затем узел.
  

36. Какую временную сложность имеет алгоритм поиска в бинарном дереве поиска?

Д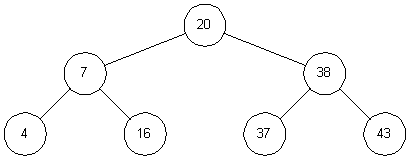воичное дерево - это дерево, у которого каждый узел имеет не более двух наследников. Предполагая, что k содержит значение, хранимое в данном узле, мы можем сказать, что бинарное дерево обладает следующим свойством: у всех узлов, расположенных слева от данного узла, значение соответствующего поля меньше, чем k, у всех узлов, расположенных справа от него, - больше. Вершину дерева называют его корнем, узлы, у которых отсутствуют оба наследника, называются листьями. Корень дерева на рис. 3.2 содержит 20, а листья - 4, 16, 37 и 43. Высота дерева - это длина наидлиннейшего из путей от корня к листьям. В нашем примере высота дерева равна 2.

Чтобы найти в дереве какое-то значение, мы стартуем из корня и движемся вниз. Например, для поиска числа 16, мы замечаем, что 16 < 20, и потому идем влево. При втором сравнении видим, что 16 > 7, и потому мы движемся вправо. Третья попытка успешна - мы находим элемент с ключом, равным 16.

К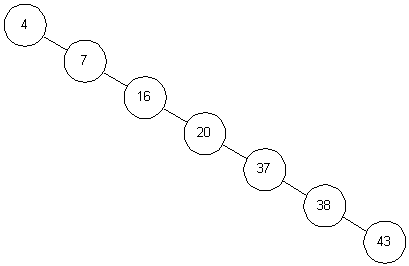аждое сравнение вдвое уменьшает количество оставшихся элементов. В этом отношении алгоритм похож на двоичный поиск в массиве. Однако, все это верно только в случаях, когда наше дерево сбалансировано. На рис. 3.3 показано другое дерево, содержащее те же элементы. Несмотря на то, что это дерево тоже бинарное, поиск в нем похож, скорее, на поиск в односвязном списке, время поиска увеличивается пропорционально числу запоминаемых элементов.