Решатель UniCalc

Вид материала

Документы

Содержание 2. Пользователи и области применения 3. Примеры использования 3.1. Нелинейное уравнение 3.2. Система линейных уравнений Гильберта 3.3. Решение разнородной системы 3.4. Решение нелинейной системы 3.5. Целочисленные задачи 3.6. Решение задачи Голомба. 3.8. Глобальный минимум функции от двух переменных 3.9. Оптимизация - функция Розенброка 3.10. Решение и исследование системы уравнений 3.13. Ряды Фурье 4. История разработки

Подобный материал:

• Msc. Nastran for Windows – возможности msc. Nastran на персональном компьютере, 172.11kb.

дополнительный раздел


Решатель UniCalc^®

Н-математика для решения широкого спектра вычислительных задач

В данный дополнительный раздел включена краткая информация о решателе UniCalc, демонстрирующая возможность создания современной коммерческой системы, использующей аппарат Н-математики для решения широкого спектра вычислительных задач. Одновременно этот раздел позволяет на ряде примеров получить представление о возможностях данного аппарата в решении нескольких классов задач, нетривиальных с точки зрения традиционных методов.

1. Введение

Если громоздкие и дорогие современные коммерческие пакеты для математических расчетов базируются на больших библиотеках различных алгоритмических методов, то в отличие от них UniCalc использует оригинальный единый вычислительный механизм, способный работать с любыми классами алгебраических задач.

UniCalc - это универсальный инструмент, совмещающий замечательную компактность с высокой эффективностью при решении произвольных алгебраических задач, в том числе тех, которые не могут быть решены традиционными методами.

Основная особенность UniCalc: он работает не с алгоритмом решения, как другие вычислительные пакеты, а непосредственно с моделью задачи, т.е. с той системой отношений (уравнений, неравенств, логических условий), которая связывает параметры решаемой задачи. В отличие от алгоритма модель:

• может быть недоопределенной;
  
• определяет все пространство решений;
  
• не делит свои параметры на входные и выходные, а симметрична по отношению к ним, поскольку в модели все они взаимозависимы; таким образом, модель не разделяет решаемые задачи на прямые и обратные, а в неявной форме содержит решение всех связанных с ней проблем.
  

Это позволяет технологии UniCalc, наряду с обычными задачами, решать алгебраические системы, в которых:

• число переменных не равно числу уравнений (т.е. недоопределенные и переопределенные системы);
  
• переменные имеют разные типы  целые и вещественные (в том числе и системы только с целочисленными переменными);
  
• наряду с любыми уравнениями и неравенствами используются логические выражения, задающие дополнительные отношения между переменными системы;
  
• параметры уравнений и неравенств (переменные, коэффициенты, константы, показатели) заданы неточно  в виде интервалов;
  
• не задано (неизвестно) начальное приближение к решению;
  
• отсутствуют стандартные методы решения.
  

Эти вышеперечисленные возможности ставят UniCalc вне конкуренции при решении широкого круга проблем  от финансовых и экономических до задач инженерного проектирования и сложных научных и промышленных расчетов. Причем многие из этих задач UniCalc решает в десятки раз эффективнее по сравнению с лучшими традиционными алгоритмами.

Аппарат недоопределенных моделей сочетается в вычислительном механизме решателя UniCalc с методами интервальной математики и компьютерной алгебры, а также оригинальными алгоритмами поиска решения. Сочетание этих подходов позволило создать универсальный инструмент для решения алгебраических задач произвольной сложности.

Взаимодействуя с моделью, UniCalc полностью меняет саму технологию решения алгебраических задач. В качестве результата он определяет пространство, которое включает все решения задачи или сообщает, что задача не имеет решений. При этом пространство решений может допускать один, несколько или бесконечное множество ответов. Вы можете оперировать с этим пространством, интерактивно корректируя модель, например - вводя новые зависимости и уточняя интервалы их параметров. При этом пространство решений реагирует на все изменения: если его сжатие произошло в нужном вам направлении, можно продолжать добавлять к системе новые ограничения для получения желательного результата.

Искомое решение можно оптимизировать по любому из параметров, последовательно сужая границы изменения соответствующих переменных, а в случае конечного множества применить процедуру автоматического поиска всех решений.

Нами соз­даны ком­мер­ческие вер­сии решателя UniCalc 3 (русский и анг­лий­ский вари­ан­ты) в MS DOS, MS Windows и версиях UNIX для платформ Sun, IBM, HP, Silicon Graphics и вычислительного ядра, используемого в ряде специализированных продуктов и технологий нашего Института. Заканчивается разработка версии UniCalc v.5 решателя следующего поколения.

2. Пользователи и области применения

UniCalc предлагает новую концепцию вычислений. В ней пользователь исходит из своей задачи, а не старается привести ее к виду, подходящему для применения того или иного известного метода традиционной вычислительной математики.

Пользователю UniCalc вообще не требуется знания вычислительных методов, специальных языков вычислительных пакетов и особенности систем (типа IMSL, MATHEMATICA, MAPLE и т.д.) При формулировании задачи не требуется приведения ее к какому-либо стандартному представлению, - пользователь может накладывать любые ограничения на любые комбинации переменных системы, может изменять и добавлять ограничения в процессе решения.

Тем самым, процесс решения становится не применением набора стандартных и заранее определенных действий, а исследованием пространства возможных решений и целенаправленным влиянием на это пространство. В силу простоты вычислительного аппарата и его практически неограниченных вычислительных возможностей пользователем решателя может быть каждый - от школьника до научного исследователя, от экономиста до инженера, выполняющего сложные проектные расчеты.

Таким образом, решатель UniCalc может эффективно применяться в любых приложениях, требующих использования математических вычислений, в частности, в таких областях как:

• инженерное проектирование и моделирование, в частности, в авиастроительной и космической промышленности;
  
• экономические и финансовые расчеты, оценки инвестиционных и других проектов с неточно и неполно заданной информацией;
  
• научные исследования, связанные с численными расчетами и численным моделированием;
  
• системы автоматического управления технологическими процессами и устройствами;
  
• технологии двойного применения;
  
• образование и др.
  

Engine (вычислительное ядро) UniCalc может использоваться как виртуальный вычислитель в специализированных технологиях, ориентированных на конкретные области приложений. В этом качестве он применятся в ряде разработанных нашим коллективом технологий, таких как

• ИНТЕГРА, электронные таблицы нового поколения,
  
• Time-EX, технология гибкого ресурсно-календарного планирования на основе н-математики и развитой временной логики,
  
• Экономика, технология разработки крупных региональных и отраслевых моделей экономики и бюджета.
  

UniCalc engine входит как составная часть в ядро ряда других наших проектов.

3. Примеры использования

Для записи решаемых задач UniCalc имеет простой входной язык, который позволяет легко записывать в общепринятом виде любые алгебраические выражения.

UniCalc позволяет решать сложные задачи размерностью в тысячи и десятки тысяч переменных, но здесь мы ограничимся рассмотрением набора небольших примеров, демонстрирующих простоту использования и уникальные вычислительные возможности решателя.


3.1. Нелинейное уравнение

В качестве первого примера рассмотрим нетривиальное нелинейное уравнение 1079 - e^{(х1.3 + i )} = (10 - x)^x, i>0,

где х - вещественное, а i - целое число. Ответом будет

i = [1, 6]; x = [0, 3.83988].

Если к уравнению добавить i = 5, то UniCalc через доли секунда даст точный ответ x = [1.67226, 1.67227]. При этом точность вычислений устанавливается пользователем и поэтому число совпадающих знаков может быть любым, например x = [1.6722643465, 1.6722643466].

Наше уравнение можно изменить как угодно, например, так:

2079 ^. i - e^{(х1.3 + i )} = (10 - x)^xx ; i<3;

ответ последует с той же скоростью i = [1, 2]; x = [1.9060359298, 2.0010736916].

Эффективность, с которой UniCalc решает этот пример, никак не связан с видом именно этого типа уравнений: тот же самый универсальной процесс будет "обжимать" пространство решений совершенно разных рассматриваемых ниже задач.

Надо отметить ту особенность решателя UniCalc, что, как правило, он решает задачу тем лучше и быстрее, чем более нелинейны используемые в ней отношения.

3.2. Система линейных уравнений Гильберта

Это пример линейной системы, не слишком простой для обычных методов.

x1/1+x2/2+x3/3+x4/4+x5/5+x6/6+x7/7+x8/8+x9/9+x10/10+x11/11 = 11;

x1/2+x2/3+x3/4+x4/5+x5/6+x6/7+x7/8+x8/9+x9/10+x10/11+x11/12 = 8.896789321789322;

x1/3+x2/4+x3/5+x4/6+x5/7+x6/8+x7/9+x8/10+x9/11+x10/12+x11/13 = 7.63973248973249;

x1/4+x2/5+x3/6+x4/7+x5/8+x6/9+x7/10+x8/11+x9/12+x10/13+x11/14 = 6.74531302031302;

x1/5+x2/6+x3/7+x4/8+x5/9+x6/10+x7/11+x8/12+x9/13+x10/14+x11/15 = 6.06041736041736;

Как видно из первых пяти уравнений, их регулярная форма определяется следующим образом:

x1/i + x2/(i+1) + x3/(i+2) + x4/(i+3) + x5/(i+4) + x6/(i+5) + x7/(i+6) + x8/(i+7) + x9/(i+8) + x10/(i+9) + x11/(i+10) = А_i;

Зададим для следующих шести уравнений правые коэффициенты:

А₆ = 5.513021700521701; А₇ = 5.062684864155453; А₈ = 4.684243452625805;

А₉ = 4.360939885707687; А₁₀ = 4.081057371421148; А₁₁ = 3.836095492055245;

Принято считать, что для полученной системы из 11 уравнений решение будет следующим:

x1 = 1, x2 = 2, x3 = 3, x4 = 4, x5 = 5, x6 = 6, x7 = 7, x8 = 8, x9 = 9, x10 = 10, x11 = 11.

UniCalc позволяет получить решения рассматриваемой системы с любой точностью, вплоть до 14-го знака:

x1 = 1.00000000591547; x2 = 1.99999935338846; x3 = 3.00001732174952;

x4 = 3.99980145334072; x5 = 5.00120664871685; x6 = 5.99568760596503;

x7 = 7.00951896254599; x8 = 7.98687100234232; x9 = 9.01101550649471;

x10 = 9.99485870739089; x11 = 11.0010234371858;

3.3. Решение разнородной системы

Для следующего примера рассмотрим задачу нахождения решений системы, включающей две вещественных x и y и одну целую k переменные. Система состоит из соотношений разного типа: двух нелинейных уравнений, одного неравенства и одного логического выражения.

x² + 6 ^. x = y - 2^k k ^. x + 7.7 ^. y = 2.4 (k - 1)² < 4

ln(y + 2 ^. x +12) < k + 5 or y > k²  x < -0.1 and y < 1.0





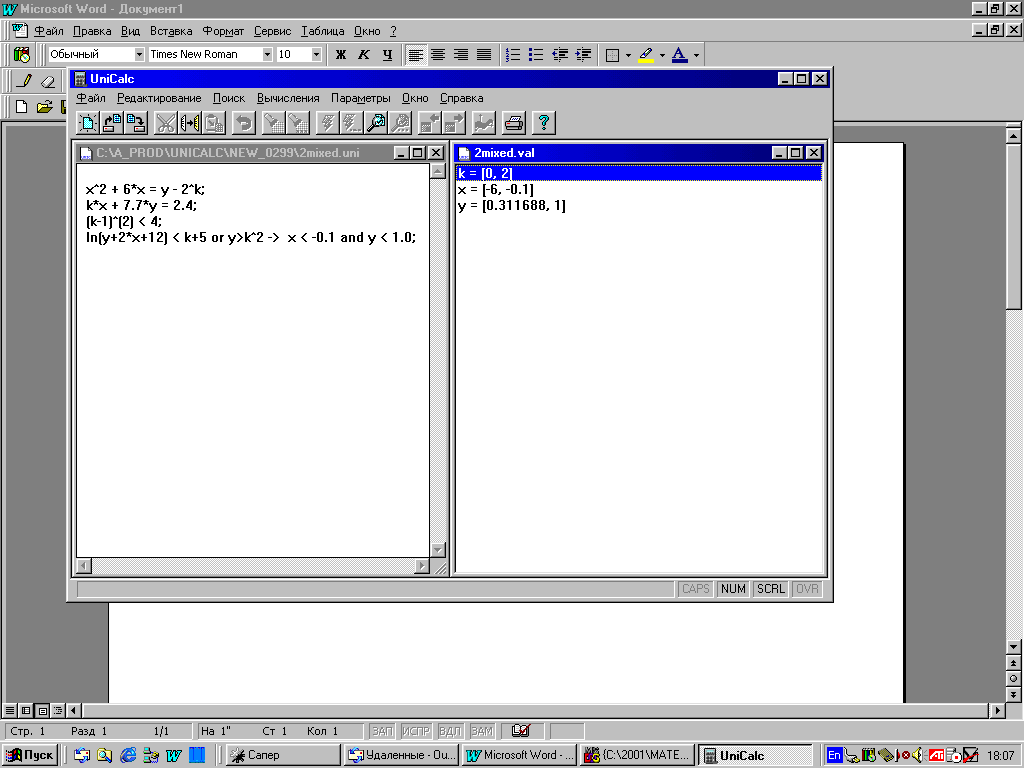
Рис.1

На экране (рис.1) задача записана на языке UniCalc, а результат показывает, что если наша система имеет решения, то они все лежат в области

k = [0, 2] x = [- 6, - 0.1], y = [0.311688, 1].

Для нахождения отдельных решений (или определения их отсутствия) можно использовать две возможности.

1. Добавить к системе дополнительные соотношения, которые либо накладывают некоторые ограничения на область решения, либо задают новые связи между переменными. Например, добавим к нашей системе логическое условие, связывающее область переменной k с ограничением на значение переменной х :
   

x < 0.0  k > 1 .

Поскольку все интервальное значение х находится в отрицательной зоне, то добавленное условие приводит к точному решению k = 2 , x = -0.658, y = 0.4827.

2. Использовать встроенный механизм поиска корней, с помощью которого мы найдем четыре корня:
   

r1 = {k = 0, x = -5.883, y = 0.3117}; r2 = {k = 0, x = -0.117, y = 0.3117};

r3 = {k = 1, x = -0.289, y = 0.349}; r4 = {k = 2, x = -0.658, y = 0.4827}.

3.4. Решение нелинейной системы

В качестве примера возьмем следующую систему из двух уравнений:

3 ^. ln (x) + sin³(x) + cos(y) = 1.0;

0.5 ^. tg (e^{y - x}) ^. x³ – cos(x) = 4;

Решения, полученные UniCalc с помощью команды ПОИСК КОРНЕЙ:

x₁ = 1.06463755, y₁ = 1.42724098;

x₂ = 1.3998655, y₂ = 2.88024679.

Те же решения можно получить, добавляя к системе ограничение y>2 или y<2.

3.5. Целочисленные задачи

Рассмотрим решение на UniCalc целочисленных задач. Поскольку UniCalc позволяет решать несколько задач одновременно, если используемые в них имена переменных не пересекаются, решим сразу три задачи:

• Разложение на сумму квадратов:
  

i ² + j ² = 61²; i > 0; j > i.

Решение: i = 11, j = 60.

• Разложение на целочисленные множители:
  

k ^. L = 1333; k > 1; L > k.

Решение: k = 31, L = 43.

• Решение Диофантовых уравнений:
  

31 ^. m + 43 ^. n = 997; m > 0; n > 0;

Решение: m = 28, n = 3.

Добавим к этим примерам целочисленную функцию Biggs EXP6 из статьи J.J.More. B.S. Garbow, K.E. Hillstrom. Testing Unconstrained Optimization Software. ACM Trans. Math. Softw. 7, 1981, N1, pp. 17 - 41.

t(i) ⁼ 0.1 ^. i;

g(i) ⁼ e ^-t(i) - 5 ^. e^{-10 . t(i)} + 3 ^. e^{-4 . t(i)};

f(i) ⁼ k3 ^. e^{-0.1. i . k1} - k4 ^. e^{-0.1 . i . k2} + k6 ^. e^{-0.1 . i . k5} - g(i);

y1 = f(1);

y = y1² + f(2)² + f(3)² + f(4)² + f(5)² + f(6)² + f(7)² + f(8)² + f(9)² + f(10)² + f(11)² + f(12)² + f(13)²;

y = 0;

k1 > 0; k2 > 0; k3 > 0; k4 > 0; k5 > 0; k6 > 0;

Результат: k1 = 1; k2 = 10; k3 = 1; k4 = 5; k5 = 4; k6 = 3;

3.6. Решение задачи Голомба.

Эта задача комбинаторной целочисленной оптимизации используется в радио-астрономических приложениях. Найти минимальное значение последнего члена монотонно возрастающей целочисленной последовательности, причем разность между любыми двумя членами этой последовательности должна быть различной. Рассмотрим задачу для 5 членов последовательности, для которой эта задача запишется следующим образом:

i1 = 0; i1 < i2; i2 < i3; i3 < i4; i4 < i5;

При этом разности всех пар членов различны, т.е.:

i1 - i2 ≠ i2 - i3; i1 - i2 ≠ i2 - i4; i1 - i2 ≠ i2 - i5;

i1 - i2 ≠ i3 - i4; i1 - i2 ≠ i3 - i5; i1 - i2 ≠ i4 - i5;

i1 - i3 ≠ i2 - i4; i1 - i3 ≠ i2 - i5; i1 - i3 ≠ i3 - i4;

i1 - i3 ≠ i3 - i5; i1 - i3 ≠ i4 - i5; i1 - i4 ≠ i2 - i3;

i1 - i4 ≠ i2 - i5; i1 - i4 ≠ i3 - i5; i1 - i4 ≠ i4 - i5;

i1 - i5 ≠ i2 - i3; i1 - i5 ≠ i2 - i4; i1 - i5 ≠ i3 - i4;

i2 - i3 ≠ i3 - i4; i2 - i3 ≠ i3 - i5; i2 - i3 ≠ i4 - i5;

i2 - i4 ≠ i3 - i5; i2 - i4 ≠ i4 - i5; i2 - i5 ≠ i3 - i4;

i3 - i4 ≠ i4 - i5;

Цель – найти минимальную длину правила, т.е. минимизировать значение i5.

i2 - i1 < i5 - i4; i5 < 100;

Первый же найденный корень будет искомым оптимальным решением i5 = 11. Значения остальных переменных будут равны: i2 = 2, i3 = 7, i4 = 10.

Заметим, что решение для i2, i3, i4 не единственно, но это не важно, так как мы ищем минимальное значение для i5, которое единственно и не зависит от выбранной стратегии поиска.

3.7. Sudoku - японская логико-математическая игра

В задаче ищутся коэффициенты k_i,j в матрице 9 ^. 9. Суть игры sudoku в заполнении матрицы целыми числами так, чтобы в каждом столбце и строке было по одному числу от 1 до 9. То же требуется и в граничных квадратах 3 ^. 3 и в центральном квадрате. Вариантов решений может быть много. Обычно с самого начала задаются 28 чисел из 81, причем обычными методами на решение тратится значительное время. UniCalc находит правильное решение менее чем за 1 сек. При использованием группового квантора all формулировка получается достаточно компактной:

all (i=1,1,9; all (j=1,1,9; k_i,j = [1,9] ));

all (i=1,1,9; all (m=1,1,9; all (n=1,1,9; (m=n) or (k_i,m ≠ k_i,n); // строки //

(m=n) or (k_m,i ≠ k_n,i) // столбцы // )) );

// несовпадение на диагоналях не требуется, но его можно включить


all (j=1,1,9; (i=j)or(k_i,i ≠ k_j,j); // главная диагональ //

(i=j)or(k[i,10-i] ≠ k[j,10-j]) // вторая диагональ // ); //

all (m=1,3,7; all (n=1,3,7; //индексы начальных элементов малых квадратов//

all (mm=0,1,2; all (nn=0,1,2; // индексы внутри малых квадратов //

all (mmm=0,1,2; all (nnn=0,1,2; // индексы внутри малых квадратов //

((mm=mmm) and (nn=nnn)) or ( k_m+mm,n+nn ≠ k_m+mmm,n+nnn ) // малые квадраты // )) )) ));


При начальных данных


k_1,2 = 3_; k_1,6 = 4_;

k_2,4 = 9_; k_2,6 = 7_; k_2,7 = 1_;

k_3,5 = 6_; k_3,7 = 8_; k_3,8 = 9_; k_3,9 = 7_;

k_4,1 = 1_; k_4,4 = 8_; k_4,5 = 2_; k_4,8 = 4_;

k_5,3 = 5_; k_5,7 = 2_;

k_6,2 = 2_; k_6,5 = 3_; k_6,6 = 5_; k_6,9 = 1_;

k_7,1 = 7_; k_7,2 = 1_; k_7,3 = 8_; k_7,5 = 9;

k_8,3 = 9_; k_8,4 = 3_; k_8,6 = 6_;

k_9,4 = 4_; k_9,8 = 2_;


После сужения пространства и поиска корней (около 0.2 сек. ) выдается первый ответ:

k_1,1 = 9 _; k_1,2 = 3 _; k_1,3 = 7 _; k_1,4 = 1 _; k_1,5 = 8 _; k_1,6 = 4 _; k_1,7 = 6 _; k_1,8 = 5 _; k_1,9 = 2 _;

k_2,1 = 6 _; k_2,2 = 8 _; k_2,3 = 2 _; k_2,4 = 9 _; k_2,5 = 5 _; k_2,6 = 7 _; k_2,7 = 1 _; k_2,8 = 3 _; k_2,9 = 4 _;

k_3,1 = 4 _; k_3,2 = 5 _; k_3,3 = 1 _; k_3,4 = 2 _; k_3,5 = 6 _; k_3,6 = 3 _; k_3,7 = 8 _; k_3,8 = 9 _; k_3,9 = 7 _;

k_4,1 = 1 _; k_4,2 = 7 _; k_4,3 = 6 _; k_4,4 = 8 _; k_4,5 = 2 _; k_4,6 = 9 _; k_4,7 = 3 _; k_4,8 = 4 _; k_4,9 = 5 _;

k_5,1 = 3 _; k_5,2 = 9 _; k_5,3 = 5 _; k_5,4 = 7 _; k_5,5 = 4 _; k_5,6 = 1 _; k_5,7 = 2 _; k_5,8 = 8 _; k_5,9 = 6 _;

k_6,1 = 8 _; k_6,2 = 2 _; k_6,3 = 4 _; k_6,4 = 6 _; k_6,5 = 3 _; k_6,6 = 5 _; k_6,7 = 9 _; k_6,8 = 7 _; k_6,9 = 1 _;

k_7,1 = 7 _; k_7,2 = 1 _; k_7,3 = 8 _; k_7,4 = 5 _; k_7,5 = 9 _; k_7,6 = 2 _; k_7,7 = 4 _; k_7,8 = 6 _; k_7,9 = 3 _;

k_8,1 = 2 _; k_8,2 = 4 _; k_8,3 = 9 _; k_8,4 = 3 _; k_8,5 = 7 _; k_8,6 = 6 _; k_8,7 = 5 _; k_8,8 = 1 _; k_8,9 = 8 _;

k_9,1 = 5 _; k_9,2 = 6 _; k_9,3 = 3 _; k_9,4 = 4 _; k_9,5 = 1 _; k_9,6 = 8 _; k_9,7 = 7 _; k_9,8 = 2 _; k_9,9 = 9 _;

3.8. Глобальный минимум функции от двух переменных

Задана функция от двух переменных

f(x,y) = (x² + y²)/200 - cos(x) ^. cos(y/(2^0.5)) + 1,

для которой необходимо найти глобальный минимум.

Необходимые условия существования минимума этой функции :

fx(x,y) = dif(f(x,y), x); fx(x,y) = 0;

fy(x,y) = dif(f(x,y), y); fy(x,y) = 0;

fxx(x,y) = dif(f(x,y), x:2); fxx(x,y) > 0;

fyy(x,y) = dif(f(x,y), y:2); fxy(x,y) = dif(f(x,y), x, y);

det = fxx(x,y) ^. fyy(x,y) - fxy(x,y)²; det > 0; fmin = f(x,y);

На данном диапазоне значений аргументов функция имеет несколько минимумов.

det = [10^-10, 0.5151], fmin = [0, 1.60218], x = [-6.28319, 6.28319], y = [-8.88577, 8.88577].

При добавлении к системе fmin =0; результат определяет глобальный минимум:

det = 0.5151; x = 0; y = 0.

3.9. Оптимизация - функция Розенброка

Для демонстрации возможностей UniCalc рассмотрим известную оптимизационную задачу – определение глобального минимума для функции Розенброка:

_N

y = (1 - x₁)² + 100 ^.  (x_i+1 - x_i²)²;

^{i = 1}

Ответ для нее известен: это y = 0 при всех x_i = 1. Однако лучшие традиционные методы оптимизации решают эту проблему для N не более 10. UniCalc позволяет решить ее практически для любого значения N. Ниже мы покажем это на примере функции Розенброка для N=50, преобразованной из функции в уравнение:

₅₀

y - (1 - x₁)² = 100 ^.  (x_i+1 - x_i²)²;

^{i = 1}

Сама попытка решения уравнения четвертой степени для 52 переменных (y и пятьдесят один x) кажется невозможной. Однако UniCalc позволяет определить пространство решений этого уравнения на ПК за доли секунды. На рис.3 А приведено графическое представление этого пространства в логарифмической шкале Легко видеть, что первые сорок восемь х получили Н-значение [-17783.3, 17783.3].

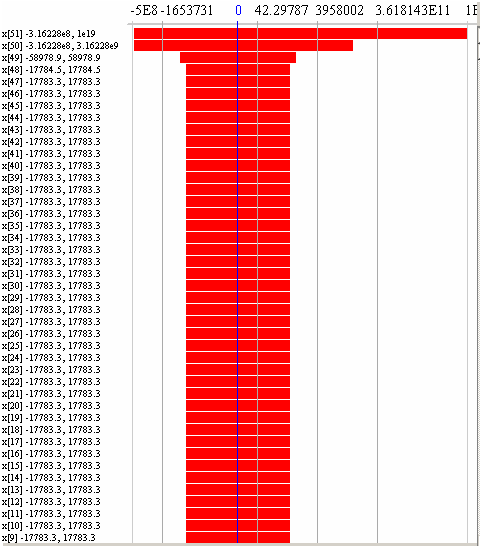
Рис. 3 А

Конечно, для массива х это пространство слишком широко. Однако при этом y = [0, 10^-19] (хотя на рис.3А этого не видно), т.е. определяемый минимум y равен 0. Если мы добавим y = 0 к исходному уравнению, мы получим значение 1 для всех переменных x, что и является ответом при поиске глобального минимума.

Но возможности UniCalc гораздо шире: он может работать со всей областью недоопределенного значения y, сокращая ее до узкой окрестности нуля: например, если мы добавим неравенство y <=0.00001 к основному уравнению, то получим гораздо более узкое пространство, которое представлено на рис.3 Б.

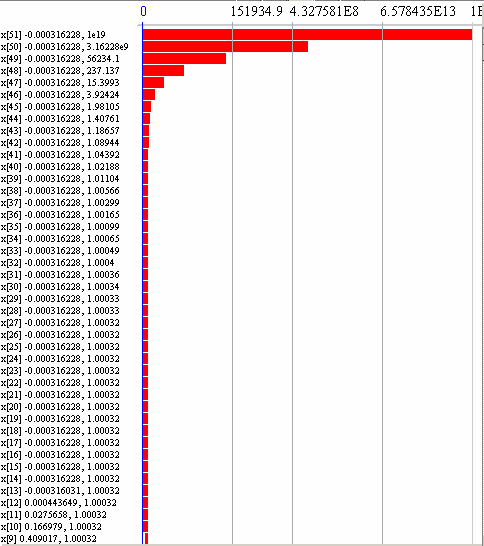
Рис. 3 Б

Рис.3 В

Для того, чтобы продемонстрировать способность UniCalc работать со всем пространством решений и всеми переменными, мы добавим к модели еще одно ограничение, например, x₄₉ <= 2.05. На рис. 3 В мы видим как новое состояние пространства (красное) реагирует на это дополнительное ограничение (светлая часть диаграммы отражает исключенную часть предыдущего состояния).

В данном случае мы взяли для простоты графической иллюстрации пример для N=50., хотя Есть сообщения, что для решения этой задачи при N=100 в США несколько лет назад использовался суперкомпьютер Cray. UniCalc тратит на это меньше секунды, а новая версия UniCalc решает эту задачу для 50 тысяч переменных меньше чем за полминуты.

3.10. Решение и исследование системы уравнений

Приведем пример трудной для решения имеющимися пакетами реальной задачи из статьи Meintjes K. and Morgan A.P. Chemical Equilibrium Systems as Numerical Test Problems (ACM Transactions on Mathematical Software. 1990. N2. pp.143-151). Предлагаемая в этой работе система уравнений описывает горение пропана в воздухе с образованием десяти продуктов. Эта система записывается следующим образом:

x1 + x4 - 3 = 0;

2 ^. x1 + x2 + x4 + x7 + x8 + x9 + 2 ^. x10 - R = 0;

2 ^. x2 + 2 ^. x5 + x6 + x7 - 8 = 0;

2 ^. x3 + x9 - 4 ^. R = 0;

xT = x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10;

pxT = p / xT;

aK5 ^. x2 ^. x4 - x1 ^. x5 = 0;

aK6 ^. (x2 ^. x4)^0.5- (x1)^{0.5 .} x6 ^. (pxT)^0.5 = 0;

aK7 ^. (x1 ^. x2) ^0.5 - (x4)^{0.5 .} x7 ^. (pxT)^0.5 = 0;

aK8 ^. x1 - x4 ^. x8 ^. pxT = 0;

aK9 ^. x1 ^. (x3)^0.5 - x4 ^. x9 ^. (pxT)^0.5 = 0;

aK10 ^. x1² - x4^{2 .} x10 ^. pxT = 0;

aK5 = 1.93^.10^-1; aK6 = 2.597^.10^-3; aK7 = 3.448^.10^-3; aK8 = 1.799^.10^-5;

aK9 = 2.155^.10^-4; aK10 = 3.846^.10^-5; p = 40; R = 10;

где xi - это переменные, обозначающие получаемые продукты, aKi и p -константы (p - атмосферное давление), а параметр R определяет относительное количество воздуха и топлива. Для получения физического решения R должно быть больше 3, причем при R<10 мы имеем случай "обогащенного" горения, а при R>10 - "бедного". Надо найти единственное решение системы, в котором все xi положительны.

В статье утверждается, что в данной постановке система сложна для имеющихся методов и поэтому сводится к полиномиальной системе, которая может быть решена, хотя и остается трудной для ряда "стандартных" решателей (при этом необходимо задавать начальные приближения для каждой переменной системы!).

UniCalc легко решает эту проблему в исходной постановке без всяких начальных приближений. Так, на ПК решение было получено за доли секунды при R = 10, т.е. в режиме "нормального" горения. Для задания положительности решения можно либо добавить к данной системе набор неравенств вида xi > 0 для всех i.

Полученное с помощью механизма поиска корней решение имеет следующий вид (использованная точность решения – 10^-6):

x1 = [2.915718, 2.915733] x6 = [0.000722, 0.000723]

x2 = [3.960938, 3.960946] x7 = [0.033198, 0.033204]

x3 = [19.986278, 19.986313] x8 = [0.000421, 0.000421]

x4 = [0.084277, 0.084281] x9 = [0.027414, 0.027416]

x5 = [0.022095, 0.022096] x10 = [0.031141, 0.031146]

Однако, UniCalc позволяет не только находить решение проблемы, но и проводить ее исследование по определению решений с различными свойствами. Например, пусть в рассмотренной задаче требуется найти значение параметра R, при котором выброс углекислого газа (переменная x1) минимален. Установив диапазон возможных значений параметра R в интервале от 3 до 40, т.е. заменив выражение R = 10 на выражение R = [3, 40] и решив полученную систему уравнений, мы определим, что требуемое решение получается при R = 3.0, и оно равно:

x1 = [2.22044.10-16, 2.21817.10-10]; x2 = [2.22044.10-16, 1.14931.10-9]; x3 = [6, 6]; x4 = [3, 3]; x5 = [2, 2.00002];

x6 = [3.99996, 4]; x7 = [2.22044.10-16, 3.98047.10-7]; x8 = [2.22044.10-16, 3.34456.10-10]; x9 = [2.22044.10-16, 1.36069.10-8]; x10 = [2.22044.10-16, 9.75862.10-8];

1. 3.11. Система из четырех квадратных уравнений
   

Предлагаемый пример приведен как сложный в работе R.B. Kearfott. Some Tests of Generalized Bisection. ACM Transactions on Mathematical Software, v.13, 1987, N3, p.197 - 220.

f(x1, x2) = (x1 - 0.1)² + x2 - 0.1;

f(x1, x2) = 0; f(x2, x3) = 0; f(x3, x4) = 0; f(x4, x1) = 0;

Система имеет два решения, заключенных в четырехмерный куб

x1 = [-0.9, 0.1]; x2 = [-0.9, 0.1]; x3 = [-0.9, 0.1]; x4 = [-0.9, 0.1];

При добавлении ограничения xi >0 для любой из четырех переменных результат определят один из корней x1 = 0.1; x2 = 0.1; x3 = 0.1; x4 = 0.1,

а при добавлении xi < 0 определяется второй корень:

x1 = -0.9; x2 = -0.9; x3 = -0.9; x4 = -0.9;

2. 3.12. Решение обратных задач
   

Как уже было сказано, в Н-моделях нет деления на входные и выходные параметры. Поэтому с помощью UniCalc можно решать как прямые, так и обратные задачи.

Рассмотрим задачу восстановления коэффициентов функции по известным значениям функции и ее первых двух производных в некоторых точках. Пусть эти значения даны с некоторой погрешностью. Требуется найти интервалы значений параметров, для которых известны лишь пределы их изменения. Подобного рода задачи часто возникают при обработке результатов наблюдений и измерений, например при поиске параметров регрессионных зависимостей. Выберем для рассмотрения функцию (k – целая, остальные - вещественные):

f (x) = a ^. x^k + b ^. e^{0.1 . x + 1.2} – c .

Тогда первая и вторая производные функции будут выглядеть так:

f1(x) = a ^. k ^. x^k-1 + 0.1 ^. b ^. e^{0.1 . x + 1.2}

f2(x) = a ^. k ^. (k-1) ^. x^k-2 + 0.01 ^. b ^. e^{0.1 . x + 1.2}

Пусть значения коэффициентов функции ограничены следующим образом:

a = [1,100]; b = [2,16]; c = [0,100]; k = [1,10];

А значения самой функции и ее производных заданы в нескольких точках:

f(2.13) = [10.8, 10.9]; f(14.91) = [7646.1, 7646.3]; f1(2.13) = [32.5, 32.7];

f1(4.06) = [115.2, 115.4]; f2(2.13) = [29.4, 29.6]; f2(10.28) = [142.1, 142.3];

f2(14.91) = [206.1, 206.3];

После вычислений UniCalc выдает следующее решение для коэффициентов:

a = [2.29865, 2.30134]; b = [2.86548, 3.44134]; c = [23.0854, 25.5771]; k = 3;

Если же ограничиться тремя точками, например:

f(2.13) = [10.8, 10.9]; f1(2.13) = [32.5, 32.7]; f2(14.91) = [206.1, 206.3];

То решение будет несколько менее точным:

a = [2.29812, 2.30134]; b = [2.86548, 3.45879]; c = [23.0803, 25.6488]; k = 3;

Графики нашей функции f (x) = a ^. x^k + b ^. e^{0.1 . x + 1.2} – c и ее производных f1 и f2 будет выглядеть как :

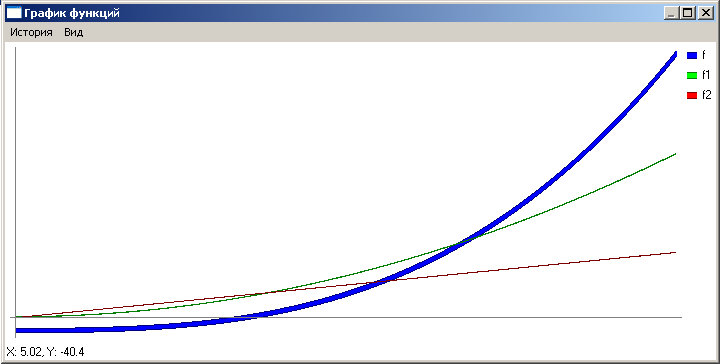Рис.4

3.13. Ряды Фурье

Разложение функции в ряд Фурье - одна из наиболее востребованных вычислительных технологий. В данном случае мы выбрали трапециидальную функцию и ее представление в форме ряда размерностью в 200 членов :

_i

f(x) = 1/2 +  ( (-4 ^. ( -2 ^. cos(n ^. ) - n ^.  ^. sin(n ^. ) + 2 ^. cos(1/2 ^. n ^. )) ^. cos(n ^.  ^. x/4) / (n^{2 .} ²) );

ⁿ⁼¹

Для x= [-4,4]; i=200 UniCalc считает около секунды (график рис.5а), а для i = 5 практически мгновенно (график рис.5б).



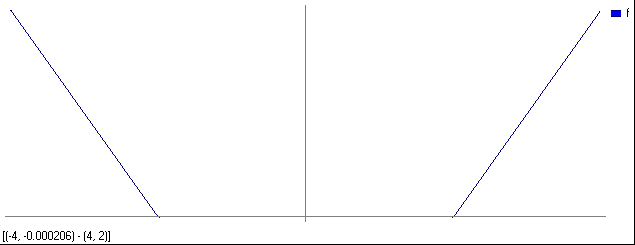
рис.5а



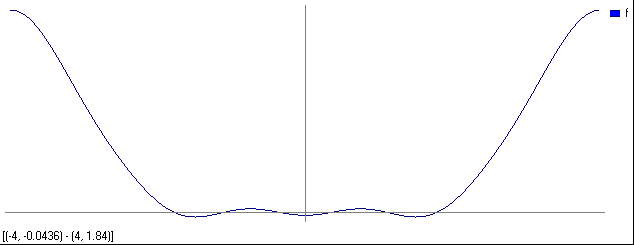
рис.5б

Выше формула ряда Фурье оперировала с обычной переменной х. Однако ее можно изменить, превратив аргумент в x + d, где d = [-0.02,0.02]:

_i

f(x) = 1/2 +  ( (-4 ^. ( -2 ^. cos(n ^. ) - n ^.  ^. sin(n ^. ) + 2 ^. cos(1/2 ^. n ^. )) ^. cos(n ^.  ^{. (}x+d)/4) / (n^{2 .} ²) );

ⁿ⁼¹

Тогда для i=200 график будет выглядеть таким образом (рис.6А):



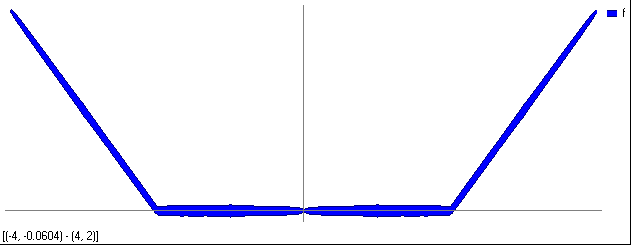
Рис. 6а

А для i=5 так как на рис. 6Б:



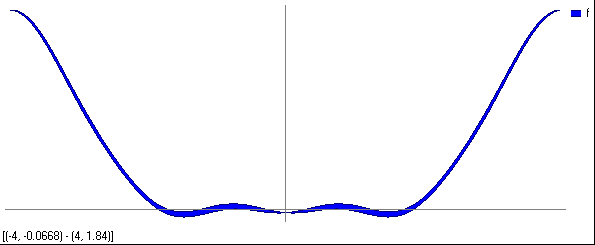
Рис. 6б

4. История разработки

Решатель UniCalc создан в Российском НИИ искусственного интеллекта. В основе используемого вычислительного механизма решателя лежит аппарат недоопределенных моделей (или Н-моделей), который позволяет обрабатывать данные с неполной и неточной информацией, в том числе эффективно решать различные системы алгебраических уравнений и неравенств. Таким образом, данный механизм может быть использован в разнообразных программных продуктах, что было подтверждено созданием на базе аппарата Н-моделей целого ряда оригинальных программных систем, включая решатель UniCalc.

Первая макетная реализация решателя была выполнена в 1987 году в операционной среде Unix, а в 1991 году появилась версия решателя UniCalc, предназначенная для работы в MS DOS на персональных компьютерах IBM PC и совместимых с ними. Она имела ограничения по размеру обрабатываемой модели, которые диктовались размерами доступной тогда памяти. Тем не менее, решатель привлек внимание пользователей своей простотой и эффективностью и был приобретен рядом промышленных предприятий и конструкторских бюро для выполнения проектных работ и инженерных расчетов.

В 1994 году появилась версия решателя UniCalc для Windows 3.1, которая обеспечивала новые интерфейсные и вычислительные возможности, снимающие частично ограничения на размер решаемых задач. В 1995 году был осуществлен перенос решателя на рабочие станции Sun в операционную систему Solaris с использованием библиотеки Motif, а в 1996 году появились версии UniCalc для Windows 95 и Windows NT, а также для рабочих станций IBM RS-6000, Hewlett-Packard и Silicon Graphics.

Решатель UniCalc был экспонатом крупнейшей международной компьютерной выставке CeBIT в Германии, ряда Российских компьютерных выставок Softool, Информатика, КомТек, а также нескольких региональных выставок.

В 1995 г. UniCalc /DOS прошла тестирование в фирме SAIC (США), в рецензии которой было отмечено, что при работе с решателем:

пользователь может не знать, какого типа задачу он хочет решить – UniCalc сам определит это и найдет решение надлежащим способом. Средства оптимизации … следует отметить, что UniCalc легко решает задачу нелинейной оптимизации, которую Excel решить не может. …вычислитель обладает достаточными преимуществами перед конкурентами, чтобы компенсировать затраты на его доработку и сделать его конкурентоспособным для тех пользователей, которым не хотят тратить время на изучение интерфейса тяжеловесных пакетов таких популярных продуктов как Mathematica или Maple.

Универсальность и естественный способ описания задач в UniCalc являются важными преимуществами. UniCalc может быть полезен людям, занимающимся экономическим и финансовым моделированием, а также может использоваться как модуль для программных пакетов CAD/CAM.

UniCalc нашел применение во многих научных, учебных, промышленных и конструкторских организациях и предприятиях в России и за рубежом. Среди них можно назвать АвтоВАЗ, Новосибирский завод химконцентратов, авиазавод им. Бериева, ОАО «Камов» (Россия), Dassault Aviation и Dassault Systemes (Франция). Вычислительное ядро решателя UniCalc встроено в известную систему Eclⁱps^e в качестве инструмента для решения задач с вещественными переменными.