Задачи : 495 (Замораживание Фибоначчи), 900 (Кирпичная стена), 10450 (Шум мирового кубка), 11000 (Пчела)
| Вид материала | Документы |
- Московский Государственный Строительный Университет Институт фундаментального образования, 357.08kb.
- Общество с ограниченной ответственностью «Торговый дом «кирпичная компания», 74.62kb.
- Автор: Довгаль Сергей, 459.74kb.
- Церковь Гроба Господня; ГолгофаЗападная стена (Стена плача). программа, 167.37kb.
- Этот шум, напоминавший шум моря, был сильнее всего по утрам, 124.84kb.
- Виброакустические вредные факторы Производственный шум Шум, 193.23kb.
- Итоговый протокол кубка ОАО «нлмк» по мини-футболу среди цехов и подразделений дс «Нептун», 34.87kb.
- И шум, 12.02kb.
- Природа шума и вибраций, 737.79kb.
- Аналитический отчет российский рынок теплоизоляционных материалов, 502.81kb.
ЗАНЯТИЕ 8
1. Числа Фибоначчи. Рекурсивный и циклический методы вычисления. Рекурсивный метод вычисления с запоминанием. Формула Бине. Свойства чисел Фибоначчи.
2. Класс string. Обработка строк с помощью класса string: инициализация, конкатенация, ввод-вывод, вставка, удаление, поиск. Обработка подстрок. Потоковое чтение из строки.
3. Задачи
ссылка скрыта: 495 (Замораживание Фибоначчи), 900 (Кирпичная стена), 10450 (Шум мирового кубка), 11000 (Пчела).
ссылка скрыта: SRM 178 (Простой калькулятор), SRM 210 (Заглавная строка), SRM 246 (Склеивание), SRM 257 (Код замены), SRM 305 (Мультичтение).
1. ЧИСЛА ФИБОНАЧЧИ
В XIII веке итальянский математик Леонардо Фибоначчи исследовал решение следующей задачи:
Фермер выращивает кроликов. Когда кролик становится взрослым (ему исполняется два месяца), то каждый месяц он дает потомство в одного кролика. Сколько кроликов будет у фермера через n месяцев, если сначало у него был только один (считается, что кролики не умирают и дают потомство по выше описанной схеме)?
Очевидно, що в начале первого и второго месяца у фермера один кролик, поскольку потомства еще нет. На третий месяц будет два кролика. На четвертый месяц первый кролик даст еще одного, а второй потомства не даст, так как ему еще один месяц. Таким образом на четвертый месяц будет три кролика.
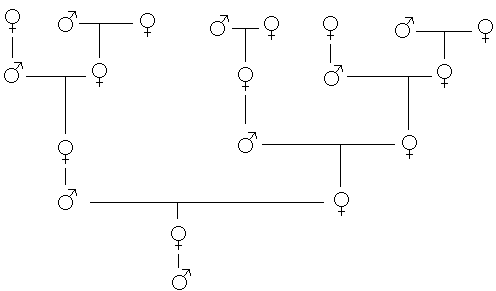
Количество кроликов в n - ый месяц будет равно количеству кроликов, которое было в n – 1 месяце, плюс количество родившихся. Последних будет столько, сколько кроликов дают потомство (которым уже исполнилось 2 месяца). Их число равно количеству кроликов в n – 2 месяц.
Если через Fn обозначить количество кроликов после n - го месяца, то имеет местоследующее рекуррентное соотношение:
Fn = Fn-1 + Fn-2, F1 = F2 = 1
Положим F0 = 0, при этом соотношение при n = 2 останется истиным. Таким образом образовалась последовательность
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... ,
которая называеться последовательностью Фибоначчи.
Рассмотрим несколько функций f(n) вычисляения n - го числа Фибоначчи. Для нахождения f(n) с линейной сложностью без запоминания значений f(1), f(2), …, f(n – 1) можно использовать циклический вариант:
int f(int n)
{
int i, temp, a = 0, b = 1;
for(i = 0; i < n; i++)
temp = a, a = b, b = temp + a;
return a;
}
Максимальным числом Фибоначчи, которое помещается в тип int, является F46 = 1836311903. В 64-битовый целочисленный тип long long (__int64) помещается максимум F92. Если в задаче требуется находить значения f(n) для n > 92, то следует воспользоваться длинной арифметикой.
В случае необходимости запоминания всех чисел Фибоначчи f(1), f(2), …, f(n), заведем массив m, в котором положим m[i] = f(i), 0 i n. Реализация может быть как циклическая, так и рекурсивная с запоминанием:
-
#include
#include
int i, n, m[47];
void main(void)
{
memset(m,0,sizeof(m));
m[0] = 0; m[1] = 1;
scanf("%d",&n);
for(i = 2; i <= n; i++)
m[i] = m[i-1] + m[i-2];
while(scanf("%d",&i) == 1)
printf("%d\n",m[i]);
}
#include
#include
int i, n, m[47];
int f(int n)
{
if (m[n] >= 0) return m[n];
if (n == 0) return m[0]=0;
if (n == 1) return m[1]=1;
return m[n] = f(n-1) + f(n-2);
}
void main(void)
{
memset(m,-1,sizeof(m));
scanf("%d",&n); f(n);
while(scanf("%d",&i) == 1)
printf("%d\n",m[i]);
}
При вычислении чисел Фибоначчи Fn для больших аргументов (n > 92) следует воспользоваться классом BigInteger:
BigInteger f(int n)
{
BigInteger a(0),b(1),temp(0);
for(int i = 0; i < n; i++)
temp = a, a = b, b = temp + a;
return a;
}
Формула Бине выражает в явном виде значение Fn как функцию от n:
Fn =
= 
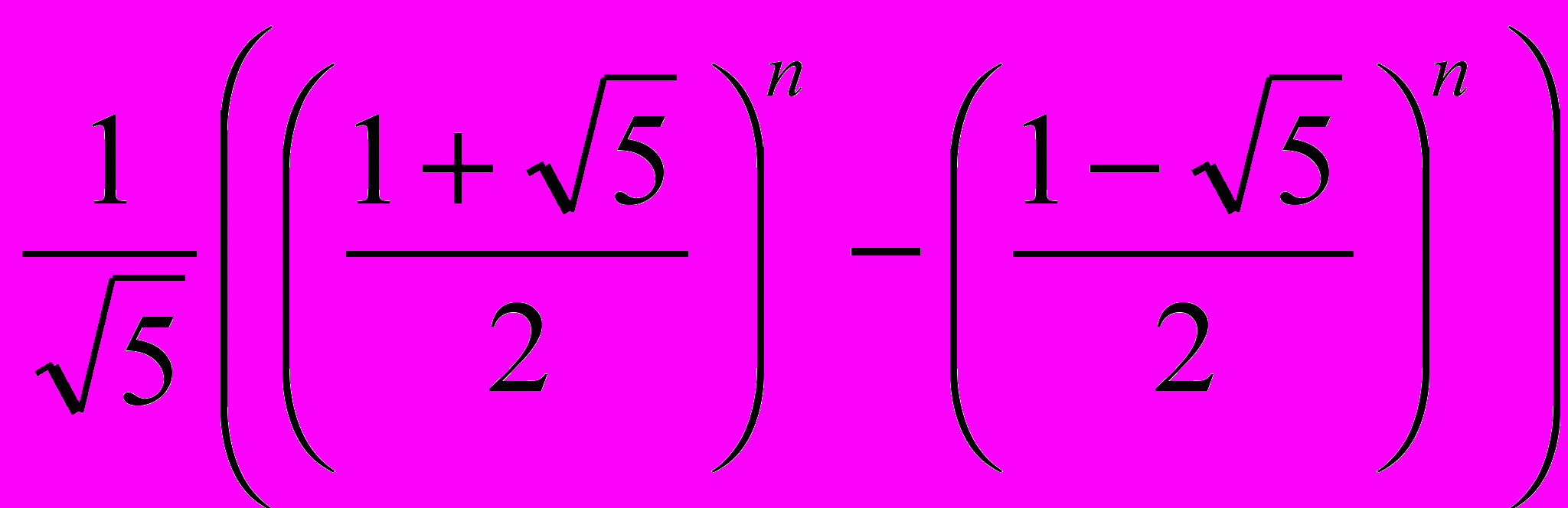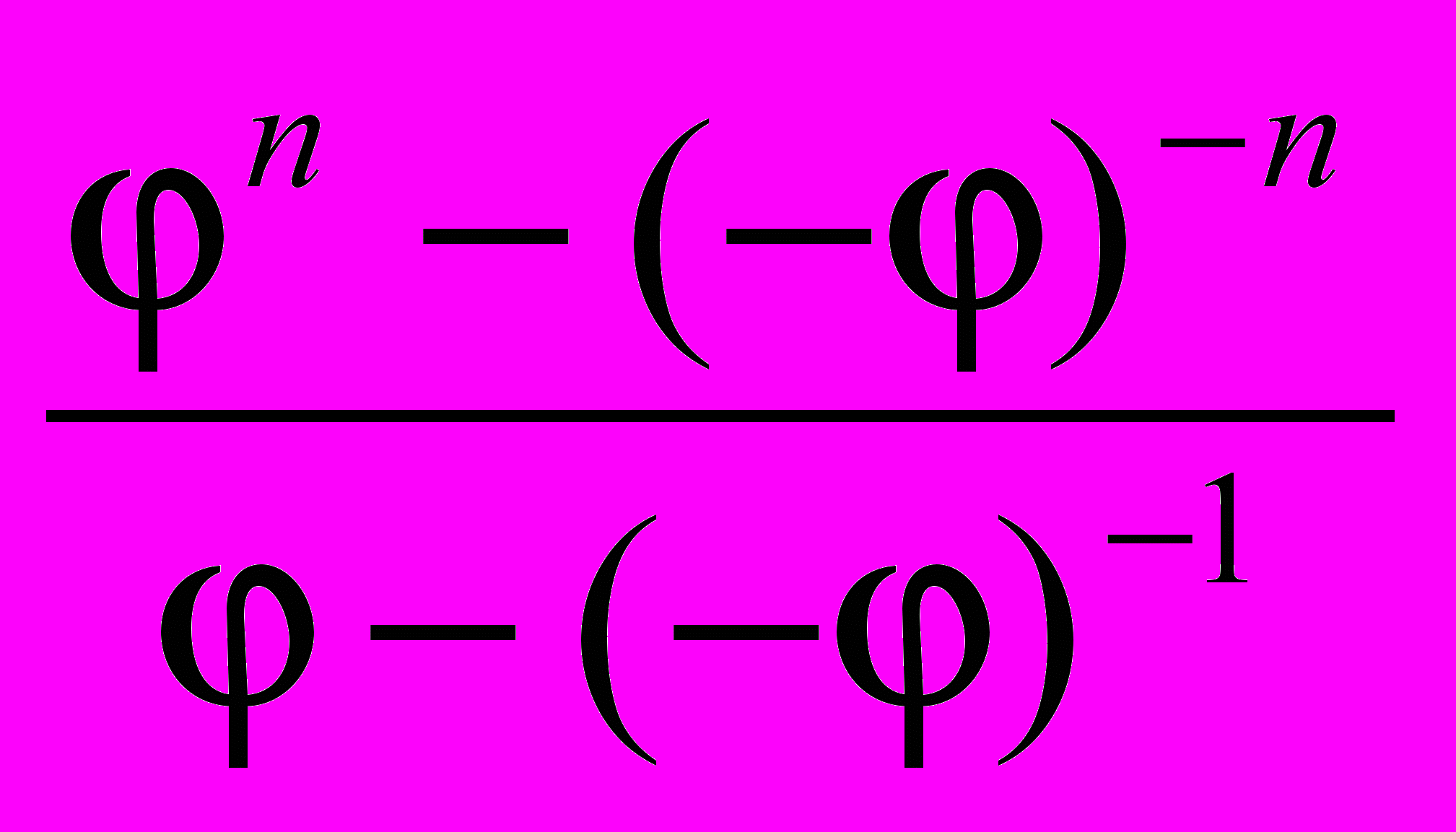,где =
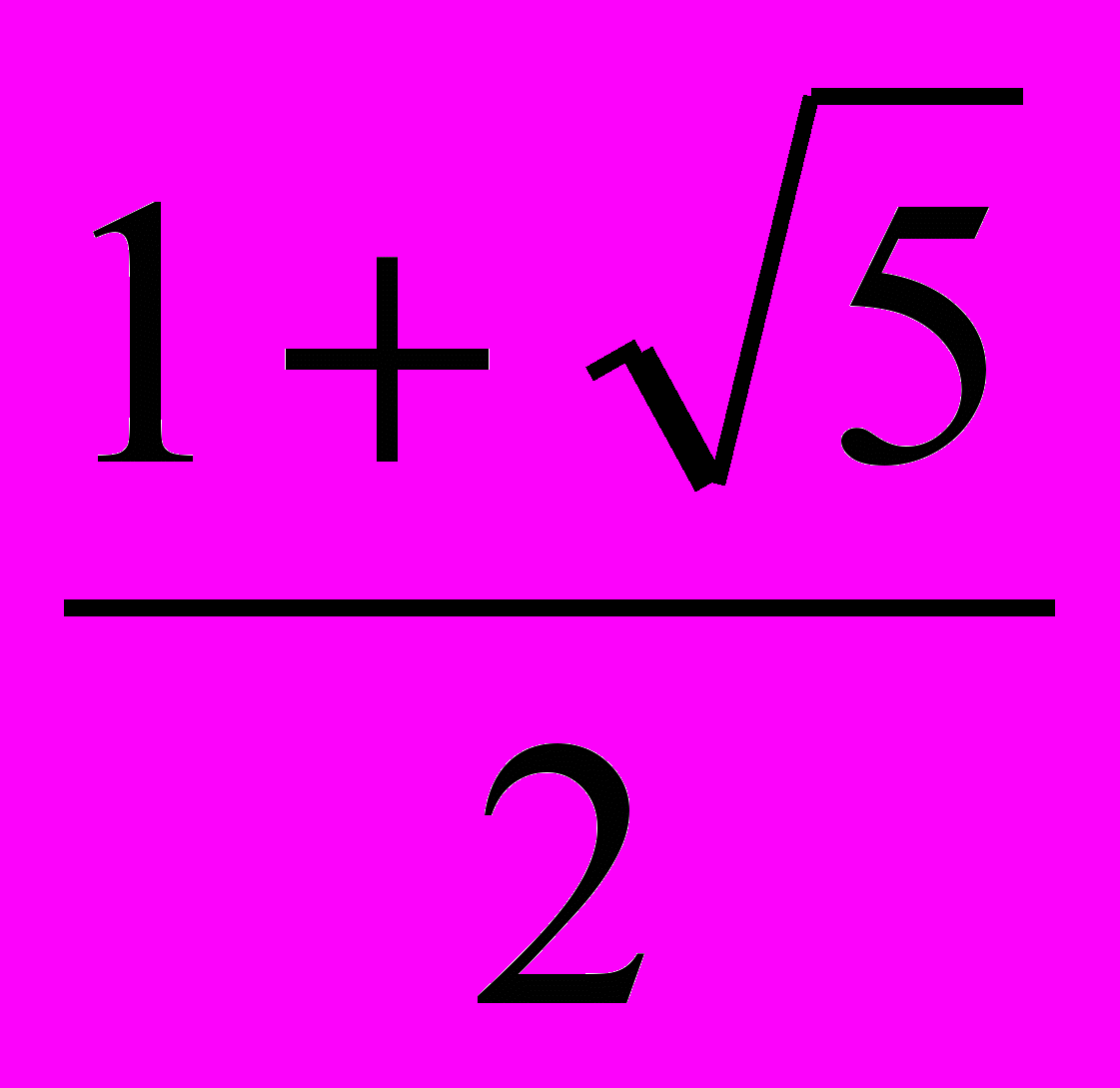– золотое сечение. При этом и (-)-1 = 1 – являются корнями квадратного уравнения x2 – x – 1 = 0.Следствие. Для всех n 0 имеет место приближение Fn
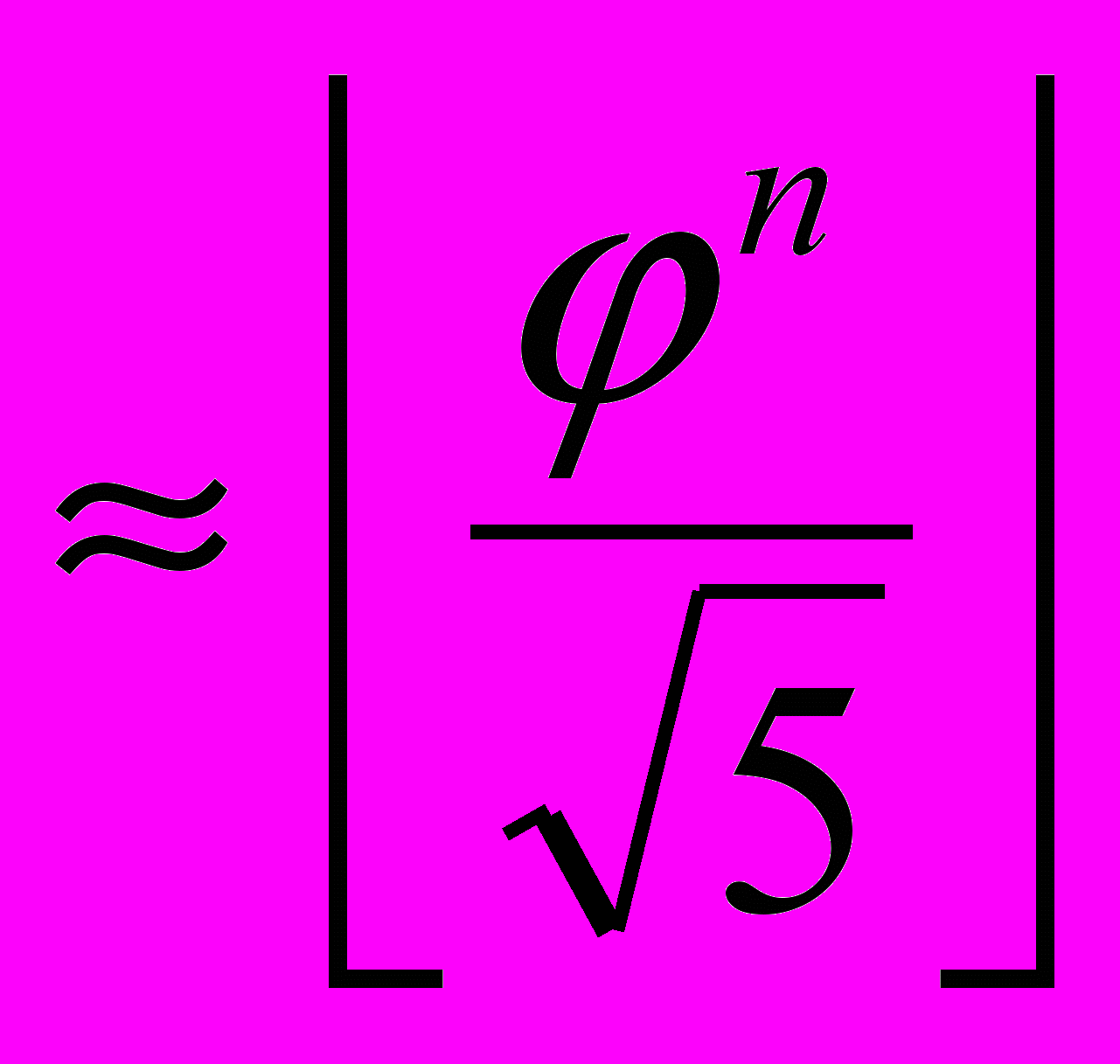.Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, то есть
НОД(Fn, Fm) = FНОД(n,m)
Следствие 1. Fm делится на Fn тогда и только тогда, когда m делится на n (за исключением n = 2).
Следствие 2. Fn может быть простым только для простых n (за исключением n = 4).
Упражнение 1.1. Свойства чисел Фибоначчи. Доказать следующие свойства:
а) F0 + F1 + F2 + F3 + … + Fn = Fn+2 – 1;
б) F1 + F3 + F5 + … + F2n-1 = F2n;
в) F0 - F1 + F2 - F3 + … - F2n-1 + F2n = F2n-1 – 1;
г) F02 + F12 + F22 + F32 + … + Fn2 = Fn * Fn+1;
д) Fn+1Fn-1 – Fn2 = (-1)n (Равенство Ж. Д. Кассини);
е) Fn+m = Fm Fn+1 + Fm-1 Fn;
Упражнение 1.2. Лестница. Необходимо пройти по лестнице, состоящей из n ступенек. Из очередной ступеньки можно перейти или на следующую ступеньку, или перешагнуть через одну. Сколько существует вариантов прохождения лестницы?
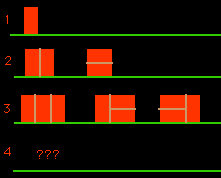
Упражнение 1.3. Кирпичная стена [Вальядолид, 900]. Высота кирпича равна 2, ширина – 1. Необходимо построить стену высоты 2 и длиной n. Сколькими способами можно это сделать в зависимости от значения n?
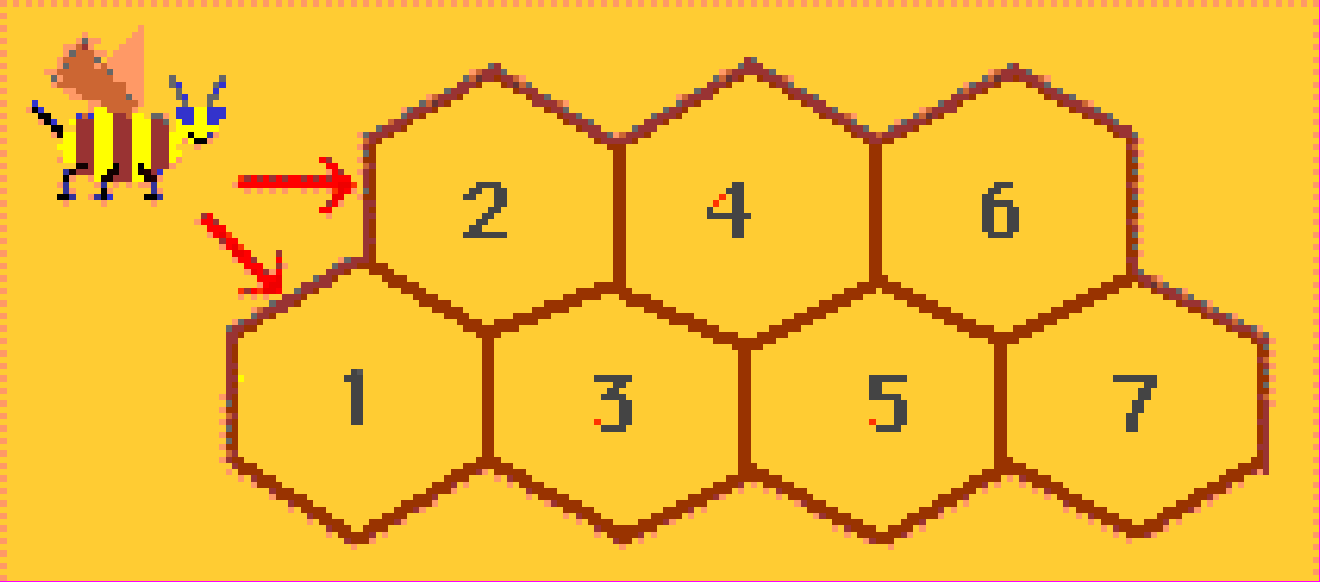
Упражнение 1.4. Путь пчелы. Пчела начинает свой путь с клетки 1 или 2 и направляется в клетку с номером n. Двигаться пчеле можно только по соседним клеткам от меньшего номера к большему. Сколькими разными путями пчела может попасть в клетку с номером n?
Упражнение 1.5. Новости по телефону. n друзей проживают в разных городах и разговаривают между собой только по телефону. Один телефонный звонок всегда длится одну минуту. Один из друзей желает поделиться новостью со всеми друзьями за наименьшее время. Найти наименьшее время, за которое все друзья будут знать новость, если каждый может совершить не более 2 звонков.
Упражнение 1.6. Резисторы. n одинаковых резисторов, с сопротивлением 1 Ом каждый, соединили как показано на рисунке (к первому резистору подсоединены резисторы с четными номерами последовательно, а с нечетными – параллельно). Найти сопротивленние всей системы из n резисторов.
n = 1 n = 2 n = 3 n = 4 n = 5 n = 6
Упражнение 1.7. Замораживание Фибоначчи [Вальядолид, 495]. Последовательность чисел Фибоначчи (0, 1, 1, 2, 3, 5, 8, 13, 21, ....) определяется рекуррентным соотношением:
f0 = 0, f1 = 1,
fi = fi-1 + fi-2, i 2
Следует написать программу, которая вычисляет числа Фибоначчи.
Вход. Каждая строка содержит целое неотрицательное число n (n 5000).
Выход. Для каждого входного n вывести n - ое число Фибоначчи в соответствии с ниже приведенным форматом.
-
Пример входа
Пример выхода
5
The Fibonacci number for 5 is 5
7
The Fibonacci number for 7 is 13
11
The Fibonacci number for 11 is 89
Упражнение 1.8. Шум мирового кубка [Вальядолид, 10450]. По заданному числу n вычислить количество последовательностей из 0 и 1 длины n, в которых две единицы не стоят рядом.
Вход. Первая строка содержит количество тестов. Каждая следующая строка является отдельным тестом и содержит число n (0 < n < 51).
Выход. Для каждого теста вывести его номер и количество последовательностей из 0 и 1 длины n, в которых две единицы не стоят рядом.
-
Пример входа
Пример выхода
2
Scenario #1:
3
5
1
Scenario #2:
2
Упражнение 1.9. Пчела [Вальядолид, 11000]. В Африке живет специальный вид пчел. Каждый год самка производит на свет одого самца, а самец – самца и самку, после чего родители погибают. Ученые изобрели магическую самку пчелу, которая плодится как обыкновенная самка, но при этом является бессмертной. Необходимо вычислить число самцов и общее количество пчел в семействе, если изначально была лишь одна магическая самка пчела.
Вход. Каждая строка содержит целое n (n 0).Последний тест содержит n = -1 и не обрабатывается.
Выход. Для каждого значения n вывести число самцов и общее количество пчел в семействе через n лет. Выводимые числа не более 232.
-
Пример входа
Пример выхода
1
1 2
3
4 7
-1
Упражнение 1.10. Флаги [Тимус 1225]. Флаг состоит из n вертикальных полос белого, красного и синего цвета. Соседние полосы не могут иметь одинаковый цвет, а синяя полоса всегда должна находиться между красной и белой. Сколькими способами можно покрасить флаг из n полос?
Вход. Число полос n (1 n 45) на флаге.
Выход. Количество способов, которыми можно покрасить флаг из n полос.
-
Пример входа
Пример выхода
3
4
2. ОБРАБОТКА СТРОК С ПОМОЩЬЮ КЛАССА STRING
Строкой называется последовательность символов, оканчивающаяся нуль-байтом. Для работы со строками (типом string) следует подключить библиотеку
#include
using namespace std;
Конструкторы. Создание строки производится одним из следующих конструкторов:
string a; // Создание пустой строки
string b("Hello"); // Создание строки с инициализацией данными
string c(10,'a'); // Создание строки, состоящей из 10 букв ‘a’
string d = b; // Создается строка d и в нее копируется одержимое строки b
string e(b,1,2); // В создавемую строку e копируются 2 символа строки b,
// начиная с позиции 1. Значение созданой строки e равно “el”
Конкатенация. Опрерация ‘+’ используется для объединения (конкатенации) строк:
string a(“This”); string b(“cat”);
string c = a+b; // Значение c равно “Thiscat”
Итераторы. Итератор string::begin() указывает на начало, a string::end() на конец строки.
string a("ABCDEFGH");
string b(a.begin()+1,a.end()-1); // b = “BCDEFG”
Ввод-вывод. При использовании функций библиотеки
string a("Hello");
printf("%s\n",a.c_str());
Ввод строки при помощи функции scanf следует совершать в символьный массив. Далее массив символов можно преобразовать в тип string при помощи конструктора
char s[100];
string a;
scanf("%s",s); a = string(s);
printf("%s\n",a.c_str());
Форматированный ввод из строки осуществляется функцией sscanf. Чтение чисел со строки и вычисление их суммы:
int x, y;
string a("23+4");
sscanf(a.c_str(),"%d+%d",&x,&y);
printf("%d+%d=%d\n",x,y,x+y);
Нумерация индексов элементов строк начинается с нуля. i - ый символ строки a можно получить операцией индексирования a[i] или выполнением функции at(i):
string a("This is a hat");
printf("Second letter is %c or %c\n",a[1],a.at(1));
Размер строки a равен a.size(). Посимвольный вывод строки a:
string a("This is a hat");
for(i = 0; i < a.size(); i++) printf("%c",a[i]);
Подстроки. Если a – переменная типа string, то a.substr(pos, l) является подстрокой, начинающейся с позиции pos и имеющей длину l. Если второй аргумент отсутствует, то выделяется подстрока с позиции pos до коца строки.
string a("This is a hat");
string b = a.substr(2,4); // b = “is i”
string c = a.substr(3); // c = “s is a hat”
printf("%s\n%s\n",b.c_str(),c.c_str());
Функция is_prefix возвращает 1, если строка a является префиксом строки b.
int is_prefix(string a, string b)
{
return b.substr(0,a.size()) == a;
}
Поиск. Если a и b – переменные типа string, то то a.find(b) возвращает первую позицию вхождения строки b в строку a. Если b не является подстрокой a, то метод find возвращает -1.
string a = "qwertwqy";
string b = "qw";
int pos = a.find(b); // pos = 0
Используя метод find, функцию is_prefix можно переписать так:
int is_prefix(string a, string b)
{
return (b.find(a) == 0);
}
Поиск в строке s подстроки b, начинающейся не раньше i - ой позиции, следует при помощи метода find(b, i) класса string:
string s = "abcdabcabc";
int pos = s.find("ab",1); // pos = 4
Удаление подстрок. Если t является подстрокой s, то находим позицию i, с которой она начинается и удаляем при помощи метода erase.
string s = "Hello thisis world";
string t = "this";
int i = s.find(t);
s.erase(i,t.size()); // s = "Hello is world"
Удаление всех вхождений строк t в качестве подстрок в строку s можно совершить в цикле:
string s = "thisHello thisis world this isthis";
string t = "this";
while((i = s.find(t)) >= 0)
s.erase(i,t.size()); // s = "Hello is world is"
Разбиение. Разбиение строки s на несколько подстрок при помощи разделителя c совершается при помощи функции split. Разделитель c может встречаться в строке в любом месте и в любом количестве.
vector
{
vector
int i = 0, j = s.find(c);
while(j >= 0)
{
if (s[i] != c) res.push_back(s.substr(i,j-i));
i = ++j;
j = s.find(c,j);
}
res.push_back(s.substr(i));
return res;
}
Вызов функции и вывод результата:
string s = " g this is a test 9";
vector
for(i = 0; i < v.size(); i++) printf("%s ",v[i].c_str());
Замена. Пример замены всех вхождений пробелов в строке v на точку:
string s = "This is a text";
replace(s.begin(),s.end(),' ','.'); // s = "This.is.a.text"
Обращение. Обращение строки можно совершить при помощи функции reverse, объявленной в
s = "This";
reverse(s.begin(),s.end()); // s = “sihT”
Потоковое чтение из строки. Занесение чисел, содержащихся в строке s, в массив m, можно совершить при помощи потокового вывода:
#include
#include
#include
using namespace std;
void main(void)
{
string s = "2 34 55 9 111";
int m[10], ptr = 0, i, a;
stringstream in(s);
while (in >> a) m[ptr++] = a;
for(i = 0; i < ptr; i++) printf("%d ",m[i]); printf("\n");
}
Упражнение 2.1. Простой калькулятор [Топкодер, раунд 178, дивизион 2, уровень 1]. Калькулятор умеет вычислять четыре арифметических действия и имеет один из следующих входных форматов:
Класс: SimpleCalculator
Метод: int calculate(string input)
Ограничения: 1
Вход. Строка input, содержащая одно из арифметических выражений.
Выход. Результат вычисления арифметческой операции.
Пример входа
-
input
5/3
15*3
1-10000
17+18
Пример выхода
1
45
-9999
35
Упражнение 2.2. Заглавная строка [Топкодер, раунд 210, дивизион 2, уровень 1]. В заданной строке необходимо заменить все первые буквы слов на заглавные. Слова в строке разделены пробелами.
Класс: TitleString
Метод: string toFirstUpperCase(string title)
Ограничения: строка title содержит от 0 до 50 символов, строка title содержит символы ‘a’ – ‘z’ и пробелы.
Вход. Строка title.
Выход. Строка title, в которой все первые буквы слов заменены на заглавные.
Пример входа
-
title
introduction to algorithms
more than one space between words
the king and i
Пример выхода
Introduction To Algorithms
More Than One Space Between Words
The King And I
Упражнение 2.3. Склеивание [Топкодер, раунд 246, дивизион 2, уровень 1]. Задана строка conglutination, состоящая из цифр, и целое число expectation. Можно ли строку разбить на два числа A и B так, чтобы A + B = expectation?
Класс: Conglutination
Метод: String split(String conglutination, int expectation)
Ограничения: conglutination содержит от 2 до 20 цифр, первая цифра не 0, 1 expectation 1000000000.
Вход. Строка цифр conglutination и ожидаемое значение суммы expectation.
Выход. Если строку conglutination невозможно разбить на части, сумма чисел в которых равна expectation, то вывести пустую строку. Иначе вывести строку в виде “A+B”.
Пример входа
| conglutination | Expectation |
| “22” | 4 |
| “536” | 41 |
| “123456000789” | 1235349 |
| “123456789” | 4245 |
Пример выхода
“2+2”
“5+36”
“1234560+00789”
“”
Упражнение 2.4. Код замены [Топкодер, раунд 257, дивизион 2, уровень 1]. В задаче следует декодировать строку символов code. Каждая цифра закодирована буквой. Ключом является строка key из 10 букв. Цифра ‘1’ соответствует первой букве ключа key, цифра ‘2’ – второй букве и так далее. Цифра ‘0’ соответствует последней букве. Буквы закодированной строки code, которые не встречаются в ключе key, игнорируются.
Класс: SubstitutionCode
Метод: int getValue(String key, String code)
Ограничения: code содержит от 1 до 9 символов ‘A’ – ‘Z’, key содержит в точности 10 разных символов, code содержит хотя бы один символ, содержащийся в key.
Вход. Две строки символов key и code.
Выход. Декодированная строка.
Пример входа
-
key
code
“TRADINGFEW”
“LGXWEV”
“ABCDEFGHIJ”
“XJ”
“CRYSTALBUM”
“MMA”
Пример выхода
709
0
6
Упражнение 2.5. Мультичтение [Топкодер, раунд 305, дивизион 2, уровень 1]. В компьютерных системах несколько процессов могут одновременно читать данные, но только один процесс может выполнять операцию записи в течении одного такта времени. Строка trace содержит историю работы системы и состоит из символов ‘R’ (чтение) и ‘W’ (запись). Вычислить минимальное время, за которое могут быть произведены все операции procs процессами.
Класс: MultiRead
Метод: int minCycles(string trace, int procs)
Ограничения: trace содержит от 1 до 50 символов ‘R’ и ‘W’, 1 procs 10.
Вход. Строка trace и число procs.
Выход. Количество тактов времени, за которое может быть выполнена последовательность операций чтения/записи, заданная строкой trace, procs процессами.
Пример входа
-
trace
procs
“RWWRRR”
3
“RWWRRRR”
3
“RRRRRRRRRR”
4
Пример выхода
4
5
3
УКАЗАНИЯ К РЕШЕНИЮ УПРАЖНЕНИЙ
Упражнение 1.1. Свойства чисел Фибоначчи.
Доказательство всех равенств проводим по индукции.
а) База. n = 0. F0 = F2 – 1, что верно.
Шаг. F1 + F2 + F3 + … + Fn = (F1 + F2 + F3 + … + Fn-1) + Fn =
= Fn+1 – 1 + Fn = Fn+2 – 1.
б) База. n = 1. F1 = F2, что верно.
Шаг. F1 + F3 + F5 + … + F2n+1 = (F1 + F3 + F5 + … + F2n-1) + F2n+1 =
= F2n + F2n+1 = F2n+2.
в) База. n = 1. F0 – F1 + F2 = 0 – 1 + 1 = 0, F1 – 1 = 1 – 1 = 0.
Шаг. (F0 – F1 + F2 – F3 + … – F2n-1 + F2n) – F2n+1 + F2n+2 =
= F2n-1 – 1 – F2n+1 + F2n+2 = F2n-1 – 1 – F2n+1 + F2n + F2n+1 =
= F2n-1 + F2n – 1 = F2n+1 – 1.
г) База. n = 0. F02 = F0 * F1, что верно.
Шаг.
+ 
+ … + 
= ( + + … + 
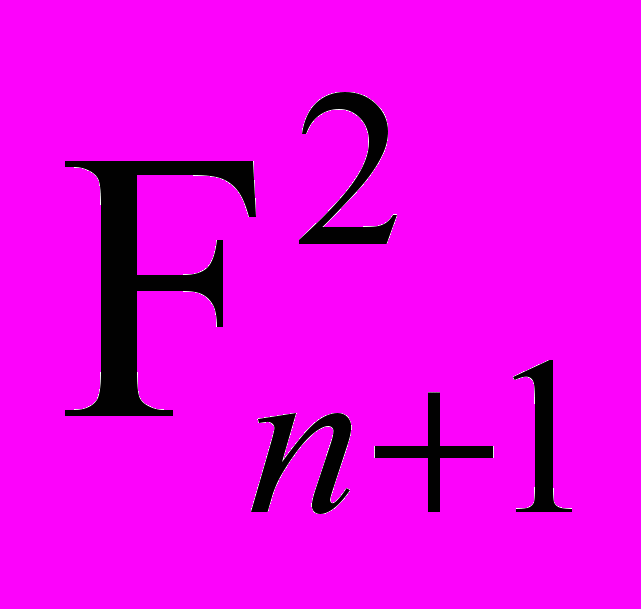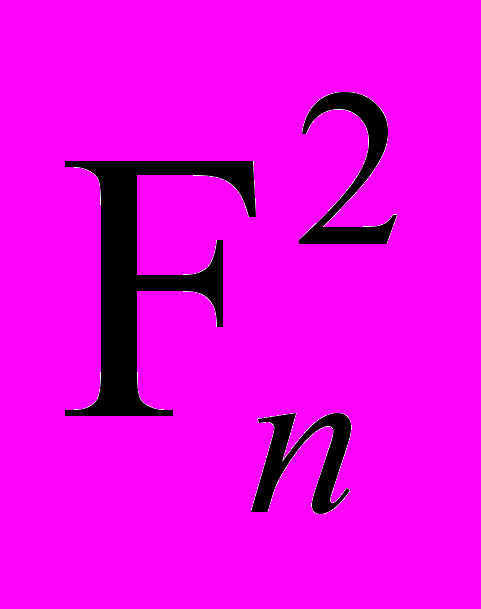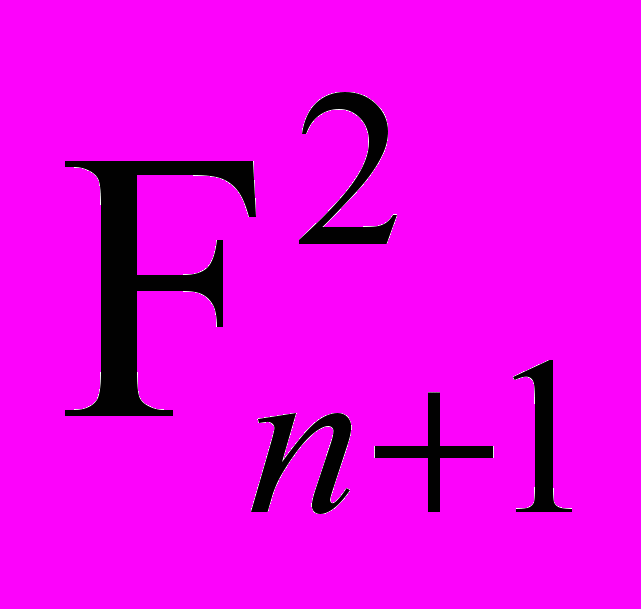) + = = Fn * Fn+1 +
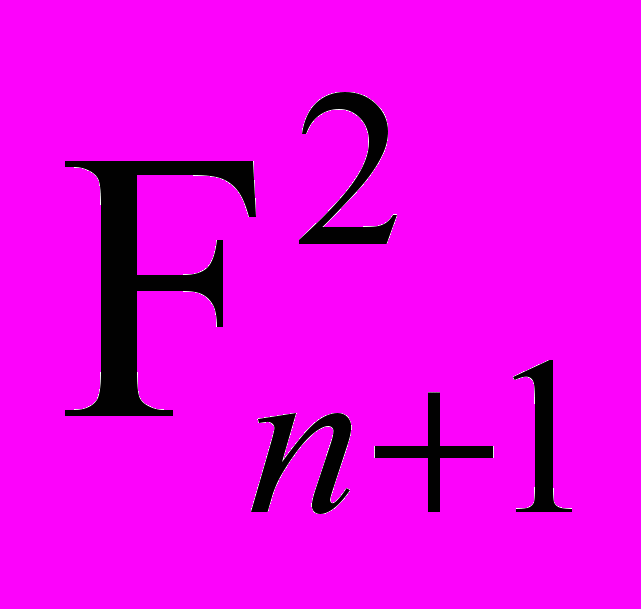= Fn+1 * (Fn + Fn+1) = Fn+1 * Fn+2.д) Равенство получается из матричного тождества
= 
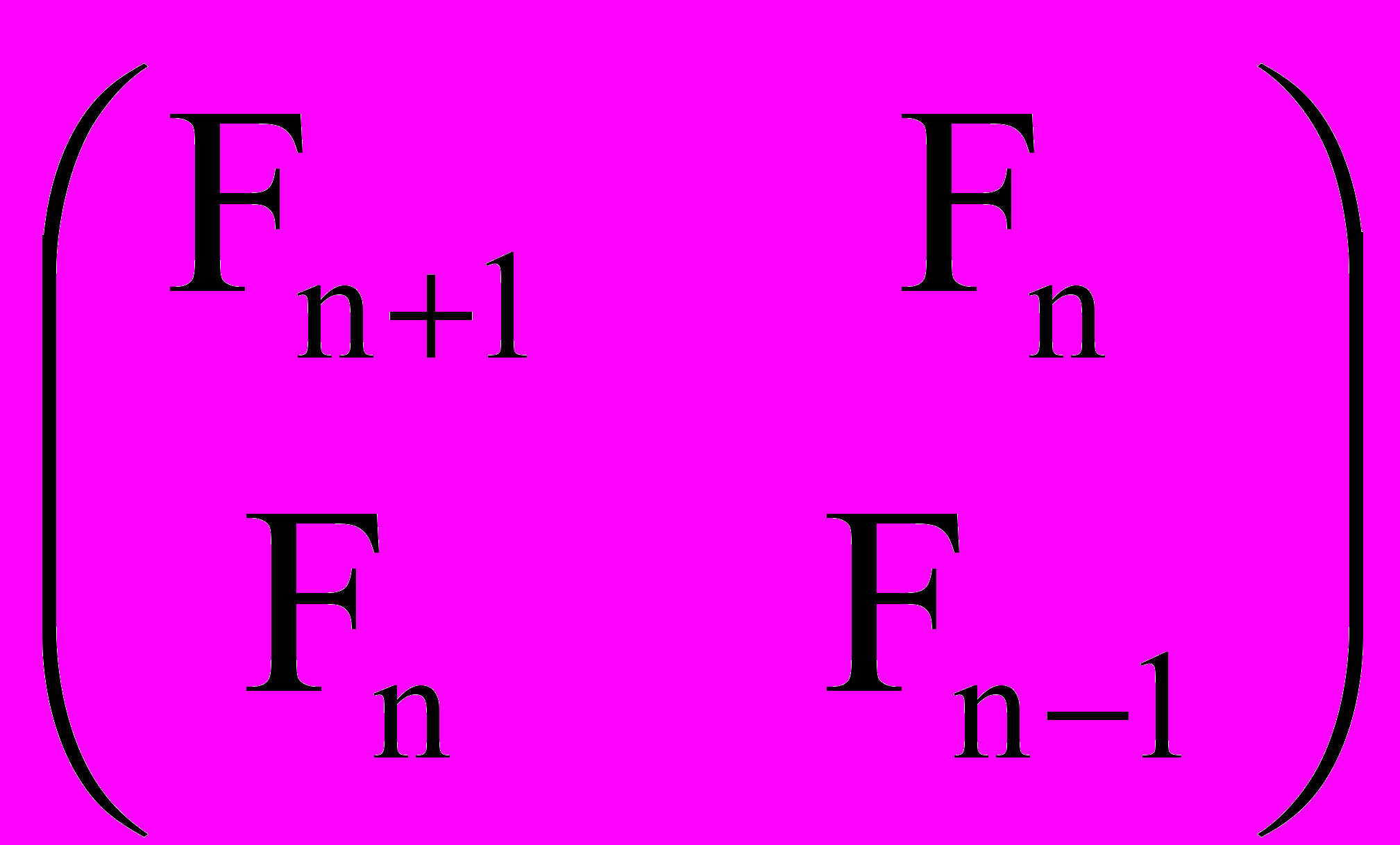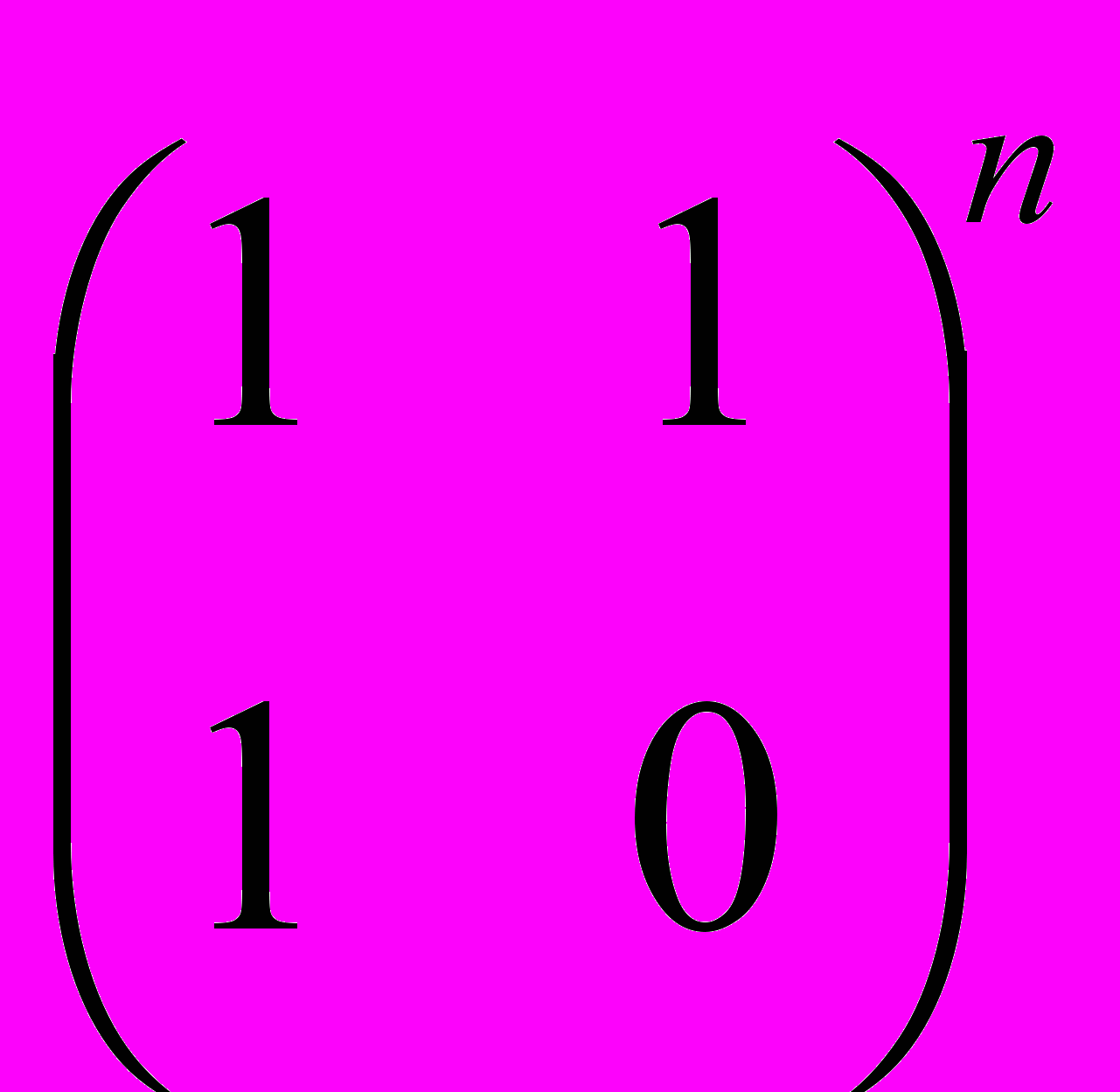после вычисления определителей.е) Индукция по m. База. m = 1. Fn+1 = F1Fn+1 + F0Fn = 1 * Fn+1 + 0 * Fn = Fn+1, что верно.
Шаг. Fn+m+1 = Fn+m + Fn+m-1 = Fm Fn+1 + Fm-1Fn + Fm-1 Fn+1 + Fm-2Fn =
(Fm + Fm-1) Fn+1 + (Fm-1 + Fm-2) Fn = Fm+1 Fn+1 + Fm Fn.
Упражнение 1.2. Лестница. Пусть f(n) – количество вариантов, которыми можно пройти по n ступенькам. С n - ой ступеньки можно перейти или на (n – 1) - ую, или на (n – 2) - ую. Количество вариантов пройти n ступенек равно количеству вариантов пройти n – 1 ступенек плюс количество вариантов пройти n – 2 ступеньки, тоесть f(n) = f(n – 1) + f(n – 2). Очевидно, что f(1) = 1 и f(2) = 2. Таким образом f(n) является (n + 1) - ым числом Фибоначчи.
Упражнение 1.3. Кирпичная стена [Вальядолид, 900]. Обозначим через f(n) количество способов, которыми можно построить кирпичную стену высоты 2 и длины n. Тогда можно положить один кирпич вертикально и далее строить стену длины n – 1 f(n – 1) способом, или положить два кирпича горизонтально и строить стену длины n – 2 f(n – 2) способами. То есть f(n) = f(n – 1) + f(n – 2). Также имеем: f(1) = 1 (один вертикальный кирпич), f(2) = 2 (два вертикальных или два горизонтальных кирпича). То есть f(n) является (n + 1) - ым числом Фибоначчи.
Упражнение 1.4. Путь пчелы. Из клетки с номером n пчела может попасть или в клетку с номером n + 1, или с номером n + 2. Задача сводится к движению по ступенькам лестницы. Количество разных путей до клетки с номером n равно Fn.
Упражнение 1.5. Новости по телефону. Звонки между друзьями следует организовать так, как показано на рисунке 4. Тогда на i - ой минуте о новости узнают еще Fi+1 друзей. Наименьшее число минут, за которое новость распространится среди n – 1 друзей (изначально не знающие новости), равно такому наименьшему значению k, для которого F2 + F3 + … + Fk + Fk+1 n – 1. Учитывая, что F0 + F1 + F2 + F3 + … + Fn = Fn+2 – 1, неравенство можно переписать в виде: Fk+3 – 1 n. Считаем, что F1 = 1 (личность, которая распространяет новость) и F2 = 1 (друг, которому сделан первый звонок).
личность, распространяющая новость
/----------------\
первая минута A \
/--------\ \
вторая минута C \ B
/----\ \ /----\
третья минута D \ E F \
/---\ \ /----\ /----\ \
... ... ... ... ... ... ... ...
Например, при n = 4 необходимо k = 2 минуты (трем друзьям A, B и C распространяется новость). Неравенство F5 – 1 4 имеет место.
Упражнение 1.6. Резисторы. Обозначим через f(n) сопротивление системы из n резисторов. Очевидно, что f(1) = 1, f(2) = 2. Докажем по индукции, что
f(n) =
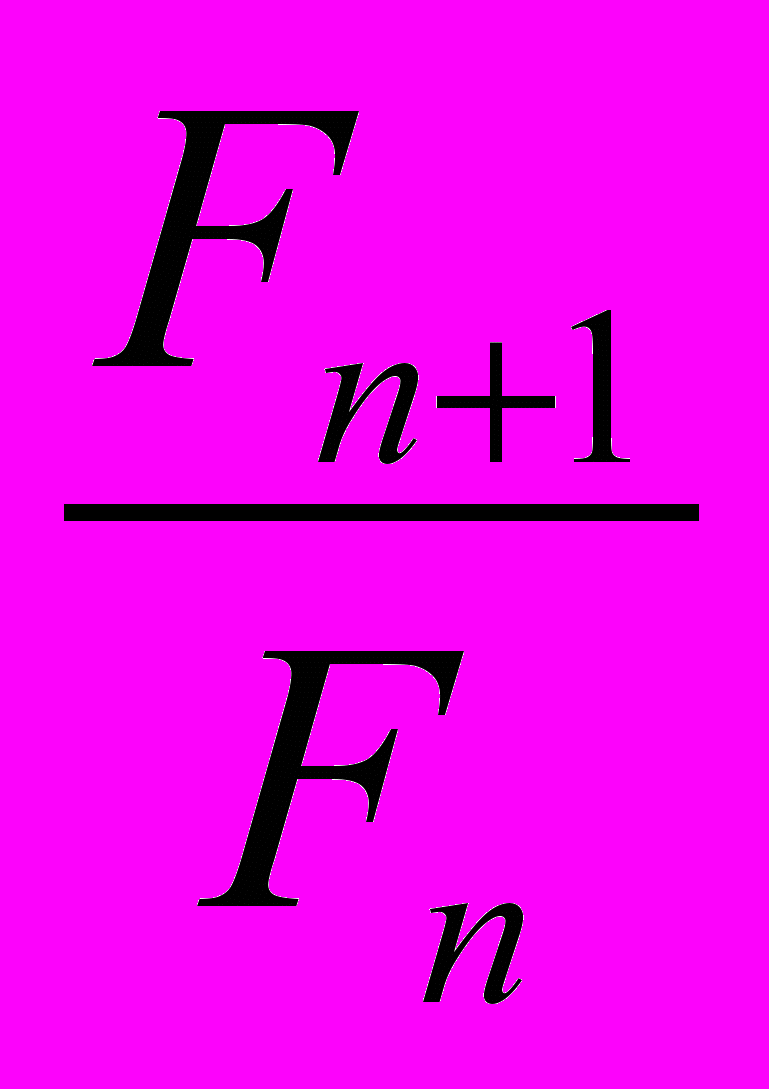при четном n и f(n) = 
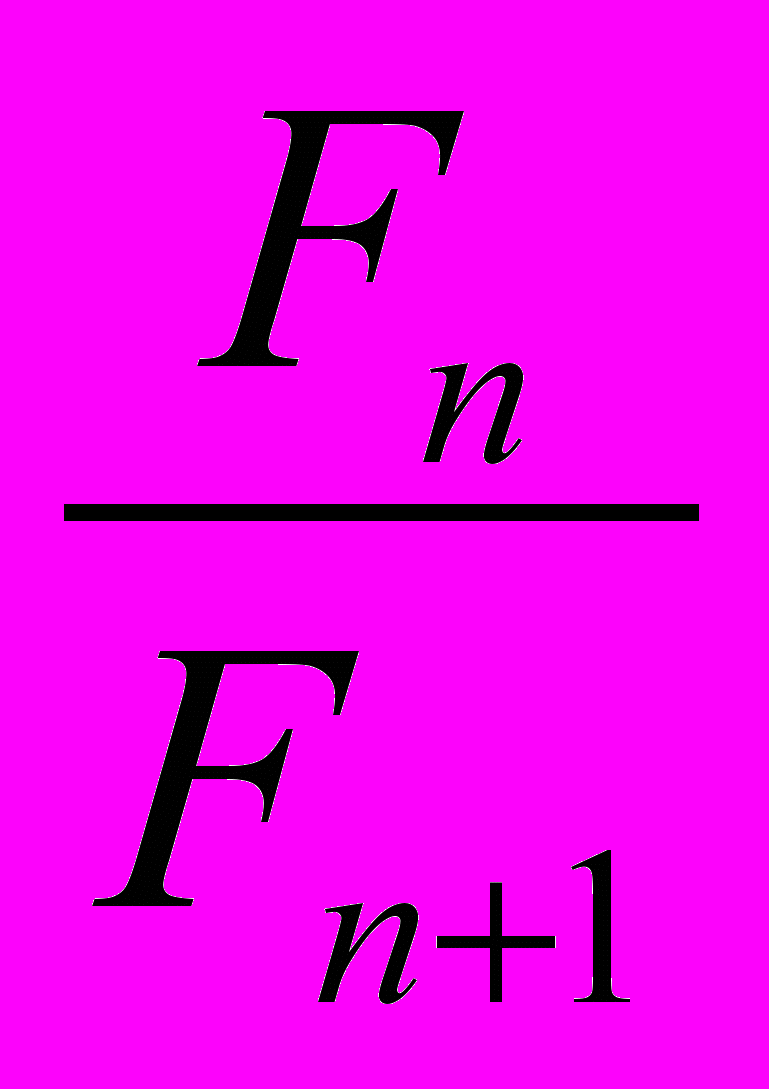при нечетном n.Если система состоит из четного количества резисторов, то следующий резистор соединяется параллельно и результирующее сопротивление равно
= 
= 
= 
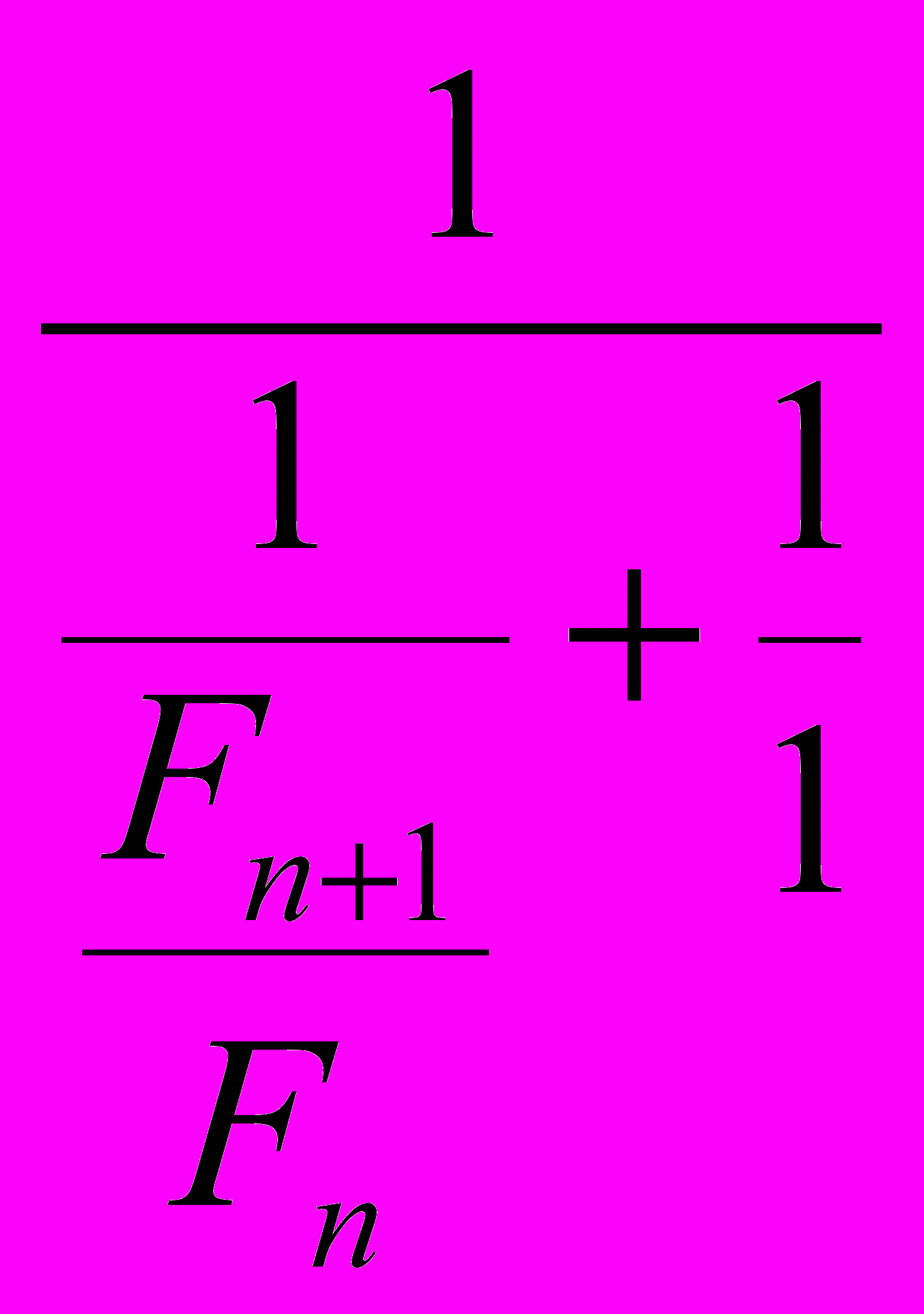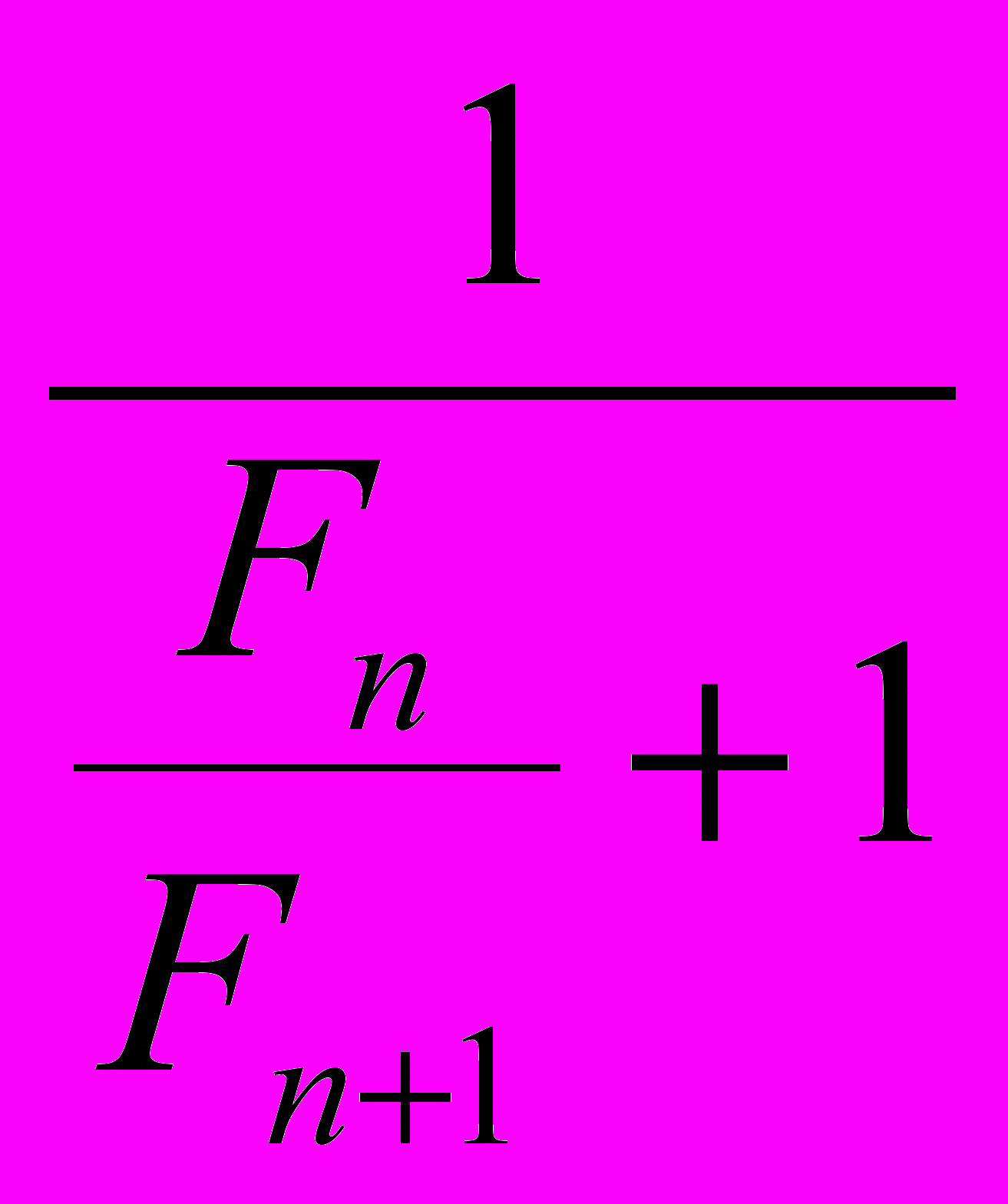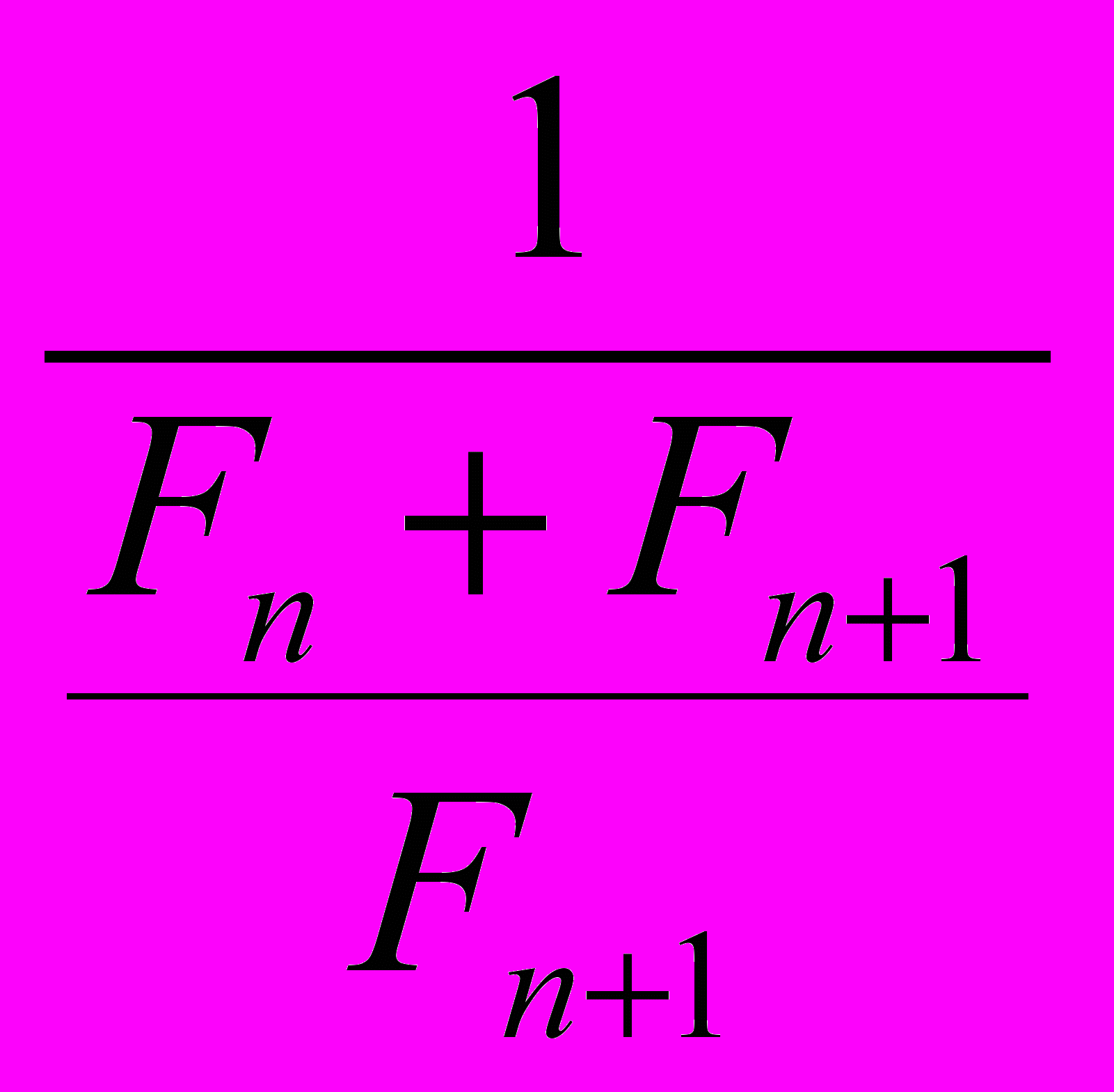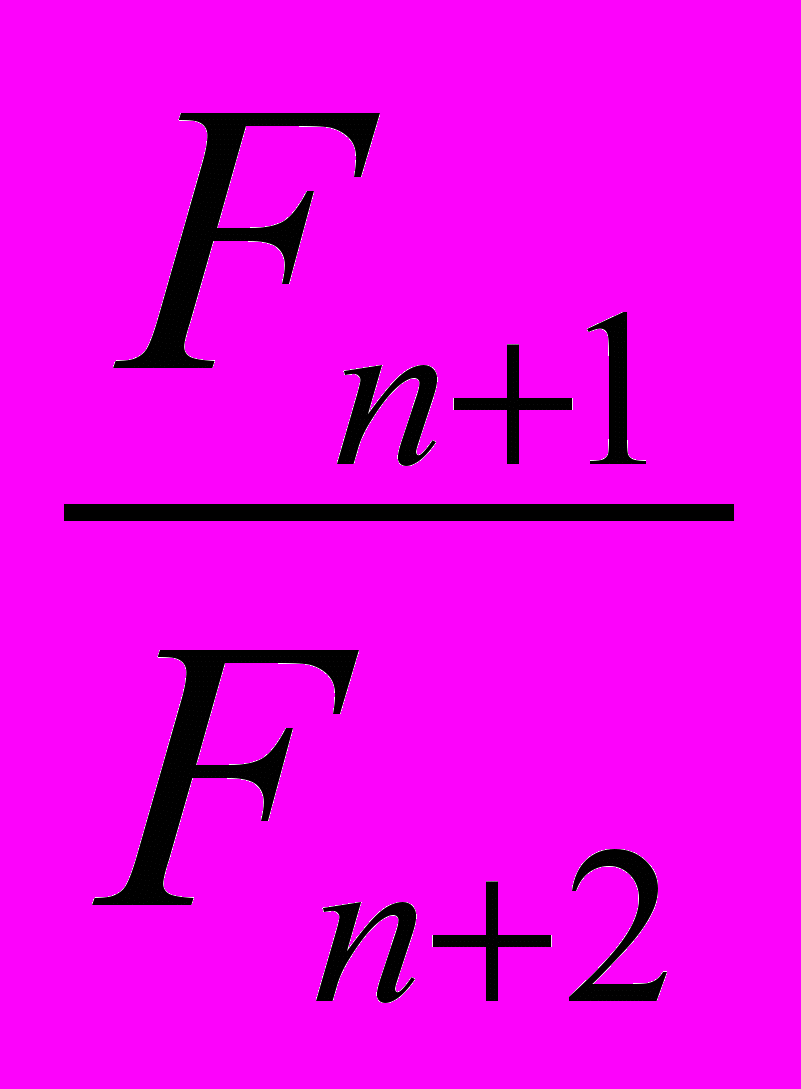
В случае нечетного количество резисторов соединение со следующим резистором происходит последовательно и результирующее сопротивление равно
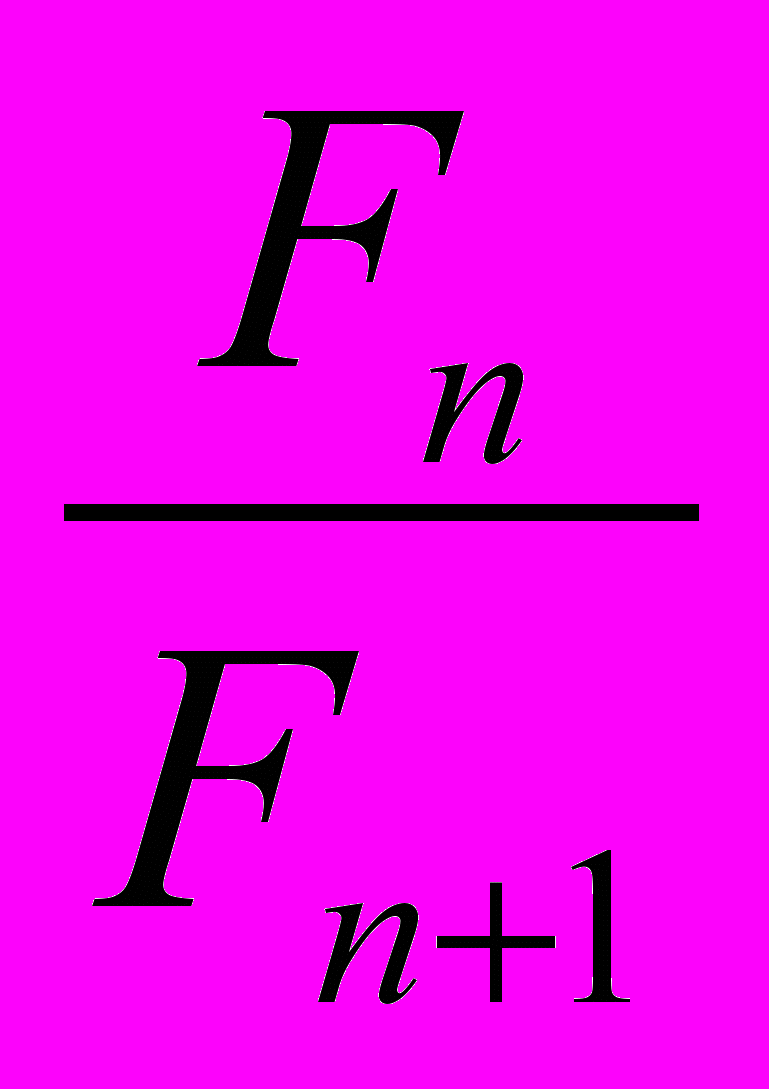+ 1 =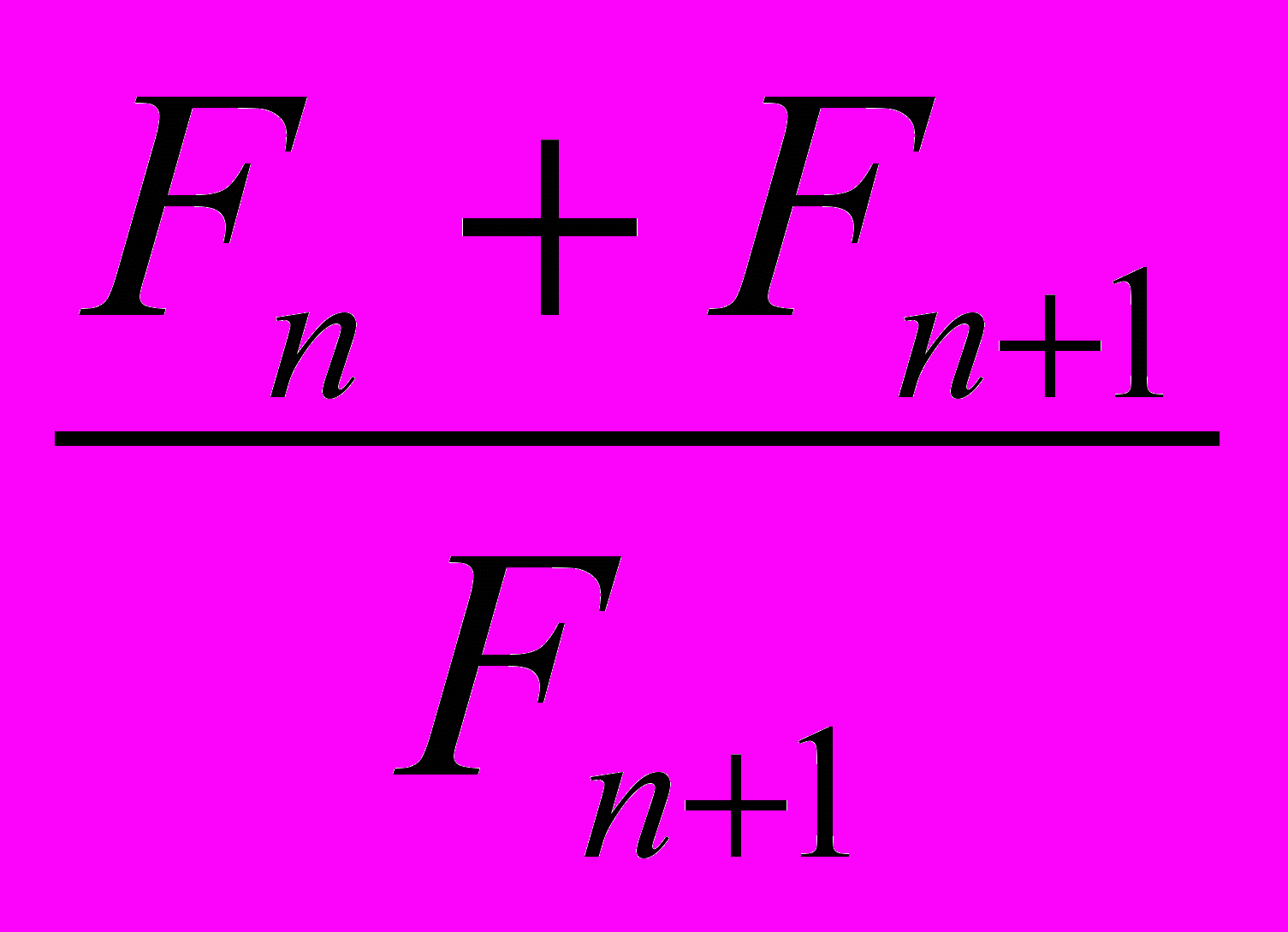 
= 
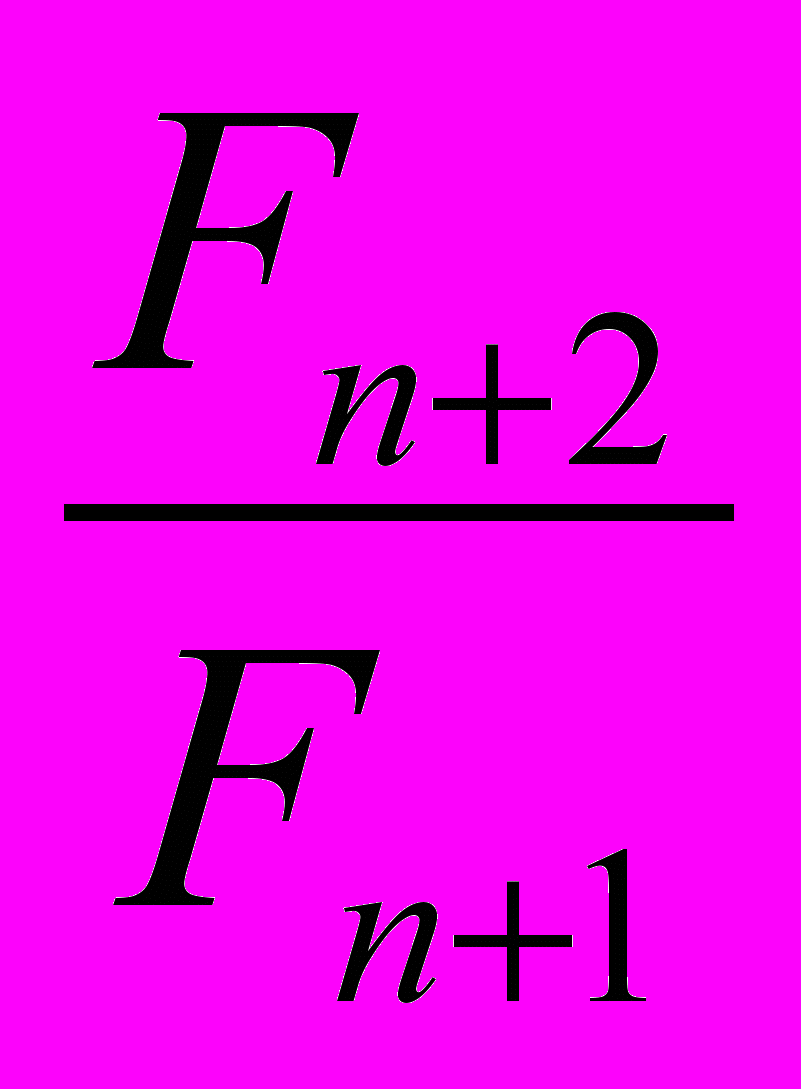
Упражнение 1.7. Замораживание Фибоначчи [Вальядолид, 495]. Поскольку n 5000, то для нахождения fn следует воспользоваться классом BigInteger. Найдем и запомним в массиве m все значения fn (0 n 5000) и для каждого входного n будем выводить m[n] = fn.
Реализация. Вычислим все значения fn (0 i 5000) и занесем их в массив m[5001]. Поскольку f5000 содержит не более 1100 десятичных знаков, то установим MAXLENGTH = 1100.
#include
#include
#define MAXLENGTH 1100
class BigInteger{ . . .};
BigInteger m[5001];
void main(void)
{
int i,n;
Положим m[1] = 1 и воспользуемся рекуррентной формулой m[i] = m[i -1] + m[i - 2].
m[1] = BigInteger(1);
for(i=2;i<5001;i++) m[i] = m[i-1] + m[i-2];
Для каждого входного значения n выводим fn = m[n] в соответствии с требуемым форматом.
while(scanf("%d",&n) == 1)
printf("The Fibonacci number for %d is ",n),m[n].print();
}
Упражнение 1.8. Шум мирового кубка [Вальядолид, 10450]. Обозначим через f(n) количество искомых последовательностей из 0 и 1 длины n. Если на первом месте последовательности будет находиться 0, то начиная со второго места можно построить f(n – 1) последовательностей. Если на первом месте стоит 1, то на втором месте обязательно должен стоять 0, а на последующих n - 2 свободных местах можно построить f(n – 2) последовательностей.
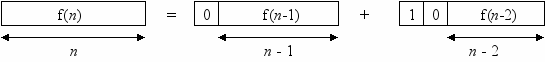
При этом f(1) = 2 (имеем две последовательности длины 2: 0 и 1), f(2) = 3 (последовательности 00, 01, 10). Значения f(n) образуют числа Фибоначчи . Известно, что f0 = 0, f1 = 1, f2 = 1, fi = fi-1 + fi-2. Учитывая начальные условия, получим: f(n) = fn+2.
Пример. Рассмотрим второй тест. Всего существует 5 последовательностей из 0 и 1 длины 3, в которых две единицы не стоят рядом: 000, 001, 010, 100, 101.
Реализация. В массиве fib вычислим значения f(n): f(n) = fib[n]. Для n > 44 значения f(n) будут выходить за границы типа int, поэтому воспользуемся 64 - битовым целочисленным типом long long (в среде Microsoft Visual Studio C++ – тип __int64).
#include
int tests,i,n;
long long fib[51];
void main(void)
{
Нахождение значений f(n) совершим в цикле:
fib[1] = 2; fib[2] = 3;
for(i=3;i<51;i++) fib[i] = fib[i-1] + fib[i-2];
Читаем количество тестов и для каждого входного n выводим значение fib[n].
scanf("%d",&tests);
for(i=1;i<=tests;i++)
{
scanf("%d",&n);
printf("Scenario #%d:\n",i);
printf("%lld\n\n",fib[n]);
}
}
Упражнение 1.9. Пчела [Вальядолид, 11000]. Обозначим n - ое число Фибоначчи через f(n). Тогда через n лет число самцов в пчелином семействе будет равно f(n) – 1, а общее число пчел f(n + 1) – 1. Через n = 0 лет семейство состоит из единственной пчелы самки, то есть имеется 0 самцов и 1 пчела. Положим f(0) = 1, f(1) = 2. Далее по индукции докажем справедливость приведенного утверждения. После n + 1 года число самцов равно суммарному числу самок и самцов после n - го года, то есть f(n + 1) – 1. Число самок после n + 1 года равно числу самцов после n - го года плюс одна бессмертная самка, то есть f(n) – 1 + 1 = f(n). Таким образом общее число пчел после n + 1 года равно f(n + 1) – 1 + f(n) = f(n + 2) – 1.
Реализация. Искомые числа Фибоначчи не превосходят 232. Вычислим их первые 50 значений и занесем в массив f типа long long.
#include
long long f[50];
void main(void)
{
int i,n;
Заполним массив f числами Фибоначчи.
f[0] = 1; f[1] = 2;
for(i=2;i<50;i++) f[i] = f[i-1] + f[i-2];
Для каждого входного n выведем результат.
while(scanf("%d",&n),n >= 0)
printf("%lld %lld\n",f[n]-1,f[n+1]-1);
}
Упражнение 1.10. Флаги [Тимус 1225]. Обозначим через fred(n) и fwhite(n) количество способов раскраски флага из n полос при условии, что первой полосой будет соответственно красная или белая. Тогда
fred(n) = fwhite(n – 1) + fwhite(n – 2), fred(1) = 1, fred(2) = 1;
fwhite(n) = fred(n – 1) + fred(n – 2), fwhite(1) = 1, fwhite(2) = 1.
Если f(n) – искомое общее количество способов раскраски, то
f(n) = fred(n) + fwhite(n)
Поскольку fred(1) = fwhite(1) = 1, fred(2) = fwhite(2) = 1, а fred(n) и fwhite(n) одинаковыми формулами выражаются друг через друга, то fred(n) = fwhite(n) = fn, где fn – n-ое число Фибоначчи. Таким образом f(n) = 2 * fn.
Реализация. В массиве fib вычислим значения fred(n): fred(n) = fib[n]. Для n > 44 значения fred(n) будут выходить за границы типа int, поэтому воспользуемся 64 - битовым целочисленным типом __int64.
__int64 fib[46];
Читаем входное значение n. Нахождение значения fib[n] совершим в цикле:
scanf("%d",&n);
fib[1] = 1; fib[2] = 1;
for(i=3;i<=n;i++) fib[i] = fib[i-1] + fib[i-2];
Выводим результат f(n) = 2* fred(n) = 2 * fib[n]:
printf("%I64d\n",2*fib[n]);
Упражнение 2.1. Простой калькулятор [Топкодер, раунд 178, дивизион 2, уровень 1]. Следует воспользоваться форматированным чтением данных при помощи функции scanf.
#include
#include
using namespace std;
class SimpleCalculator
{
public:
int calculate(string input)
{
int a,b,res;
char c;
sscanf(input.c_str(),"%d%c%d",&a,&c,&b);
if (c == '+') res = a + b; else
if (c == '-') res = a - b; else
if (c == '*') res = a * b; else
if (c == '/') res = a / b;
return res;
}
};
Упражнение 2.2. Заглавная строка [Топкодер, раунд 210, дивизион 2, уровень 1]. Проходим по строке, каждую первую букву слова заменяем на заглавную при помощи функции toupper, объявленной в библиотеке
#include
#include
#include
using namespace std;
class TitleString
{
public:
string toFirstUpperCase(string title)
{
for(int i=0;i
if ((!i || title[i-1] == ' ') && isalpha(title[i]))
title[i] = toupper(title[i]);
return title;
}
};
Упражнение 2.3. Склеивание [Топкодер, раунд 246, дивизион 2, уровень 1]. Задача решается полным перебором вариантов разбиения строки на две части. Если размер входной строки равен len = conglutination.size(), то следует перебрать len – 1 разбиений: левая часть строки содержит i цифр, правая len – i цифр, 1 i len – 1.
Если a – переменная типа string, то a.substr(pos, l) является подстрокой, начинающейся с позиции pos и имеющей длину l. Если второй аргумент отсутствует, то выделяется подстрока с позиции pos до коца строки.
Функция a.c_str() преобразовывает строку a в массив символов, с которым работают функции ввода-вывода библиотеки <stdio.h>. Чтение форматированных данных из строки совершается функцией sscanf.
Требуемое разбиение строки на два числа не будет найдено, если по окончанию цикла переменная i будет содержать значение len.
#include
#include
using namespace std;
class Conglutination
{
public:
string split(string conglutination, int expectation)
{
string a,b,res="";
int x,y;
for(int i = 1; i < conglutination.size(); i++)
{
a = conglutination.substr(0,i);
b = conglutination.substr(i);
sscanf(a.c_str(),"%d",&x);
sscanf(b.c_str(),"%d",&y);
if (x + y == expectation) break;
}
if (i < conglutination.size()) res = a + '+' + b;
return res;
}
};
Упражнение 2.4. Код замены [Топкодер, раунд 257, дивизион 2, уровень 1]. Для каждой i - ой буквы из кода code следует найти ее позицию pos в ключе key при помощи метода find класса string. Если буква не найдена, метод возвратит -1. Если соответствующая буква найдена в ключе, то припишем к результату res цифру (pos + 1) % 10.
#include
#include
using namespace std;
class SubstitutionCode
{
public:
int getValue(string key, string code)
{
int i,pos,res=0;
for(i=0;i
{
pos = key.find(code[i]);
if (pos >= 0) res = res*10+(pos+1)%10;
}
return res;
}
};
Упражнение 2.5. Мультичтение [Топкодер, раунд 305, дивизион 2, уровень 1]. Просматриваем строку trace. При встрече операции записи увеличиваем искомое число тактов времени res на 1. Длину каждой группы из операций чтения заносим в переменную с. с операций чтения можно выполнить procs процессами за
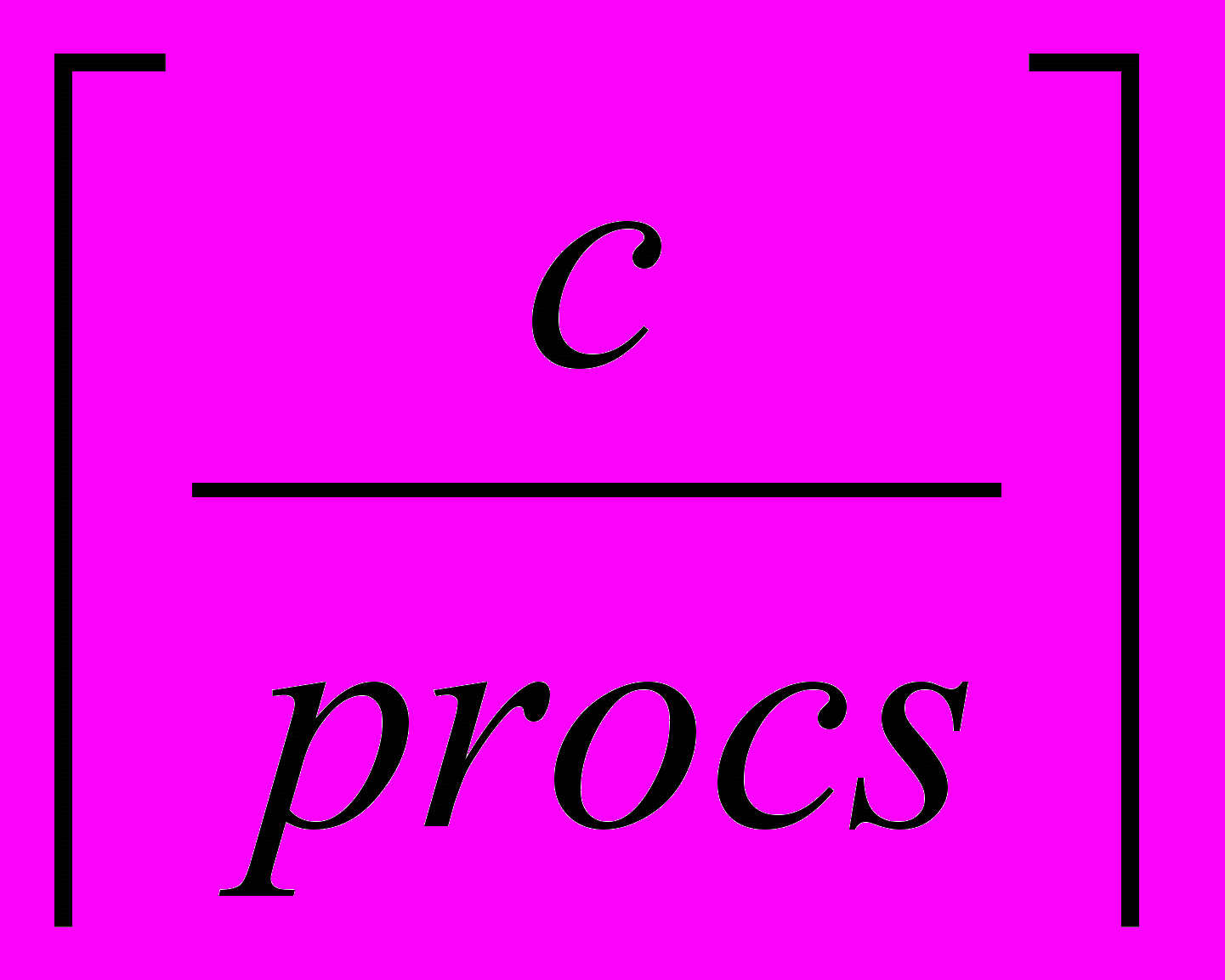временных тактов. Заметим, что 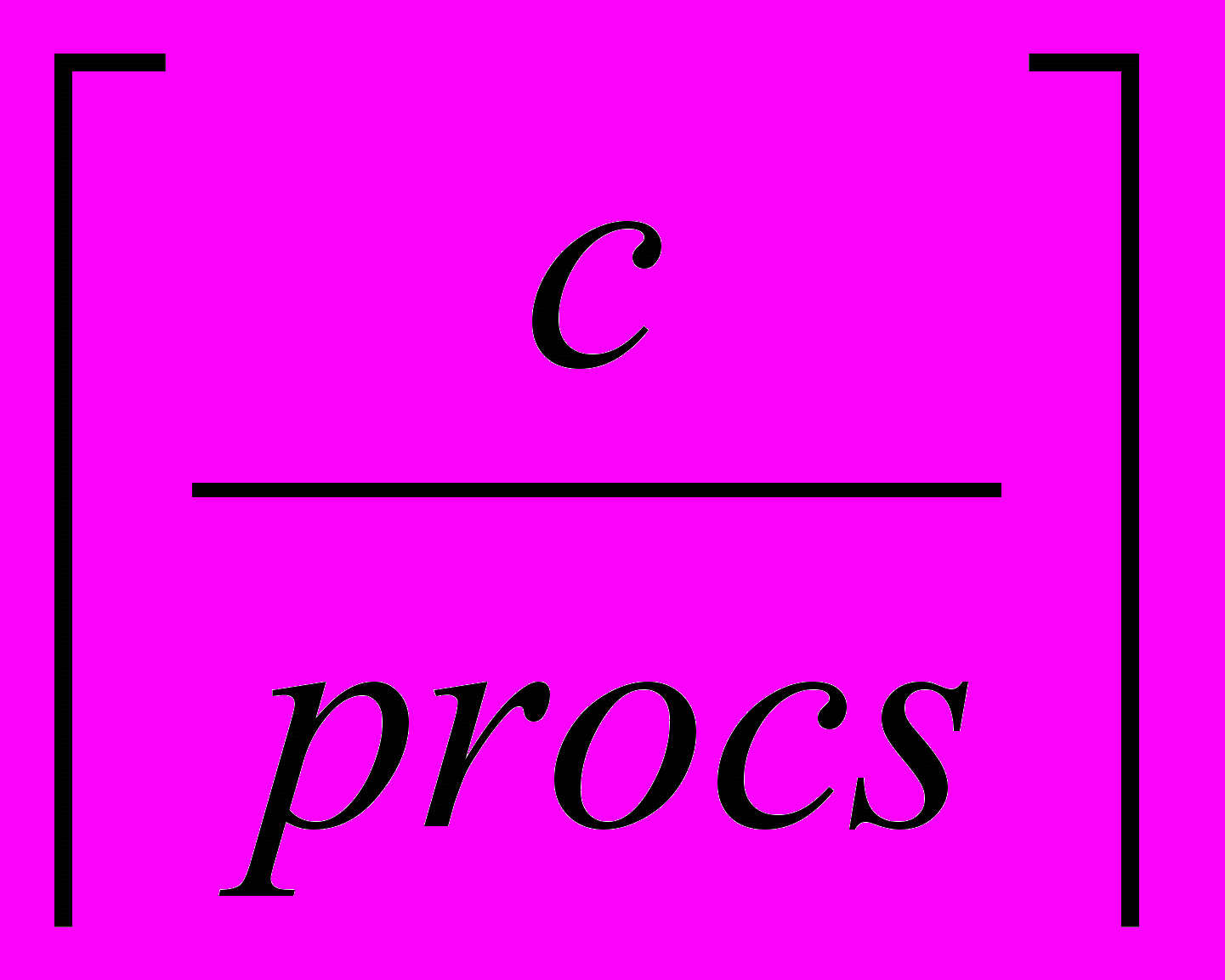= (c + procs – 1) / procs,где деление является целочисленным. Добавим это число к переменной res.
#include
#include
using namespace std;
class MultiRead{
public:
int minCycles(string trace, int procs)
{
int res,i,c;
for(res=i=0;i
if (trace[i] == 'W') res++; else
{
c=0;while((trace[i] == 'R') && (i < trace.size())) {c++;i++;} i--;
res += (c + procs - 1)/procs;
}
return res;
}
};