Конспект лекций по курсу "Алгоритмические языки и программирование". Тема "Рекурсия"

Вид материала

Содержание

Базисное утверждение
Рекурсивное утверждение
1.2. Рекурсивные процедуры и функции. Взаиморекурсия.
Прямая или явная
1.3. Фрейм активации.
Базисное утверждение
Базисное утверждение
Рекурсивное утверждение
Базисные утверждения
Глава 2. Полный и ограниченный перебор. Рекурсия при программировании ограниченного перебора.
2.2. Использование рекурсии при реализации ограниченного перебора.

Подобный материал:

Иванова Г.С., Ничушкина Т.Н.

Конспект лекций

по курсу "Алгоритмические языки и программирование".

Тема "Рекурсия".

Глава 1. Рекурсия. Основные положения.

1.1. Рекурсивные алгоритмы.

Строгое определение некоторых понятий может опираться на то же понятие. Существует доступная математическая форма определений, согласно которой определяемое понятие используется как заголовок определения и как его элемент. Эта форма называется рекурсивной или индуктивной.

Рекурсия является особенно мощным средством в математических определениях. Известны примеры рекурсивных определений натуральных чисел, древовидных структур и некоторых функций.

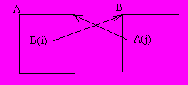
Пример 1. Определение отношения "Кубик А находится в башне над кубиком В."

1. Если кубик А лежит непосредственно на кубике В, то кубик А находится в

башне над кубиком В.

2. Если кубик А лежит непосредственно на кубике С и этот кубик находится в

башне над кубиком В, то кубик А находится в башне над кубиком В.

Первое утверждение носит название базисного. Базисное утверждение нерекурсивно.

Рис. 1

Второе утверждение носит название рекурсивного или индуктивного. Оно строится так, чтобы полученная в результате повторных применений цепочка определений редуцировалась к базисному утверждению.

При этом базисное утверждение определяет один или более случаев, удовлетворяющих определению, а рекурсивное утверждение показывает, как надо применять определение, чтобы проверить, удовлетворяют ли ему другие случаи.

Применительно к примеру, это выглядит следующим образом. Если требуется определить, находится ли синий кубик в башне над зеленым, то необходимо действовать следующим образом:

а) Проверяем первое утверждение "Синий кубик находится в башне над зеленым, если он лежит на зеленым". Оно ложно, следовательно, переходим к проверке второго.

б) Второе утверждение "Синий кубик находится в башне над зеленым, если синий кубик лежит на красном, а красный находится в башне над зеленым" требует доказательства того, что красный кубик находится в башне над зеленым. А это значит, что надо вновь применить правило 1 и проверить, находится ли красный кубик непосредственно на зеленом. Поскольку это положение истинно, значит истинно и то, что синий кубик находится в башне над зеленым.

Пример 2. Рекурсивное определение понятия "нечетное число".

Базисное утверждение: Число 1 является нечетным.

Рекурсивное утверждение: Если i является нечетным числом, то нечетными являются и числа i-2 и i+2.

Определить, являются ли числа 7 и -7 нечетными.

а) 7-2 -> 5 5-2 -> 3 3-2 -> 1 1 - нечетное число, следовательно, число 7 - нечетное.

б) -7+2 -> -5 -5+2 -> -3 -3+2 -> -1 -1+2 -> 1 - нечетное число, следовательно, число -7 - нечетное.

Очень важной областью применения рекурсии является синтаксис языков программирования.

Пример 3. Определение целой константы.

Базисное утверждение: Числа от 0 до 9 являются целыми константами.

Рекурсивное утверждение: Добавление десятичной цифры к записи целой константы образует новую целую константу.

Соответствующая форма Бэкуса-Наура записывается следующим образом:

<цифра>:: = 0|1|2|3|4|5|6|7|8|9 - базис

<целая константа>:: =<цифра>|<целая константа> - рекурсивная часть

Таким образом, мощность рекурсии заключается в том, что она позволяет определить бесконечное множество объектов с помощью конечного количества высказываний.

В программировании рекурсия используется как при определении структур данных, так и при разработке алгоритмов.

1.2. Рекурсивные процедуры и функции. Взаиморекурсия.

Рекурсивной процедурой называется такая процедура, которая в процессе выполнения вызывает сама себя.

Различают следующие виды рекурсии:

Прямая или явная рекурсия характеризуется существованием в теле процедуры оператора обращения к самой себе.

Косвенная или неявная рекурсия образуется в случае цепочки вызовов других процедур, которые в конечном итоге приведут к вызову начальной.

Для описания на Паскале прямой рекурсии никаких дополнительных операторов не требуется. При описании неявной рекурсии возникает проблема: при определении первой из нескольких взаиморекурсивных процедур или функций возникает необходимость обращения к подпрограмме, которая еще не определена, что в Паскале недопустимо. В этом случае используется специальная директива Паскаля forward, которая позволяет выполнять предописание:

сначала задаются прототипы подпрограмм с параметрами, за которыми вместо тела подпрограммы следует forword;
затем описываются тела этих подпрограмм (причем параметры второй раз можно уже не описывать).

Например, описание взаиморекурсивных процедур A и B можно выполнить следующим образом: procedure B(j:byte);forward;

procedure A(j:byte);

begin ... B(i); ... end;

procedure B;

begin ... A(j); ... end;

Рис.2.

1.3. Фрейм активации.

Каждое обращение к процедуре вызывает независимую активацию этой процедуры. С процедурой принято связывать некоторое множество локальных объектов (переменных, констант, типов и процедур), которые определены локально в этой процедуре, а вне ее не существуют или не имеют смысла. Совокупность данных, необходимых для одной активации называется фреймом активации.

Фрейм активации содержит независимые копии всех локальных переменных и формальных параметров процедуры, в которых оставляют "следы" операторы текущей активации.

Если процедура обращается к себе несколько раз, образуется несколько одновременно существующих активаций и, соответственно, несколько фреймов активации. Обычно все фреймы являются различными экземплярами одной и той же структуры и размещаются в стеке. При некотором количестве вызовов возможно переполнение стека. На размер фрейма активации влияет способ передачи параметров в процедуру: при использовании параметров-переменных фрейм содержит адреса данных (по 4 байта на каждый параметр), а при использовании параметров-значений - сами данные, которые могут занимать достаточно много места (например, массивы).

Размер фрейма активации можно примерно определить следующим образом:

V= <размер области параметров>+2(адрес возврата)+2..8(для сохранения содержимого регистров)+<размер области локальных переменных>+<размер строки результата, если это функция, возвращающая результат - строку>

Пример 4. Вычисление НОД двух чисел (алгоритм Евклида).

Базисное утверждение: Если два числа равны, то их НОД равен этим числам.

Рекурсивное утверждение: НОД двух чисел равен НОД их разности и меньшего из чисел.

Таким образом, редуцирование происходит при замене большего из чисел на их разность.

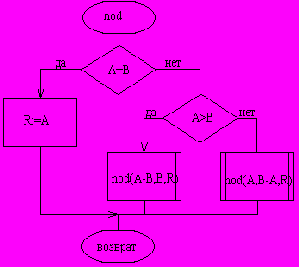
Рекурсивная подпрограмма может быть реализована и как процедура и как функция. При реализации в виде процедуры в список параметров добавляется параметр R, передаваемый по ссылке, через который процедура возвращает результат. Схема алгоритма рекурсивной процедуры и текст программы, содержащей рекурсивную процедуру, представлены ниже.

program ex;

var a,b,r:integer;

procedure nod(a,b:integer; var r:integer);

begin if a=b then r:=a {базис}

else if a>b then nod(a-b,b,r)

else nod(a,b-a,r)

end;

begin readln(a,b);

nod(a,b,r);

writeln(r);

end.

Рис.3.

При выполнении программы Паскаль будет использовать стек, в который будут записываться фреймы активации каждого вызова. Например, для а=20 и b=12 стек будет выглядеть следующим образом (запись в стек идет словами, то есть по 2 байта, как и изображено на рисунке):

Рис.4.

Если вместо процедуры использовать рекурсивную функцию, то фрейм активации уменьшится, так как сократится список параметров. Соответствующая программа будет выглядеть следующим образом:

program ex;

var a,b,r:integer;

function nod(a,b:integer):integer;

begin if a=b then nod:=a {базис}

else if a>b then nod:=nod(a-b,b) {рекурсивные утверждения}

else nod:=nod(a,b-a)

end;

begin readln(a,b);

r:=nod(a,b);

writeln(r);

end.

Пример 5. Определение корней уравнения y=x²-2 на заданном отрезке методом половинного деления.

Для простоты будем считать, что отрезок задается таким образом, что корень на нем есть (иначе основная программа должна содержать проверку наличия корня).

Метод половинного деления для непрерывных функций заключается в следующем:

Базисное утверждение: Если абсолютная величина функции в середине отрезка не превышает заданного значения точности, то координата середины отрезка и есть корень.

Рекурсивное утверждение: Корень расположен между серединой отрезка и тем концом, значение функции в котором по знаку не совпадает со значением функции в середине отрезка.

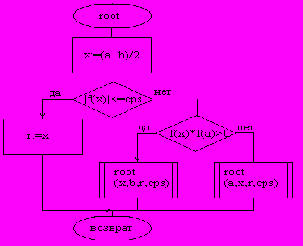
program ex;

var a,b,eps,x:real;

procedure root(a,b,eps:real,var r):real;

var f,x:real;

begin x:=(a+b)/2; f:=x*x-1;

if abs(f)>eps then

begin

if (a*a-1)*f>0 then root(x,b,eps,r)

else root(a,x,eps,r)

end;

end;

begin readln(a,b,eps);

root(a,b,eps,x);

writeln(x);

end.

Рис.5.

Одной из наиболее часто встречающихся ошибок при создании рекурсивных процедур является "зациклившаяся" или бесконечная рекурсия, при которой базисное утверждение не достигается, и, соответственно, вновь и вновь вызывается рекурсивная подпрограмма. От бесконечного цикла бесконечная рекурсия отличается тем, что каждая активация требует дополнительной памяти для размещения фрейма активации, и, следовательно, программа, содержащая бесконечную рекурсию, обычно завершается аварийно при исчерпании доступной памяти. Так для рассмотренного примера, если, например, задать отрезок, не содержащий корня, то произойдет "зацикливание", что вызовет аварийное завершение программы. Таким образом, причиной "зацикливания" может являться, как ошибка в программе, так и ошибка в данных.

Пример 6. Проверка чередования букв и цифр в заданной строке (первый символ - обязательно буква).

Базисные утверждения: Строка допустима, если она пустая.

Строка не допустима, если обнаружен не допустимый символ.

Рекурсивное утверждение: Если текущий символ строки допустим, то допустимость строки определяется оставшейся частью строки.

Для написания данной программы используем взаиморекурсивные подпрограммы. Первая будет проверять, является ли текущий символ буквой, и, если "да", будет удалять этот символ и вызывать вторую. Вторая - будет проверять, является ли текущий символ цифрой, и, если "да", будет удалять эту цифру и вызывать первую. Выход из рекурсии - по достижению конца строки. Параметр - строка передается по значению.

program ex2;

var s:string;

function f_char(st:string):boolean;forward;

function f_value(st:string):boolean;

begin if length(st)=0 then f_value:=true

else if (st[1]<='9') and (st[1]>='0') then f_value:=f_char(copy(st,2,length(st)-1))

else f_value:=false;

end;

function f_char;

begin if length(st)=0 then f_char:=true

else if (st[1]<='Z') and (st[1]>='A') then f_char:=f_value(copy(st,2,length(st)-1))

else f_char:=false;

end;

begin writeln('Введите строку'); readln(s);

if f_char(s) then writeln(' Строка корректна')

else writeln('Строка не корректна');

end.

Данная программа построена не удачно, так как размер фрейма активации V»260 байт. Для уменьшения размера фрейма следует подумать об изменении способа передачи параметра. Действительно, если гарантировать, что исходная строка изменяться не будет, то ее можно передавать по ссылке. Переход к следующему символу можно осуществить, добавив еще один параметр - индекс, передаваемый по значению. Размер фрейма активации при этом сократится (V»10). Кроме этого, в программе использована более удобная проверка (с использованием множеств).

program ex2;

var s:string;

function f_char(var st:string;i:word):boolean;forward;

function f_value(var st:string;i:word):boolean;

begin if i>length(st) then f_value:=true

else if (st[i] in ['0'..'9'])then f_value:=f_char(st,i+1)

else f_value:=false;

end;

function f_char;

begin if i>length(st) then f_char:=true

else if (st[i] in ['A'..'Z','a'..'z']) then f_char:=f_value(st,i+1)

else f_char:=false;

end;

begin writeln('Введите строку');

readln(s);

if f_char(s,1) then writeln('Строка корректна')

else writeln(' Строка не корректна');

end.

Таким образом, по возможности, в рекурсивных подпрограммах при передаче строк и массивов следует использовать передачу по ссылке, что приводит к уменьшению размера фрейма активации.

Пример 7. Из заданного массива, завершающегося нулем, распечатать сначала положительные значения, а затем - отрицательные в любом порядке.

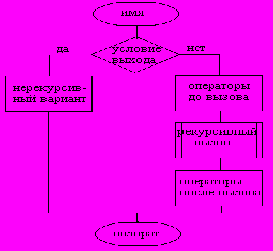
Нерекурсивная программа для решения данной задачи должна содержать, по крайней мере, два цикла не считая цикла ввода. Рекурсивный вариант может использовать так называемый "рекурсивный возврат" для вывода оставшихся элементов.

Структура рекурсивной подпрограммы имеет в общем случае вид, представленный на рисунке 6. Операторы, которые на схеме помечены как "операторы после вызова" будут выполняться после возврата управления из рекурсивно вызванной подпрограммы. Если попытаться изобразить последовательность действий, то она будет выглядеть так, как показано на рисунке 7.

Рис 6

Рис. 7.

Таким образом, сначала выполняются операторы до вызова всех активаций, затем, при достижении условия выхода, нерекурсивная часть, а затем, в порядке, обратном порядку вызова, операторы, записанные после рекурсивного вызова (!!!). Используя это свойство, построим решение следующим образом: в области до вызова запрограммируем печать положительных чисел, в области после вызова - печать отрицательных чисел, а нерекурсивная часть будет содержать вывод звездочек.

program ex;

type mas=array[1..10] of real;

var x:mas;

i:integer;

procedure print(var x:mas;i:integer);

begin if x[i]=0 then writeln('***')

else

begin

if x[i]>0 then writeln(i,x[i]);

print(x,i+1); {рекурсивный вызов}

if x[i]<0 then writeln(i,x[i]);

end

end;

begin i:=0;

repeat i:=i+1;read(x[i]) until x[i]=0;

readln;

print(x,1);

end.

Примечание. Обратите внимание, что значение i при каждом вызове свое, и оно не меняется все время обработки данного вызова: одно и то же, как до вызова, так и после него.

Глава 2. Полный и ограниченный перебор. Рекурсия при программировании ограниченного перебора.

2.1. Понятие полного перебора. Основные приемы его осуществления.

Существует класс задач, в которых необходимо из некоторого количества вариантов выбрать наиболее подходящий. Для таких задач далеко не всегда удается найти алгоритм, который позволил бы получить решение без анализа всех или большого количества вариантов, т.е. без осуществления перебора.

В качестве примера рассмотрим классическую "задачу о сдаче".

Пример 1. Разработать программу выдачи сдачи минимальным количеством монет при ограниченном количестве монет каждого достоинства в кассе.

Попытка использовать известный алгоритм, при котором сдача выдается начиная с монет большего достоинства и включает максимальное возможное количество монет каждого достоинства, в этом случае не дает оптимального решения. Например, если необходимо выдать сдачу 47 копеек, и в кассе имеется достаточное количество монет достоинством 1,2,3, 5,10,15,20 копеек, то алгоритм работает: 47=20*2+5*1+2*1 - 4 монеты. Но при отсутствии в кассе 5 копеечных монет вариант 47=15*3+2*1 ( 4 монеты) лучше варианта 47=20*2+3*2+1*1 (5 монет). При таких условиях для решения этой задачи используется метод перебора вариантов.

К задачам, при решении которых используется перебор, относятся также задачи из области искусственного интелекта, решения которых ищутся методом "проб и ошибок"., например, задача о расстановке n ферзей на доске n*n таким образом, чтобы они не били друг друга. К этой же группе относятся задачи, в которых требуется получить все возможные перестановки каких-то элементов, например, все перестановки букв от A до F.

Существует две стратегии решения задач данного типа. При первой - мы генерируем вариант, а затем определяем его пригодность. При второй - вариант генерируется по одному элементу, и проверка пригодности осуществляется после добавления каждого элемента. Поскольку вычислительная сложность задач данного типа - nⁿ, то есть при увеличении размерности задачи время вычислений возрастает как nⁿ, вторая стратегия предпочтительней.

Общий алгоритм решения задачи с использованием полного перебора по первой стратегии может быть представлен следующим образом:

цикл-пока еще есть варианты

генерировать вариант

если вариант удовлетворяет условию,

то обработать набор

все-если

все-цикл

Для генерации вариантов используют либо вложенные циклы, применение которых существенно уменьшают универсальность программы, либо программно-реализуемый счетчик, который в каждом разряде считает от минимального до максимального значений элементов в данной позиции. Каждое состояние такого счетчика соответствует варианту. Для генерации следующего варианта в младший разряд счетчика добавляют 1 и "протряхивают" межразрядные переносы.

Пример 2. Написать программу, которая генерирует следующие комбинации: 1111, 1112, 1113, 1121, 1122, 1123, 1131, 1132, 1133, 1211, ..., 3333.

В процессе решения необходимо программно реализовать 4-разрядный счетчик, который в каждом разряде будет считать от 1 до 3.

program ex;

const a:array[1..4] of byte=(1,1,1,1);

var i:integer;

begin

while a[1]<4 do {условие "сброса" счетчика}

begin for i:=1 to 4 do write(a[i],' '); writeln; {вывод комбинации}

a[4]:=a[4]+1; {добавление 1 в последний разряд}

for i:=4 downto 2 do { анализ и осуществление переносов}

if a[i]>3 then

begin a[i]:=1; a[i-1]:=a[i-1]+1; end;

end

end.

Этот прием можно использовать и для решения других задач данного класса.

Пример 3. Задача о расстановке ферзей.

Разработка программы решения начинается с выявления некоторых деталей.

Определим форму представления данных задачи. С первого взгляда кажется, что доска должна представляться матрицей, а местоположение ферзей - индексами в матрице. Однако при некотором размышлении можно заменить, что доска может быть представлена вектором, в котором индекс соответствует номеру столбца доски, а значение - номеру строки.

Рис.8.
Определим, что для векторного представления означает "бьет". Ферзь "бьет" другую фигуру, если она расположена на той же диагонали, вертикали или горизонтали, т.е. если

pole[ j ]=pole[ i ] или | pole[ j ]-pole[ i ] | =| j- i |

Полностью решение выглядит следующим образом:

program ex;

type p=array[1..100] of integer;

var pole:p; i,m:integer;

function new_r(m:integer;pole:p):boolean; {функция проверки комбинации}

var i,j:integer;

begin new_r:=true;

for i:=1 to m-1 do

for j:=i+1 to m do

if (pole[i]=pole[j]) or (abs(pole[j]-pole[i])=j-i) then

begin new_r:=false;

exit;

end;

end;

function Variant(m:integer; var pole:p):boolean; {генератор вариантов}

var i:integer;

begin

pole[m]:=pole[m]+1; {добавление единицы в младший разряд счетчика}

for i:=m downto 2 do {обработка переносов}

if pole[i]>m then

begin pole[i]:=1;

pole[i-1]:=pole[i-1]+1;

end;

if pole[1]<=m then Variant:=true {фиксируем наличие ранее не рассмотренных}

else Variant:=false; {вариантов}

end;

begin writeln('Введите размер доски'); readln(m);

for i:=1 to m do pole[i]:=1; {исходная комбинация}

repeat

if New_r(m,pole) then

begin for i:=1 to m do write(pole[i]:2); writeln; end;

until not Variant(m,pole);

end.

Недостаток примененного метода, как уже говорилось, заключается в m^m-ой зависимости времени выполнения от значения m.

2.2. Использование рекурсии при реализации ограниченного перебора.

Попробуем сократить количество рассматриваемых вариантов за счет как можно более раннего отбрасывания неперспективных комбинаций. На рис.9 представлена часть дерева промежуточных и завершенных вариантов.

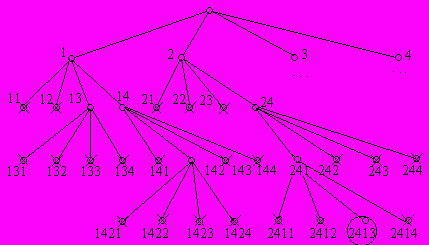
Рис. 9.

Крестиками отмечены комбинации, уже содержащие комбинации при которых ферзи "бьют" друг друга. Генерацию таких вариантов можно не продолжать, существенно уменьшая общее количество просматриваемых вариантов. В принципе возможна не рекурсивная реализация данного подхода, но рассмотрим вариант с использованием рекурсии.

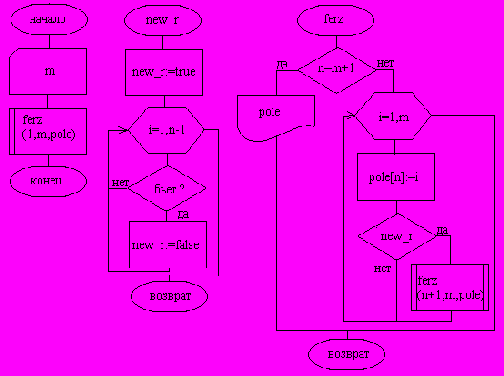
Рис. 10.

program ex;

type p=array[1..100] of integer;

var pole:p; k,integer;

function new_r(n:integer;pole:p):boolean;

var j:integer;

begin new_r:=true;

for j:=1 to n-1 do

if (pole[j]=pole[n]) or (abs(pole[j]-pole[n])=n-j) then

begin new_r:=false;

exit;

end;

end;

procedure ferz(n,m:integer; var pole:p);

var i:integer;

begin

if n=m+1 then

begin for i:=1 to m do write(pole[i]:2);writeln; end

else

for i:=1 to m do

begin

pole[n]:=i;

if new_r(n,pole) then ferz(n+1,m,pole);

end;

end;

begin writeln('Введите размер доски:');

readln(m);

k:=0;

ferz(1,m,pole);

end.

Процедура new_r используется для проверки уже сгенерированной комбинации (уровень n соответствует попытке установить n-го ферзя). Процедура ferz рекурсивна. На каждом уровне она может породить до m рекурсивных вызовов (в соответствии c деревом генерации вариантов). Однако общее количество рассматриваемых вариантов резко уменьшается, что можно наглядно видеть по таблице 1.

Таблица 1.

Размер доски	Всего вариантов	Рассмотрено вариантов	Количество решений
4*4	256	17	2
5*5	3125	54	10
6*6	46656	153	4
7*7	823543	552	40
8*8	16777216	2057	92

Выводы.

Рекурсию следует использовать тогда, когда рекурсивный алгоритм значительно проще нерекурсивного.
При использовании рекурсии следует обязательно проверять наличие и правильность условия выхода из рекурсии.
Не следует забывать о необходимости оценки размера фрейма активации и соотношения этой оценки с размером стека (с учетов развертывания рекурсии).

Blog