Программа по математике для проведения вступительных испытаний в колледж (на правах факультета)

Вид материала

Программа

Содержание Абитуриент должен знать Абитуриент должен уметь Абитуриент должен знать Раздел № 5. Функции и графики. Абитуриент должен знать определения понятий

Подобный материал:

• Программа вступительных испытаний по литературе для лиц, поступающих на базе среднего, 187.85kb.
• Программа вступительного экзамена по математике, 535.41kb.
• Программа и правила проведения вступительных испытаний по физике правила, 71.18kb.
• Программа вступительных испытаний по английскому языку предназначена для абитуриентов, 28.23kb.
• Программа вступительных испытаний по общеобразовательным предметам и правила их проведения, 335.79kb.
• Программа по литературе для вступительных испытаний в мгакхиС, 45.65kb.
• Программа вступительных испытаний и правила их проведения в фгбоу впо «ргэу (ринх)», 72.28kb.
• Программа для проведения вступительных испытаний для поступления в магистратуру, 921.84kb.
• Программа для проведения вступительных испытаний для поступления в магистратуру, 626kb.
• Председатель приемной комиссии назначается директором образовательного учреждения, 17.57kb.

Программа по математике

для проведения вступительных испытаний в

колледж (на правах факультета)

МГГУ им. М.А. Шолохова


(для поступающих на базе основного общего образования)


Раздел № 1. Числа и вычисления.


Содержание раздела.

Множество действительных чисел и его подмножества: натуральные, целые, рациональные и иррациональные числа. Обыкновенная и десятичная записи чисел. Периодические дроби.

Основные понятия теории делимости на множестве натуральных чисел.

Модуль (абсолютная величина) числа.

Степень числа. Корень n-ой степени из числа.


Абитуриент должен знать:

1. правила арифметических действий с натуральными, целыми и рациональными числами в обыкновенной и десятичной записи, правила обращения десятичных дробей в обыкновенные, и наоборот, правила сравнения чисел;
   
2. свойства и признаки делимости натуральных чисел, определения и примеры простых и составных чисел, понятия НОД и НОК, их свойства и взаимосвязь;
   
3. определение и свойства модуля (абсолютной величины) действительного числа;
   
4. определение и свойства степени с натуральным, целым и рациональным показателями, определение и свойства корня n-ой степени из числа;
   
5. приближенное значение числа  , с точностью до сотых;
   

Абитуриент должен уметь:

1. находить значения числовых выражений различной степени сложности, содержащих все арифметические действия над числами в обыкновенной и десятичной записи;
   
2. обращать периодическую дробь в обыкновенную;
   
3. приводить примеры простых и составных чисел, раскладывать составные числа на простые множители;
   
4. находить НОД и НОК двух и более натуральных чисел, приводить примеры взаимно простых чисел;
   
5. находить значения числовых выражений, содержащих модули, степени и корни;
   
6. приводить примеры иррациональных чисел (кроме ).
   

Абитуриент должен иметь представление о:

1. иррациональных числах;
   
2. приближенных вычислениях, погрешностях, округлении чисел;
   
3. записи чисел римскими цифрами.
   

Абитуриент должен понимать:

1. свойства действий над числами;
   
2. приемы, упрощающие техническую сторону устных и письменных вычислений;
   
3. различия понятия корня и арифметического корня, правила использования символа ;
   
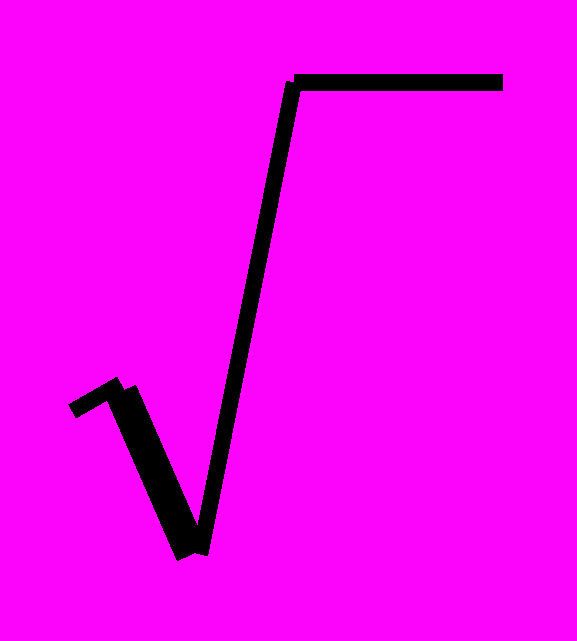4. доказательства свойств степени и корня.
   

Раздел № 2. Выражения и их преобразования.


Содержание раздела.

Буквенно-числовые и буквенные выражения.

Одночлены. Многочлены. Алгебраические дроби. Формулы сокращенного умножения. Преобразования рациональных выражений. Преобразования иррациональных выражений.

Основные определения и формулы тригонометрии. Простейшие преобразования тригонометрических выражений.


Абитуриент должен знать:

1. правила действий с одночленами, многочленами, алгебраическими дробями;
   
2. способы разложения многочленов на множители;
   
3. основные формулы сокращенного умножения;
   
4. определения синуса, косинуса, тангенса и котангенса, исходя из тригонометрического круга;
   
5. значения тригонометрических функций основных углов,
   
6. основные тригонометрические формулы: основные тригонометрические тождества, формулы сложения, формулы двойного, тройного и половинного аргументов, формулы понижения степени, формулы приведения;
   

Абитуриент должен уметь:

1. проводить преобразования рациональных выражений, используя правила действий с одночленами, многочленами, алгебраическими дробями, способы разложения многочленов на множители, основные формулы сокращенного умножения;
   
2. проводить вычисления с арифметическими корнями и преобразования выражений, содержащих арифметические корни, используя свойства корней;
   
3. проводить тригонометрические вычисления и преобразования тригонометрических выражений, используя основные формулы тригонометрии;
   
4. проводить тригонометрические преобразования сумм в произведения и произведений в суммы;
   

Абитуриент должен иметь представление о:

1. допустимых и недопустимых значениях букв в буквенно-числовых выражениях;
   

Абитуриент должен понимать:

1. сущность понятий тождество и тождественное преобразование;
   
2. классификацию математических выражений;
   
3. особенности преобразований выражений различных классов;
   
4. тригонометрический круг;
   
5. доказательства основных тригонометрических формул;
   
6. конкретные примеры применения преобразований выражений к решению различных математических задач.
   

Раздел № 3. Уравнения и неравенства.


Содержание раздела.

Уравнение и его корни. Классификация уравнений. Сущность процесса решения уравнений. Методы и приемы решения уравнений. Равносильные и неравносильные уравнения.

Линейные уравнения. Квадратные уравнения. Целые рациональные уравнения. Дробные рациональные уравнения.

Неравенства. Числовые промежутки. Рациональные неравенства. Метод интервалов.

Системы неравенств.

Простейшие системы уравнений.


Абитуриент должен знать:

1. определения понятий: уравнение, корень уравнения, равносильные уравнения;
   
2. классификацию уравнений, существенные признаки уравнений различных классов;
   
3. формулу корней квадратного уравнения (с выводом);
   
4. формулу разложения квадратного трехчлена на линейные множители;
   
5. теорему Виета и ей обратную для квадратного уравнения (без доказательств);
   
6. алгоритм метода интервалов для решения рациональных неравенств;
   
7. основные теоремы о равносильности уравнений (без доказательства);
   
8. основные теоремы о равносильности неравенств (без доказательства);
   
9. определение понятий: система уравнений, решение системы уравнений;
   
10. основные теоремы о равносильности систем уравнений (без доказательств).
    

Абитуриент должен уметь:

1. приводить конкретные примеры уравнений с различным количеством корней;
   
2. решать линейные и квадратные уравнения;
   
3. решать целые рациональные уравнения, сводимые к линейным и квадратным элементарными алгебраическими преобразованиями;
   
4. решать биквадратные уравнения;
   
5. находить корни многочленов, целых и дробных рациональных уравнений методом разложения на множители;
   
6. решать рациональные неравенства методом интервалов;
   
7. записывать решения неравенств в виде объединения числовых промежутков;
   
8. решать системы и совокупности неравенств;
   
9. применять метод введения новой переменной при решении уравнений и неравенств;
   
10. решать простейшие системы рациональных уравнений;
    
11. решать системы уравнений, не являющихся рациональными;
    
12. осуществлять графическое решение уравнений с одной переменной;
    

Абитуриент должен иметь представление о:

1. графическом решении уравнений, неравенств, систем;
   

Абитуриент должен понимать:

1. сущность процесса решения уравнений;
   
2. особенности использования равносильных и неравносильных преобразований уравнений;
   
3. сущность метода разложения на множители при решении уравнений;
   
4. сущность метода введения новой переменной при решении уравнений;
   
5. возможности графических рассуждений при решении уравнений;
   
6. обоснование метода интервалов решения рациональных неравенств;
   

Раздел № 4. Сюжетные задачи.


Содержание раздела.

Сюжетная задача и ее решение. Арифметическое и алгебраическое решение сюжетных задач. Классификации сюжетных задач.

Деление на части, пропорции, проценты. Отношения «больше – меньше» в сюжетных задачах. Задачи с геометрическим содержанием. Задачи с физическим содержанием. Торгово-денежные отношения в сюжетных задачах. Соотношения между натуральными числами в сюжетных задачах. Задачи на движение. Задачи на работу. Задачи на смеси и сплавы.

Последовательности. Арифметическая прогрессия. Геометрическая прогрессия. Сюжетные задачи на прогрессии.


Абитуриент должен знать:

1. правила нахождения части от целого и целого по части;
   
2. понятие пропорции, применение пропорций к решению сюжетных задач в случаях прямой и обратной пропорциональности;
   
3. определения и основные свойства арифметической прогрессии;
   
4. определение и основные свойства геометрической прогрессии;
   

Абитуриент должен уметь:

1. анализировать условие сюжетной задачи, составлять его краткую запись в форме удобной для поиска пути решения задачи;
   
2. проводить процентные вычисления;
   
3. решать сюжетные задачи различных типов;
   
4. приводить примеры и контрпримеры арифметической и геометрической прогрессий;
   
5. проводить вычисления по формулам прогрессий;
   

Абитуриент должен иметь представление о:

1. о последовательностях, не являющихся прогрессиями;
   

Абитуриент должен понимать:

1. процесс решения сюжетной задачи как процесс математического моделирования, особенности этапов составления модели, внутримодельного решения, интерпретации результатов;
   
2. сущность основных эвристик, применяемых при решении сюжетных задач.
   

Раздел № 5. Функции и графики.


Содержание раздела.

Понятие функции. Основные функциональные понятия: область определения и множество значений функции.

График функции. Свойства функций. Нули функции. Промежутки знакопостоянства функции. Четность и нечетность функций.

Элементарные функции. Линейная функция. Функция y = x. Степенная функция с целым показателем. Функция у = 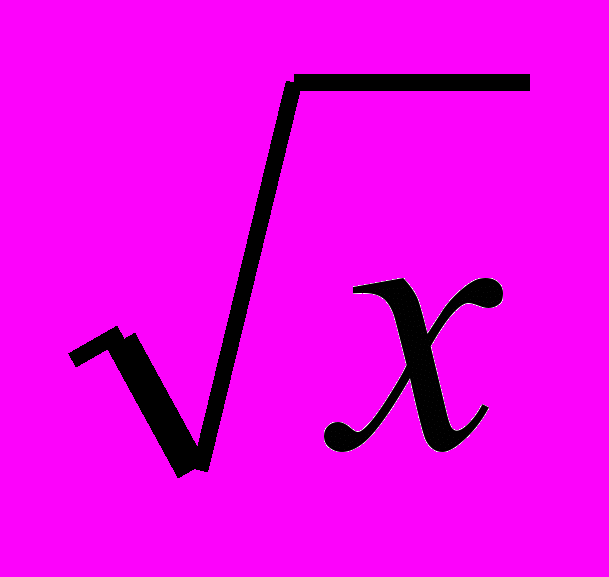. Функция у = .

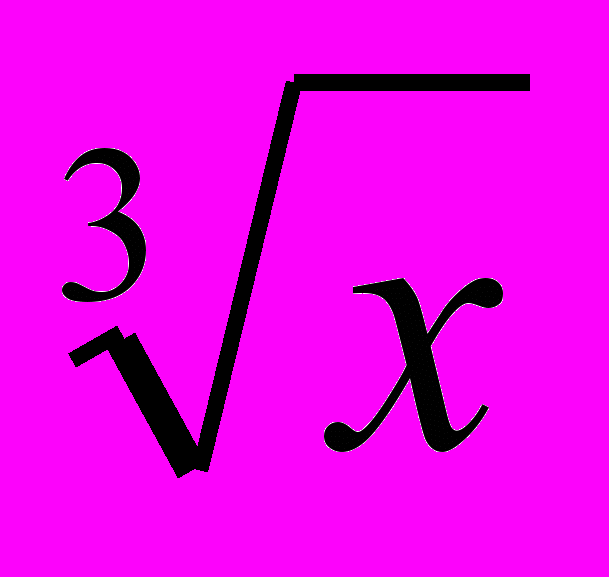Геометрические преобразования графиков функций.

Исследование функций элементарными средствами.


Абитуриент должен знать:

1. определения основных функциональных понятий;
   
2. определения четной и нечетной функций;
   
3. определения возрастающей и убывающей функций, точек экстремума;
   
4. графики и свойства важнейших элементарных функций: линейной, квадратичной, функция y = x, дробно-линейной, степенной функции с целым показателем, функции у = 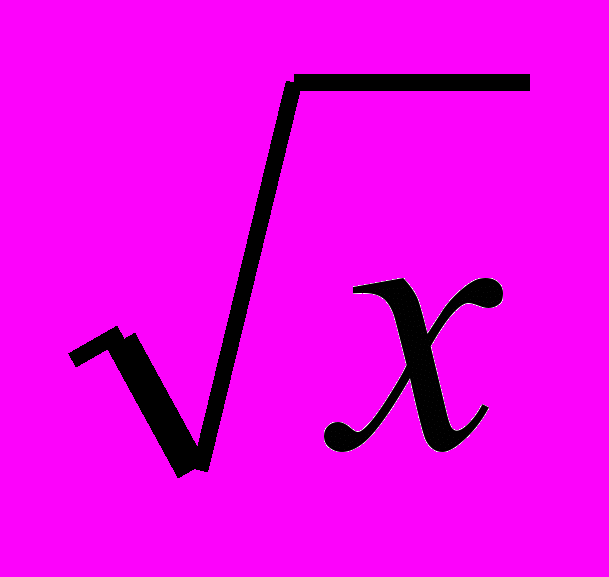, функции у = .
   

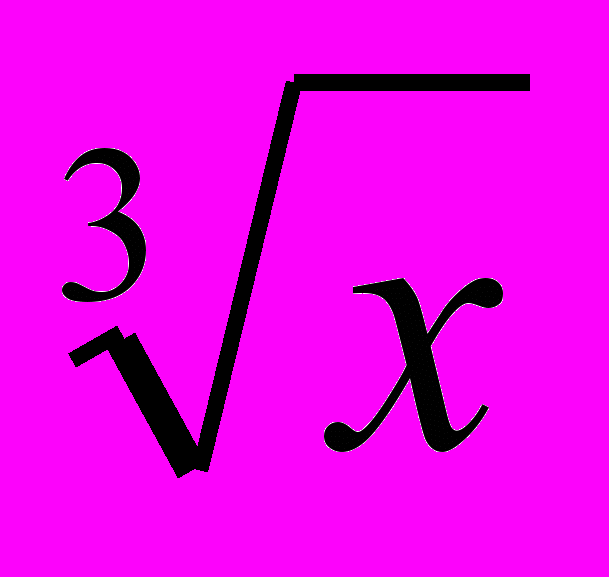Абитуриент должен уметь:

1. находить область определения аналитически заданной функции;
   
2. находить множество значений аналитически заданной функции (в очевидных случаях);
   
3. «переходить» от одного способа задания функции к другому;
   
4. осуществлять геометрические преобразования графиков функций;
   
5. строить графики функций по заданному набору свойств;
   
6. «читать» графики функций;
   
7. уметь находить нули функции, промежутки знакопостояества функции;
   
8. исследовать функцию на четность и нечетность;
   
9. исследовать функции на монотонность и экстремумы элементарными средствами;
   

Абитуриент должен иметь представление о:

1. свойствах четных и нечетных функций;
   

Абитуриент должен понимать:

1. сущность функционального соответствия, особенности функциональной символики;
   
2. особенности различных способов задания функций;
   

Раздел № 6. Планиметрия.


Содержание раздела.

Аксиомы планиметрии. Луч, отрезок, угол. Параллельность и перпендикулярность на плоскости.

Треугольники. Равенство и подобие треугольников. Пропорциональные отрезки. Медианы, биссектрисы, высоты. Метрические соотношения в треугольнике.

Окружность, круг, дуга, хорда, диаметр. Углы, связанные с окружностью. Секущая и касательная к окружности. Треугольники и окружность. Четырехугольники. Параллелограмм, прямоугольник, ромб, квадрат. Трапеция. Четырехугольники и окружность.

Многоугольники. Выпуклые многоугольники. Правильные многоугольники.

Площади плоских фигур.

Векторы и их применение к решению задач. Система координат на плоскости. Основные задачи аналитической геометрии. Различные уравнения прямой. Уравнение окружности.

Преобразования фигур. Движение. Подобие. Гомотетия.

Задачи на построение.

Абитуриент должен знать определения понятий:

1. угол; прилежащие углы, смежные углы, вертикальные углы; развернутый, прямой, острый, тупой углы; соответственные, внутренние и внешние односторонние, внутренние и внешние накрест лежащие углы; треугольник, внешний угол треугольника, средняя линия треугольника;
   
2. окружность и круг; дуга, хорда, диаметр окружности; центральный и вписанный углы, секущая и касательная к окружности; круговой сектор, круговой сегмент;
   
3. параллелограмм, прямоугольник, ромб, квадрат, трапеция;
   
4. вектор, движение, симметрия, поворот, параллельный перенос, подобие, гомотетия.
   

Абитуриент должен знать формулировки теорем:

1. критерий параллельности прямых;
   
2. свойства равнобедренного треугольника;
   
3. признаки равенства треугольников;
   
4. признаки подобия треугольников;
   
5. о пропорциональных отрезках в произвольном треугольнике;
   
6. о пропорциональных отрезках в прямоугольном треугольнике;
   
7. об углах, связанных с окружностью;
   
8. свойства касательной к окружности;
   
9. о центрах окружностей вписанной в треугольник и описанной около треугольника;
   
10. теорема синусов;
    
11. теорема косинусов;
    
12. свойства параллелограмма, прямоугольника, ромба, квадрата;
    
13. свойства произвольной и равнобедренной трапеций;
    
14. площадях подобных треугольников;
    
15. о разложении вектора по двум неколлинеарным векторам.
    

Абитуриент должен знать формулировки и доказательства теорем:

1. о сумме углов треугольника;
   
2. о средней линии треугольника;
   
3. теорема Фалеса;
   
4. теорема Пифагора;
   
5. о сумме квадратов диагоналей трапеции;
   
6. о сумме внутренних углов произвольного многоугольника;
   
7. о выражении скалярного произведения векторов через их координаты.
   

Абитуриент должен знать формулы:

1. площади прямоугольника;
   
2. площади параллелограмма;
   
3. основную формулу площади треугольника;
   
4. формулу площади треугольника, связанную с радиусом описанной окружности;
   
5. формулу Герона площади треугольника;
   
6. площади трапеции;
   
7. длины окружности;
   
8. площади круга;
   
9. уравнение окружности;
   
10. выражение длины вектора в координатах;
    

Абитуриент должен уметь:

1. грамотно воспроизводить теоретические знания по планиметрии в письменной форме;
   
2. решать различные геометрические задачи на вычисление, применяя указанные выше теоремы и формулы;
   
3. проводить геометрические задачи доказательства, применяя указанные выше теоремы;
   
4. грамотно составлять чертежи, адекватно иллюстрирующие заданные геометрические ситуации;
   
5. решать простейшие (основные) задачи на построение;
   
6. применять методы аналитической геометрии в процессе решения задач.
   

Абитуриент должен иметь представление о:

1. свойствах углов с соответственно параллельными и соответственно перпендикулярными сторонами;
   
2. свойствах медиан, высот и биссектрис треугольника;
   
3. о вписанных и описанных четырехугольниках;
   
4. о вписанных и описанных правильных многоугольниках;
   
5. об операциях над векторами и их свойствах;
   
6. о свойствах преобразования движения;
   
7. о свойствах преобразования подобия;
   
8. о способах решения задач на построение.
   

Абитуриент должен понимать:

1. логическое строение геометрии и планиметрическую аксиоматику;
   
2. различные случаи взаимного расположения прямых на плоскости;
   
3. сущность отношения равенства на множестве геометрических фигур;
   
4. сущность понятия площади;
   
5. сущность векторно-координатного метода в планиметрии;
   
6. сущность геометрических преобразований движения и подобия, возможности их применения при решении задач;
   
7. принципиальную схему решения задач на построение.