Биография Евдокс Книдский известен прежде всего как математик и астроном, но кроме того он писал книги по философии, географии, музыке и медицине.

Вид материала

Подобный материал:

Теория отношений Евдокса.

Биография

Евдокс Книдский известен прежде всего как математик и астроном, но кроме того он писал книги по философии, географии, музыке и медицине. О жизни Евдокса известно следующее. Евдокс родился около 408 г. до н. э. в городе Книде (Малая Азия). Это первый из астрономов в истории человечества, о жизни и деятельности которого сохранились хоть какие-то письменные свидетельства. В молодости он изучал математику у Архита в Таренте и медицину у Филистиона в Сицилии. В 23-летнем возрасте, привлеченный славой Платона, он отправился в Афины «вместе с врачом Феомедонтом, который его содержал, а, по мнению некоторых, и был его любовником». Там они пробыли два месяца, и все это время Евдокс посещал Платоновскую академию. Будучи очень бедным, Евдокс поселился в гавани Пирея, откуда ежедневно ходил пешком в платоновскую Академию и обратно. Вскоре после возвращения домой Евдокс уехал в Египет, где год и четыре месяца под руководством жрецов изучал состояние тамошней науки. На обратном пути он задержался в Кизике — милетской колонии на южном берегу Мраморного моря у персидского царя Мавсола – и основал там свою школу. В Книд Евдокс вернулся уже тридцатилетним. Здесь он основал школу астрономов и математиков, сыгравшую важную роль в развитии греческой науки. На родине ученый пользовался большим почетом за свои знания и труды; сограждане называли его «славным». Умер Евдокс около 355г. до н.э., окруженный славой и почетом.

К сожалению, научные труды Евдокса не сохранились, и мы знаем о них только по цитатам, которые содержатся в манускриптах его учеников и последователей.

Математические работы:

Евдокс был великим математиком. Развивая то, что было сделано другими учеными в области теории пропорций, он построил общую теорию отношений, основанную на новом определении величины. До Евдокса теоремы теории отношений приходилось доказывать отдельно для чисел, отрезков и площадей. Он же ввел понятие величины, включавшее в себя как числа, так и любые непрерывные величины. Данное понятие определялось с помощью общих аксиом равенства и неравенства, к которым Евдокс добавил еще одну, теперь обычно называемую аксиомой Архимеда: “Две величины находятся между собой в определенном отношении, если любая из них, взятая кратно, может превзойти другую”. Исходя из этих аксиом, Евдокс разработал строгую теорию отношений, изложенную Евклидом в 5ой книге “Начал”. Глубину этой теории смогли по-настоящему оценить лишь во второй половине XIX столетия. Дедекинд проделал для современной математики то, что сделал Евдокс для греческой. Существует большое сходство между дедекиндовым сечением, с помощью которого современные математики определяют иррациональные числа, и античной теорией Евдокса, как она изложена в пятой книге “Начал” Евклида”.

Другим важнейшим вкладом Евдокса в математику являлась разработка так называемого “метода исчерпывания”, заложившего основы теории пределов и подготовившего почву для позднейшего развития математического анализа. В основе “метода исчерпывания” лежит следующее положение [1]: если от какой-либо величины отнять половину или более, затем ту же операцию проделать с остатком, и так поступать дальше и дальше, то через конечное число действий можно дойти до величины, которая будет меньше наперед заданного числа.

С помощью данного метода Евдокс впервые строго доказал, что:

площади двух кругов относятся как квадраты их диаметров (само это положение было известно ранее);
объем пирамиды равен 1/3 объема призмы с теми же основанием и высотой;
объем конуса равен 1/3 объема цилиндра с теми же основанием и высотой.

В дальнейшем “метод исчерпывания” был развит Архимедом. Он также изложен в “Началах” Евклида.

Теория отношений:

После кризиса математики, вызванного апориями Зенона, новые основы – строгие методы предельных переходов (метод исчерпывания) и общее учение об отношениях – были созданы Евдоксом. При этом актуальная бесконечность была отвергнута. В основе теории лежала новая концепция величины.

Известно, что и до Евдокса были попытки обосновать общую теорию отношений. Одна из них (автор скорее всего Теэтет) основана на применении алгоритма Евклида, т.е. на сравнении непрерывных дробей. Однако в старой теории отношений основные предложения приходилось доказывать отдельно для чисел, отрезков, площадей, т.е. ее приходилось строить для разного рода величин заново. И определить операции над отношениями общим образом тоже не удавалось. Поэтому она была оставлена.

Понятие величины у Евдокса охватывает собой и числа, и непрерывные величины: отрезки, площади, объемы. Оно водится с помощью аксиом, определяющих отношения равенства и неравенства. У Евклида эти аксиомы формулируются так:

Равные одному и тому же, равны между собой.
Если к равным прибавляются равные, то целые будут равны.
Если от равных отнимаются равные, от остатки будут равны.
Совмещающиеся друг с другом равны между собой.
Целое больше части.

Только 4 аксиома относится к геометрическим величинам.

Область величин, определяемых этими аксиомами, слишком велика, чтобы определить в ней понятие отношения. Чтобы исключить актуально бесконечно малые и актуально бесконечно большие величины, Евдокс вводит аксиому (аксиома Евдокса-Архимеда): «Величины имеют отношение между собой, если они, взятые кратно, могут превзойти друг друга».Т.е. если даны две величины a и b, то должны существовать такие целые числа n и m, что naархимедовыми. Пример неархимедовых величин – роговидные углы.

Для определения того, когда две пары архимедовых величин a, b и c, d имеют одно и тоже отношение, Евдокс пользуется сопоставлением кратных этих величин (na, mb, nc и md): величины a, b имеют то же отношение, что и c, d, если для любых целых m, n:

либо ma>nb и mc>nd

либо ma=nb и mc=nd

либо ma

Две пары величин, имеющих одно и то же отношение, называются в «Началах» пропорциональными.

Доказывается: Транзитивность свойства пропорциональности.

Симметричность свойства пропорциональности.

Т.о. пропорциональность есть отношение типа равенства.

Все пары величин разбиваются на классы пропорциональных друг другу пар, а отношение – это то общее, что имею все пары величин данного класса (определение через равенство).

Отношения Евдокс упорядочивает по величине: a:b больше c:d, если существуют такие целые m и n, что ma>nb и одновременно mc
По сути, осмысленная до конца теория отношений Евдокса дает теорию сечений Дедекинда, если добавить к ней аксиому непрерывности. Но это было сделано лишь во второй половине 19в. Однако есть и серьезные отличия в этих теориях. У Дедекинда любое сечение области рациональных чисел определяет некоторое действительное число. У Евдокса отношение задается парой архимедовых величин, а затем уже строится сечение пар целых чисел. Ниоткуда не следует, что, наоборот, произвольному сечению будет отвечать пара величин a:b, которая и определяет это сечение. Второе различие состоит в том, что Дедекинд оперирует с областью рациональных чисел, а Евдокс – с парами целых, для которых не определены ни арифметические операции, ни отношения порядка.

В «Началах» над отношениями величин совершается только одна операция – составление отношений, которая соответствует нашему умножению. Евклид не дает прямого определения этой операции, но называет отношение a:c составленным из a:b и b:с.Запишем это так: .

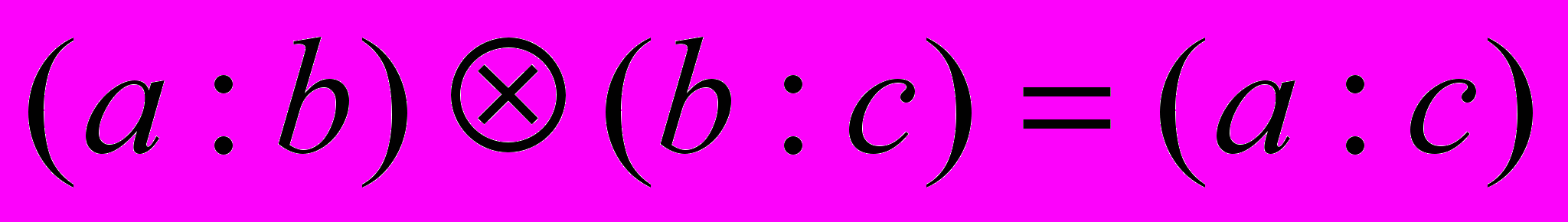Если a:b=b:c, то a:c называется двойным отношением, если a:c составляется из трех одинаковых отношений, то тройным, и т.д.

Если надо составить отношения a:b и c:d, то в «Началах» используется существование четвертой пропорциональной – принцип, доказанный Евклидом только для отрезков. Для отношения c:d отыскивается равное ему, первый член которого есть b - c:d=b:x. Величина х и есть четвертая пропорциональная к величинам c, d, b. Тогда

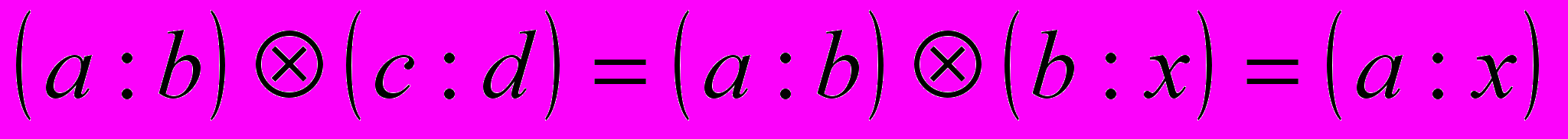
Для введения обратной операции не требуется никаких специальных определений. Евклид доказывает, что если a=b, то a:c=b:c и c:a=c:b. Он свободно пользуется обращением отношений: из a:b=c:d следует b:a=d:c.

В «Началах» устанавливаются два основных свойства операции составления отношений.

1. Доказывается, что если a:b=f:g и b:c=g:h, то a:c=f:h, т.е. результат операции составления не зависит от того, какие именно представители из класса пар берутся.

2. Показывается, что если a:b=g:h и b:c=f:g, то a:c=f:h, т.е. операция составления коммутативна.

Метод исчерпывания – ответ школы Платона Зенону. Метод устранял ловушки бесконечно малого, сводя все проблемы к формальной логике. (Чтобы доказать, что А=В, достаточно знать, что эти величины сравнимы и показать, что абурдно предположение, что А<В и А>В.) Недостаток метода – надо заранее знать, что доказывать.

Евдокс строго доказал следующие теоремы:

Теорема: площади кругов относятся как квадраты из диаметров.

Теорема: объем пирамиды равен 1/3 объема призмы с тем же основанием и высотой.

Теорема: объем конуса равен 1/3 объема цилиндра с тем де основанием и высотой.

Астрономические работы

Фактически Евдокса можно считать создателем античной теоретической астрономии как самостоятельной науки. Евдокс был не только теоретиком, но и первоклассным астрономом-наблюдателем. При своей школе в Кизике он организовал первую греческую обсерваторию, где его ученики вели систематические наблюдения за небесными светилами. Он дал детальное описание созвездий, видимых на широте Греции, составил каталог звездного неба. До нас дошли названия двух его сочинений в области астрономии — “Явления” и “Зеркало”, которые были посвящены одним и тем же вопросам и различались лишь в деталях. На основе этих сочинений древнегреческий поэт Арат написал в III в. до н. э. дидактическую (т.е. “поучительную”) поэму, первая часть которой содержала красочное описание созвездий и связанных с ними легенд (вторая часть поэмы касалась в основном вопросов метеорологии). Поэма Арата, называвшаяся, как и книга Евдокса, “Явления”, пользовалась в древности большой популярностью и в течение долгого времени была важнейшим источником астрономических сведений.

Евдокс дал геометрическое обоснование платоновской модели мироздания. Ученый создал систему мира, в центре которого находилась Земля. Вокруг нее обращались Солнце, Луна и пять известных в то время планет: Меркурий, Венера, Марс, Юпитер и Сатурн. Эти небесные тела были «прикреплены» к внутренней стороне воображаемых хрустальных сфер разного размера, вращавшихся с различными угловыми скоростями. Для объяснения всех видимых движений Евдоксу понадобилось 27 сфер: одна для звезд, по три для Солнца и Луны и по четыре для каждой из планет. Например, одна лунная сфера совершала полный оборот вокруг Земли за месяц, другая делала то же самое, но в противоположную сторону, за 18,5 лет и т. д. Все это остроумное изобретательство предпринималось с тем, чтобы примирить "теорию и практику". Евдокс совершенно откровенно занимался "подгонкой решения под ответ", - тем, что античные греки называли "спасением явления". Евдоксу потребовалось 27 сфер, но явные аномалии все же оставались. Важно отметить, что модель Евдокса была чисто демонстрационной, наглядной, а не расчетной.

Ученику Евдокса Калипу для объяснения всех видимых движений небесных тел понадобилось уже 33 сферы, а Аристотелю — еще больше: 56 сфер. Причем, Аристотель считал сферы не фиктивными, как Евдокс и Калип, а реальными, сделанными из идеально прозрачного хрустального вещества. Система мира Аристотеля была признана христианской церковью единственно верной и просуществовала целых 19 веков, до появления учения Коперника.

Чтобы исправить «погрешности» календаря, Евдокс первым предложил один раз в четыре года вводить високосные годы, что было сделано лишь три столетия спустя при реформе календаря, осуществленной Юлием Цезарем.

Архимед упоминает и о вычисленном Евдоксом отношении расстояний до Луны и Солнца (1 : 12).

Blog

Биография Евдокс Книдский известен прежде всего как математик и астроном, но кроме того он писал книги по философии, географии, музыке и медицине.