Методика и содержание подготовки учащихся к олимпиадам по программированию. Дистанционный курс. Небольшое отступление
| Вид материала | Документы |
СодержаниеУтверждение: любой цикл можно заменить рекурсией и наоборот. Обработка последовательностей и массивов Классические задачи с рекурсивным решением Небольшие общие примечания |
- Методика и содержание подготовки учащихся к олимпиадам по программированию. Дистанционный, 57.33kb.
- М. Е. Литвак секс в семье и на работе, 5263.69kb.
- Курс предпрофильной подготовки учащихся с ориентацией на информационно-технологический, 59.17kb.
- Дистанционный курс Современные технологии открытого образования Занятие, 92.07kb.
- Фейгина Евгения Алексеевна, Методист моу дод «цит» Г. Кировск 2010 содержание содержание, 534.9kb.
- Пояснительная записка Курс предназначен для учащихся 9-х классов общеобразовательных, 47.51kb.
- Дистанционный курс подготовки к егэ по математике, 48.14kb.
- Дистанционный курс «Немецкий язык для студентов заочной формы обучения» Тип эвм: Intel, 617.94kb.
- Положение о всероссийском конкурсе «содержание, технологии и методики подготовки, 70.96kb.
- Предлагаем вам пройти дистанционный курс «Обучение в сотрудничестве». Каждое занятие, 171.18kb.
Методика и содержание подготовки учащихся к олимпиадам по программированию. Дистанционный курс.
Небольшое отступление
В этом курсе не идет речь о подготовке школьников к олимпиадам Российского уровня. Для этого есть специальные сборы, семинары (как очные, так и дистанционные), летняя компьютерная школа (ссылка скрыта). В конце концов, для этого есть самоподготовка школьника. Разумеется, очень желательно чтобы преподаватель разбирался не только в тех базовых алгоритмах, которые приведены в этом курсе, но и в более сложных.
Материалы данного в основном о «содержании» подготовки учащихся. Возможно использование этих материалов учащимися непосредственно или после какой-то обработки преподавателем. Суть в том, что необходимо знать и слабые места тех или иных алгоритмов, уметь показать школьнику причину ошибочного поведения программы. А таких причин, как уже отмечалось в первой лекции, может быть великое множество. И если такие вещи как переполнение промежуточных результатов или другие тонкости можно научиться «отлавливать» только приобретя определенный опыт, то неаккуратная реализация того или иного «стандартного» алгоритма – это скорее признак неглубокого или поверхностного изучения.
Темой данного занятия является рекурсия. Опыт показывает, что использование графической библиотеки является довольно мощным средством для демонстрации этого приема программирования. Если учащиеся в младших классах познакомились с этим приемом на базе среды «Логомиры» или какой-либо другой – это сильно облегчит задачу объяснения этой темы. Графическая библиотека также может использоваться для демонстрации геометрических и графических алгоритмов и обычно повышает у учащихся мотивацию к изучения математики (в частности тригонометрии).
В качестве упражнений для учащихся здесь сгодятся практически любые задания, которые давались на циклы.
Еще один довольно сильно стимулирующий прием – это проведение соревнований между программами по какой-либо игре. Возьмем, к примеру, «уголки». И попросим учеников написать программу, которая прочитает из файла игровую позицию и сделает один ход фигурой определенного цвета, запишет результат в тот же файл и завершится. Затем запустим программу-соперника, которая также прочитает игровую позицию и сделает ход фигурой другого цвета. Конечно, здесь требуется разработка проверяющей программы (которая как минимум контролирует корректность хода, а может быть и показывает графическое изображение игровой позиции). Проведение таких соревнований стимулирует изучение элементов теории игр и отработку навыков написания стандартных алгоритмов.
Рекурсия
«Итерация от человека, рекурсия — от Бога»
(Питер Дойч)
«Чтобы понять рекурсию, нужно сначала понять рекурсию»
(фольклор)
«РЕКУРСИЯ — см. РЕКУРСИЯ
РЕКУРСИЯ БЕСКОНЕЧНАЯ — см. БЕСКОНЕЧНАЯ РЕКУРСИЯ
БЕСКОНЕЧНАЯ РЕКУРСИЯ — см. РЕКУРСИЯ БЕСКОНЕЧНАЯ»
(шуточный словарь)
Рекурсия — это прием программирования, при котором решение задачи сводится к некоторым действиям плюс решение такой же задачи, но в более простом случае. Под более простым подразумевается либо случай с меньшими входными данными, либо с меньшим их количеством.
Пример: возведение числа X в натуральную степень N.
По определению, XN=X*X*X*…*X (N раз).
Преобразуем равенство: XN=X*(X*X*…*X). Выражение в скобках содержит произведение числа X само на себя N-1 раз, что по определению равно XN-1.
Таким образом XN=X*X(N-1)
В словесной формулировке результаты преобразований будут звучать так: чтобы найти N-ю степень числа надо найти N-1-ю степень числа и умножить ее на число. Таким образом решение задачи с параметром N свелось к решению задачи с параметром N-1. В свою очередь, используя аналогичные рассуждения можно свести задачу с параметром N-1 к задаче с параметром N-2, а ту, в свою очередь к N-3 и так далее. В какой-то момент мы сведем задачу к N=1 или N=0 — параметрам, при которых дальнейшее упрощение смысла не имеет, так как нулевая или первая степень не требуют вычислений.
На этом примере видно, что для описания рекурсивного решения необходимы две четко определенные вещи:
- правило, по которому решение задачи в сложном случае сводится к решению такой же задачи, но в более простом случае;
- условие, при котором дальнейшее упрощение нужно прекратить (терминальное условие). При отсутствии этого условия упрощение будет продолжаться до бесконечности и получится вечный цикл, чего при написании программ обычно не хочется.
С точки зрения программирования рекурсивное решение записывается в виде подпрограммы (процедуры или функции), содержащей вызов самой себя. Для примера со степенью возможна, к примеру, такая реализация:
function power(x : real; n : integer): real;
begin
if n=0 then power := 1
else power := x * power (x, n — 1);
end;
Первая строка представляет собой терминальное условие (если нужно возвести в нулевую степень, то ответ будет 1 и работа подпрограммы будет закончена), вторая строка — это правило перехода от более сложной задачи к менее сложной (вычислить такую же функцию с параметром (n — 1), ее результат домножить на x и закончить работу функции.
Рассмотрим подробнее как данная конструкция будет работать на компьютере. Пусть в программе записана такая строка:
b := power(2, 2);
Упоминание имени функции в правой части выражения приводит к тому, что программа переходит к описанию функции и начинает его исполнять с заданными значениями параметров.
| power(2, 2) требуется вычислить 22 begin if n=0 then power := 1 n=2, следовательно условие неверно и функция будет вычислена по второй строке: else power := x * power (x, n — 1); в этом выражении значение x известно, и чтобы найти результат функции нужно найти значение power (2, 2-1). В этот момент функция «подвисает» и запускает копию самой себя, чтобы вычислить 21 | | |
| Основная функция не может завершиться, потому что не вычислено значение внутренней функции. | power(2, 1) требуется вычислить 21 begin if n=0 then power := 1 n=1, следовательно условие неверно и функция будет вычислена по второй строке: else power := x * power (x, n — 1); данное выражение также не может быть вычислено пока неизвестно значение power (2, 1-1). В этот момент и эта функция также «подвисает» и запускает копию самой себя (уже вторую, не считая основной), чтобы вычислить 20 | |
| Основная функция не может завершиться, потому что не вычислено значение внутренней функции. | Эта копия функции тоже не может завершиться, так как не вычислено значение ее внутренней функции. | power(2, 0) требуется вычислить 20 begin if n=0 then power := 1 n=0, следовательно условие верно и эта копия функции может сразу завершиться с ответом power=1. Это означает, что предыдущая копия получит нужные для завершения вычислений данные. |
| Основная функция не может завершиться, потому что не вычислено значение внутренней функции | x=2, значение внутренней функции=1. Эта копия вычисляет свой результат power:=2*1 завершает работу. Теперь и у основной функции достаточно данных, чтобы найти свое значение. | |
| x=2, значение внутренней функции равно 2, основная функция может вычислить свой результат (2*2) и завершиться. | | |
Если изобразить написанное в таблице в виде схемы, то получится цепочка рекурсивных вызовов:
power(2,2) — power(2,1) — power(2,0)
Длина такой цепочки называется глубиной рекурсии.
Основной идеей рекурсивного решения является «вера» в то, что внутренняя функция успешно справится с решением своей более простой задачи. А это вполне возможно, так как внутренняя функция может быть либо последней в цепочке рекурсии (тогда она выдает простой ответ), либо от нее цепочка будет тянуться дальше, тогда все зависит от правильности рекурсивного соотношения.
Утверждение: любой цикл можно заменить рекурсией и наоборот.
Однако, в некоторых задачах рекурсивное решение является более изящным и легким для написания.
Р
 ассмотрим пример.
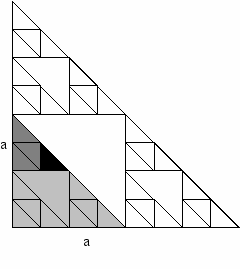
ассмотрим пример.Пусть требуется написать программу, для построения такой фигуры (см рисунок):
Фигура представляет собой равнобедренный прямоугольный треугольник с длиной катета равной a. Внутри него располагаются три равных треугольника (также прямоугольных и равнобедренных). Катеты внутренних треугольников в 2 раза меньше катетов внешнего. Каждый из внутренних треугольников также содержит внутри себя по три треугольника, которые в свою очередь могут содержать еще более маленькие треугольники и так далее.
Собственно, в самом описании геометрической фигуры полностью изложен механизм рекурсивного решения данной задачи. Любой внутренний треугольник по структуре ничем не отличается от внешнего. Таким образом, требуется написать подпрограмму, которая построит треугольник, а затем вызовет саму себя для построения трех меньших треугольников внутри данного. Терминальным условием в этом случае будет ситуация, когда длина катета меньше либо равна 1 (катет превращается в одну точку).
Подпрограмма для решения такой задачи может выглядеть, например, так:
procedure triangle(x,y,a:integer); {пусть (x,y) — положение прямого угла, a — длина катета}
begin
line(x, y, x + a, y);
line(x, y, x, y - a);
line(x + a, y, x, y - a); {построили контур большого треугольника}
if (a>1) then begin {если наш треугольник должен содержать внутренние — построим их по тому же правилу что и большой}
triangle(x, y, a div 2); {меньший треугольник, у которого общий с большим прямой угол}
triangle(x, y — a div 2, a div 2); {верхний треугольник}
triangle(x + a div 2, y, a div 2); {правый треугольник}
end;
end;
При написании данной процедуры считается, что ось Y экрана направлена сверху вниз, поэтому чем выше точка, тем меньше будет ее координата.
Кстати, на примере этого решения хорошо видно, что рекурсию не всегда легко заменить циклом.
Р
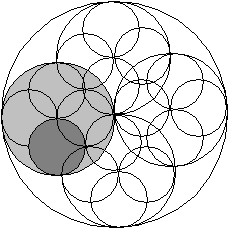 ассмотрим еще один пример. Пусть требуется написать подпрограмму для изображения серии вложенных окружностей. Окружность диаметра d содержит внутри себя 4 одинаковых окружности диаметра d/2, которые касаются ее в верхней, нижней, правой и левой точках. С свою очередь каждая из четырех внутренних окружностей также содержит внутри еще по 4 окружности меньшего диаметра и так далее.
ассмотрим еще один пример. Пусть требуется написать подпрограмму для изображения серии вложенных окружностей. Окружность диаметра d содержит внутри себя 4 одинаковых окружности диаметра d/2, которые касаются ее в верхней, нижней, правой и левой точках. С свою очередь каждая из четырех внутренних окружностей также содержит внутри еще по 4 окружности меньшего диаметра и так далее.Аналогично предыдущей задаче, любая из внутренних окружностей есть полное подобие внешней. Окончание рекурсивных вызовов будет задаваться условием d<=1 (на каком-то уровне упрощения окружность превратилась в точку).
Подпрограмма для решения этой задачи может выглядеть, например, так:
procedure circles(x,y, r : integer); {пусть (x,y) — координаты центра окружности, r - радиус }
begin
circle(x,y,r);
if (r>=2) then begin
circles(x — r div 2, y, r div 2);
circles(x + r div 2, y, r div 2);
circles(x, y — r div 2, r div 2);
circles(x, y + r div 2, div 2);
end;
end;
Аналогично предыдущей задаче данная подпрограмма строит только контур большой окружности, а всю работу по построению внутренних перекладывает на свои собственные копии, но вызванные с другими параметрами.
Обработка последовательностей и массивов
Пусть дан массив из N целых чисел и требуется найти максимальное среди них. Разумеется, эту задачу вовсе необязательно на практике реализовывать рекурсией. Здесь речь идет скорее о том, чтобы потренироваться в написании рекурсивных решений, в замене цикла на рекурсию. В данной задаче можно сделать это таким образом: разобьем массив на «голову» - первый элемент и «хвост» - остальные элементы, начиная со второго. При этом «хвост» тоже будет массивом, просто его нумерация будет немного отличаться от нумерации исходного массива. Отсюда можно вывести такой способ сведения задачи к более простой:
«Найти максимальное число в массиве» = «Найти максимальное число в части массива, которая начинается со второго элемента» + «Сравнить найденный максимум с первым числом». В свою очередь, можно «хвост» массива обрабатывать по этой же схеме. То есть отделить от него начальный элемент и еще меньший «хвост».
Пусть существует такое описание:
const
N = 100;
var
a : array [1..N] of integer;
Тогда функция нахождения максимального числа может быть записана так:
function Max(Start : integer) : integer;
var
m : integer;
begin
if Start=N then Max:=a[Start]
else begin
m:=Max(Start+1); {Найдем максимальное число среди всех, которые справа от номера Start}
if m>a[Start] then Max:=m {Сравним найденное с первым числом и вернем}
else Max:=a[Start]; {максимальное из этих значений}
end;
end;
В программе функция будет использована так:
x := Max(1);
Параметром функции является номер того элемента, с которого начинается поиск максимума. С каждым шагом рекурсии этот параметр будет увеличиваться и приближаться к правой границе массива. Отсюда и получается терминальное условие – если Start=N (то есть это последний шаг упрощения – дошли до рассмотрения массива из одного элемента, который и будет максимальным).
Классические задачи с рекурсивным решением
Ханойские башни
Д
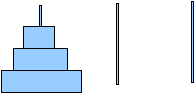 ано три стержня. На первом стержне в начальный момент времени нанизано N колец различного диаметра, так что они образуют пирамидку.
ано три стержня. На первом стержне в начальный момент времени нанизано N колец различного диаметра, так что они образуют пирамидку.Требуется перенести все кольца с первого стержня на третий за минимальное количество ходов, соблюдая два правила:
- можно брать только свободное кольцо (то, на котором ничего не лежит);
- взятое кольцо можно нанизывать на любой стержень, но нельзя класть большее кольцо на меньшее.
Рассмотрим случай, когда N=1. Здесь решение очевидно, необходимо просто перенести кольцо с первого стержня на третий.
При N=2 решение также очевидно. Необходимо перенести верхнее кольцо на второй стержень, затем освободившееся нижнее на 3-й, а потом маленькое кольцо также перенести на 3-й стержень.
При N=3 можно сделать следующее замечание. Пока верхние два кольца куда-нибудь не денутся с нижним кольцом по правилам ничего сделать нельзя. Поэтому можно временно про нижнее кольцо «позабыть» и решать только задачу переноса двух верхних колец на второй стержень. После этого свободное нижнее кольцо можно перенести на третий стержень, а затем опять вернуться к задаче о перемещении первых двух колец. Таким образом задача для N=3 сводится к двум задачам для N=2 и одной задаче для N=1.
Аналогично, для N=4 задача сводится к переносу трех верхних колец на второй стержень, переносу нижнего кольца на третий стержень и переносу на него трех колец со второго стержня. А задачи переноса трех верхних колец, как мы уже убедились, сводятся к задаче переноса двух.
Из этих рассуждений можно получить как схему упрощения задачи и сведения ее решения к более простому случаю (действительно, для произвольного N нужно сначала N-1 кольцо поместить на второй стержень, потом перенести самое большое на третий, и поверх него поместить N-1).
Факториал
Факториалом натурального числа N называется произведение всех натуральных чисел от 1 до N включительно: N!=1*2*3*...*N. Рассуждения в этой задаче полностью аналогичны задаче о возведении числа в натуральную степень.
Действительно, N!=1*2*3*...*N=(1*2*3*..*(N-1))*N. По определению, выражение в скобках есть (N-1)! (так как это произведение всех натуральных чисел от 1 до (N-1). Отсюда окончательно получается правило, по которому решение задачи сводится к более простому случаю. N!=(N-1)!*N.
Функция для вычисления факториала может быть записана, например, так:
function Factorial(n : integer) : longint;
begin
if N=1 then Factorial:=1 {терминальное условие}
else Factorial:=Factorial(N-1)*N;
end;
Последовательность Фибоначчи
Требуется найти k-е число ряда 1,1,2,3,5,8,13,21,34,55...
Первое и второе число ряда F1=F2=1, каждое следующее число равно сумме двух предыдущих: Fk=Fk-1 + Fk-2.
В данной задаче само определение следующего числа ряда уже дано рекурсивно, поэтому можно сразу записать реализацию подпрограммы для ее решения.
function F(k : integer): integer;
begin
if k<=2 then F:=1
else F:=F(k-1) + F (k-2);
end;
Наибольший общий делитель (НОД)
Дано два натуральных числа. Требуется найти их наибольший общий делитель, то есть максимальное из чисел, на которое оба исходных числа делятся без остатка.
- Найдем остаток от деления большего числа на меньшее.
- Если остаток не равен нулю, то повторим шаг №1 для меньшего числа и остатка.
- Если остаток равен нулю, то последнее число, на которое делалось последнее деление и будет НОД
Функция вычисления НОД двух чисел может быть записана таким образом:
function NOD(a, b : integer) : integer;
var
c : integer;
begin
if b>a then begin {сделаем так, чтобы в a находилось большее значение}
c:=a;
a:=b;
b:=c;
end;
c:=a mod b;
if c=0 then NOD:=b
else NOD:=NOD(b,c);
end;
Небольшие общие примечания
Рекурсия может быть не только прямой (когда подпрограмма содержит вызов самой себя), но и косвенной (когда подпрограмма X вызывает подпрограмму Y, которая опять вызывает подпрограмму X и так далее).
Хотя рекурсия и является довольно мощным приемом, особенно там, где это касается организации перебора, она не всегда является оптимальным способом решения задачи (когда именно это происходит подробно разобрано в главе о динамическом программировании)
К
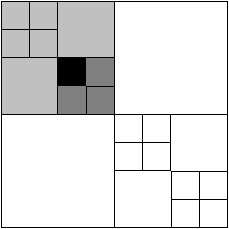 роме того, каждый новый вызов подпрограммы сопровождается выделением памяти под ее локальные переменные и параметры, поэтому в случае достаточно глубокой рекурсии возможны ошибки, связанные с недостатком памяти для работы программы.
роме того, каждый новый вызов подпрограммы сопровождается выделением памяти под ее локальные переменные и параметры, поэтому в случае достаточно глубокой рекурсии возможны ошибки, связанные с недостатком памяти для работы программы. Упражнения
- Напишите рекурсивную программу построения фигуры (см. рисунок).
- Напишите рекурсивную функцию нахождения суммы цифр натурального числа.
- Напишите рекурсивную подпрограмму переворота строки (последний символ на первое место, предпоследний — на второе и так далее).
- Напишите рекурсивную подпрограмму нахождения суммы элементов массива.
- Напишите рекурсивную подпрограмму подсчета количества слов в строке (словом считается последовательность символов, внутри которой нет пробелов). Слова отделены друг от друга одиночными пробелами.
- * Напишите подпрограмму для открытия клетки в игре «сапер». Поле задано двумерным массивом. Даны также координаты открываемой клетки. Если вокруг есть заминированные, то нужно подсчитать их количество, если вокруг мин нет, то нужно также открыть все соседние клетки.
- * Дана шахматная доска, на которой есть несколько черных шашек и одна белая. Напишите программу, для определения максимального количества черных шашек, которые можно съесть за один ход.
МЦНМО, 2007/08 учебный год
