Geum.ru

2012 умови вступу на програму спеціаліст Наукма

Вид материалаДокументы

Содержание


Listening Comprehension
А. математика
Б. інформатика
Подобный материал:

2012

УМОВИ ВСТУПУ

на програму спеціаліст НаУКМА




«Інформаційні управляючі системи

та технології»



присвоєна кваліфікація – 7.05010101

інформаційні управляючі системи та технології


I. Зарахування абітурієнтів студентами на програму спеціаліста відбувається на підставі результатів вступних випробувань:

▪ письмового екзамену з української мови;

▪ письмового тестування з англійської мови;

▪ письмового екзамну зі спеціальності

Вступний рейтинг визначається за результатами екзамену зі спеціальності за умови позитивної оцінки з української та англійської мов.


ІІ. Вступний іспит з української мови складається з двох частин: диктанту та редагування 10 речень. Необхідною умовою позитивної оцінки є грамотність викладу, ґрунтовне знання нині чинного «Українського правопису», а також успішне засвоєння лінгвістичного курсу:«Ділова українська мова та культура мовлення».

Курс передбачає засвоєння орфоепічних та правописних норм, граматичних і синтаксичних особливостей української мови, специфіки ділового мовлення, основ практичної стилістики з урахуванням майбутньої спеціалізації.


ЛІТЕРАТУРА:

  1. Антоненко-Давидович Б. Д. Як ми говоримо. – К.: Українська книга, 1997. – 336 с.
  2. Великий тлумачний словник сучасної української мови. – К.: Перун, 2003; 2005; 2007.
  3. Вирган І. О., Пилинська М. М. Російсько-український словник сталих виразів. – Харків: Прапор, 2000; 2002.
  4. Головащук С. І. Російсько-український словник сталих словосполучень. – К.: Наукова думка, 2001. – 639 с.
  5. Головащук С. І. Словник-довідник з українського літературного слововживання. – К.: Наукова думка, 2004. – 448 с.
  6. Гуць М. В., Олійник І. Г., Ющук І. П. Українська мова у діловому спілкуванні. – К.: Біноватор, 2005. – 352 с.
  7. Караванський С. До зір крізь терня, або хочу бути редактором. – Л.: БаК, 2008. – 118 с.
  8. Караванський С. Практичний словник синонімів української мови. – Л.: БаК, 2008. – 512 с.
  9. Культура фахового мовлення: Навчальний посібник / За ред. Н. Д. Бабич. – Чернівці: Книги – ХХІ, 2006. – 496 с.
  10. Новий російсько-український словник-довідник: близько 100 тисяч слів. – К.: Довіра, 1999. – 878 с.
  11. Новий тлумачний словник української мови / уклад. В. Яременко, О. Сліпушко: в 4-х тт. – К., 1998, 1999; в 3-х тт. – К., 2004.
  12. Орфографічний словник української мови: 4-е вид., доопр. / А. А. Бурячок. – К.: Наукова думка, 2002. – 460 с.
  13. Пономарів О. Д. Культура слова: мовностилістичні поради. – К.: Либідь, 2001; 2002; 2008. – 238 с.
  14. Пономарів О. Д. Стилістика сучасної української літературної мови. – К.: Богдан, 2000. – 246 с.
  15. Російсько-український словник / за ред. В. В. Жайворонка. – К.: Абрис, 2003. – 1402 с.
  16. Сербенська О., Волощак М. Актуальне інтерв’ю з мовознавцем. – К.: Вид. центр «Просвіта», 2001. – 204 с.
  17. Сучасний словник іншомовних слів. – К.: Довіра, 2006. – 790 с.
  18. Словник синонімів української мови: у двох томах / ред. А. А Бурячок та ін. – К.: Наукова думка, 2001; 2006.
  19. Словник української мови: в 11-ти тт. – К.: Наукова думка, 1971-1981.
  20. Українська мова. Енциклопедія. – К.: «Українська енциклопедія», 2000; 2004; 2007.
  21. Український орфографічний словник. – К.: Довіра, 2005; 2006; 2007.
  22. Український правопис. – К.: Наукова думка, 2008. – 288 с.
  23. Українсько-російський словник / упор. Г. П. Їжакевич. – К.: Наукова думка, 2004. – 1008 с.
  24. Читай і знай!: довідник-практикум з граматики та стилістики сучасної української мови / Н. Я. Дзюбишина-Мельник, О. Я. Лаврінець, К. С. Симонова, Л. Ф. Ціпцюра. – К.: Вид. дім «Києво-Могилянська академія», 2007. – 197 с.
  25. Читай і знай!-2: довідник-практикум з фонетики, орфоепії, орфографії, лексикології, фразеології сучасної української мови/ О.Я. Лаврінець, К.С. Симонова, І.А. Ярошевич.-К.: Вид.дім «Києво-Могилянська академія», 2009.-206 с.
  26. Шевельов Ю. Українська мова в першій половині двадцятого століття (1900-1941). Стан і статус. – Чернівці: Рута, 1998. – 207 с.
  27. Ющук І. П. Практикум з правопису української мови. – К.: Освіта, 1997; 2000. – 254 с.
  28. Ющук І. П. Українська мова. – К.: Либідь, 2006. – 640 с.


III. Тест з англійської мови передбачає перевірку практичного володіння англійською мовою на рівні бакалаврських програм; оцінювання знань і навичок, здобутих бакалаврами в результаті успішного засвоєння курсу англійської мови. Письмовий тест з англійської мови складається з трьох розділів:
  1. Listening Comprehension – перевіряє уміння абітурієнта сприймати на слух інформацію монологічного або діалогічного характеру (визначення основної ідеї, вилучення конкретної інформації).

2. Reading Comprehension – перевіряє знання нормативної граматики та лексики рівня Upper-Intermidiate Level.

3. Writing передбачає написання невеликого тексту (10 – 15 речень) на запропоновану тему, що перевіряє уміння грамотно і логічно викладати власну думку. Абітурієнт повинен мати уявлення про структуру (Introduction, Body, Conclusion) та типи письма (Narrative, Persuasive, Cause and Effect, Comparison and Contrast).


Література


Raymond Murphy. English Grammar in Use (Intermediate Level).

Headway Intermadiate (Students Book + Workbook).

The Heinemann English Grammar.

Michael Vince. First Certificate Language Practice.


IV. Питання для підготовки до іспиту зі спеціальності:

А. МАТЕМАТИКА



Основи математичного аналізу
  1. Числові послідовності. Границі.
  2. Збіжність послідовності 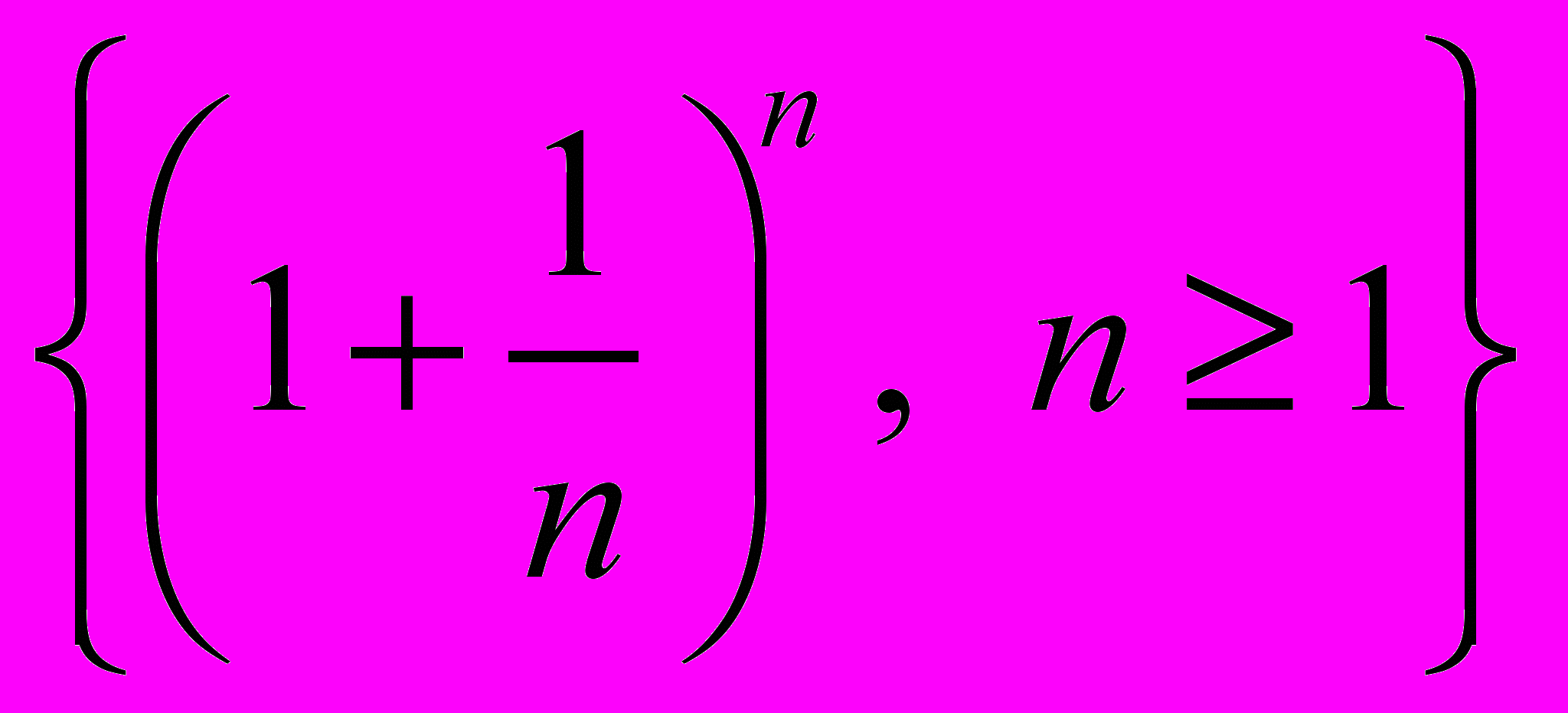. Число e.
  3. Границя функції в точці. Означення по Коші і по Гейне, їх еквівалентність.
  4. Поняття неперервності функції, неперервність функції в точці, точки розриву.
  5. Дослідження функції за допомогою похідних. Монотонність та похідна. Локальний екстремум.
  6. Опуклість, точки перегину. Знаходження найбільшого та найменшого значень функції, заданої на відрізку.
  7. Алгоритм побудови графіка функції.
  8. Числові ряди. Необхідна умова збіжності числового ряду. Гармонійний ряд.
  9. Розклад функцій в ряд Тейлора, основні розклади.
  10. Поняття тригонометричного ряду, розклад функцій в ряд Фур’є.


Диференціальні рівняння
  1. Звичайне диференціальне рівняння першого порядку, розв’язане відносно похідної. Означення розв'язку, загального розв'язку. Особливі розв’язки.
  2. Основні типи диференціальних рівнянь першого порядку, які інтегруються в квадратурах.
  3. Лінійні диференціальні рівняння першого порядку, методи розв’язання.
  4. Лінійні диференціальні рівняння з сталими коефіцієнтами.


Аналіз функцій багатьох змінних
  1. Поняття про m-вимірний простір Rm. Відстань між двома точками. Збіжність послідовності точок в Rm.
  2. Локальний екстремум функції багатьох змінних. Необхідні умови екстремуму.

17. Достатні умови екстремуму функції двох змінних.


Алгебра та теорія чисел
  1. Основні алгебраїчні структури: поле, кільце, група. Означення, приклади.
  2. Арифметика цілих чисел. Прості числа, розподіл простих чисел, решето Ератосфена.

Основна теорема арифметики.
  1. Властивості лишків при діленні з остачею. Кільця лишків.
  2. Кільця лишків за модулем m як фактор-кільце кільця цілих чисел.
  3. Теорема Ейлера, мала теорема Ферма.
  4. Китайська теорема про лишки.
  5. Побудова кільця многочленів від однієї змінної. Ділення многочленів з остачею.

Теорема Безу.
  1. НСД, НСК многочленів. Алгоритм Евкліда.
  2. Теорема про лінійне подання НСД многочленів однієї змінної.


Основи дискретної математики
  1. Числення висловлювань. Операції над висловлюваннями та їх властивості. Основні

    тавтології та правила логічного наслідку.
  1. Бульові функції, операції над ними. Застосування до побудови релейно-контактних

    схем. диз’юнктивні та кон’юнктивні нормальні форми
  1. Метод математичної індукції.
  2. Основні поняття теорії множин. Парадокс Рассела. Діаграми Ейлера-Вена. Способи

    представлення множин в пам’яті комп’ютера. Операції над множинами та їх

    властивості. Закони де Моргана. Декартів добуток множин. Поняття функції , способи

    її задання.
  1. Основні принципи комбінаторики. Розміщення , перестановки, комбінації (з

    повтореннями і без). Біноміальні коефіцієнти та їх інтерпретації Поліноміальні

    коефіцієнти. Формули включень та виключень.
  1. Відношення, та відповідності задані на множинах. Графіки та графи бінарних

    відношень. Операції над відношеннями .
  1. Спеціальні типи відношень. Функціональні відношення. Відношення еквівалентності,

    поняття фактор-множини Відношення часткового порядку, решітки.
  1. Основні поняття теорії графів. Ейлерові та гамільтонові графи.
  2. Дерева та їх властивості.



Лінійна алгебра та аналітична геометрія
  1. Поле комплексних чисел: означення ( побудова ); дії над комплексними числами в

    алгебраїчній та тригонометричній формі; формула Муавра, видобування кореня n-го

    степеня з комплексного числа; логарифм та експонента комплексного числа, формула

    Ейлера.
  1. Векторний (лінійний) простір, лінійна залежність і лінійна незалежність векторів,

    базис, розмірність, координати вектора в різних базисах. Лінійний підпростір, способи

    його задання. Сума і перетин лінійних підпросторів .
  1. Системи лінійних рівнянь: еквівалентність, сумісність,визначеність.

    Метод Жордана – Гауса. Теорема Кронекера – Капеллі.
  1. Лінійні оператори. Алгебра лінійних операторів. Ізоморфізм алгебри лінійних

    операторів алгебри матриць розмірності.
  1. Лінійні оператори, матриці оператора в різних базисах.
  2. Власні числа та власні вектори лінійного оператора та квадратної матриці.
  3. Геометрія тривимірного евклідового простору: рівняння прямої на площині та в

    просторі, рівняння площини. Векторний та мішаний добуток векторів.
  1. Криві другого порядку: означення, властивості.
  2. Зведення загального рівняння квадратичної форми до канонічного виду, класифікація

    кривих другого порядку


Теорія алгоритмів та математична логіка
  1. Формальні мови. Числення висловлювань та числення предикатів, як формальна мова.
  2. Формальні теорії. Числення висловлювань та числення предикатів, як формальні

теорії.
  1. Теорії першого порядку. Приклади ( теорія часткового порядку, теорія груп і т.і.).
  2. Примітивно-рекурсивні та рекурсивні функції.
  3. Рекурсивні та рекурсивно зліченні множини ( предикати ). Властивості таких множин.
  4. Поняття універсальної функції для класу рекурсивних функцій.Показати, що

універсальна функція класу примітивно рекурсивних функцій не належить цьому

класу.
  1. Машина Тьюринга. Теза Черча. Еквівалентність концепцій алгоритму за Гьоделем та

Тьюрінгом.
  1. Алгоритмічно нерозв’язні проблеми. Проблема застосовності для машин Тьюринга.

Класичні алгоритмічно нерозв’язні проблеми.

Теорія ймовірностей
  1. Поняття ймовірності. Умовні ймовірності. Формули повної ймовірності та Байєса.
  2. Дискретні випадкові величини. Розподіл дискретної випадкової величини. Функція

розподілу.
  1. Схема Бернуллі. Біноміальний розподіл. Його числові характеристики.
  2. Геометричний розподіл. Його основна властивість і числові характеристики.
  1. Числові характеристики випадкових величин.
  2. Незалежні дискретні випадкові величини.
  3. Основні розподіли (рівномірний розподіл, показниковий розподіл, нормальний

розподіл.

60. Функції від випадкових величин. Математичне сподівання. Моменти випадкової

величини.

61. Числові характеристики залежності випадкових величин.

62. Граничні теореми для біноміального розподілу.

Література:

  1. Ляшко И.И., Боярчук А.К., Гай Я.Г., Калайда А.Ф. Математический анализ. Т.1,2. – К., 1983.
  2. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т.1-3.- М.1959.
  3. Новиков Ф.А. Дискретная математика (для программистов).
  4. Уилсон Р. Введение в теорию графов.- М. Мир, 1977.
  5. Капітонова Ю.В., Кривий С.Л., Летичевський О.А., Луцький Г.М., Печурін М.К.

Основи дискретної математики. – Київ, Наукова думка, 2002.
  1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.,1985.
  2. Беклемишев Д.В., Петрович А.Ю., Чубаров И.А. Зборник задач по аналитической геометрии и линейной алгебре. – М.,1987.
  3. Калужнін Л. А., Вишенський В., Шуб Ц. Лінійні простори. – К., 1961.
  4. Мальцев А. И. Основы линейной алгебры. – М., 1975.
  5. Курош А. Г. Курс высшей алгебры. – М., 1975.
  6. Феллер В. Введение в теорию вероятностей. В 2-х т. – М.,1984.
  7. Гихман И.И., Скороход А.В., Ядренко М.И. Теория вероятностей и математическая статистика. – К.,1988.

Б. ІНФОРМАТИКА


Загальні питання
  1. Поняття алгоритму.
  2. Основні поняття об’єктно орієнтованого програмування.
  3. Принципи криптографічного захисту інформації.
  4. Базові принципи фон Нейманівської архітектури.
  5. Основні принципи побудови і функціонування компіляторів.
  6. Основні поняття об’єктно-орієнтованого програмування.
  7. Класифікація сучасного апаратного забезпечення.


Комп'ютерні мережі
  1. Internet, головні принципи побудови та використання.
  2. Поняття гіпертексту; Основні елементи мови HTML.
  3. Поняття моделі відкритої системи та стеку протоколів. Концепція еталонної моделі OSI.
  4. Стек протоколів TCP/IP: топологічні особливості, функції рівнів.
  5. Основні види протоколів, що застосовуються в мережах.


Системи управління базами даних
  1. Загальні концепції СУБД; три моделі даних: реляційна, ієрархічна, мережева. Вимоги до СУБД.
  2. Мова SQL та її діалекти.
  3. Проектування реляційних баз даних: аномалії реляційної моделі, функціональні залежності, нормальні форми та декомпозиція.
  4. Захист баз даних: цілісність, безпечність, адміністрування.
  5. СУБД в мережах: головні концепції, транзакції, дедлоки, паралельний доступ.
  6. Нормальні форми баз даних.
  7. Реляційне числення та поняття реляційної повноти.
  8. Основні операції реляційної алгебри.


Основи комп’ютерних алгоритмів
  1. Спискові структури даних.
  2. Основні алгоритми на графах.
  3. Часова складність алгоритмів.
  4. Формальні мови й граматики.
  5. Метод резолюцій та його застосування в логічному програмуванні.
  6. Дерева та графи; їх подання в пам’яті комп’ютера.
  7. Метод перебору з поверненнями (back tracking).
  8. Метод „розділяй і пануй”, його часова оцінка та застосування.
  9. Метод динамічного програмування та його застосування.
  10. Фреймова модель задання знань.
  11. Семантичні мережі.
  12. Метод резолюцій, як основа логічного виведення.
  13. Функціональна мова програмування ЛІСП.
  14. Логічна мова програмування ПРОЛОГ.
  15. Застосування методу динамічного програмування до задачі добутку матриць.
  16. Алгоритм впорядкування злиттям.
  17. Метод найшвидшого спуску.
  18. Знаходження найкоротших шляхів у графі.
  19. Задання дерев у пам’яті.
  20. Фундаментальна множина циклів графу.
  21. Алгоритми розфарбовування графів.
  22. Алгоритми генерування всіх перестановок.
  23. Алгоритми пошуку на графах.
  24. Стеки та черги.
  25. Алгоритми знаходження остового дерева найменшої вартості.
  26. Ізоморфізм дерев.
  27. Задача про розташування n ферзів.
  28. Метод гілок і границь.
  29. Бінарний пошук.
  30. Планування в просторі станів і в просторі задач.



Основи штучного інтелекту
  1. Семантичні мережі та фрейми.
  2. Моделі прийняття рішень.



Паралельне програмування
  1. Класифікація архітектур паралельних систем.
  2. Головні парадигми паралельної обробки інформації.
  3. Механізми синхронізації в паралельних обчисленнях.
  4. Засоби паралельного програмування мови Java.

Література:

  1. Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных

алгоритмов. – М.,1979.
  1. Бородич Ю.С. Разработка прикладных систем на языке Паскаль. – Минск, 1992.
  2. Вирт Н. Алгоритмы+Структуры данных=Программы. – М.,1985.
  3. Зуев Е.Ф. Система программирования Turbo Pascal. – М.,1992..
  4. Кнут Д. Искусство программирования. В 3-х тт.
  5. Глибовець М. М., Олецький О.В. Штучний інтелект.-Київ, Видавничий дім “КМ

Академія”, 2002., с.365.
  1. Глибовець М. М. Основи комп’ютерних алгоритмів.- Київ, Видавничий дім “КМ Академія”, 2002., с.452.
  2. Ульман Дж. Основы системы баз данных. – М.,1985.
  3. Мартин Дж. Организация баз данных в вычислительных системах. – М.,1980.
  4. Дрибас Д. П. Реляционные модели баз данных. – Минск, 1982.
  5. Керниган Б., Ритчи Д., Фюэр А. Язык программирования Си. Задачи по языку. –

М.,1985.
  1. Проценко В.С., Чаленко П.І., Ставровський А.Б. Техніка програмування мовою Сі. –

К.,1993.
  1. Буч Г. Объектно-ориентированое проектирование с примерами применения. –

СПб,1998.
  1. Страуструп Б. Язык программирования С++. В 2-х ч. – К.,1993.
  2. Мюллер Дж. Visual C++ 5. – СПб, 1998.
  3. Калужнин Л.А., Введение в общую алгебру.- Наука,1973.
  4. Мендельсон Э. Введение в математическую логику.- М. Наука, 1971.
  5. Мальцев А. Алгоритмы и рекурсивные функции.- М. Наука, 1986


V. Випускники факультету інформатики НаУКМА 2012 року,

які мають диплом з відзнакою і бажають продовжити навчання на програмі спеціаліст «Інформаційні управляючі системи та технології», мають право на першочергове зарахування. Зазначене право надається за інших рівних умов за черговістю, визначеною пунктом 10.1 Правил прийому до Національного університету «Києво-Могилянська академія» у 2012 році на підготовку фахівців за спеціальностями освітньо-кваліфікаційного рівня «спеціаліст».


Віце-президент з навчальної роботи В.М. Ожоган


Декан ФІН М.М. Глибовець