Моделирование радиоцеребральных эффектов при комбинированном действии факторов экстремальной интенсивности 05. 13. 01. Системный анализ, управление и обработка информации (медицинские науки)
| Вид материала | Автореферат диссертации |
- Системный анализ параметров вектора состояния организма женщин репродуктивного возраста, 689.14kb.
- Системный анализ параметров вектора состояния организма человека, проживающего в условиях, 694.75kb.
- Комплекс программных средств поддержки принятия решений при сетевой обработке информации, 192.61kb.
- Системный анализ параметров сердечно-сосудистой системы учащихся югры 05. 13. 01 системный, 641.8kb.
- Прогнозирование риска и пользы эндоскопических транспапиллярных вмешательств у пациентов, 589.85kb.
- Модели и алгоритмы периоперационной лучевой визуализации желчевыводящих протоков, 426.55kb.
- Метод и алгоритмы обработки информации в системе прогнозирования качества агломерата, 229.88kb.
- Эволюционный метод синтеза непрерывно дискретных систем управления, 288.26kb.
- Высокоточное нейросетевое распознавание в системах технического зрения, 248.39kb.
- Краткосрочное прогнозирование на основе технологии нейросетевого пространственно-параметрического, 194.81kb.
Для определения приоритета каждого морфологического критерия и построения математической модели проведен сравнительный анализ зависимостей изменений при изолированном и совместном воздействии изучаемых факторов (рис.1).
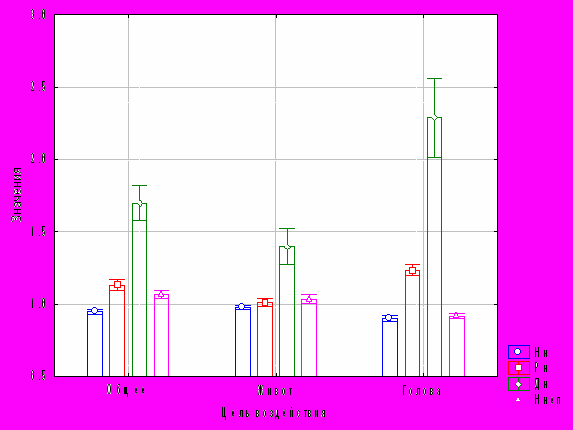
Рис. 1. График средних и доверительных интервалов 95 % для нормохромных, реактивных, деструктивных нейроцитов и нейроцитов на единицу площади
Из рис. 1 следует, что наибольшие изменения наблюдаются при облучении головы по количеству нервных клеток с необратимыми изменениями. Поэтому, интерес представляет прогноз состояния головного мозга после облучения этой области.
Модель изменения показателей морфофункционального состояния нейронов головного мозга крыс при облучении головы, составленную с помощью регрессионного анализа можно представить следующим уравнением:
ЗП = á0 + á1х + a2y + a3z + a4xy + a5xz + a6yz + a7x2 + a8y2 + a9z2 + a10xyz,
где ЗП – зависимый показатель, x – доза облучения, y – время наблюдения, z – содержание кислорода, xy, xz, yz, xyz, x2, y2, z2 – взаимные влияния параметров x, y, z и нелинейное влияние каждого из этих параметров. При построении регрессионной модели незначимые коэффициенты (p>0,05) параметров элиминировались, а рассматривались только параметры для коэффициентов с уровнем значимости р<0,05.
Модель состояния морфофункциональных показателей головного мозга при раздельном и сочетанном воздействии факторов на количество деструктивных нейроцитов (ДН) представлена в табл. 1.
Таблица 1
Зависимость деструктивных нейроцитов от дозы облучения, времени после воздействия и содержания кислорода
| Показатель | Оценка коэффициента | Стандартная ошибка | Т-статистика | Коэффициент достоверности |
| Константа | 1,2062 | 0,0966 | 12,4796 | <1,00E-19 |
| a1 | -1,7274 | 0,3106 | -5,5605 | 1,19E-7 |
| a2 | 2,3606 | 0,4645 | 5,0815 | 1,09E-6 |
| a3 | 3,4255 | 0,6669 | 5,1363 | 8,53E-7 |
| a4 | 2,9191 | 0,7806 | 3,7397 | 2,61E-4 |
| a5 | 1,5352 | 0,3095 | 4,9607 | 1,87E-6 |
| a6 | -1,7732 | 0,7204 | -2,4612 | 0,01 |
| a7 | 2,5478 | 0,3413 | 7,4644 | 6,18E-12 |
| a8 | -2,1621 | 0,3494 | -6,1874 | 5,48E-9 |
| a9 | -2,9849 | 0,6024 | -4,9549 | 1,92E-6 |
| a10 | 3,0397 | 1,5181 | 2,0022 | 0,05 |
Анализируя коэффициенты регрессионной модели, можно заключить, что наибольшее влияние на увеличение количества деструктивных клеток оказывает совместное воздействие трех изучаемых факторов. Вместе с тем, при увеличении показателей изолированного воздействия и совместного влияния дозы облучения с кислородом и временем после воздействия, количество деструктивных нейроцитов также будет возрастать. Однако, повышение содержания кислорода в среде с увеличением времени после воздействия будет способствовать уменьшению деструктивных нейроцитов.
Оценка сочетанного действия факторов на уровень значимости модели представлена в табл.2.
Таблица 2
Оценка адекватности математической модели влияния параметров на динамику изменений деструктивных нейроцитов
| Параметр | Сумма квадратов отклонений | Степени свободы | Средний квадрат | F-статистика | Коэффициент достоверности |
| Модель | 744,687 | 11 | 67,698 | 665,164 | <1,00E-19 |
| Остаток | 15,368 | 151 | 0,101 | | |
| Коэффициент корреляции R= 0,90049 Коэффициент детерминации R²= 0,81089 | |||||
Из табл. 2 следует, что построенная модель статистически значима и ее коэффициент детерминации достигает 0,8109.
Уравнение регрессии, описывающее динамику воздействия изучаемых факторов на изменение деструктивных нейроцитов, выглядит следующим образом:
ДН=1,2061+1,7273х+2,3606у+3,4254z+2,919ху+1,5352хz–1,7732yz-2,5478х2-
-2,1620у2-2,9849z2+3,0396хуz.
На рис.2. графически представлена зависимость деструктивных нейроцитов от воздействия экспериментальных факторов.
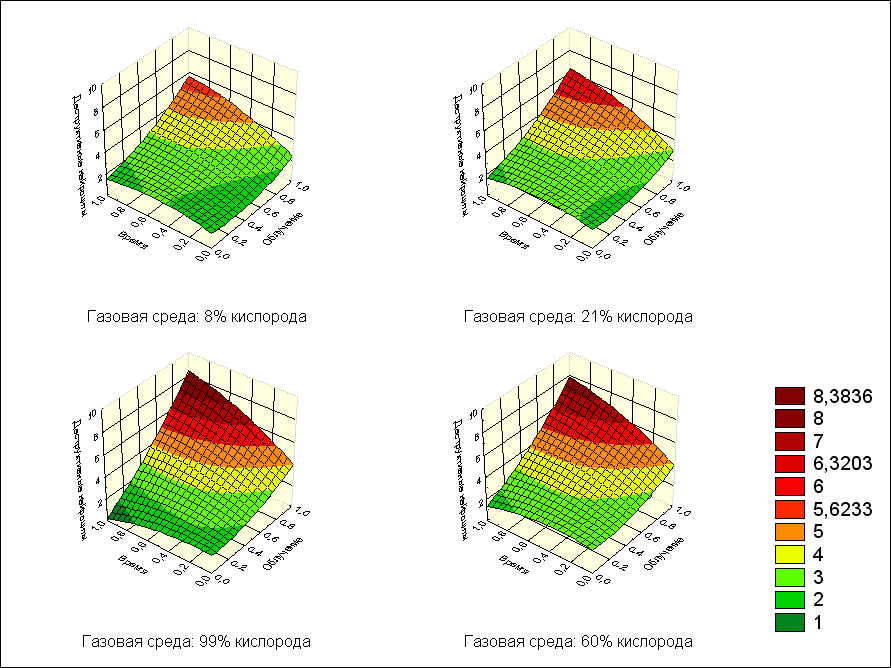
Рис. 2. Зависимость деструктивных нейроцитов от дозы облучения и времени после воздействия с фиксированными значениями кислорода
Точки, полученные в результате расчета по уравнению регрессии, аппроксимированы поверхностью методом наименьших квадратов. Очевидно, что при возрастании совместного влияния всех изучаемых параметров количество деструктивных нейроцитов будет повышаться.
Количество нормохромных клеток (НХ) в условиях эксперимента уменьшалось при возрастании дозы облучения, содержания кислорода и времени после воздействия. Построенная модель являлась статистически значимой, и коэффициент детерминации составлял R2=0,50605. Уравнение регрессии, описывающее динамику воздействия изучаемых факторов на изменение нормохромных нейроцитов, выглядит следующим образом:
НХ=1,0348+0,0641х–0,0785у–0,5531z–0,1685х2+0,5003z2.
Состояние нервных клеток с реактивными изменениями (РН) имеет прямую зависимость от совместного воздействия дозы облучения, времени после воздействия и содержания кислорода.
Уравнение регрессии, описывающее динамику воздействия изучаемых факторов на изменение реактивных нейроцитов, выглядит следующим образом:
РН=0,8494+0,3458х+0,6107у+0,8972z–0,1671хz–0,3132уz–0,5037у2-0,7792z2+ +1,1876хуz.
Построенная модель являлась статистически значимой, и коэффициент детерминации составлял R2=0,7599.
Степень участия экспериментальных факторов в изменении количества реактивных нейроцитов представлена на рис. 3.
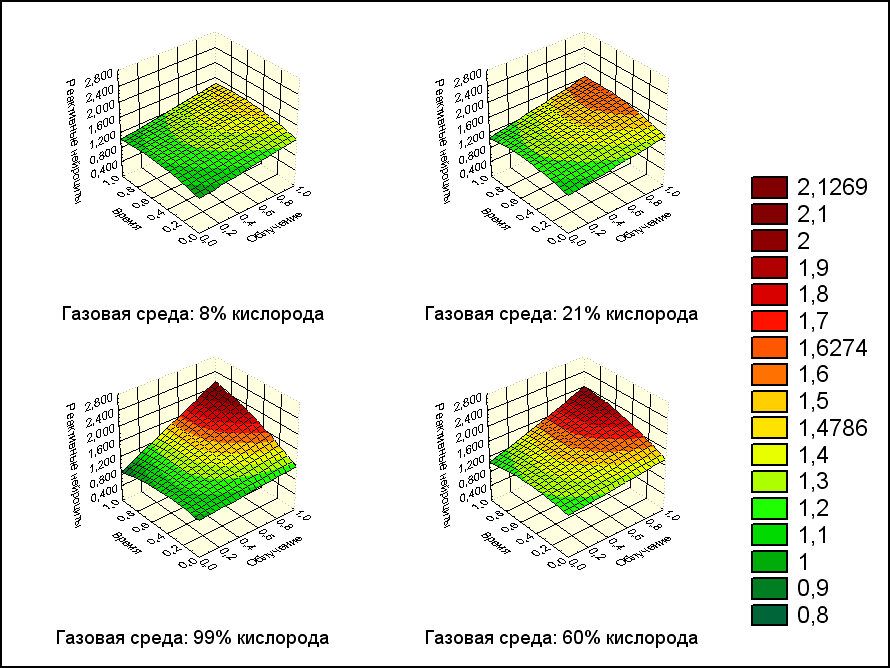
Рис. 3. Зависимость реактивных нейроцитов от дозы облучения и времени после воздействия с фиксированными значениями кислорода
Очевидно, что с увеличением содержания кислорода в среде, повышением дозы облучения и времени после воздействия, количество реактивных клеток будет увеличиваться.
Количество нейроцитов на единице площади (НеП) зависит от содержания кислорода. Результаты математического моделирования свидетельствуют о статистически значимом эффекте воздействия рассматриваемого фактора. Однако, значимость самого параметра в моделировании морфофункционального состояния головного мозга невелика, и коэффициент детерминации составляет R2=0,1177. Уравнение регрессии, описывающее динамику воздействия изучаемых факторов на изменение нейроцитов на единице площади, выглядит следующим образом:
НеП=1,0170–0,5159z+0,4762z2.
Результаты регрессионного анализа зависимости количества глиальных клеток на единице площади (ГеП) от воздействия факторов выявили, что с увеличением дозы облучения и времени после воздействия, количество глиоцитов на единице площади будет повышаться, но их совместное влияние приведет к уменьшению изучаемого показателя. Построенная модель была статистически достоверной, а коэффициент детерминации R2=0,4243. Уравнение регрессии, описывающее динамику воздействия изучаемых факторов на изменение глиоцитов на единице площади, выглядит следующим образом:
ГеП = 0,9405+0,2475x - 0,7312y - 1,11192xy + 0,2169yz + 0,8582y².
Показатель количества сателлитной глии (СГ) достоверно зависел от всех факторов. Очевидно, что с увеличением дозы облучения количество сателлитной глии будет увеличиваться. Повышение содержания кислорода вызывало уменьшение клеток глии. Коэффициент детерминации в построенной модели R2=0,5765. Уравнение регрессии, описывающее динамику воздействия изучаемых факторов на изменение сателлитной глии, выглядит следующим образом:
СГ=1,18358–0,29957x–1,24467z–1,0861xy+0,43146x2+0,30493y2+ +1,11157z2.
Результаты регрессионного анализа для сателлитной глии у измененных нейроцитов (СГиН) установили, что на увеличение клеток сателлитной глии оказывало влияние повышение содержания кислорода в среде и дозы облучения в сочетании со временем после воздействия. Оценка сочетанного действия факторов свидетельствовала об их статистически достоверном (р=1,00Е-19) влиянии. Величина коэффициента детерминации R2=0,6191 подтверждала довольно высокую активность сателлитной глии у измененных нейроцитов в математической модели.
Уравнение регрессии, описывающее динамику воздействия изучаемых факторов на сателлитную глию у измененных нейроцитов, выглядит следующим образом: СГиН=0,9891+5,1584z+4,5728xy–1,1764y2–4,5351z2.
Результаты регрессионного анализа показателя нервно-клеточного индекса (НКИ) в зависимости от воздействующих факторов установили, что на его изменение наибольшее влияние оказывает содержание кислорода, которое уменьшает показатель. Зависимость сочетанного воздействия факторов оказалась незначимой. Коэффициент детерминации участия НКИ в построении математической модели составлял R2=0,4560. Уравнение регрессии выглядит следующим образом: НКИ=1,0569–0,3993x–0,1758у–0,6071z+0,54634z2.
Общее облучение собак.
Зависимость количества нормохромных клеток от действия изучаемых факторов в регрессионном уравнении выглядела следующим образом:
НХ=0,7481–0,0519x+0,1226y+0,0317z–0,1753y2+0,0156z2.
Коэффициент детерминации для построенной модели R2=0,9245. Очевидно, что с увеличением дозы и времени количество нормохромных клеток будет уменьшаться, а повышение содержания кислорода приводит к некоторому их увеличению (рис.4).
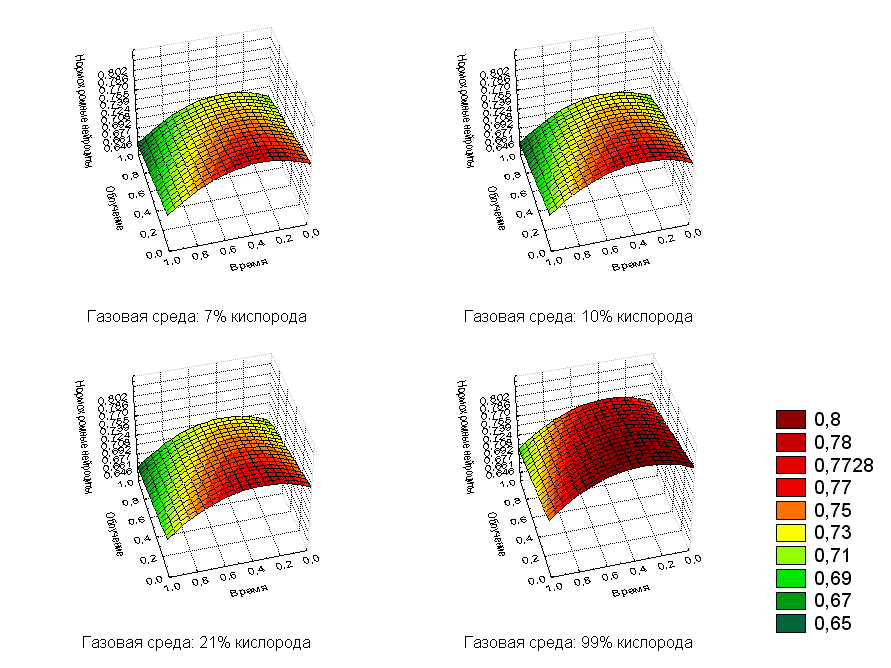
Рис. 4. Регрессионная зависимость нормохромных нейроцитов от дозы облучения и времени после воздействия с фиксированными значениями кислорода
Уравнение регрессии, описывающее динамику воздействия изучаемых факторов на изменение количества реактивных нейроцитов, выглядит следующим образом: РН=0,2563+0,0399x–0,0168y–0,5985z–0,0041y2+0,4975z2.
Анализируя коэффициенты уравнения регрессии, можно заключить, что с увеличением дозы облучения количество реактивных нейроцитов будет возрастать, а увеличение времени после воздействия и содержания кислорода способствовали уменьшению нейроцитов данного типа. Коэффициент детерминации участия реактивных нейроцитов в построении математической модели составил R2=0,8138.
Для деструктивных нейроцитов сенсомоторной коры уравнение регрессии выглядит следующим образом:
ДН=0,1876+0,0117x–0,0968y+0,4528z+0,1598y2–0,4151z2.
Очевидно, что с увеличением дозы облучения и времени после воздействия количество деструктивных нейроцитов будет возрастать. Кислород нелинейно влияет на изучаемый показатель, но, в целом, для каждой из доз кислорода количество деструктивных клеток возрастает с увеличением времени воздействия и дозы облучения (рис.5). Построенная модель была статистически достоверной, а коэффициент детерминации составлял R2=0,7326.
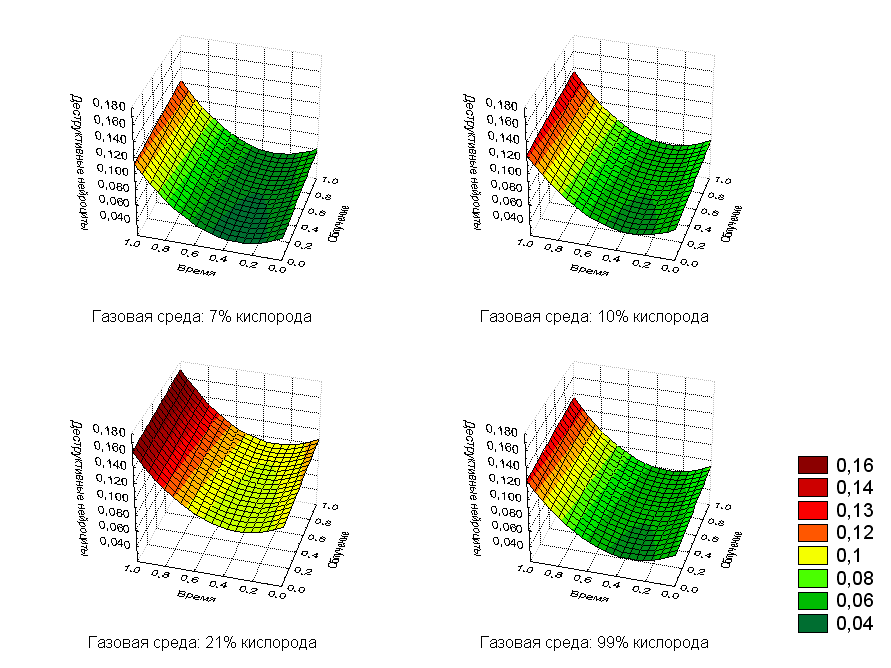
Рис.5. Регрессионная зависимость деструктивных нейроцитов от дозы облучения и времени после воздействия с фиксированными значениями кислорода
Динамика изменений количества глиальных клеток имеет прямую зависимость от содержания кислорода и дозы облучения. Их возрастание приводило к повышению количества глии. Время после воздействия играет существенную роль в уменьшении количества клеток, особенно это заметно при малых дозах облучения. Построенная модель была статистически значимой, и коэффициент детерминации составлял R2=0,6935. Уравнение регрессии, описывающее динамику воздействия изучаемых факторов на изменение количества глиальных клеток, выглядит следующим образом: ГК=0,5979+0,0580x–0,1109y–0,3770z–0,0262y2+0,3596z2.
Количество сателлитной глии увеличивалось пропорционально времени после воздействия. Возрастание дозы облучения снижало количество клеток глии. С повышением содержания кислорода в среде количество клеток глии увеличивалось, но при нахождении в чистом нормобарическом кислороде количество сателлитной глии снижалось. Построенная модель была статистически достоверной, и коэффициент детерминации составлял R2=0,8751.
Для сателлитной глии уравнение регрессии выглядит следующим образом:
СГ=0,4008–0,05837x+0,10049y+0,37098z+0,03751y2–0,3533z2.
При общем облучении клетки Пуркинье отличались выраженным полиморфизмом по сравнению с нейроцитами сенсомоторной коры.
Для нормохромных нейроцитов уравнение регрессии, описывающее динамику воздействия изучаемых факторов, выглядит следующим образом:
НХ=0,6915–0,1136х+0,2301y+0,2875z–0,2518y2–0,3163z².
Построенная модель являлась статистически значимой, и коэффициент детерминации составлял R² =0,8247.
Для реактивных нейроцитов коэффициент детерминации составлял R2=0,9211. Уравнение регрессии, описывающее динамику воздействия изучаемых параметров на количество реактивных нейроцитов, выглядело следующим образом: РH=0,1388+0,0462x–0,0706y+0,2337z+0,1082y2–0,1893z2.
Для деструктивных нейроцитов уравнение регрессии, описывающее динамику воздействия изучаемых факторов, выглядит следующим образом:
ДН=0,0877+0,0451х–0,0951y–0,277z+0,1003y2+0,2885z2 .
Построенная модель являлась статистически значимой, и коэффициент детерминации составлял R² =0,8358.
Из результатов регрессионного анализа следует, что при увеличении дозы, времени и содержания кислорода количество нервных клеток, не имеющих изменений – нормохромные (рис.6), будет уменьшаться, а количество нейроцитов с реактивными и деструктивными изменениями возрастать.
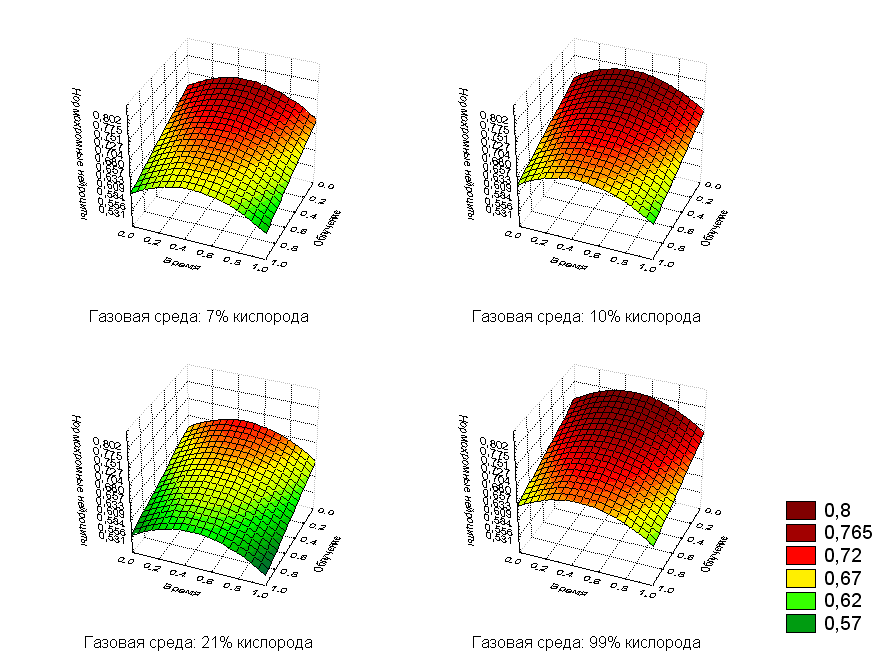
Рис.6. Регрессионная зависимость нормохромных нейроцитов от дозы облучения и времени после воздействия с фиксированными значениями кислорода
Облучение головы собак.
Количество нормохромных нейроцитов уменьшалось при изолированном и при совместном действии изучаемых факторов. Величина коэффициента детерминации составляла R2=0,6714. Уравнение регрессии для нормохромных нейроцитов выглядит следующим образом:
НХ=0,6867 - 0,1116x - 0,2647y+0,3525z+0,3832yz+0,1272x2+0,117y² - 0,2947z²--0,2862xyz.
Динамика изменений реактивных клеток прямо зависела от увеличения дозы облучения, времени после воздействия и совместного влияния факторов. Повышение содержания кислорода уменьшало количество клеток. Коэффициент детерминации составлял R2=0,8913. Уравнение регрессии для реактивных нейроцитов выглядит следующим образом:
РН=0,2014+0,1018x+0,2353y-0,2179z-0,1817yz-0,1394x²-0,1527y2+0,1811z2+ +0,1047xyz
Количество деструктивных нейроцитов увеличивалось с повышением дозы облучения и времени после воздействия. Особенно эта тенденция заметна при увеличении содержания кислорода (рис.7). Коэффициент детерминации для построенной модели составлял R2=0,8838.
Уравнение регрессии, описывающее динамику воздействия изучаемых параметров на деструктивные нейроциты, выглядит следующим образом:
ДН=0,1204+0,0149х+0,0351у-0,1606z-0,360yz-0,0061x2+0,0449y²+0,1383z²+ +0,3637xyz
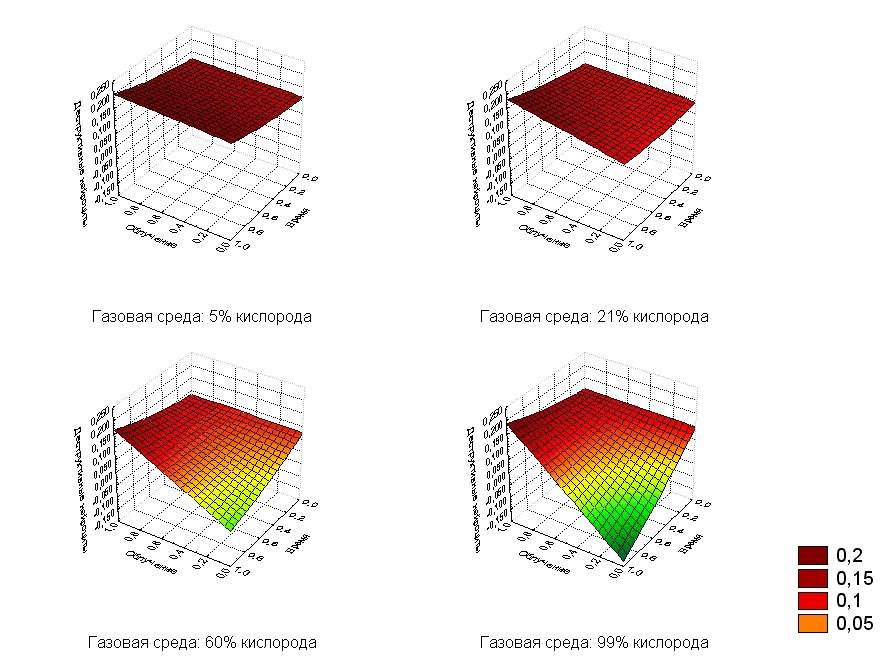
Рис.7. Регрессионная зависимость деструктивных нейроцитов от дозы облучения и времени после воздействия с фиксированными значениями кислорода
Динамика глиальных клеток имела статистически значимую зависимость от воздействия всех факторов. Очевидно, что с повышением дозы облучения и содержания кислорода, а также при совместном действии факторов, количество клеток глии уменьшалось. Коэффициент детерминации в построенной модели составлял R2=0,8325.
Уравнение регрессии, динамики воздействия изучаемых факторов на изменение количества глиальных клеток, выглядит следующим образом:
ГК=0,6045+0,0461x+0,0743y-0,4644z-0,1984yz-0,1292х2+0,0437y2+0,4253z²-
-0,0126xyz.
Повышение дозы облучения и содержания кислорода будут увеличивать количество клеток сателлитной глии. Построенная модель являлась статистически значимой, и коэффициент детерминации составлял R2=0,9181.
Для сателлитной глии уравнение регрессии выглядит следующим образом:
СГ=0,3956–0,0461x–0,1057y+0,4564z+0,2774yz+0,2111x²–0,0281y2–0,4204z2-
-0,0671xyz.
При облучении головы собак уравнения регрессии, описывающие динамику воздействия изучаемых факторов на клетки Пуркинье мозжечка, выглядят следующим образом:
НХ=0,6781–0,2147х+0,0246у+0,1279z+0,0986x2–0,1234y2–0,1055z2-
-0,6192xyz.
Для построенной модели коэффициент детерминации R2=0,8474
PH=0,1669+0,1245x–0,0242y+0,1582z–0,0675x2+0,4268y2-0,1403z2+ +0,1516xyz.
Для построенной модели коэффициент детерминации R2=0,7658.
ДН=0,1066+0,0466x+0,0174y–0,2783z+0,0114х2+0,0544y2+0,2704z2+ +0,2405xyz
Для построенной модели коэффициент детерминации R2=0,9246.
Графическая зависимость действия изучаемых факторов на количество деструктивных нейроцитов представлена на рис.8.
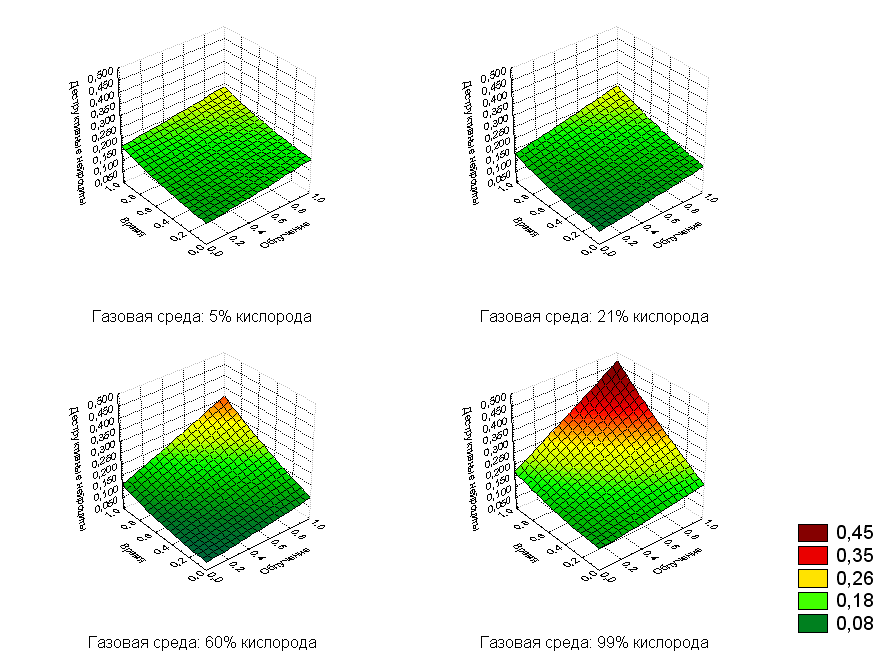
Рис.8. Регрессионная зависимость деструктивных нейроцитов от дозы облучения и времени после воздействия с фиксированными значениями кислорода
Из результатов регрессионного анализа следует, что между количеством измененных (реактивных и деструктивных) нейроцитов и действующими факторами существует прямая зависимость: при увеличении параметров каждого фактора и при их совместном действии возрастает количество как реактивных, так и деструктивных нервных клеток. Для нормохромных нейроцитов обратная зависимость. Кроме того, при увеличении дозы кислорода уменьшение количества нормохромных нейроцитов особенно заметно при больших дозах облучения и времени.
Математическое моделирование многоуровневых и разнонаправленных сочетаний факторов на морфологические показатели головного мозга.
Для оценки влияния многоуровневого и разнонаправленного сочетания факторов на состояние нервных и глиальных клеток сенсомоторной коры использован однофакторный дисперсионный анализ, основой которого является разделение дисперсии на части, обусловленные влиянием контролируемых факторов, и остаточную дисперсию, объясняемую неконтролируемыми факторами или случайными событиями. Обозначим группы: а1 – гамма-облучение в воздухе; а2 – гамма-облучение в ГГС; а3 – гамма-облучение в кислороде; а4 – ГГС, затем гамма-облучение в воздухе; а5 – кислород, затем гамма-облучение в воздухе; а6 – гамма-облучение, затем ГГС; а7 – гамма-облучение, затем кислород; а8 – ГГС, затем гамма-облучение в ГГС, затем снова ГГС; а9 – кислород, затем гамма-облучение в кислороде, затем снова кислород; а10 – без воздействий.
Таблица 3
Зависимость показателя нервно-клеточного индекса от параметров воздействия
| Фактор | Оценка коэффициента | Критерий Стьюдента 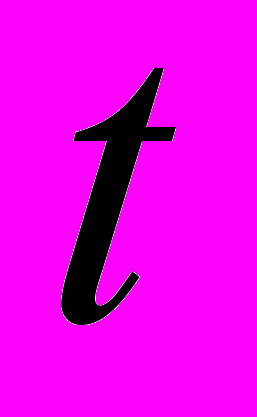 | Коэффициент достоверности 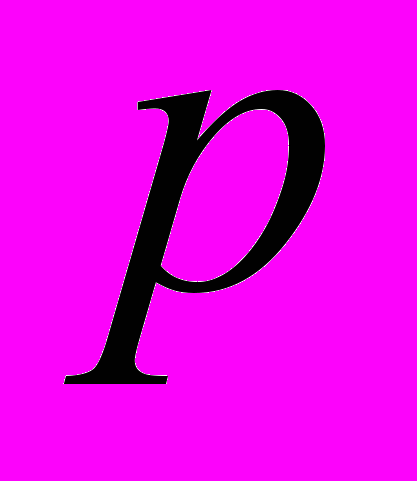 | Сила влияния фактора (диагностическая значимость) 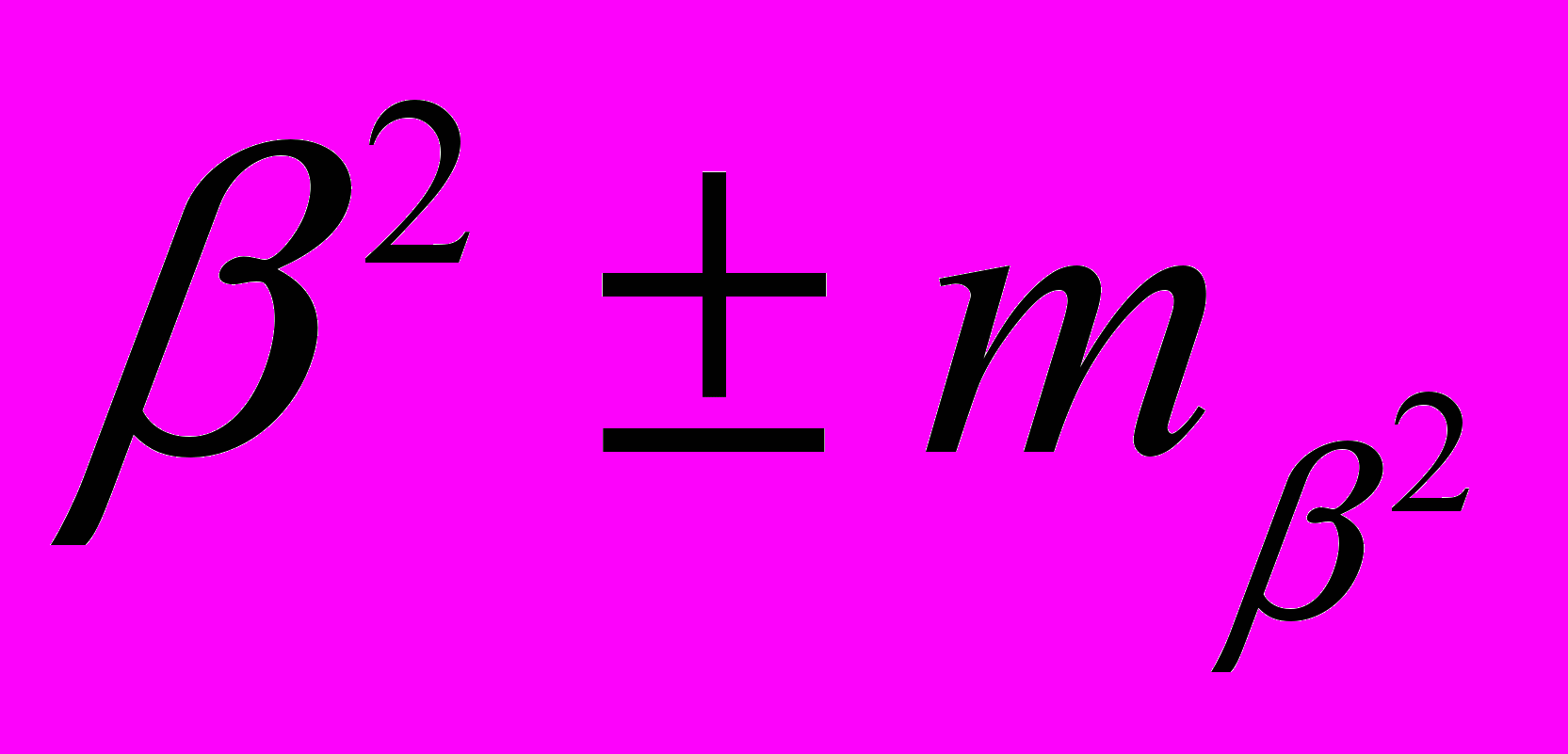 |
| Константа | 0,8527 | 138,41 | <1,00E-19 | |
| а1 | -0,0217 | -1,175 | 0,25 | 0,127±0,077 |
| а2 | 0,0613 | 3,316 | 1,95E-3 | 0,358±0,056 |
| а3 | -0,0349 | -1,889 | 0,07 | 0,204±0,070 |
| а4 | 0,0394 | 2,136 | 0,04 | 0,231±0,068 |
| а5 | -0,0667 | -3,609 | 8,43E-4 | 0,390±0,054 |
| а6 | 0,0135 | 0,7185 | 0,48 | 0,077±0,081 |
| а7 | -0,0495 | -2,679 | 0,01 | 0,290±0,063 |
| а8 | -0,0027 | -0,147 | 0,88 | 0,015±0,087 |
| а9 | -0,0857 | -4,638 | 3,72E-5 | 0,502±0,044 |
Из табл. 3 очевидно, что на снижение показателя нервно-клеточного индекса максимально влияет кислород с облучением в различных комбинациях (а9).
Воздействие кислорода до (а5) и после (а7) облучения вызывало аналогичный эффект, но сила влияния этих параметров была незначительной. Показатель увеличивался при облучении в ГГС (а2) и применении ГГС до облучения (а4), но коэффициент диагностической значимости оказался невысоким. Из табл. 4 следует, что построенная модель статистически достоверна при коэффициенте детерминации R2=0,7396.
Таблица 4
Оценка влияния смены факторов воздействия на нервно-клеточный индекс
| Пара-метр | Коэффи-циент корреля-ции  | Коэффи-циент детермина-ции 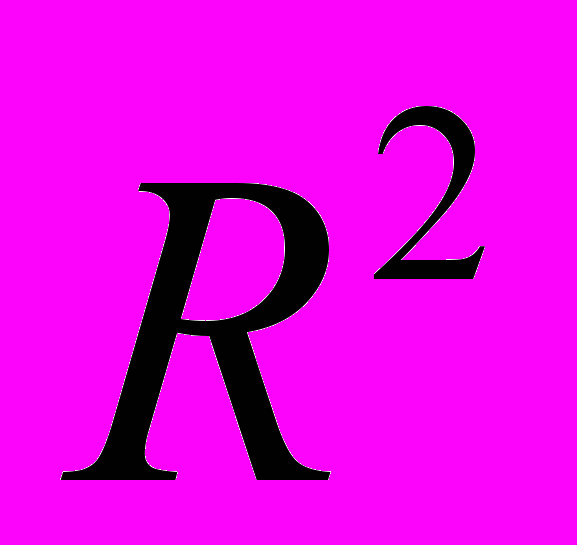 | Сумма квадратов отклоне-ний | Степе-ни свобо-ды | Средние квадраты отклоне-ний | 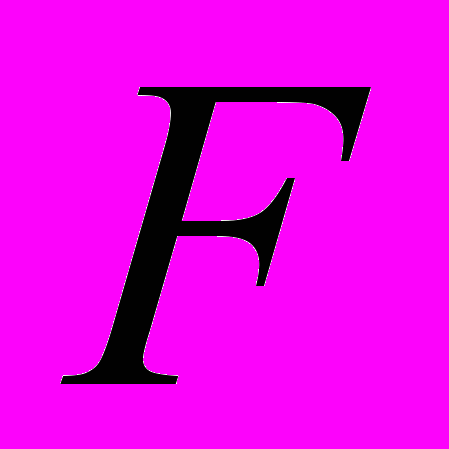 -статистика -статистика | Коэффициент достоверности 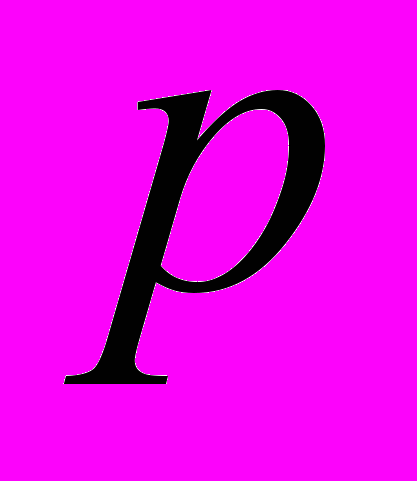 |
| Мо-дель | 0,8601 | 0,7397 | 0,2157 | 9 | 0,0239 | 12,626 | 3,37E-9 |
| Оста-ток | | | 0,0759 | 40 | 0,0019 | | |
На показатель нервно-клеточного индекса влияет количество нейроцитов на площади и их состояние (нормохромные, реактивные, деструктивные). Так, на увеличение количества клеток с реактивными изменениями оказывает воздействие кислород (а9), а также его влияние до (а5) и после (а7) облучения. Модель сочетанного действия факторов имеет высокий уровень значимости (р=1,07Е-12) и информативности (R2=0,8292). Сила влияния (а9) на деструктивные клетки оказалась наибольшей, что приводило к увеличению их количества. Аналогичный эффект оказывало воздействие кислорода до (а5) и после облучения (а7), также как и действие одного облучения. Вместе с тем, применение ГГС до (а4) или после (а6) облучения способствует уменьшению количества деструктивных нейроцитов, но диагностическая значимость их коэффициентов была невысокой. В свою очередь, величина коэффициента детерминации (R2=0,9175) указывает на довольно высокую степень участия изучаемого показателя в морфофункциональной организации головного мозга в условиях различных сочетаний гамма-облучения в пороговых дозах с измененной газовой средой.
Снижению кариометрических показателей способствует применение ГГС до (а4) и после (а6) облучения (коэффициент диагностической значимости β²=0,54±0,04 и β²=0,43±0,05 соответственно). Такой же эффект вызывало и применение кислорода в аналогичных сочетаниях (а5) и (а7), но диагностическая значимость этих воздействий была незначительной. Построенная модель являлась статистически значимой (р=2,91Е-13), и коэффициент детерминации составлял R2=0,8403.
Количество нейроцитов на единице площади достоверно зависело от двух факторов а5 и а6, причем в противоположных направлениях. Построенная модель статистически достоверна (р=5,6Е-3), но коэффициент детерминации оказался невысоким (R2=0,4161), что может свидетельствовать о незначительной роли изучаемого показателя в моделировании морфофункционального состояния головного мозга. На количество глиальных клеток статистически значимое влияние оказывают факторы а1, а3, а4, а5, а7, причем сила влияния факторов максимальна. Построенная модель статистически значима (р=1,17Е-10), а диагностическая значимость самого показателя в моделировании радиоцеребральных эффектов измененной газовой средой весьма существенна при коэффициенте детерминации R2=0,7819. Сателлитную глию существенно уменьшает влияние а4 (β²=0,573±0,037) и а7. Наибольший эффект увеличения сателлитной глии получен при воздействии а3 (β²=0,515±0,043) и а5 (β²=0,453±0,048) и незначительный в а4, а8. Оценка влияния смены факторов имеет достаточный уровень значимости, при коэффициенте детерминации (R2=0,6028), что указывает на диагностическую значимость показателя количества сателлитной глии в построении математической модели. Количество сателлитной глии измененных нейроцитов существенно увеличивало воздействие факторов а1 (β²=0,627±0,033) и а9 (β²=0,702±0,026). Аналогичный эффект получен в а7 и а8, но коэффициент диагностической значимости этих воздействий был невысоким. Применение кислорода до облучения (а5) значительно уменьшало количество сателлитной глии у измененных нервных клеток. Также действовали факторы а2, а4, и а6, но сила их влияния была незначительной. В тоже время, данный показатель в построенной модели имеет высокий уровень значимости: достоверность модели составляет менее 1,0·10-19 при коэффициенте детерминации R2=0,9536.
Для сравнения влияния всех факторов на морфологические показатели по построенным моделям составлена графическая зависимость (рис. 9).
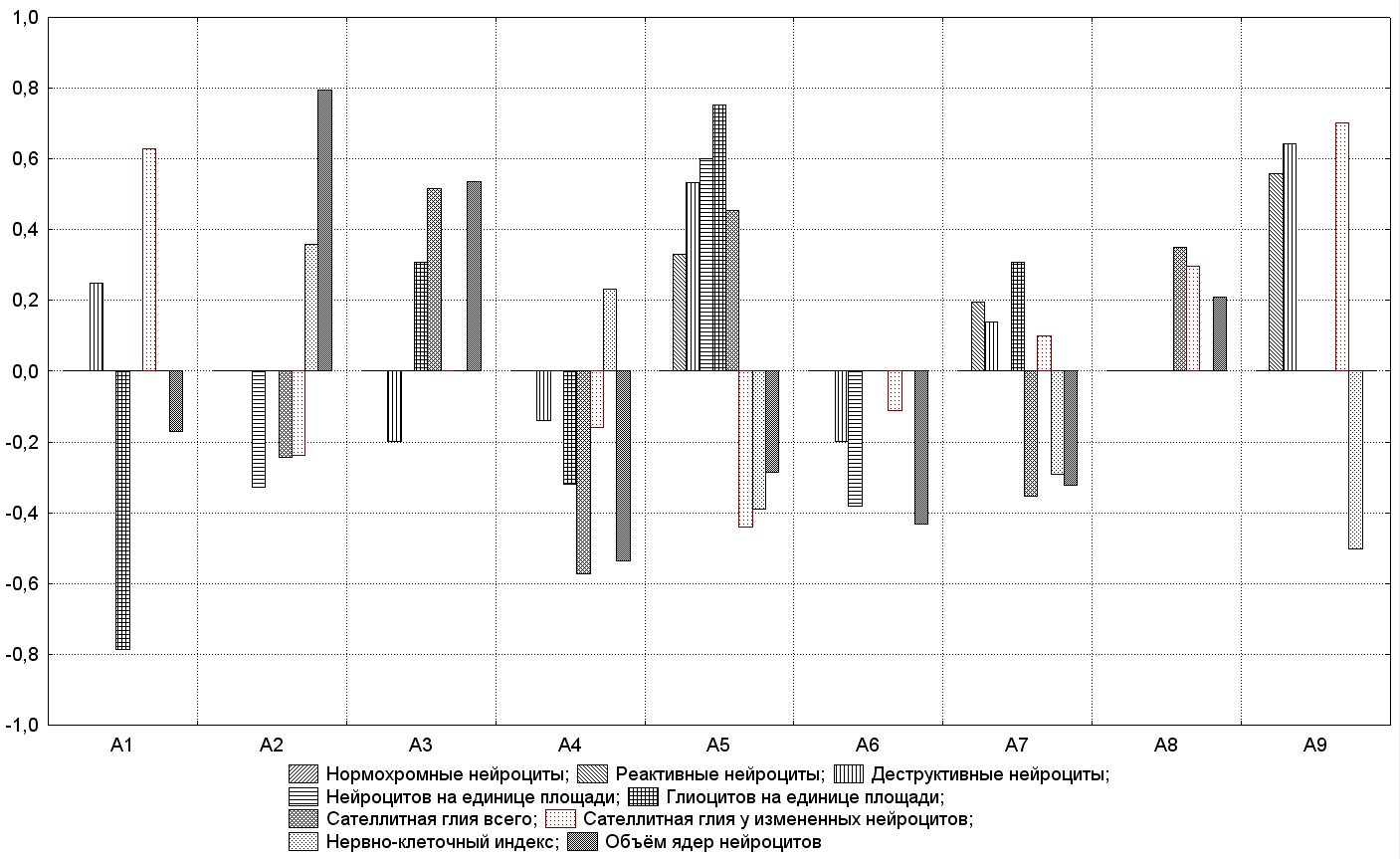
Рис. 9. Зависимость морфологических показателей от воздействия облучения и измененной газовой среды в различных сочетаниях
Математическое моделирование радиоцеребральных эффектов динамическими факторами полета и микроволнами.
В качестве инструментального метода сравнения использован однофакторный дисперсионный анализ. Изучалось влияние следующих сочетанных воздействий: вибрация – облучение, облучение – вибрация, перегрузка – облучение, облучение – перегрузка, ЭМИ – облучение, облучение – ЭМИ.
Вибрация.
Изменения деструктивных нервных клеток представлены в табл. 5.
Очевидно, что сила влияния вибрации после облучения на увеличение деструктивных клеток была максимальной. Облучение и применение вибрации до облучения вызывали аналогичный эффект, но диагностическая значимость этих показателей существенно ниже. Вместе с тем, вибрация, примененная в отдельности, уменьшала количество деструктивных нейроцитов.
Таблица 5
Зависимость деструктивных нейроцитов от параметров воздействия
| Фактор | Оценка коэффициента | Критерий Стьюдента 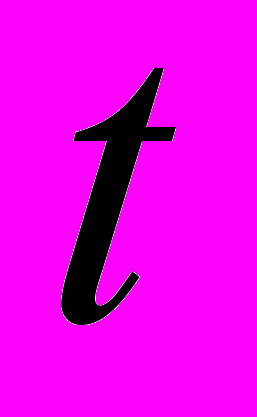 | Коэффициент достоверности 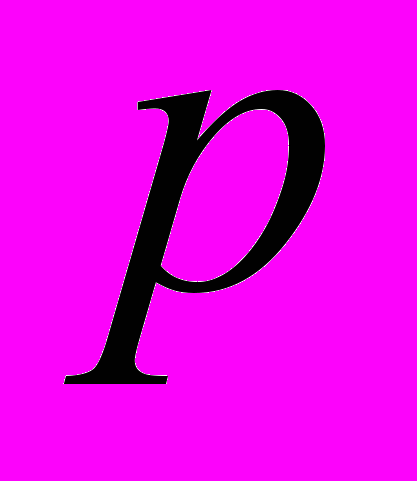 | Сила влияния фактора (диагностическая значимость) β2±mβ2 |
| Константа | 1,6017 | 238,8974 | <1,00Е-19 | |
| Вибрация | -0,4694 | -35,0018 | <1,00Е-19 | 0,659±0,068 |
| Облучение | 0,3492 | 26,0440 | 1,11E-16 | 0,490±0,101 |
| Вибрация + Облучение | 0,2138 | 15,9468 | 7,74E-13 | 0,300±0,139 |
| Облучение + Вибрация | 0,50804 | 37,8863 | <1,00Е-19 | 0,713±0,057 |
Построенная модель статистически значима, а величина коэффициента детерминации (R2=0,9956) подтверждает высокую активность деструктивных нейроцитов в математической модели (табл.6).
Таблица 6
Оценка влияния смены факторов воздействия на деструктивные нейроциты
| Параметр | Коэффи-циент корреля-ции  | Коэффи-циент детермина-ции 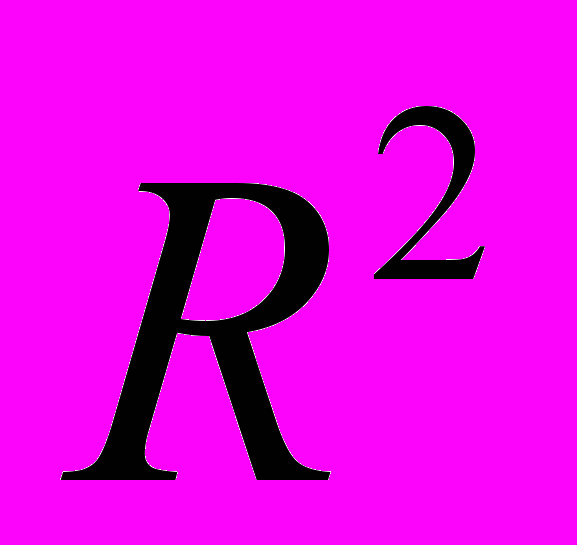 | Сумма квадра-тов отклоне-ний | Степе-ни свобо-ды | Средние квадра-ты отклоне-ний | 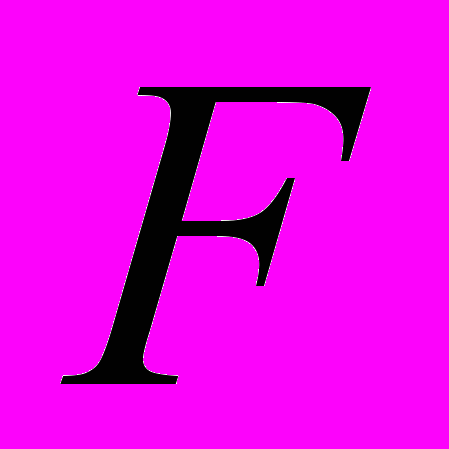 -статисти-ка -статисти-ка | Коэффициент достоверности 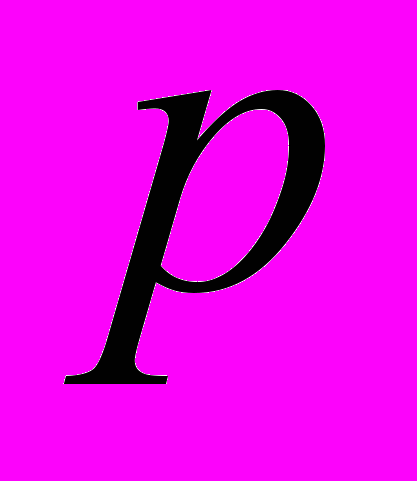 |
| Модель | 0,9978 | 0,9956 | 5,0411 | 4 | 1,2602 | 1121,38 | <1,0Е-19 |
| Остаток | | | 0,0225 | 20 | 0,0011 | | |
Аналогичные таблицы строились и для других показателей с расчетом соответствующих коэффициентов. Так, для реактивных нейроцитов модель статистически значима, а коэффициент детерминации составлял R²=0,87742. Существенное увеличение количества реактивных клеток вызывало действие вибрации после облучения (β2=0,888±0,022). Этот же параметр вызывал значительное уменьшение количества нормохромных клеток. Вибрация и облучение с последующим действием вибрации приводили к уменьшению объема ядер нейроцитов. Облучение и применение вибрации до облучения вызывали увеличение кариометрических показателей. Следует отметить, что эффект воздействия изучаемых параметров на объем ядер довольно высокий: уровень значимости р=2,22·10-16 при коэффициенте детерминации R²=0,9787. Для оценки влияния факторов на морфологические показатели по полученным моделям была построена их графическая зависимость (рис.10).
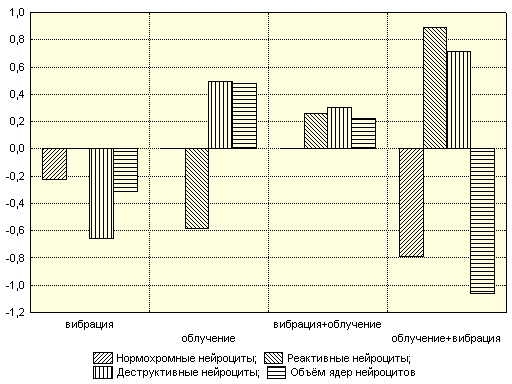
Рис. 10. Зависимость морфологических показателей от воздействия вибрации и облучения в различных комбинациях
Очевидно, что облучение с последующей вибрацией значительно моделирует радиоцеребральные эффекты, утяжеляя по всем показателям.
Перегрузка, как предшествующая, так и следующая за облучением, увеличивает количество реактивных клеток (табл.7).
Таблица 7
Зависимость реактивных нейроцитов от параметров воздействия
| Фактор | Оценка коэффициента | Критерий Стьюдента 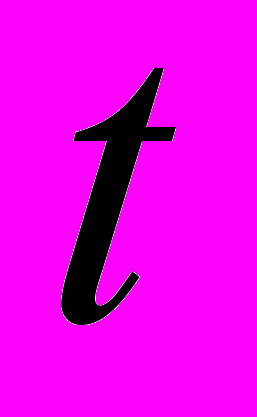 | Коэффициент достоверности 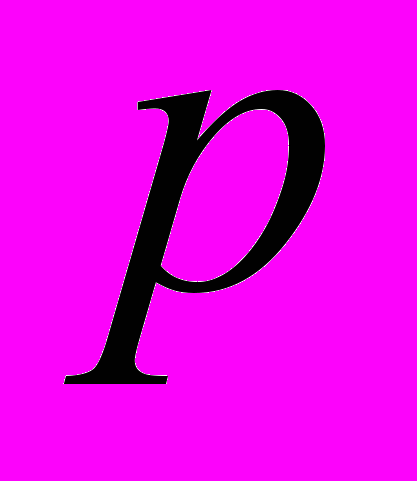 | Сила влияния фактора (диагностическая значимость) 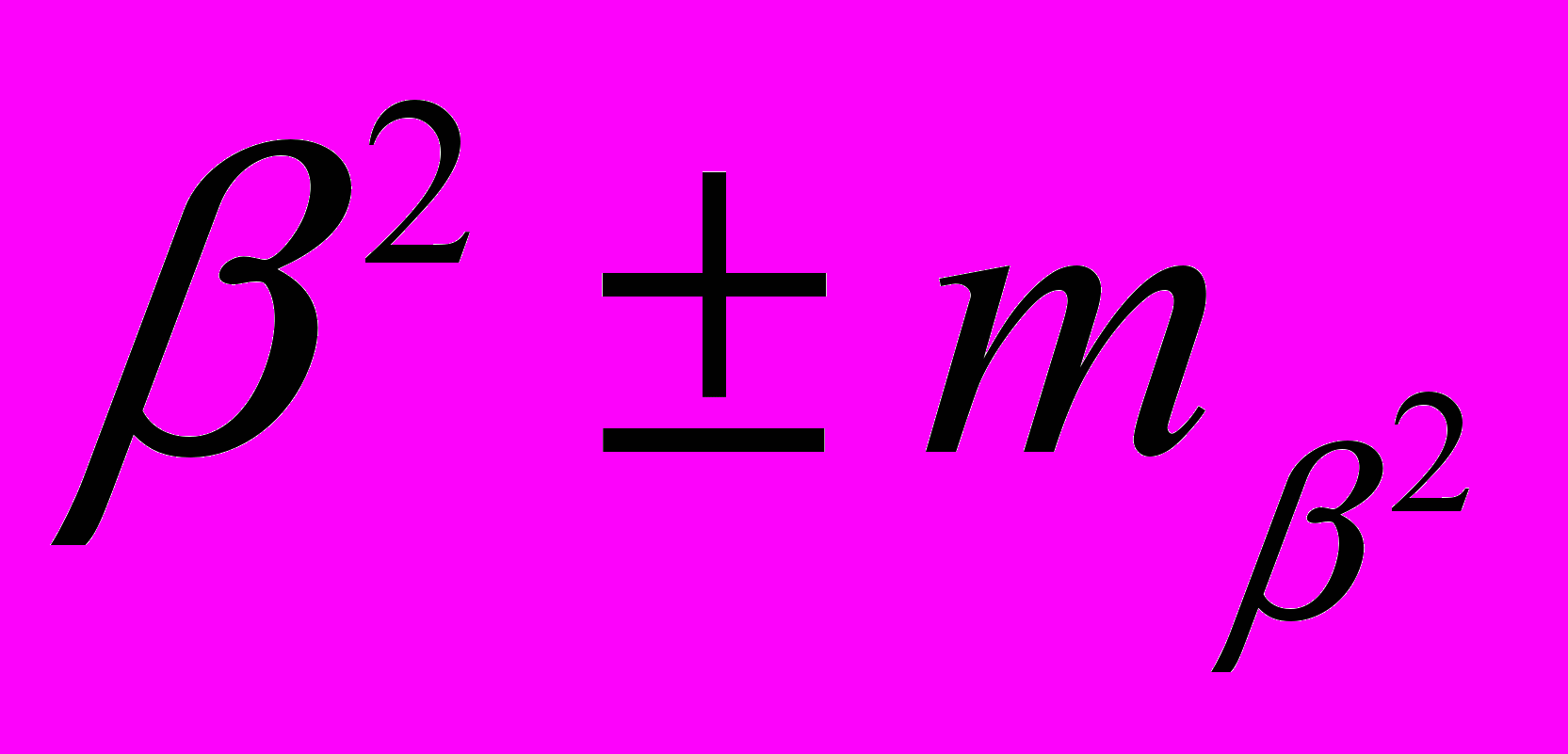 |
| Константа | 1,1222 | 218,2988 | <1,00E-19 | |
| Перегрузка | -0,0380 | -3,6960 | 1,43E-3 | 0,245±0,156 |
| Облучение | -0,0984 | -9,5708 | 6,58E-9 | 0,557±0,088 |
| Перегрузка + Облучение | 0,1240 | 12,0607 | 1,24E-10 | 0,703±0,059 |
| Облучение + Перегрузка | 0,1346 | 13,0917 | 2,88E-11 | 0,763±0,047 |
Сила влияния этих факторов существенна, β2=0,703±0,059 и β2=0,763±0,047 соответственно. Облучение головы приводило к уменьшению показателя, а воздействие перегрузкой, хотя и снижало показатель, но сила влияния незначительна.
Построенная модель статистически достоверна, а коэффициент детерминации составлял R²=0,9575.
Количество деструктивных клеток облучение с предшествующей или последующей перегрузкой увеличивало, причем последующее воздействие с наибольшим эффектом (β2=0,693±0,061). Построенная модель статистически достоверна, и коэффициент детерминации составлял R²=0,9968.
При действии перегрузки на облученный организм количество нормохромных нейроцитов будет заметно уменьшаться, и сила влияния этого фактора весьма существенна (β2=0,706±0,058). Модель статистически значима при R²=0,616.
Продольная перегрузка увеличивала объем ядер, а облучение вызывало противоположный эффект. Облучение с предшествующей или последующей перегрузкой моделировало кариометрические показатели, но сила влияния этих факторов оказалась незначительной. Построенная модель для ядер нейроцитов статистически достоверна, и коэффициент детерминации составлял R²=0,9194.
По полученным моделям построена графическая зависимость, представленная на рис.11.
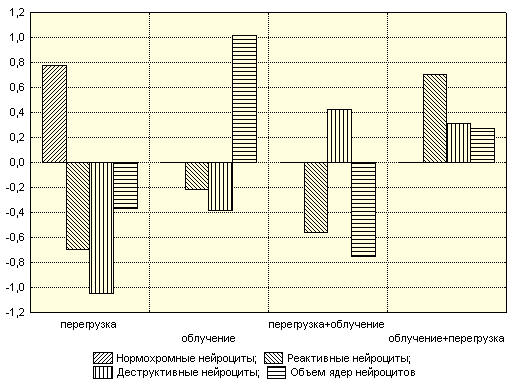
Рис. 11. Зависимость морфологических показателей от воздействия перегрузки и облучения в различных комбинациях
Электромагнитное излучение
Гамма-облучение и облучение с последующим действием ЭМИ значительно уменьшают количество нормохромных клеток (табл. 8).
Таблица 8
Зависимость нормохромных нейроцитов от параметров воздействия
| Фактор | Оценка коэффициента | Критерий Стьюдента 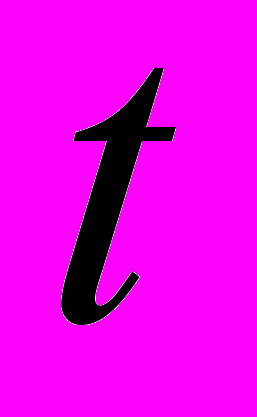 | Коэффициент достоверности 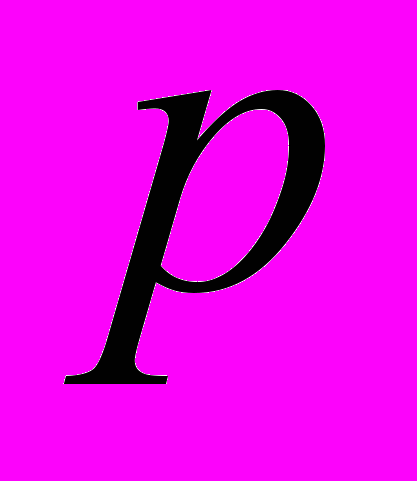 | Сила влияния фактора (диагностическая значимость) 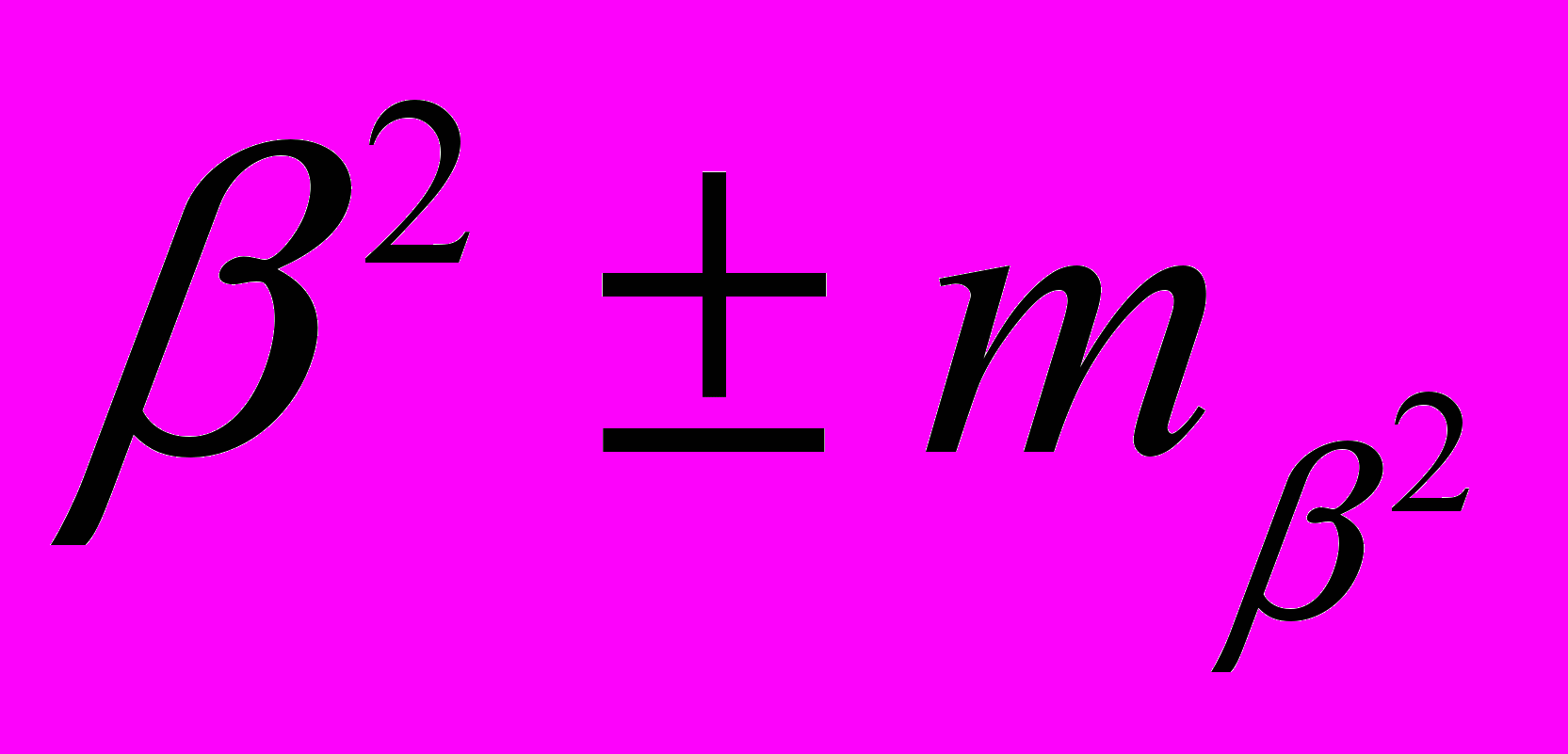 |
| Константа | 0,9709 | 238,457 | <1,00E-19 | |
| ЭМИ | 0,0222 | 2,7309 | 0,01 | 0,438±0,112 |
| Облучение | -0,0229 | -2,8194 | 0,01 | 0,452±0,109 |
| ЭМИ + Облучение | 0,0106 | 1,3065 | 0,21 | 0,259±0,158 |
| Облучение + ЭМИ | -0,0389 | -4,7841 | 1,13E-4 | 0,767±0,046 |
Модель статистически значима, а степень участия параметров довольно высокая (R²=0,6783). Количество реактивных клеток увеличивалось после облучения с последующим действием ЭМИ (β2=0,878±0,024). Модель статистически значима при R²=0,8833. Облучение головы увеличивало количество деструктивных нейроцитов, а воздействие ЭМИ после облучения значительно увеличивало этот показатель (β2=0,802±0,039). Само ЭМИ, а также его действие до гамма-облучения уменьшало количество нервных клеток с деструктивными изменениями, но сила влияния этих воздействий незначительна. Гамма-облучение снижало кариометрические показатели, а ЭМИ оказывало противоположный эффект. Построенная модель статистически достоверна при коэффициенте детерминации R²=0,9680.
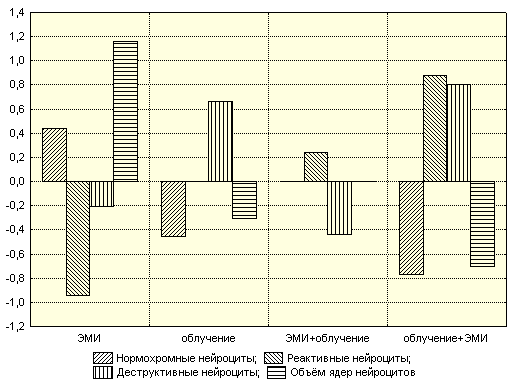
Рис. 12. Зависимость морфологических показателей от воздействия ЭМИ и облучения в различных комбинациях
