Р ахштадт Ю. А
| Вид материала | Документы |
СодержаниеВторое начало Системы макроскопические Система термодинамическая Теплоемкость тела Т и ускорение свободного падения g |

Р
ахштадт Ю.А.
ГЛОССАРИЙ
К УЧЕБНОЙ ОБЩЕУНИВЕРСИТЕТСКОЙ ДИСЦИПЛИНе
ФИЗИКА
ПОНЯТИЯ, определения, формулы, уравнения
РАЗДЕЛ 2. молекулярная физика
РАЗДЕЛ 2. молекулярная физика | ||
Понятие | Определение, формула, уравнение | См. в Конспекте лекций (семестр 2) |
Абсолютный нуль | См. Нуль абсолютный | 4.3 |
| Адиабата | График адиабатического процесса в координатах P-V. | 4.4 |
| Вероятность термодинамическая | Термодинамическая вероятность состояния системы  – число способов, которыми может быть реализовано данное состояние макросистемы (число микросостояний, осуществляющих данное макросостояние, или статистический вес данного макросостояния). – число способов, которыми может быть реализовано данное состояние макросистемы (число микросостояний, осуществляющих данное макросостояние, или статистический вес данного макросостояния). | 4.5 |
| Вес статистический | См. Вероятность термодинамическая | |
| Время свободного пробега среднее | Среднее время свободного пробега время между двумя последовательными столкновениями; зависит от средней скорости v молекул и средней длины свободного пробега 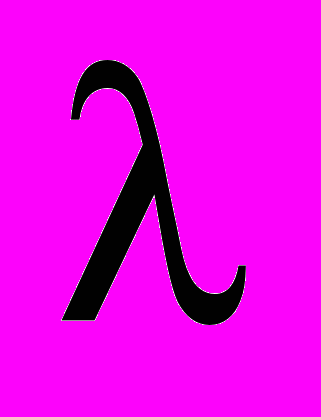 : :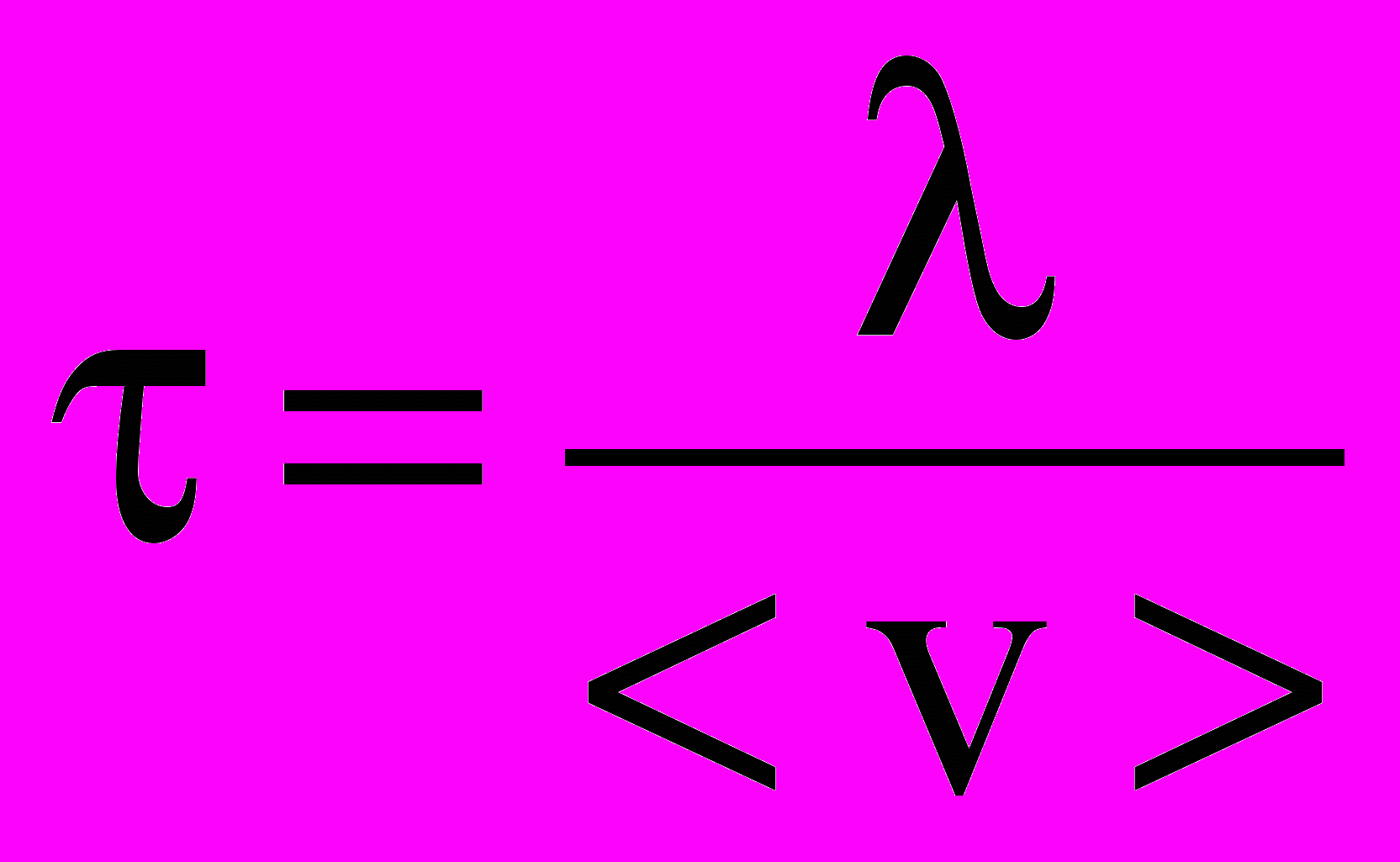 . . | 4.1 |
| Газ идеальный | Если в газе средняя потенциальная энергия взаимодействия молекул значительно меньше их средней кинетической энергии, то такой газ называется идеальным. Реальный газ близок по своим свойствам к идеальному при достаточном разрежении. | 4.1 4.2 |
| Давление |
и среднему значению кинетической энергии поступательного движения молекулы газа. | 4.1 |
| Двигатель тепловой | Устройство, преобразующее энергию сгорающего топлива в полезную работу, приводя в движение какой-либо механизм. | 4.5 |
| Длина свободного пробега средняя | Средняя длина свободного пробега – среднее расстояние, пробегаемое молекулой газа между двумя последовательными столкновениями, определяется формулой: 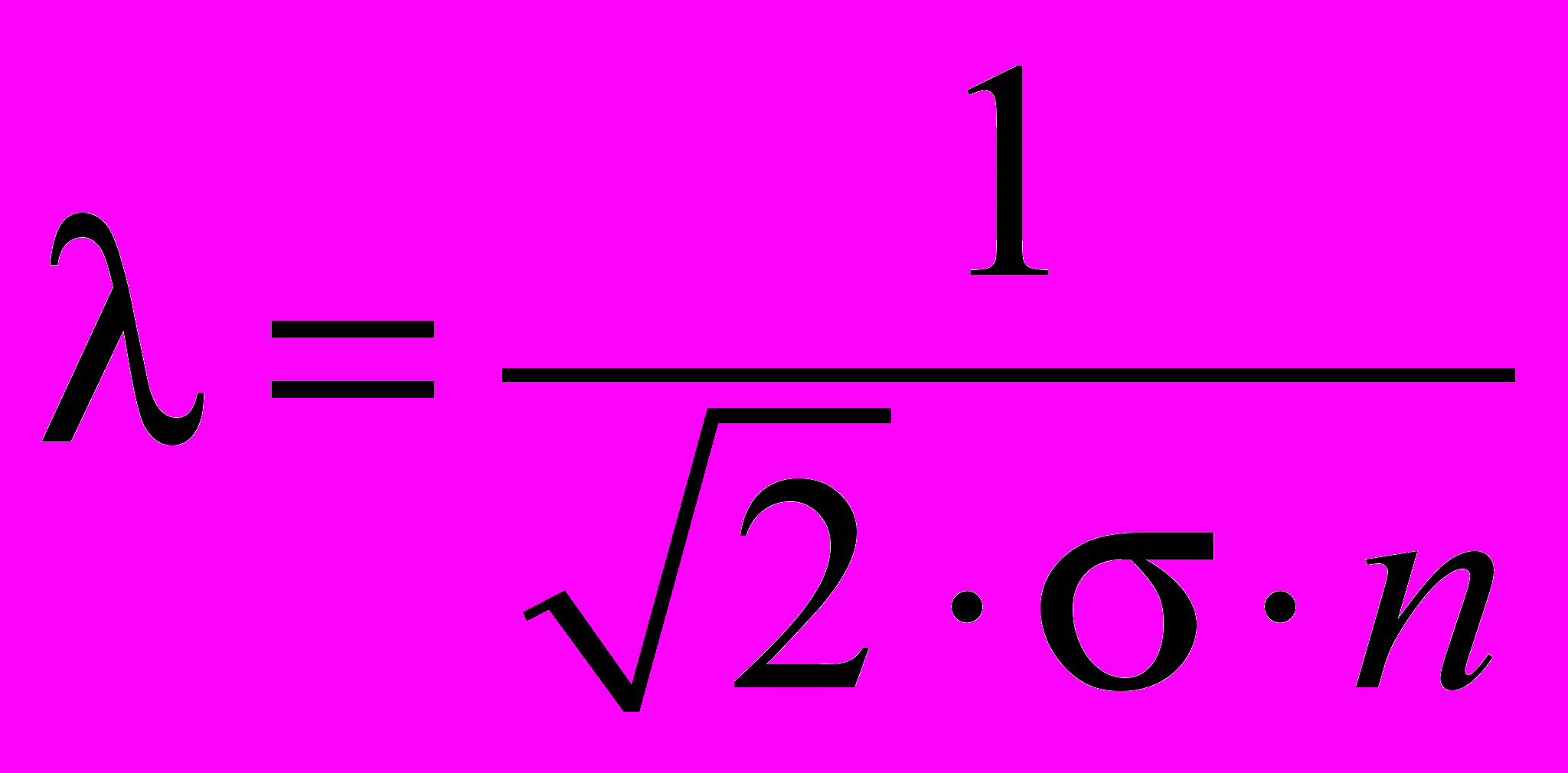 , ,где σ- площадь эффективного поперечного сечения соударения молекул, n- концентрация молекул. | 4.1 |
| Закон возрастания энтропии (неравенство Клаузиуса) | Энтропия изолированной системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов): 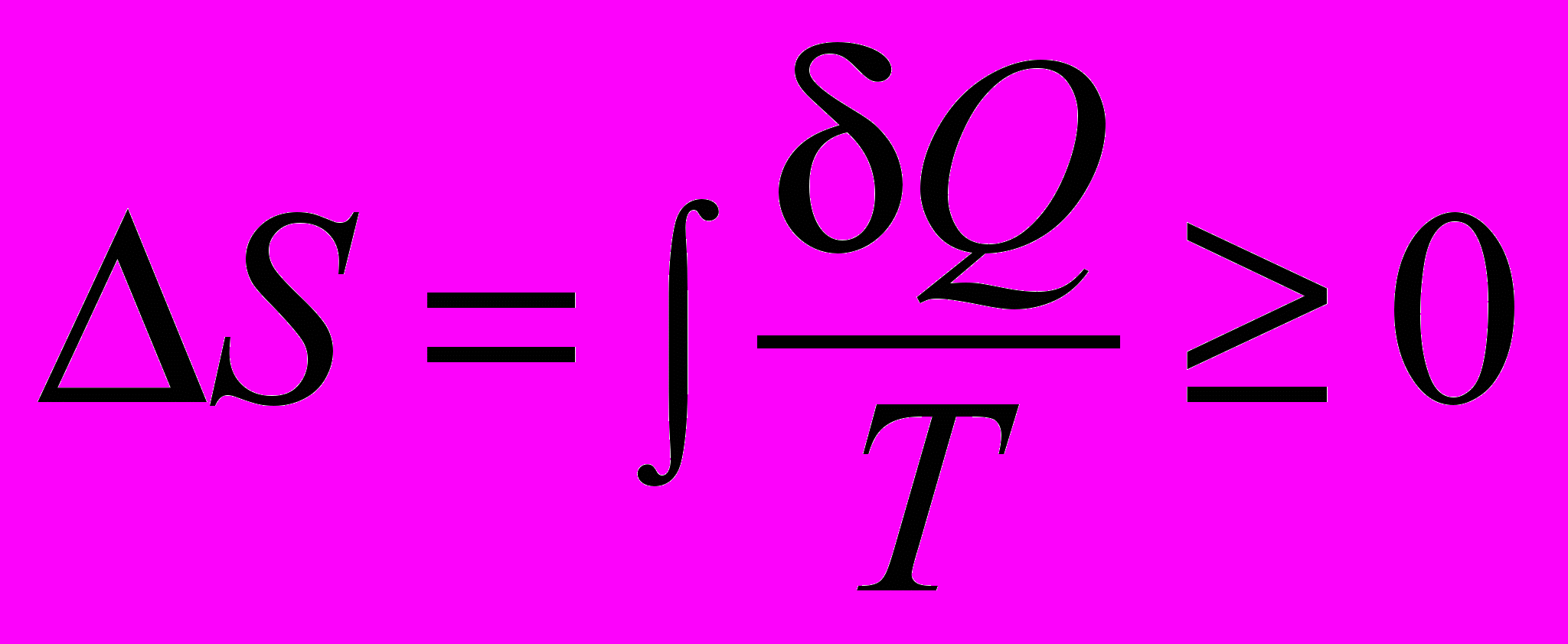 . . | 4.5 |
| Закон Бойля-Мариотта для изотермического процесса | 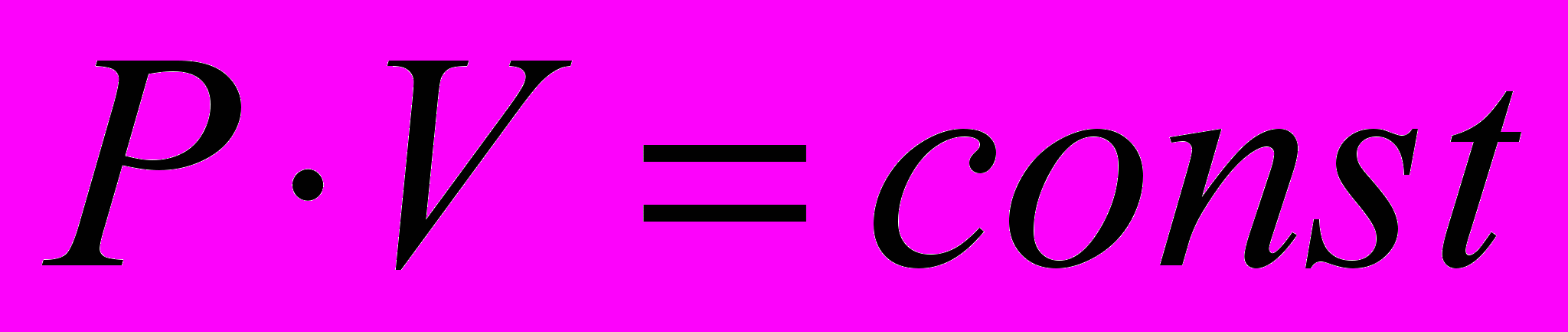 , ,если количество вещества и температура T постоянны. | 4.4 |
| Закон Гей-Люссака для изобарического процесса | 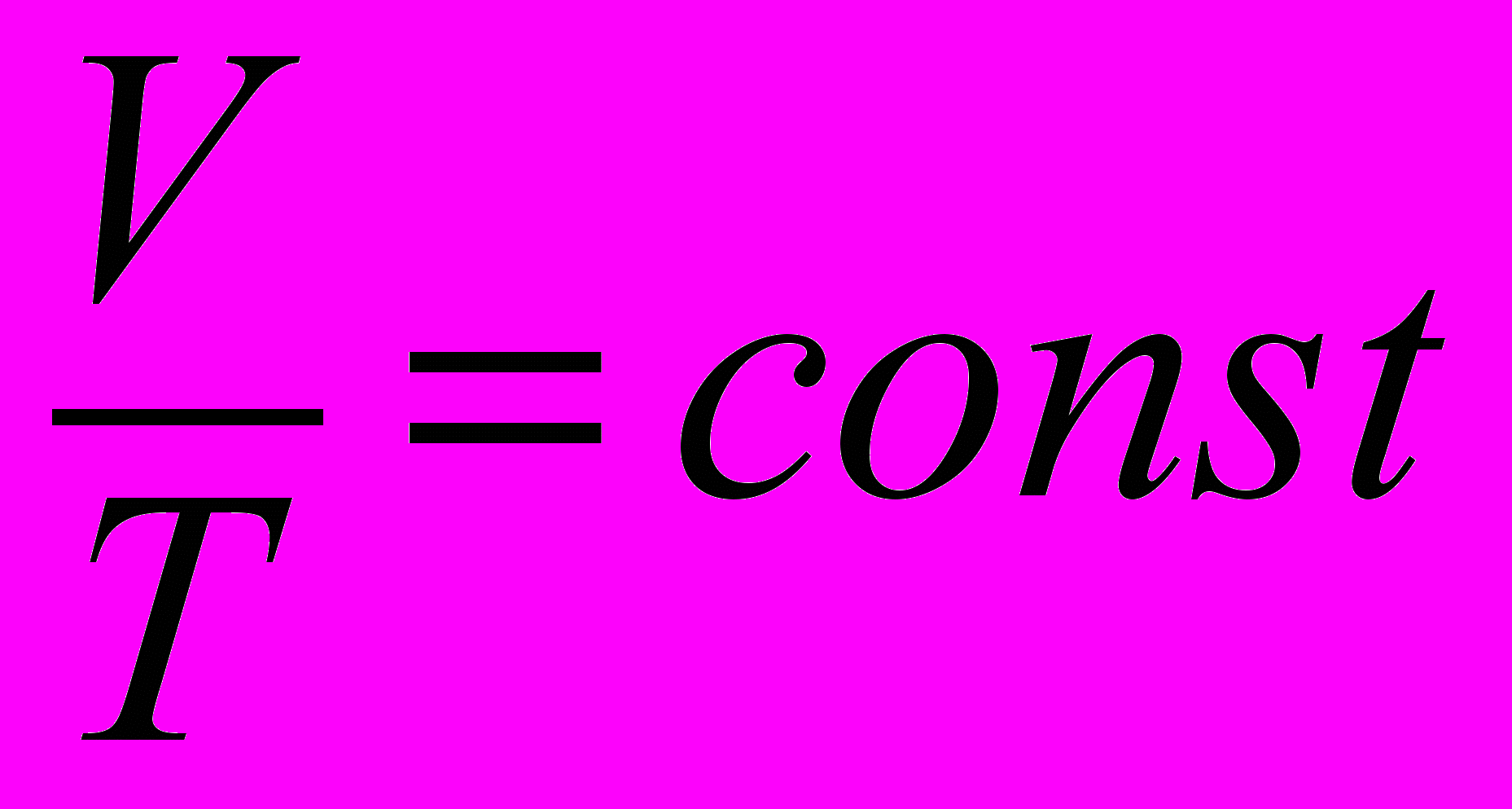 если количество вещества и давление P постоянны. | 4.4 |
| Закон Шарля для изо-хорического процесса | 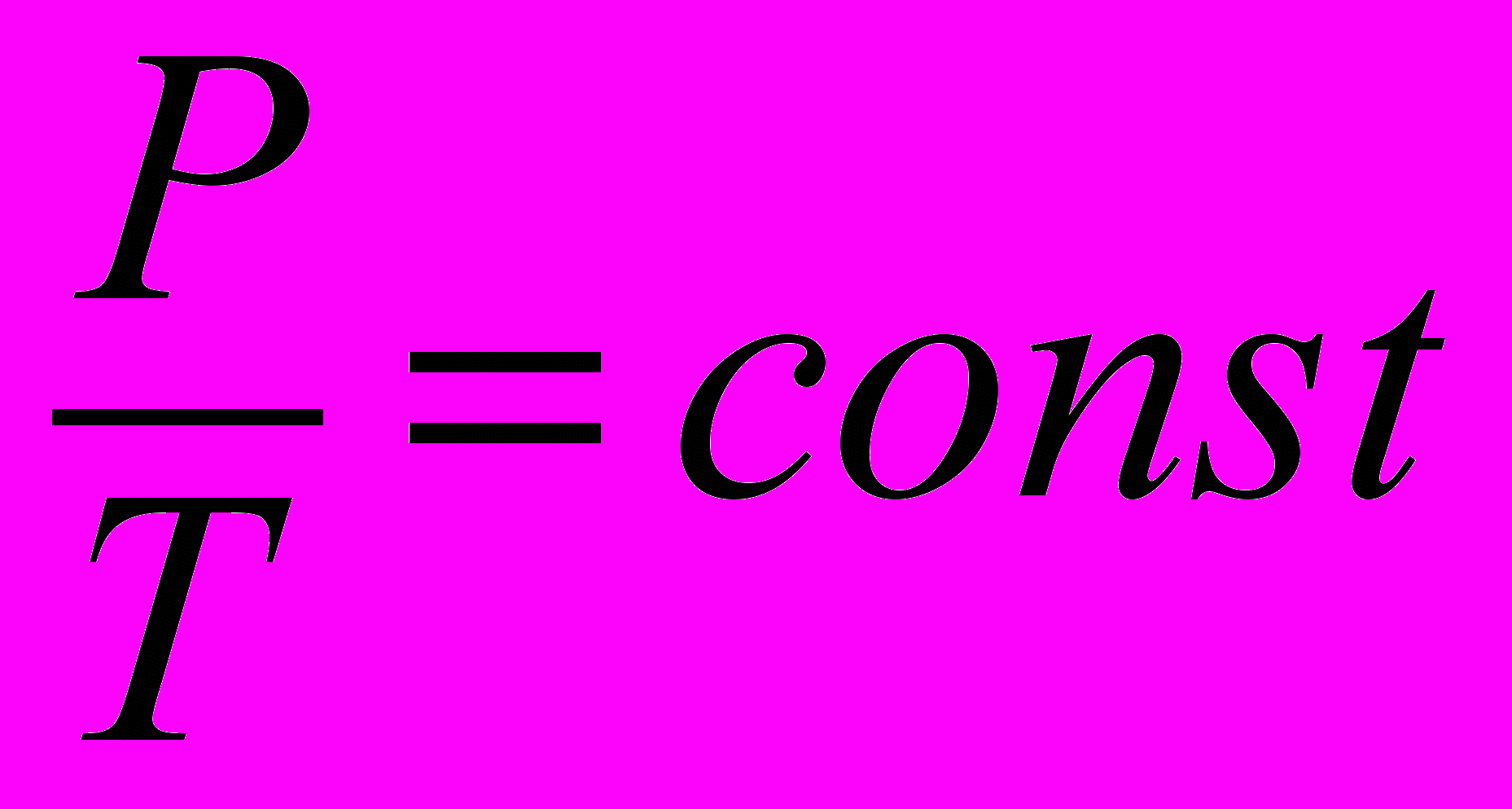 если количество вещества 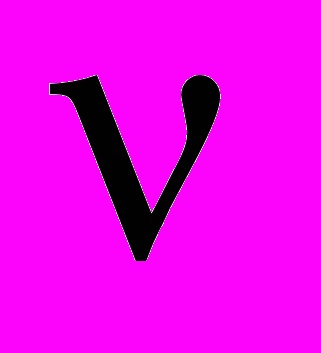 и объем V постоянны. и объем V постоянны. | 4.4 |
| Изобара | График изобарического процесса в координатах V-T. | 4.4 |
| Изохора | График изохорического процесса в координатах P-T | 4.4 |
| Изотерма | График изотермического процесса в координатах P-V | 4.4 |
| Изэнтропа | График адиабатического процесса в координатах T-S | 4.4 |
| Концентрация | Концентрация n – число частиц в единице объема, связана с плотностью, молярной массой и числом Авогадро соотношением: 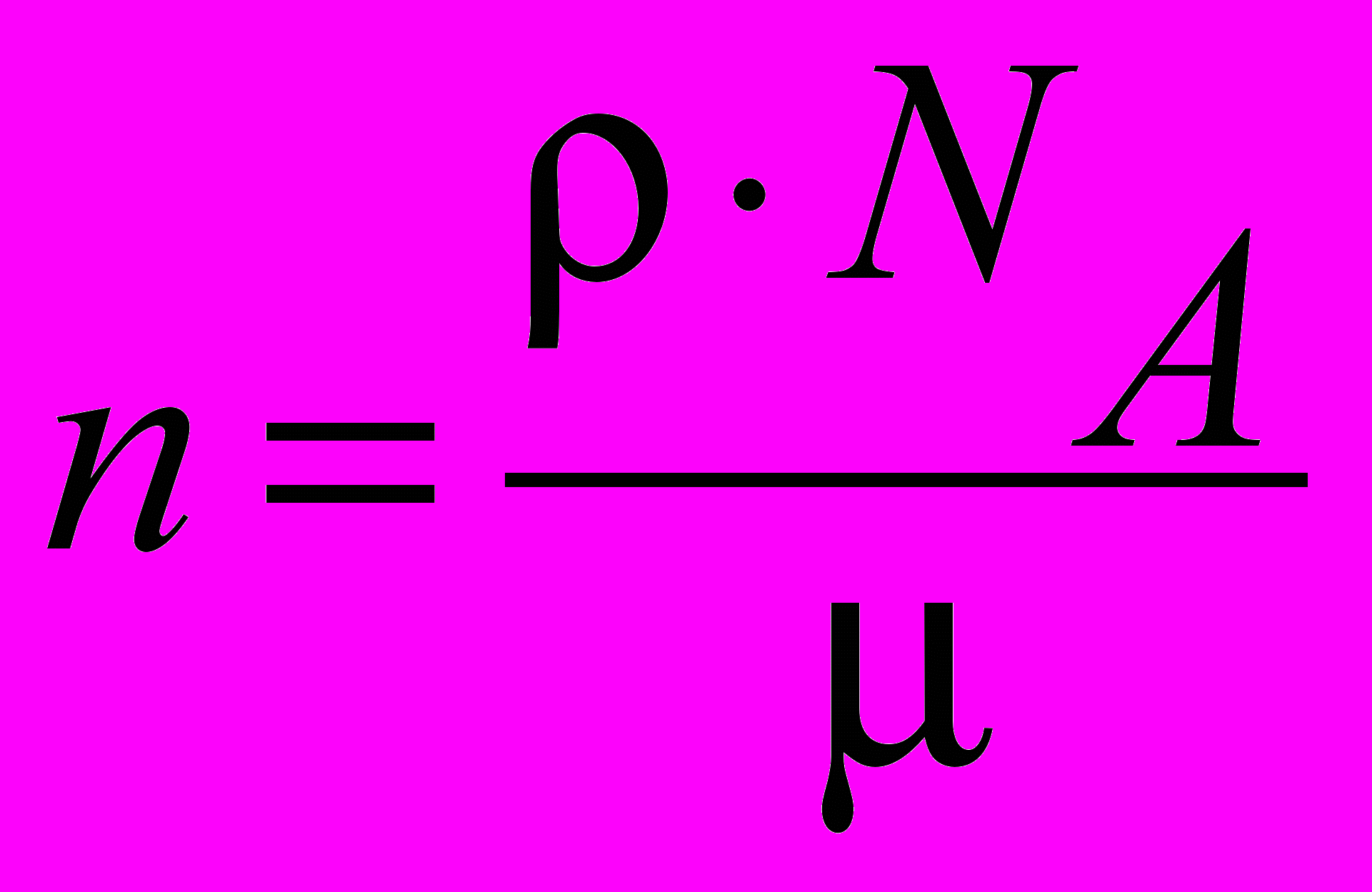 . . | |
| Количество тепла | Количество энергии, переданное системой (системе) в процессе теплообмена, называют количеством теплоты, или теплотой Q | 4.3 |
| Коэффициент полезного действия термический | 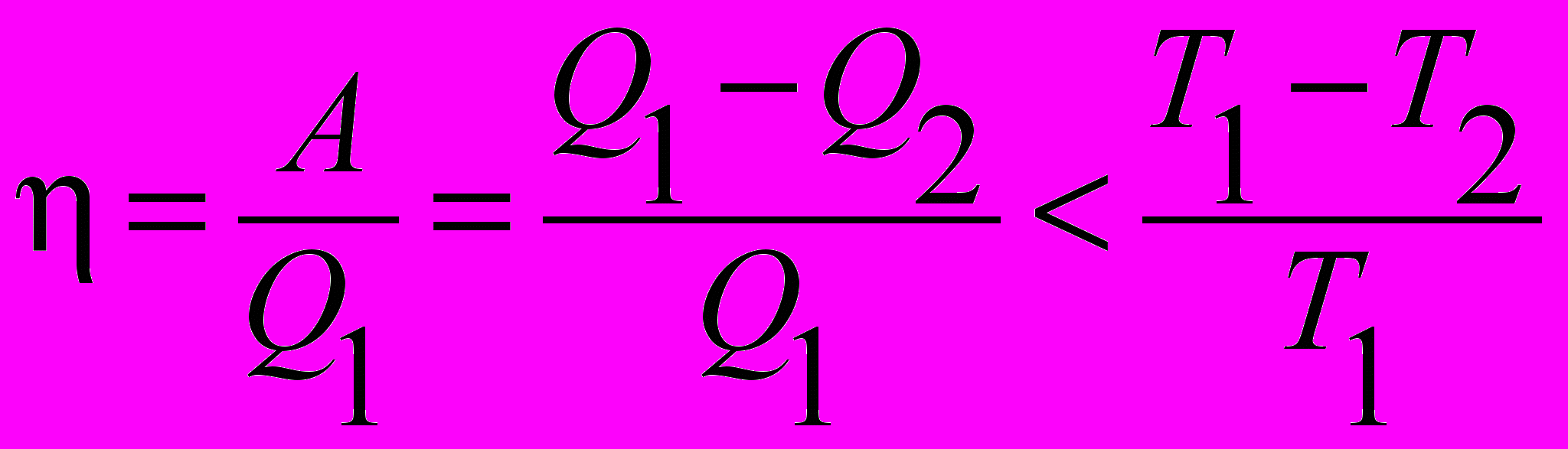 . .Термический коэффициент полезного действия любой тепловой машины, работающей в интервале температур Т1 и Т2 , не может быть больше КПД машины, работающей по циклу Карно в том же интервале температур. | 4.5 |
| Коэффициент полезного действия цикла Карно | 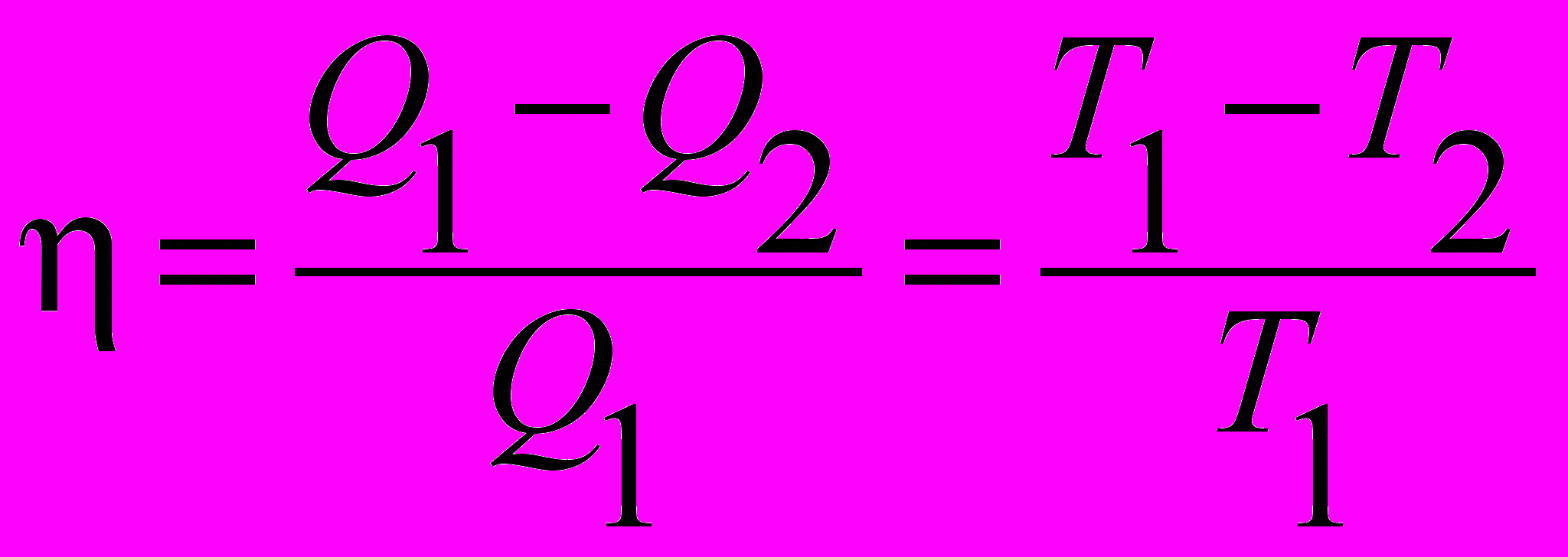 КПД идеального цикла Карно зависит только от температуры нагревателя и холодильника. | 4.5 |
| Коэффициент Пуассона | 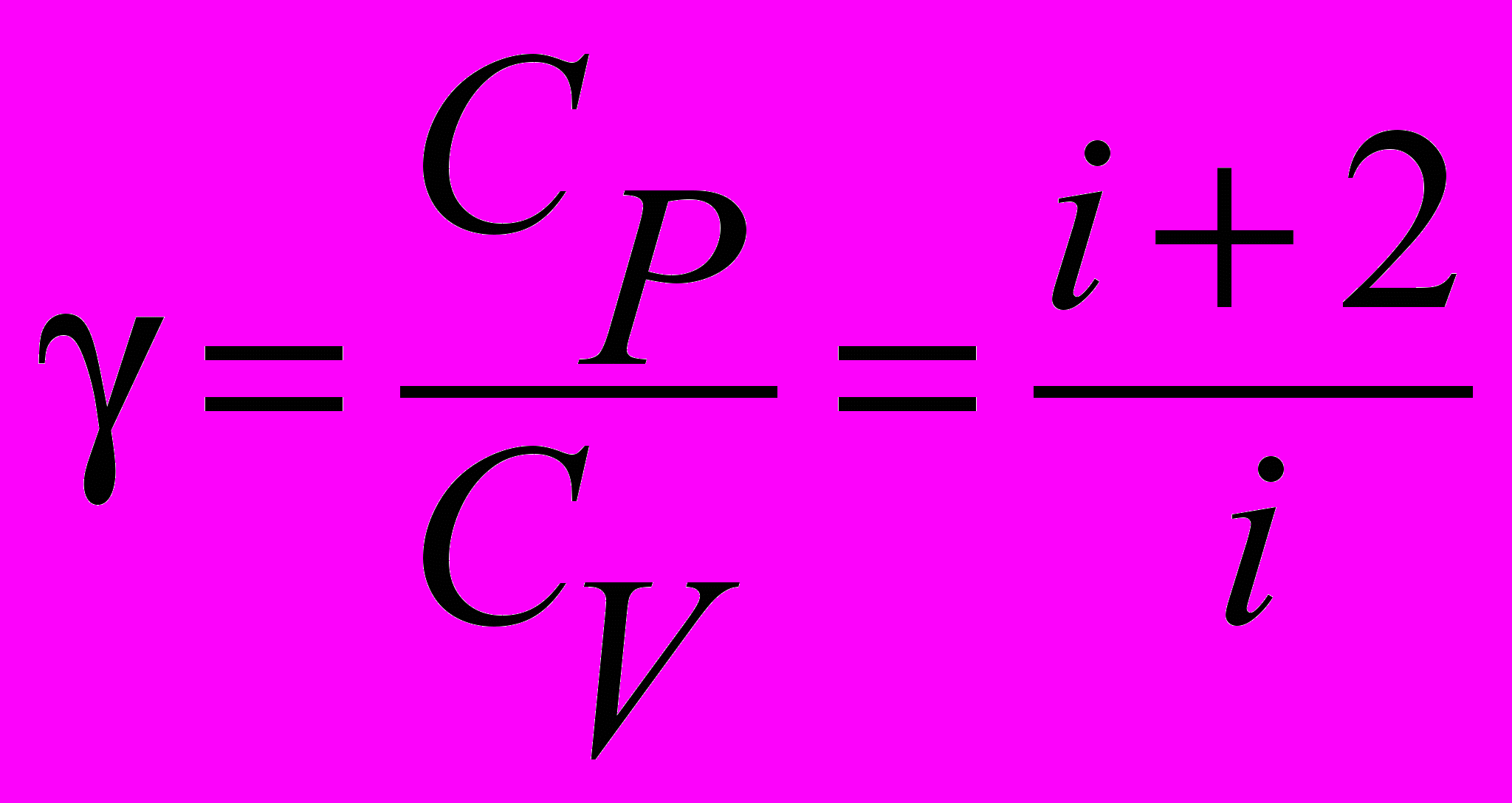 | 4.4 |
| КПД | См. Коэффициент полезного действия | |
| Масса молярная | Масса одного моля вещества. Молярная масса  измеряется в кг/моль, связана с массой одной молекулы m0 (N = 1) соотношением: измеряется в кг/моль, связана с массой одной молекулы m0 (N = 1) соотношением: 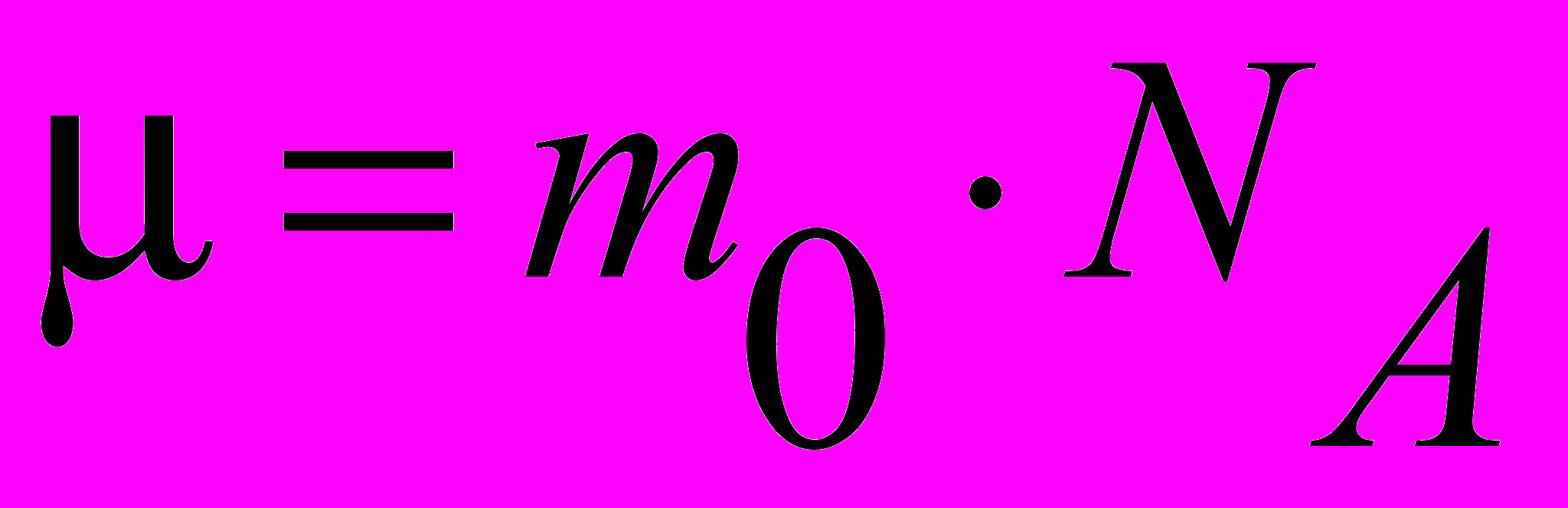 | 4.1 |
| Метод статистической физики | Метод статистической физики состоит в изучении свойств макроскопических тел, исходя из свойств частиц (молекул, атомов), составляющих тела, и из взаимодействий этих частиц. | 4.1 |
| Молекулярная физика | молекулярная физика изучает состояние и поведение макроскопических объектов при внешних воздействиях (нагревании, деформации, действии электромагнитного поля), процессы переноса (теплопроводность, вязкость, диффузию), фазовые превращения (кристаллизацию, плавление, испарение и т.д.) | 4.1 |
| Молекулярно-кинетическая теория (МКТ) | Молекулярно-кинетическая теория (МКТ) основана на статистическом методе, поэтому иногда ее называют статистической физикой. МКТ изучает микроскопическую структуру макроскопических объектов. | 4.1 |
| Моль | Количество вещества, которое содержит столько же частиц (атомов или молекул), сколько атомов содержится в 12 граммах углерода. | 4.1 |
| Нагреватель | Тело, температура которого больше, чем температура рабочего тела. | 4.5 |
| Начало термодинамики второе | Второе начало определяет условия, при которых возможны эти превращения, то есть определяет возможные направления протекания процессов. Возможны несколько эквивалентных формулировок второго закона термодинамики: -невозможно протекание самопроизвольного процесса, сопровождающееся уменьшением энтропии системы, ибо это означало бы самопроизвольный переход системы в менее вероятное состояние; -невозможен самопроизвольный переход тепла от тела менее нагретого к телу более нагретому; -невозможны такие процессы, единственным конечным результатом которых был бы переход тепла от тела, менее нагретого, к телу, более нагретому; -невозможен вечный двигатель второго рода, т.е. такой периодически действующий двигатель, который получал бы тепло от одного источника и превращал бы это тепло полностью в работу. В формулировке Зоммерфельда второе начало термодинамики звучит так: «При реальных (в современной терминологии - необратимых) процессах энтропия замкнутой системы возрастает": 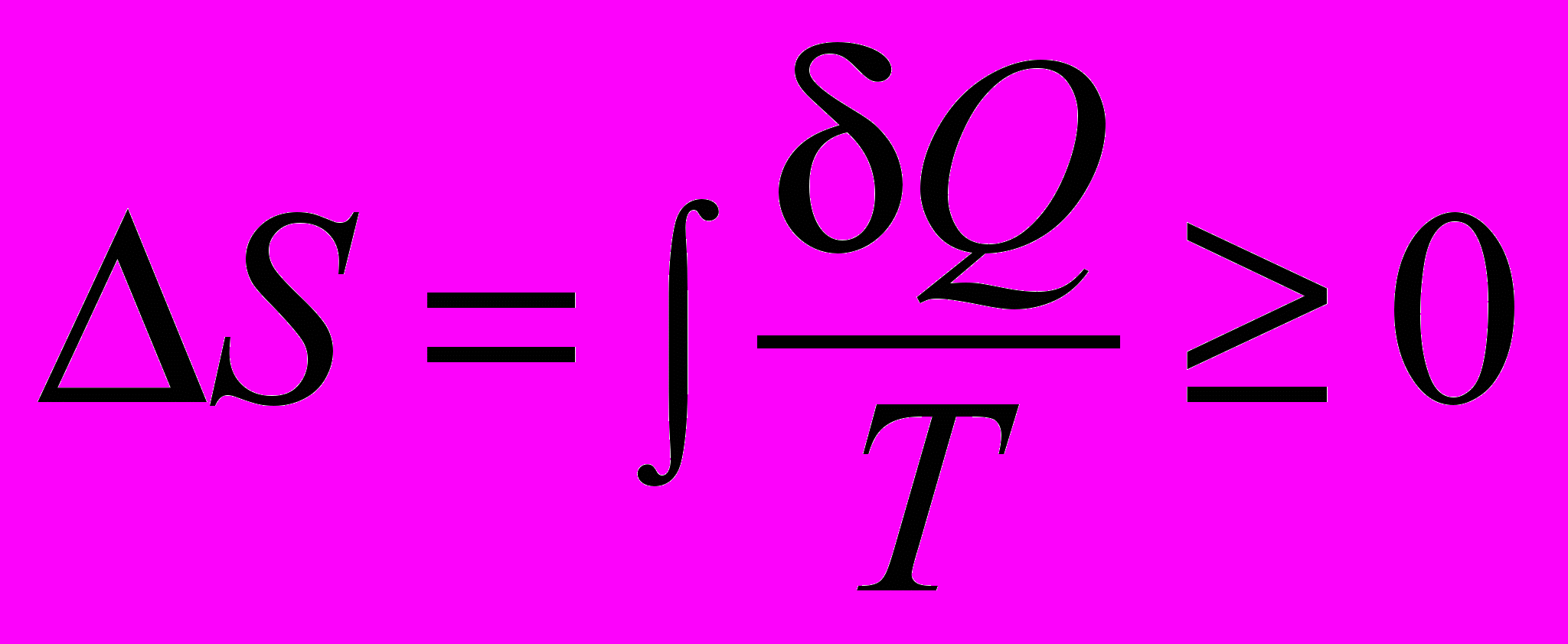 или или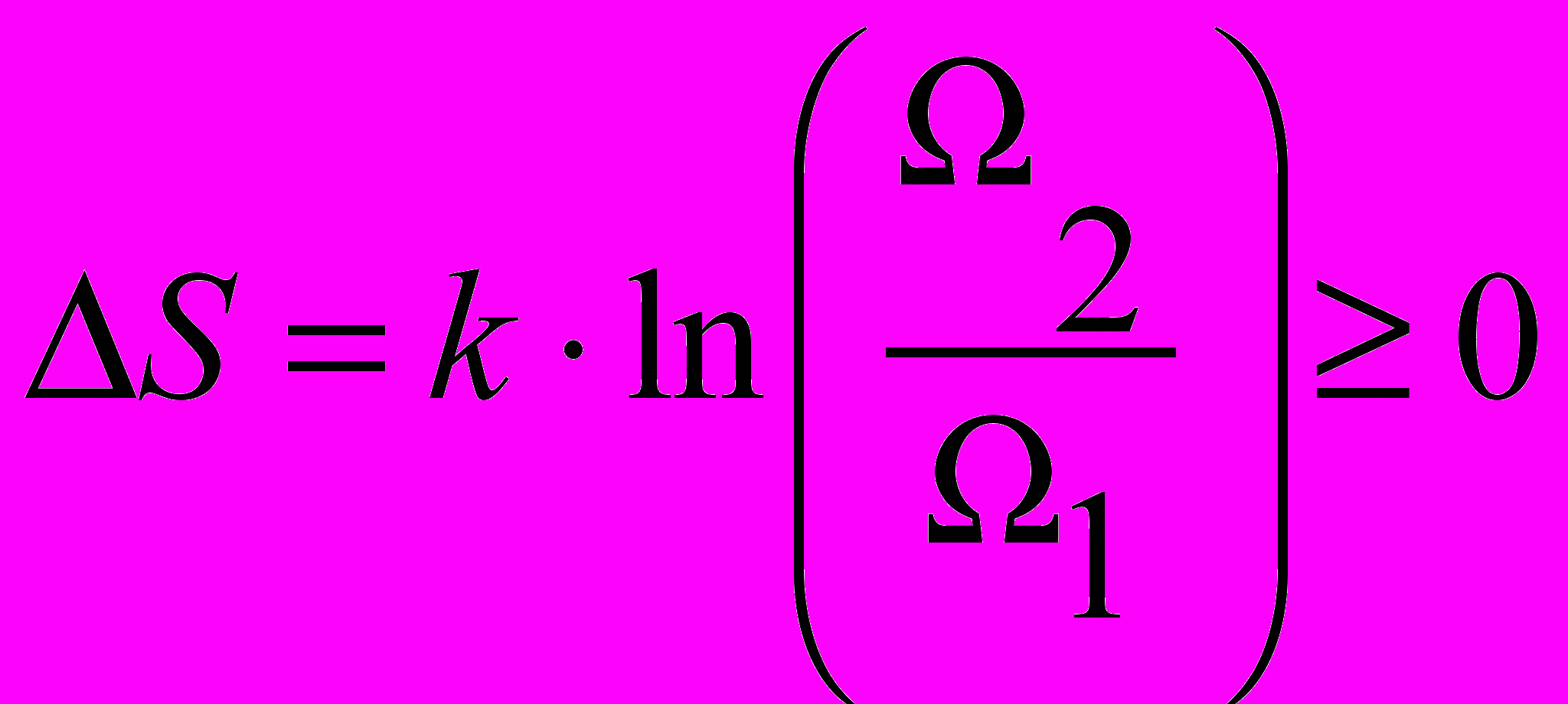 | 4.5 |
| Начало термодинамики первое | Первое начало термодинамики (закон сохранения энергии): количество тепла, сообщенное системе, идет на приращение внутренней энергии системы и на совершение работы над внешними телами. Первое начало устанавливает количественные соотношения, имеющие место при превращениях энергии из одних видов в другие. Первое начало не позволяет установить направление протекания термодинамических процессов. | 4.3 |
| Начало термодинамики первое – уравнение в дифференциальной форме | 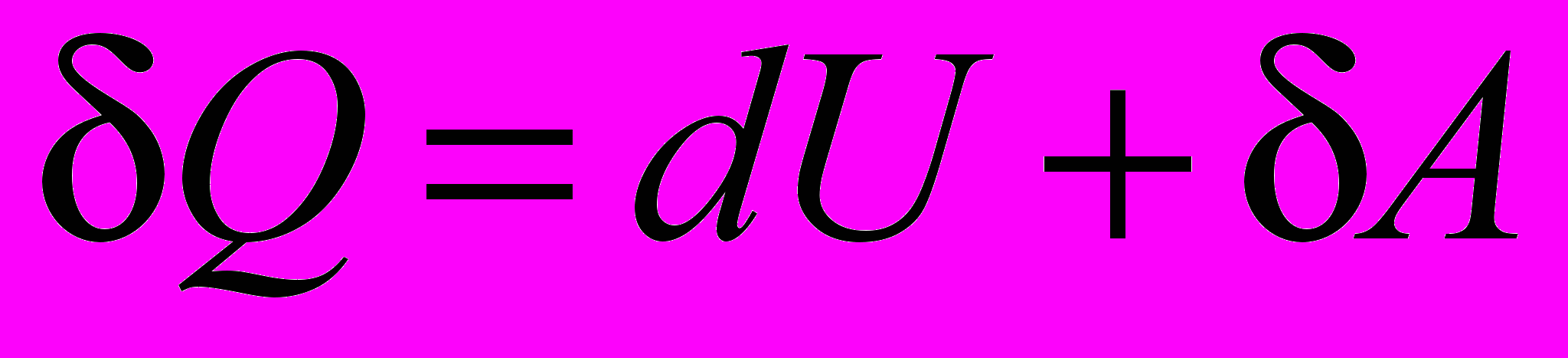 | 4.3 |
| Начало термодинамики первое – уравнение в интегральной форме | 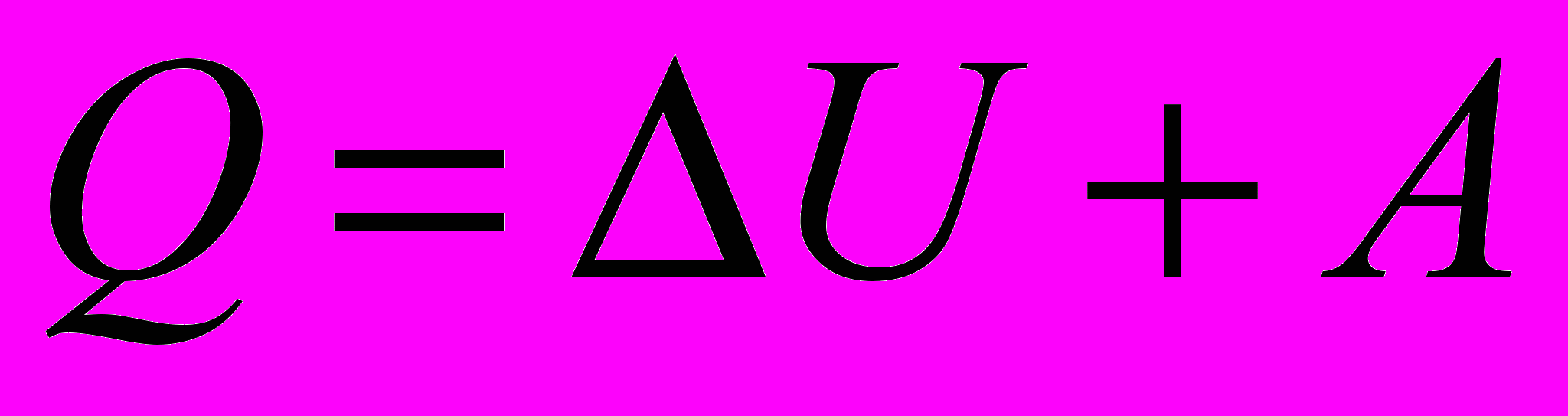 | 4.3 |
| Начало термодинамики первое – уравнение для изотермического процесса | dU=0 → δQ = δA; Q=A= 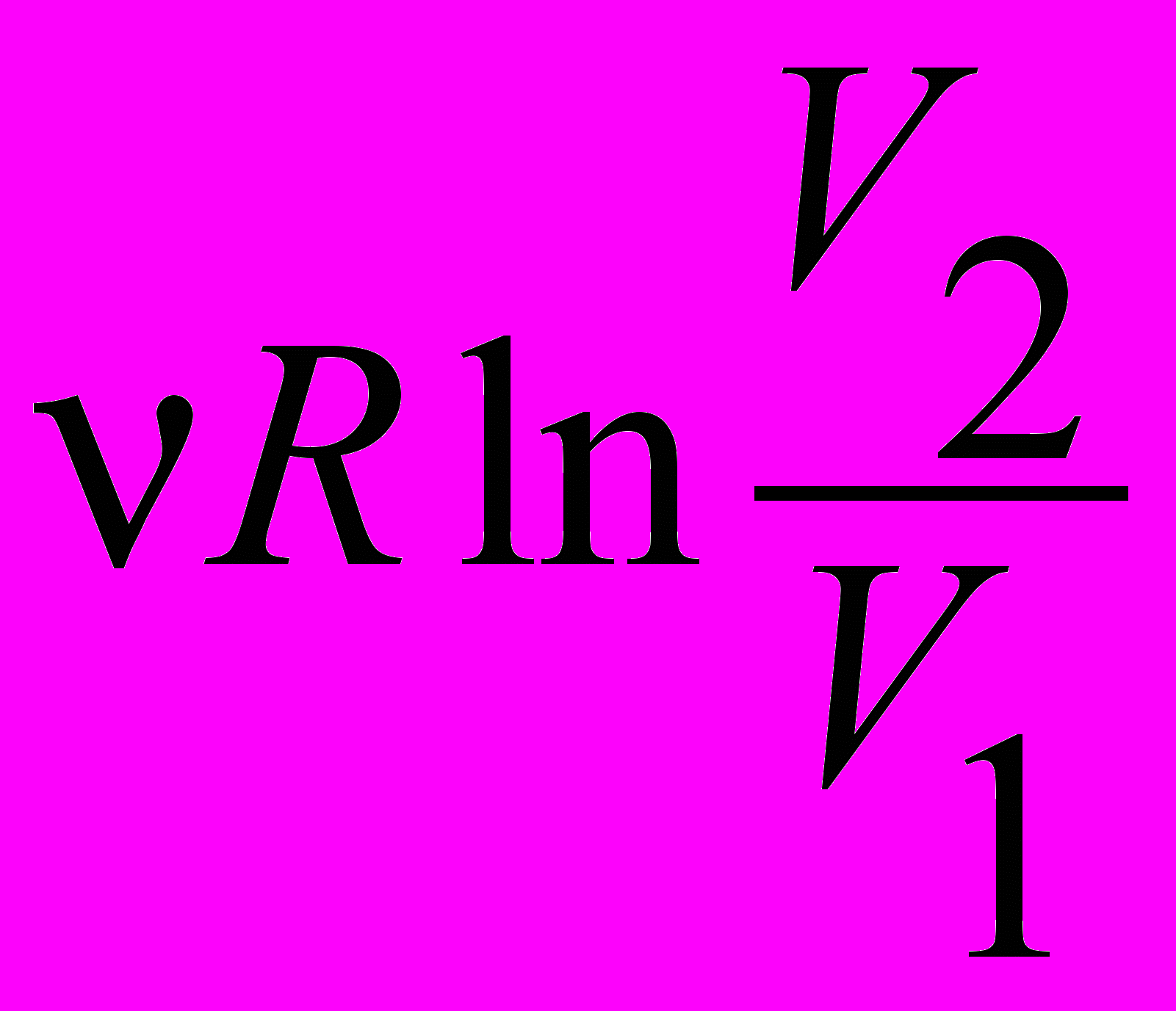 | 4.3 |
| Начало термодинамики первое – уравнение для изобарического процесса | δQ= dU+ δA = CV·dT + RdT = CРdT; Q = νCР·ΔT | 4.3 |
| Начало термодинамики первое – уравнение для изохорического процесса | δQ = dU = CV·dT Q = CV·ΔT. | 4.3 |
| Начало термодинамики первое - уравнение для адиабатического процесса | δQ = 0; δA = –dU; 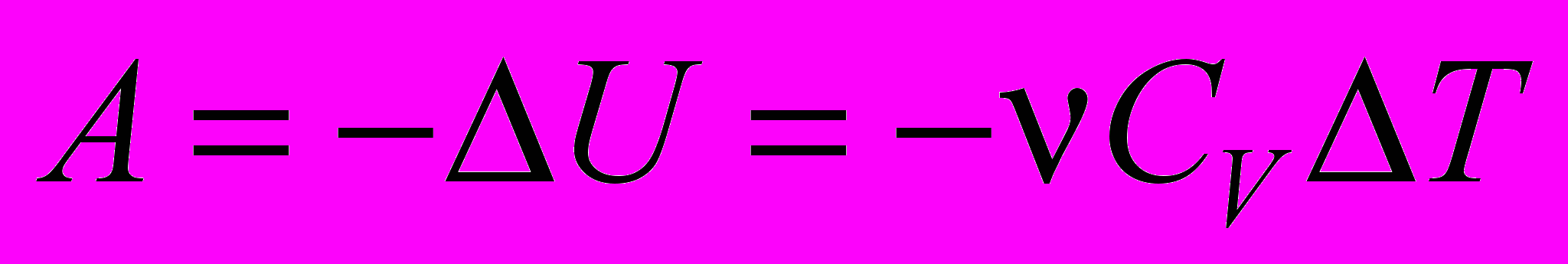 . . | 4.3 |
| Неравенство Клаузиуса | 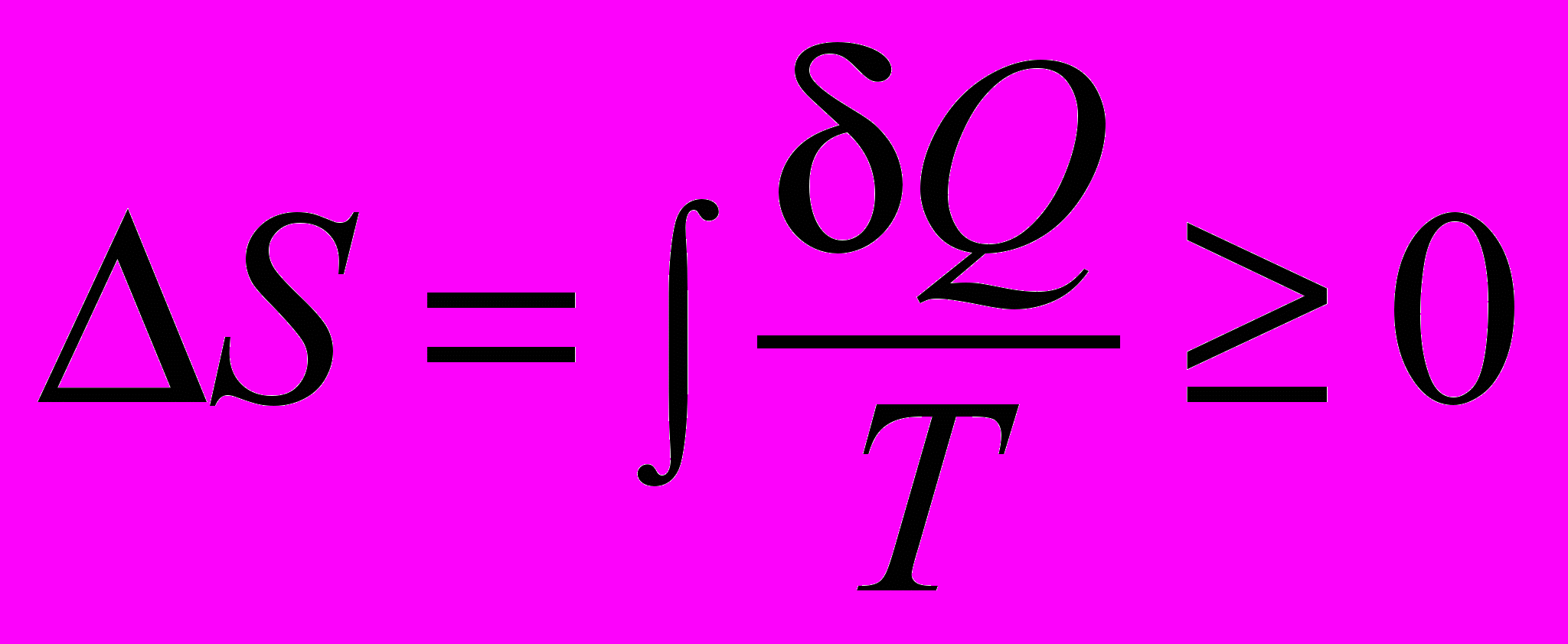 - - - энтропия изолированной системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов) | 4.5 |
| Нормальные условия | Давление 101,3 кПа = 1 атм = 760 мм рт. ст., температура 273 К = 0ºС | 4.1 |
| Нормировки условие для функции плотности вероятности | 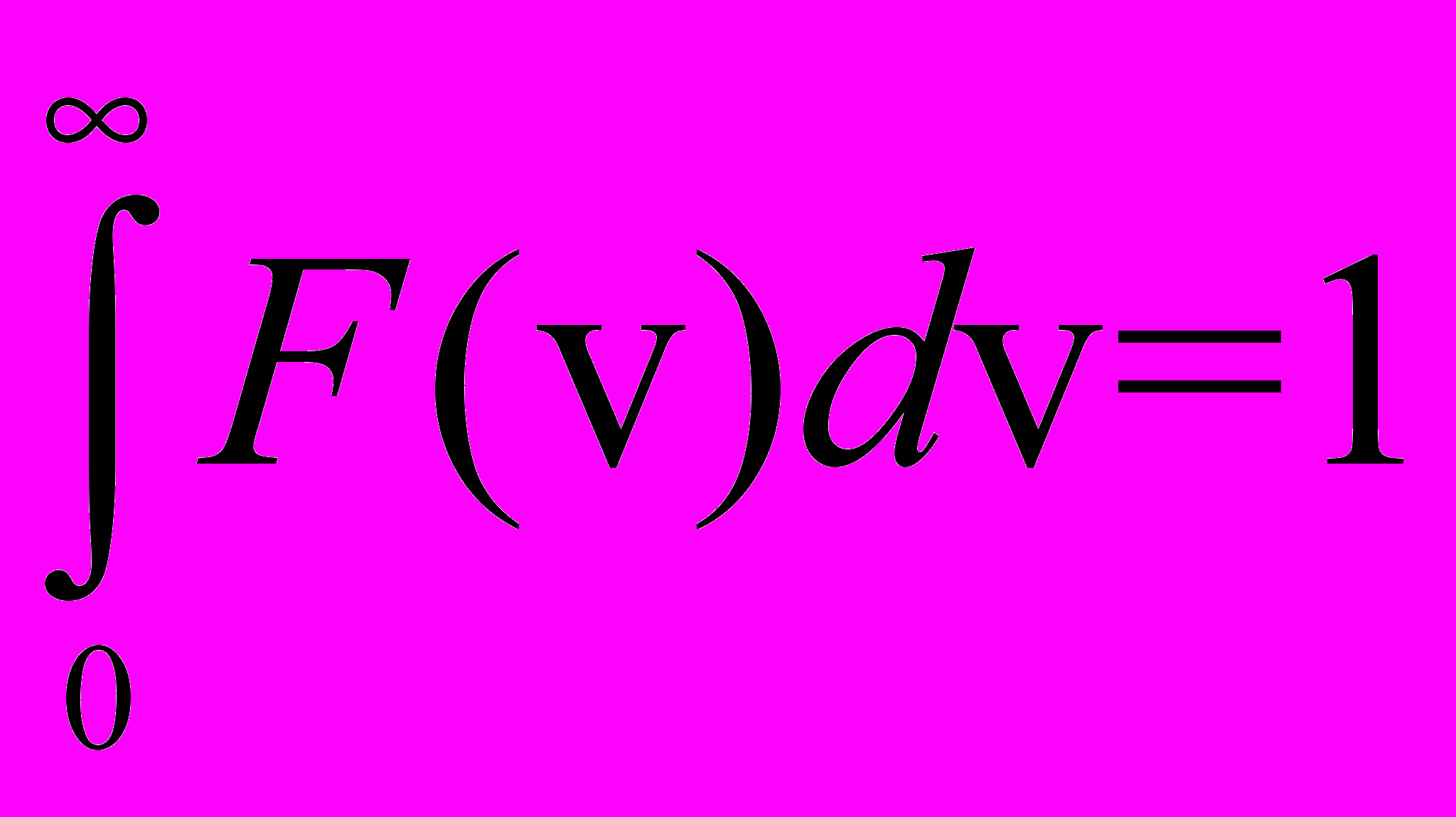 | 4.2 |
| Нуль температуры абсолютный | Начало отсчета по шкале Кельвина. Характеризует основное состояние системы многих частиц, т.е. состояние , обладающее наименьшей возможной энергией, которой соответствуют «нулевые» колебания атомов. При абсолютном нуле энтропия любого тела должна равняться нулю (теорема Нернста). Температура, при которой объем газа приближается к нулю при постоянном давлении газа. | 4.3 |
| Параметры состояния термодинамической системы внутренние | Внутренние параметры – это величины, характеризующие свойства самой системы – например, давление P и температура T. | 4.3 |
| Параметры состояния термодинамической системы внешние | Внешние параметры – это величины, характеризующие свойства внешних тел. В отсутствие внешних полей газ имеет единственный внешний параметр – объем V. | 4.3 |
| Плотность вещества | Величина, характеризующая распределение массы в пределах тела. Для однородных тел: 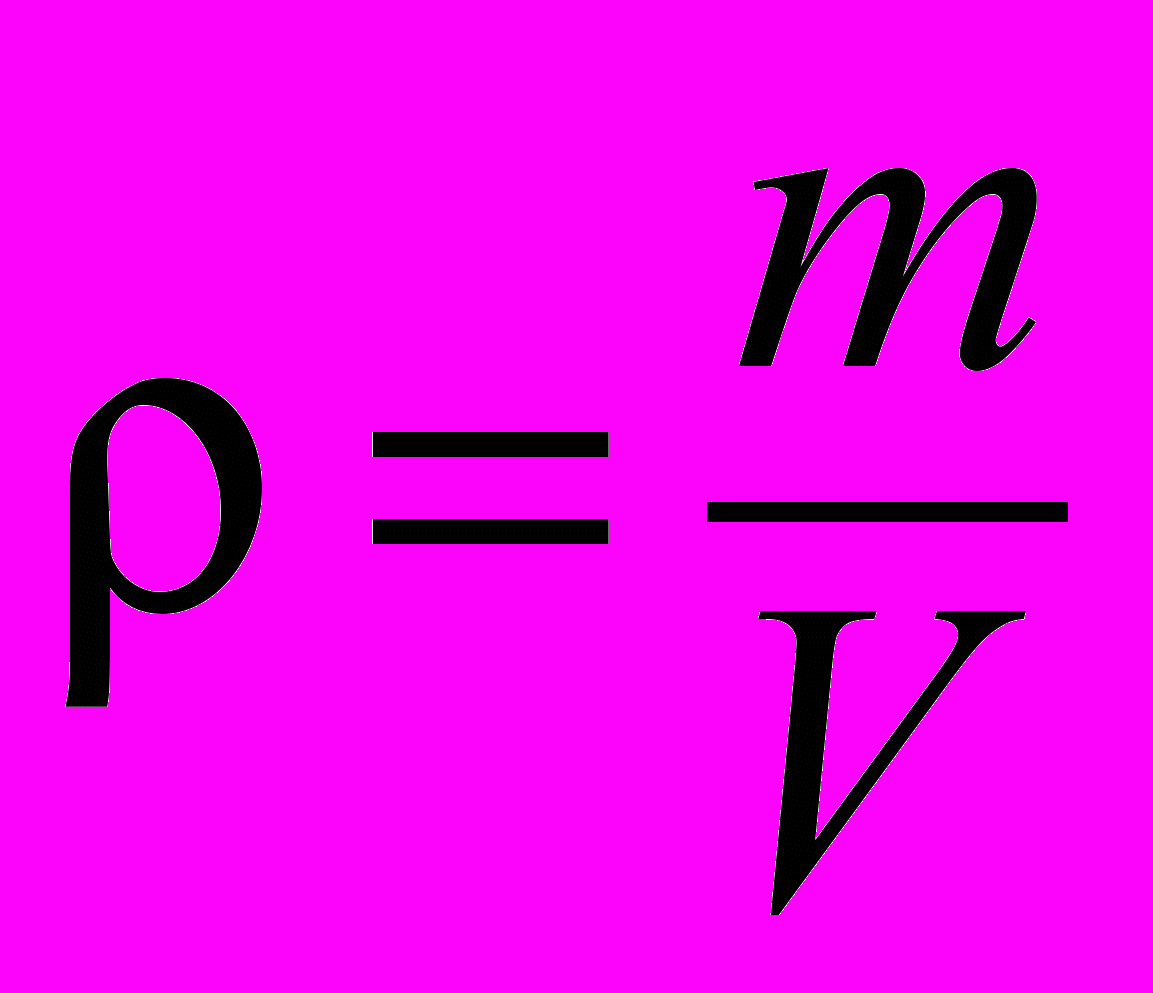 , ,для неоднородных тел плотность в данной точке: 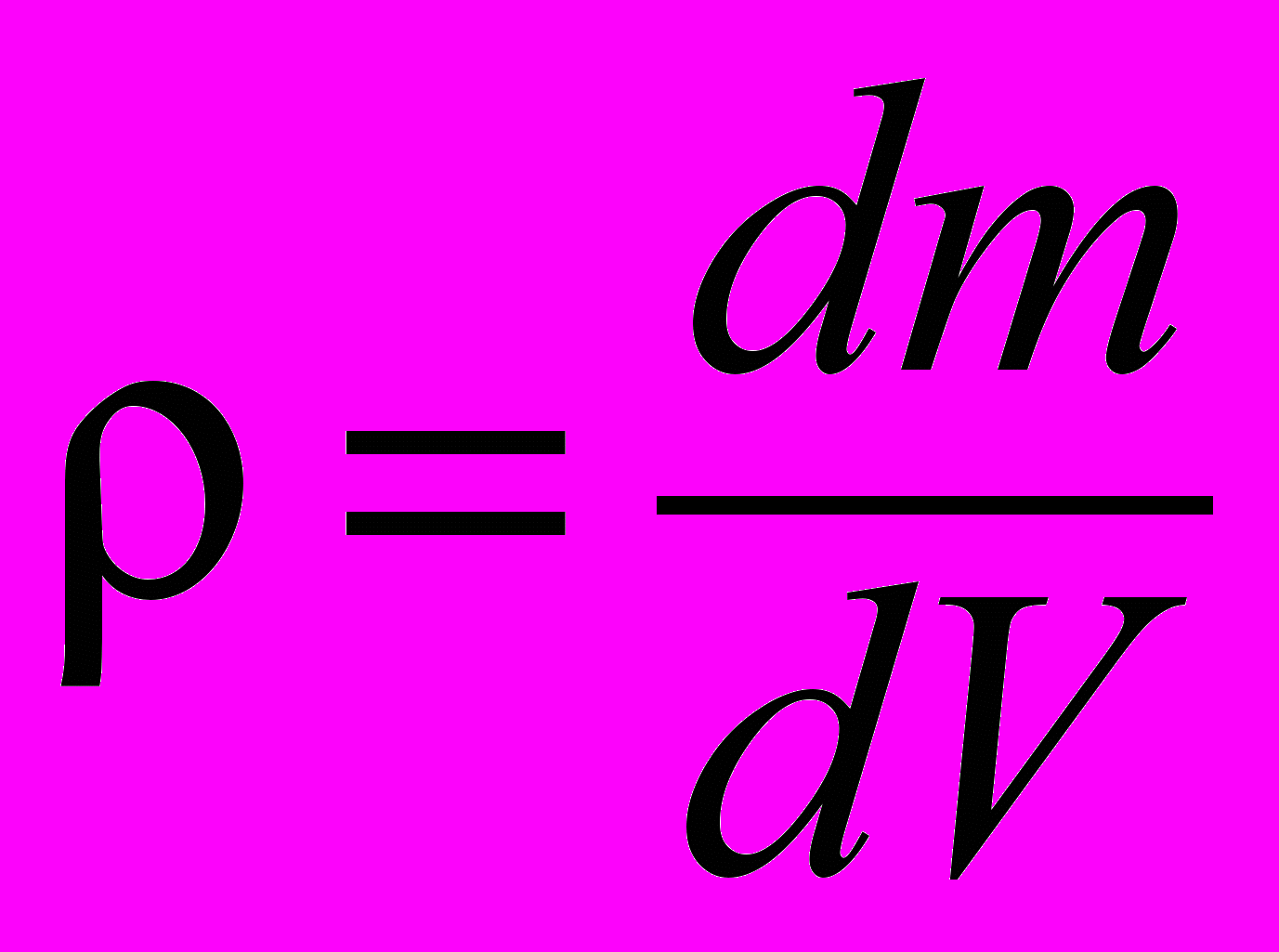 . . | 4.1 |
| Плотность вероятности распределения молекул по скоростям | См. функция распределения молекул по скоростям. | 4.2 |
| Показатель степени адиабаты | См. Коэффициент Пуассона | 4.4 |
| Поперечное сечение соударения молекул эффективное | = d2 , где d – удвоенный радиус молекулы. | 4.2 |
| Постоянная Больцмана | 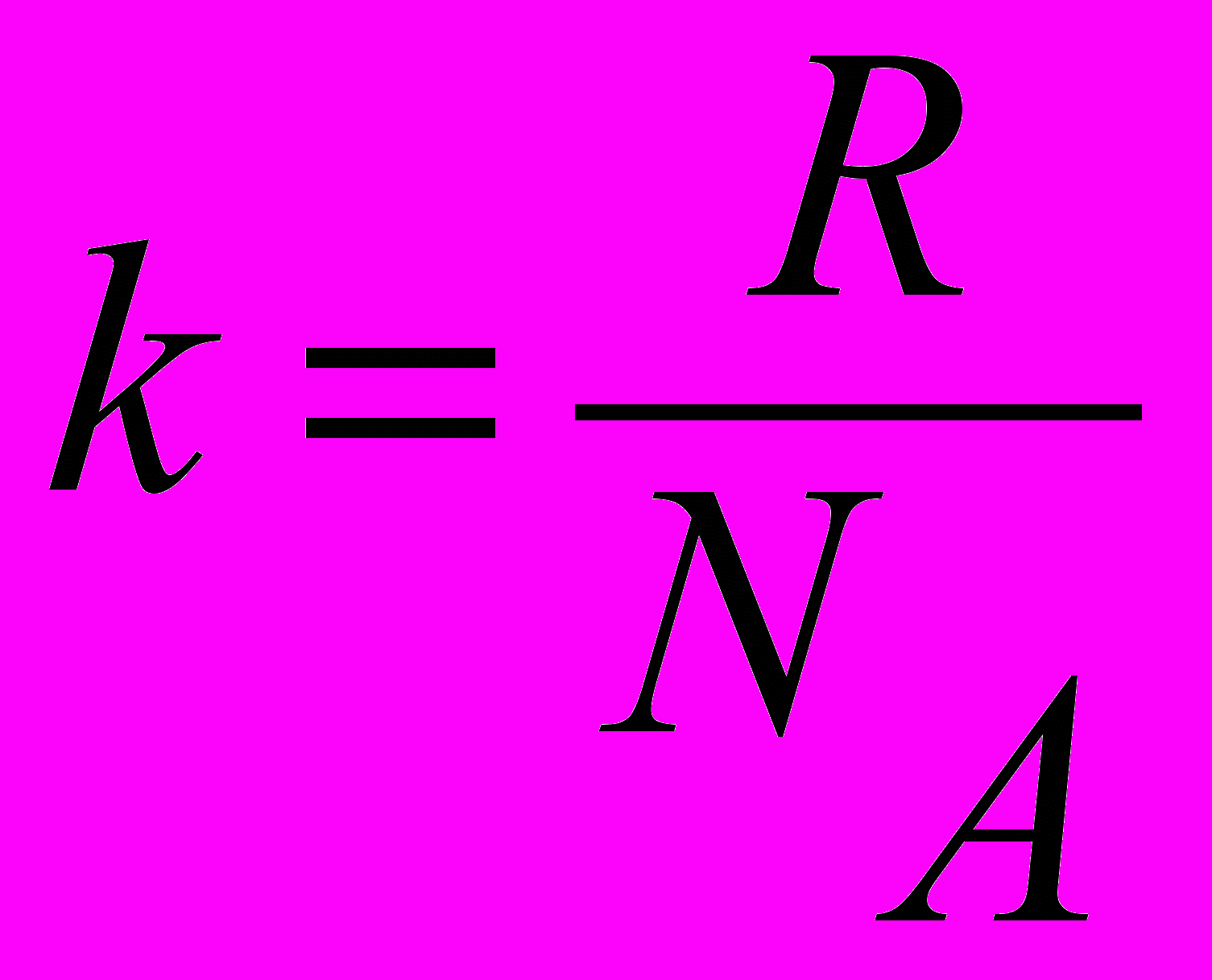 , ,где 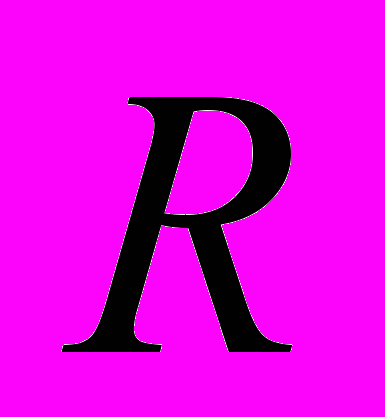 - универсальная газовая постоянная, - универсальная газовая постоянная, 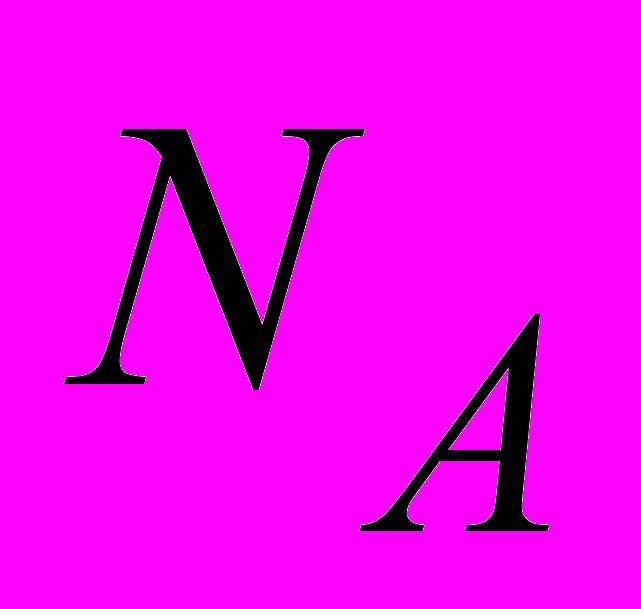 - число Авогадро. - число Авогадро. 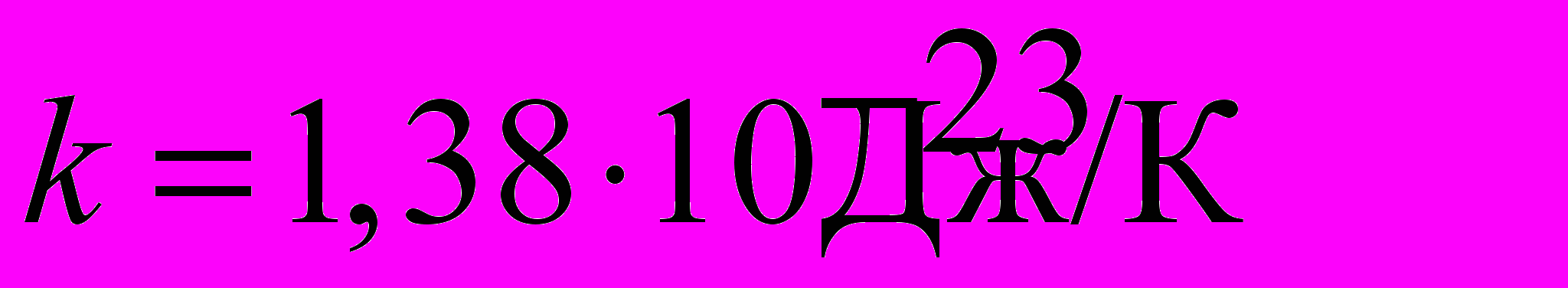 | 4.1 |
| Постоянная Пуассона | См. Коэффициент Пуассона | |
| Постоянная газовая универсальная | R= 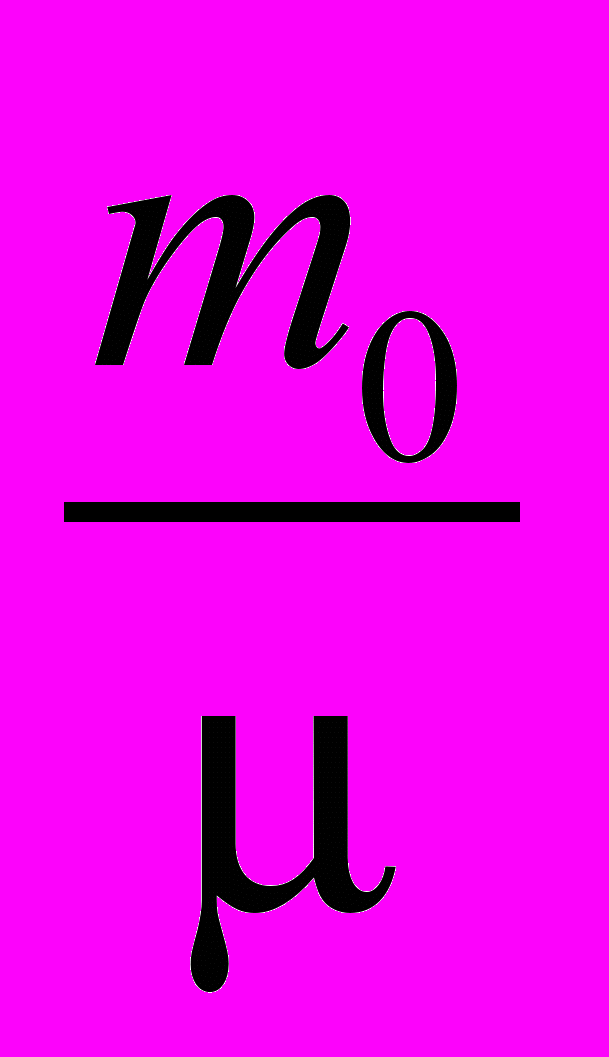 , ,где 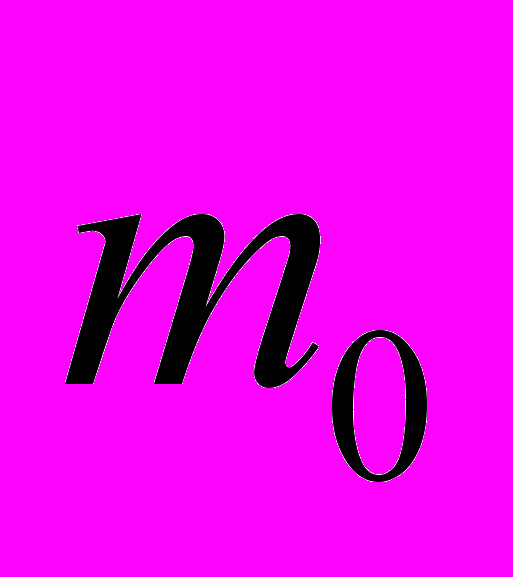 - масса одной молекулы газа, - масса одной молекулы газа,  - молярная масса этого газа - молярная масса этого газаR =8,31 Дж/К·моль | 4.1 4.3 |
| Принцип Больцмана | см. формула Больцмана | |
| Процесс адиабатический (изэнтропический) | Адиабатический процесс осуществляется в термодинамической системе без теплообмена с внешней средой. Математически условие адиабатического процесса записывается в виде: Q = 0. | 4.4 |
| Процесс изобарический | Процесс, протекающий без изменения давления в термодинамической системе. | 4.4 |
| Процесс изотермический | Процесс, протекающий без изменения температуры термодинамической системы. | 4.4 |
| Процесс изохорический | Процесс, протекающий без изменения объема термодинамической системы. | 4.4 |
| Процесс неравновесный (необратимый) | Процесс, который не является равновесным (см. процесс равновесный). Неравновесный процесс является необратимым. | 4.3 |
| Процесс равновесный (квазистатический, обратимый) | Процесс называют равновесным, если внешние условия меняются так медленно, что в любой момент времени систему можно считать равновесной. Равновесным может быть только бесконечно медленный, или квазистатический процесс. Равновесный процесс можно провести в обратном направлении, при этом система проходит через те же состояния, что и при прямом процессе, такой процесс называется обратимым. | 4.3 |
| Процесс термодинамический | Переход термодинамической системы из одного состояния в другое, сопровождающийся изменением хотя бы одного из параметров системы. | 4.3 |
| Работа термодинамической системы | Количество энергии А, переданное системой (системе) в процессе расширения или сжатия газа, называют работой 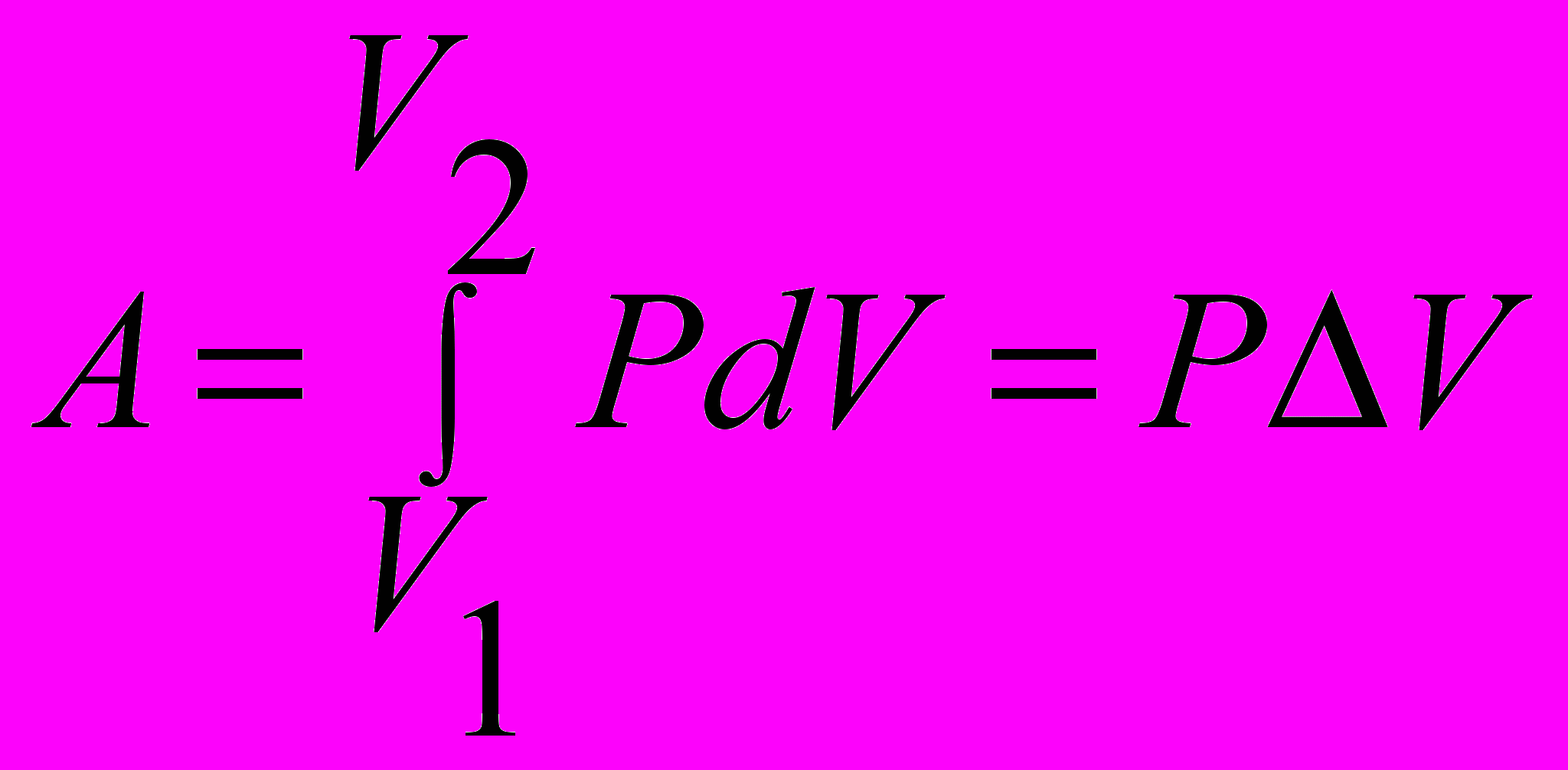 | 4.3 4.4 |
| Работа идеального газа в изотермическом процессе | 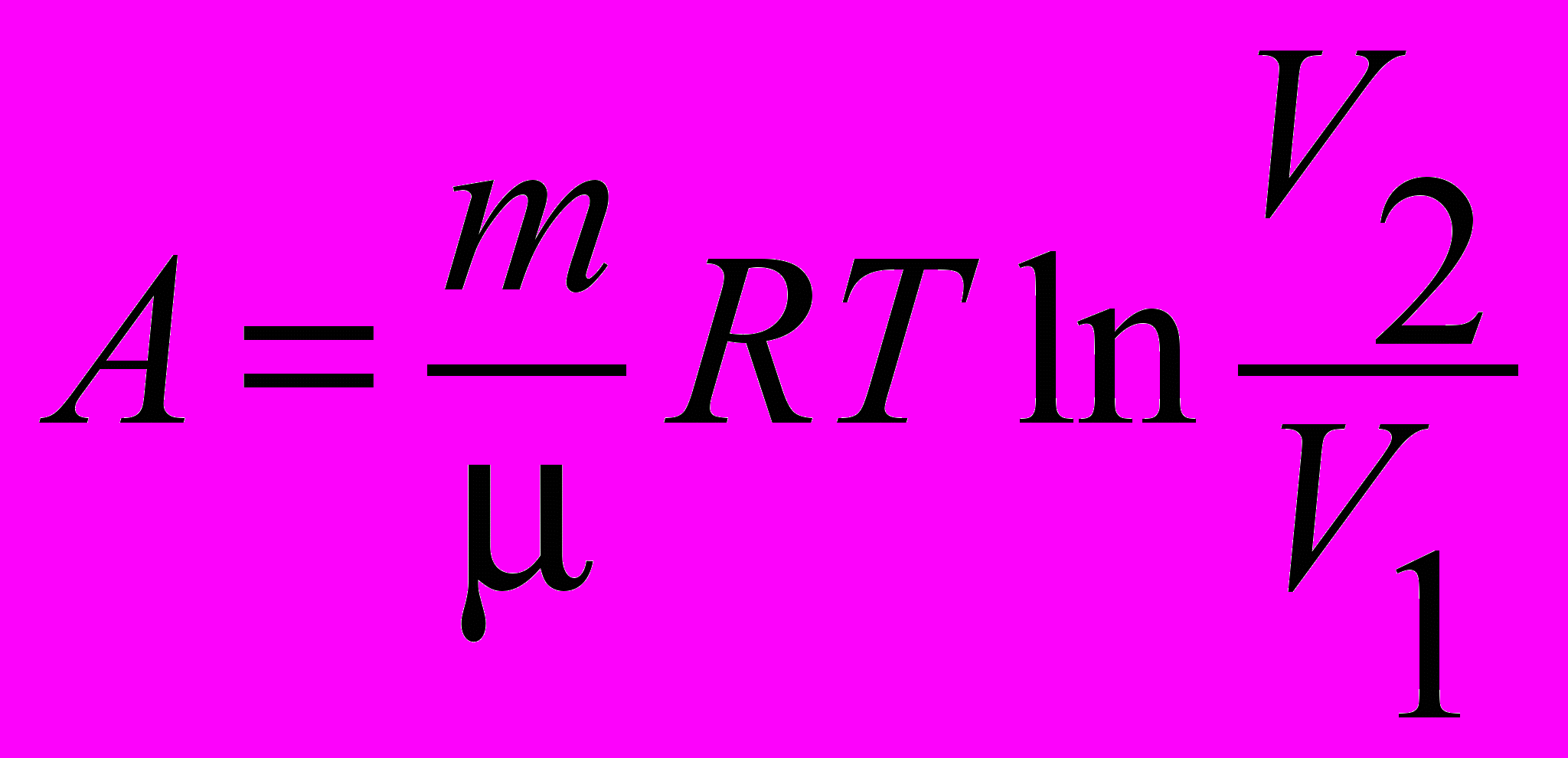 | 4.4 |
| Работа идеального газа в изобарическом процессе | 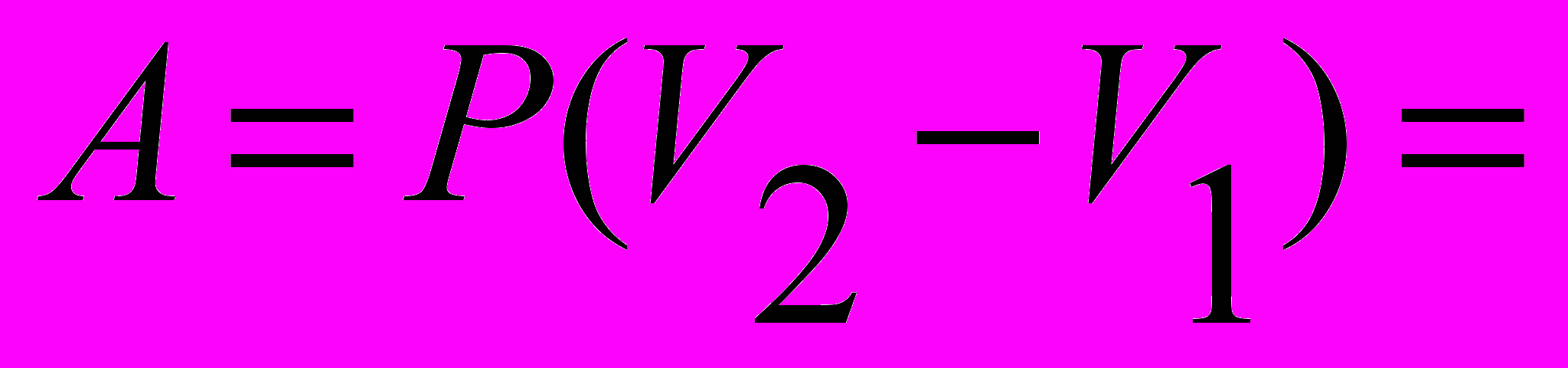 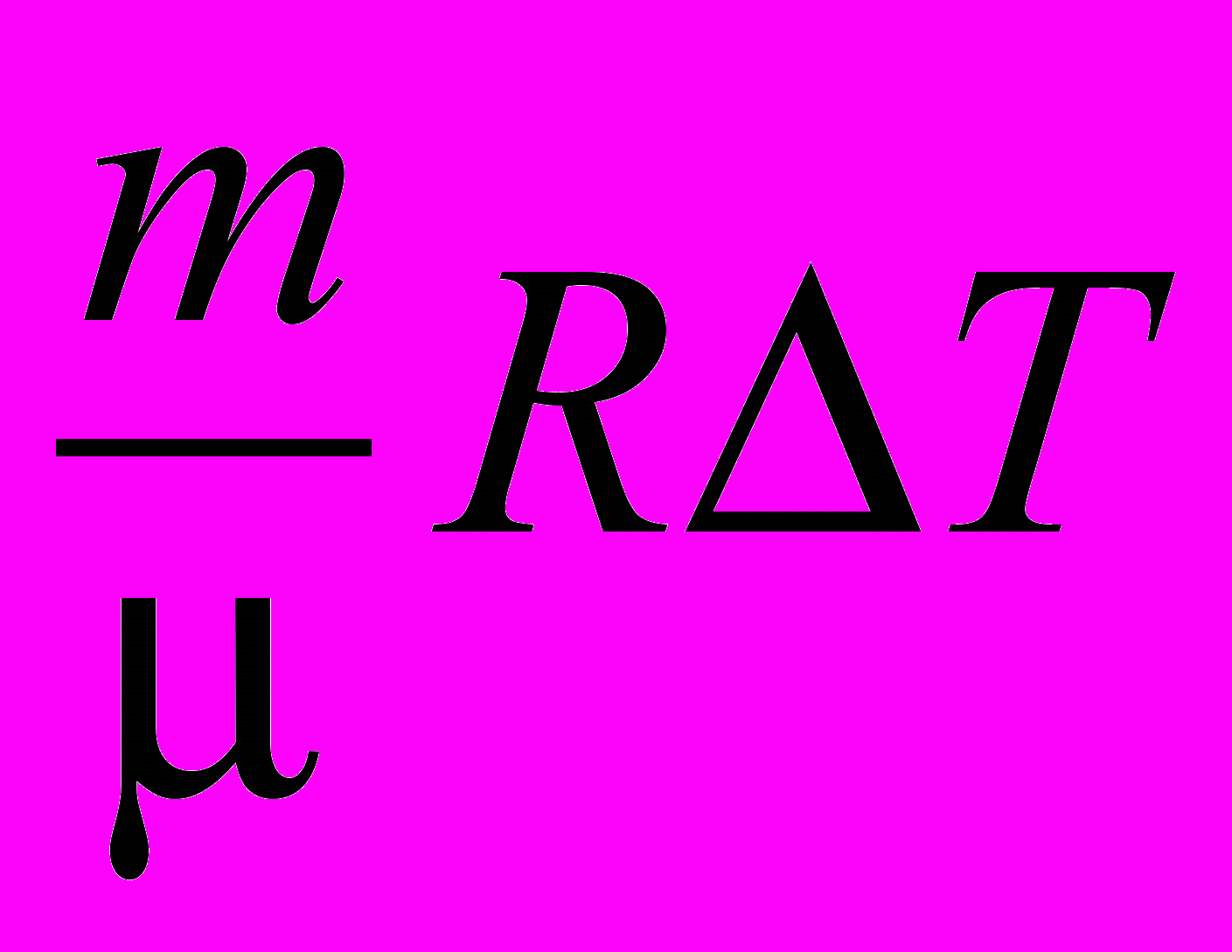 | 4.4 |
| Работа идеального газа в изохорическом процессе | А = 0, так как V = 0. | 4.4 |
| Работа идеального газа в адибатическом процессе | 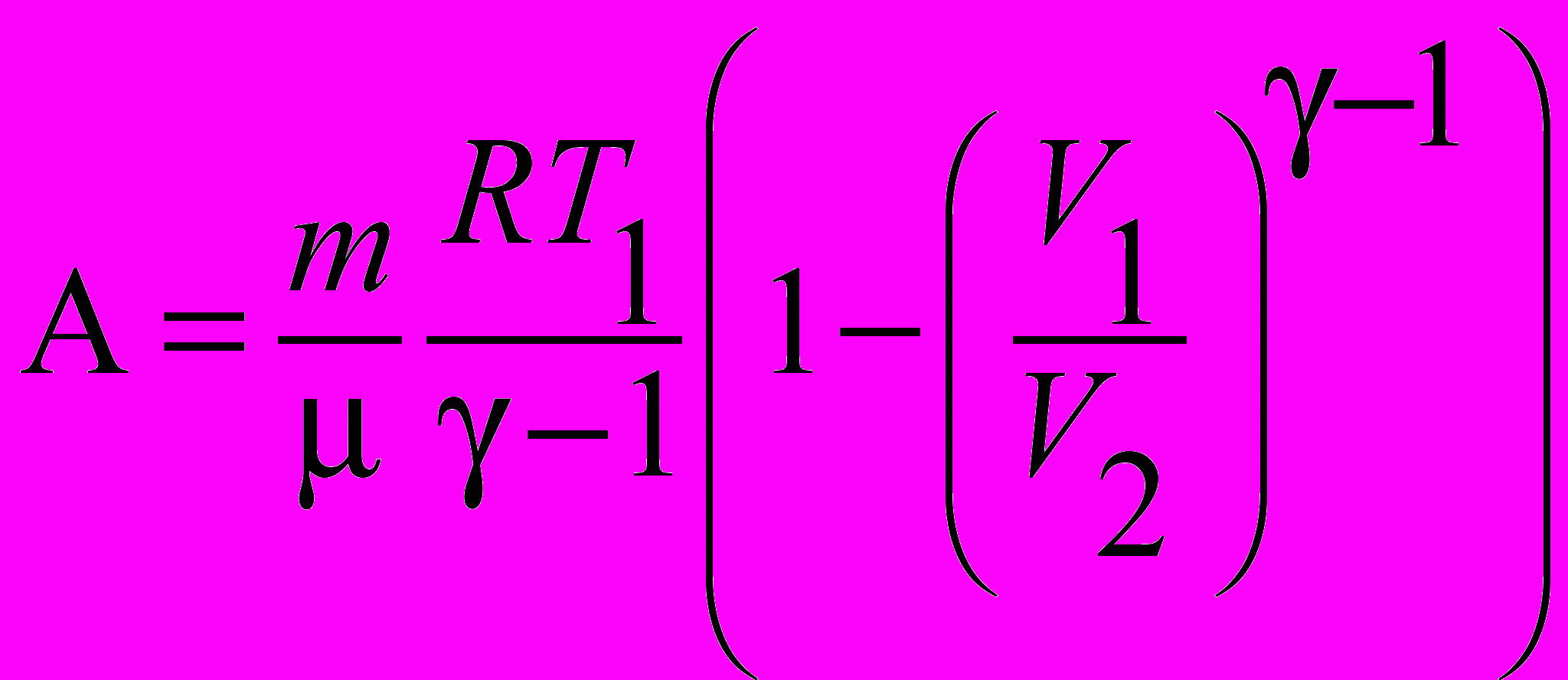 , ,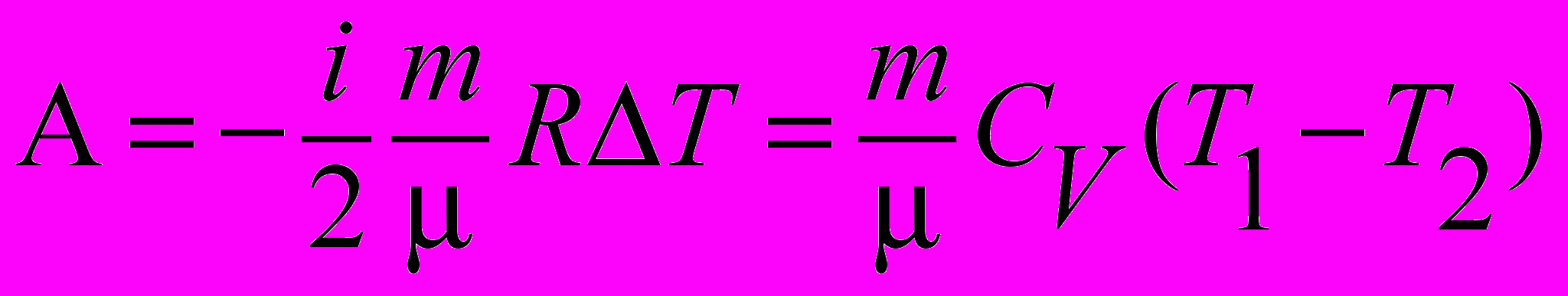 . . | 4.4 |
| Рабочее тело | Газ или пар, который совершает работу при расширении. | 4.3 4.4 |
| Система адиабатически изолированная | Если система не поглощает и не отдает тепло, то она называется адиабатически изолированной. | 4.3 |
| Система замкнутая | Система может считаться замкнутой, если отсутствует обмен веществом между системой и окружающей средой. | 4.3 |
Системы макроскопические | Это такие тела, масштабы которых привычны для человека. Макроскопические системы состоят из большого числа частиц (молекул или атомов) | 4.3 |
Система термодинамическая | Термодинамической системой называют совокупность макроскопических тел, которые могут взаимодействовать между собой и с другими телами (внешней средой) – обмениваться с ними энергией и веществом. | 4.3 |
| Скорость наиболее вероятная | 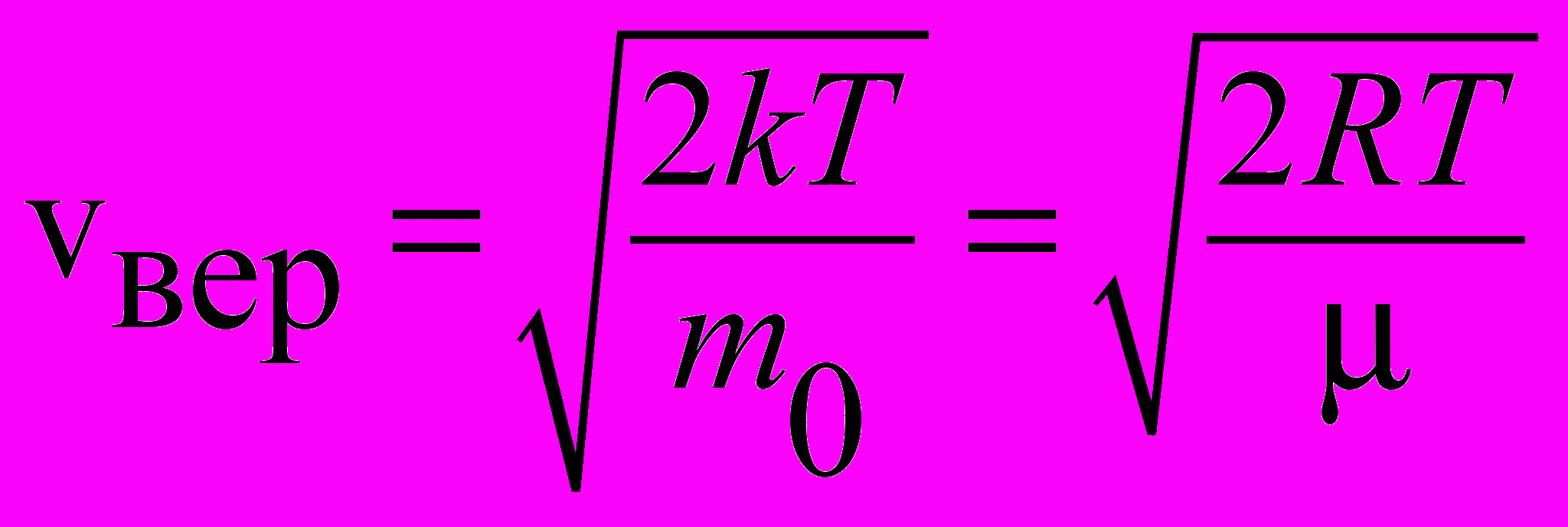 | 4.2 |
| Скорость средняя квадратичная | 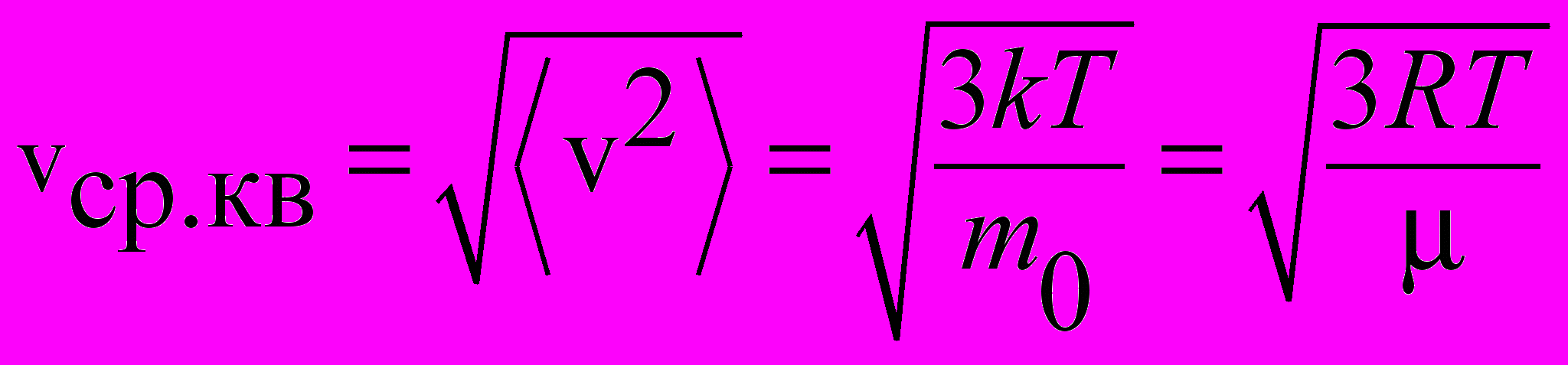 | 4.2 |
| Скорость средняя | 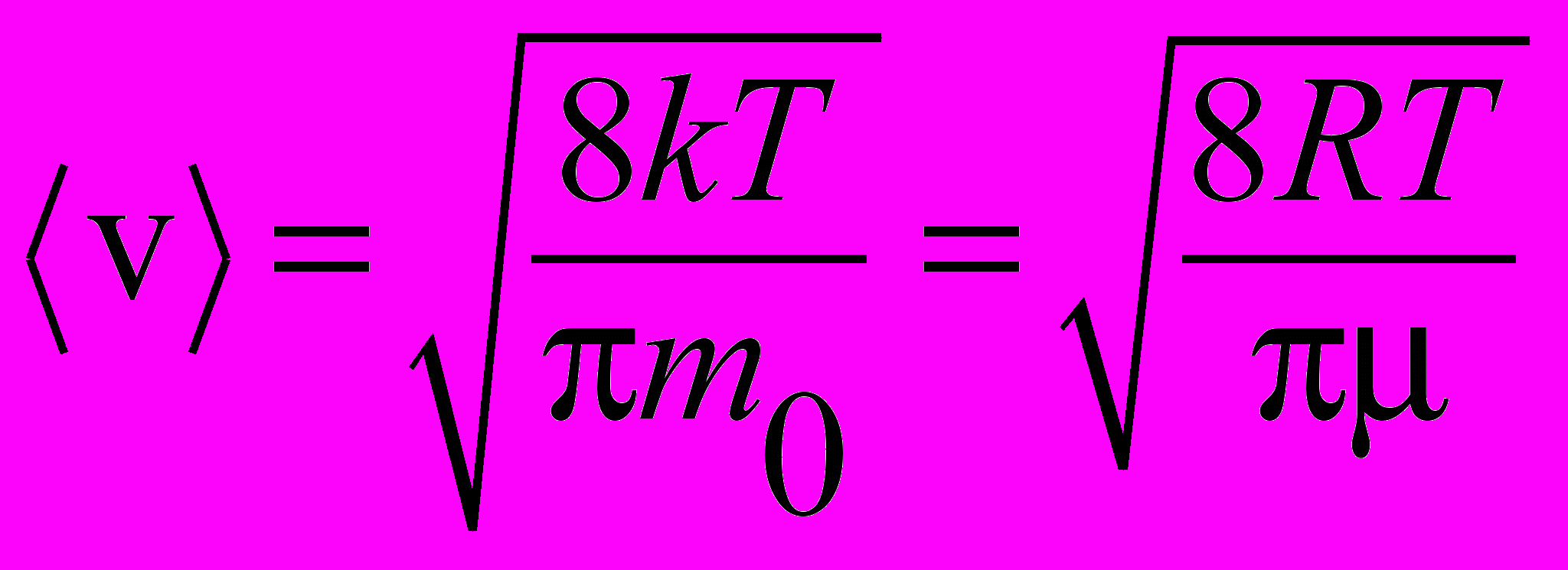 | 4.2 |
| Состояние равновесное | Если все параметры макроскопической системы имеют определенные значения, остающиеся при неизменных внешних условиях постоянными сколь угодно долго, то такое состояние системы называется равновесным, или статическим. | 4.3 |
| Состояние неравновесное | состояние термодинамической системы называется неравновесным, если c течением времени параметры термодинамической системы изменяются. | 4.3 |
| Среда окружающая | Тела, не входящие в термодинамическую систему, называются внешними телами или окружающей средой. | 4.3 |
| Степеней свободы число | Числом степеней свободы молекулы называется количество независимых координат, с помощью которых может быть однозначно задано положение молекулы в пространстве | 4.2 |
| Температура абсолютная | Измеряется по шкале Кельвина. Температура в кельвинах и температура в градусах Цельсия связаны следующим соотношением: 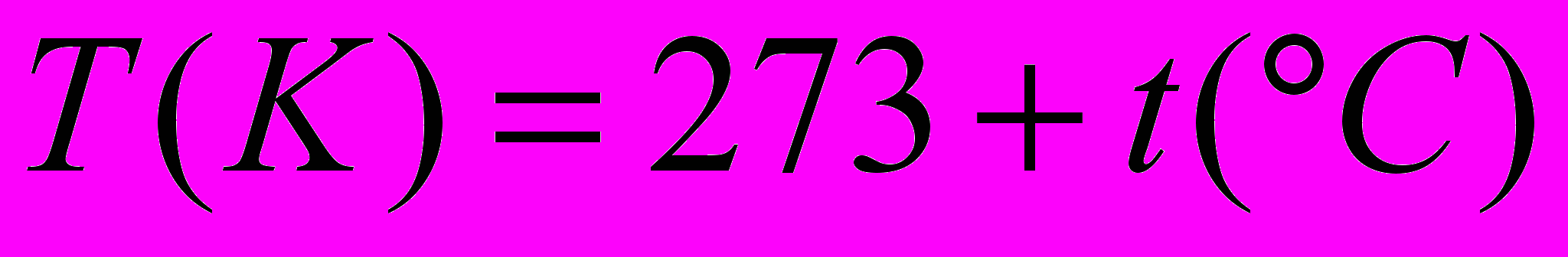 . . | 4.3 |
| Теорема о равнораспределении энергии по степеням свободы | На каждую поступательную и вращательную степень свободы молекулы приходится средняя энергия равная 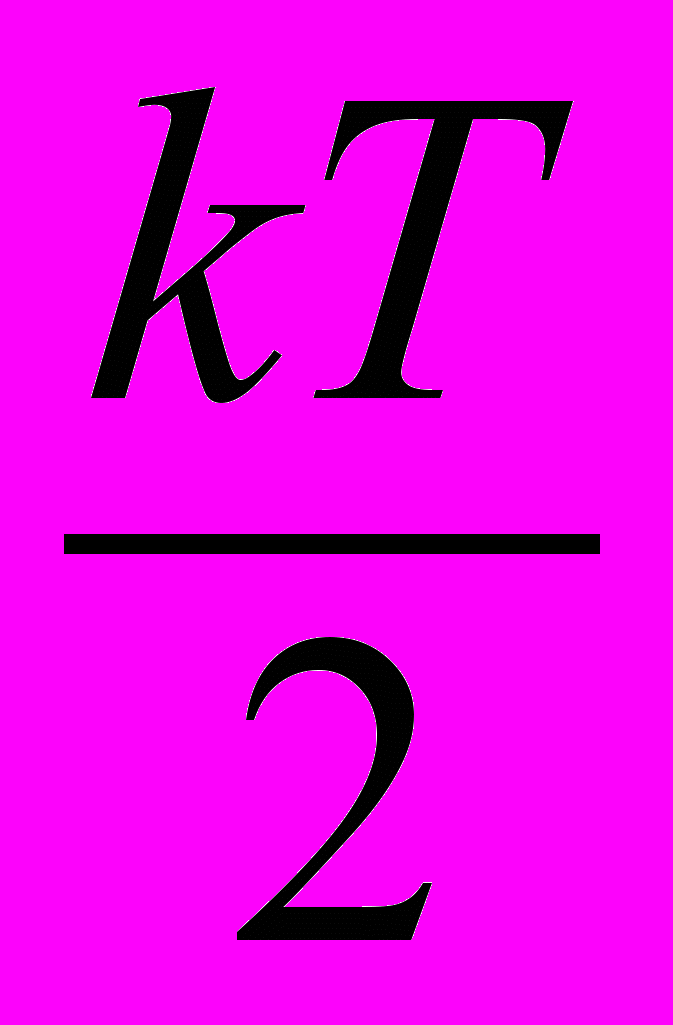 , а на каждую колебательную степень свободы приходится средняя энергия, равная kT, которая делится поровну между потенциальной и кинетической энергией. , а на каждую колебательную степень свободы приходится средняя энергия, равная kT, которая делится поровну между потенциальной и кинетической энергией. | 4.2 |
| Теорема Карно | КПД цикла Карно является верхним пределом для КПД тепловых машин, работающих в заданном интервале температур, не зависит от рабочего тела и от конструкции двигателя. | 4.5 |
Теплоемкость тела | Теплоемкостью тела (системы) называют количество тепла, которое необходимо сообщить этому телу, чтобы увеличить его температуру на один кельвин: 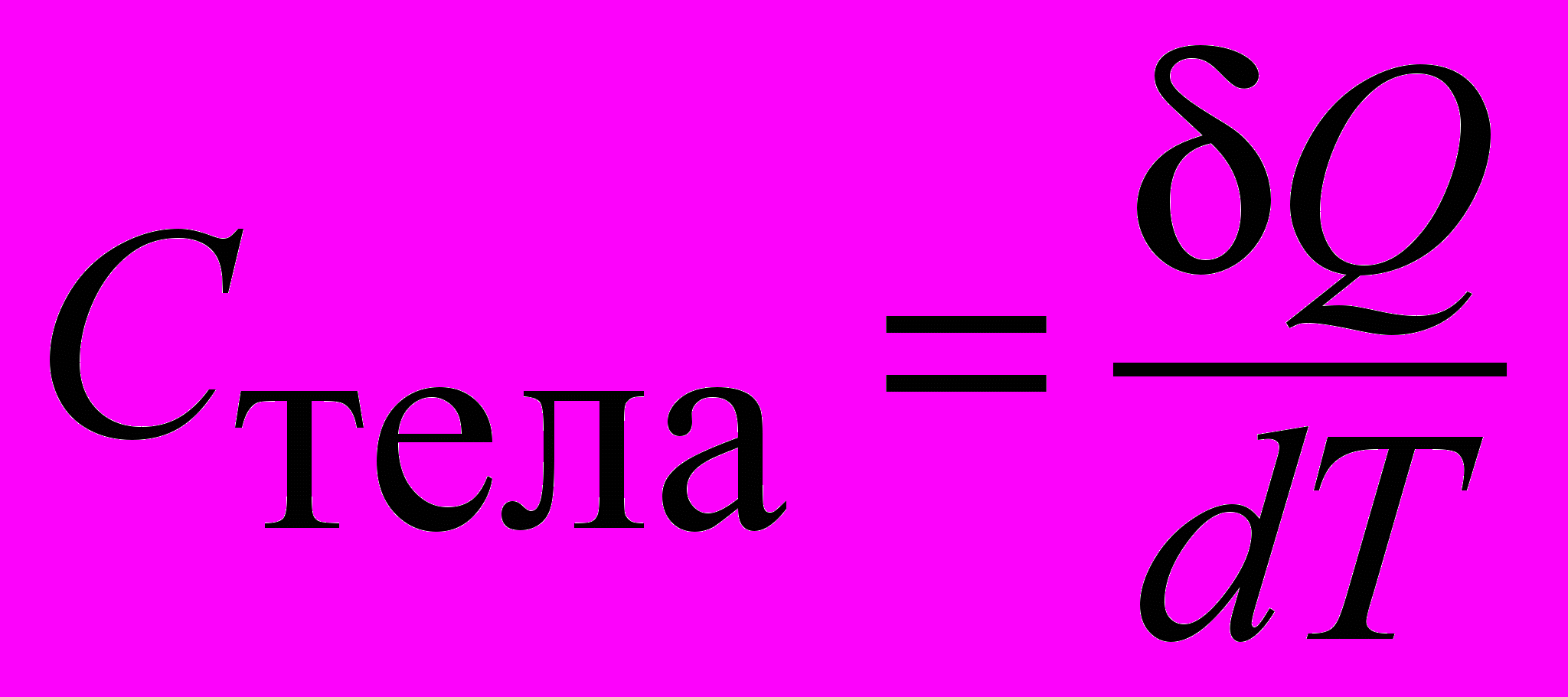 . . Размерность теплоемкости 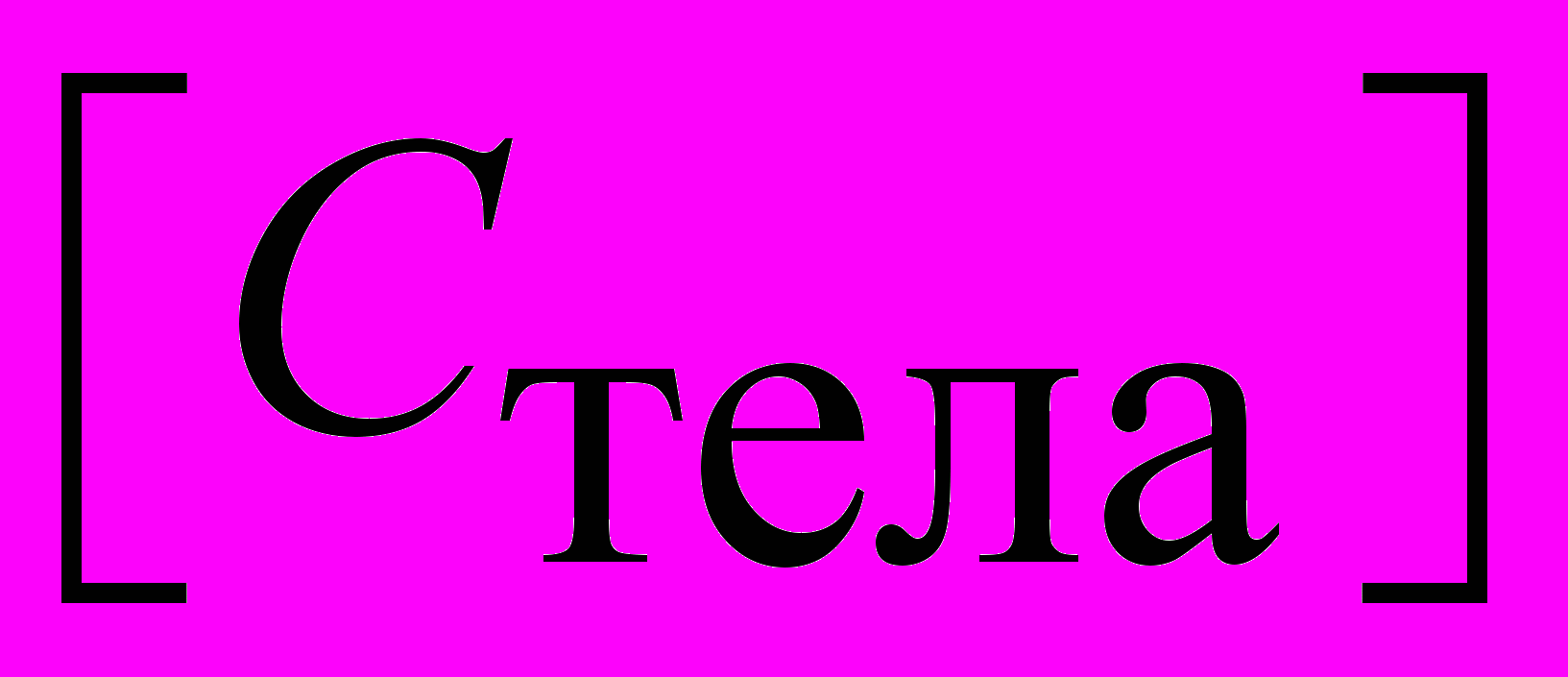 = = 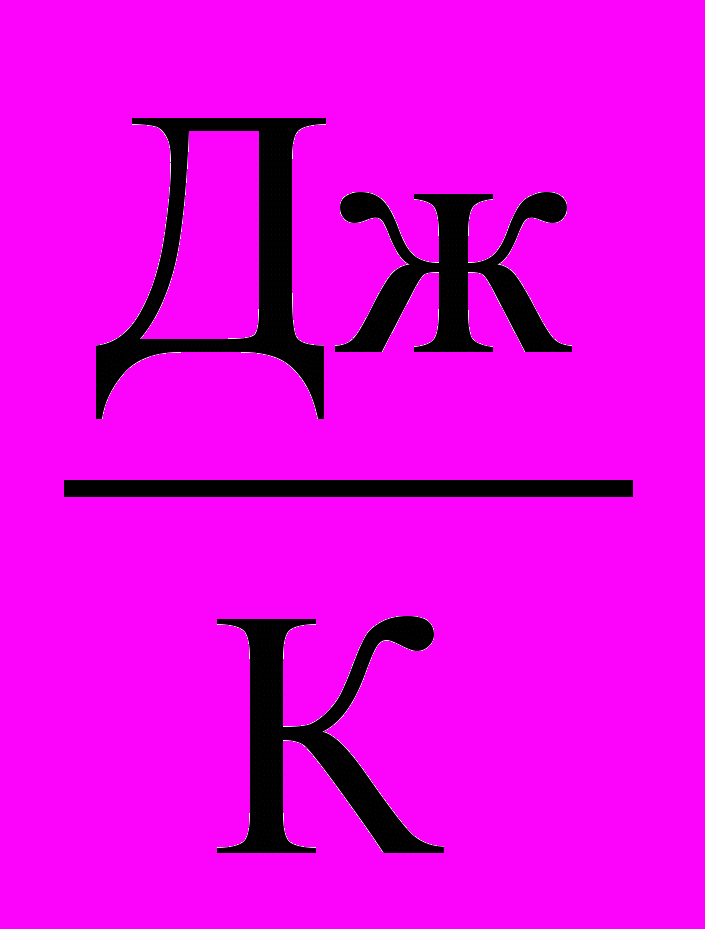 . . | 4.3 |
| Теплоемкость молярная | Теплоемкость, отнесенная к одному молю вещества, называется молярной теплоемкостью (C): 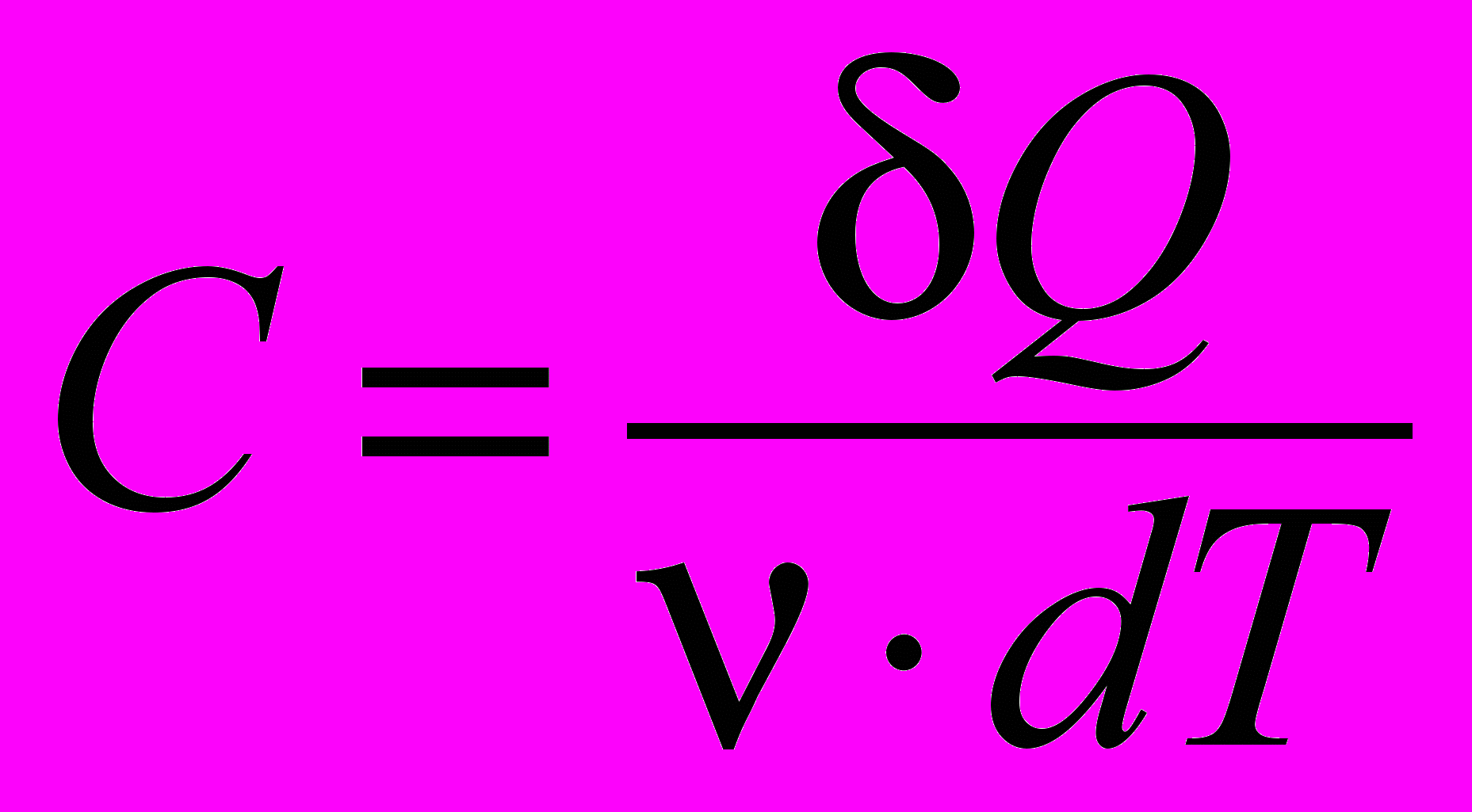 . .Размерность молярной теплоемкости [C] = 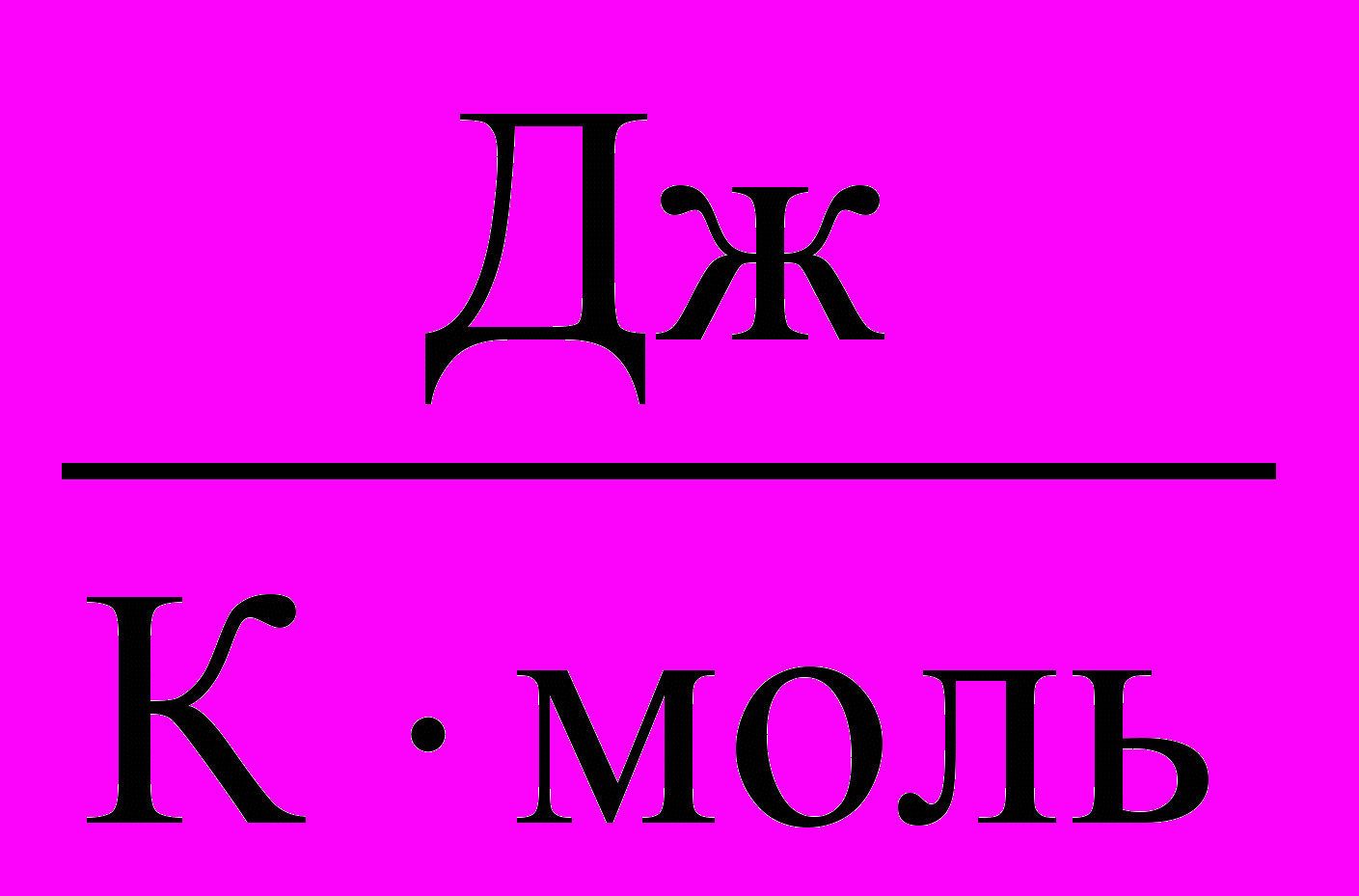 . . | 4.3 |
| Теплоемкость молярная изохорическая идеального газа | 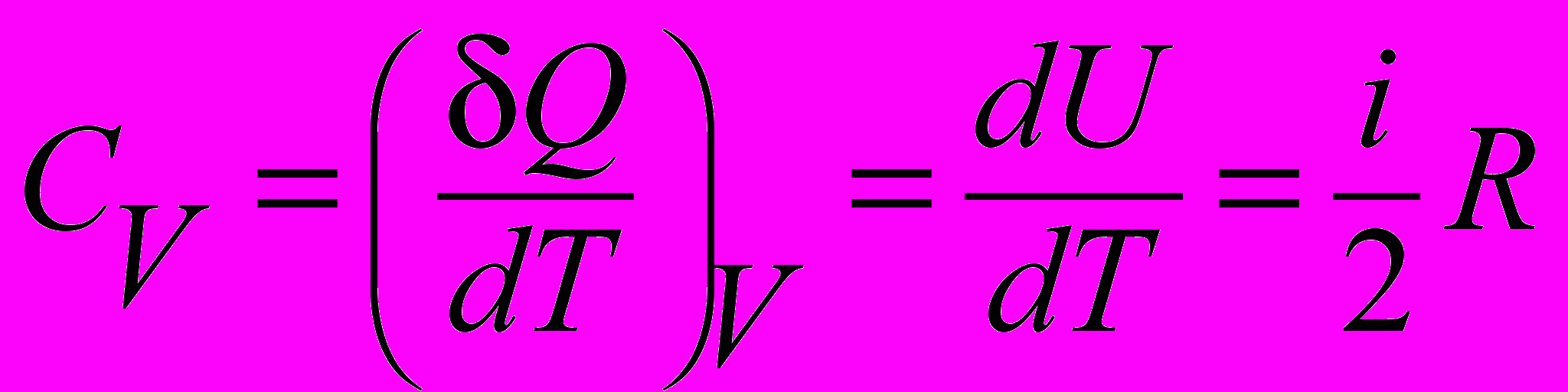 | 4.3 |
| Теплоемкость молярная изобарическая идеального газа | 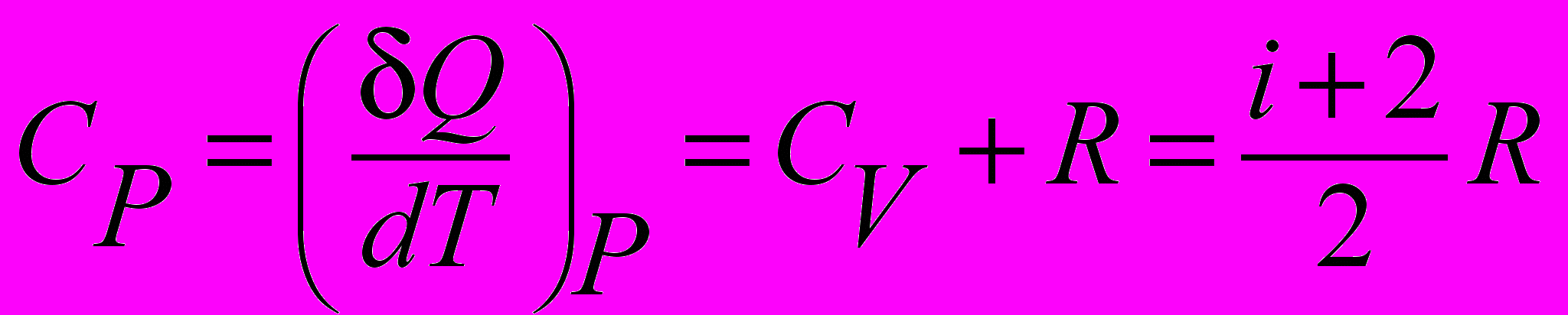 | 4.3 |
| Теплоемкость удельная | Теплоемкость, отнесенная к единице массы вещества, называется удельной теплоемкостью (c): 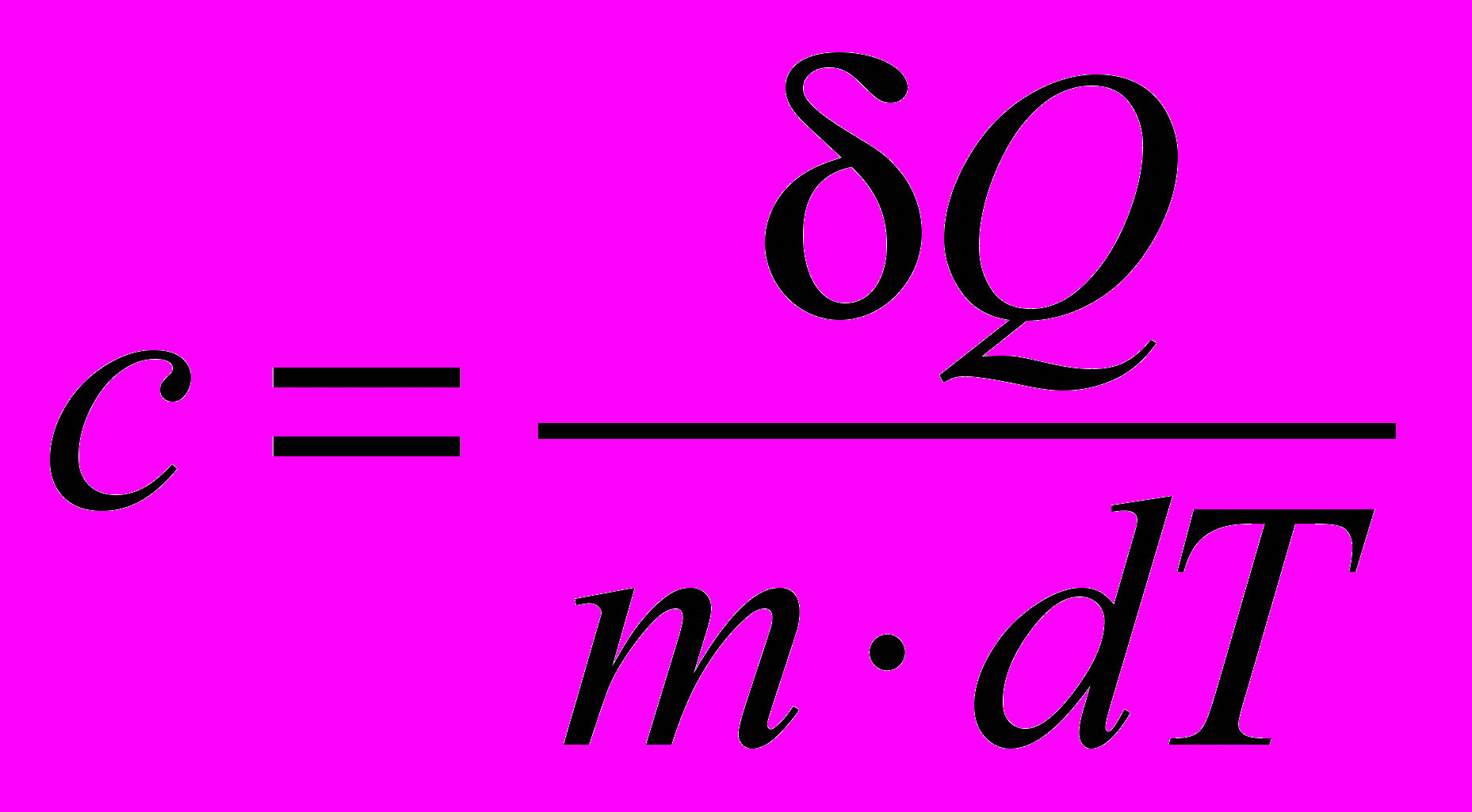 . . Размерность удельной теплоемкости [с] = 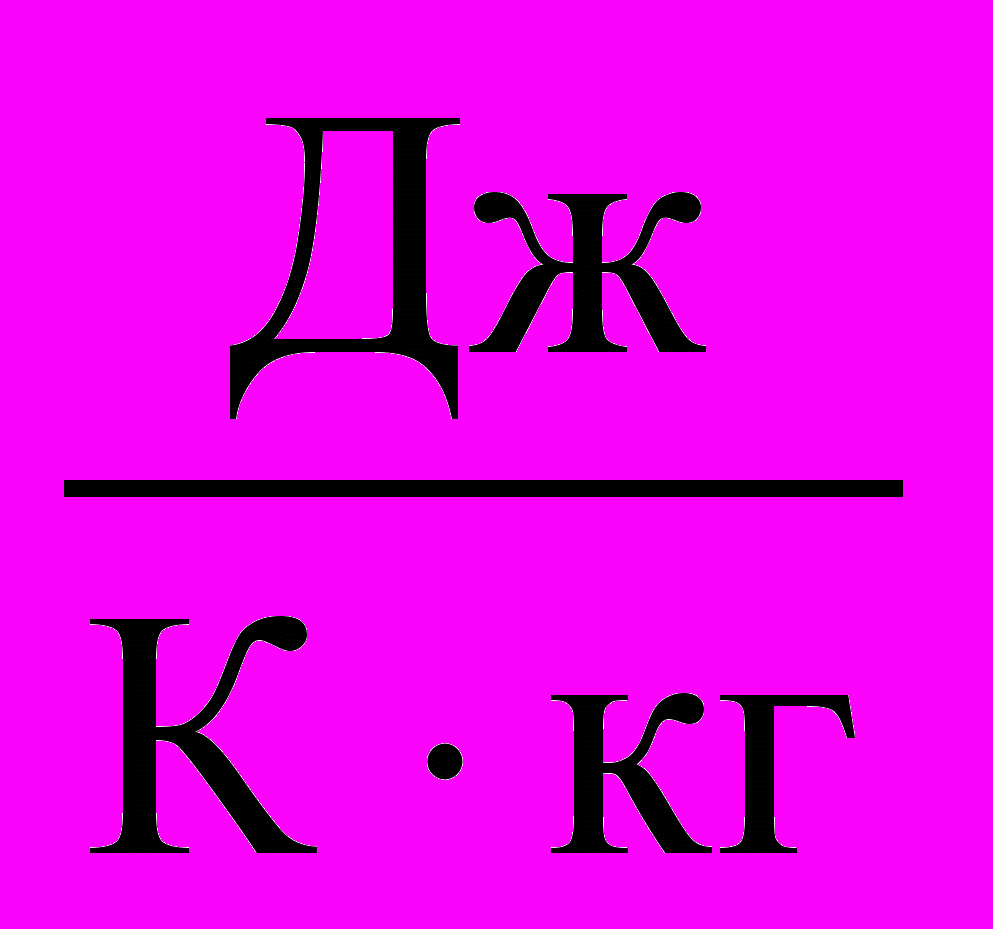 | 4.3 |
| Теплопередача | Процесс передачи тепла термодинамической системе без совершения работы над системой. | 4.3 4.5 |
| Теплота приведенная | Отношение количества теплоты, полученного системой в изотермическом процессе, к температуре этого процесса называется приведенной теплотой. | 4.5 |
| Термодинамика | Термодинамика – раздел физики, основанный на термодинамическом методе изучения макроскопических объектов как сплошной среды, не имеющей внутренней структуры. В основе термодинамики лежат несколько основных законов (начал), которые являются обобщением экспериментальных данных и выполняются независимо от конкретной природы макроскопической системы. Термодинамика возникла как наука о движущих силах, возникающих при тепловых процессах, о закономерностях превращения энергии в различных макросистемах, как теория тепловых машин. | 4.3 |
| Термодинамический метод | Термодинамический метод описания макроскопической системы состоит в изучении физических свойств системы путем анализа условий и количественных соотношений для процессов превращения энергии в системе. | 4.3 |
| Уравнение основное МКТ | 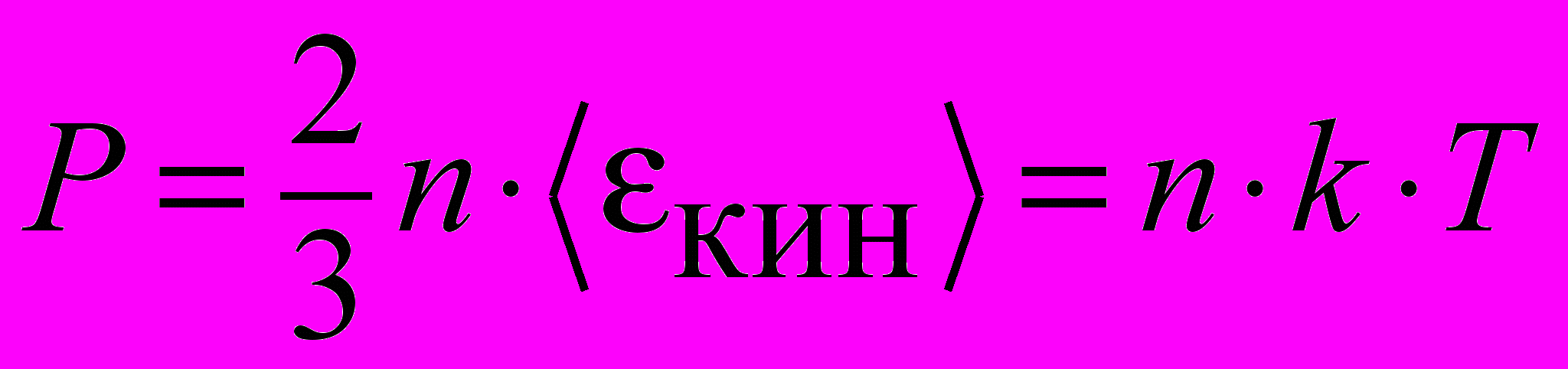 | 4.1 |
| Уравнение Пуассона | 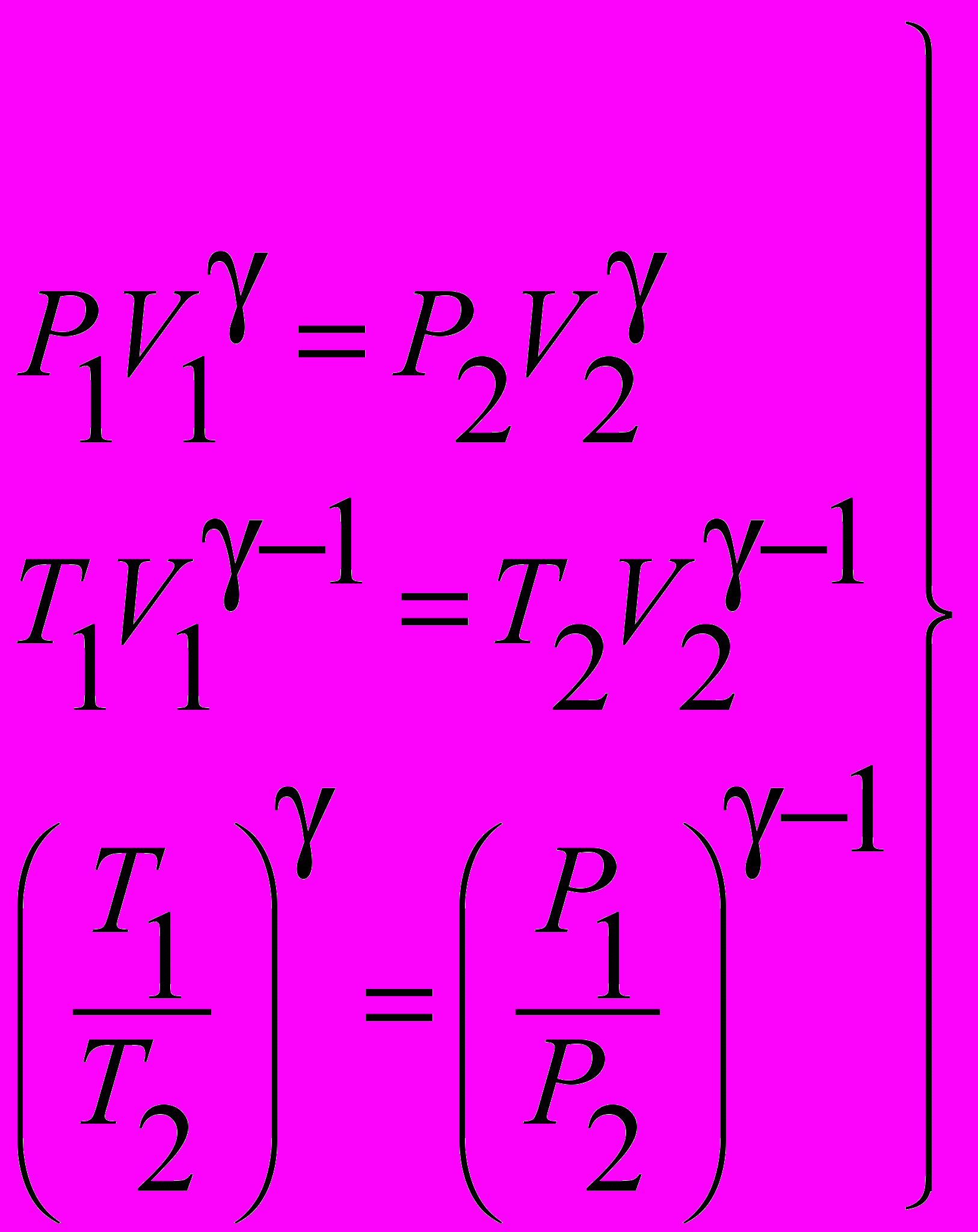 | 4.4 |
| Уравнение состояния идеального газа (Менделеева-Клапейрона) | 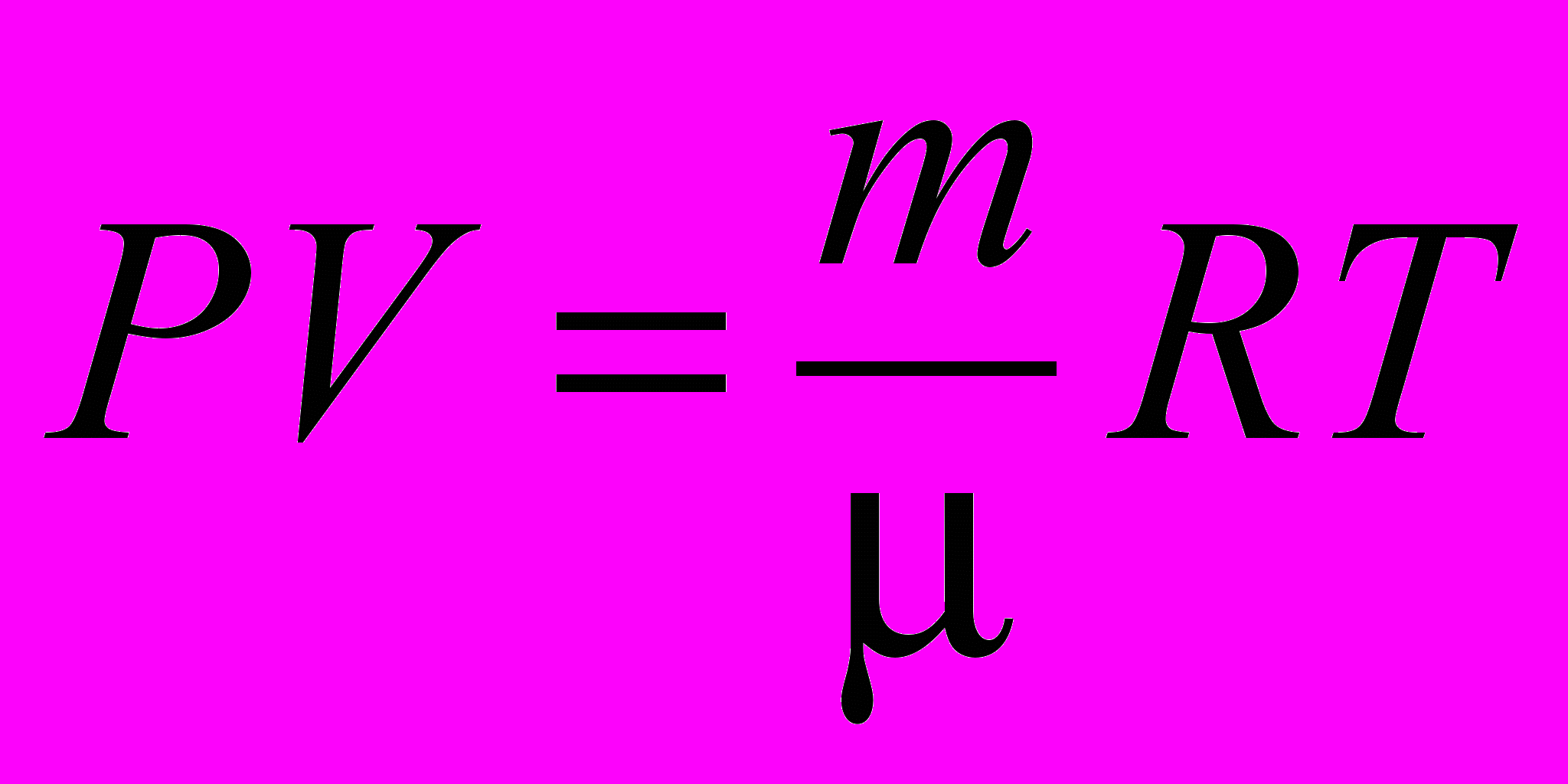 | 4.1 |
| Уравнение Майера | 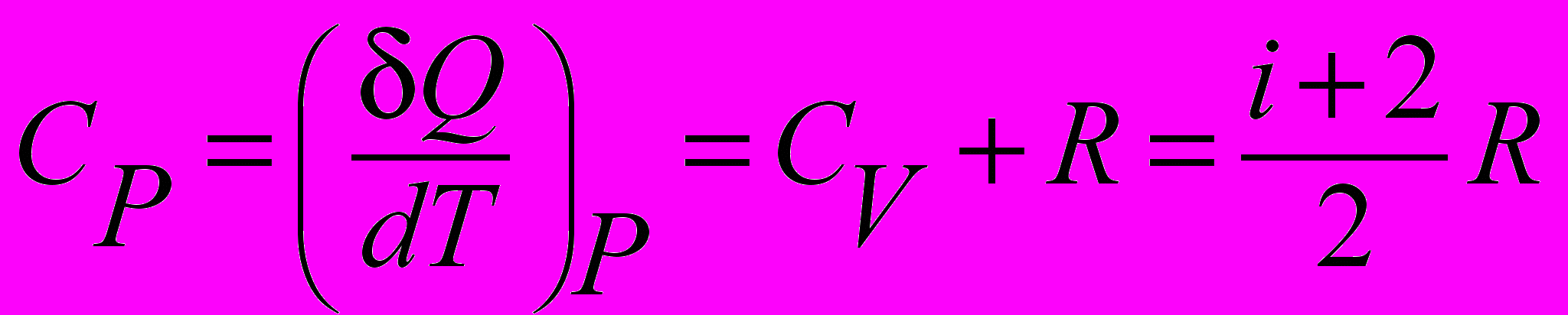 | 4.3 |
| Уравнение основное термодинамики | Если система совершает равновесный переход из состояния 1 в 2 , то изменение энтропии равно: 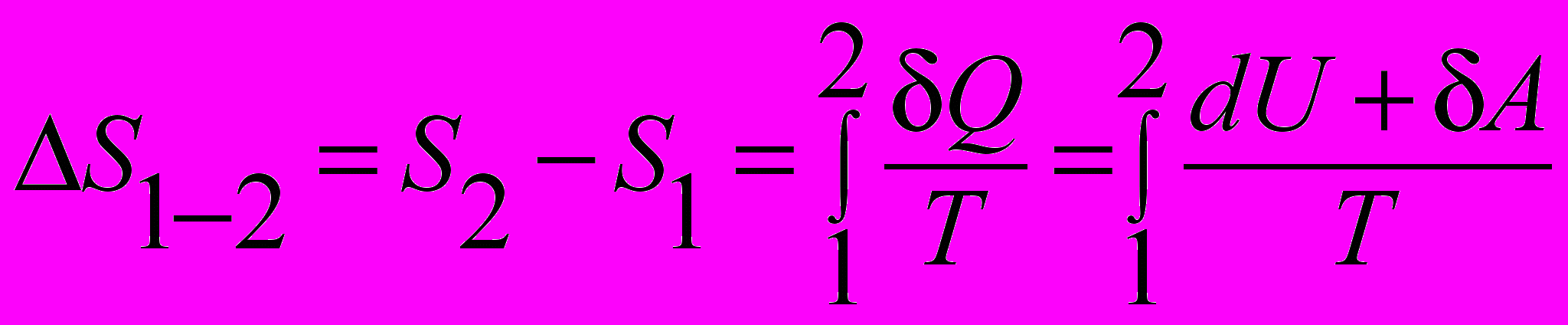 . . | 4.5 |
| Условие нормировки для функции плотности вероятности | См. Нормировки условие для функции плотности вероятности | |
| Формула Больцмана для энтропии (принцип Больцмана) | 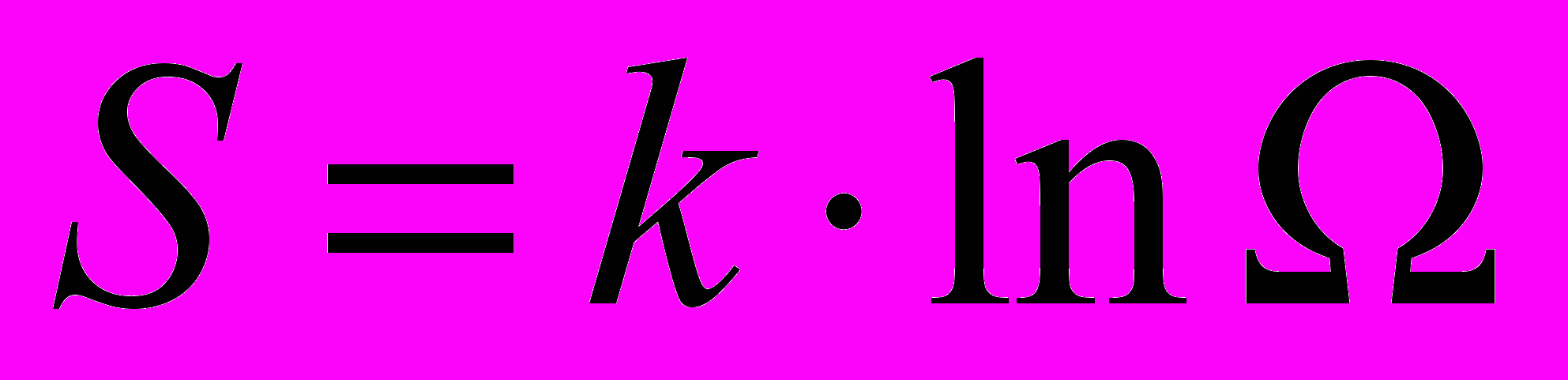 , ,где Ω – термодинамическая вероятность состояния системы. | 4.5 |
| Формула барометрическая | Если температура воздуха Т и ускорение свободного падения g не меняются с высотой, то давление воздуха Р на высоте h, отсчитанной от некоторого уровня, принятого за начальный, связано с давлением Р0 на этом начальном уровне экспоненциальной зависимостью: 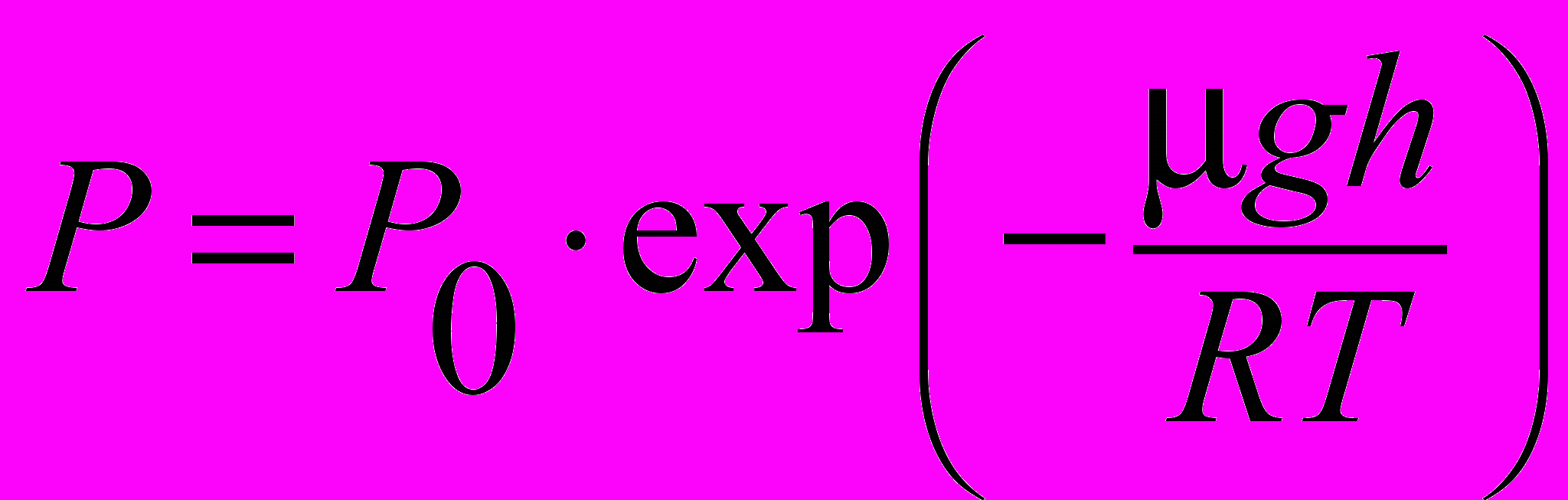 . . | 4.2 |
| Функция Максвелла для распределения молекул по скоростям | 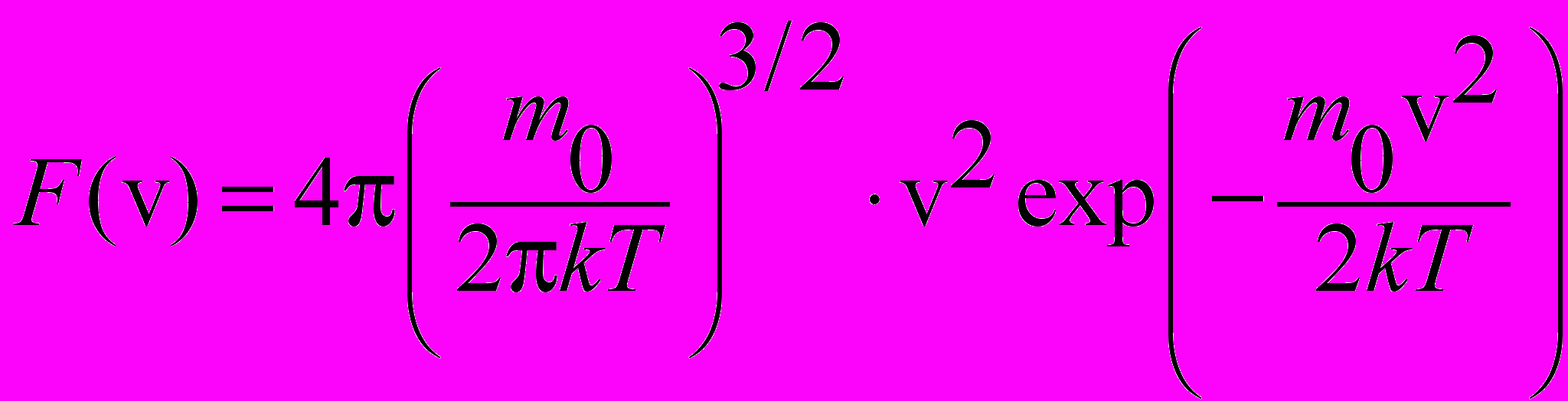 | 4.2 |
| Функция Максвелла для распределения молекул по кинетическим энергиям | 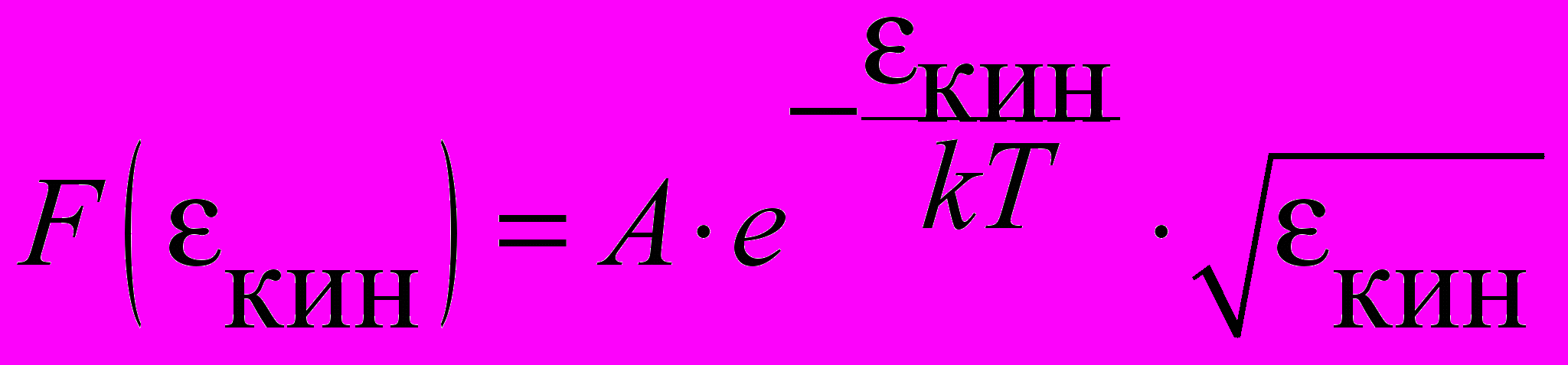 , ,где А 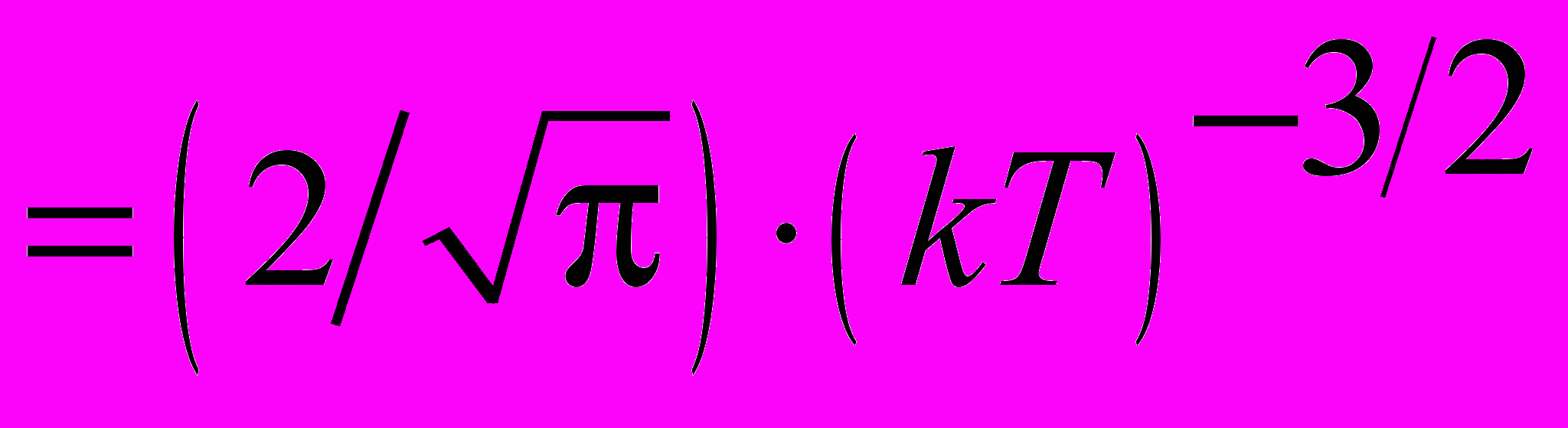 – нормировочный множитель. – нормировочный множитель. | 4.2 |
| Функция Больцмана для распределения молекул по потенциальным энергиям | 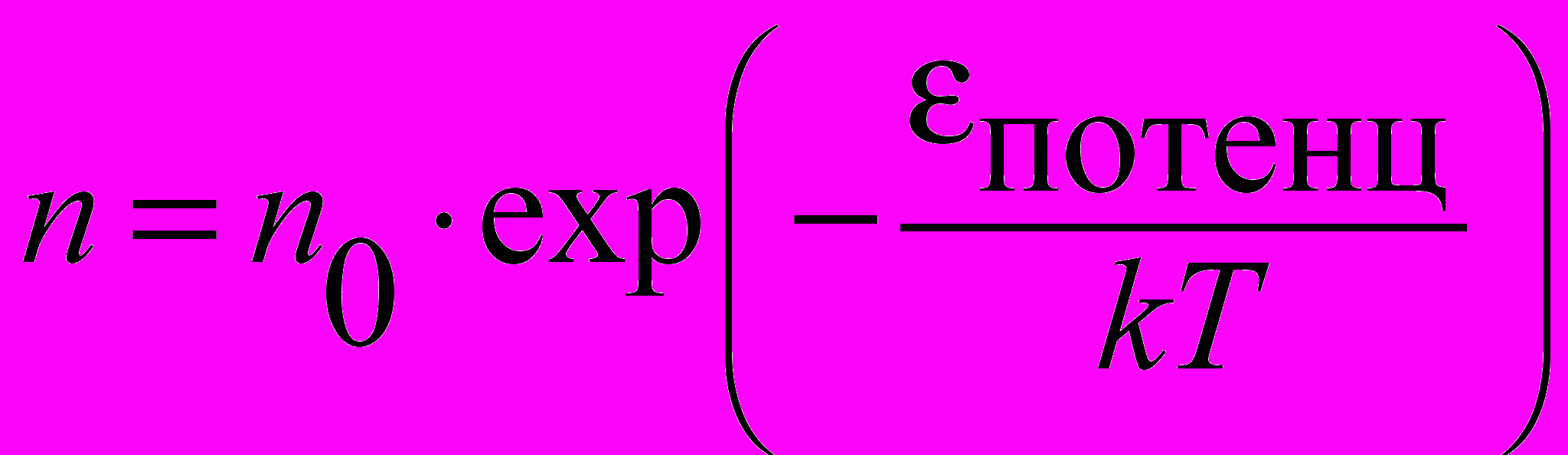 | 4.2 |
| Холодильник | Тело, температура которого меньше температуры рабочего тела. | 4.5 |
| Функция Больцмана для распределения молекул по высоте | 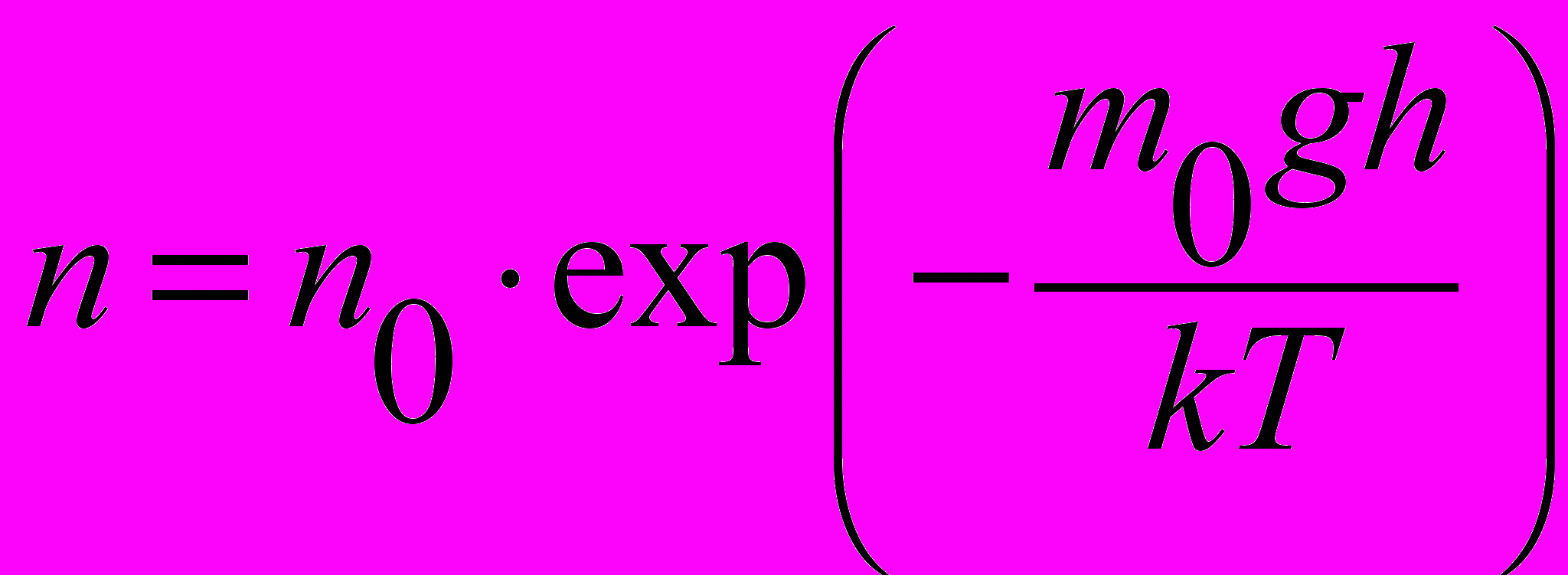 | 4.2 |
| Цикл | Круговым процессом или циклом, называют такой процесс, в результате которого термодинамическая система возвращается в исходное состояние. | 4.5 |
| Цикл Карно | Обратимый циклический процесс, состоящий из двух изотерм и двух адиабат. | 4.5 |
| Цикл прямой | Если за цикл газ совершает положительную работу, то такой круговой процесс называется прямым циклом, или циклом тепловой машины (теплового двигателя). При прямом цикле система получает некоторое количество тепла, и газ совершает работу за счет сообщенной ему теплоты. | |
| Цикл обратный | Если за цикл газ совершает отрицательную работу, то такой круговой процесс называется обратным циклом, или циклом холодильной машины (холодильника). В обратном цикле над газом совершается работа и от него отводится тепло. | 4.5 |
| Число Авогадро | числом Авогадро называется число атомов, содержащееся в 12 граммах углерода или в одном моле вещества: 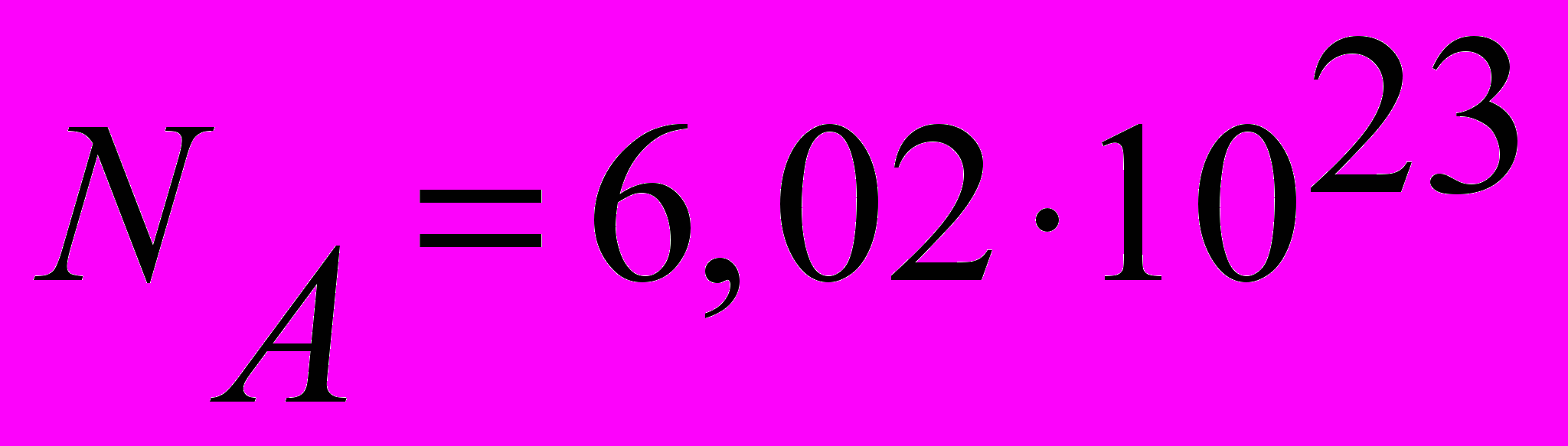 моль-1. моль-1. | 4.1 |
| Число степеней свободы | См. Степеней свободы число | 4.2 |
| Энергия внутренняя идеального газа | Внутренняя энергия идеального газа равна суммарной кинетической энергии движения молекул: 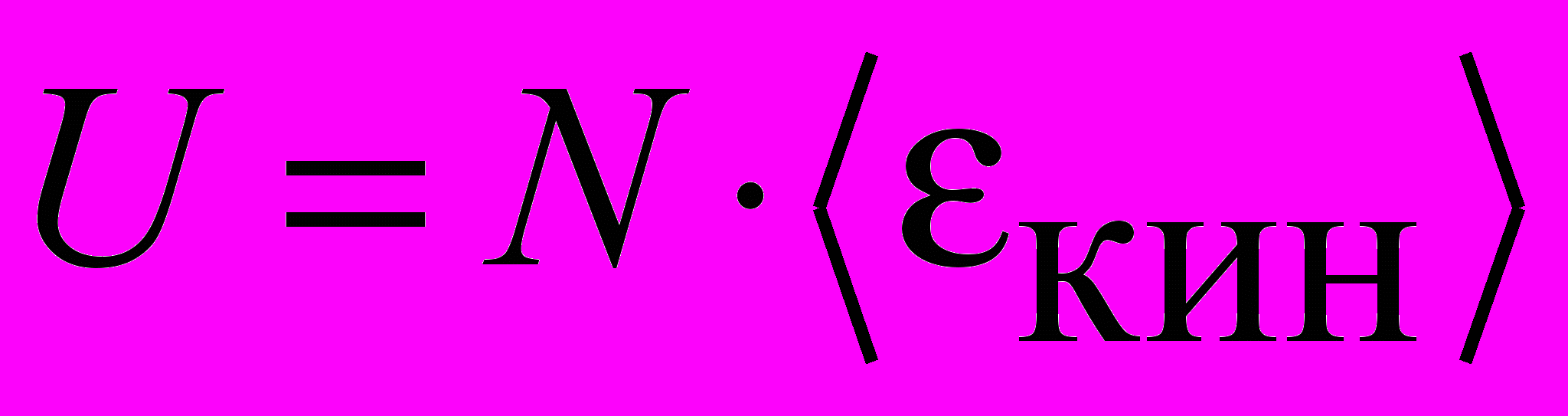 . .U – функция состояния газа, зависящая только от параметров газа в данном состоянии и не зависящая от способа, каким газ был приведен в это состояние. Внутренняя энергия идеального газа зависит только от температуры газа. | 4.3 |
| Энергия внутренняя одного моля идеального газа | 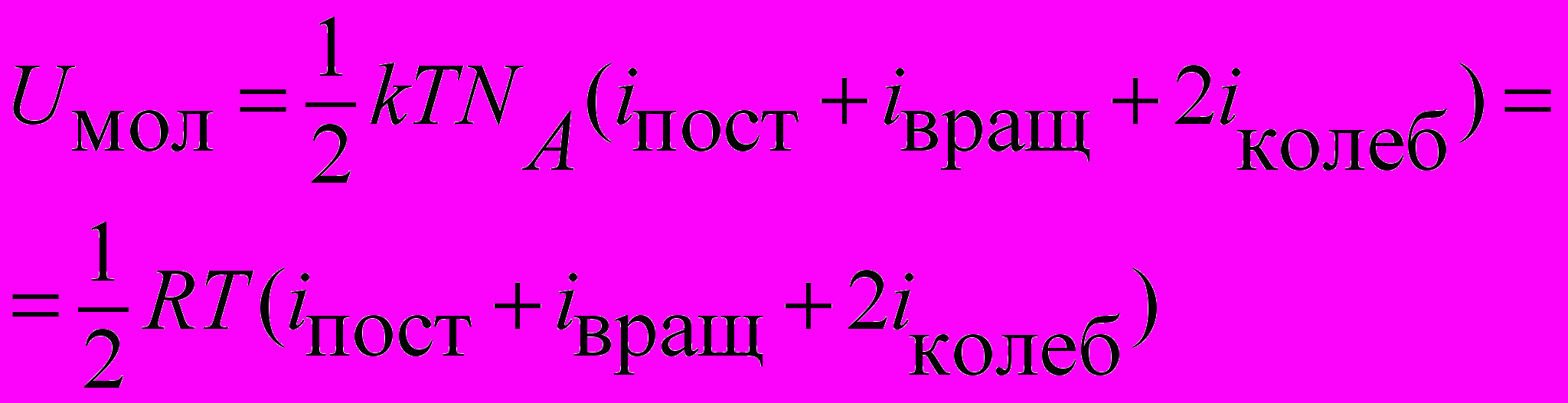 | 4.3 |
| Энергия внутренняя произвольной массы газа идеального газа | 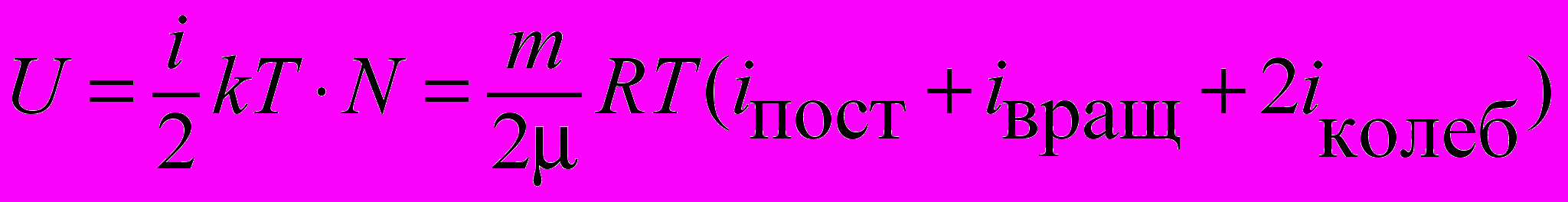 | 4.3 |
| Энергия внутренняя термодинамической системы | Аддитивная функция состояния термодинамической системы. Внутренней энергией термодинамической системы называется энергия тел, входящих в систему, за вычетом кинетической энергии тел, как целого и потенциальной энергии взаимодействия с телами, не входящими в систему. | 4.3 |
| Энергия средняя кинетическая поступательного движения | 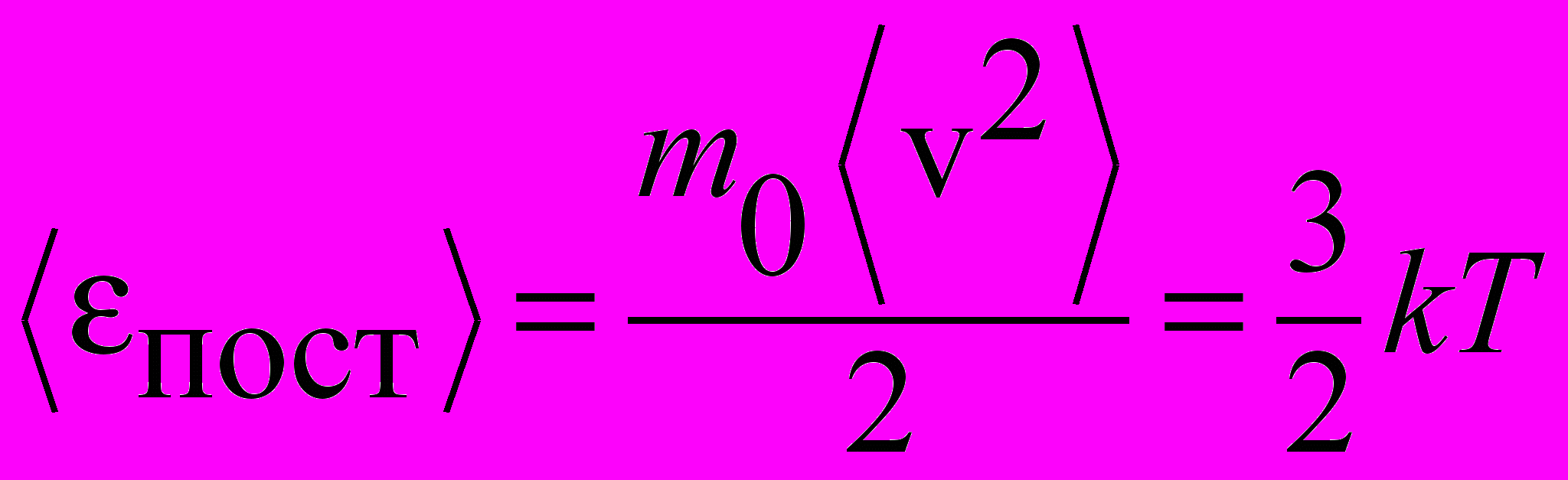 | 4.2 |
| Энтропия | Понятие энтропии в термодинамике применяется для определения меры необратимого рассеяния энергии как однозначная аддитивная функция состояния термодинамической системы, остающаяся постоянной при равновесных адиабатических процессах: 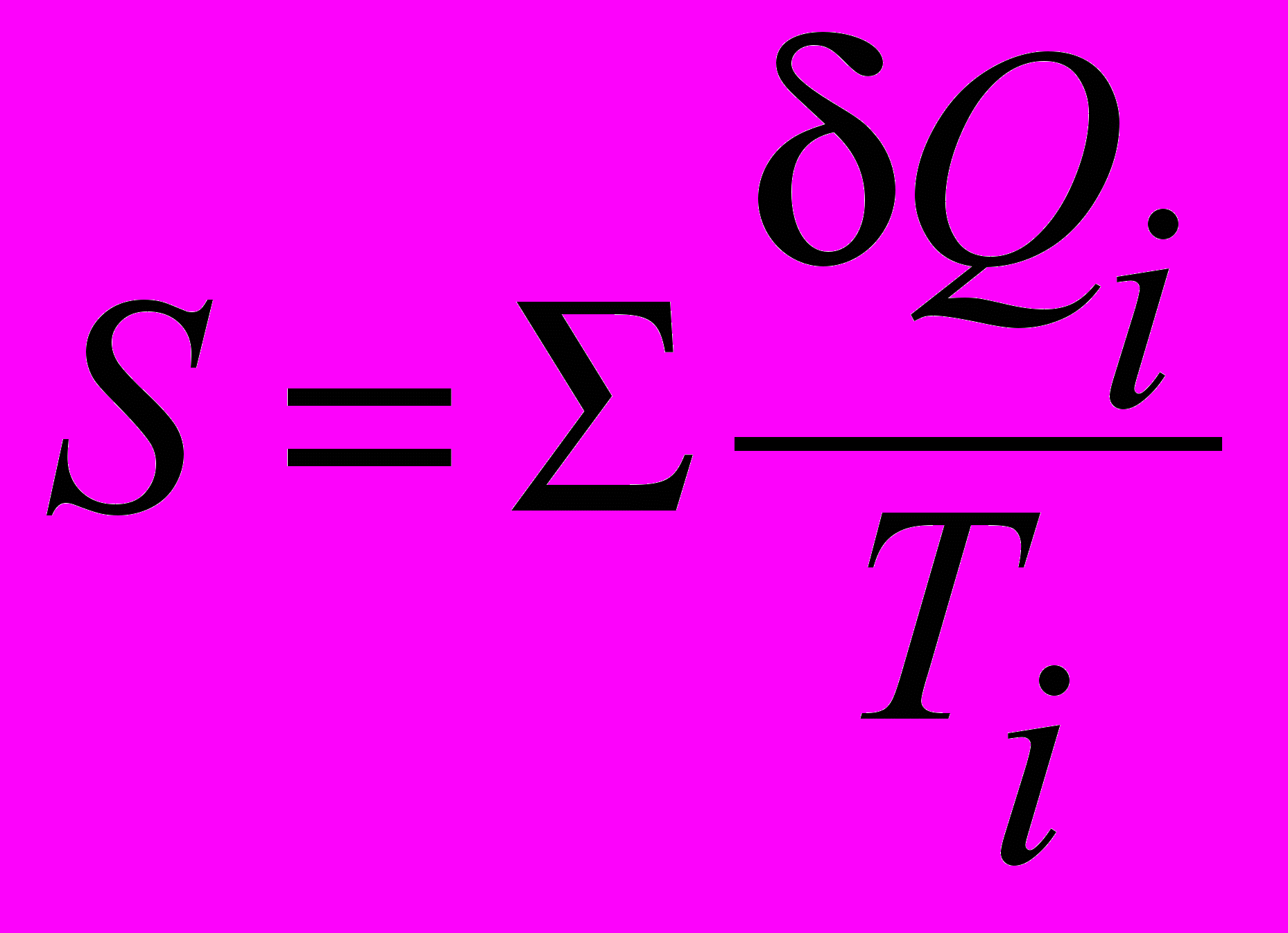 В статистической физике - как мера вероятности осуществления данного макроскопического состояния системы. | 4.5 |
| Энтропия –изменение в изолировангных системах в обратимых процессах | 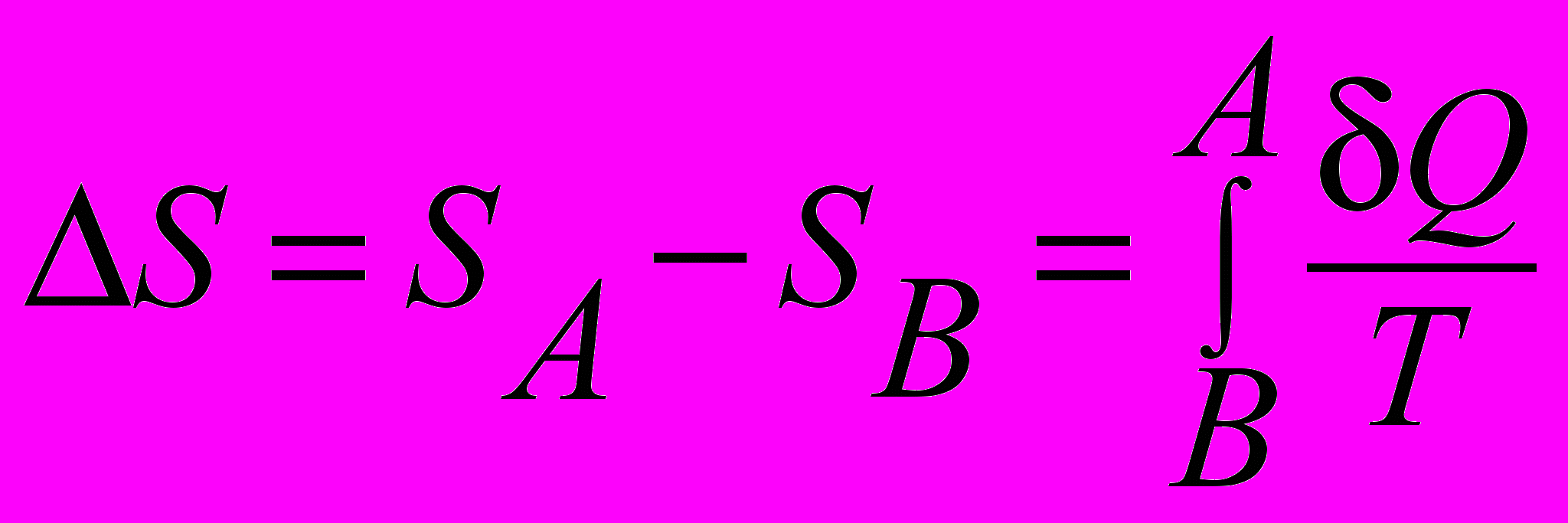 | 4.5 |
| Энтропия–изменение в изолированных в необратимых процессах | 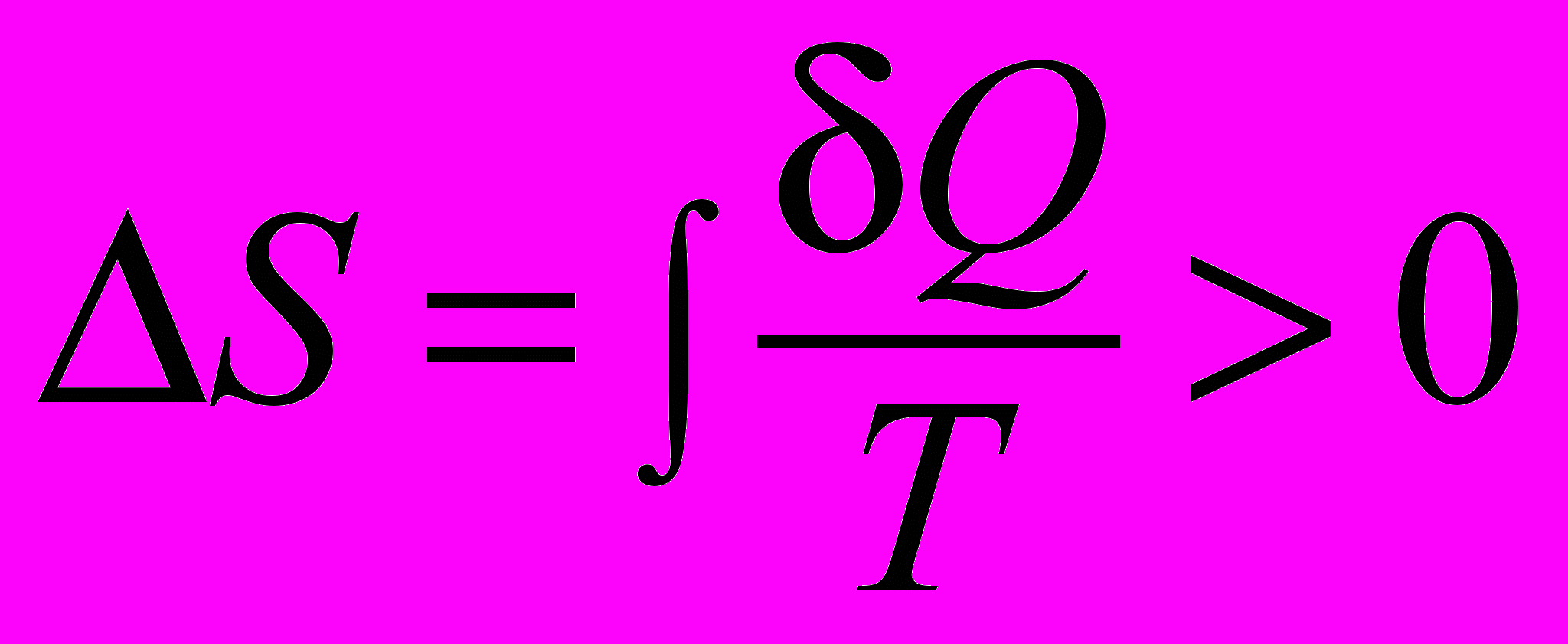 | 4.5 |
| Энтропия – изменение в открытых системах | Энтропия открытых (неизолированных) систем может вести себя любым образом. | 4.5 |
