Geum.ru

Винокур, В. Н. Орлов, А. Г. Иванов, В. Л

Вид материалаДокументы

Содержание


Расчет циклической компоненты в аддитивной
Расчет скорректированной циклической компоненты
Расчет выровненных значений T + E, построенного тренда T
Расчет линейного тренда T
Подобный материал:
Т.Ю. Винокур, В.Н. Орлов, А.Г. Иванов, В.Л. Сусликов


РАЗРАБОТКА МАТЕМАТИЧЕСКОЙ МОДЕЛИ ДЛЯ ОЦЕНКИ ДИНАМИКИ ЗАБОЛЕВАЕМОСТИ И СМЕРТНОСТИ ОТ СЕРДЕЧНО-СОСУДИСТЫХ ЗАБОЛЕВАНИЙ НА ТЕРРИТОРИИ ЧУВАШСКОЙ РЕСПУБЛИКИ


ГУЗ «Республиканский кардиологический диспансер»

ФГОУ ВПО «Чувашская государственная сельскохозяйственная академия»

ФГОУ ВПО «Чувашский государственный университет им. И.Н. Ульянова»


Сохраняющаяся в течение длительного времени (более 25 лет) территориальная неравномерность показателей заболеваемости и смертности по классу МКБ ВОЗ № I 00  I 99 «Болезни системы кровообращения» населения Чувашской Республики, что констатируется в ежегодных государственных докладах, требует сосредоточения внимания на разработку мер по первичной профилактике этих болезней.

Исследователями было установлено, что сердечно-сосудистые заболевания сердца (ССЗ) территориально приурочены к юго-западной части республики [14,6]. Здесь на протяжении последних 10 лет c 1996 по 2005 годы наблюдается динамический рост показателей распространенности ССЗ с учетом возрастной стандартизации по переписи 2002 года. Оценивая динамику показателя распространенности ССЗ в Алатырском, Шумерлинском и Порецком районах, следует отметить его нарастание за этот период на 35%. В то же время в ряде районов восточной части республики стабильно регистрируются низкие показатели распространенности Проведенное нами ССЗ. К ним относятся: Батыревский, Янтиковский и Комсомольский районы.

В соответствии с последними данными, полученными нами из ежегодных Государственных докладов, в структуре смертности, на первом месте стоят болезни системы кровообращения и составляют в среднем 50,7%.

Анализируя сведения Республиканского медицинского информационно-аналитического центра об умерших от острого инфаркта миокарда (ОИМ), мы обратили внимание на то обстоятельство, что самые высокие показатели смертности регистрируются в юго-западной части республики (Алатырский, Порецкий, Шумерлинский районы). В то же время в восточной части республики выделяются районы (Янтиковский, Батыревский, Комсомольский), в которых показатели смертности от ОИМ в 2 раза ниже средне-республиканских показателей и в 4 раза ниже данных по юго-западной части республики.

Сравнительный анализ половозрастных, национальных и профессиональных особенностей распространения ССЗ выявил вышеуказанные закономерности, о которых сообщалось ранее многочисленными исследователями [13,6].

На основании данных заболеваемости и смертности от ССЗ за 10 лет (1996 – 2005 гг.) на территории Чувашской Республики нами были построены математические модели тенденции развития указанных выше показателей заболеваемости и смертности за рассматриваемый период методом скользящей средней и учетом циклической компоненты [5], как для опытных (Алатырский, Порецкий), так и для контрольных (Батыревский, Янтиковский) территорий. Не утомляя многочисленными расчетами, для представления алгоритма [5] его проведения, ниже приводим вычисления и графики показателя заболеваемости ССЗ и математической модели ее развития для Порецкого района.


Таблица 1

Расчет циклической компоненты в аддитивной

модели заболеваемости в Порецком районе


Номер года
Показатель заболеваемости болезней сердца
Сумма за 4 периода
Скользящая средняя за 4 периода
Централизован-ная скользящая средняя
Оценка циклической компоненты

1
22,53






























2
30,06


















120,56
30,14






3
29,2






31,6875
-2,4875







132,94
33,235






4
38,77






34,065
4,705







139,58
34,895






5
34,91






38,08
-3,17







165,06
41,265






6
36,7






43,06625
-6,36625







179,47
44,8675






7
54,68






47,265
7,415







198,65
49,6625






8
3,18






























9
54,09













Таблица 2

Расчет скорректированной циклической компоненты

в аддитивной модели заболеваемости


Показатели
Период,

годы
Кварталы года

1
2
3
4




1






-2,4875
4,705

2
-3,17
-6,36625
7,415



За каждый год периода



-3,17
-6,36625
4,9275
4,705

Средняя оценка циклической компоненты за i -ый год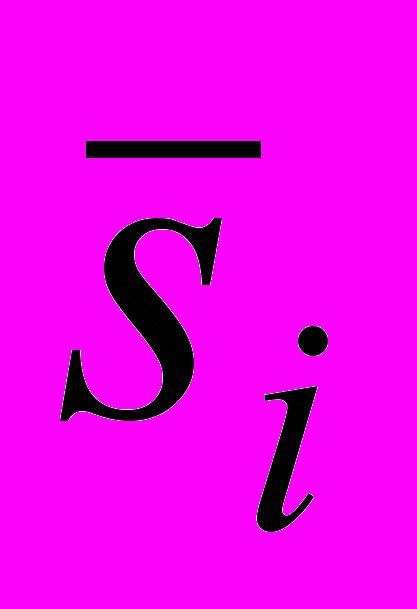




-1,585
-3,18313
2,46375
2,3525

Скорректированная циклическая компонента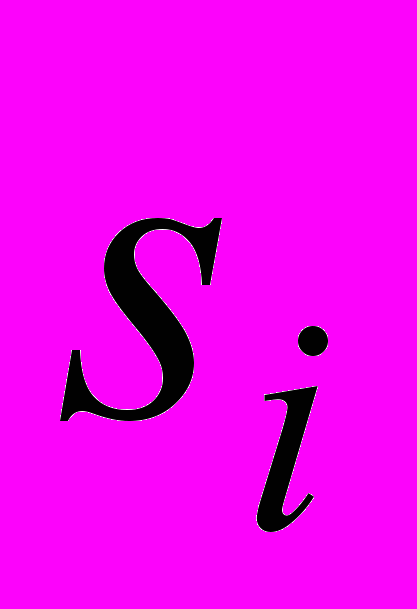




-1,59703
-3,19516
2,451719
2,340469

Расчет корректирующего коэффициента:

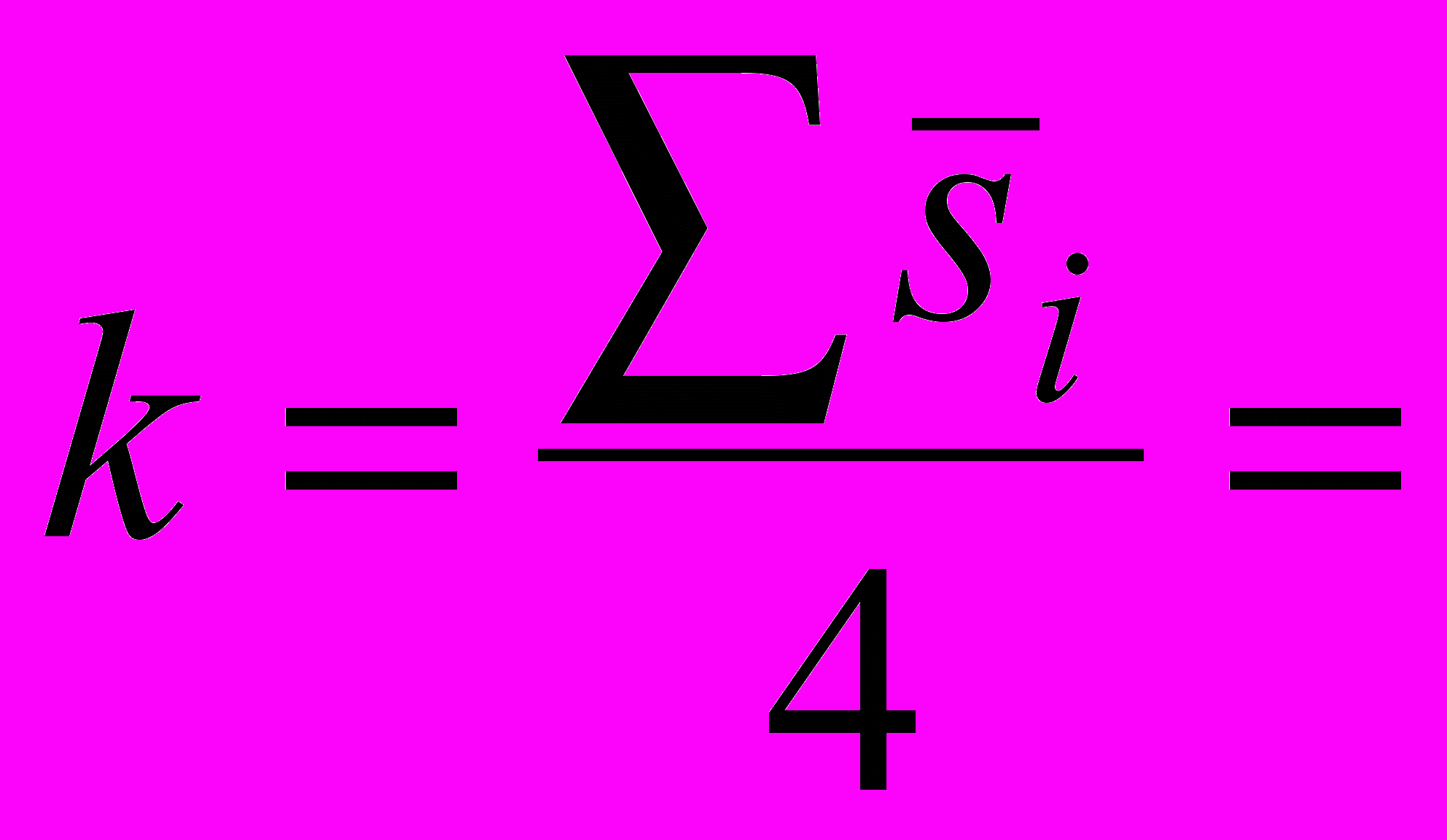0,012031,

где 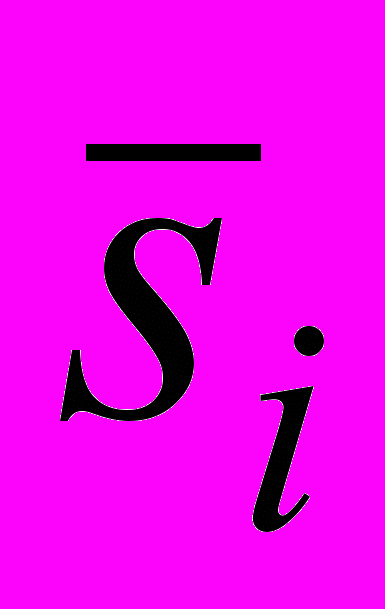 средняя оценка циклической компоненты.

Расчет скорректированной циклической компоненты по формуле:

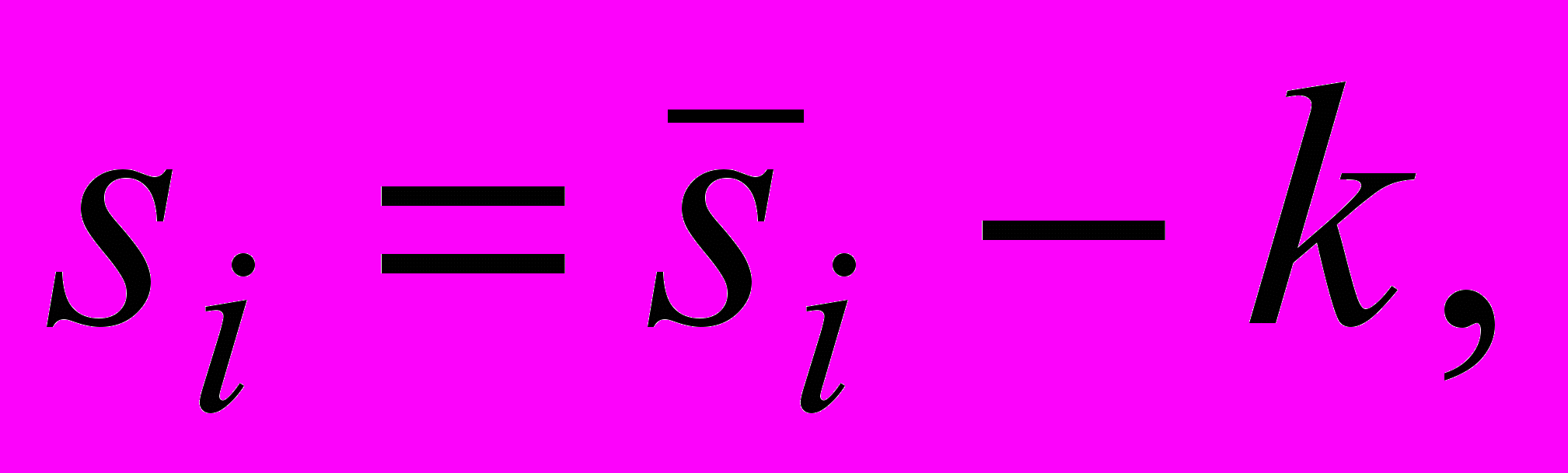i =1, 2, 3, 4.

Контроль по скорректированной циклической компоненте:



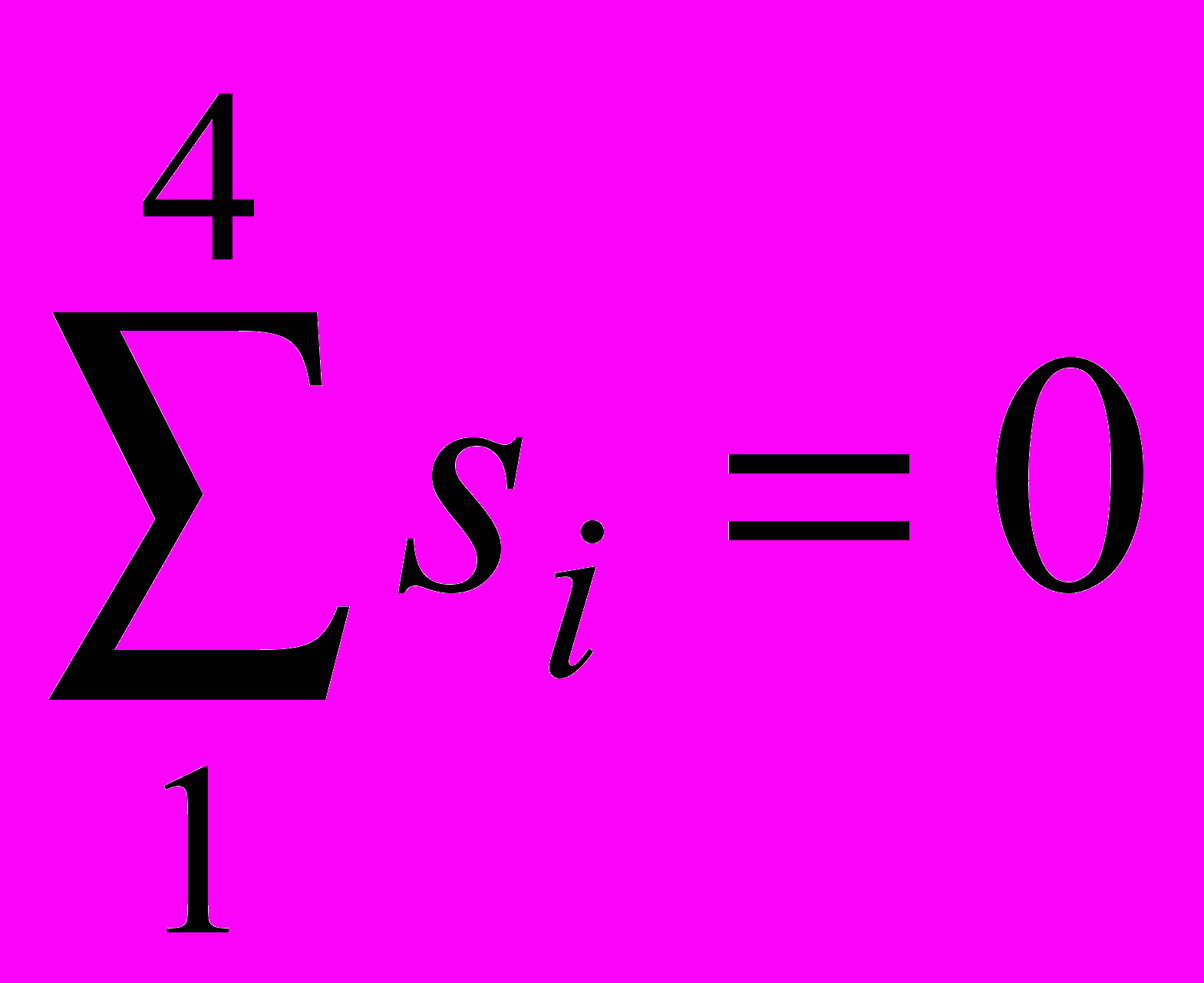
Таблица 3

Расчет выровненных значений T + E, построенного тренда T

и ошибки E в аддитивной модели


t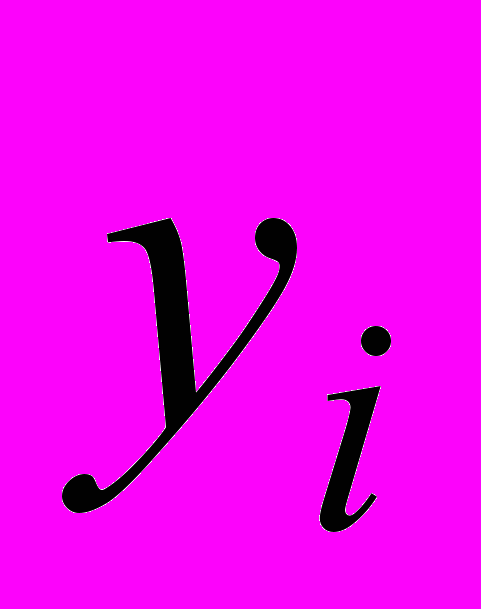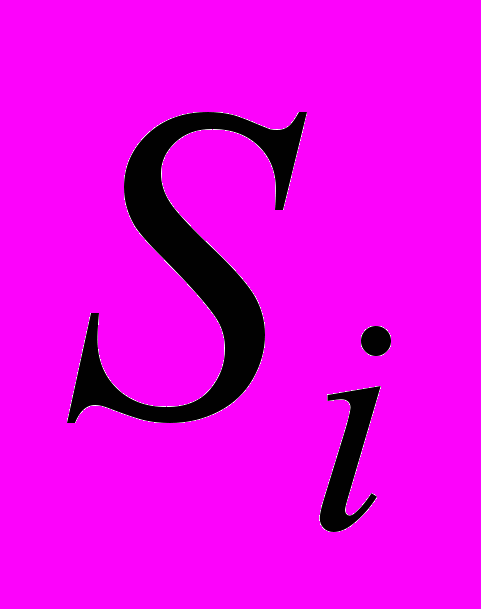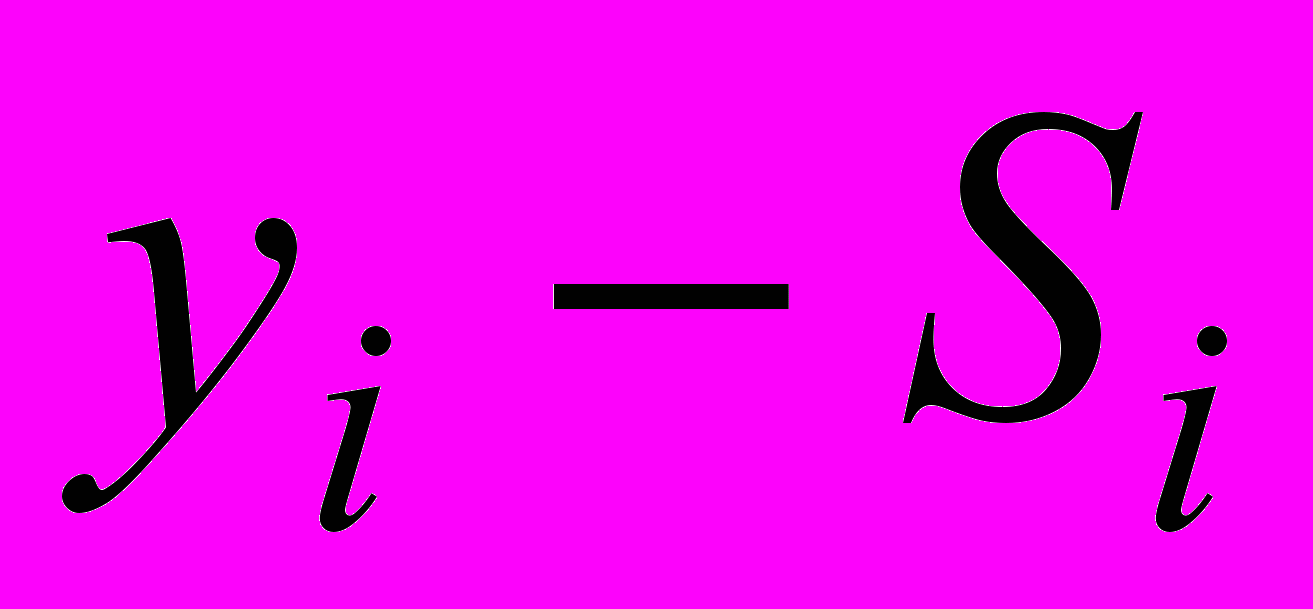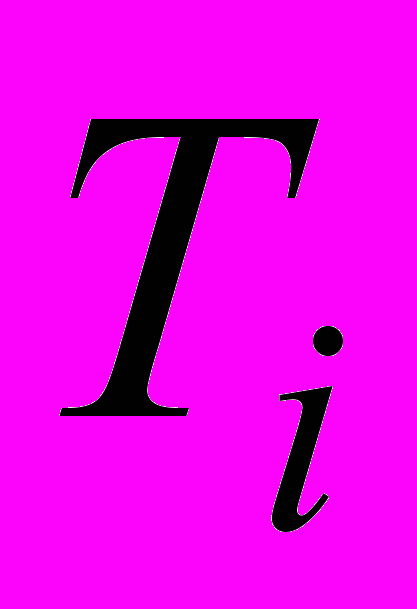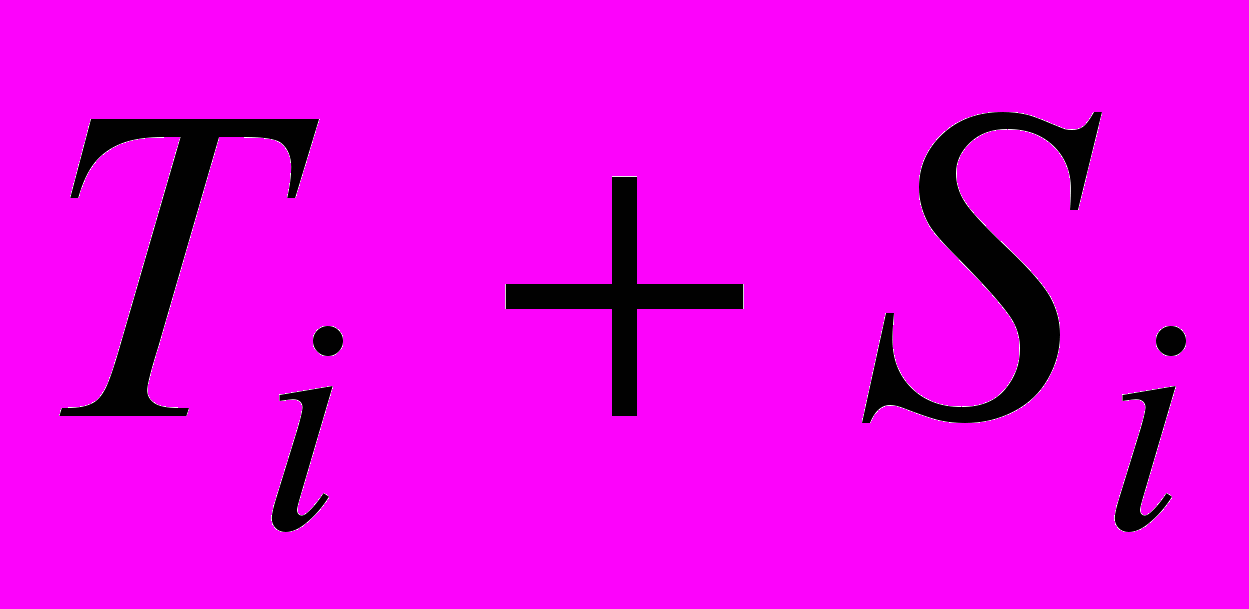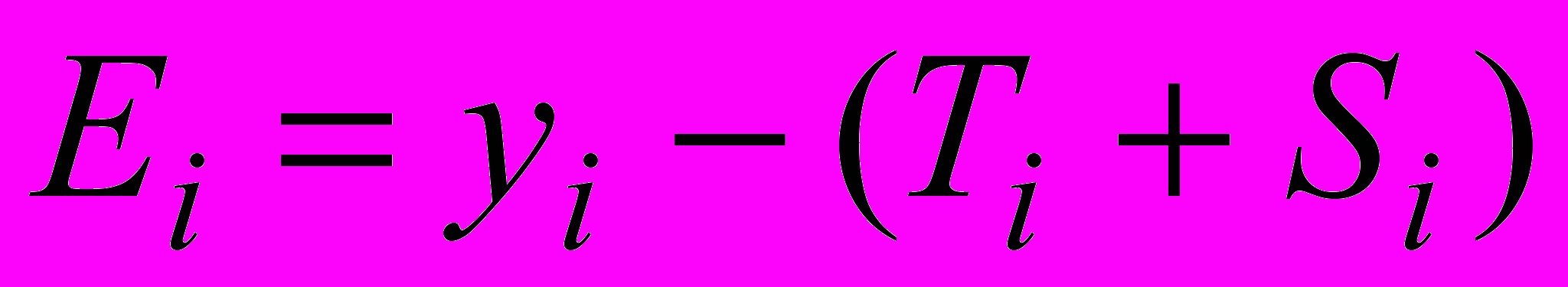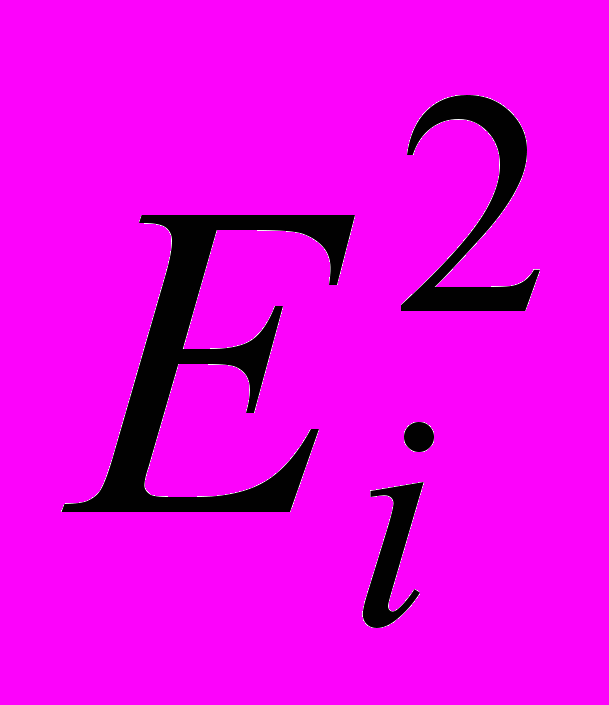














1
22,53
-1,59703
24,12703
23,96286
22,36583
0,164167
0,026951

2
30,06
-3,19516
33,25516
27,85318
24,65802
5,401979
29,18138

3
29,2
2,451719
26,74828
31,74349
34,19521
-4,99521
24,95211

4
38,77
2,340469
36,42953
35,6338
37,97427
0,795729
0,633185

5
34,91
-1,59703
36,50703
39,52411
37,92708
-3,01708
9,102792

6
36,7
-3,19516
39,89516
43,41443
40,21927
-3,51927
12,38527

7
54,68
2,451719
52,22828
47,30474
49,75646
4,923542
24,24126

8
53,18
2,340469
50,83953
51,19505
53,53552
-0,35552
0,126395

9
54,09
-1,59703
55,68703
55,08536
53,48833
0,601667
0,362003



Таблица 4

Расчет линейного тренда T




t
y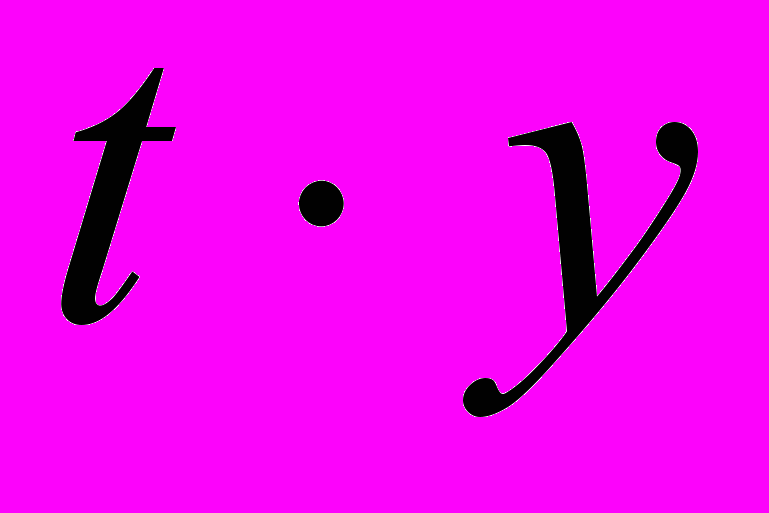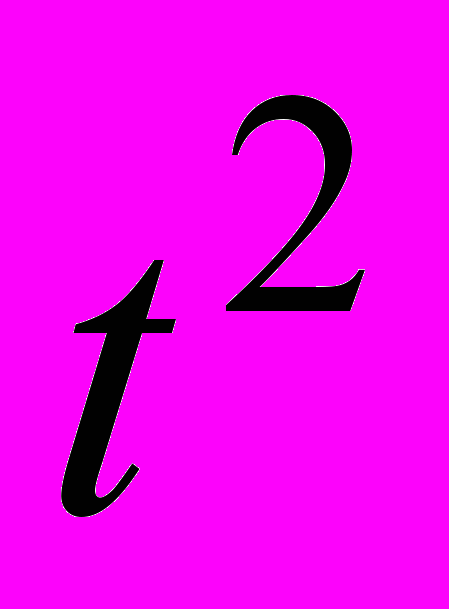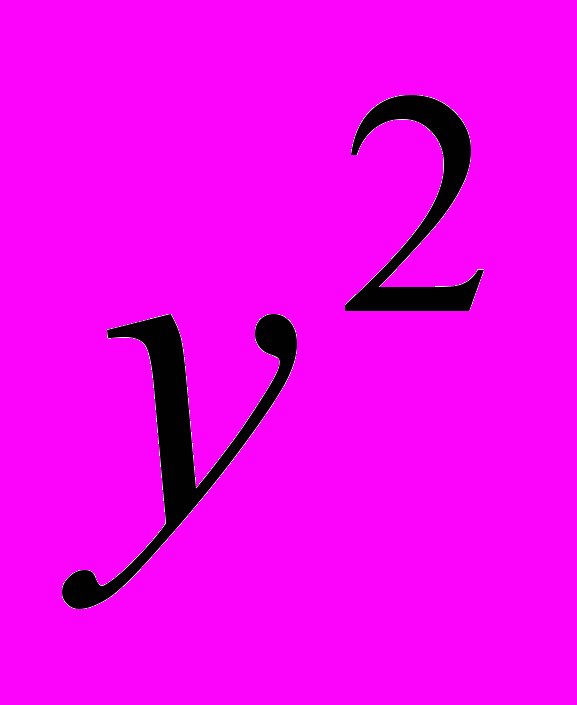






1
24,12703
24,12703
1
582,1136

2
33,25516
66,51031
4
1105,905

3
26,74828
80,24484
9
715,4705

4
36,42953
145,7181
16
1327,111

5
36,50703
182,5352
25
1332,763

6
39,89516
239,3709
36
1591,623

7
52,22828
365,598
49
2727,793

8
50,83953
406,7163
64
2584,658

9
55,68703
501,1833
81
3101,045

среднее значение
5
39,52411
223,556
31,66667
1674,276


Формулы для расчета параметров линейного тренда

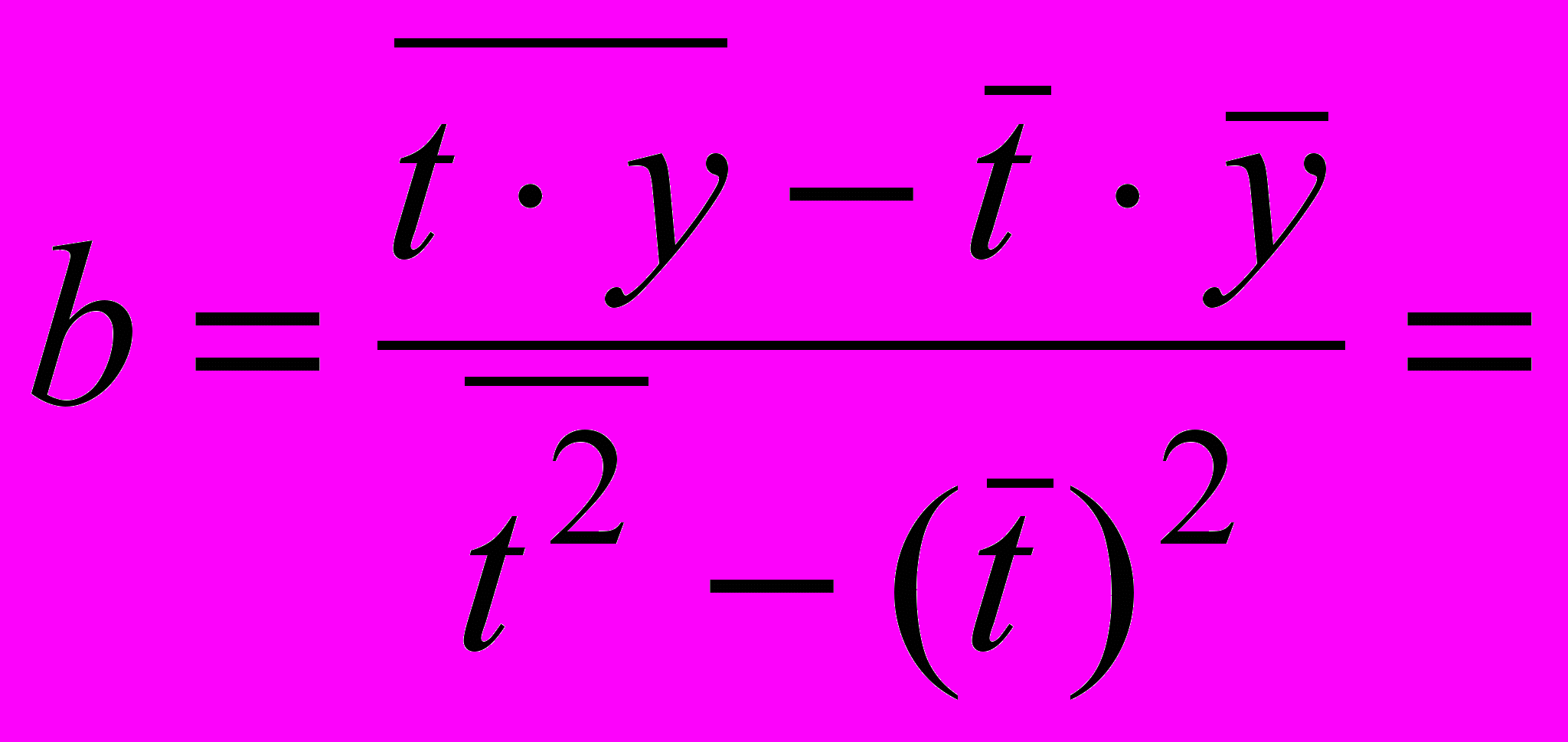3,890313, 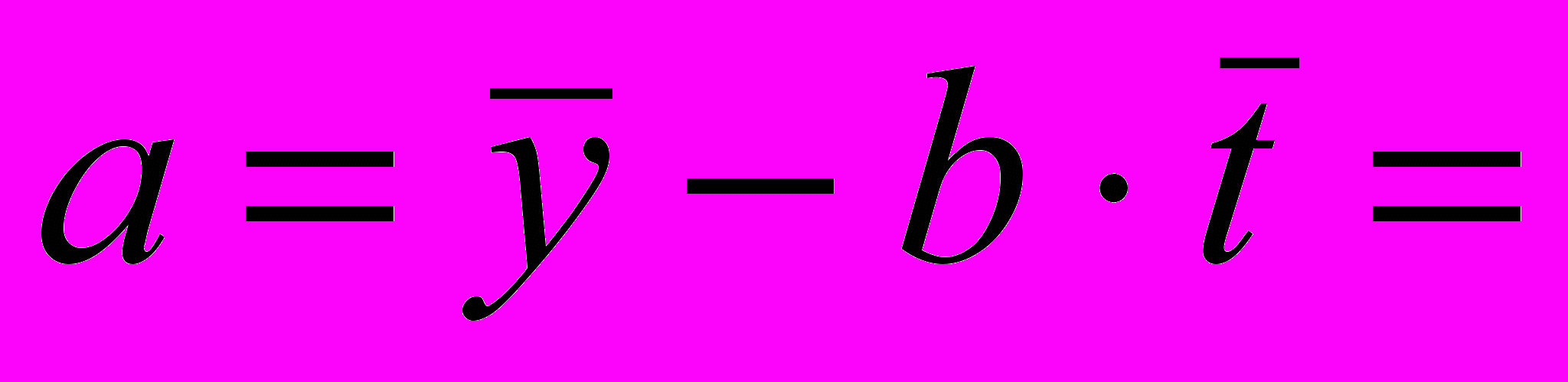20,07255.

Для расчета качества построенной модели определяем сумму квадратов отклонений значений исходного ряда от среднего значения данного ряда

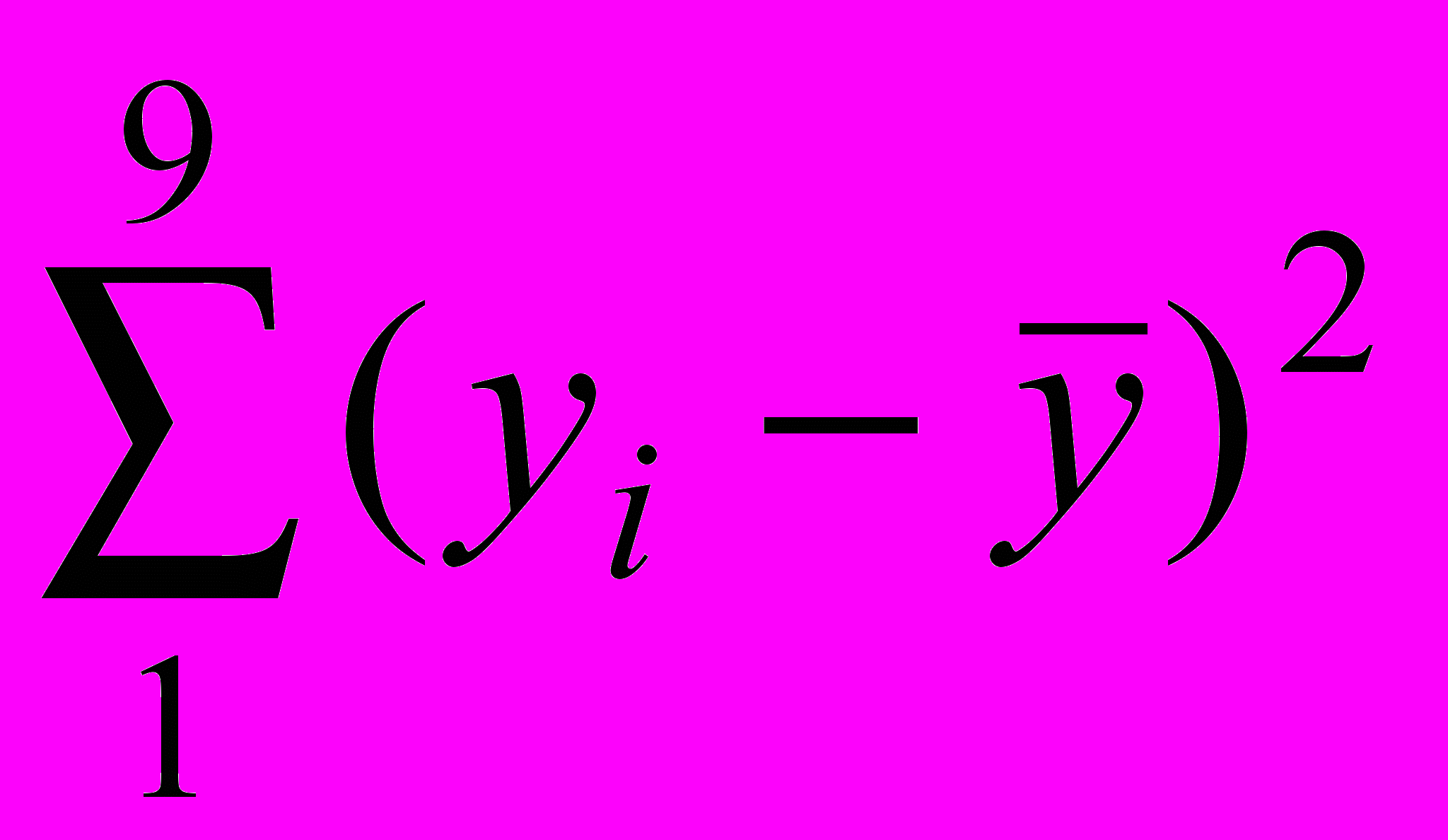=14851,5.

Для данной аддитивной модели сумма квадратов абсолютных ошибок 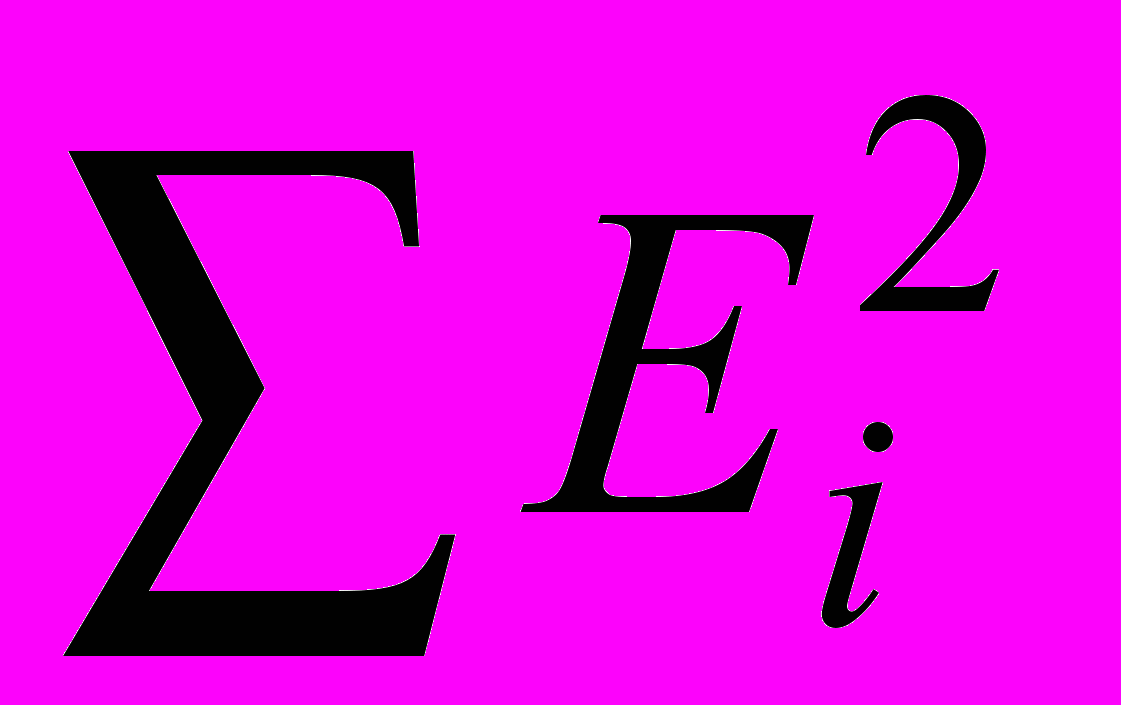(табл. 3) по отношению к общей сумме квадратов отклонений уровней ряда от его среднего значения составляет

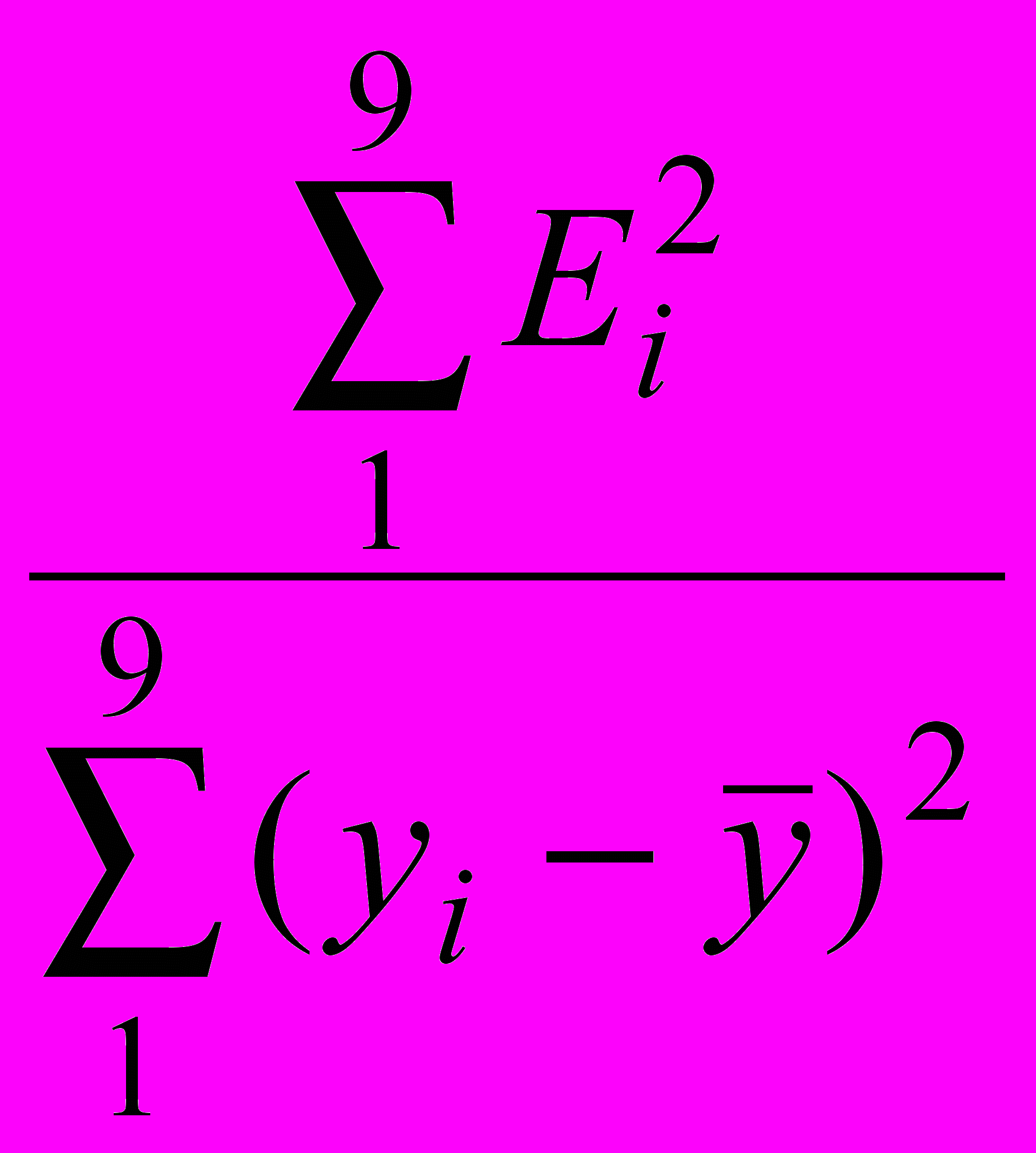= 0,680142 .

Это свидетельствует, что ошибка в данной модели составляет всего 0,680142 и модель можно использовать для прогнозирования 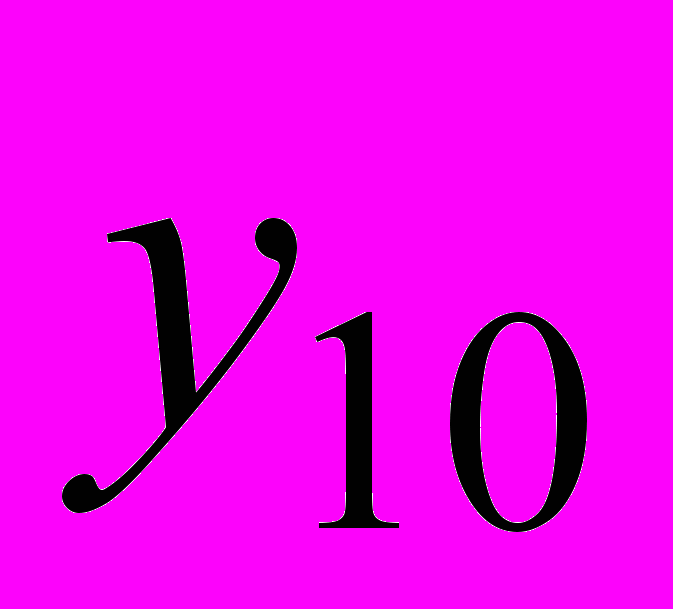и 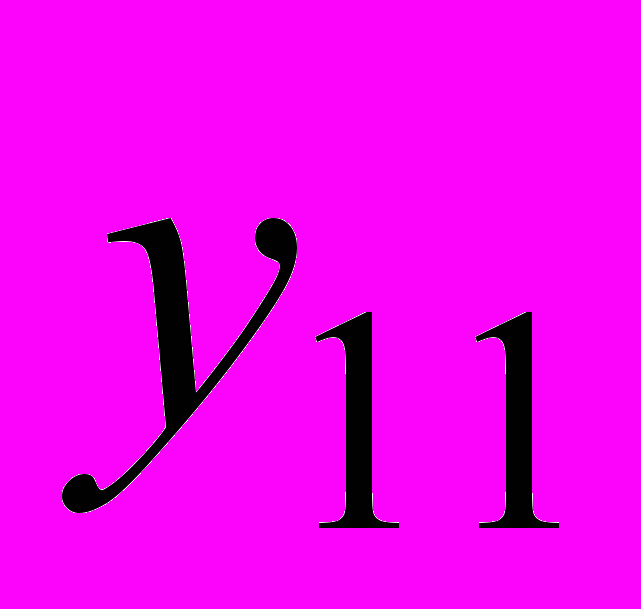, которые имеют соответственно значения:

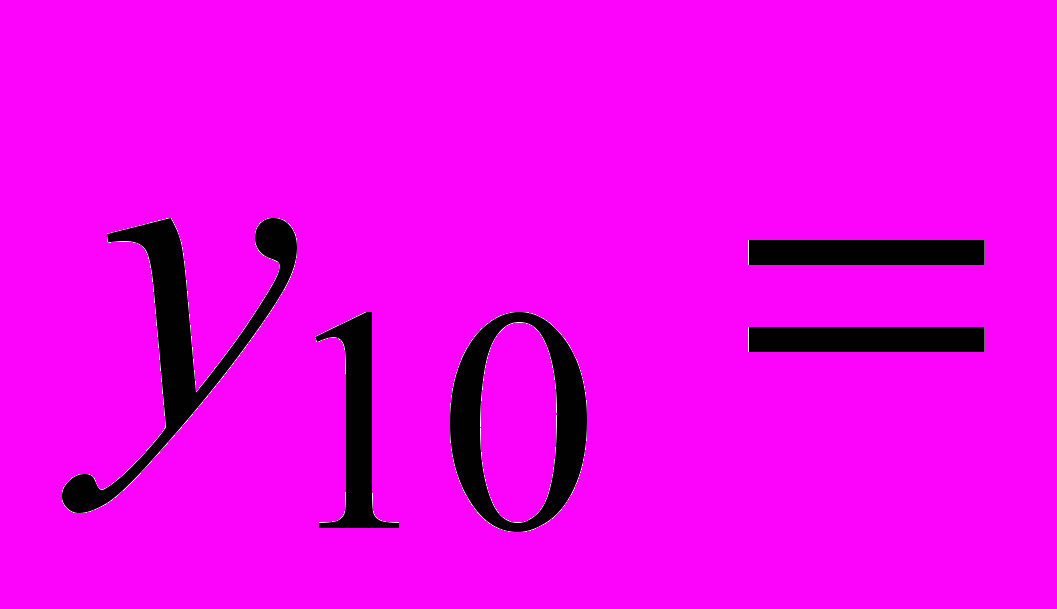55,78052, 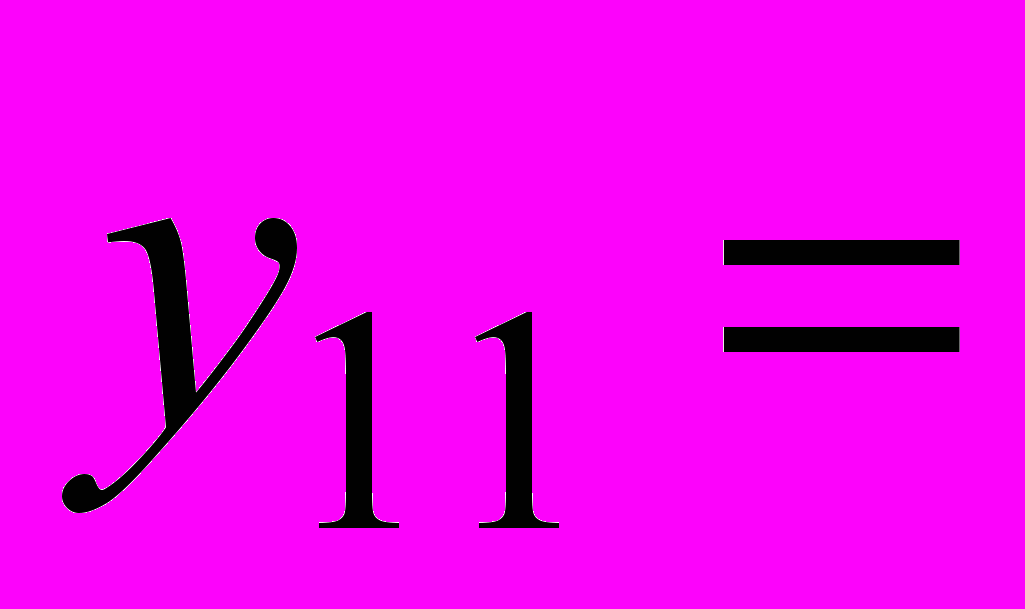65,31771.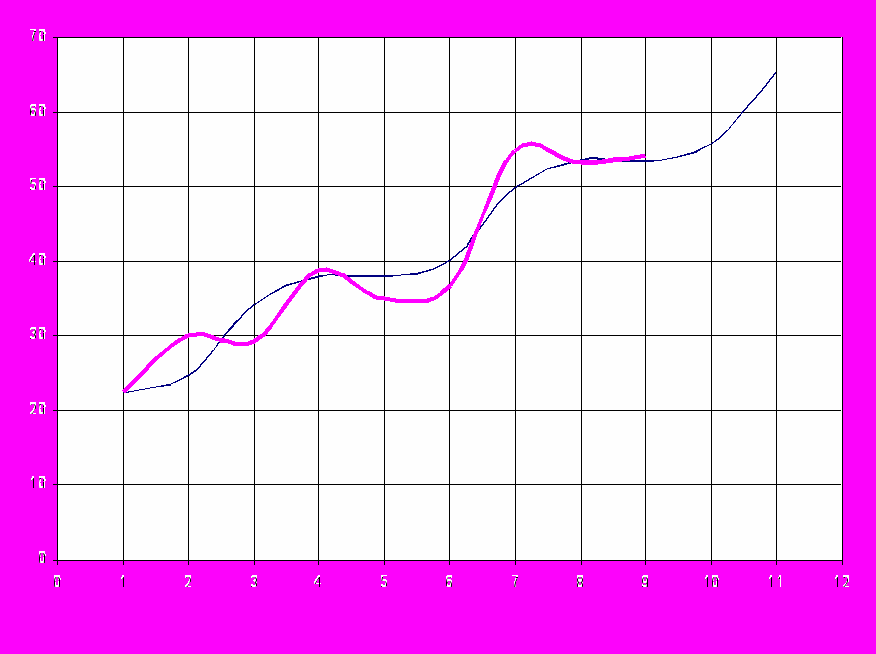


№1

№2

Показатель заболеваемости

Годы
Рис. 1. Линия №1 – построенная модель; линия №2 – исходные данные для аддитивной модели заболеваемости по Порецкому району.


Выводы. На основании проведенных расчетов по математическим моделям сравниваемых территорий, установили следующее:

1. В математической модели, по Алатырскому району, сумма квадратов абсолютных ошибок ∑Е2 по отношению к общей сумме квадратов отклонений уровней ряда от его среднего значения ∑(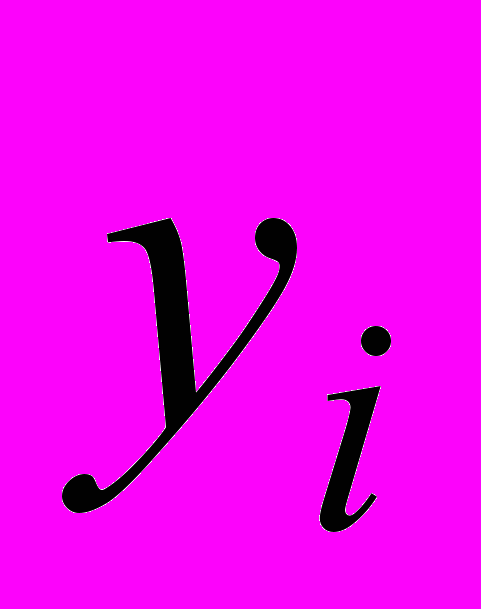- 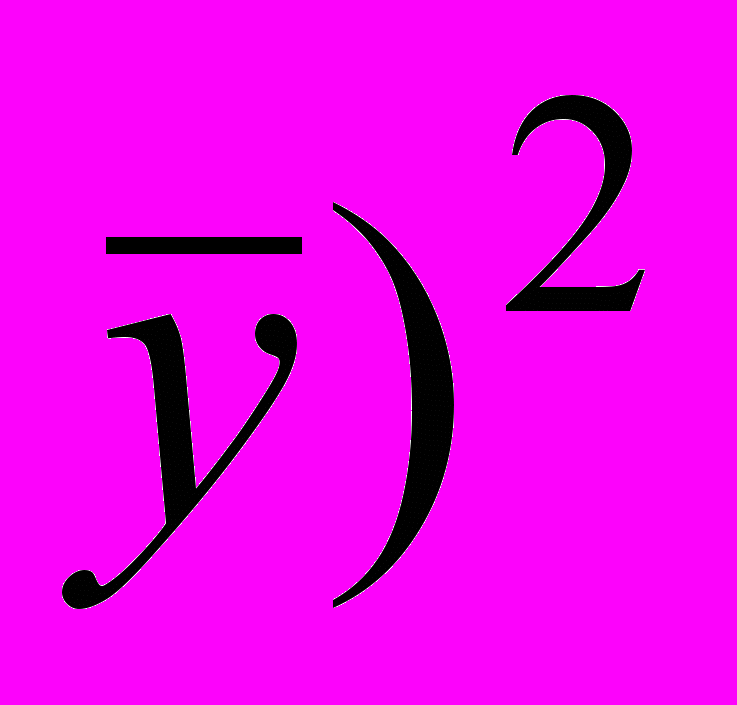составила 0,803733%, а по Порецкому району  0,680142%, что свидетельствует о высоком качестве построенных моделей.

2. В построенной модели тенденции развития указанных выше показателей заболеваемости и смертности за рассматриваемый период по Батыревскому району, ошибка составляет 0,242751%, а по Янтиковскому району – 0,282823%. Следует отметить, что ошибки моделей (независимо от района исследования) в показателях смертности выше, чем в показателях заболеваемости.

3. Нетрудно заметить, что имеет место существенная разница в показателях, характеризующих влияния ошибки в развитии ССЗ в сравниваемых территориях, которые в юго-западных раонах (Алатырский, Порецкий) в 23 раза выше данных по восточных районах (Батыревский, Янтиковский). Все факторы, влияющие на развитие ССЗ, учитываются в совокупности: социальные, возрастные, медико-организационные, эколого-биогеохимические факторы. Вместе с тем, методика построения модели свидетельствует о наличии в тенденции рассматриваемых процессов циклического характера. Кроме того, построенные модели позволяют получить прогноз исследуемых показателей, влияющих на заболеваемость и смертность от ССЗ на ближайшее время с возможностью принятия определенных профилактических мероприятий для их снижения.

В данной работе рассматривается первый шаг в изучении и оценки динамики заболеваемости и смертности ССЗ на территории Чувашской Республики, которую можно разделить на следующие задачи:

1. Построение математической модели тенденции развития ССЗ на территории Чувашии.

2. Выделение экзогенных и эндогенных факторов риска, влияющих на развитие ССЗ и разделение их по группам.

3. Изучение влияния составляющих факторов в каждой группе на ССЗ.

4. Исследования степени влияния каждой группы на развитие ССЗ.

ЛИТЕРАТУРА

  1. Сапожников С.П. Влияние эколого-биогеохимических факторов среды обитания на функциональное состояние и здоровье населения Чувашии: Автореф. дисс. … докт. мед. наук. М., 2001. 44 с.
  2. Степанов Р.В. Материалы к изучению причинно-следственных связей инфаркта миокарда: Автореф. дисс. … канд. мед. наук. Казань, 1992. 25 с.
  3. Сусликов В.Л. Гигиеническое районирование методическая основа первичной профилактики хронических неинфекционных заболеваний // Здоровье и медицинское обслуживание населения: Межвузовский сб. науч. тр. Чебоксары: Изд.-во ЧувГУ, 1989. С. 49.
  4. Сусликов В.Л., Семенов В.Д. Биогеохимическое районирование Чувашской АССР. Труды биологической лаборатории. М.: Наука, 1981. Т. 19. С. 6584.
  5. Елисеева И.И. и др. Эконометрика. М.: Э-40, Финансы и статистика, 2002. 344 с.
  6. Максимов Ю.Г. Состояние здоровья населения в регионах с эколого-биогеохимическим факторами риска (по материалам Чувашской Республики): Автореф. дисс. … докт. мед. наук. М., 2000. 44 с.



Адрес для переписки




ФИО: Иванов Андрей Геннадьевич

Домашний адрес: 428025, г. Чебоксары, пр-кт М.Горького, д. 31, кв. 233


Телефон: (8352) 41-24-71, моб. 89063887515

E-mail: animax@chuvsu.ru