Продольно-поперечные движения изотропных цилиндрических оболочек, имеющих искажения в форме поперечного сечения

Вид материала

Документы

Подобный материал:

• Вопросы к теоретическому зачету по физике за Iполугодие, 17.24kb.
• Список научных статей, докладов, тезисов и т п. за 9 месяцев 2011 года, 211.68kb.
• Варианты теории оболочек с применением разложений по полиномам лежандра, 32.7kb.
• Компания метинвест азия || библиотека по кабельно проводниковой продукции, 107.75kb.
• Расчет ступенчатого бруса, нагруженного внешними осевыми силами. Построение эпюр продольных, 13.18kb.
• Лекция 10. Основные способы обработки металлов давлением, их характеристика. Прокатка, 117.37kb.
• Изучение свойств анаэробноотверждаемых клеев в цилиндрических соединениях, 194.69kb.
• Лекция №9 26. пересечение плоскости и поверхности, определение натуры сечения, 151.71kb.
• Государственный стандарт СССР гост 18979-90 "Колонны железобетонные для многоэтажных, 459.53kb.
• Роизводители транзисторных усилителей водили аудиофилов за нос, предлагая им правдоподобные, 210.83kb.

Продольно-поперечные движения изотропных цилиндрических оболочек, имеющих искажения в форме поперечного сечения

Ф. Г. Шигабутдинов, Р. З. Муртазин, Р. Ф. Мухутдинов

Казанский государственный архитектурно-строительный университет,
Казань, Россия

Геометрически нелинейные дифференциальные уравнения продольно-попереч­ных движений тонкой изотропной оболочки типа Тимошенко, учитывающие сдвиг и инерцию вращения (Галимов К.З. Теория оболочек с учетом поперечного сдвига, 1977), используются для анализа поведения цилиндрических оболочек переменной и постоянной толщины при продольных ударах абсолютно твердым телом. Начальные условия соответствуют условиям удара телом по оболочке, поверхность приведения которой не имеет начального прогиба. Общий вид оболочки показан на рис. 1. Граничные условия принимались в виде подвижной шарнирной опоры на ударяемом конце и неподвижной шарнирной опоры на втором конце. Система дифференциальных уравнений и соотношения физического закона упругости представлены в работе [2]. Для решения дифференциальных уравнений использовалась явная схема метода конечных разностей.

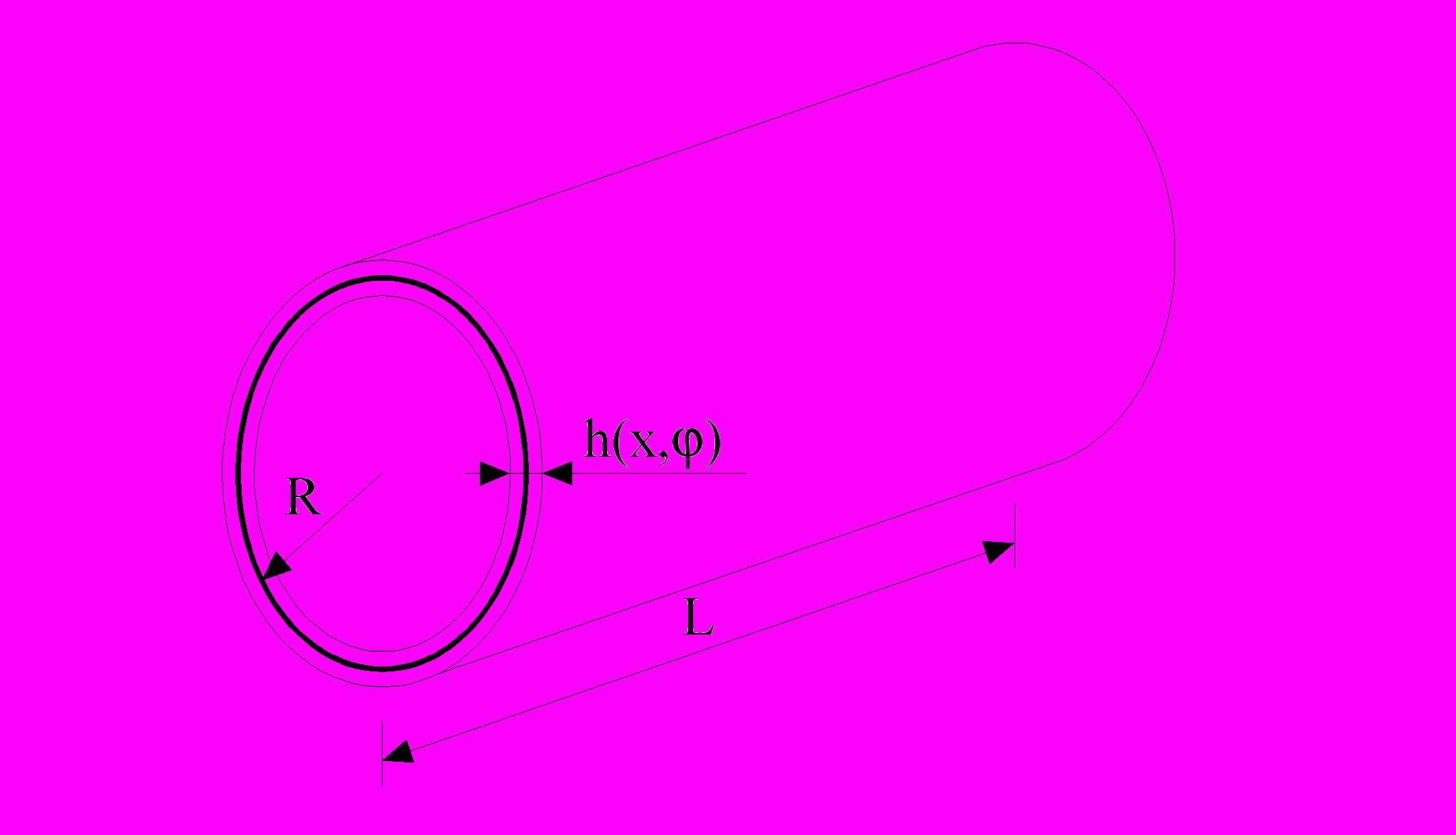	В докладе представлены результаты решения двух задач: 1. Задача о продольном ударе по цилиндрической оболочке переменной толщины. Толщина оболочки изменяется по окружной координате равномерно: hmin=0,02м, hmax=0,05м. Поперечное сечение оболочки представлено на рис. 2. 2. Задача о продольном ударе по части торцевого сечения цилиндрической оболочки постоянной толщины. На рис. 3 штриховкой показана часть поверхности торцевого сечения, подвергаемая удару.
Рис. 1
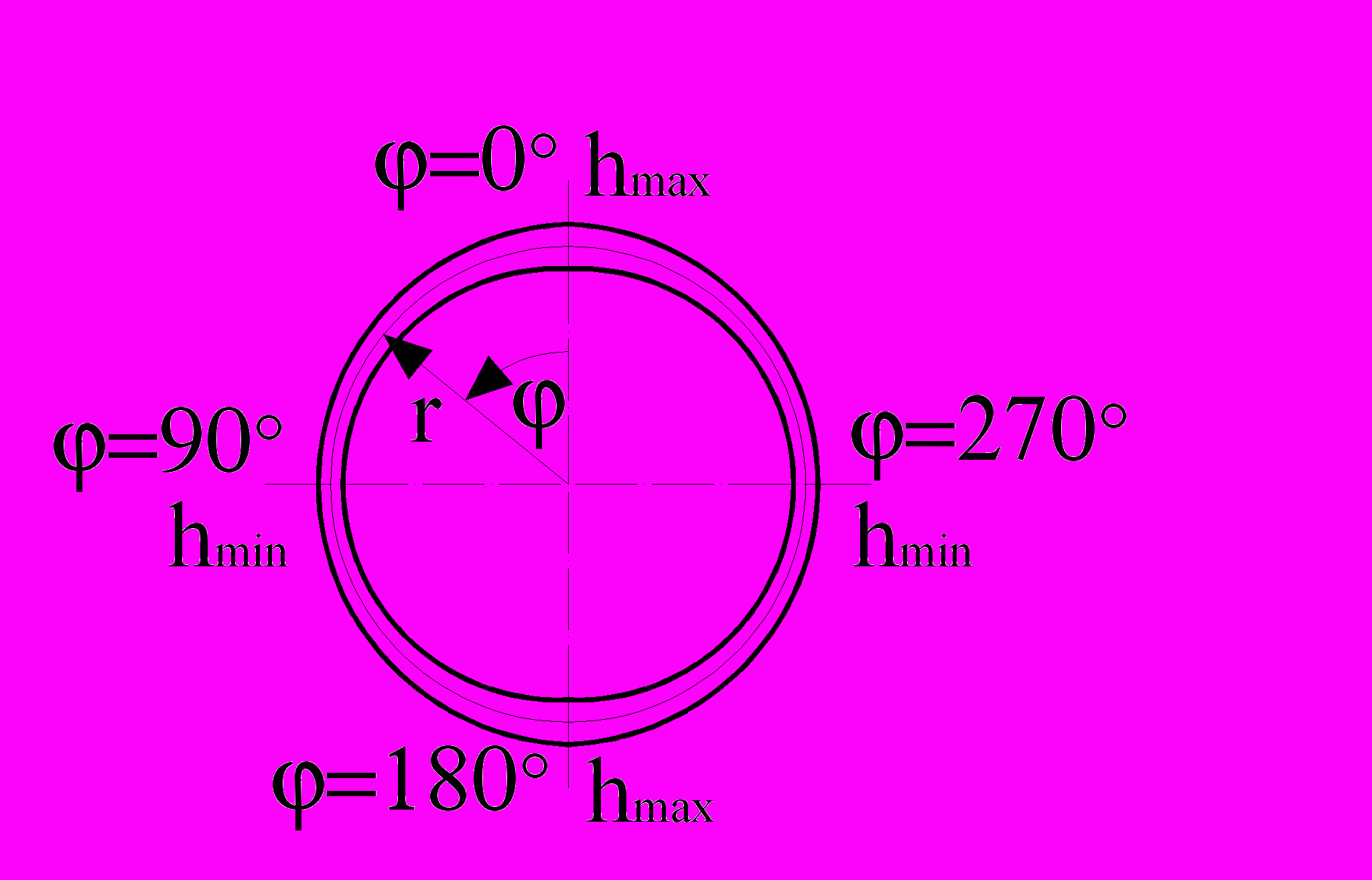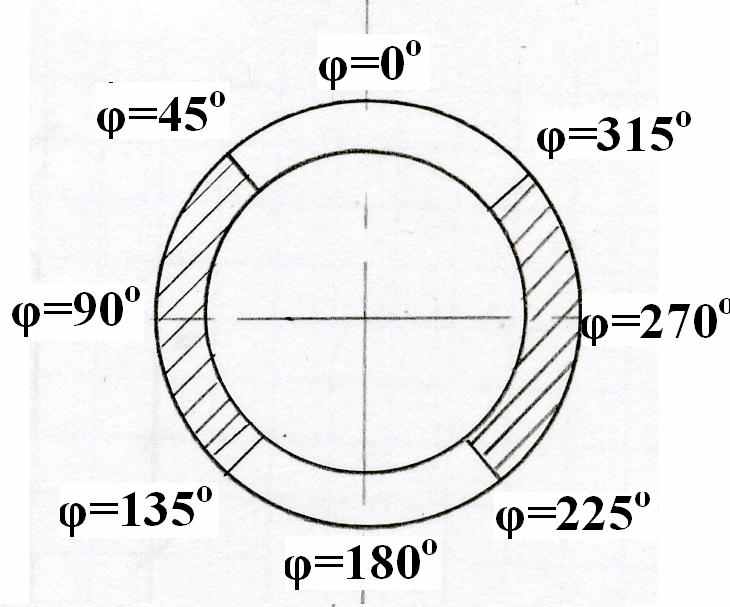Рис. 2	Рис. 3

Получены формы поперечного волнообразования (прогибы по всей длине оболочки) для девяти пробегов продольной волны вдоль оболочек. Для наглядности формы изгиба срединной поверхности оболочек приведены в виде трехмерных графиков.

Некоторые результаты решений представлены на рис. 4–9. Рисунки 4–6 соответствуют решению первой задачи, рисунки 7–9 – второй. На рисунках, с двух различных точек обзора, представлены картины волнообразования во всей оболочке в различные моменты времени T = t/t₀, t₀ – время, за которое продольная волна один раз пробегает вдоль оболочки. По одной из осей откладывается продольная координата x, по другой – угловая координата φ (от 0 до 2π). Наглядность данных пространственных представлений прогибов позволяет охватить единым взглядом всю оболочку, увидеть прогибы в любой ее точке. Отчетливо видна симметричность картины прогибов по угловой координате, обусловленная симметрией ударяемой части поверхности торцевого сечения относительно вертикальной оси.

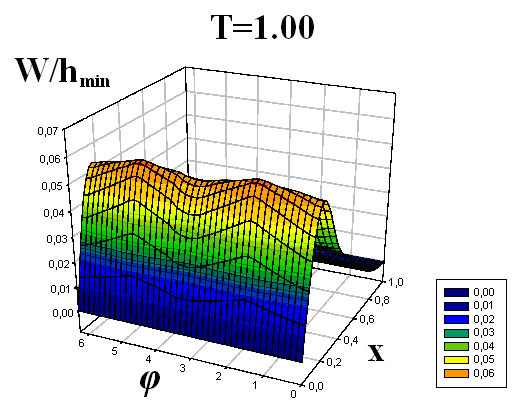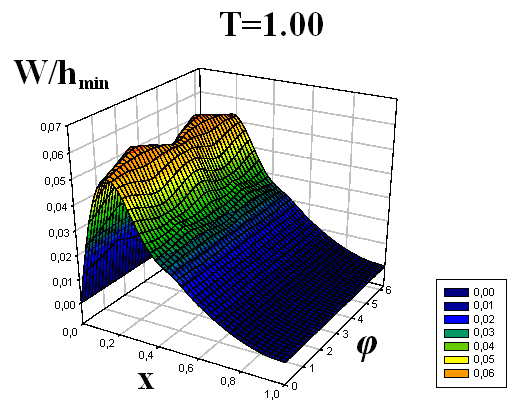Рис. 4
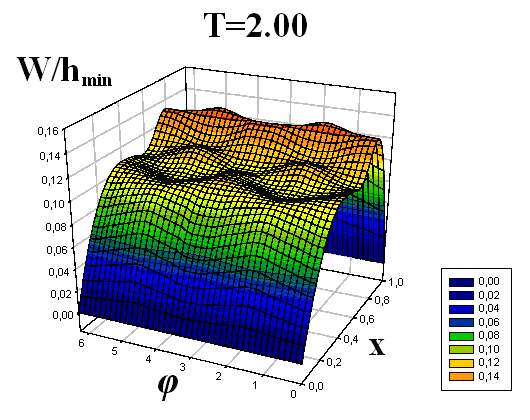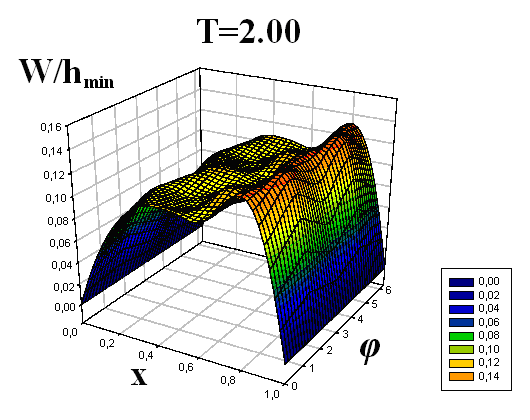Рис. 5
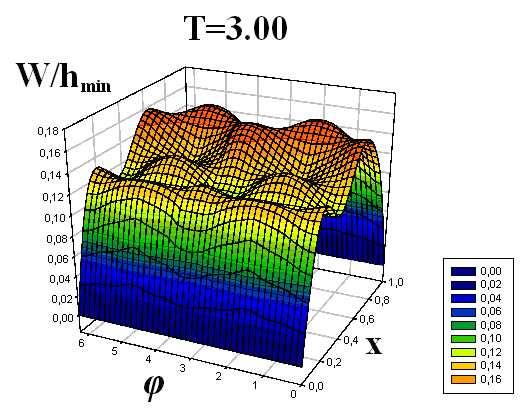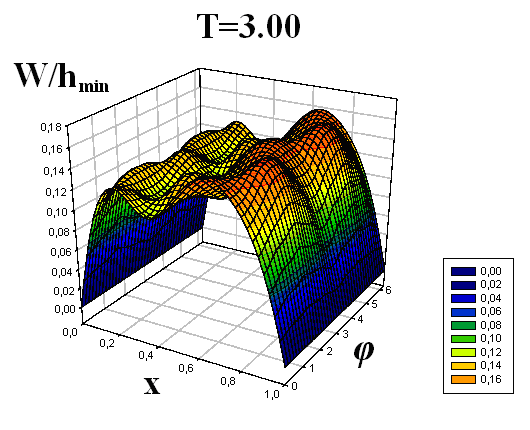Рис. 6
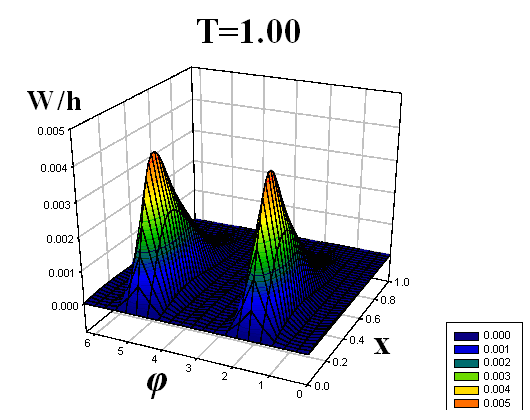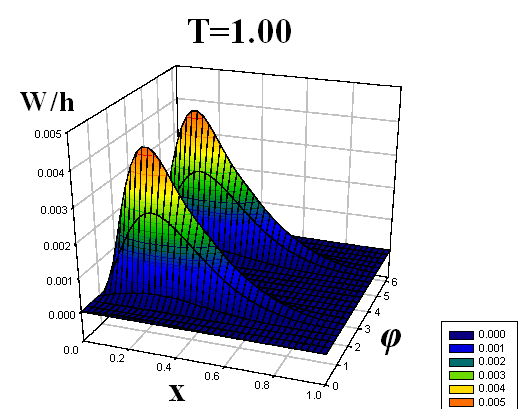Рис. 7
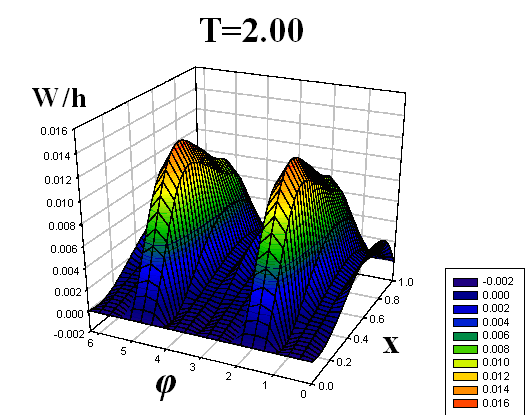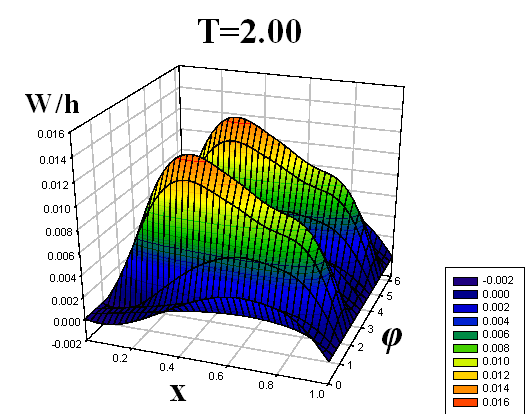Рис. 8
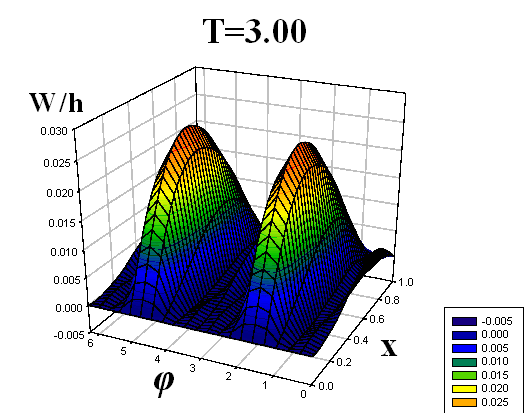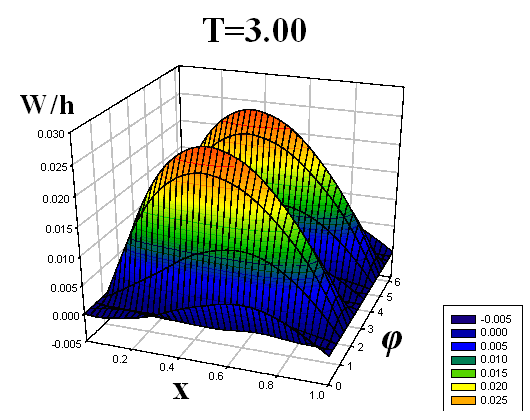Рис. 9

Литература

1. Теория оболочек с учетом поперечного сдвига / Науч. ред. проф. К. З. Галимов. – Казань: Изд-во КГУ, 1977. – С. 3–132.

2. Шигабутдинов Ф.Г., Муртазин Р.3., Мухутдинов Р.Ф. Численные эксперименты с выпучиванием оболочек переменной толщины под действием продольной ударной нагрузки // Труды XXI Международной конференции по теории оболочек и пластин. – Саратов, 2005. – С. 229–235.