Geum.ru

Гия, ресурсы и перспективы освоения нефтегазовых недр Прикаспийской впадины и Каспийского региона: Международная научно-техническая конференция «Прикаспий-2007»

Вид материалаДокументы
Подобный материал:
Ратнер С.В. Современные математические методы мониторинга грязевулканической деятельности // Геология, ресурсы и перспективы освоения нефтегазовых недр Прикаспийской впадины и Каспийского региона: Международная научно-техническая конференция «Прикаспий-2007»; Москва, 18-20 сентября 2007 г.: Избранные доклады / Под. ред. Гаврилова В.П. – М.: МАКС Пресс, 2008, стр. 273-281.


Современные математические методы мониторинга грязевулканической деятельности

Ратнер С.В., Южный научный центр РАН, Краснодар, lanarat@mail.ru


Известно, что свыше 70% всех месторождений нефти и газа в Южно-Каспийской впадине связаны с одним и более (до 6-8) грязевыми вулканами [1]. И хотя грязевые вулканы не могут рассматриваться как поисковый признак на нефть и газ, тем не менее, их связь с нефтегазоносностью неоспорима и до конца не изучена.

После Прикаспийского региона второй зоной в СНГ по масштабам проявления грязевого вулканизма является Керченско-Таманская область. Учитывая единую генетическую природу грязевого вулканизма и общность геологических процессов в осадочной толще, следствием которых является возникновение грязевулканической активности, для составления и верификации концептуальной и математических моделей используется обширный геофизический и геологический материал, накопленный в процессе изучения Таманской грязевулканической провинции.

В 2005 году в рамках комплексной эколого-геофизической экспедиции Института физики Земли РАН, Южного научного центра РАН и Института Вычислительной математики и математической геофизики СО РАН в районе Таманской грязевулканической провинции впервые в практике изучения грязевых вулканов были применены методы активной сейсмологии, которые позволяют изучить внутреннюю структуру флюидонасыщенных образований в теле вулканической постройки, включая грязевулканическую камеру и глубинные флюидогенерирующие области. В процессе проведения экспедиции основное внимание исследователей было сосредоточено на двух грязевых вулканах – вулкан Ахтанизовский и вулкан Шуго.

Анализ тонкой структуры геологической среды при возбуждении колебаний внешними поверхностными сейсмическими источниками колебаний связано с необходимостью привлечения специализированных технологий приема сейсмических сигналов. Эта задача весьма сложна в экспериментальном исполнении ввиду реального многообразия строения изучаемых объектов и в ряде случаев требует построения математической модели изучаемой среды.

Результаты интерпретации полученных экспериментальных данных в рамках традиционных моделей лучего метода, представленные в работе [2] говорят о регистрации нового эффекта и получении новых знаний о строении грязевых вулканов. Однако они также свидетельствуют о необходимости разработки более эффективных моделей интерпетации сейсмических данных. Такой альтернативой может послужить метод интегрального волнового поля.

Одно из основных преимуществ подхода, основанного на разработке и анализе математических моделей - возможность качественного учета каждой особенности строения реальной геофизической среды, что позволяет выявить все эффекты, связанные именно с данной изучаемой особенностью строения вулканической структуры.

В свою очередь, математическое моделирование позволяет по-новому подойти к постановке сложных экспериментальных работ, связанных с изучением волновых процессов в геофизической среде вулканической постройки, дать правильное толкование наблюдаемым геофизическим процессам и новым явлениями. Натурный же эксперимент регистрирует общую картину, где влияние всех элементов объединено, и зачастую сложно дать однозначное объяснение выявленного эффекта.

В силу вышеизложенного, механико-математические модели геофизической среды достаточно многообразны, обладают различной степенью сложности и общности, что определяет круг решаемых задач. Напомним, что простейшей является модель однородного полупространства, позволяющая ответить на некоторые вопросы взаимодействия поверхностных источников сейсмических колебаний с грунтом. Однако, несмотря на большое количество посвященных ее анализу публикаций, подобная модель имеет весьма ограниченный по частоте сверху диапазон применимости, что не позволяет учесть реальные резонансные свойства геофизической среды. Тем не менее, модель однородного полу-пространства - важная составная часть более сложных моделей.

Следующая по сложности модель многослойного полупространства – это модель, которая позволяет достаточно достоверно исследовать особенности возбуждения колебаний в геофизической среде вулканической постройки поверхностными источниками с учетом резонансных свойств отдельных образований и структуры выводящих каналов, а также исследовать процесс формирования волновых полей в такой среде [3]. В рамках такой модели могут быть исследованы особенности распространения поверхностных, пограничных и внутренних (продольных и поперечных) волн, их трансформация и взаимодействие. Разработанная модель, достаточно общая, она позволяет исследовать эффекты, связанные с движением нагрузок, и имеет большие, еще не исчерпанные практические возможности.

С практической точки зрения важен вопрос о резонансных свойств геофизической среды наиболее важен. Эти свойства, обусловленные слоистостью, при возбуждении колебаний поверхностными источниками могут быть достаточно подробно изучены на основе модели слоистого полупространства. Открытыми при этом остаются вопросы корректного моделирования особенностей возбуждения колебаний заглубленными источниками, а также изучения влияния имеющихся в реальных структурах полостей различной формы, природы и положения на закономерности формирования волновых полей и резонансные характеристики среды.

С определенной степенью абстрагирования для изучения динамики грязевулканической деятельности можно использовать модель слоистой упругой полуограниченной среды (слоистое полупространство или пакет слоев, лежащий на полупространстве), содержащей множественные плоско-параллельные неоднородности, которые могут быть как полостями трещинами, так и включениями. При этом модельному случаю полостей-трещин соответствует случай заполнения карманов грязевулканической постройки газами, а включениям – заполнение карманов брекчией. Переход в модельной задаче от одной неоднородности к их совокупности приводит к новым качествам, как в части локализации волнового процесса, так и в части поведения системы в условиях резонанса. Известно, что традиционные аналитические и численные методы исследования динамических задач, например, о трещинах в упругих средах при вибрации достаточно высокой частоты, становятся неэффективными даже для небольшого количества неоднородностей, особенно когда речь идет об областях больших размеров.

Механические свойства совокупностей параллельных неоднородностей оказываются достаточно неожиданными. Находясь в деформируемой среде, занимающей определенную область, в условиях вибрации они могут локализовать волновой процесс и вызвать резонансы. Они не энергоемкие – для локализации необходима лишь конечная энергия, даже если вибрирует неограниченное тело с бесконечной суммарной энергией. Они способны быть незаметными до достижения определенных условий, а в телах некоторой формы – вообще не проявлять своих резонансных свойств.

Обычно выявление лишь одного сочетания неоднородностей, локализующих волновой процесс, вскрывает целое семейство подобных сочетаний, также локализующих волновой процесс при этих же значениях параметров среды и частоте. Поэтому, исследуя влияние неоднородностей на характер волнового процесса, целесообразно рассматривать не отдельную неоднородность или их совокупность, а семейство неоднородностей или семейство совокупностей неоднородностей. В этих семействах взаимное расположение неоднородностей сохраняется, меняются лишь их размеры.

С математической точки зрения отмеченное поведение объясняется наличием у оператора соответствующей краевой задачи, описывающей поведение механической системы, состоящей из упругого тела с неоднородностями, одних и тех же спектральных свойств, например, наличия точек изолированного спектра для всего семейства неоднородностей [3]. Развитая спектральная теория послужила основой для направленного поиска механических и физических явлений, возникающих в вибрирующем теле при наличии неоднородностей той или иной природы. Для этого необходим соответствующий математический аппарат, который был развит в работах академика В.А.Бабешко и его школы как метод факторизации.

Рассмотрим коротко постановку задачи о распространении длиннопериодных волновых возмущений в анизотропной упругой среде, содержащей локальные неоднородности дилатансного типа и метод ее решения. В декартовой системе координат колебания линейно-упругой среды, обладающей произвольной анизотропией описывается системой трех дифференциальных уравнений в частных производных второго порядка:

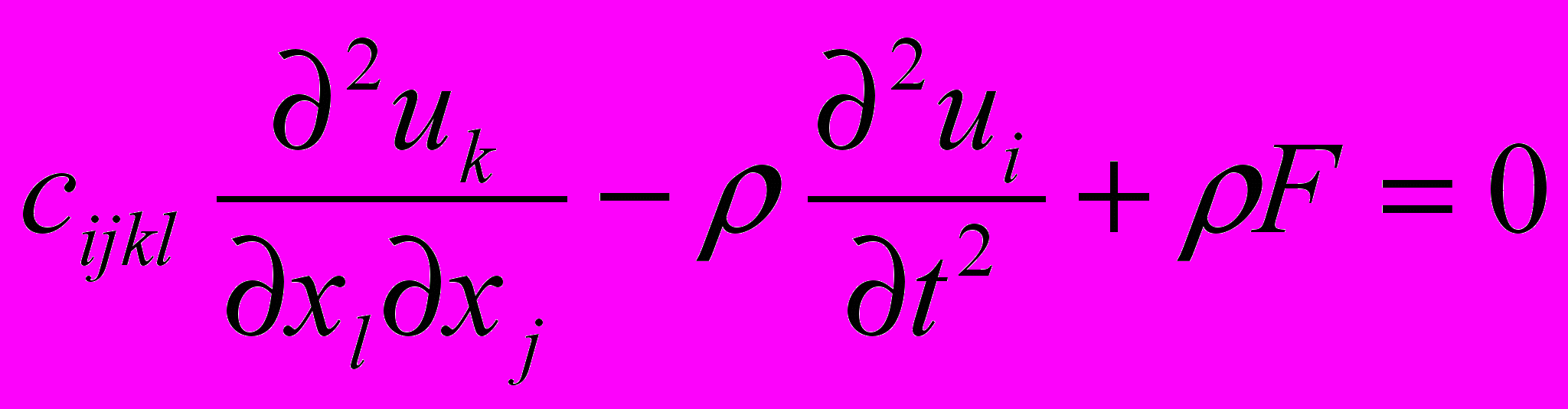, (1)

где 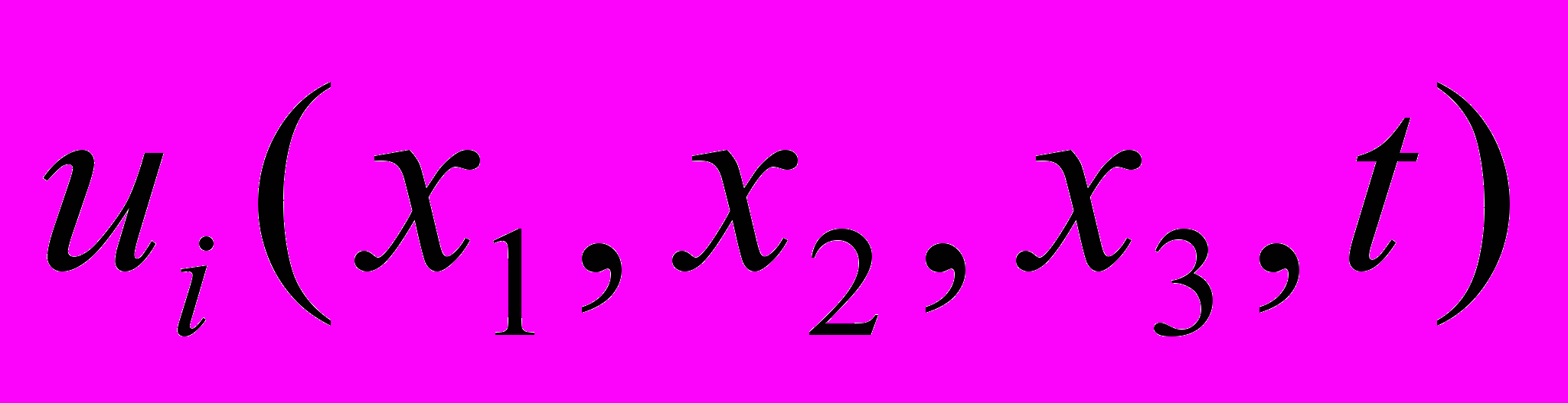- перемещения точек среды, t - время, 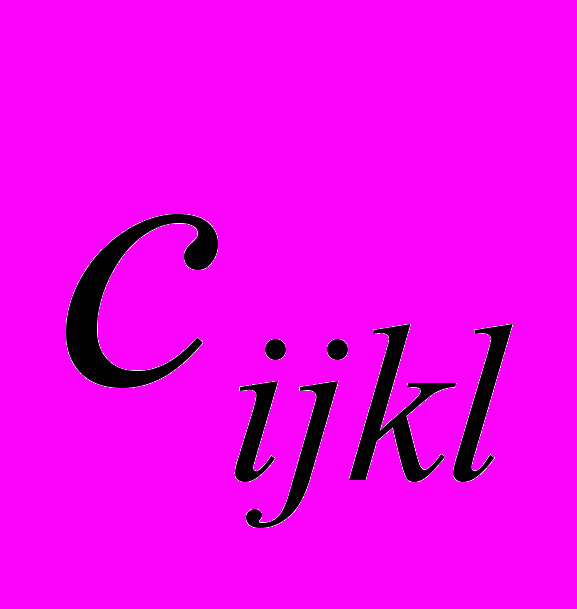- тензор упругих постоянных, 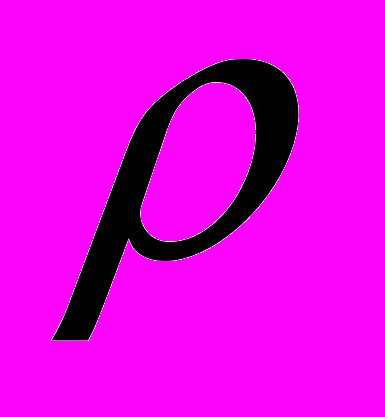- плотность среды, - вектор объемных сил.

Так как решение задачи о гармонических колебаниях является промежуточным этапом при анализе нестационарных задач, будем считать 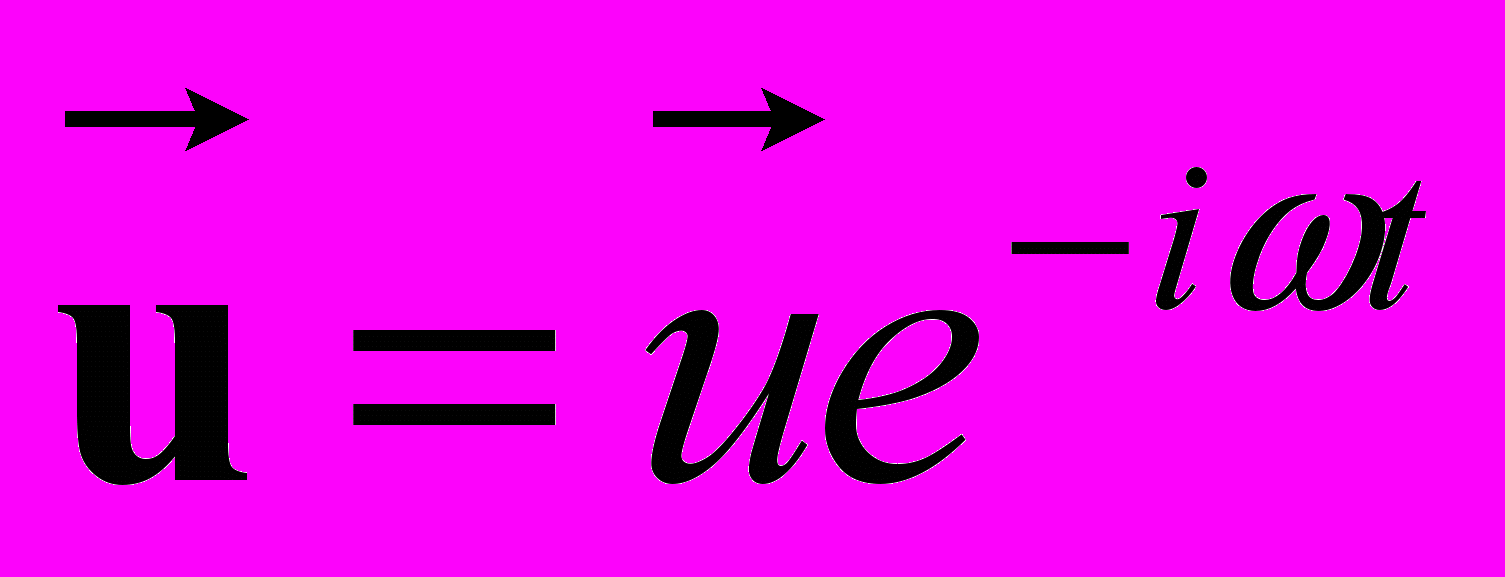. Введение комплексных амплитуд удобно тем, что они описывают одновременно амплитуду и сдвиг фазы и позволяет в выкладках избавиться от временной зависимости. Решение соответствующей нестационарной задачи строится по принципу суперпозиции колебаний в линейных системах

.

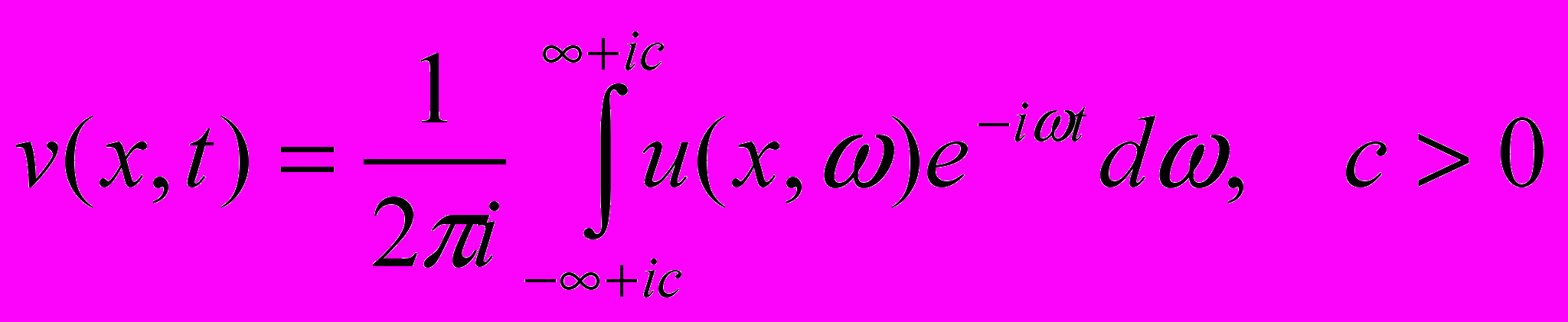Известно, что в случае неограниченных тел (объем V включает бесконечно удаленные токи) предположение об установившемся характере колебаний всего объема, являясь идеализацией, приводит к неоднозначной разрешимости. В этом случае для обеспечения единственности решение должно удовлетворять условию излучения в той или иной форме - Зоммерфельда, требующего от решения выполнение предельного дифференциального соотношения на бесконечности, принципа предельного поглощения Игнатовского - состоящего в переходе к системе без поглощения через систему с искусственным внутренним трением, предельной амплитуды - рассмотрение установившихся колебаний как предельное во времени решение задачи Коши, излучения энергии Мандельштама. На примере динамических смешанных задач для неоднородной полосы детальный анализ всех этих условий выполнил И.И.Ворович [4-5]. Им установлено, что при всех аномальных ситуациях, связанных с физикой распространения волн в сложных средах и областях, остаются эквивалентными принципы Игнатовского и Мандельштама.

Будем использовать принцип предельного поглощения Игнатовского: в качестве решения u задачи для установившихся гармонических колебаний полуограниченного идеально упругого тела берется равномерный предел единственного решения 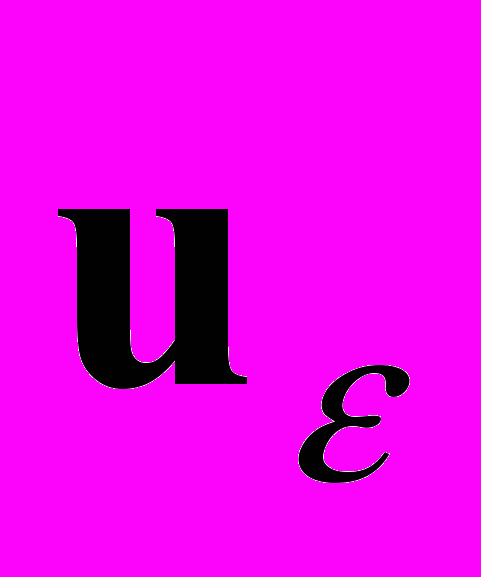аналогичной задачи для среды с поглощением, удовлетворяющего на бесконечности нулевым условиям, при стремлении параметра внутреннего поглощения 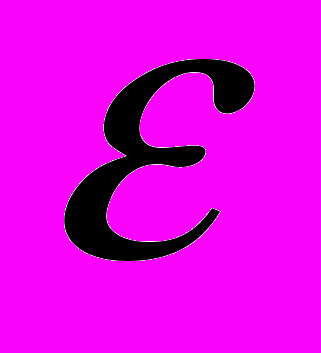к нулю: 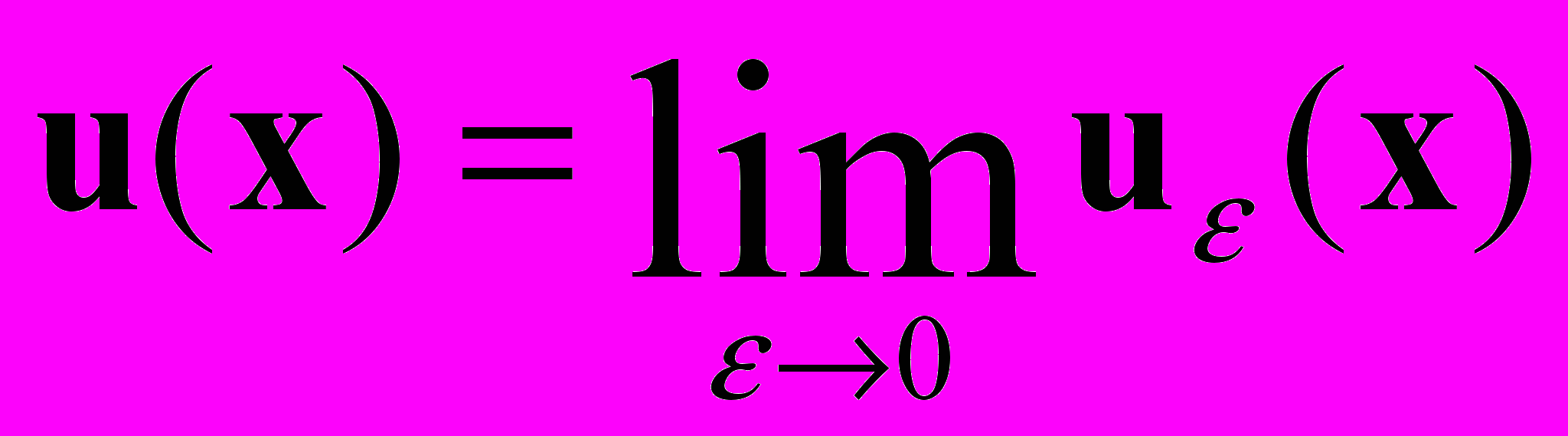. Внутренне трение приводит к появлению в среде тормозящей объемной силы, пропорциональной скорости смещения частиц: 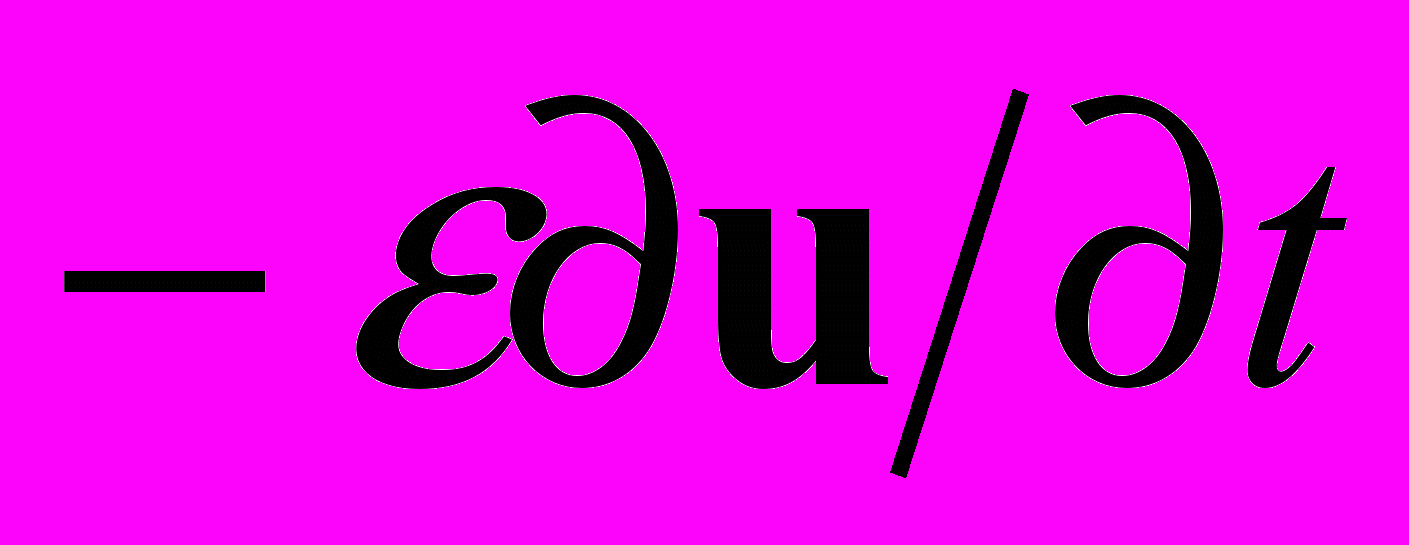, что в случае гармонических колебаний дает в уравнениях Ламе дополнительное слагаемое 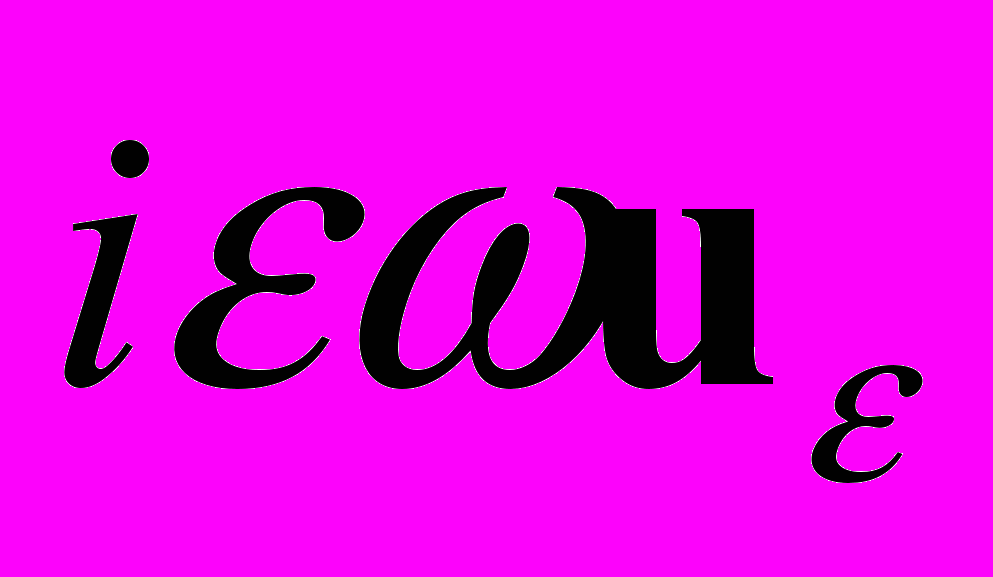. Вид уравнений остается прежним, если ввести обозначение 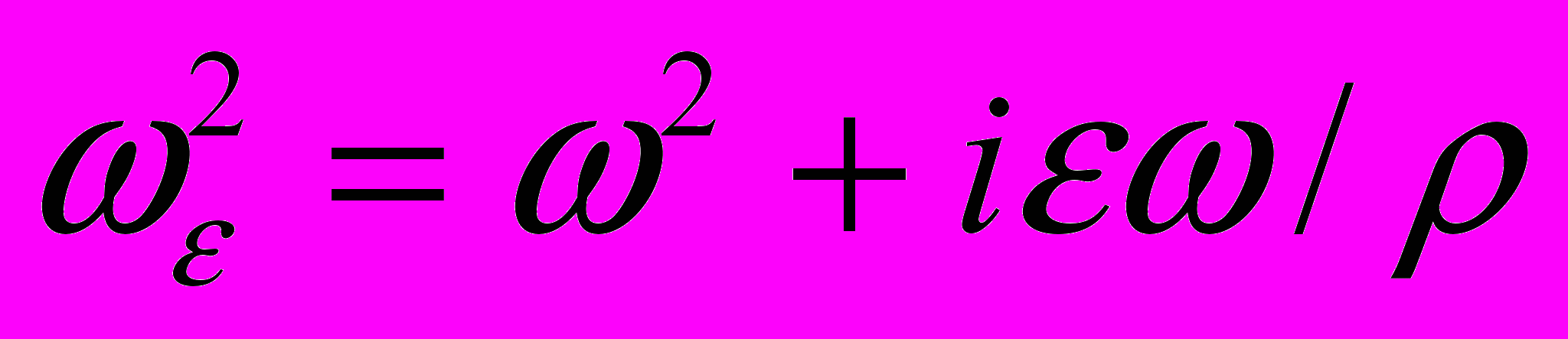, 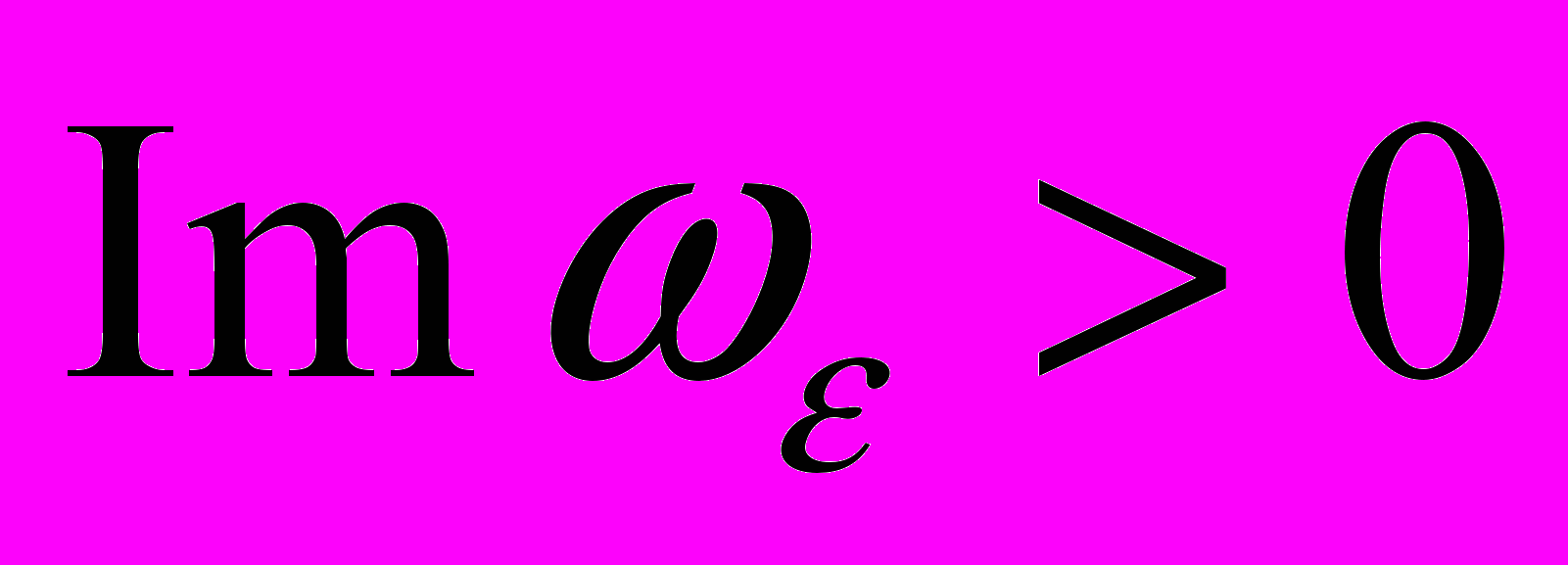. Таким образом, решение, удовлетворяющее принципу предельного поглощения, можно рассматривать как решение уравнений (1) для комплексной частоты 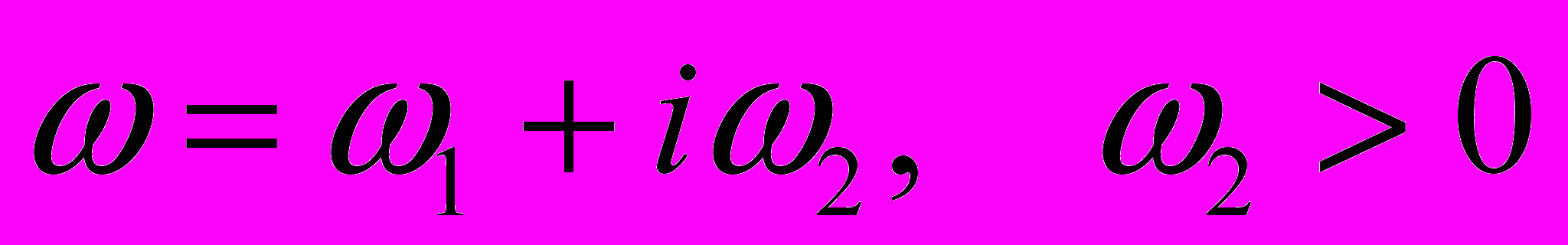при .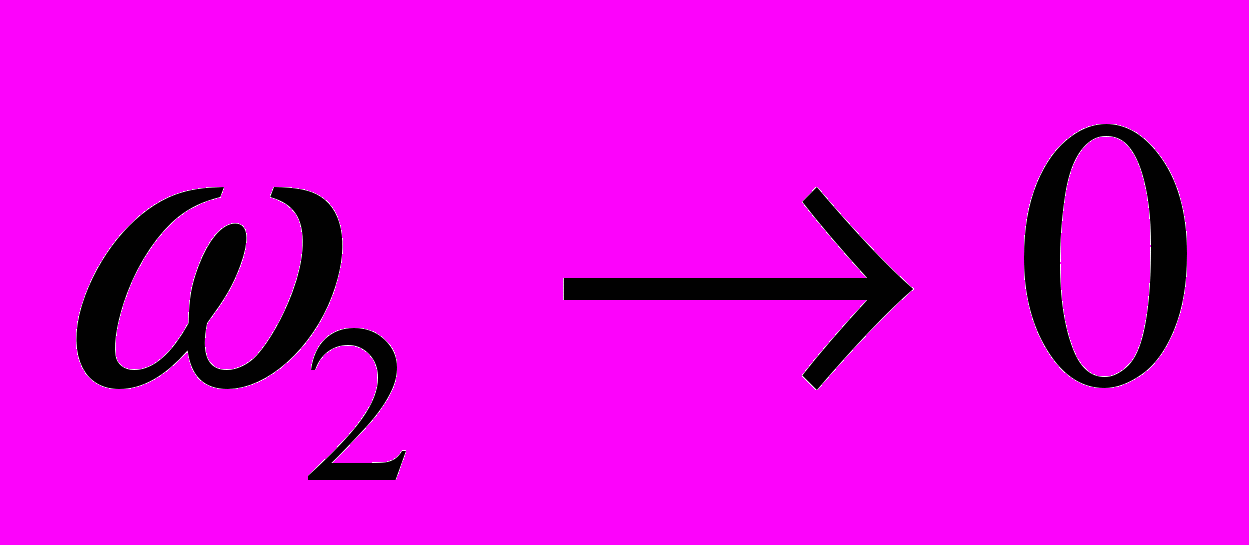

В общем случае рассматривается упругое пространство, которое параллельными горизонтальными сечениями мысленно делится на слои, верхний и нижний из которых являются полупространствами. В каждом сечении расположена плоская неоднородность. Расположив плоскость 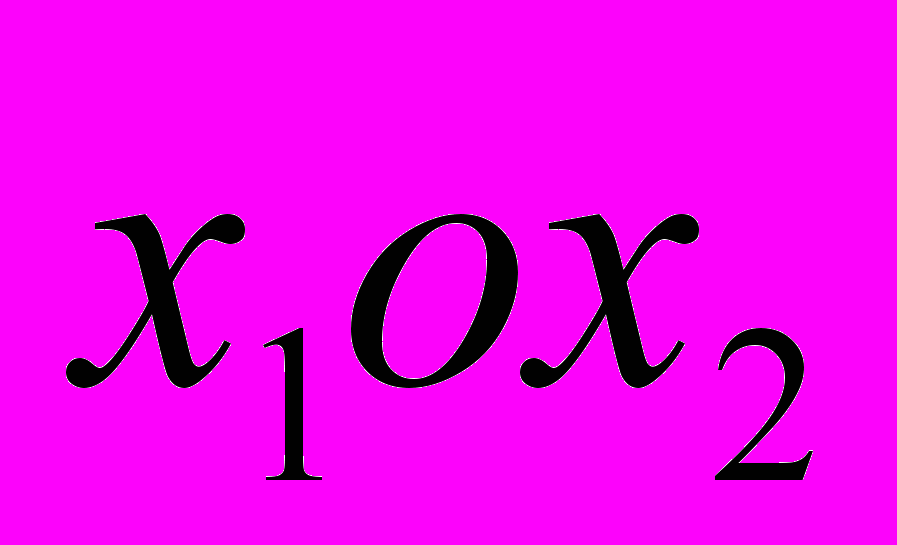параллельно плоскостям неоднородностей, приходим к задаче, когда внутри упругого пространства в сечениях 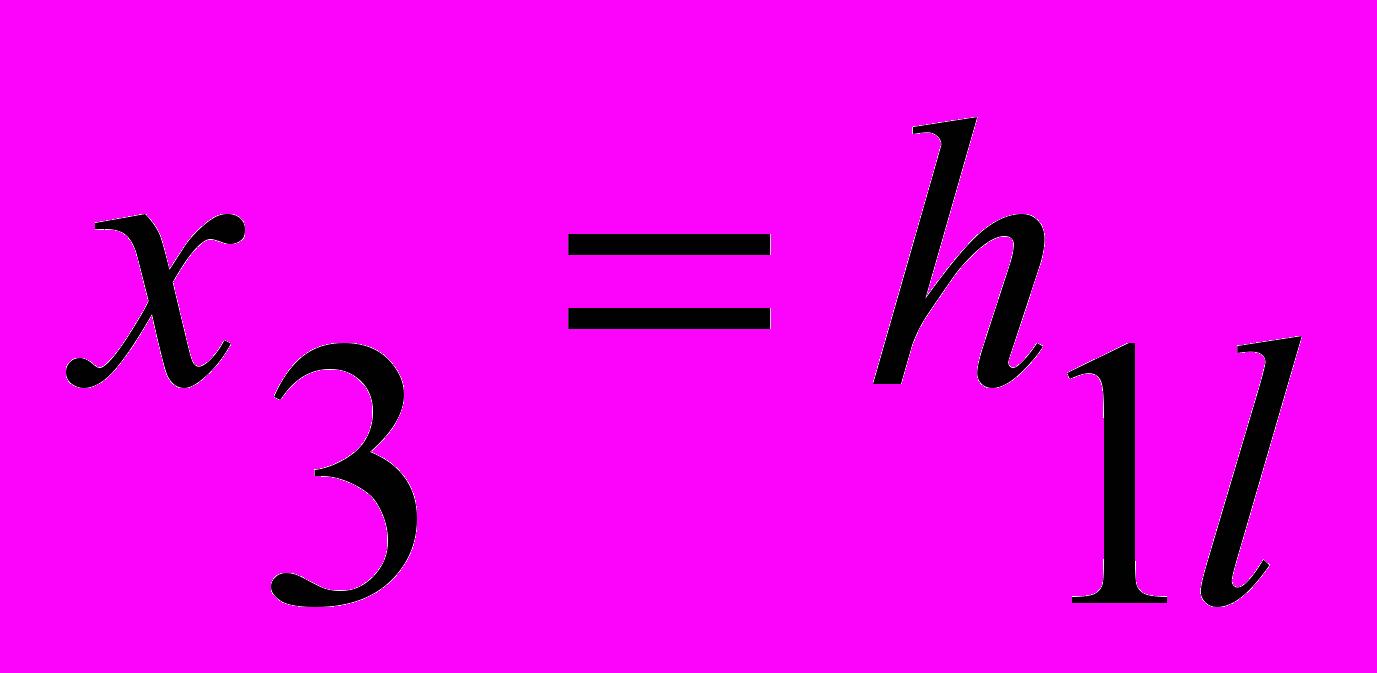, 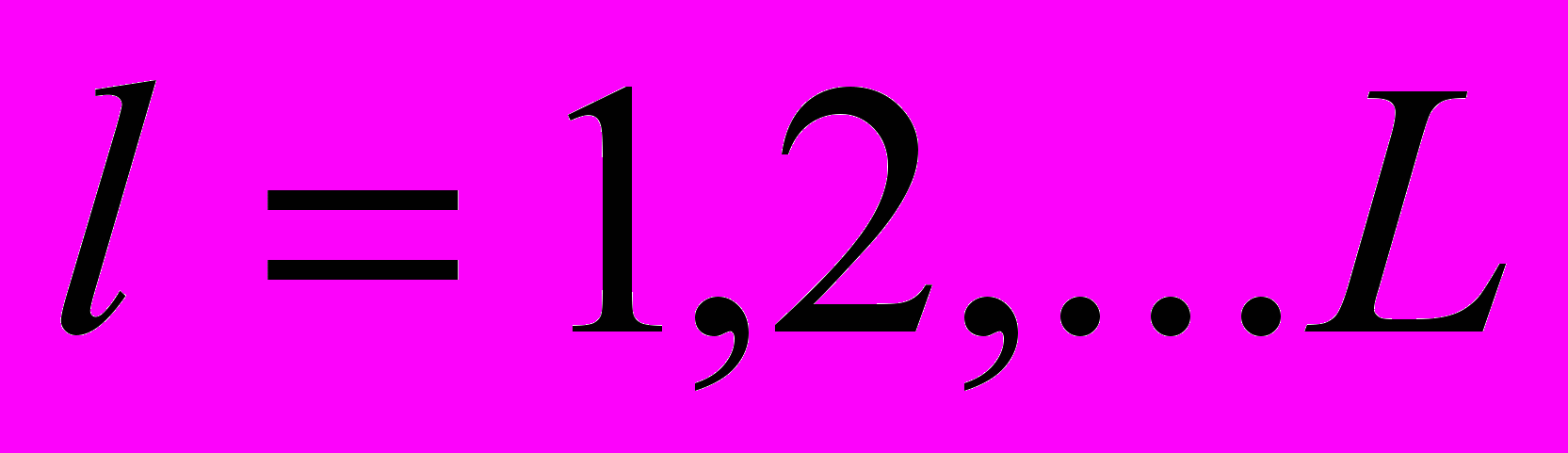имеются жесткие включения с носителями 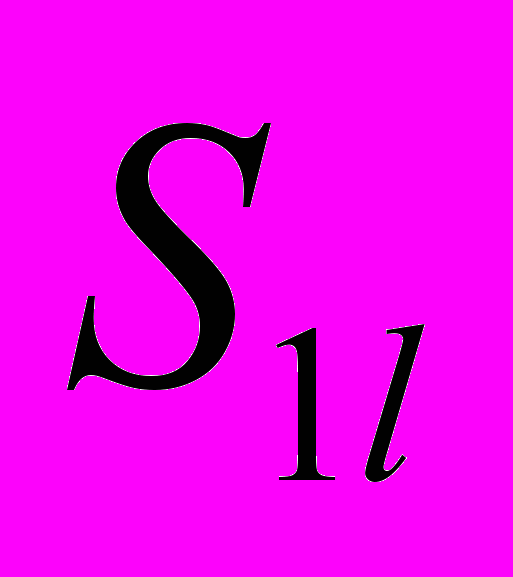, а в сечениях  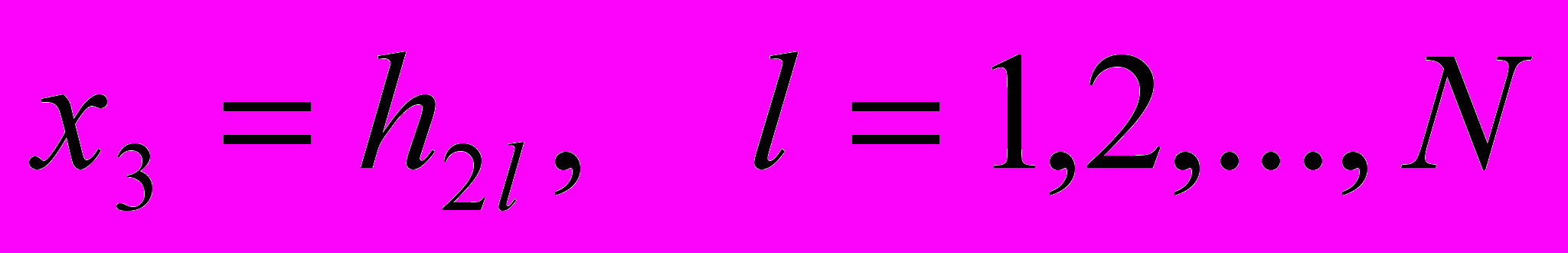— полости–трещины с носителями 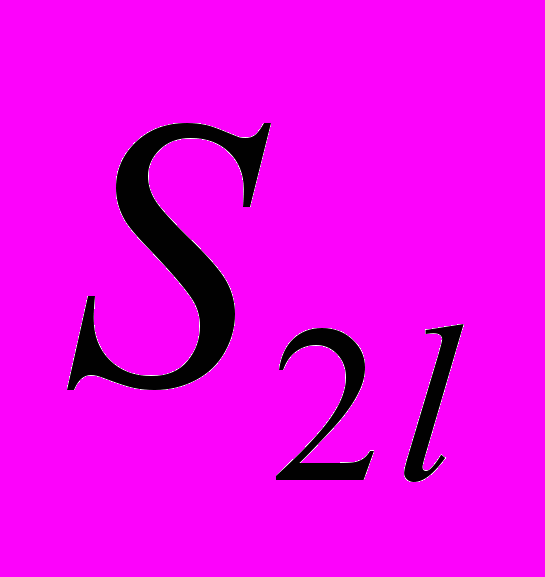. Может оказаться, что некоторые 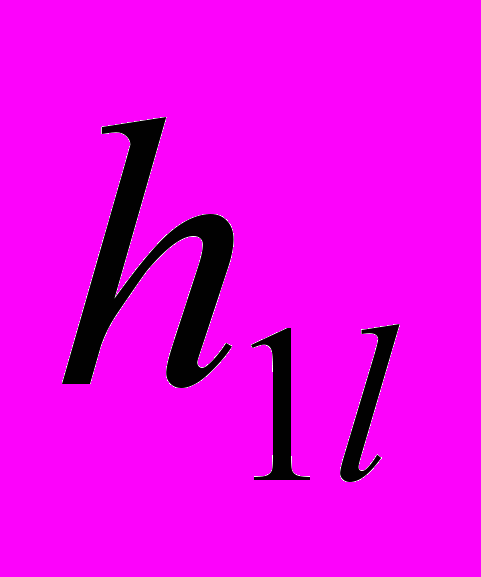и 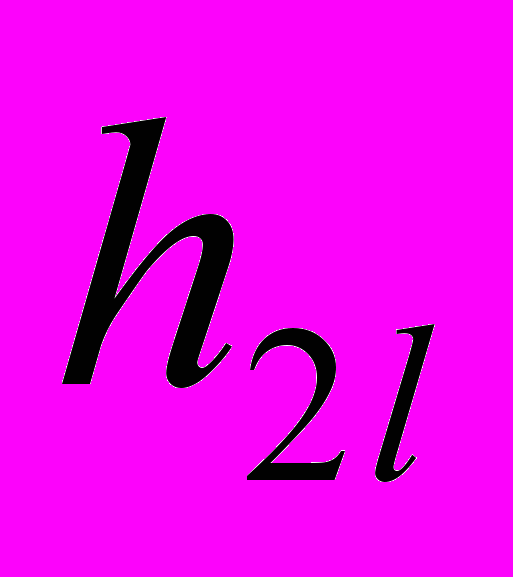совпадают. Множества, представляющее собой объединения носителей в сечениях , могут представлять собой совокупность одно или многосвязных областей.

Заметим, что данная система обозначений введена таким образом, что в случае процесса разрушения материала, начинающегося в зонах неоднородностей, плоскости, их содержащие, остаются неизменными, а области 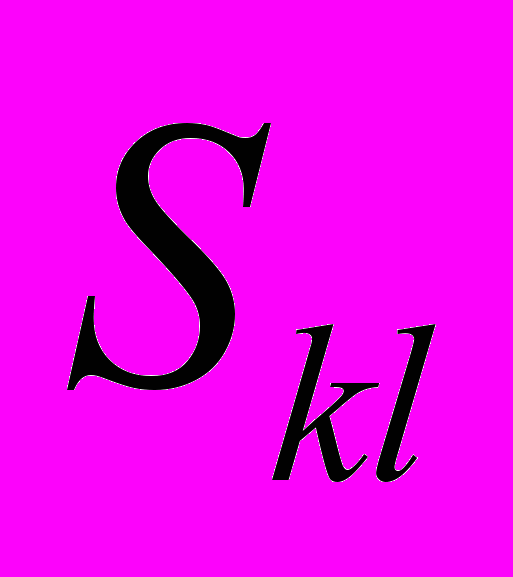могут измениться.

Интегральное представление волновых полей с помощью матрицы Грина является основой, так называемого, интегрального метода, который позволяет строить волновое поле в ближней зоне, изучать процесс подвода энергии к среде, ставить и решать задачу о формировании излучения заданной направленности с учетом взаимного влияния источников; а также изучать влияние неоднородностей среды на волновое поле, в частности резонансные особенности многослойных сред и сред, содержащих системы трещин или включений. В последнем случае источник колебаний задается без решения контактной задачи в виде некоторой элементарной сосредоточенной или равномерно распределенной в круге нагрузки.

Построив символ матрицы Грина 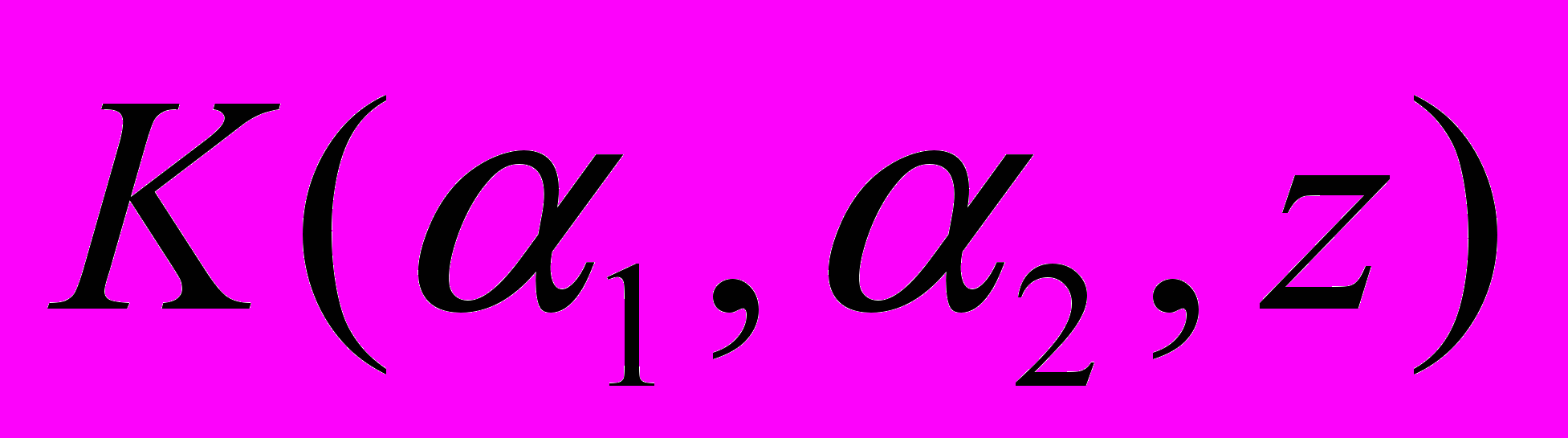, исследователь получает точное представление волнового поля с учетом бесконечного числа отражений и преломлений. Асимптотика в дальней зоне имеет тот же порядок точности, что и лучевая, но уже содержит всю информацию о наложении преломленных и отраженных волн.

Конкретный вид символа матрицы Грина определяется реальной моделью среды и строится таким образом, чтобы избежать трудностей при численной реализации, обусловленных наличием растущих экспоненциальных составляющих в фундаментальных решениях соответствующих систем дифференциальных уравнений. Для однородного полупространства и слоя явный вид матрицы K приведен в [6]. При произвольной зависимости свойств среды от глубины (стратифицированная среда) или всех пространственных координат (анизотропия), а также в слоистых средах и средах со сложными физико-механическими свойствами (термоупругие, электроупругие, термоэлектроупругие) построение матрицы Грина становится достаточно сложной задачей, которая, однако, успешно решена в [3]. Наличие систем неоднородностей приводит к существенному возрастанию порядка матрицы Грина (каждая неоднородность увеличивает размерность матрицы на 3).

В данном случае для построения матрицы Грина используется метод сведения краевых задач динамической теории упругости для неограниченных выпуклых областей с неплоской границей, изложенный в [6]. Результаты представлены в [7].

Для решения задачи, основанного на факторизации, а также анализа волновых полей необходимо знание вещественных особенностей элементов матрицы системы и ее определителя. К особенностям относятся стационарные точки показателей экспонент (фазовых функций), полюса и точки ветвления. Анализ вклада особенностей в асимптотику осцилирующих интегралов зачастую позволяет выделить из волнового поля некоторые регулярные структуры, которые в дальнейшем удается отождествить с объемными, поверхностными или каналовыми волнами. При этом вклад стационарных точек в асимптотику волновых полей в дальней зоне представляет собой объемные волны, а вклад полюсов дает слабозатухающие поверхностные и каналовые волны. Вклад точек ветвления обычно менее значителен, так как соответствует цилиндрическим волнам, распространяющимся в горизонтальном направлении, тем не менее, его оценка может понадобиться в случае анализа объемных волн, отраженных от нижних слоев слоистого полупространства в случае действия поверхностной нагрузки типа штампа.

Для одной-двух трещин проблема нахождения вещественных особенностей определителя решается достаточно легко, так как свойства матрицы - функции символа ядра позволяют воспользоваться известными алгоритмами вычисления определителей блочных матриц. Так, в случае двух трещин, определитель легко сводится к определителю третьего порядка и может быть подсчитан по правилу Саррюса. С ростом числа неоднородностей использование данного подхода становится нецелесообразным, так как возникает необходимость в обращении матриц высокого порядка, в общем случае размерности 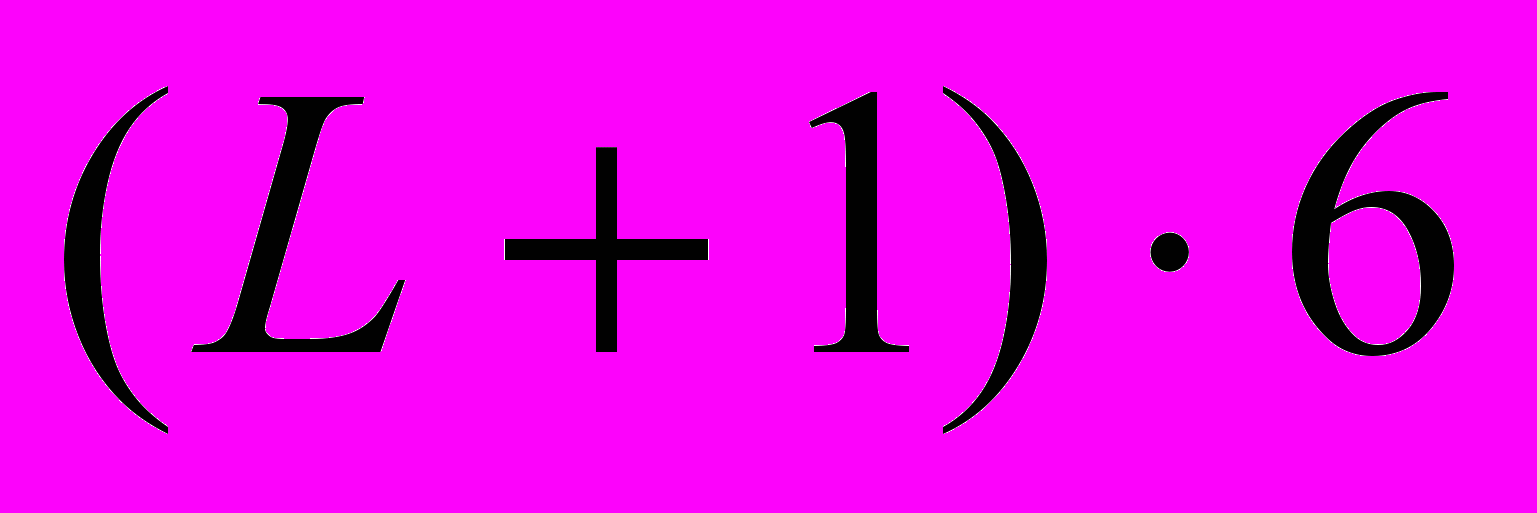. Тогда решение линейной системы уравнений относительно ее правой или левой части можно получить, обращая однотипные блоки матриц размерности 6, что в вычислительном отношении гораздо предпочтительнее.

Для реализации данного подхода разработан программный комплекс на языке FORTRAN 90, среда MS FORTRAN PowerStation, проведена серия модельных расчетов на примере трехслойной среды с разными свойствами анизотропии в каждом слое и разными расположениями полостей-трещин.

Получение окончательного решения поставленной задачи требует развития специальных численных методов изучения функций, представленных многомерными интегралами Фурье. В случае общих областей указанные интегралы являются представлениями функций на покрытиях топологического разбиения единицы. В случаях, подобных рассматриваемому, когда изучаемые области, в которых применяется дифференциальный метод факторизации, приобретают плоско-параллельные границы раздела, интегралы Фурье упрощаются.

Существует достаточно большой набор методов и программ вычисления подобных интегралов, тем не менее, представляет интерес разработка и более простых методов, учитывающих специфику подинтегральных функций. Ниже предлагается удобный для указанных задач метод вычисления обратного преобразования Фурье 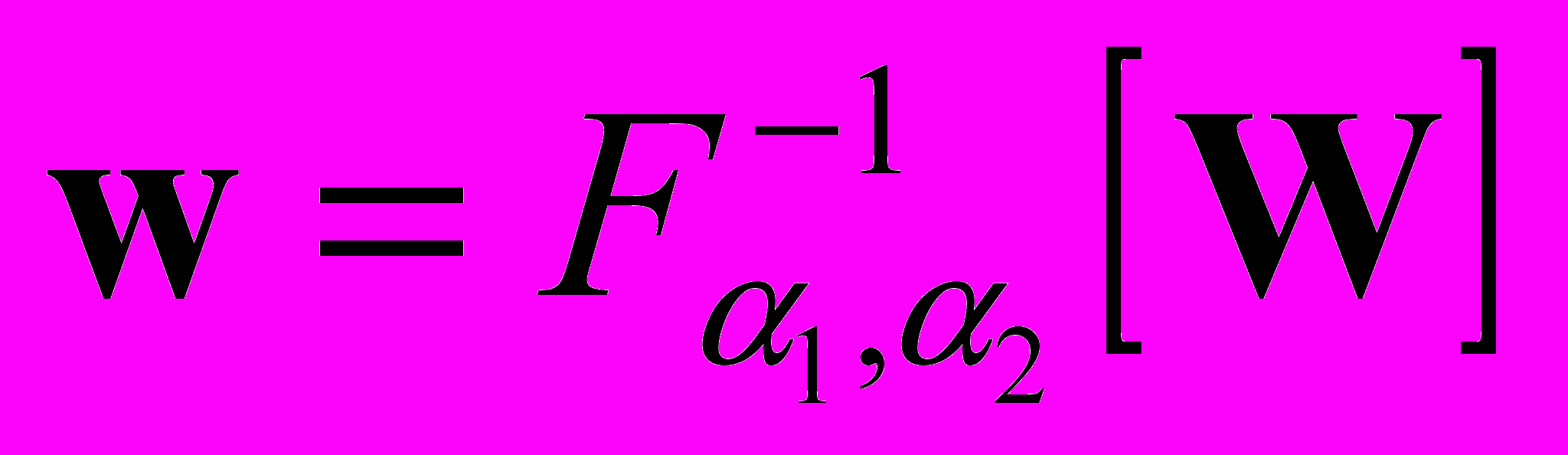при заданном векторе . Переходя к цилиндрической системе координат 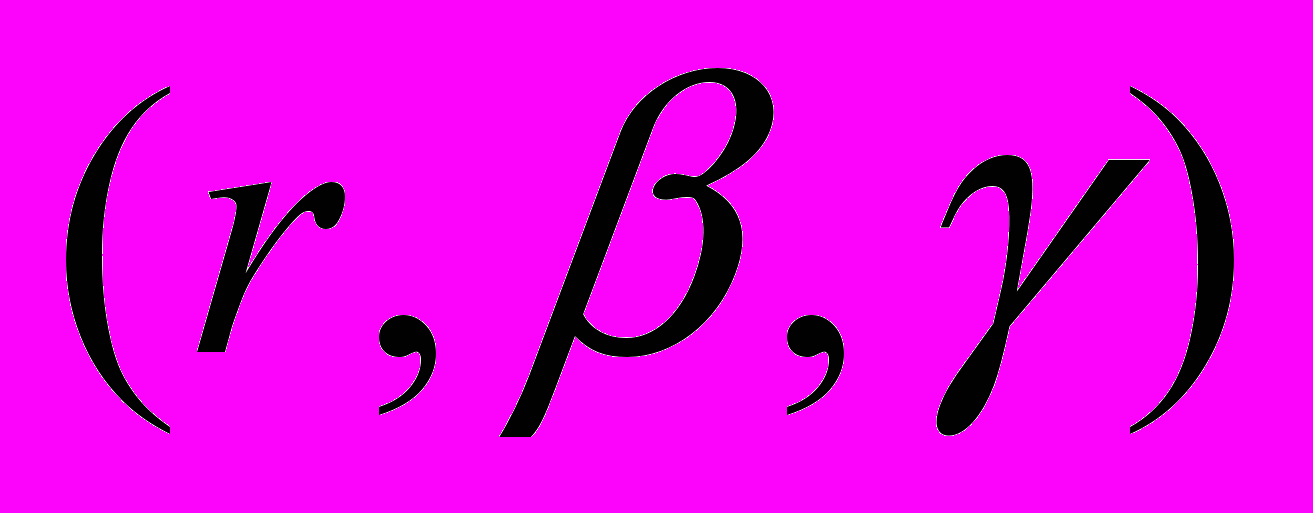и обозначая 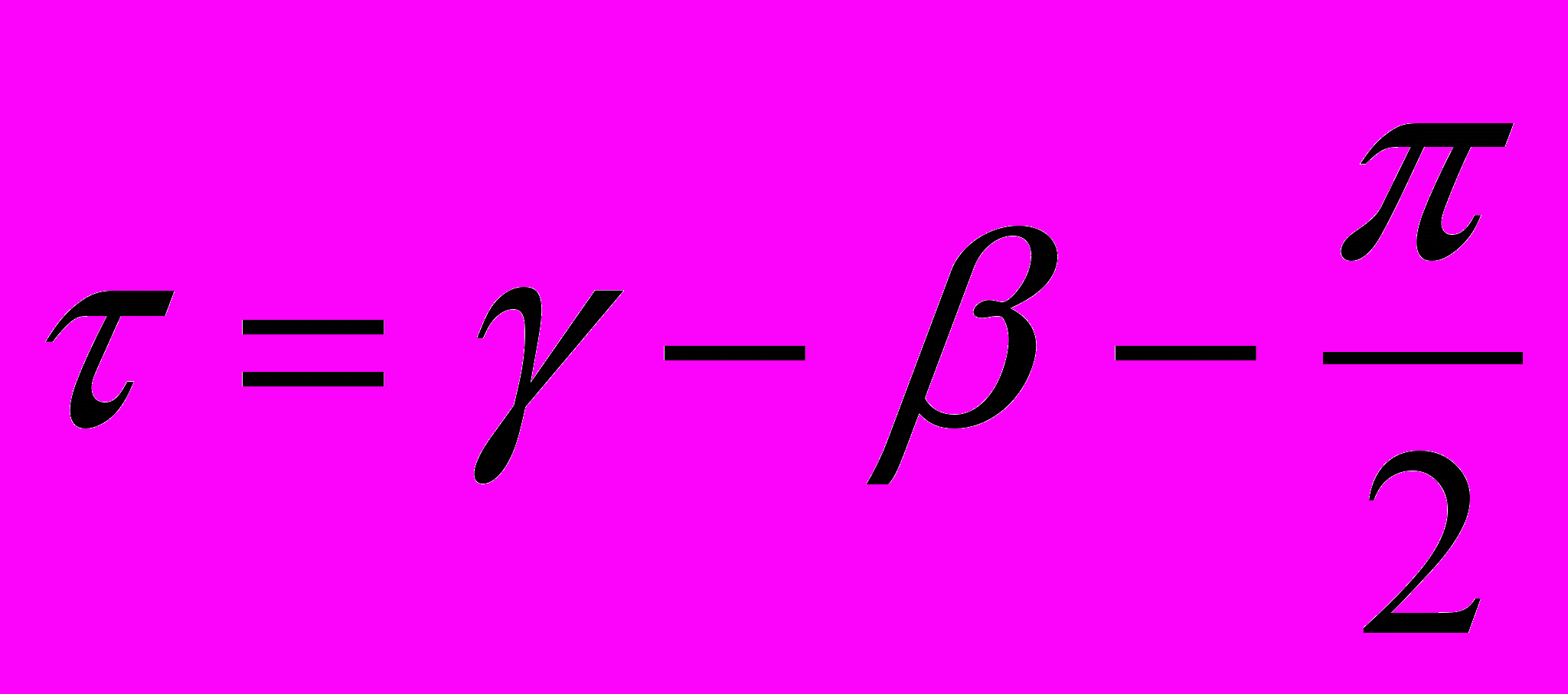, можно получить представление

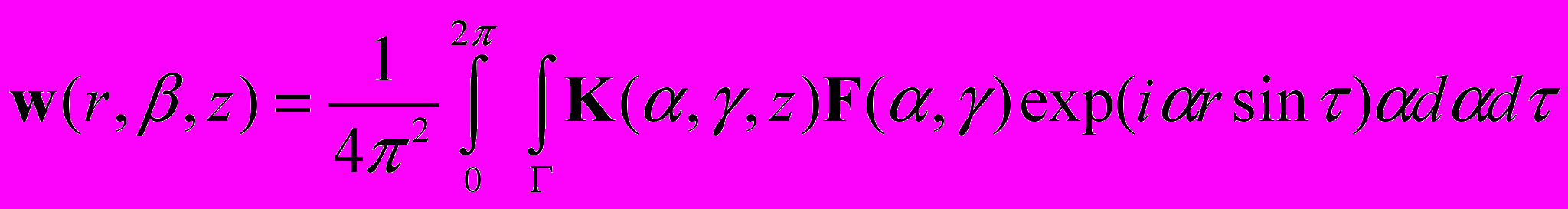(2)

Большое количество требуемых операций при вычислении матрицы 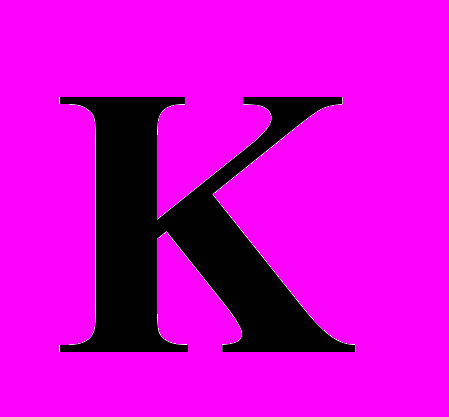, сильная осцилляция и особенности подынтегрального выражения существенно затрудняют прямой счет указанного интеграла. Для преодоления этих сложностей разработан специальный подход, позволяющий при незначительных вычислительных затратах оценить вклад вещественных полюсов и ближайших к вещественной оси комплексных полюсов в интеграл (2). Для этого представим (2) в виде суммы двух интегралов

(3)



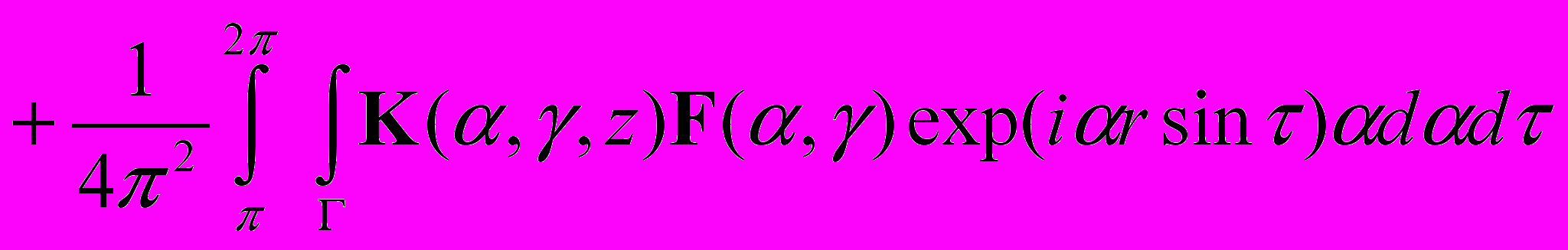
Отметим, что применение известной процедуры «разворота контура» в случае анизотропии общего вида неприемлимо. Поэтому, так как в первом интеграле (3) 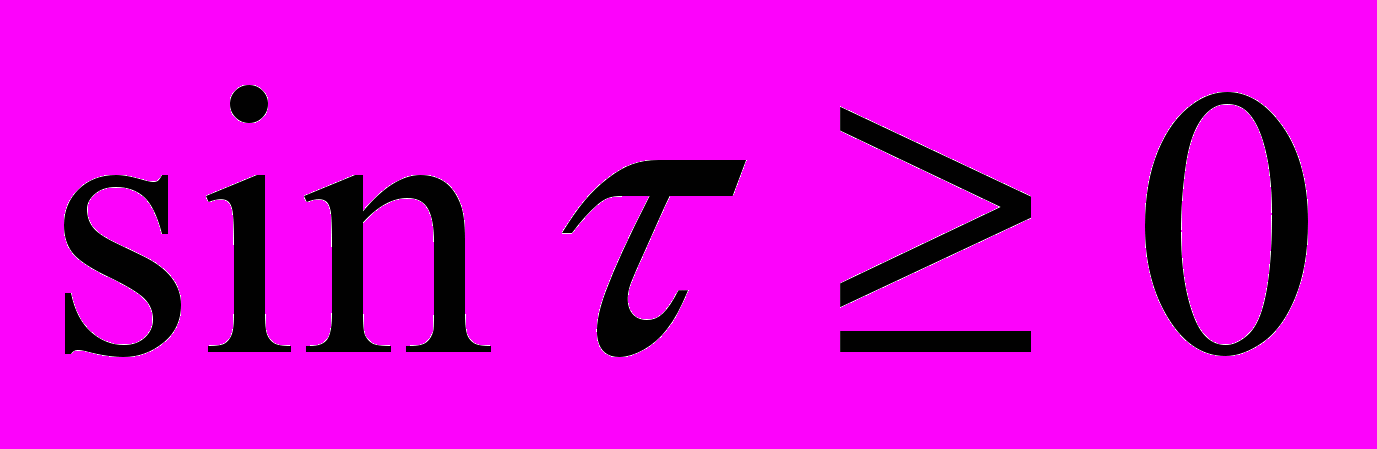и, следовательно, контур можно деформировать и замкнуть в первом квадранте, во втором интеграле 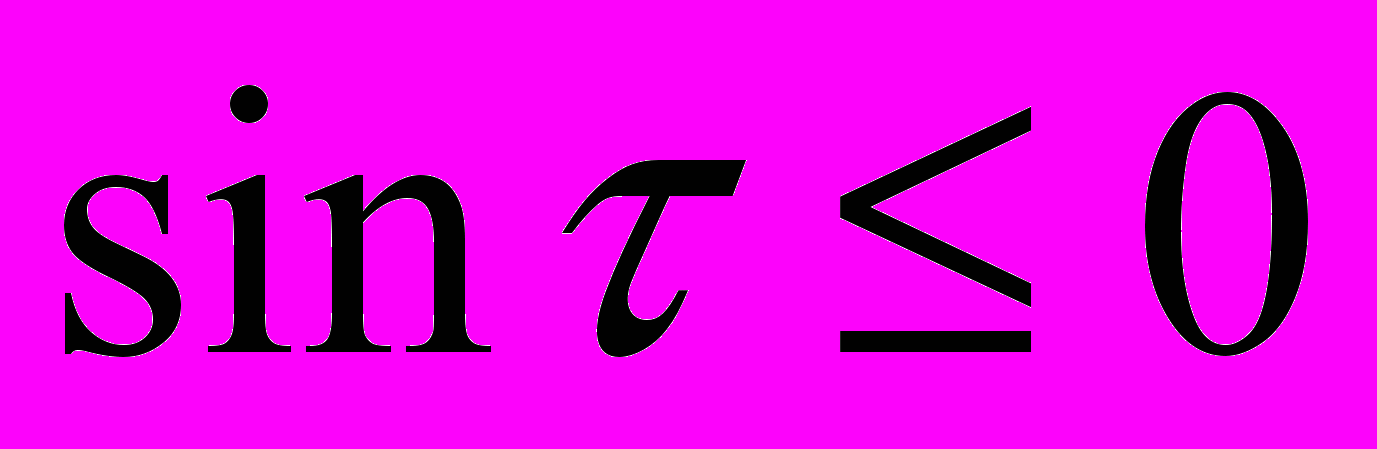и замыкается в четвертом квадранте аналогичным образом. Замкнутые контуры содержат интегралы по мнимой оси 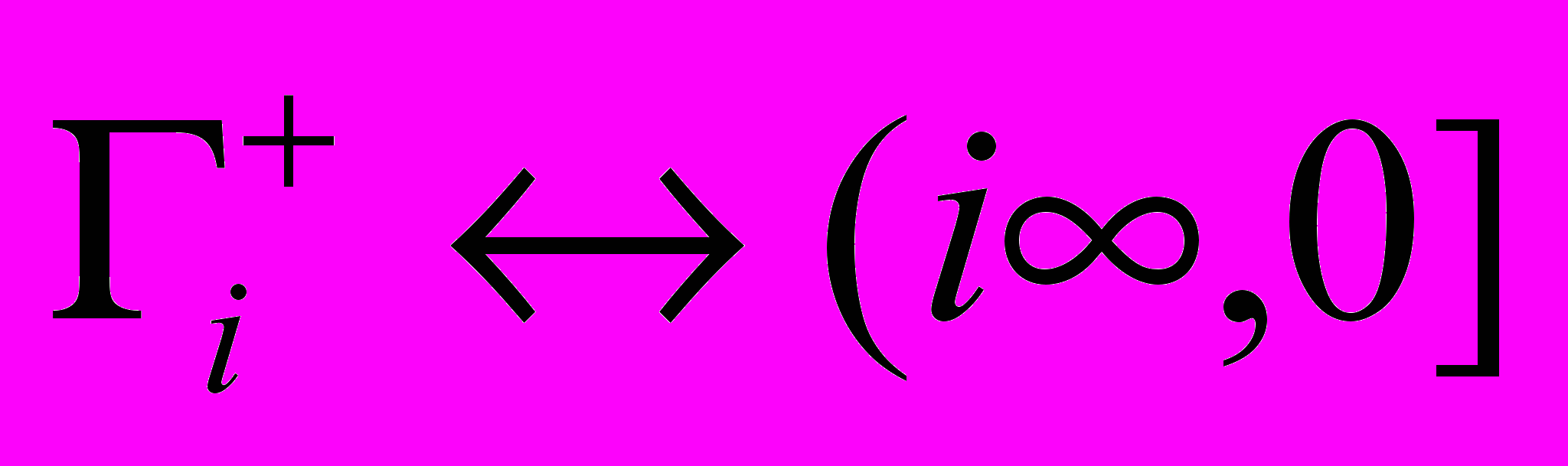, , 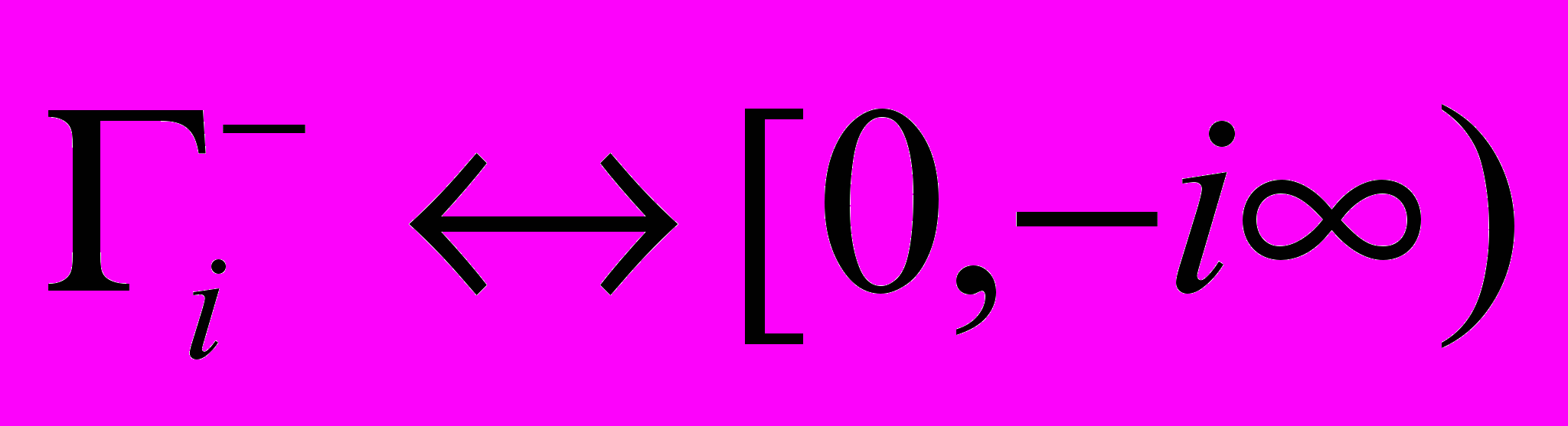по дугам четверть-окружностей в первом и 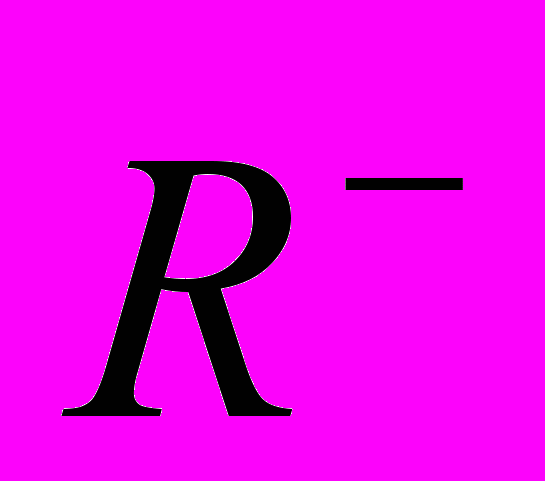в четвертом квадрантах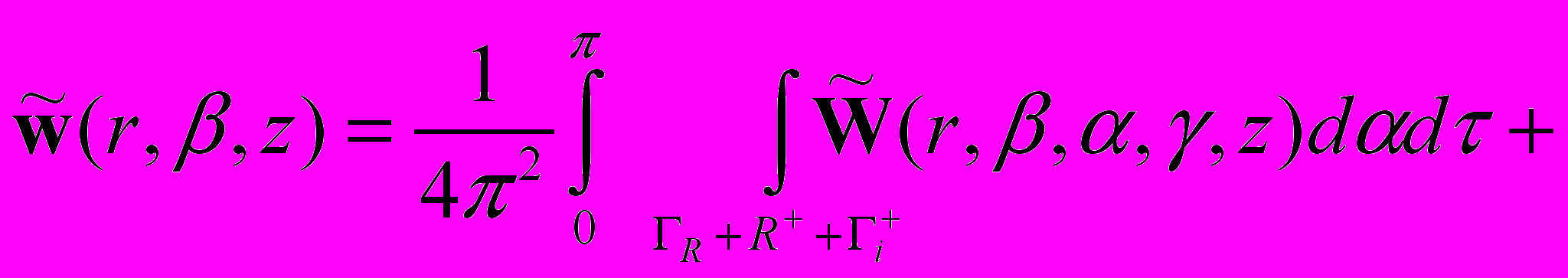

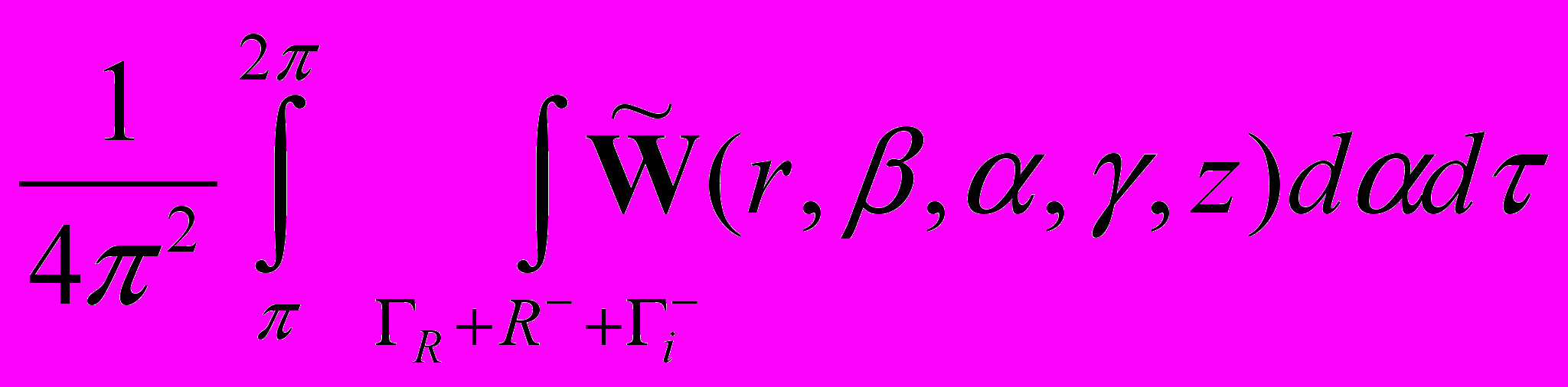(4)

Здесь 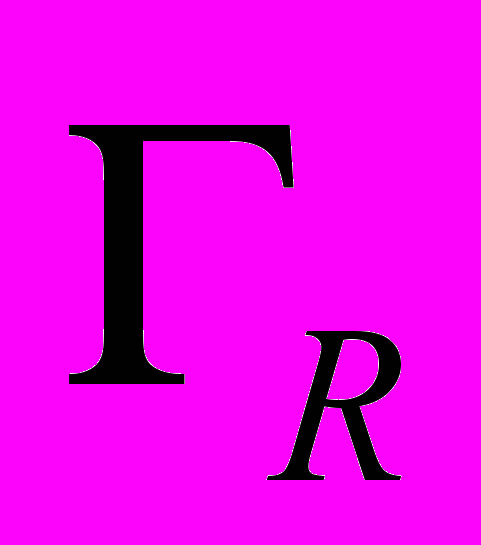- контур при 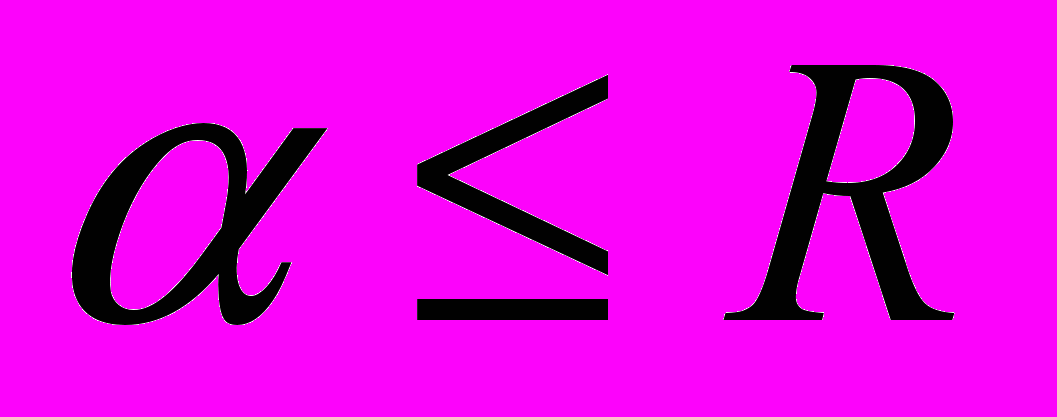. Интегралы по 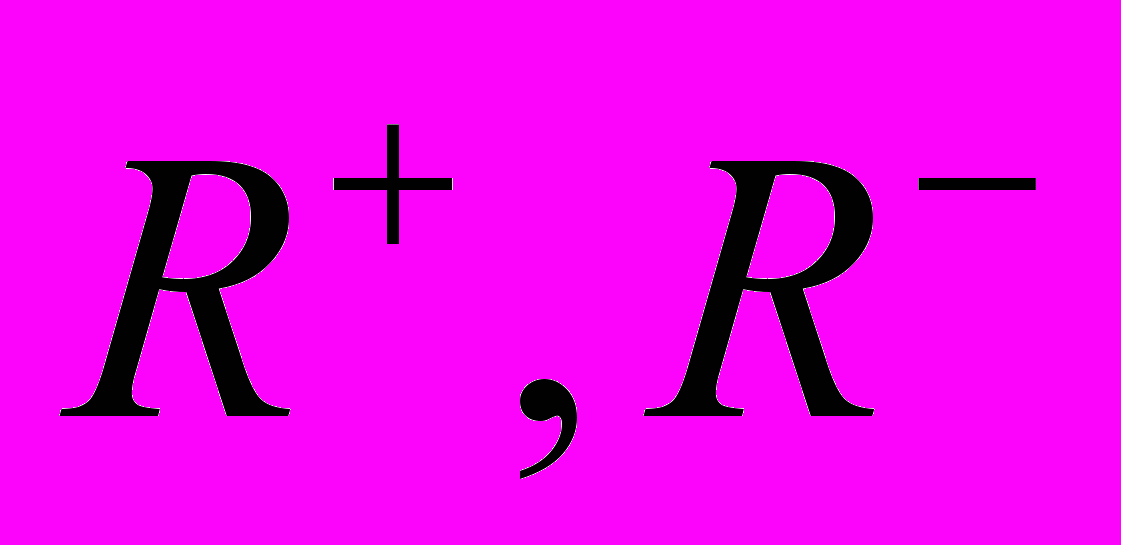по лемме Жордана при стремятся к нулю. Таким образом, для 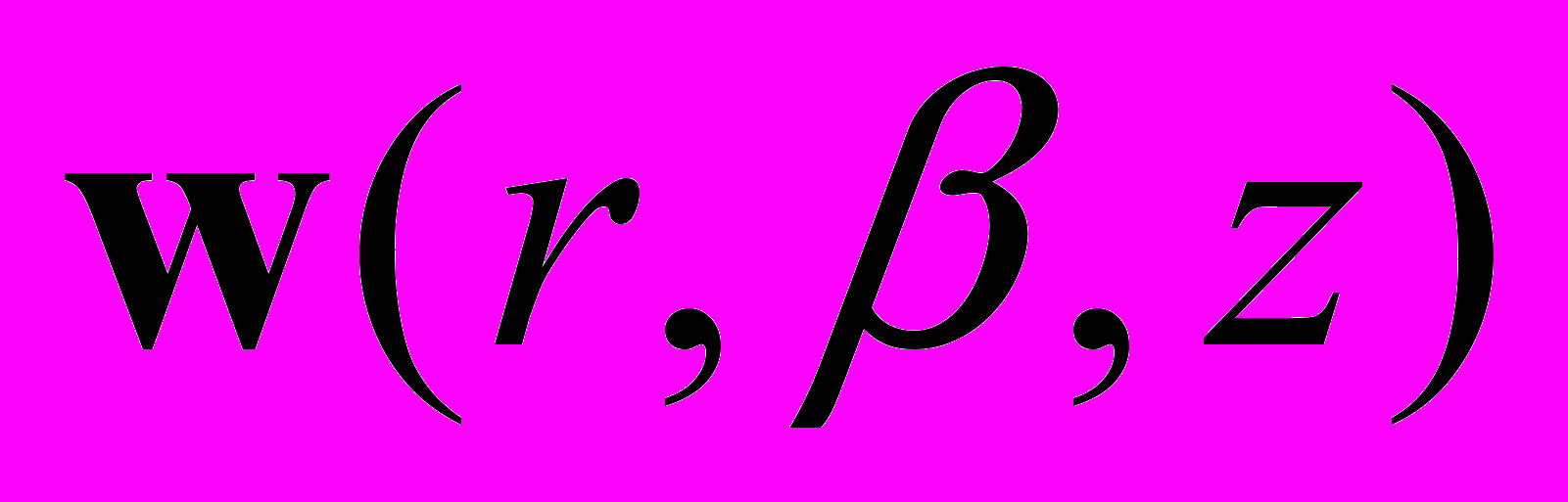в представлении (4) получаем

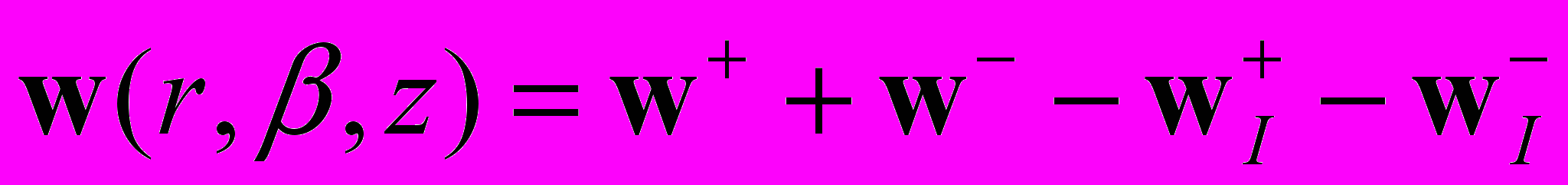(5)

где

, , , , ,

,

,

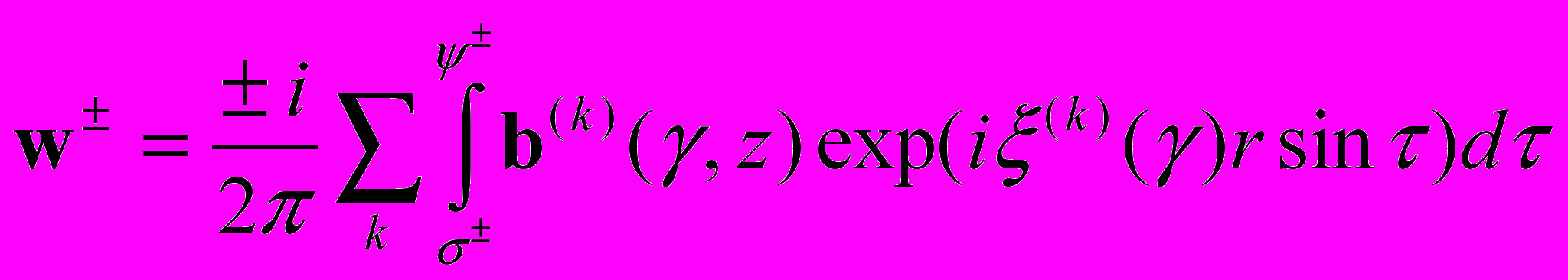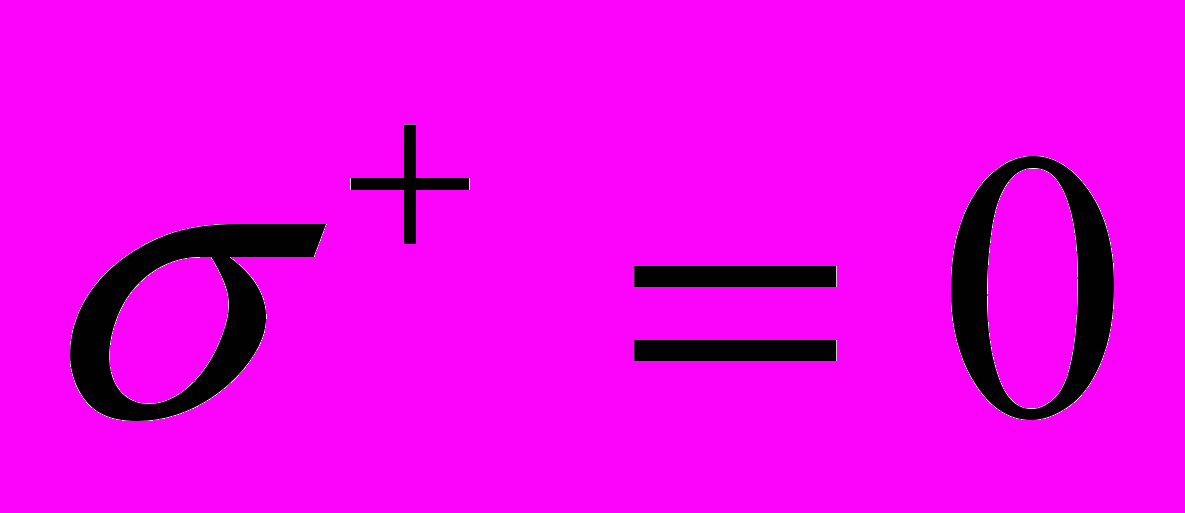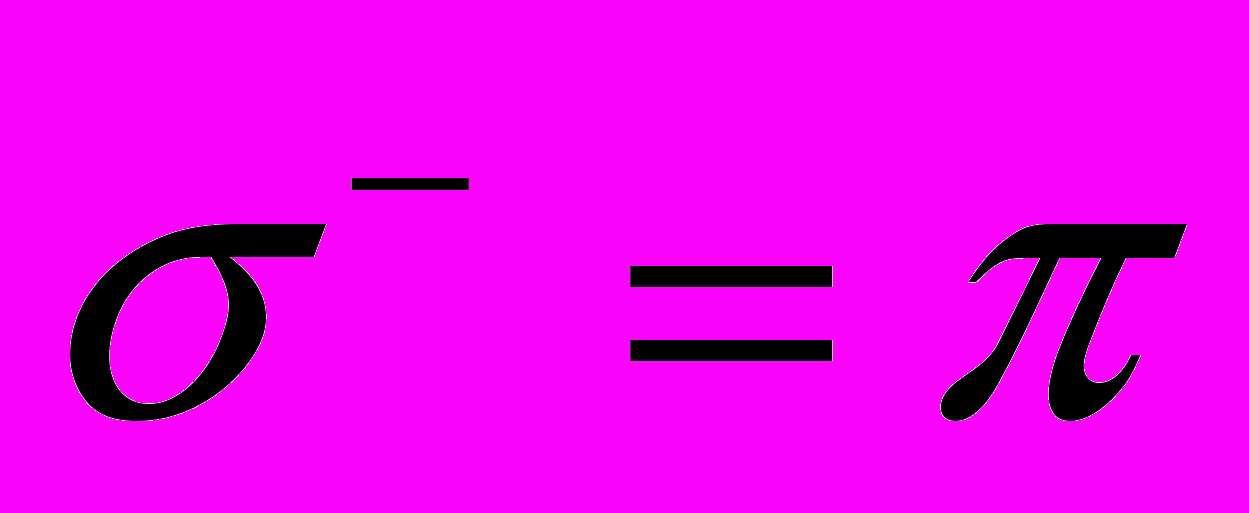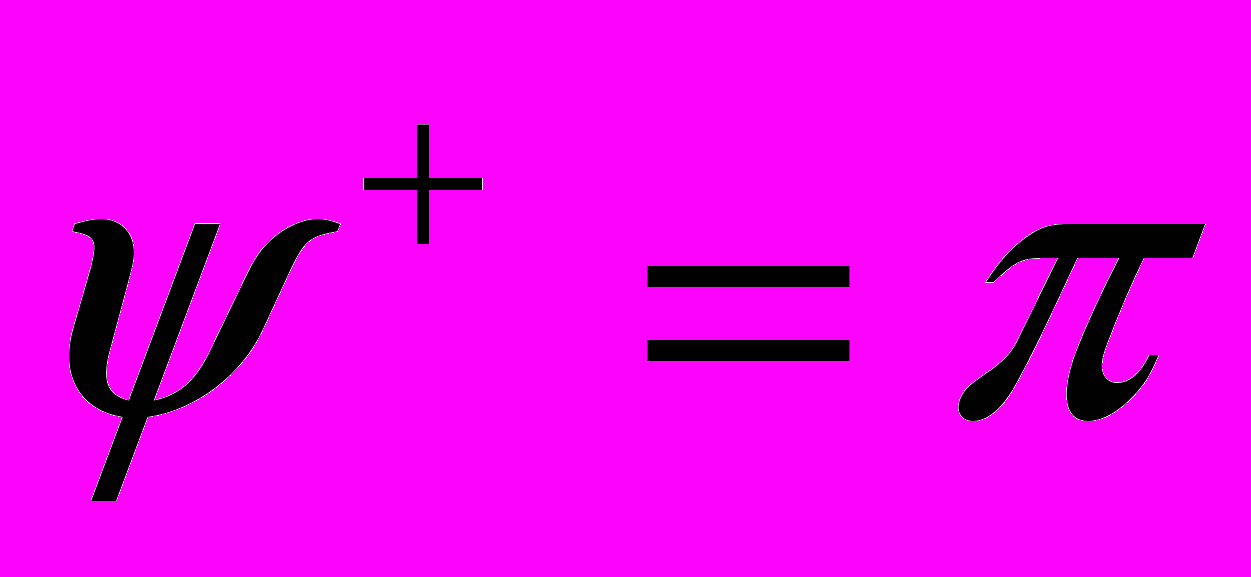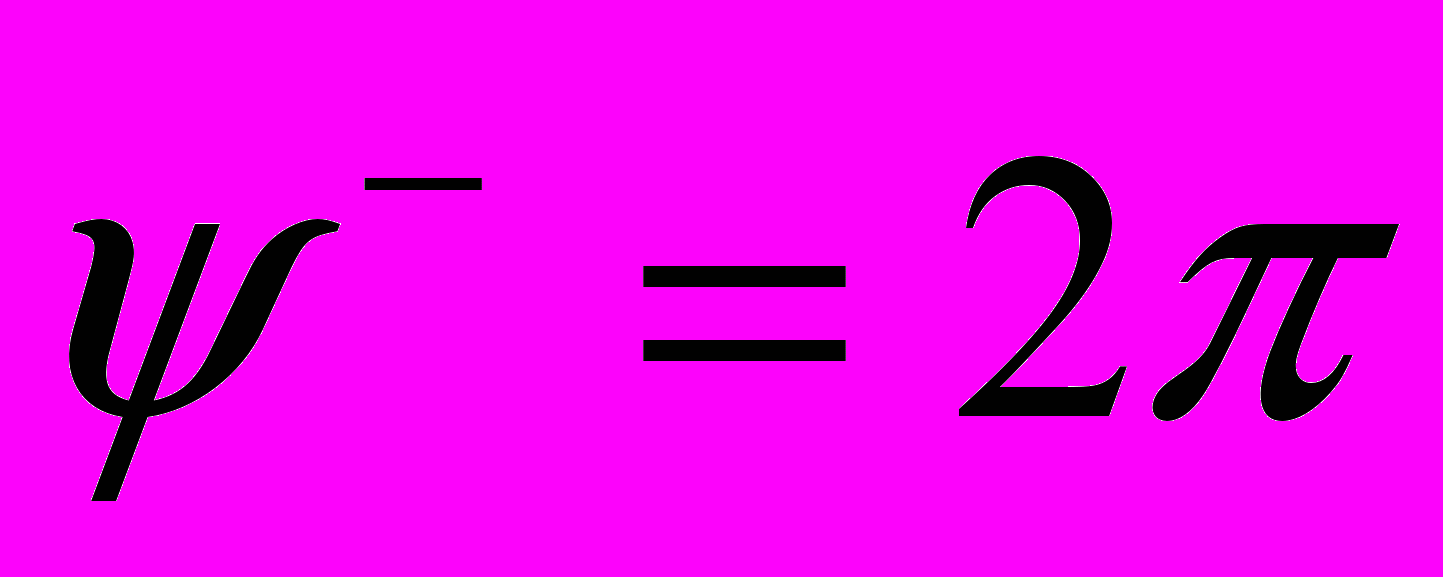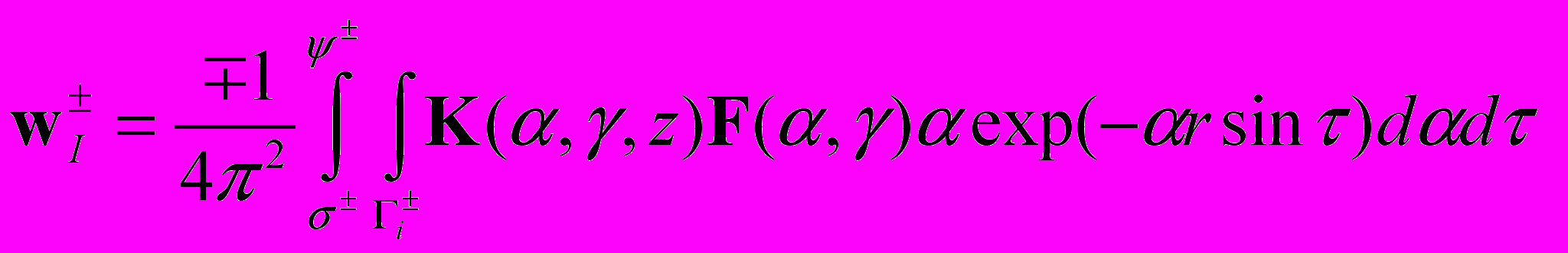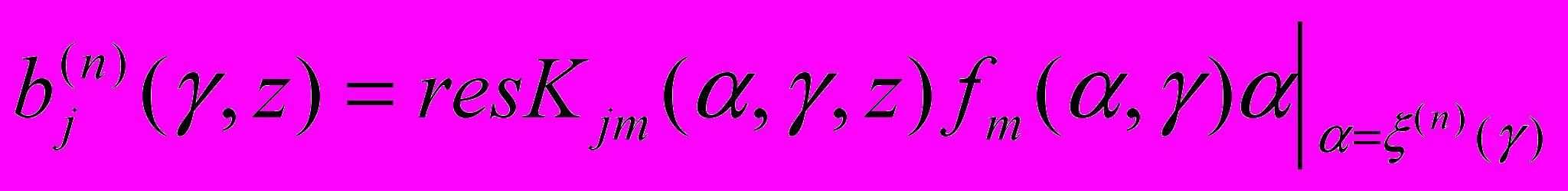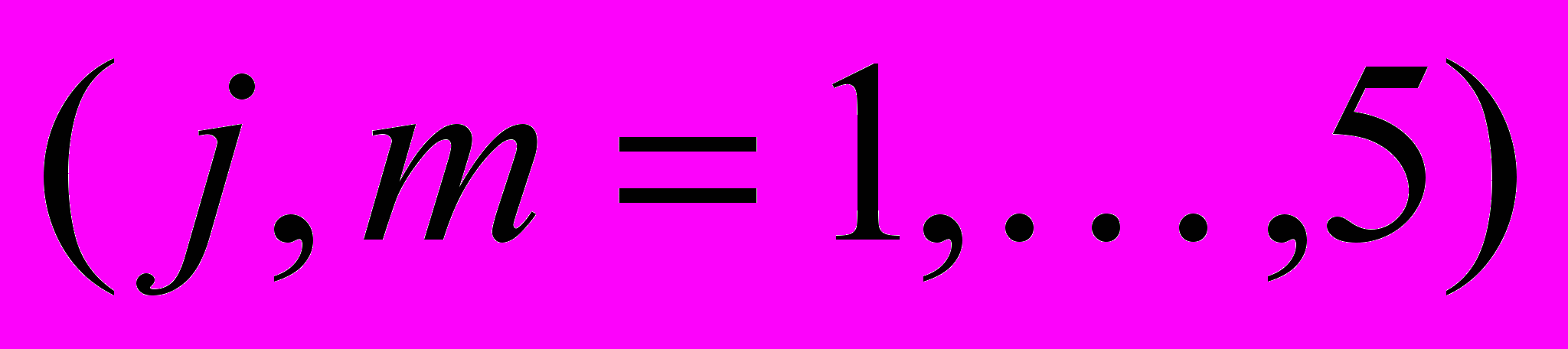
За счет убывающих экспонент вычислительная сходимость интегралов 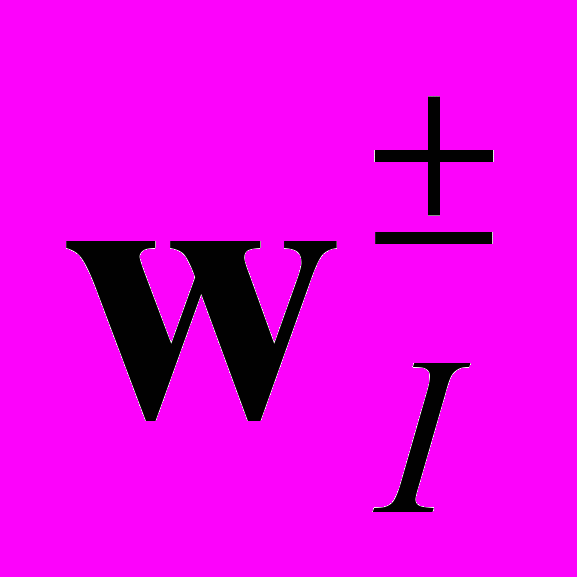по быстрее, чем . Кроме того, во всех численных экспериментах выполнялось соотношение .

Предложенный поход реализован в программах [8-9].


При некоторых существенных модификациях метод факторизации применим для исследования краевых задач в таких сложных областях, как неограниченные и многосвязные [10-11].

С практической точки зрения данная модификация метода факторизации дает возможность решать динамические задачи о вибрации полуограниченной геосреды, вмещающей грязевулканические структуры как положительной, так и отрицательной форм по единому алгоритму с учетом реального сложного (а не только плоско-параллельного) строения системы карманов, аккумулирующих сопочную брекчию, воды и газы.

Работа выполнена при поддержке Программы отделения наук о Земле РАН «Развитие технологий мониторинга, экосистемное моделирование и прогнозирование при изучении природных ресурсов в условиях аридного климата», Программы 09 Президиума РАН «Исследование вещества в экстремальных условиях», гранта РФФИ №05-01-00902, а также проекта «Исследование распределения вулканической активности на шельфе Азовского моря», финансируемого компанией «Приазовнефть».


Литература
  1. Мамедов Л.З., Гулиев И.С. Субвертикальные геологические тела в осадочном чехле Южно-Каспийской впадины // Азярбайъан милли елмляри, №3, 2003, с.139-146
  2. Глинский Б.М., Собисевич А.Л., Хайретдинов М.С. Опыт активного мониторинга сложно построенных геологических структур (на примере грязевого вулкана Шуго) // Вулканология и сейсмология. М.: «Наука». 2007.
  3. Ворович И.И., Бабешко В.А., Пряхина О.Д. Динамика массивных тел и резонансные явления в деформируемых средах – М.: Научный мир, 1999, с.246
  4. Ворович И.И., Бабешко В.А. Динамические смешанные задачи теории упругости в неограниченных областях. М.: Наука, 1979, 320 с.;
  5. Ворович И.И. Спектральные свойства краевой задачи теории упругости для неоднородной полосы. ДАН СССР,1979. Т.245, №4. С.817-820
  6. Бабешко В.А., Глушков Е.В., Зинченко Ж.Ф. Динамика неоднородных линейно-упругих сред. - М.: Наука, 1989.- 344с.
  7. Бабешко В.А., Павлова А.В., Ратнер С.В., Р. Вильямс (США). Задачи о вибрации упругого полупространства, содержащего систему внутренних полостей.// Доклады РАН, 2002, Т. 386, №1
  8. Сыромятников П.В., Ратнер С.В., Зарецкая М.В., Ломакина Л.В. Программа расчета смещений частиц упругой слоистой анизотропной среды, содержащей систему жестких включений, при возбуждении сейсмических волн внутренними источниками. Свидетельство об официальной регистрации программы для ЭВМ №2006614043 от 24.11.06
  9. Сыромятников П.В., Ратнер С.В., Зарецкая М.В., Ломакина Л.В. Программа расчета механических перемещений точек среды, возбуждаемых поверхностными гармоническими нагрузками в пакете упругих анизотропных слоев, содержащих систему трещин. Свидетельство об официальной регистрации программы для ЭВМ №2006614042 от 24.11.06
  10. Бабешко В.А., Бабешко О.М. Обобщенная факторизация в краевых задачах в многосвязных областях // ДАН. 2003. Т. 392. №2. С. 163–167.
  11. Бабешко В.А., Бабешко О.М. Метод факторизации в краевых задачах в неограниченных областях // ДАН. 2003. Т.392. № 6. C. 767–770.