Е. В. Лысь, В. В. Лисица, Г. В. Решетова, В. А. Чеверда
| Вид материала | Документы |
СодержаниеПоглощение в анизотропной среде Ограничение расчетной области Численные эксперименты Список литературы |
- «Шаг в науку, юниоры Псковщины», 118.89kb.
- Тема: Обобщающий урок по басням И. А. Крылова «Ворона и Лисица», «Волк и Ягненок»,, 55.21kb.
- Книги для самостоятельного чтения. 8 класс Русские народные песни и баллады, 29.51kb.
- Курс 5 Т. Я. Решетова Форма обучения гвд человек 26 Дата, 236.89kb.
- Майнарди Д. М14 Собака и лисица. Пер с итал. А. Б. Махов /Под ред и с предисл., 1483.51kb.
- О сотрудничестве по уголовным делам, 979.88kb.
- З. В. Лисица расписание курсов по выбору в 9 классе, 11.34kb.
- Иван Андреевич Крылов Ворона и Лисица, 17.25kb.
- Героя Советского Союза С. Н. Решетова Структура программы пояснительная записка, 2163.86kb.
- Героя Советского Союза С. Н. Решетова программа, 133.74kb.
Е.В.Лысь, В.В.Лисица, Г.В.Решетова, В.А.Чеверда
Ин-т нефтегазовой геологии и геофизикиСО РАН
(Россия, 630090, Новосибирск, пр. Коптюга, 3,
тел.(383) 3302796, E-mail: lysev@ipgg.nsc.ru)
Конечно-разностное моделирование акустического каротажа в трехмерных неоднородных трансверсально-изотропных средах с поглощением
Ведение:
Ключевое предназначение метода акустического каротажа это детальное определение структуры и механических свойств пород в околоскважинной зоне, посредством измерения и изучения волнового поля создаваемого источником сейсмоакустических волн, расположенным в скважине. Эта задача в упрощённой постановке (скважина в однородной изотропной среде) впервые была исследована в работе [2]. Впоследствии множество авторов внесло свой вклад в изучение этой проблемы [5], [6]. Однако вплоть до настоящего времени отсутствует детальное понимание особенностей процессов распространения акустических волновых полей для реалистичных неоднородных трехмерных сред с анизотропией и поглощением. Поэтому численное моделирование является, по нашему мнению, единственной возможностью изучения волнового поля, возникающего при выполнении акустического каротажа. В работе представлена модификация ранее разработанного метода конечно-разностного моделирования акустического каротажа для изотропной вязкоупругой среды [6], позволяющая проводить расчёты для трансверсально-изотропной упругой среды с поглощением. Благодаря специальному виду тензора упругих модулей в случае VTI среды можно, как и в изотропном случае применить для построения схемы сдвинутую сетку Верьё[8] и как следствие нет необходимости менять основу разработанного ранее алгоритма, включая измельчение сетки по радиусу и азимуту. Главные изменения коснулись двух областей: описания поглощения и ограничения расчётной области.
Поглощение в анизотропной среде:
Для введения поглощения предлагается естественное обобщение подхода, представленного в [9].
Для начала напомним, что в изотропной среде поглощение вводится независимо для P и S волн и определяется добротностями
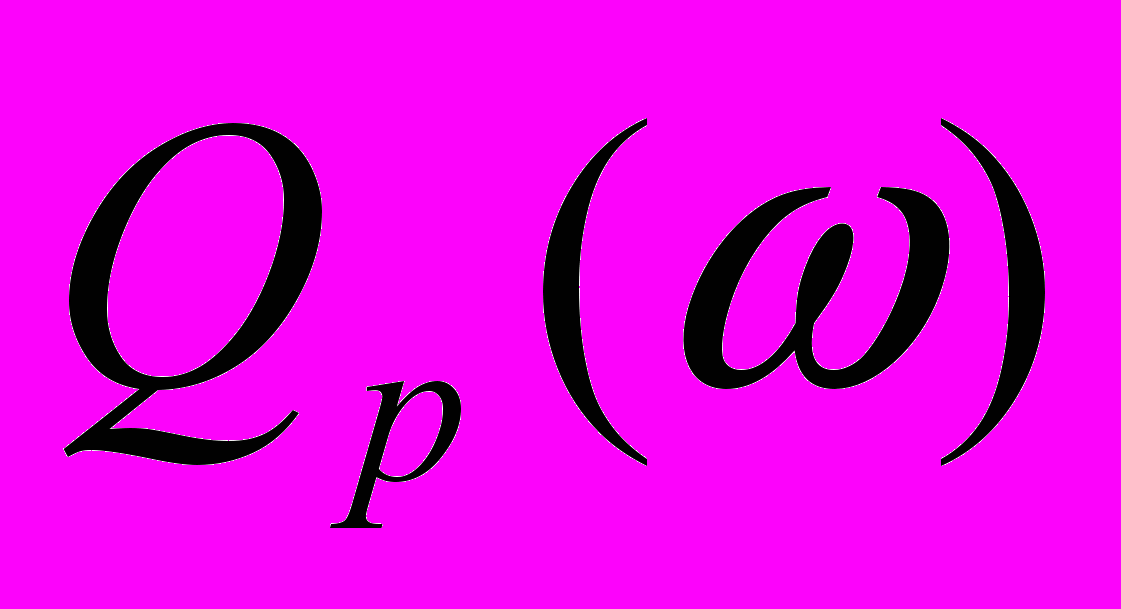 и
и 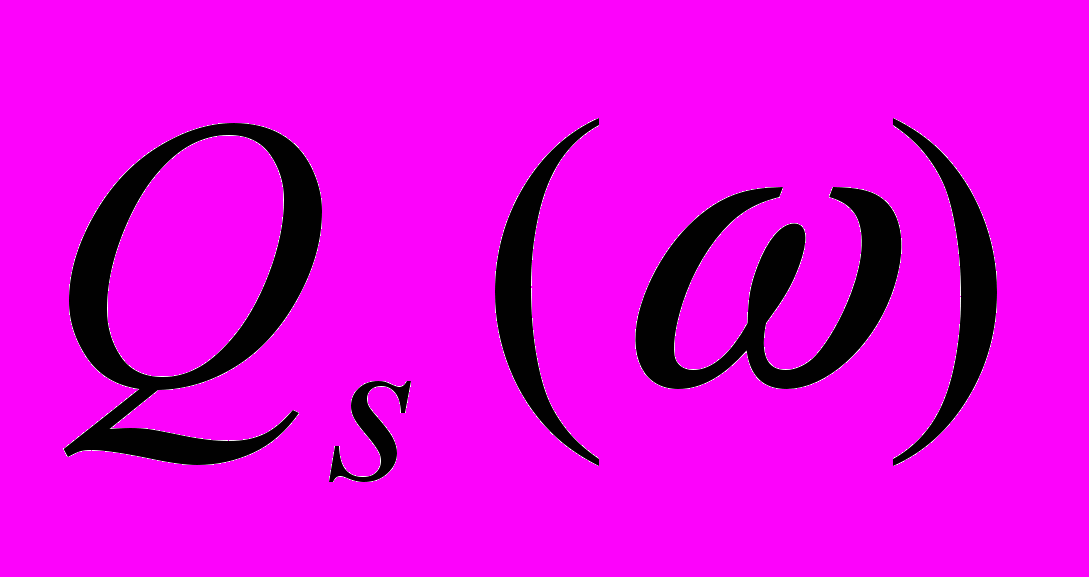 . В анизотропной среде ввести поглощение независимо для каждой из трёх волн qP, qSV и qSH не представляется возможным. Рассмотрим тензор, связывающий напряжения с деформациями вязкоупругой среды в частотной области:
. В анизотропной среде ввести поглощение независимо для каждой из трёх волн qP, qSV и qSH не представляется возможным. Рассмотрим тензор, связывающий напряжения с деформациями вязкоупругой среды в частотной области: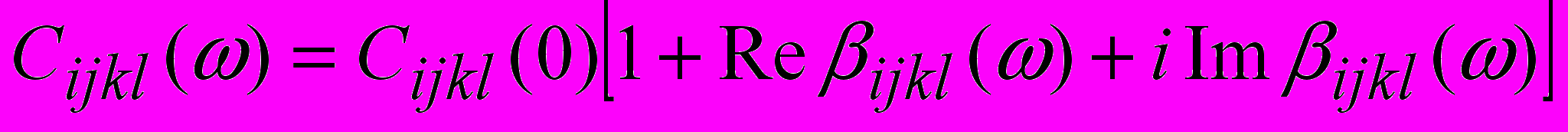 ,
,Наличие вещественной и мнимой частей у компонент тензора влечет за собой наличие вещественной и мнимой частей у фазовых скоростей, то есть:
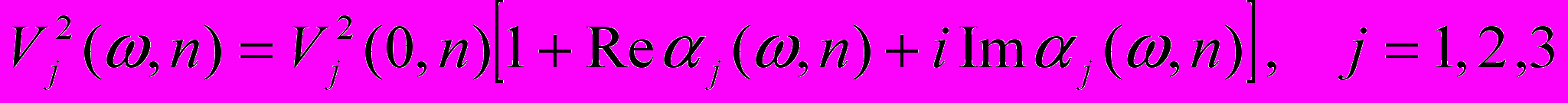
Будем считать, что мы можем измерить эти комплексные скорости для некоторых направлений на каждой временной частоте. Тогда задача отыскания компонент тензора ставится следующим образом:
Восстановить параметры
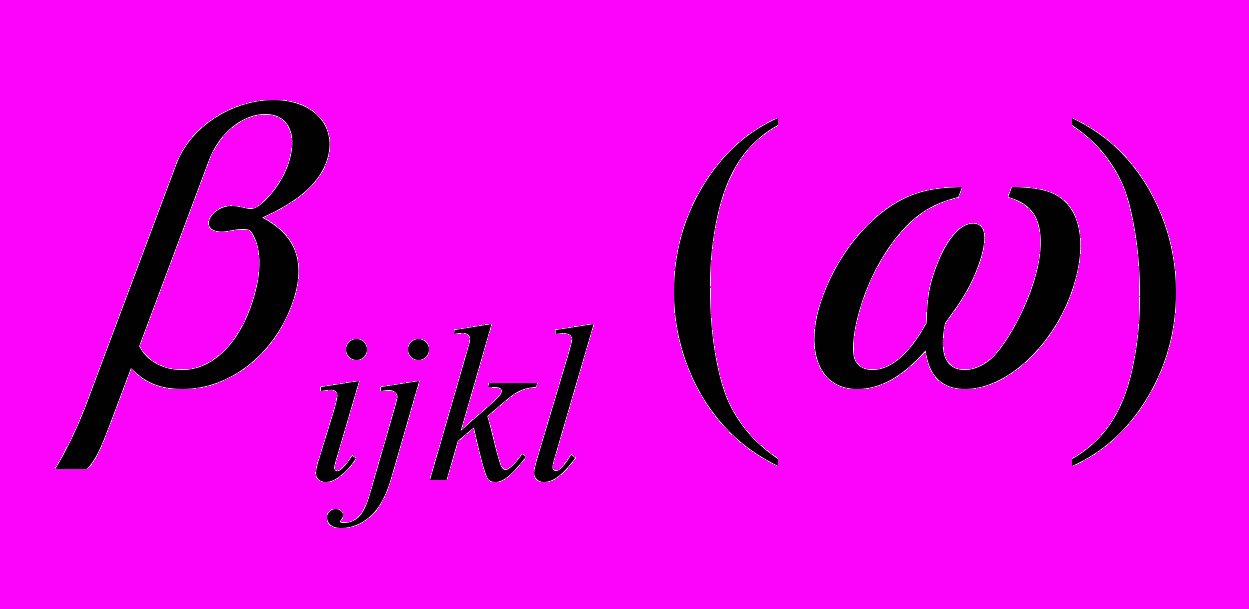 по комплексным скоростям (распространения и затухания) измеренным по ряду направлений:
по комплексным скоростям (распространения и затухания) измеренным по ряду направлений: 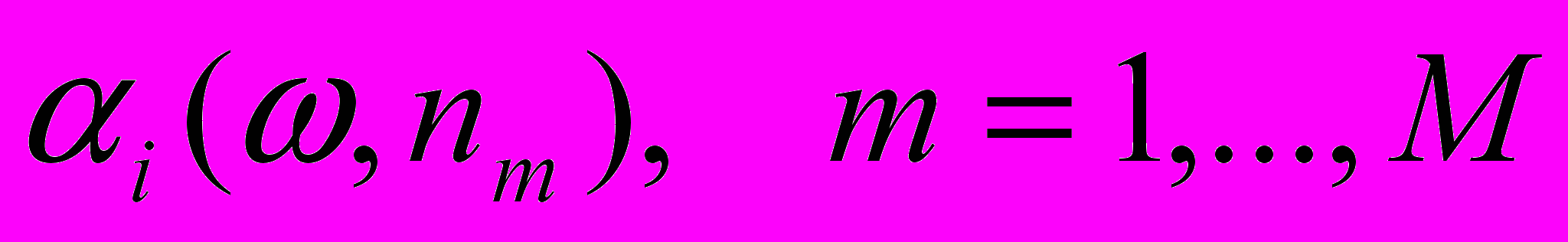
Как можно видеть, этот подход обеспечивает одинаковый тип симметрии (тип анизотропии) и для скоростей и для поглощения.
Мы разработали и применили этот подход для VTI сред со слабой анизотропией [7] и доказали, что он приводит к классической постановке задачи теории возмущений применительно к симметричной проблеме собственных значений и требуется как минимум пять независимых измерений для каждой временной частоты: четыре для qP или qSV и одно для qSH. Затем необходимо построить рациональную аппроксимацию функции добротности посредством применения обобщенной стандартной линейной модели твёрдого тела, как это сделано в [3].
Ограничение расчетной области:
Поскольку метод акустического каротажа в первую очередь нацелен на определение структуры околоскважинного пространства и не ставит задач определения сейсмических объектов на радиальном удалении большем нескольких длин волн, естественным будет ограничить область вычислений одним – двумя метрами от скважины. В вертикальном направлении размер расчетной области определяется размерами акустического прибора и не превышает, как правило, десяти – пятнадцати метров. Таким образом, целевая область имеет форму цилиндра, вытянутого по вертикали. Условия на границах целевой области должны обеспечивать минимальный уровень артефактов с тем, чтобы не исказить информативные волновые поля. Наиболее распространенным способом постановки таких условий на границах расчетной области является метод идеально согласованного слоя (PML, от английского Perfectly Matched Layer) [6], отлично зарекомендовавший себя в изотропных средах. Но для некоторых анизотропных сред он ведет к возникновению неустойчивых решений, допускающих экспоненциальный рост. Критерий устойчивости PML приведён в работе [1]:
PML в направлении r устойчив, если проекции векторов групповой и фазовой скоростей на это направление имеют один знак (Рис.1). Если этот критерий удовлетворяется, то можно применять стандартный PML. В противном случае, область вычислений расширяется на оптимальных сетках [4]. Основным преимуществом таких сеток является возможность использования весьма крупных шагов (3 точки на длину волны) и обеспечение низкого уровня паразитных отражений на границе между регулярной и оптимальной сетками.
Численные эксперименты:
Первый эксперимент демонстрирует неустойчивость PML для среды, состоящей из скважины заполненной жидкостью и трех горизонтальных слоев с толщинами 1 м, 2 м и 1 м (сверху вниз):
- isotropic
 ,
, 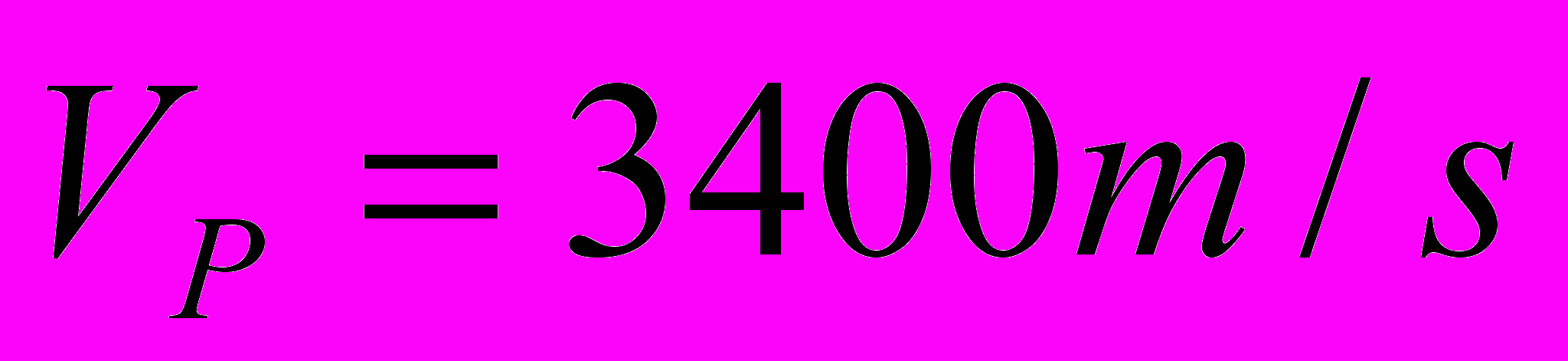 ,
, 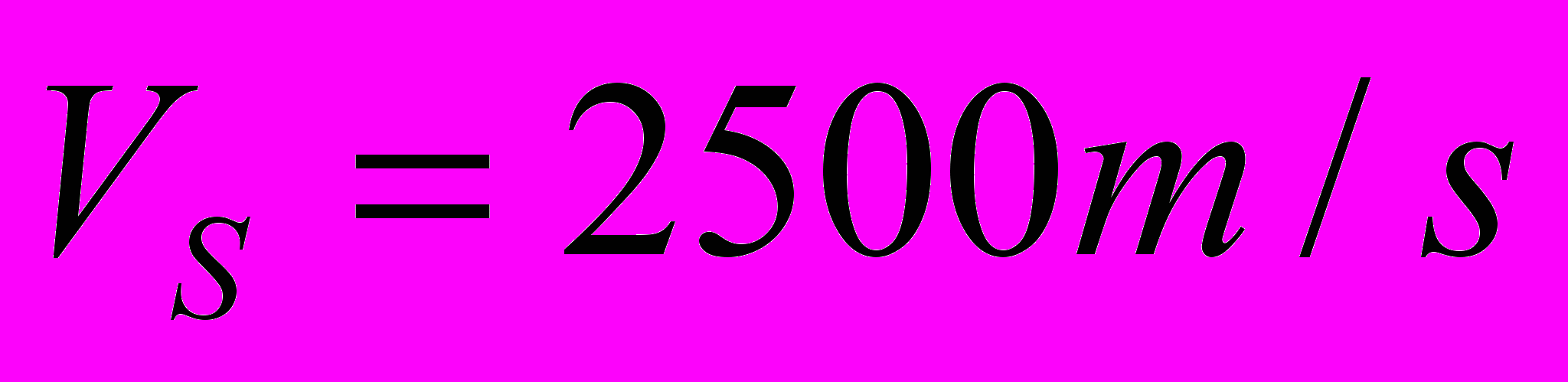 ,
, 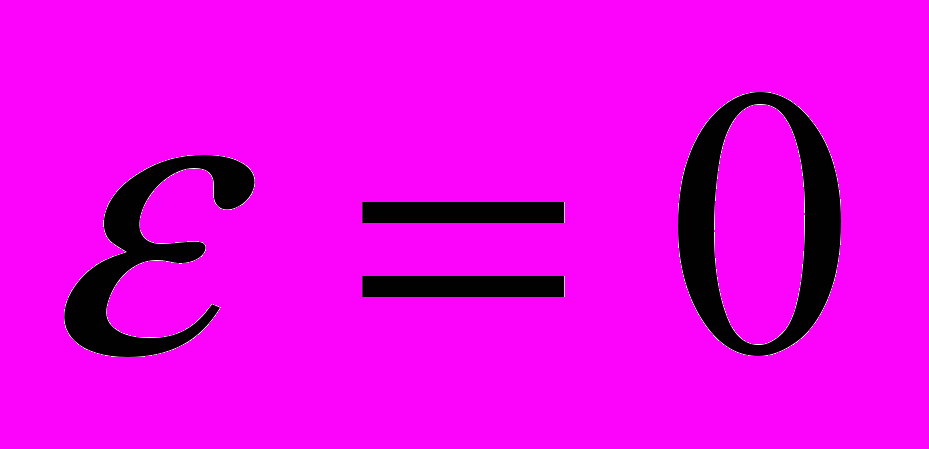 ,
, 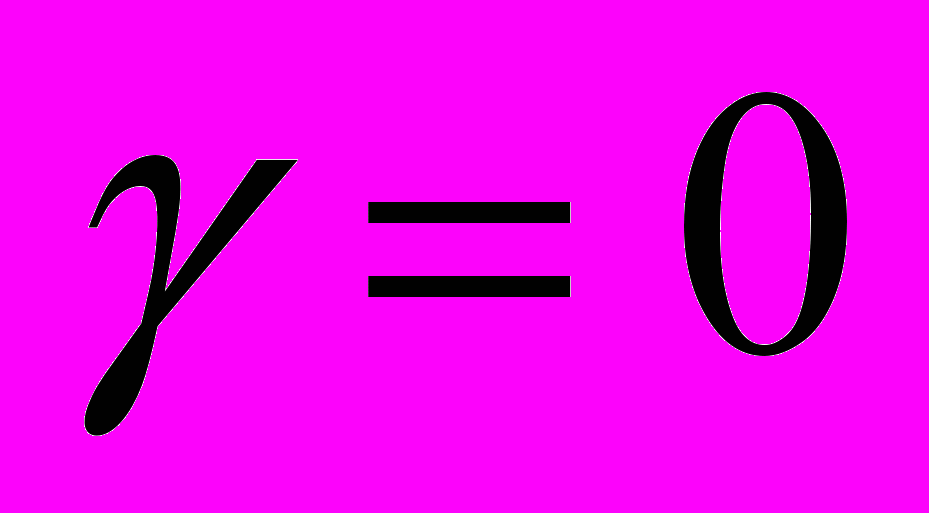 и
и 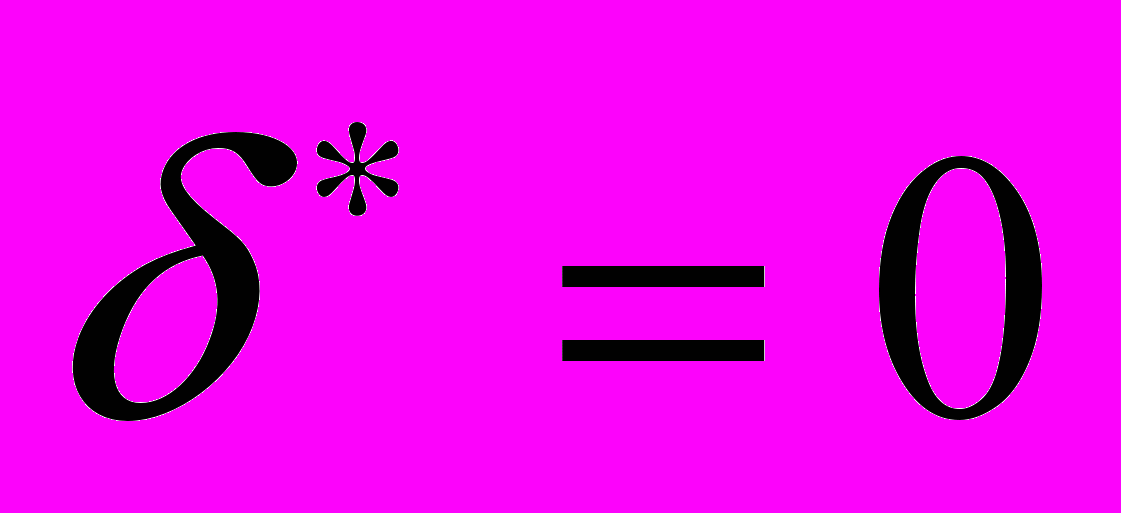 ;
;
- VTI
 ,
,  ,
, 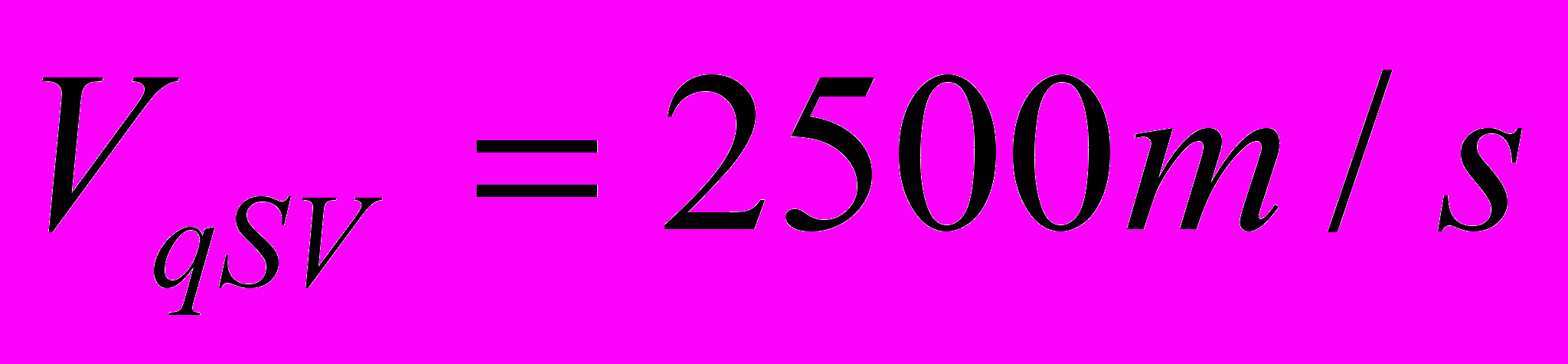 ,
, 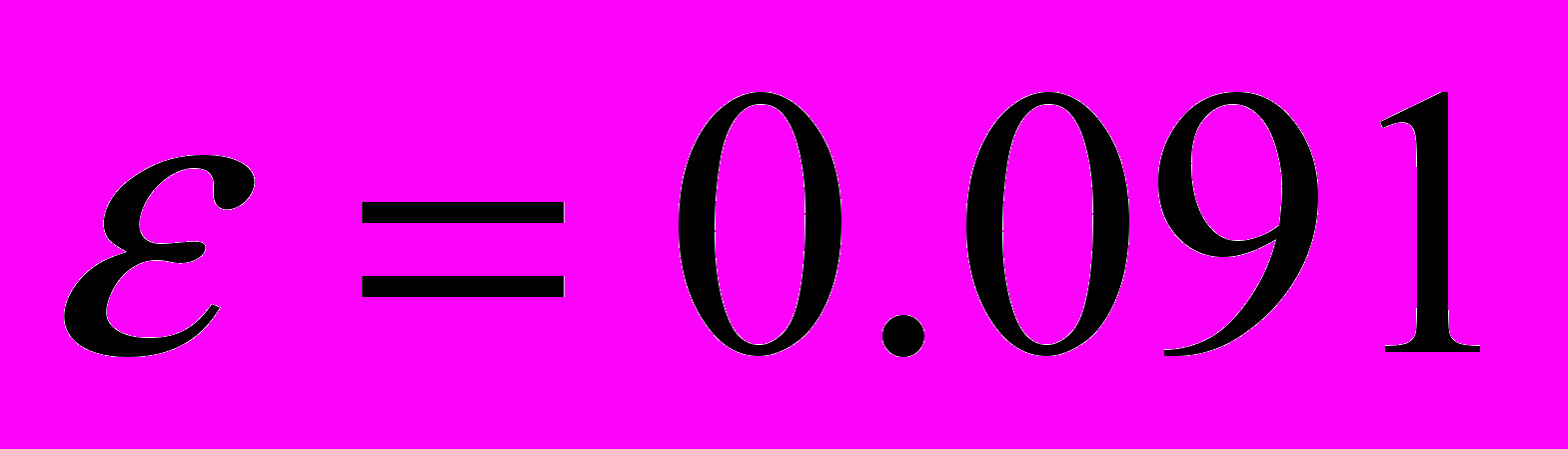 ,
, 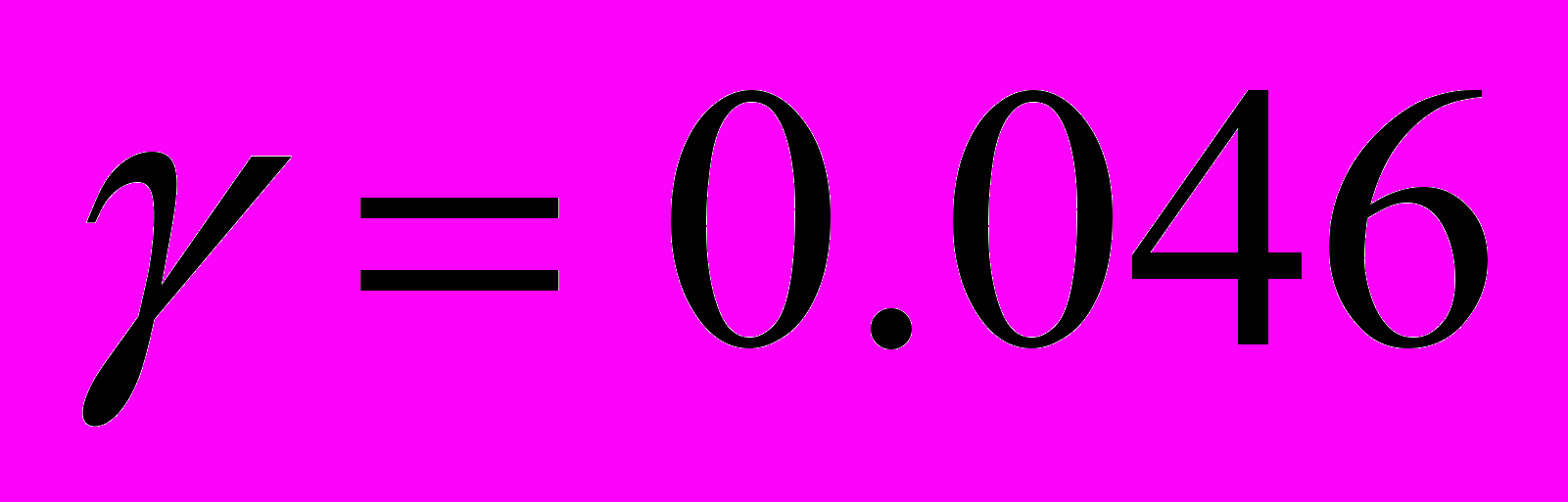 и
и  ;
;
- VTI
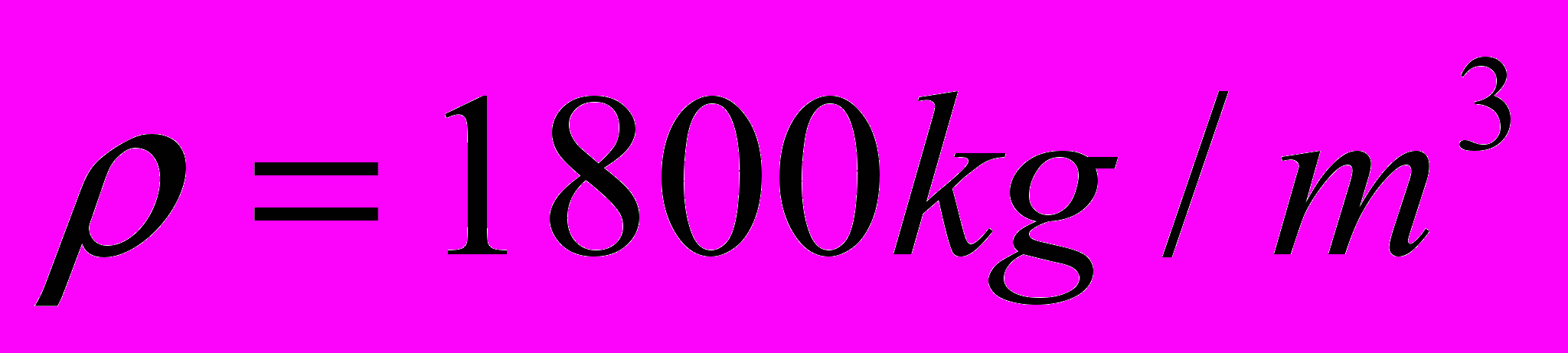 ,
, 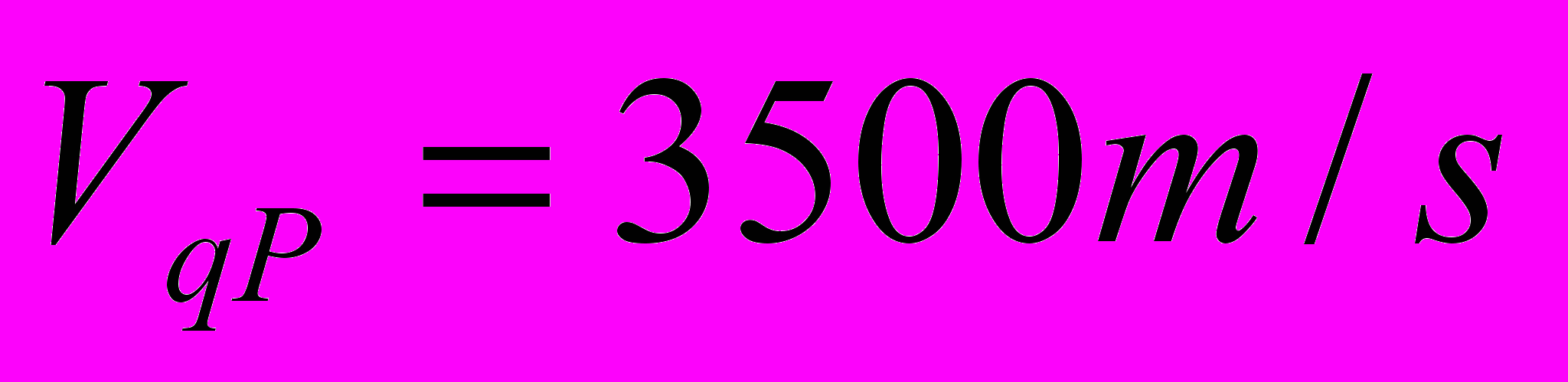 ,
, 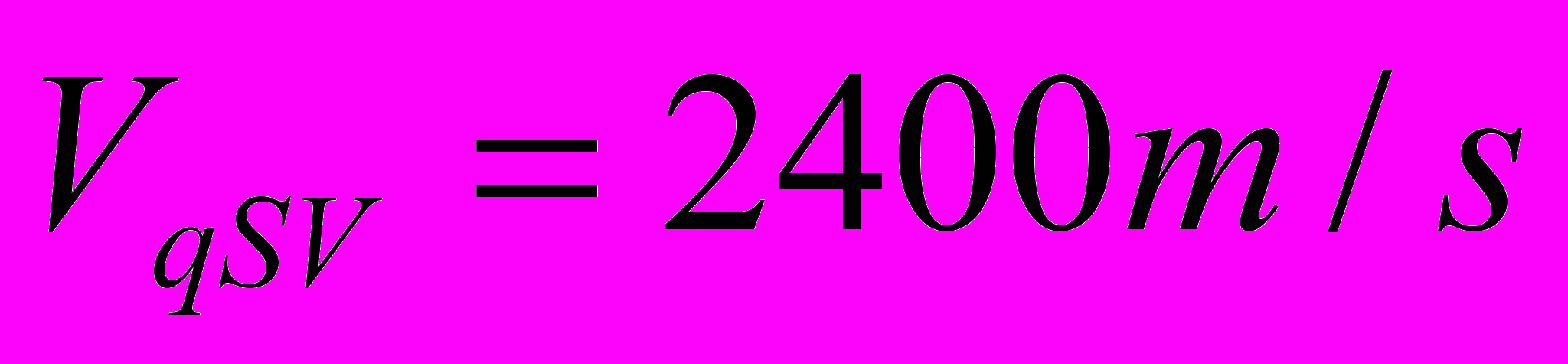 ,
, 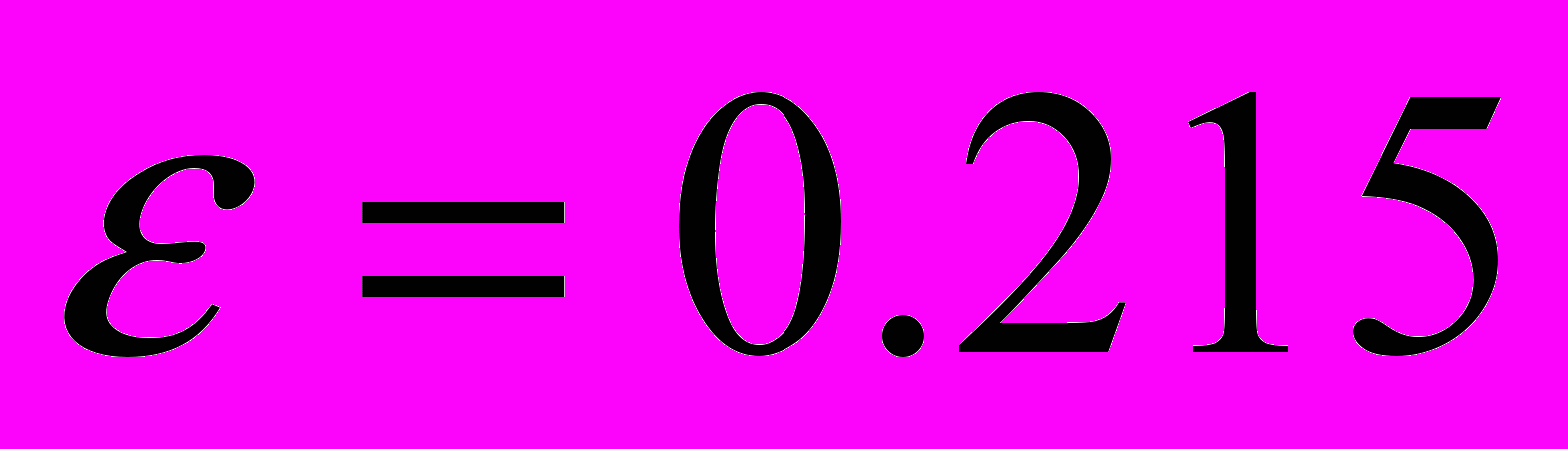 ,
, 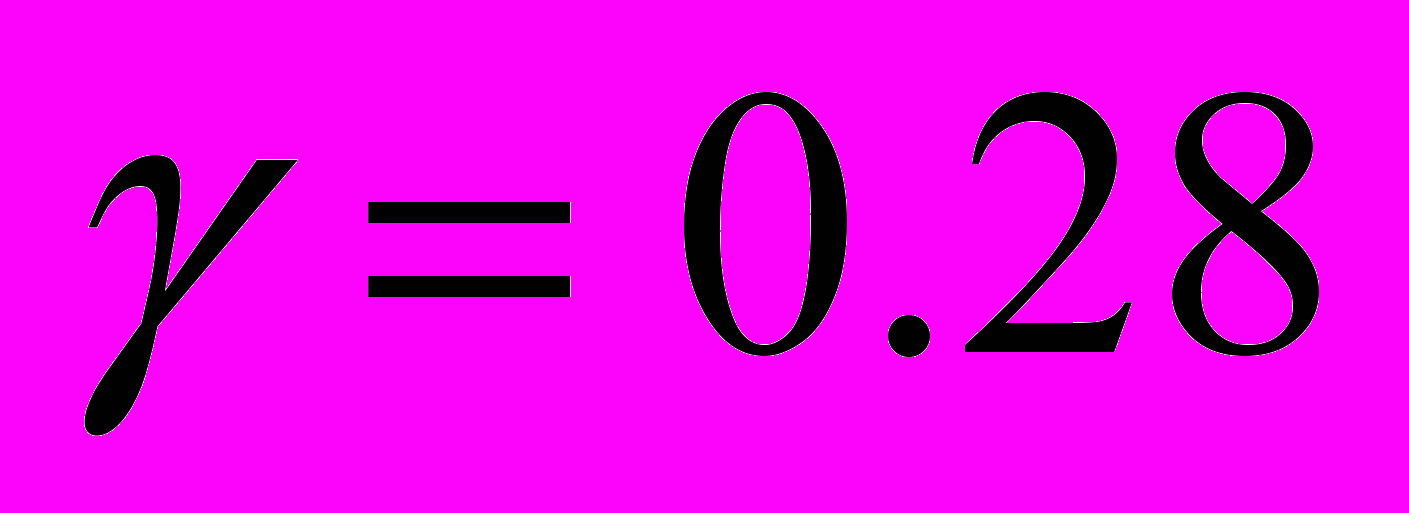 и
и 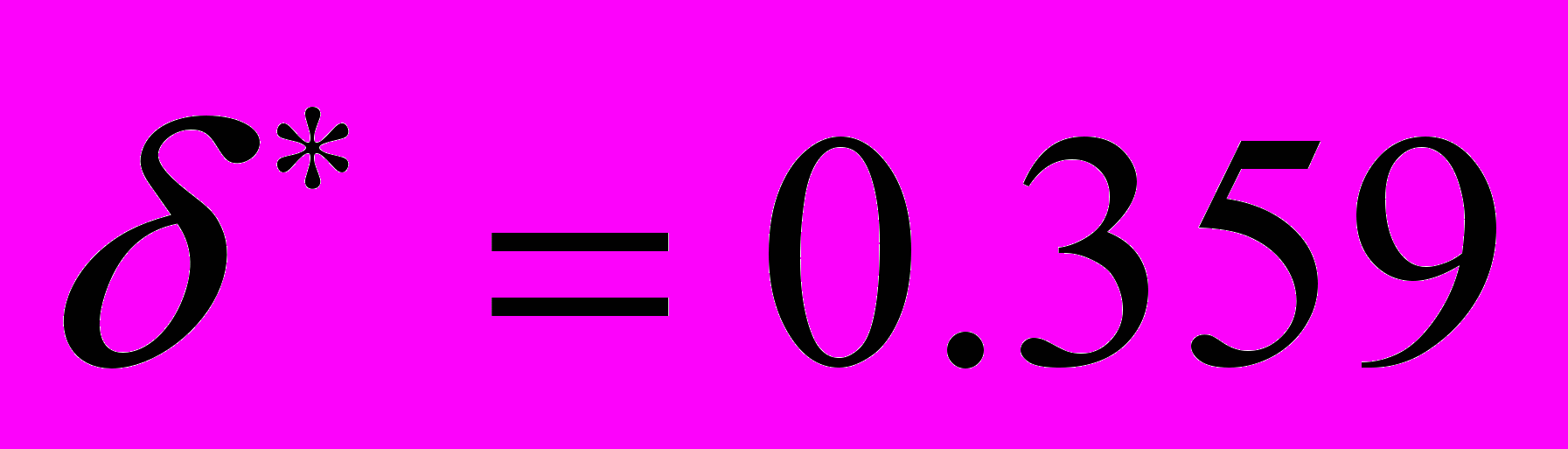 .
.
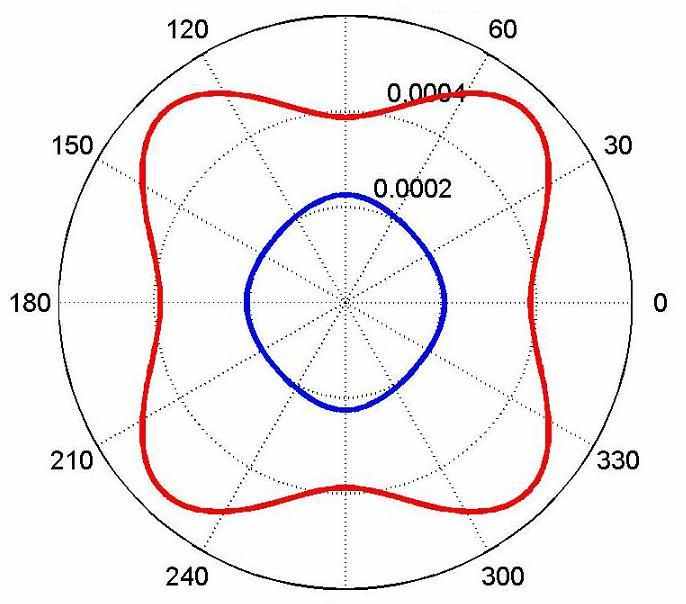
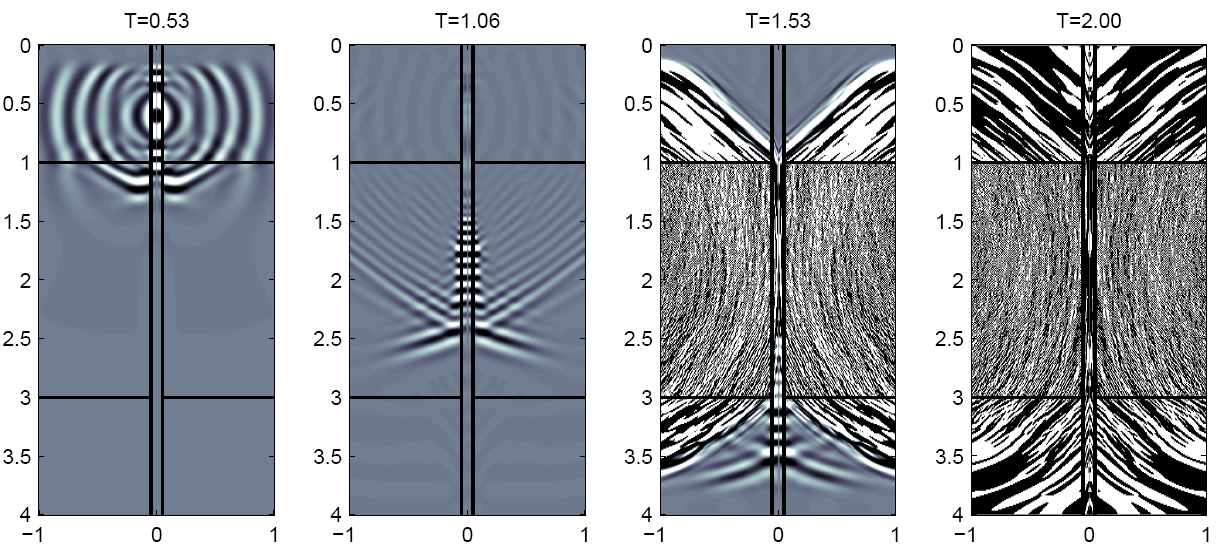
Индикатрисы фазовых и групповых скоростей в среде 2 представлены на Рис.2. На Рис.3 представлены произведения радиальных и вертикальных компонент фазовой и групповой скоростей. Как видно, для волн qSV существуют углы, при которых произведения и радиальных и вертикальных компонент отрицательны. Следовательно, для этой среды PML по обоим направлениям неустойчив. На Рис.5а представлены результаты численного моделирования с использованием PML для ограничения расчетной области, а на Рис.5b для этих целей использовано расширение расчетной области с помощью оптимальных сеток.
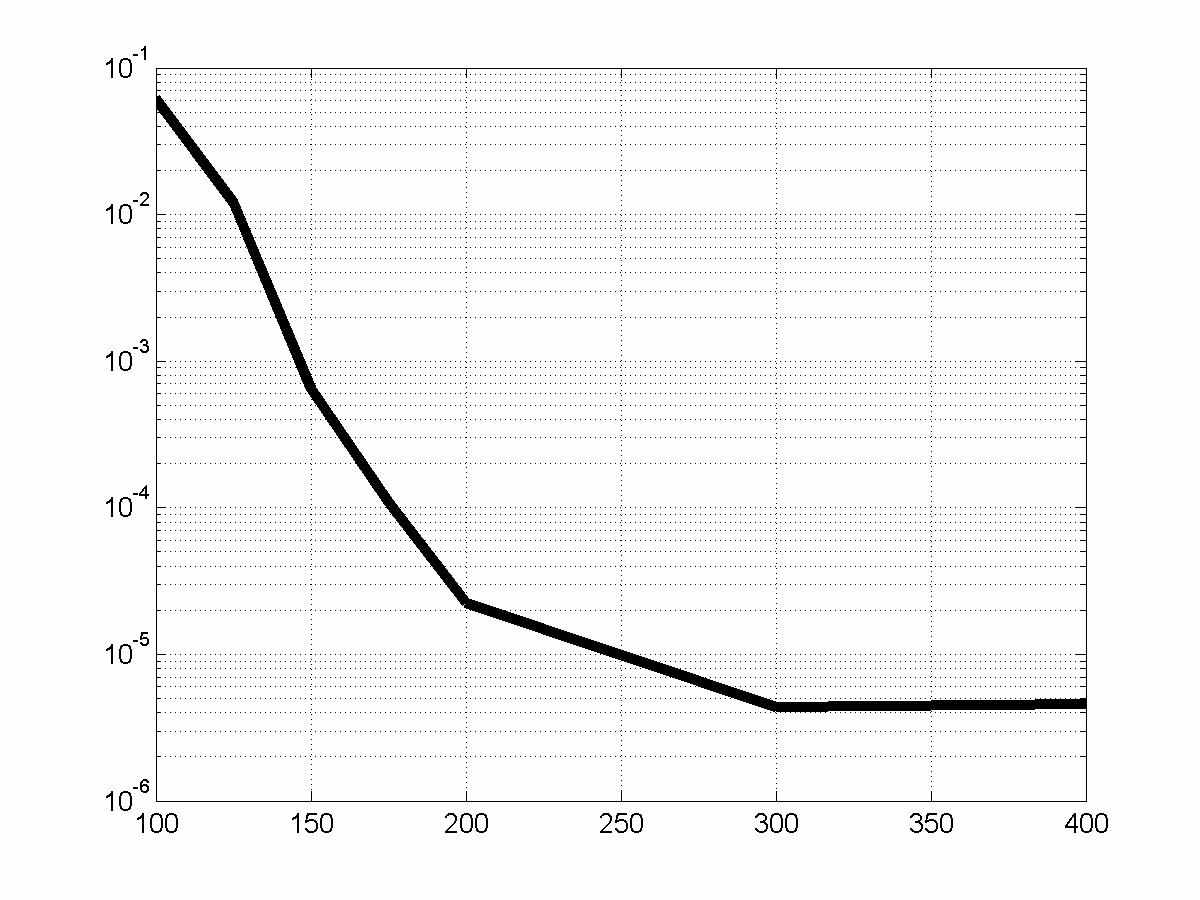
На Рис.6 представлен график зависимости относительной ошибки на оси
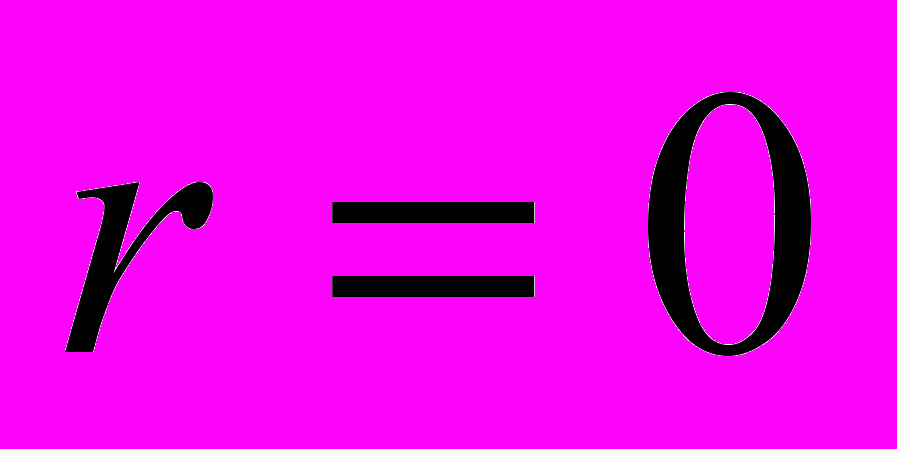 от числа точек используемых при расширении расчетной области. Как видно, относительная ошибка при использовании 150 точек в расширении составляет 0.1%.
от числа точек используемых при расширении расчетной области. Как видно, относительная ошибка при использовании 150 точек в расширении составляет 0.1%.Основной целью следующего эксперимента является наблюдение расщепления поперечных головных волн на стенке скважины. Для этого была выбрана модель среды, содержащая скважину диаметром в один метр, заполненную жидкостью и помещённую в упругую VTI среду со следующими параметрами:
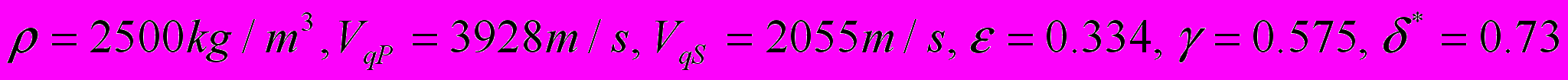 .
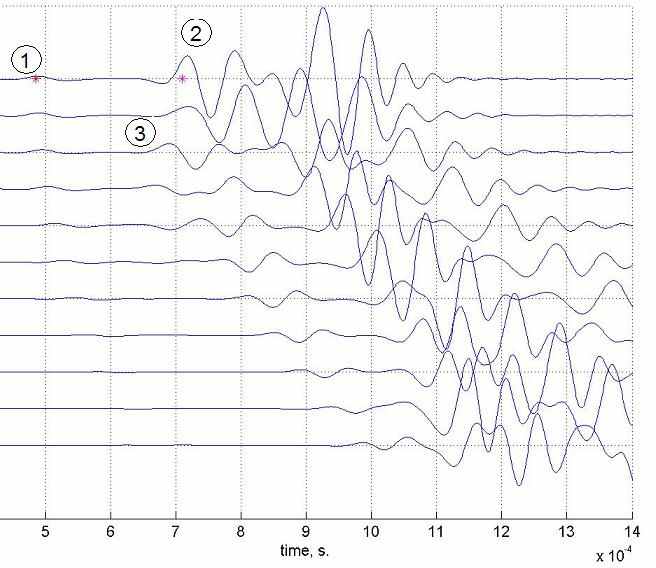
. Для неаксиально расположенного источника падающая P волна, генерирует головную qP волну и две головные qSV (медленная) и qSH (быстрая). Источник располагался на удалении 0.45 метра от оси скважины. На Рис.7 представлены сейсмограммы записанные приемниками, расположенными по окружности на стенке скважины на вертикальном удалении от источника равном 1 метру. Первая трасса соответствует приемнику расположенному наиболее близко к источнику. Сравнивая сейсмограммы Рис.7а (VTI) и Рис.7b (изотропия), можно достоверно выделить быструю qSH волну.
Благодарности:
Работа была выполнена совместно с Научно-исследовательским центром компании Schlumberger в г.Москве и частично при поддержке грантов РФФИ 06-05-64748, 07-05-00538 и 08-05-00265.
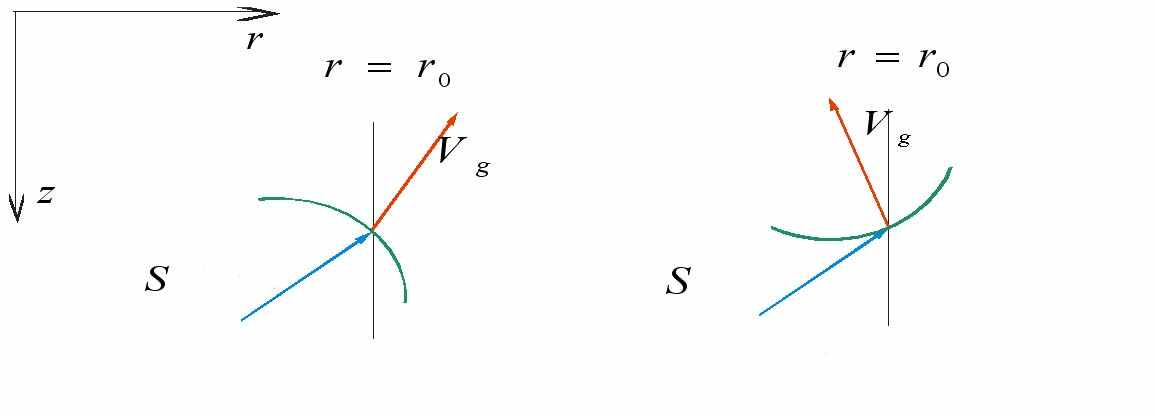
Рис.1. Критерий устойчивости PML.
 a) |  b) |
| Рис.2. Медленность (a) и групповая скорость (b) для VTI среды: qP (син.) и qSV (крас.) | |
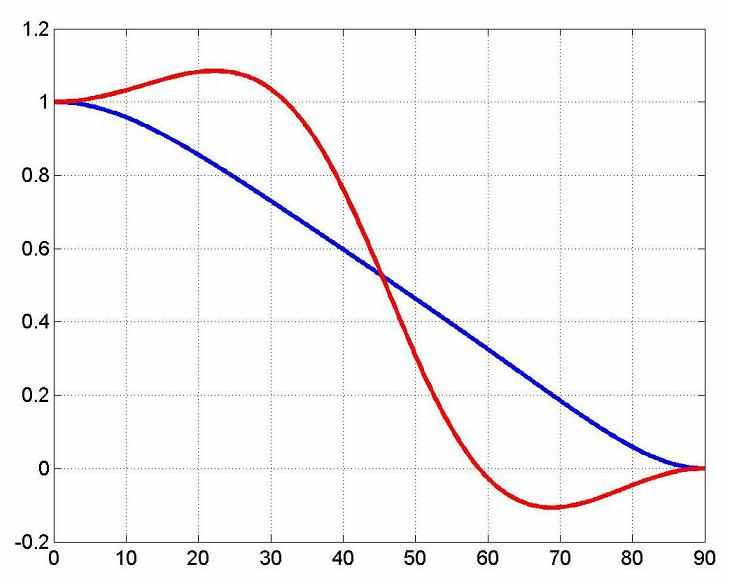 a) | 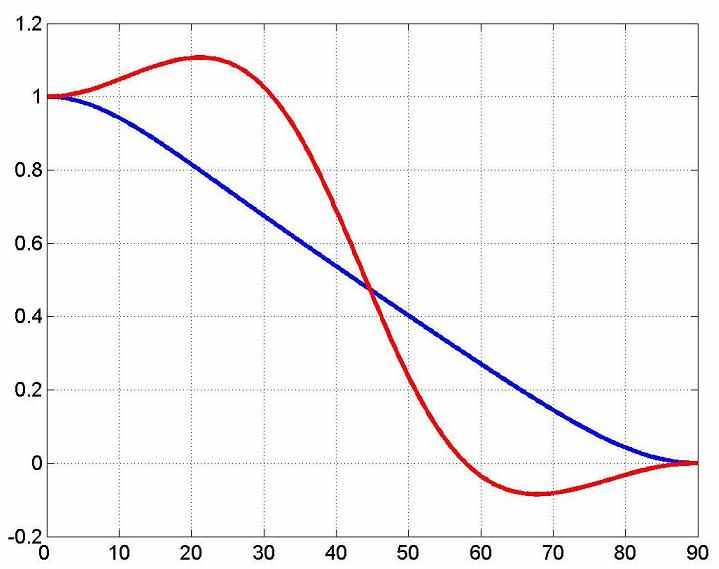 b) |
| Рис.3. признак устойчивости PML для VTI среды: qP (син.) и qSV (красн.) | |
 a) | 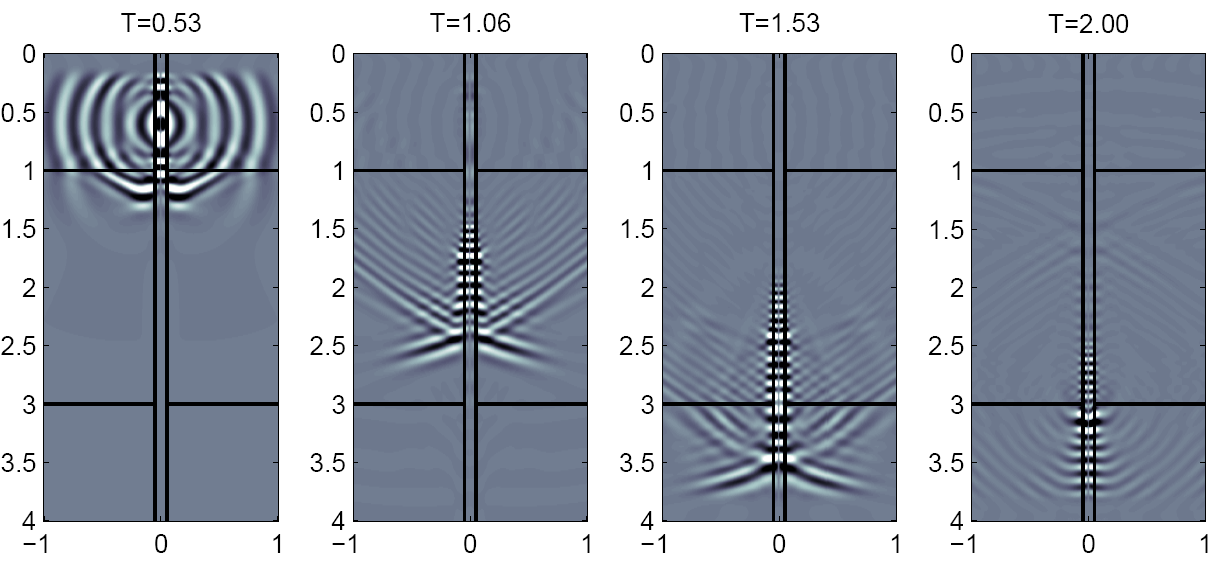 b) |
| Рис.5. Численное моделирование (a) PML (100 точек) ,(b) оптимальное расширение (150 точек). | |
 | 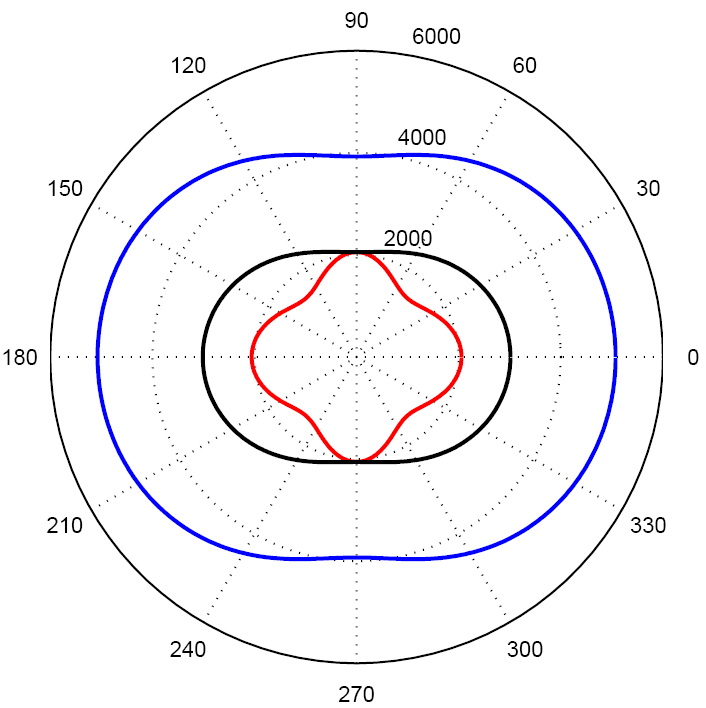 | |
| Рис.6. Относительная ошибка от числа точек в расширении | Рис. 7. Фазовые скорости в модели для разделения сдвиговых волн | |
 a) | 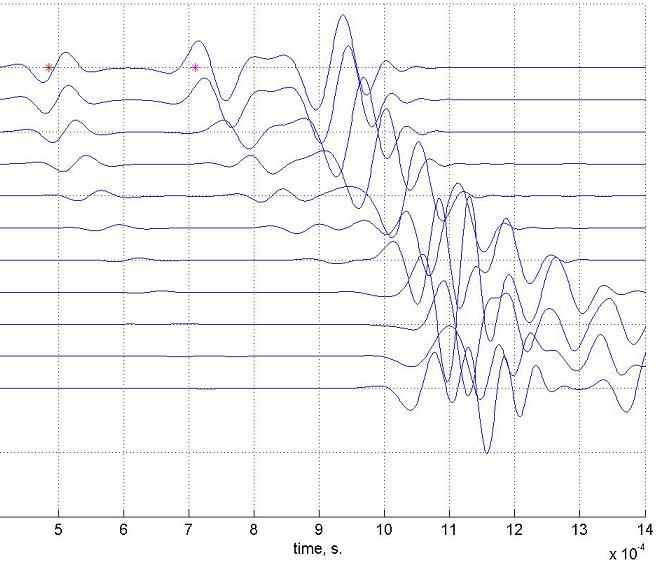 b) | |
| Рис. 7. Радиальные смещения на стенке скважины. (a) VTI. Числами обозначены первые вступления: 1 – головная P-волна: 2 – головная qSV, 3 – головная qSH. (b) Изотропия. Звёздочками обозначены первые вступления P- и S-головных волн | | |
Список литературы
- Becache, E. Stability of Perfectly Matched Layers, Group Velocities and Anisotropic Waves/ Becache, E. Fauqueux, S. Joly P.// INRIA, Rapport de recherche n° 4304, Novembre 2001, 35p.
- Biot, M.A. Propagation of elastic waves in a cylindrical bore containing a fluid/ Biot, M.A. // Journal of Applied Physics, 1952, 23, 997 -1005.
- Blanch, J.O. Modeling of a constant Q: Methodology and algorithm for an efficient and optimally inexpensive viscoelastic technique./ Blanch J.O., Robertsson J.O.A., Symes W.W. // Geophysics, 1995, 60(1), 176 - 184..
- Lisitsa, V. 2005. Optimal grids for numerical solution of a wave equation in heterogeneous media/ Lisitsa, V.// Siberian journal of numerical mathematics, 2005, 8(3), pp.219 – 229.
- Qing, H. L. A 3D cylindrical PML/FDTD method for elastic waves in fluid-filled pressurized boreholes in triaxially stressed formations/ Qing Huo Liu, Sinha Bikash K.// Geohysics, 2003, 68(5), 350 – 357.
- Kostin, V. 3D Synthetic Acoustic Log for Viscoelastic Media: Finite-Difference Approach/ Kostin V., Pissarenko D., Reshetova G., Tcheverda V.// Extended abstracts of 69th EAGE Conference and Technical Exposition, London, 11 – 14 June 2007, P096.
- Thomsen, L. Weak elastic anisotropy/ L.Thomsen// Geophysics, 1986, 51(10), 1954 – 1966.
- Virieux, J. Velocity-stress finite-difference method/ Virieux, J.// Geophysics, 1986, 51, 889 – 901
- Zhu, Y. Physical modeling and analysis of P-wave attenuation anisotropy in transversely isotropic media/ Y.Zhu, I.Tsvankin, P.Dewangan, K. van Wijk// Geophysics, 72(1), D1 – D7, 2007.
