Моделирование процесса упрочнения поверхностного слоя заготовки методом конечных элементов при деформирующем протягивании а. В. Грушко, канд техн наук, доцент; И. Ю. Ростоцкий *
| Вид материала | Документы |
- Гост 17623-87, 138.94kb.
- Надійності та безпеки в будівництві, 692.13kb.
- Гост 5382-91, 1729.88kb.
- Д. М. Лаковский (руководитель темы); И. В. Колечицкая; С. А. Резник, канд техн наук;, 203.82kb.
- Гост 14637-89: Прокат толстолистовой из углеродистой стали обыкновенного качества Технические, 310.23kb.
- Государственный стандарт союза сср здания и сооружения Методы измерения яркости, 278.78kb.
- Гост 26824-86, 248.28kb.
- Строительные нормы и правила отопление, вентиляция и кондиционирование, 2477.63kb.
- Строительные нормы и правила отопление, вентиляция и кондиционирование сниП 04. 05-91*, 1856.14kb.
- Б. В. Баркалов ), Государственным проектным конструкторским и научно-исследовательским, 2674.7kb.
МОДЕЛИРОВАНИЕ ПРОЦЕССА УПРОЧНЕНИЯ ПОВЕРХНОСТНОГО СЛОЯ ЗАГОТОВКИ МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ ПРИ ДЕФОРМИРУЮЩЕМ ПРОТЯГИВАНИИ
А.В. Грушко, канд. техн. наук, доцент;
И.Ю. Ростоцкий*, млад. науч. сотр.;
Винницкий национальный технический университет, г. Винница;
*Институт сверхтвердых материалов им. В.Н. Бакуля НАН Украины, г. Киев
Качество деталей, получаемых методами холодного пластического деформирования, существенно зависит от технологической наследственности. В значительной мере оно определяется такими параметрами, как геометрическая форма инструмента, шероховатость поверхности, остаточная пластичность материала, остаточные напряжения, отсутствие трещин, гофров, линий скольжения и степень деформационного упрочнения. При деформирующем протягивании
(рис. 1) происходит интенсивное упрочнение поверхностного слоя, которое характеризуется высокими степенями деформаций на различную глубину заготовки, остаточными напряжениями сжатия и невысоким ресурсом пластичности [1-3], что благоприятно сказывается на технологической наследственности деталей, работающих в условиях циклических нагрузок и трения. Согласно [1, 3] некоторые характеристики упрочнения поверхностного слоя, описывающие его в виде одного комплексного параметра, могут наряду с другими параметрами определить оценку качества деталей на стадии проектирования технологического процесса.
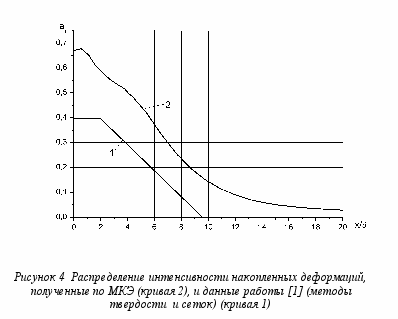
В работах [1, 3] всесторонне исследована механика деформирующего протягивания, в том числе и механизм упрочнения поверхностного слоя. Для его изучения были проведены экспериментальные и экспериментально-расчетные методы теории пластичности: метод твердости, визиопластичности, метод линий скольжения. Показано, что интенсивность накопленных деформаций определяется углом инструмента и натягом на сторону (рис. 2). При этом авторы отмечают слабое влияние остальных параметров технологического процесса.
Однако предварительное исследование процесса методом конечных элементов (МКЭ) без применения упрощающих гипотез показало большее влияние и остальных технологических параметров на деформационное упрочнение поверхностного слоя, особенно при малых натягах. Косвенным подтверждением этому также являются закономерности действия деформирующих сил, хорошо изученные в [1, 2]. МКЭ в сравнении с ранее перечисленными методами МКЭ имеет наибольшую точность и информативность. Однако как и большинство методов, имеет свои причины возникновения погрешностей при его использовании:
- Процесс протягивания в пластической области реализует сложное немонотонное нагружение металла. Немонотонное нагружение сопровождается проявлением эффекта Баушингера, деформированное состояние не соответствует однозначно напряженному [6].
- Искаженная делительная сетка, полученная в натурном эксперименте и при моделировании МКЭ (рис. 6) дает удовлетворительное соответствие, что указывает на приемлемость рассчитанного деформированного состояния. Деформации, посчитанные по методу сеток, дают меньшие значения, чем по МКЭ. Здесь следует принять во внимание нарушение континуальности заготовки при реализации эксперимента метода сеток и погрешности измерений и обработки результатов.
- Решение задачи при моделировании МКЭ основано на идеальности свойств материала – изначально изотропный материал с изотропным упрочнением согласно аппроксимации (1).
- При малых натягах на деформирование оказывает влияние поверхностная микронеровность заготовки – шероховатость.
- Модель трения может быть приближенной и этим вносить в расчеты МКЭ дополнительную погрешность неопределенной величины.
- Накопленная ошибка расчета контактных высоконелинейных задач при наличии пластических деформаций при моделировании МКЭ может составлять до 15% при прочих корректно заданных данных и условий расчета.
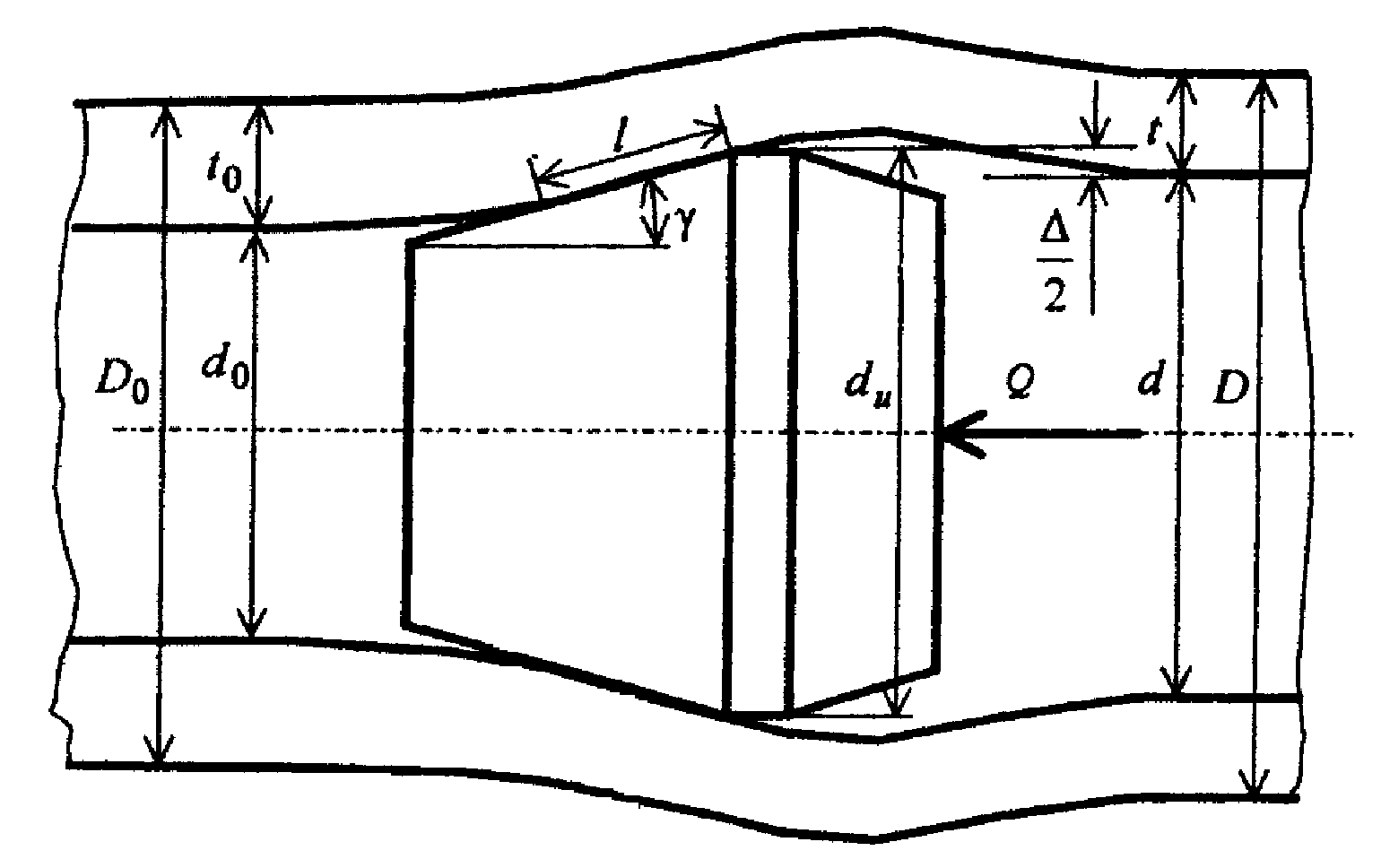
Рисунок 1 Схема и основные параметры деформирующего протягивания
hдеф
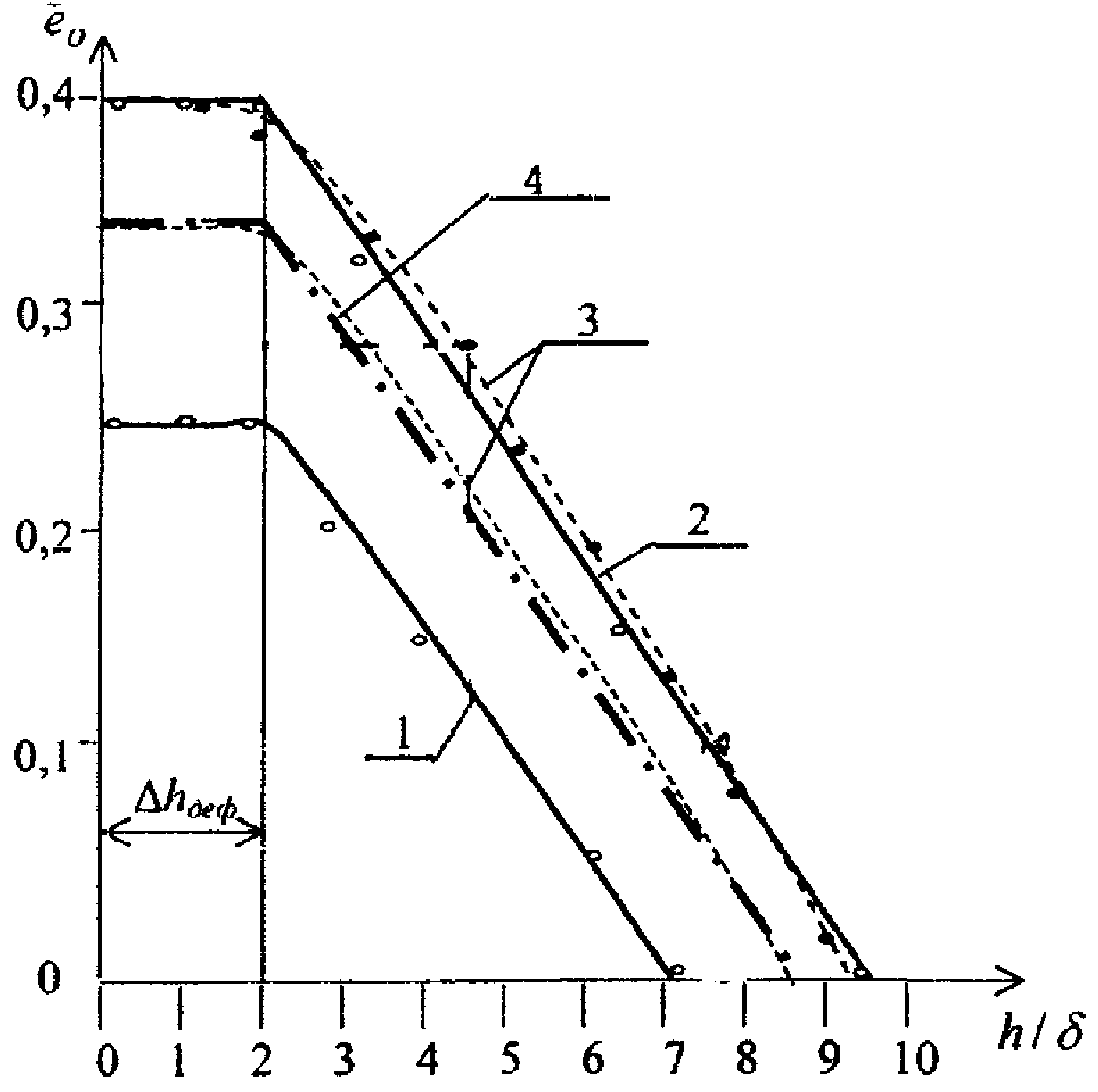
Рисунок 2 [1] Универсальные зависимости е0 от относительной глубины поверхностного слоя заготовки :
- – для деталей, обработанных инструментом с углом конусности = 5°;
- – для деталей, обработанных инструментом с углом = 10°;
- – кривые, полученные методом измерения микротвердости;
- – кривая, полученная интерполированием кривых 1 и 2 для обработки; инструментом с углом конусности = 8°
Таким образом, в модели, полученной по МКЭ, хотя и будет присутствовать погрешность, однако можно будет определить, как факторы и их сочетания влияют на особенности упрочнения поверхностного слоя.
Целью исследований является изучение зависимости упрочнения поверхностного слоя от основных технологических параметров и свойств материала при малых натягах в процессе моделирования деформирующего протягивания МКЭ.
Решали поставленную задачу с использованием конечноэлементного моделирования явным методом [4]. Использовали осесимметричную постановку задачи. Применяли модель трения по Кулону с ограничением контактных касательных напряжений напряжением текучести при сдвиге. Свойства материала задавали в виде упругих констант изотропного материала и кривой течения.
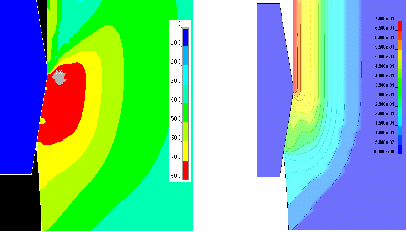
д) е)
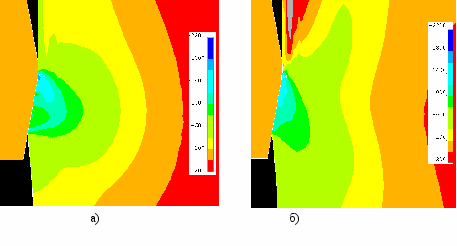
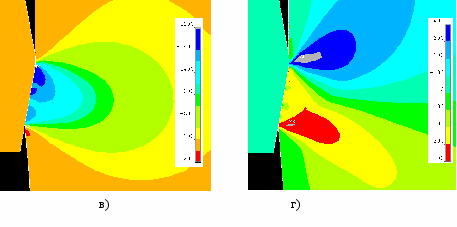
Рисунок 3 Компоненты напряженно-деформированного состояния:
а) осевые напряжения, МПа; б) радиальные напряжения, МПа; в) окружные напряжения, МПа; г) касательные напряжения, МПа;
д) нормальные напряжения, МПа; е) интенсивность деформаций
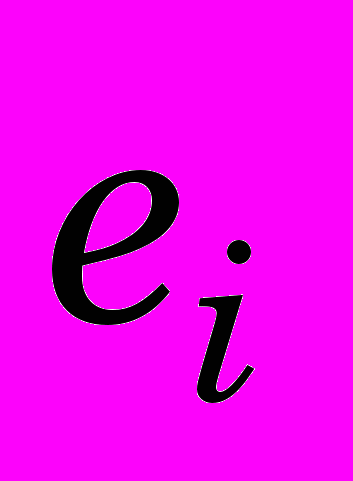
К
ривые течения обычно аппроксимируют различными функциями в зависимости от особенностей поведения материала. На наш взгляд, как в экспериментально-теоретических, так и численных расчетах при деформациях, существенно превышающих деформацию предела текучести, достаточную для большинства квазимонотонных процессов обработки давлением точность дает аппроксимация П. Людвика [4, 5]
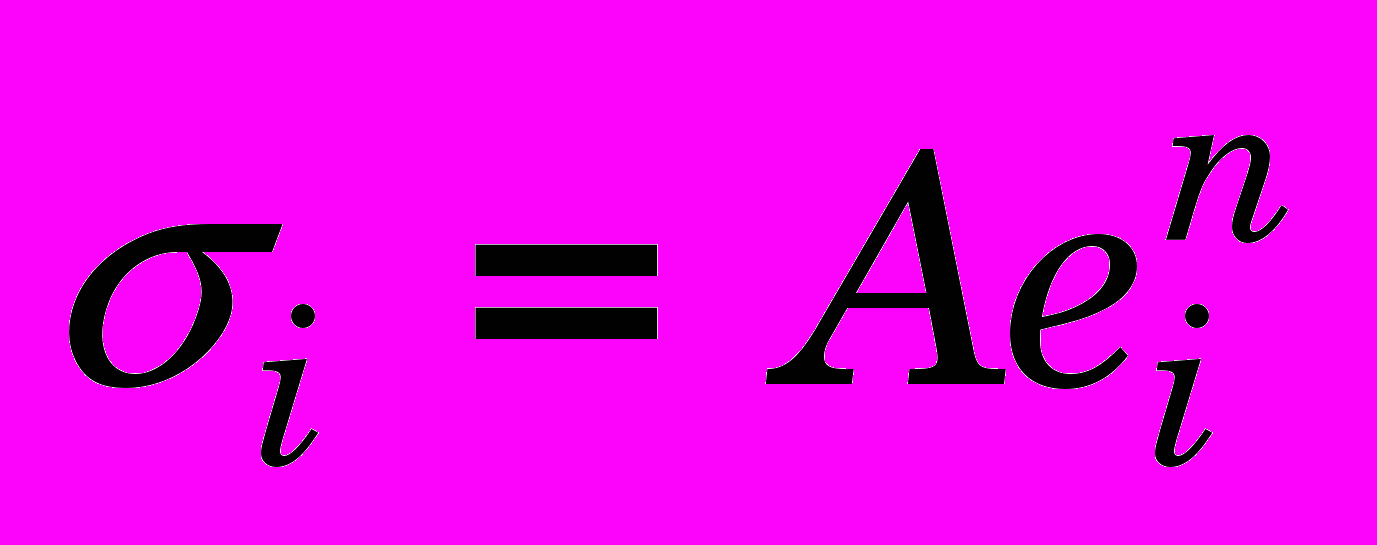 , (1)
, (1)где
 и
и 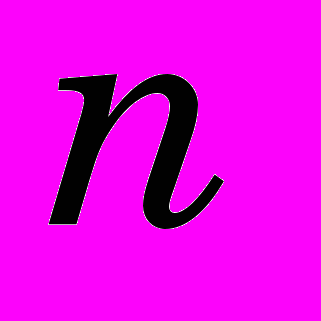 – эмпирические коэффициенты – модуль и показатель упрочнения материала;
– эмпирические коэффициенты – модуль и показатель упрочнения материала; 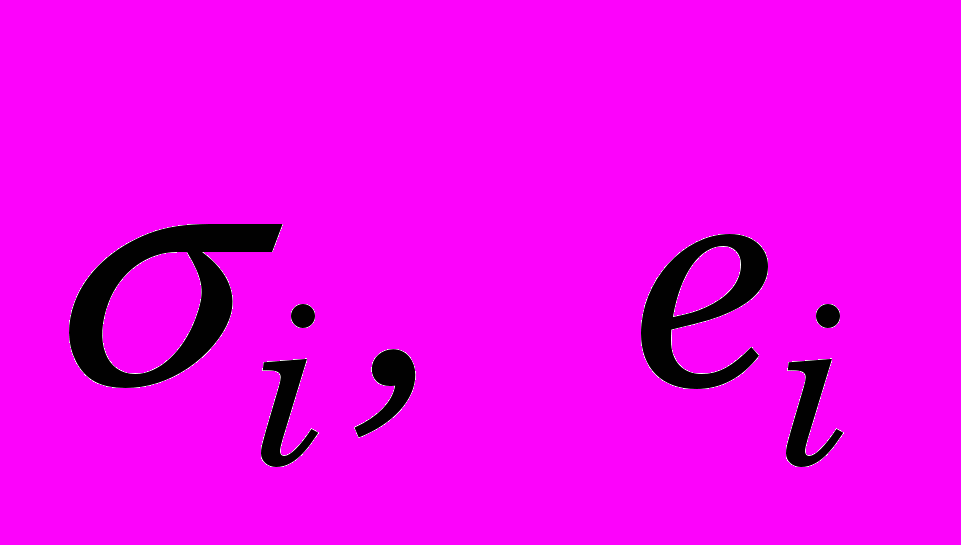 – интенсивность напряжений и деформаций.
– интенсивность напряжений и деформаций.После обработки функции (1) на ЭВМ были получены эпюры компонент тензора напряжений и интенсивности деформаций при протягивании заготовки из стали 20Х, диаметр внутренний
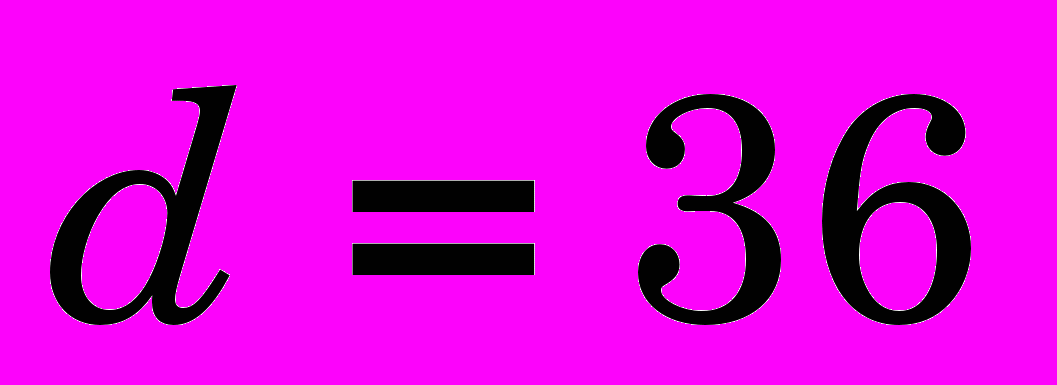 мм, толщина стенки s = 36 мм, угол инструмента = 10°, натяг на сторону
мм, толщина стенки s = 36 мм, угол инструмента = 10°, натяг на сторону = 0,6 мм. Общая картина распределения рассмотренных величин подтверждает результаты, изложенные в [1], подсчитанные деформирующие силы хорошо согласуются с экспериментальным значением (расхождение составило 10%).
Анализируя данные распределения деформаций, полученных МКЭ (рис. 4) с методами твердости и визиопластичности [1] (рис. 2), можно сказать лишь о качественном соответствии с графиками.
Анализируя рис. 5, необходимо учитывать корреляцию между твердостью и интенсивностью накопленных деформаций [1], отметим, что по МКЭ глубина распространения пластических деформаций намного больше (более чем в 2 раза). Абсолютная величина деформаций по твердости осталась неизученной в связи с отсутствием тарировочных графиков материала заготовки, который, как известно, сильно зависит от партии материала и термообработки. Таким образом, можно говорить о качественном соответствии этих двух графических зависимостей, но не количественном. Такое расхождение можно объяснить причинами возникновения погрешностей при использовании МКЭ, изложенными выше.
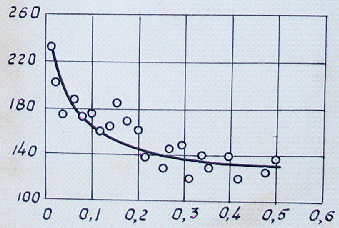
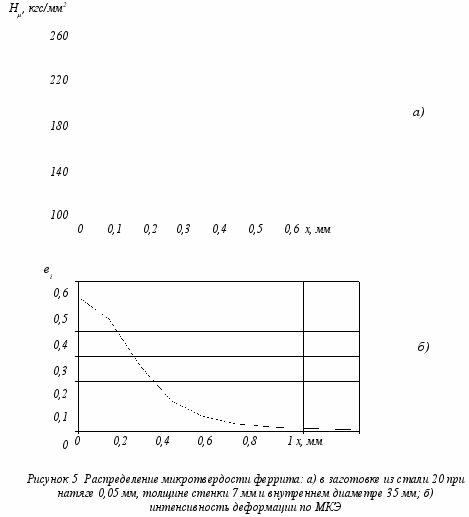
Для решения этой проблемы количественного несовпадения результатов все линейные размеры были отнесены к толщине стенки заготовки для дальнейшей работы с безразмерными величинами, исключением толщины стенки из варьируемых параметров и расширением модели. Обозначим относительный натяг на сторону
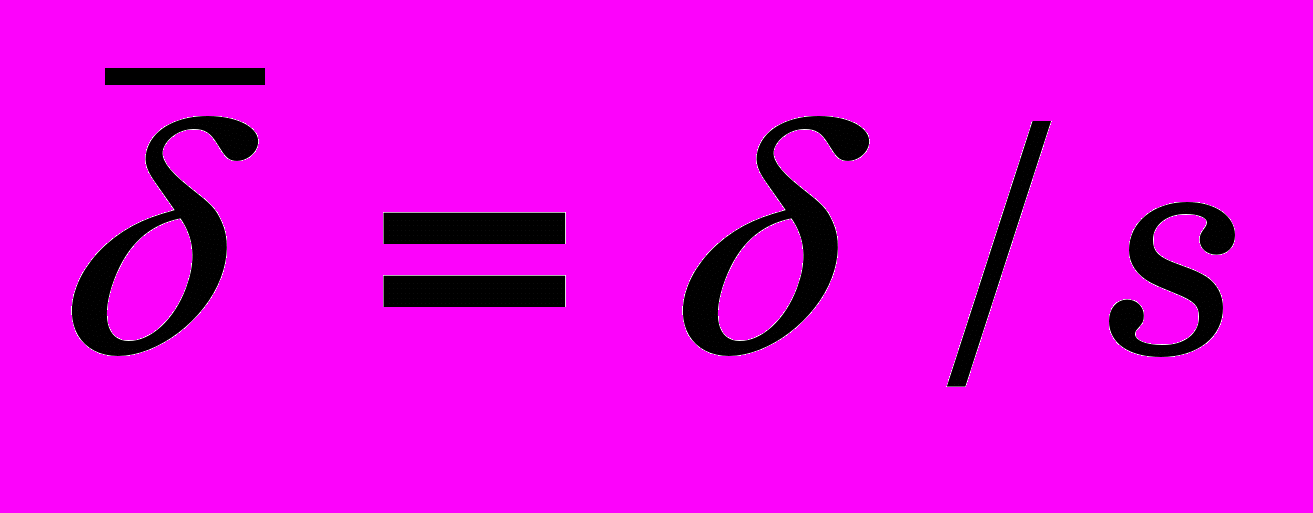 ; относительный диаметр
; относительный диаметр 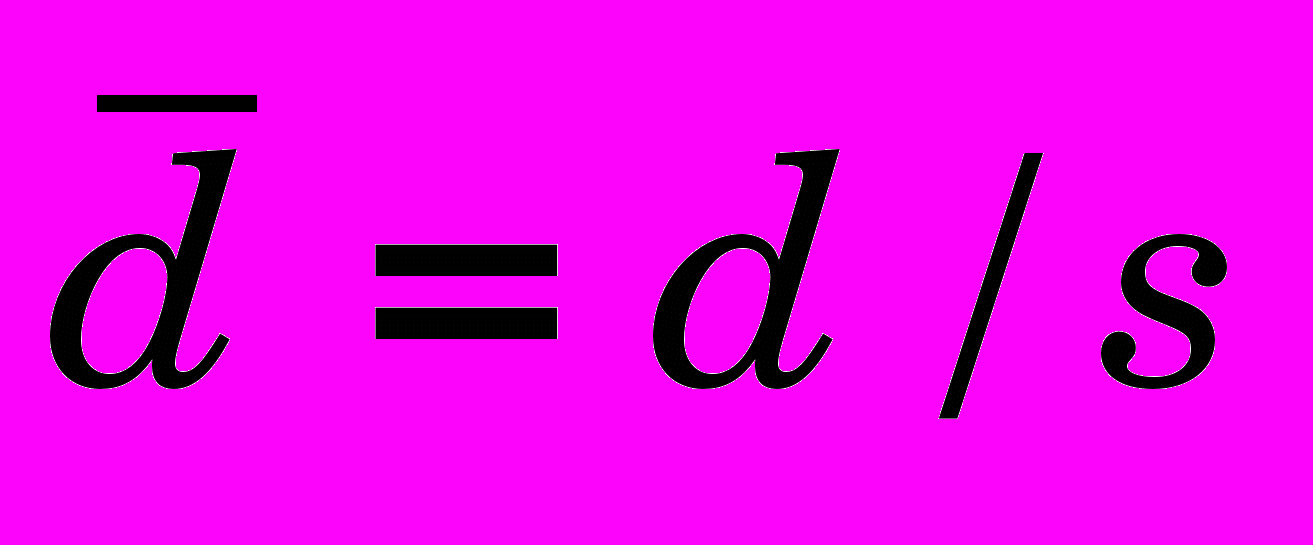 . В дальнейшем все относительные величины обозначены чертой сверху.
. В дальнейшем все относительные величины обозначены чертой сверху.Распределение интенсивности деформаций в радиальном направлении (обозначено х) носит экспоненциально убывающий характер. Характерные расчетные МКЭ графики показаны на рис. 7.
Путем многочисленных переборов различного вида функций с применением ЭВМ установлено, что наименьшие отклонения в смысле наименьшей суммы квадратов дает экспоненциально-степенная функция в виде
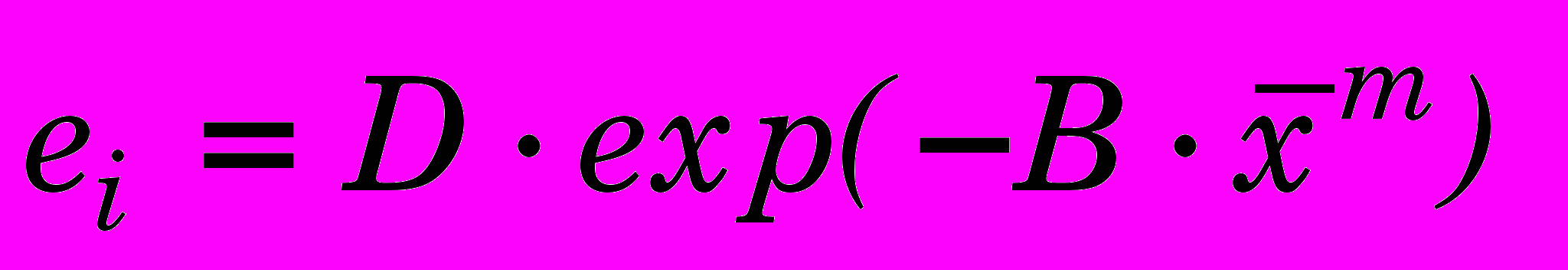 , (2)
, (2)где
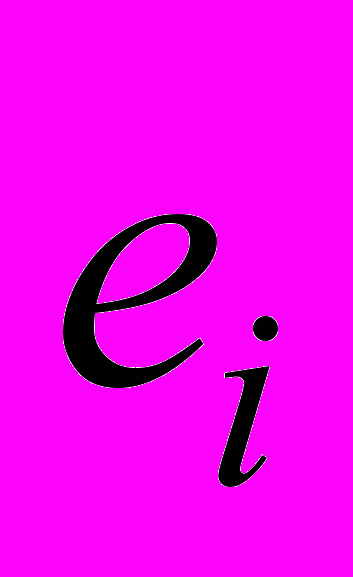 интенсивность накопленных деформаций в точке с относительной координатой
интенсивность накопленных деформаций в точке с относительной координатой 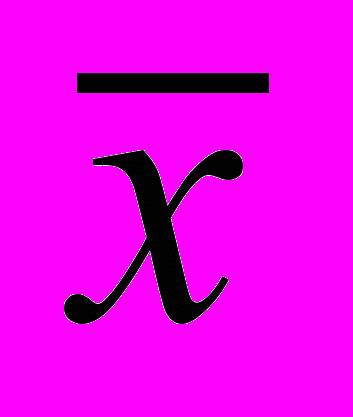 ;
; 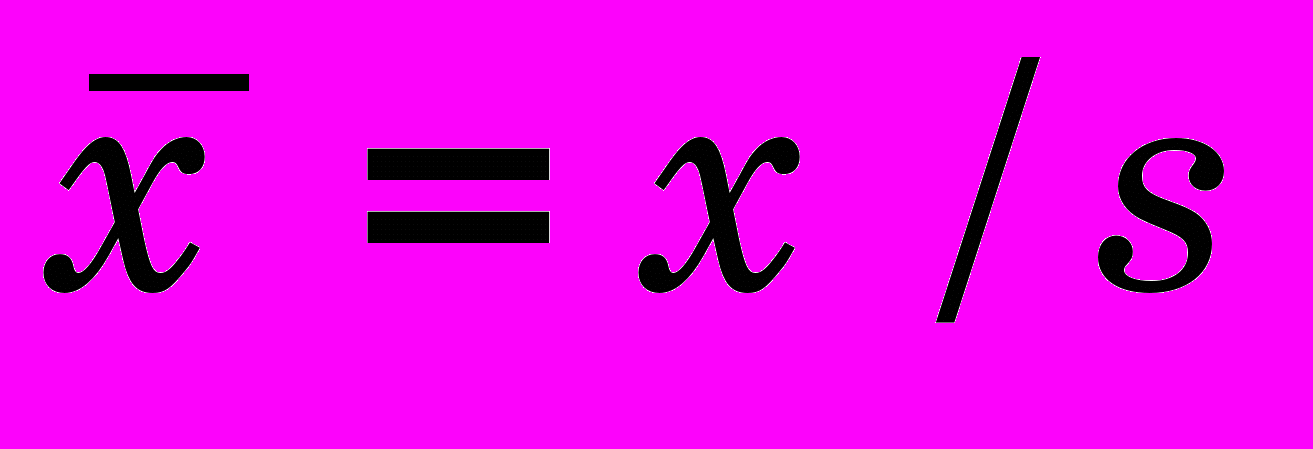 ;
; 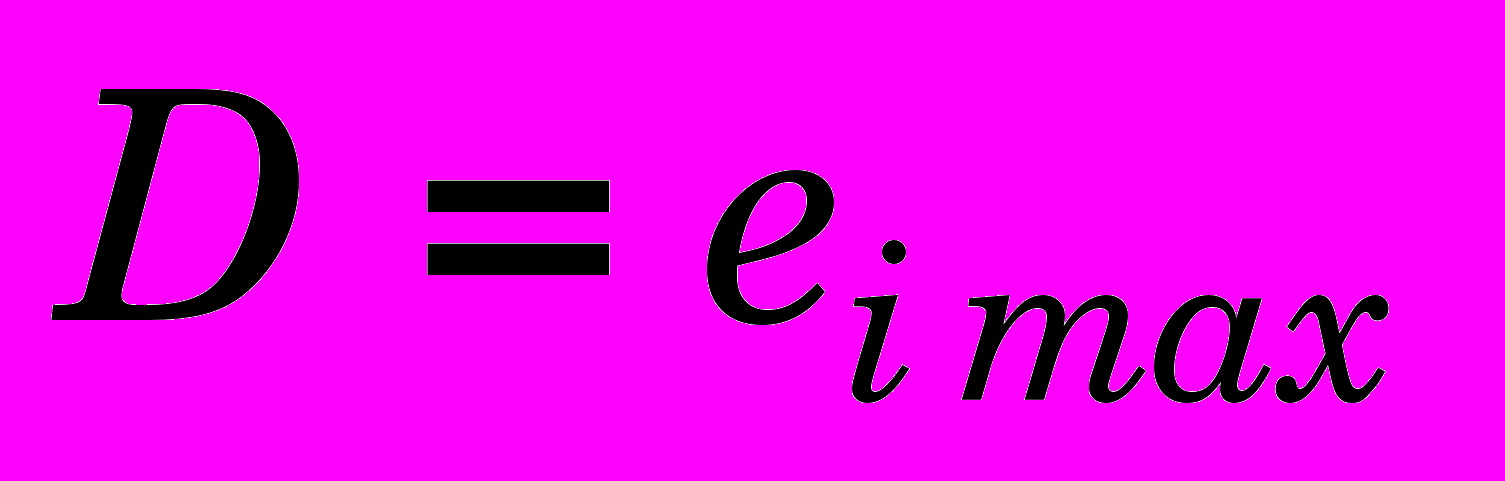 интенсивность деформаций на поверхности заготовки (она обычно максимальная или близка к максимальной при
интенсивность деформаций на поверхности заготовки (она обычно максимальная или близка к максимальной при 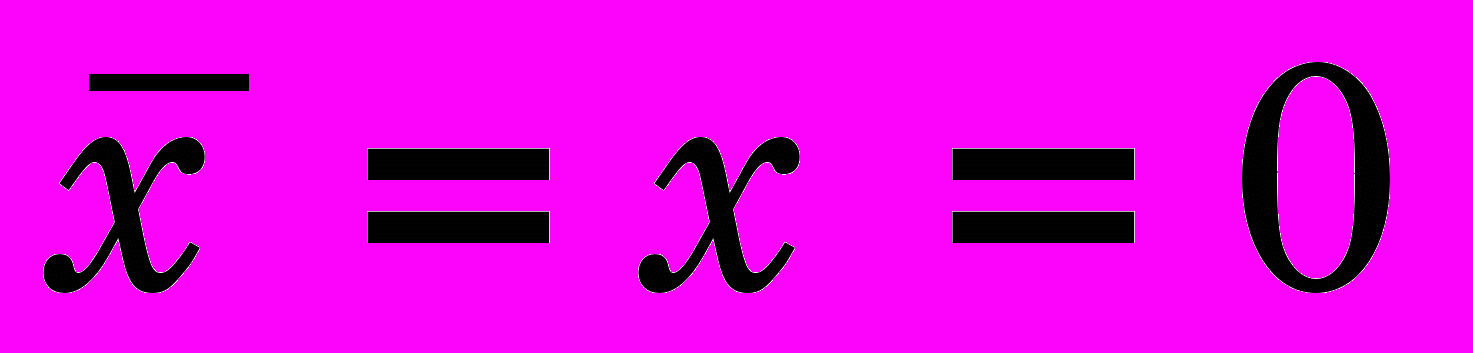 );
); 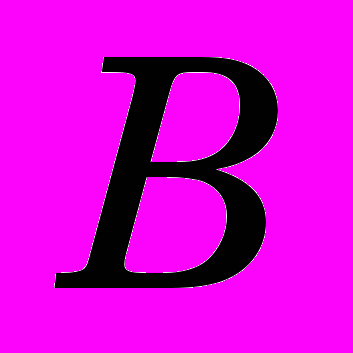 и
и 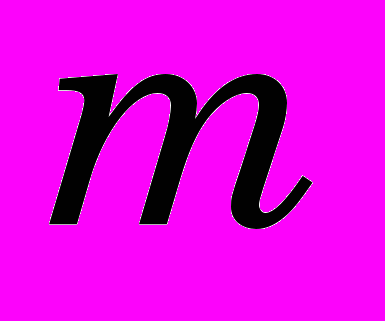 эмпирические коэффициенты.
эмпирические коэффициенты.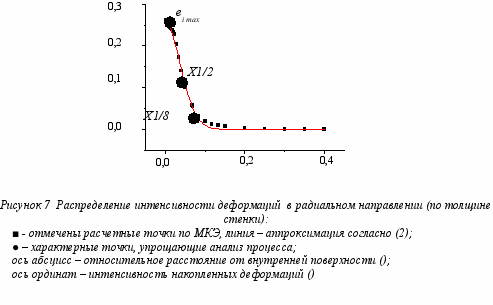
Однако коэффициенты
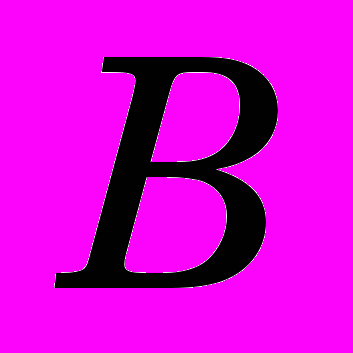 и
и 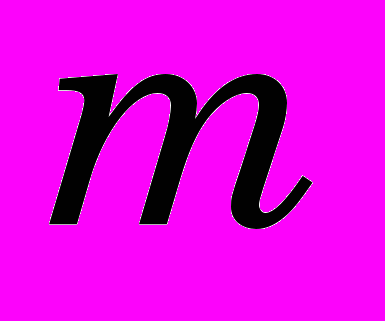 не имеют достаточно ясного физического смысла, что затрудняет анализ процесса упрочнения поверхностного слоя при деформирующем протягивании. Поэтому с помощью функции (2) впервые нами предложена методика, суть которой состоит в том, что на полученном графике мы определяем его характерные точки, связанные с деформацией и ее относительным расстоянием от поверхности заготовки. На наш взгляд, достаточно удобными точками являются:
не имеют достаточно ясного физического смысла, что затрудняет анализ процесса упрочнения поверхностного слоя при деформирующем протягивании. Поэтому с помощью функции (2) впервые нами предложена методика, суть которой состоит в том, что на полученном графике мы определяем его характерные точки, связанные с деформацией и ее относительным расстоянием от поверхности заготовки. На наш взгляд, достаточно удобными точками являются: а) расстояние
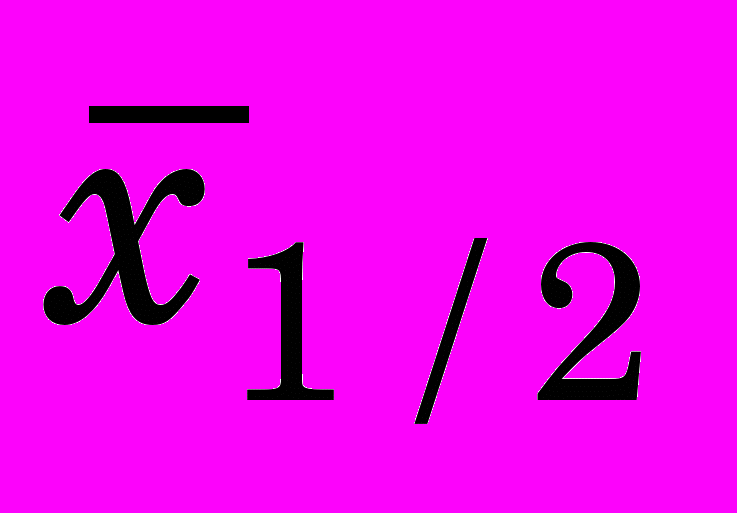 , на котором деформации достигают половины значения на внутренней поверхности, т.е.
, на котором деформации достигают половины значения на внутренней поверхности, т.е. 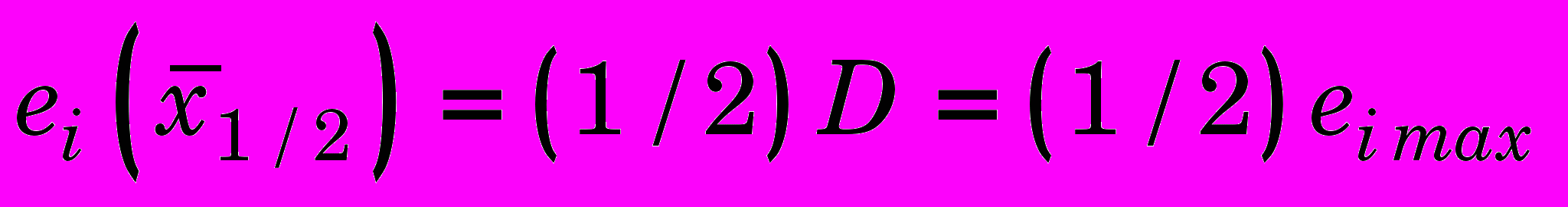 ;
;б) расстояние
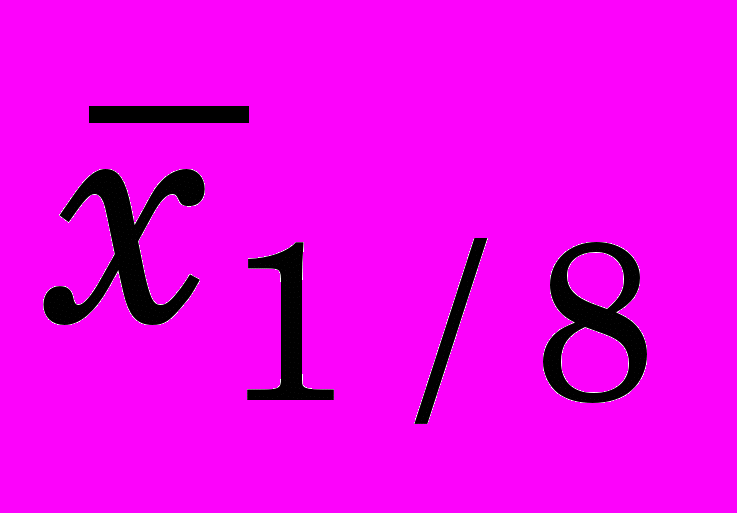 , на котором деформации достигают 1/8 значения на поверхности, т.е.
, на котором деформации достигают 1/8 значения на поверхности, т.е. 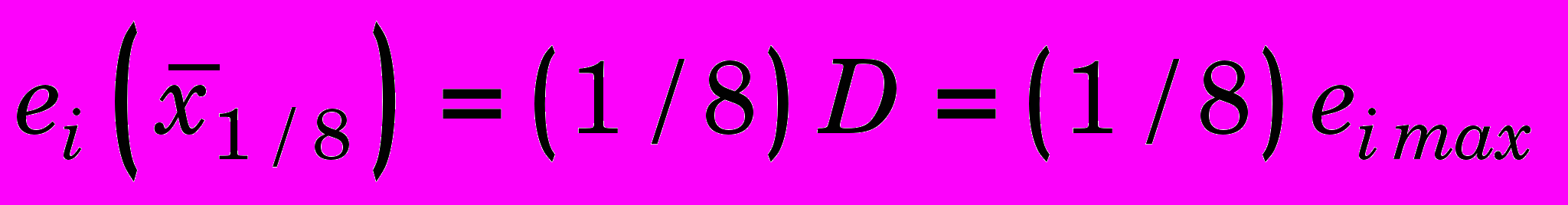 .
.Таким образом, механизм упрочнения заготовки определяется тремя параметрами с ясным физическим смыслом
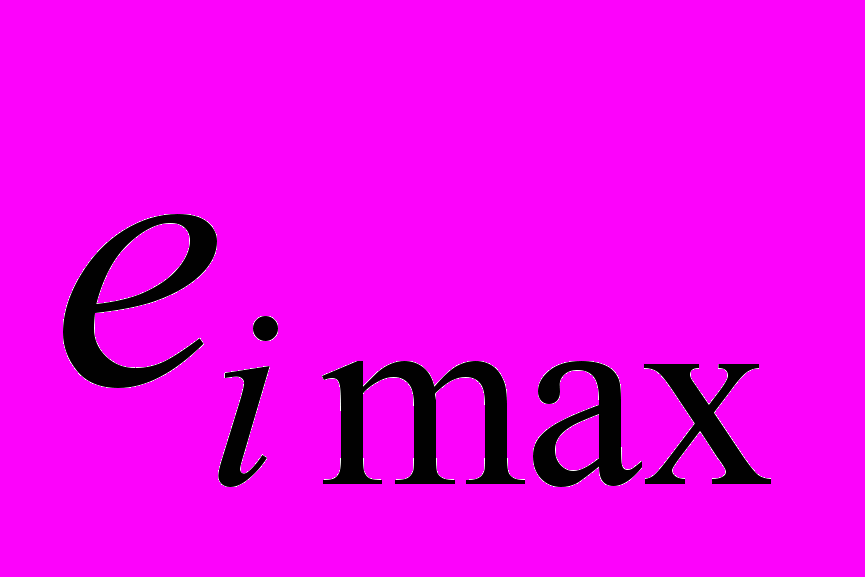 ,
, 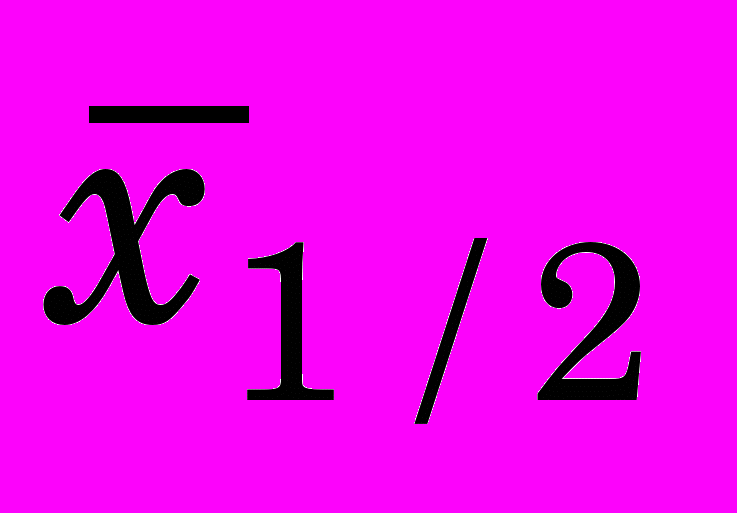 ,
, 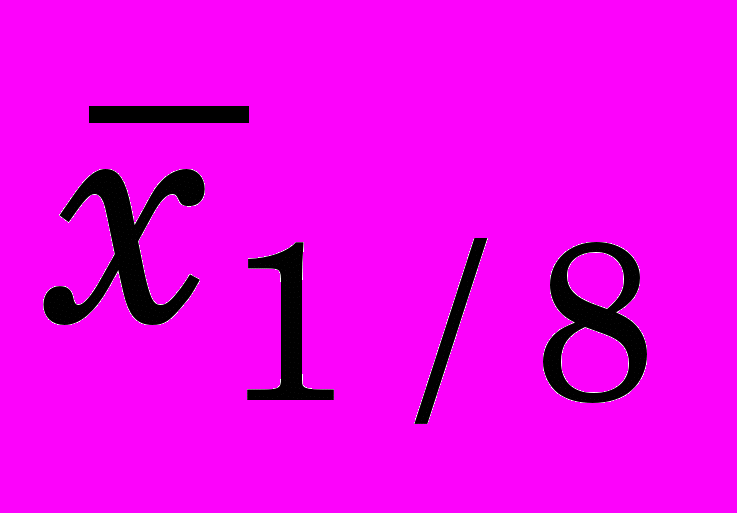 при аппроксимации функцией (2).
при аппроксимации функцией (2). Параметр
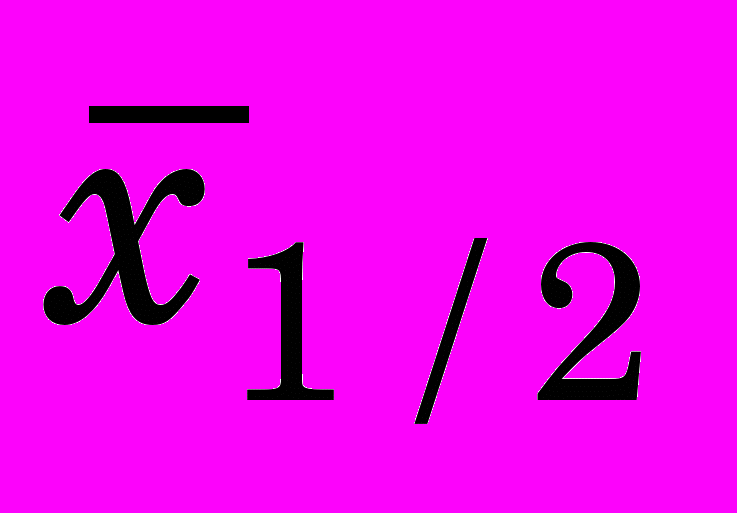 может характеризовать интенсивность убывания деформаций от поверхности, т.е. относительный градиент деформаций у поверхности (максимальный) или «крутизну» ниспадающего графика.
может характеризовать интенсивность убывания деформаций от поверхности, т.е. относительный градиент деформаций у поверхности (максимальный) или «крутизну» ниспадающего графика. Чем меньше величина
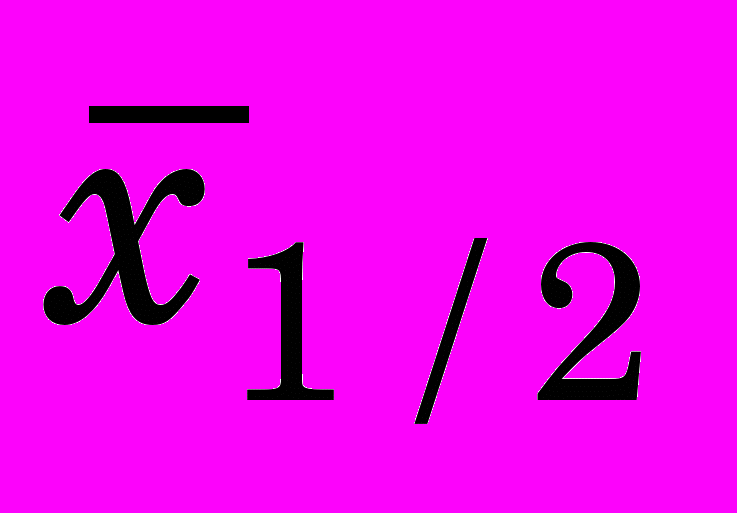 , тем интенсивнее уменьшаются деформации от поверхности и тем выше градиент деформаций.
, тем интенсивнее уменьшаются деформации от поверхности и тем выше градиент деформаций.Параметр
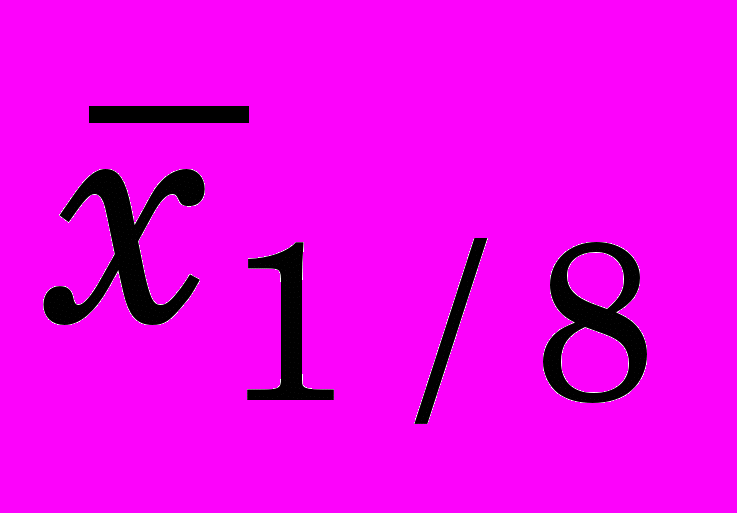 может характеризовать глубину распространения условных пластических деформаций от поверхности, т.е. «ширину» графика. Значение 1/8 принято исходя из удобства измерения
может характеризовать глубину распространения условных пластических деформаций от поверхности, т.е. «ширину» графика. Значение 1/8 принято исходя из удобства измерения 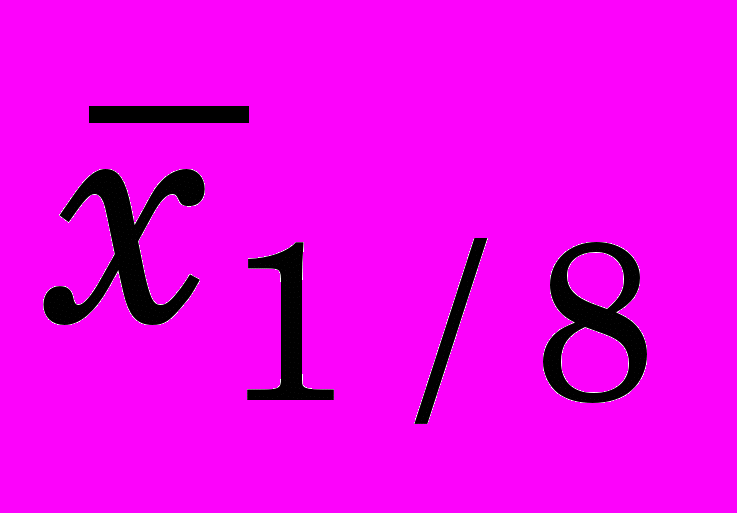 и достаточной статистической надежности этой точки на основе анализа полученных графиков. Чем больше эта величина, тем на большую глубину металл пластически деформирован.
и достаточной статистической надежности этой точки на основе анализа полученных графиков. Чем больше эта величина, тем на большую глубину металл пластически деформирован. Путем несложных математических преобразований получена связь рассмотренных величин с коэффициентами функции (2):
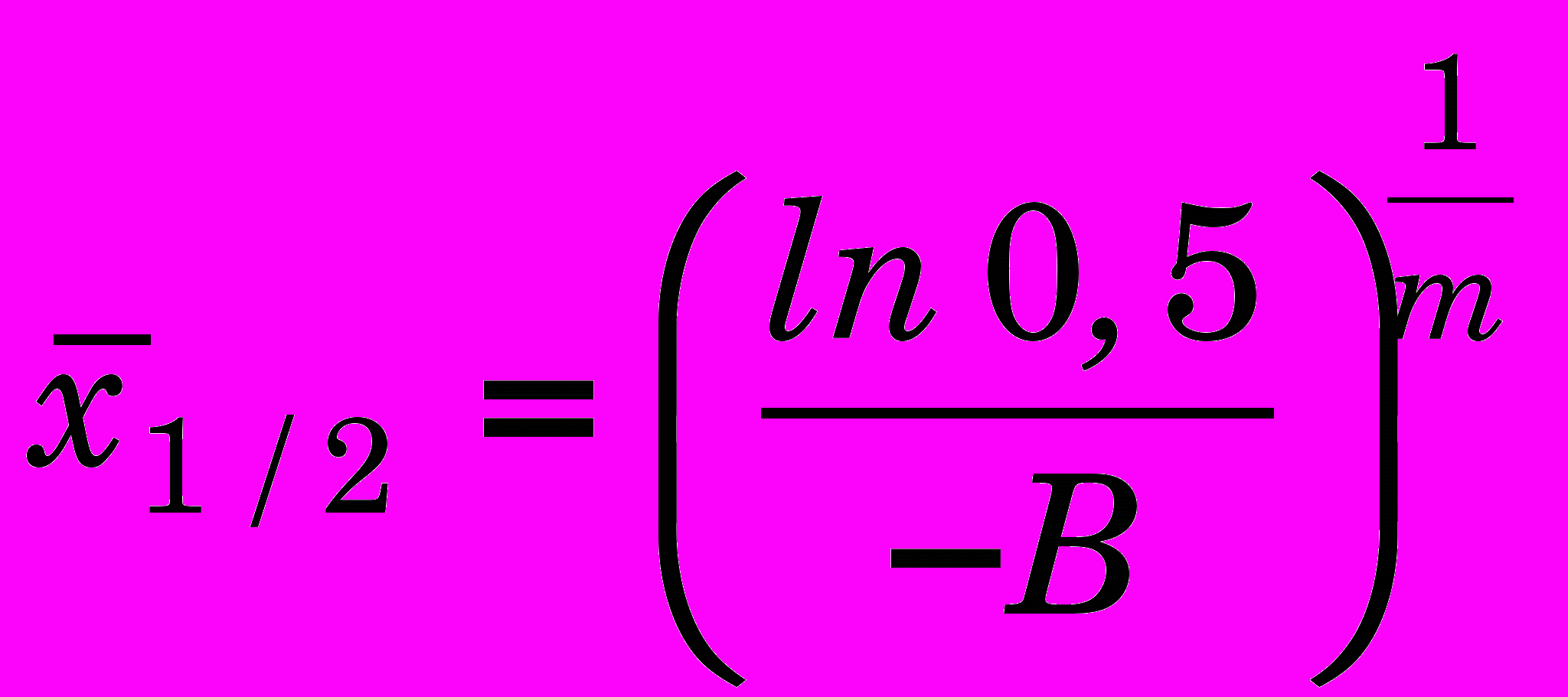 , (5)
, (5)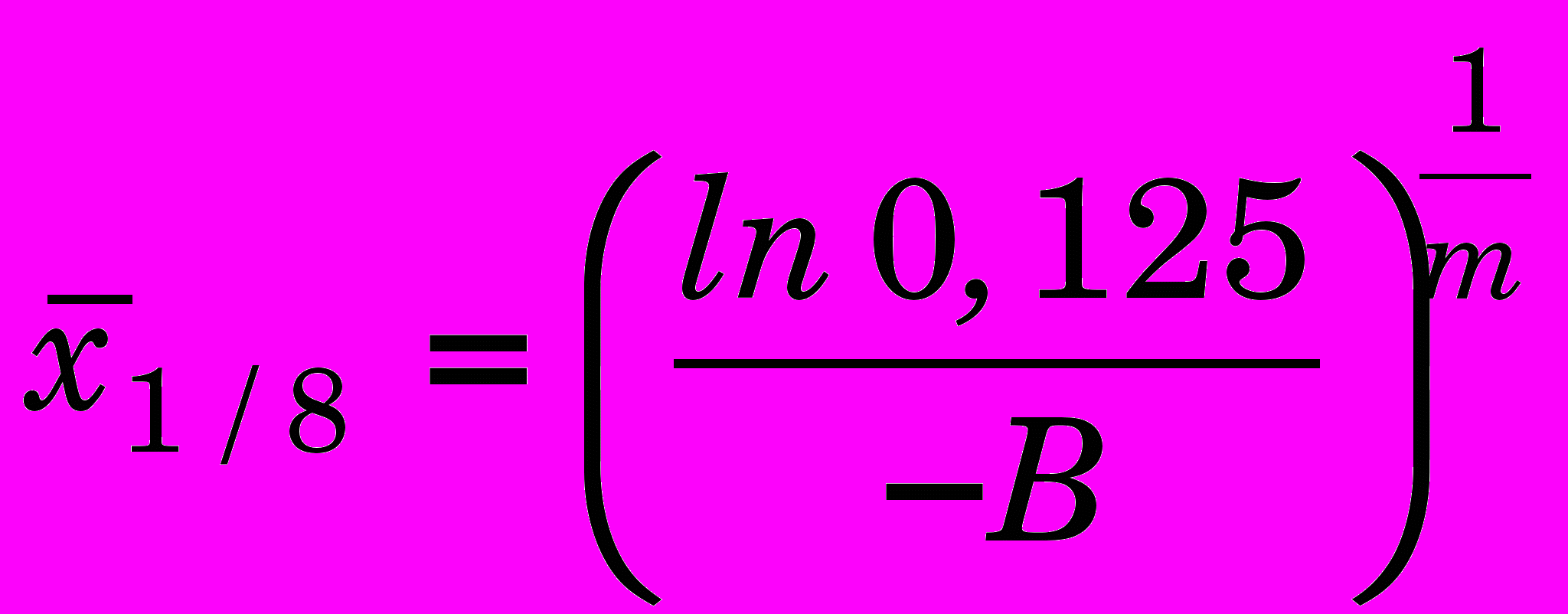 . (6)
. (6)Деформации на внутренней поверхности
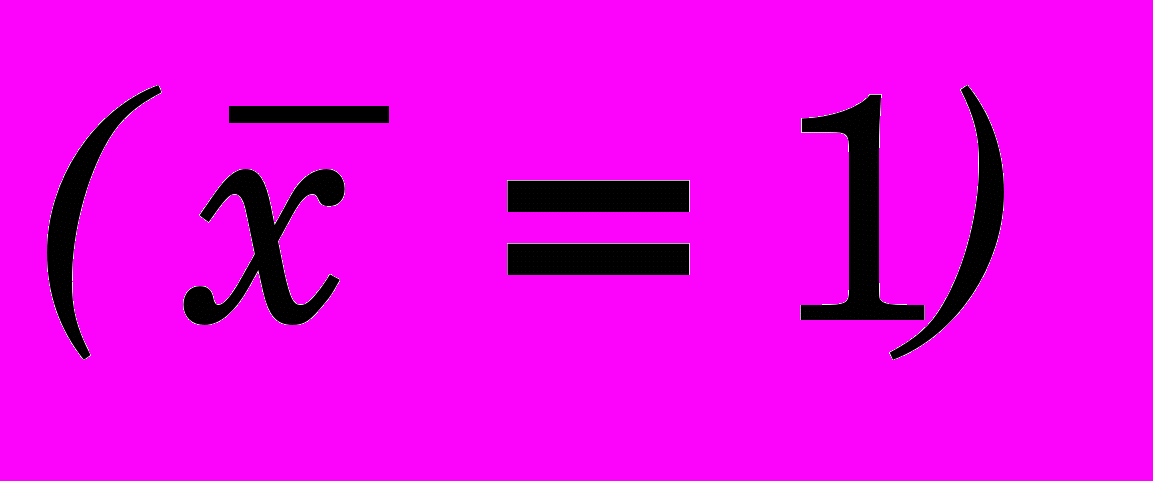
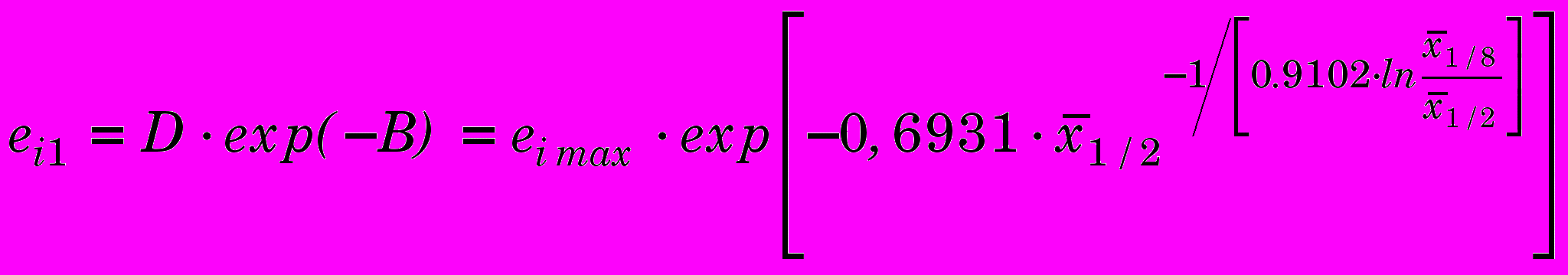 . (8)
. (8)Для исследования влияния основных параметров процесса деформирующего протягивания на коэффициенты
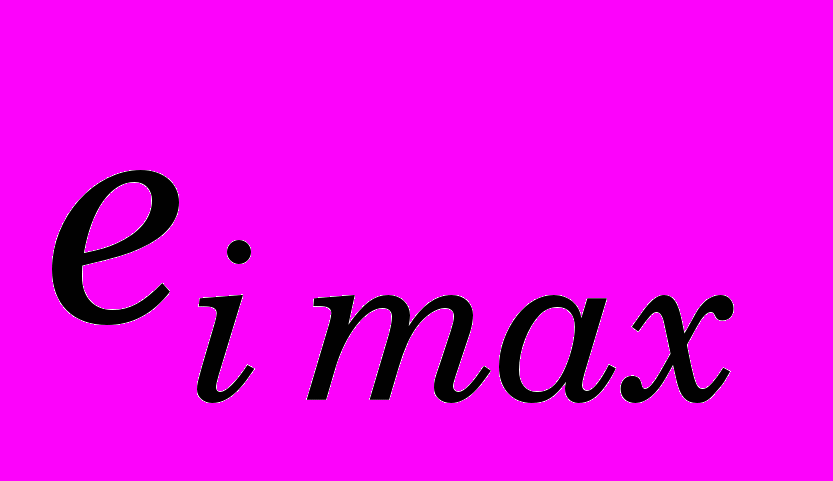 ,
, 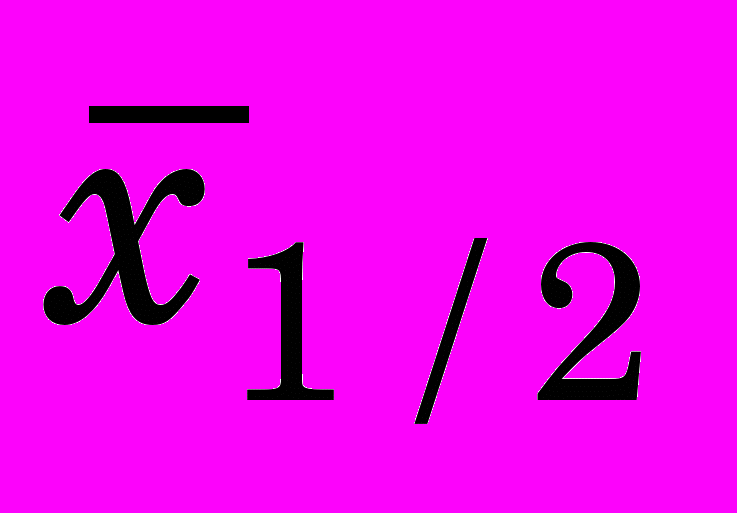 ,
, 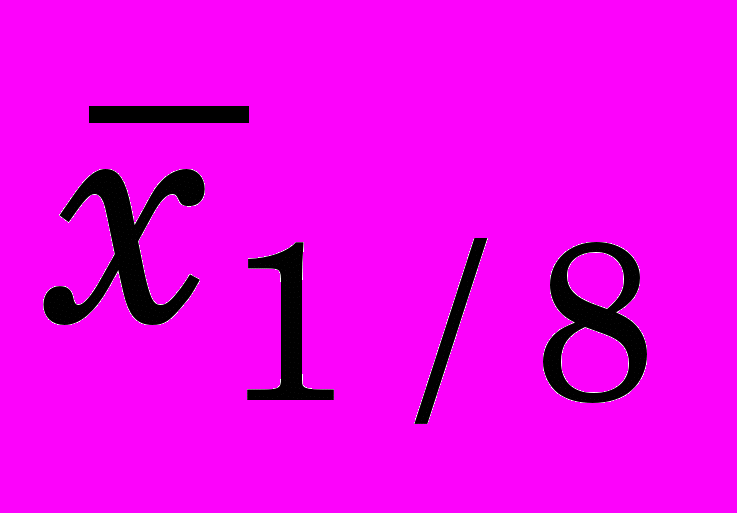 воспользуемся методом планирования эксперимента [5].
воспользуемся методом планирования эксперимента [5]. Основные влияющие факторы следующие (рис. 1):
- натяг на диаметр
 (на радиус или на сторону
(на радиус или на сторону 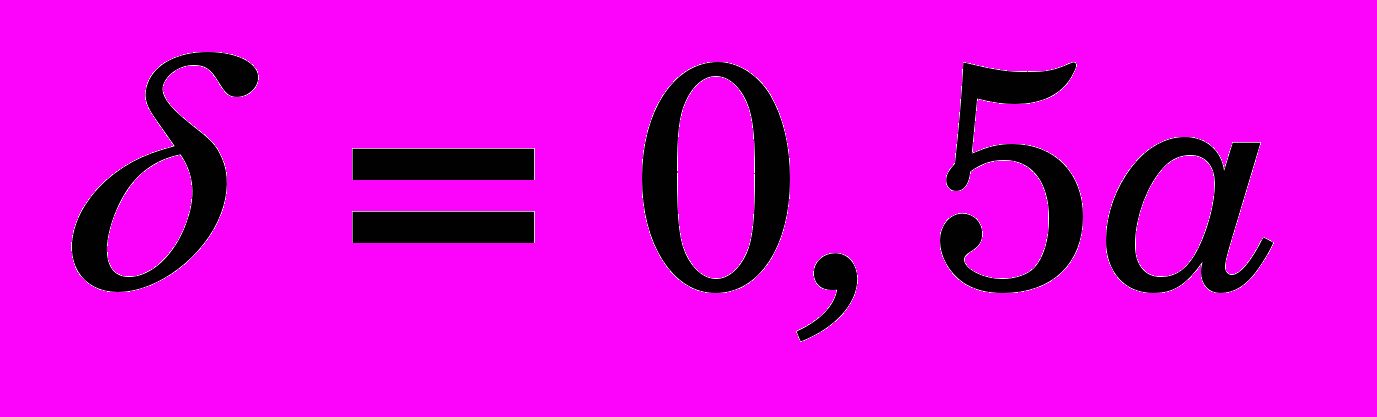 );
);
- толщина стенки заготовки
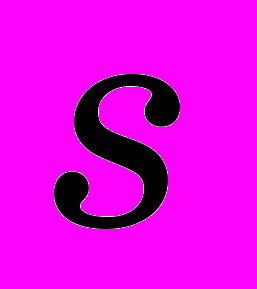 ;
;
- внутренний диаметр заготовки (исходный)
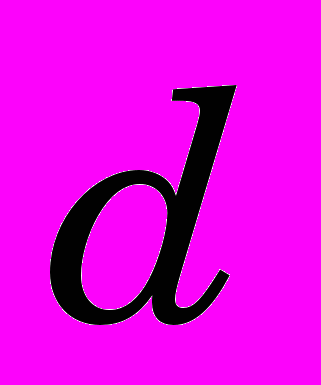 ;
;
- угол конусности деформирующего инструмента а;
- коэффициент трения
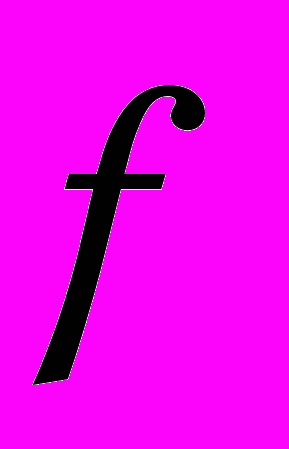 по Кулону;
по Кулону;
- модуль упрочнения материала
 ;
;
- показатель упрочнения материала
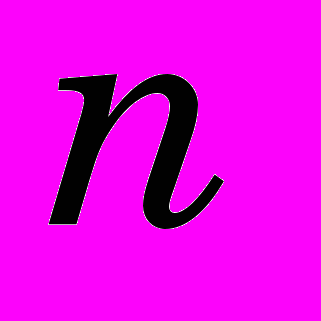 ;
;
- количество циклов деформирования
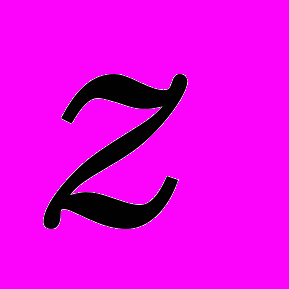 .
.
При многоцикловом протягивании отмечается линейный принцип суммирования деформаций, что соответствует проведенным расчетам и подтверждается данными работы [1]:
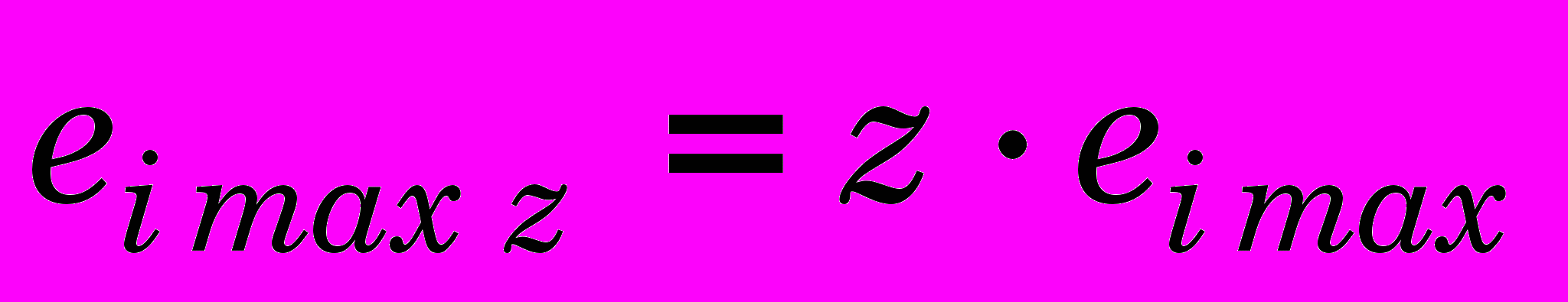 ,
, 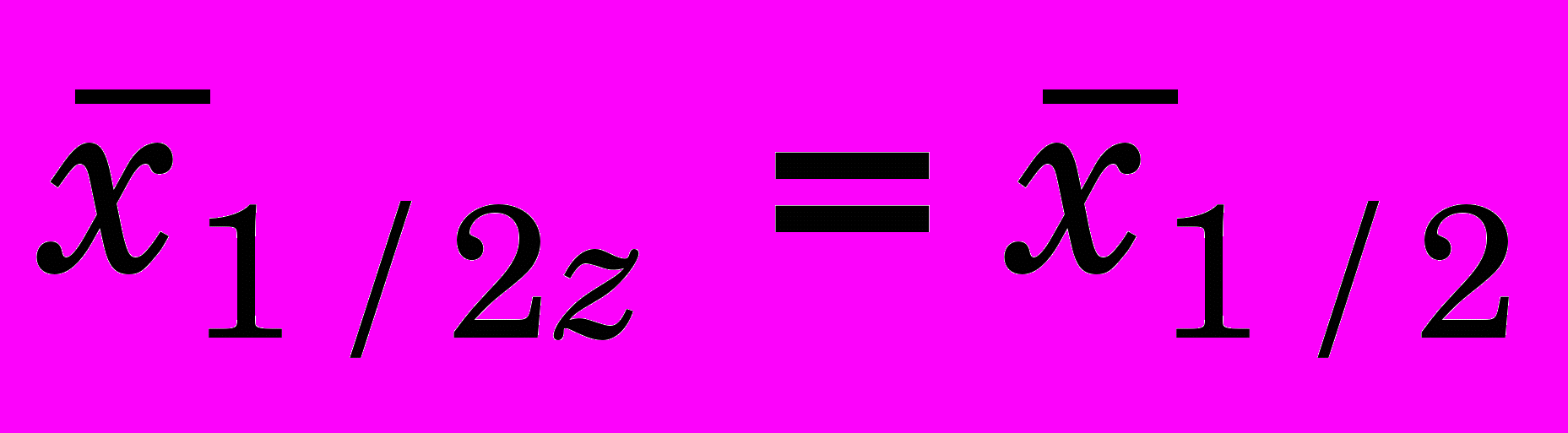 ,
, 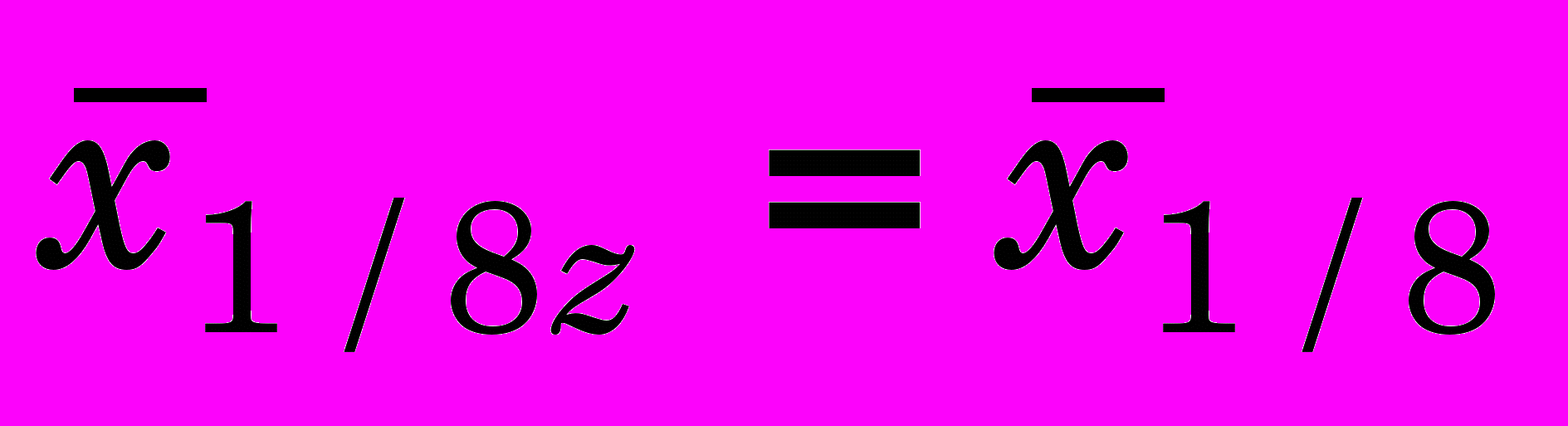 ,
,где z – количество циклов протягивания.
Отметим, что данный принцип достаточно хорошо работает при небольших суммарных натягах, не приводящих к увеличению внешнего диаметра более чем на 1-2%.
Это позволило исключить
 из строимой модели.
из строимой модели.Опираясь на опыт по проектированию технологического процесса протягивания и перспективы его применения, укажем ориентировочно предельные значения рассматриваемых величин. Ограничимся черным металлом (сталями) в связи с преимущественным их использованием при деформирующем протягивании и относительно постоянным коэффициентом Пуассона (
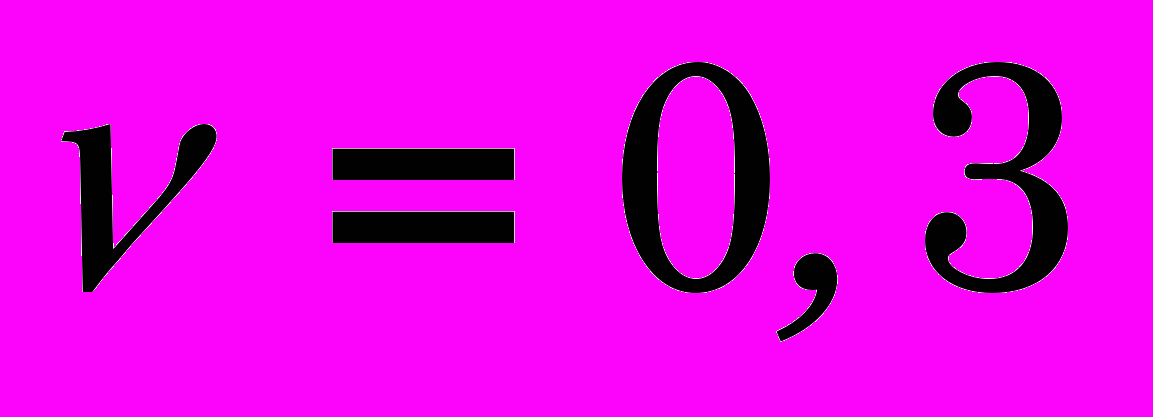 ) и модулем Юнга (
) и модулем Юнга (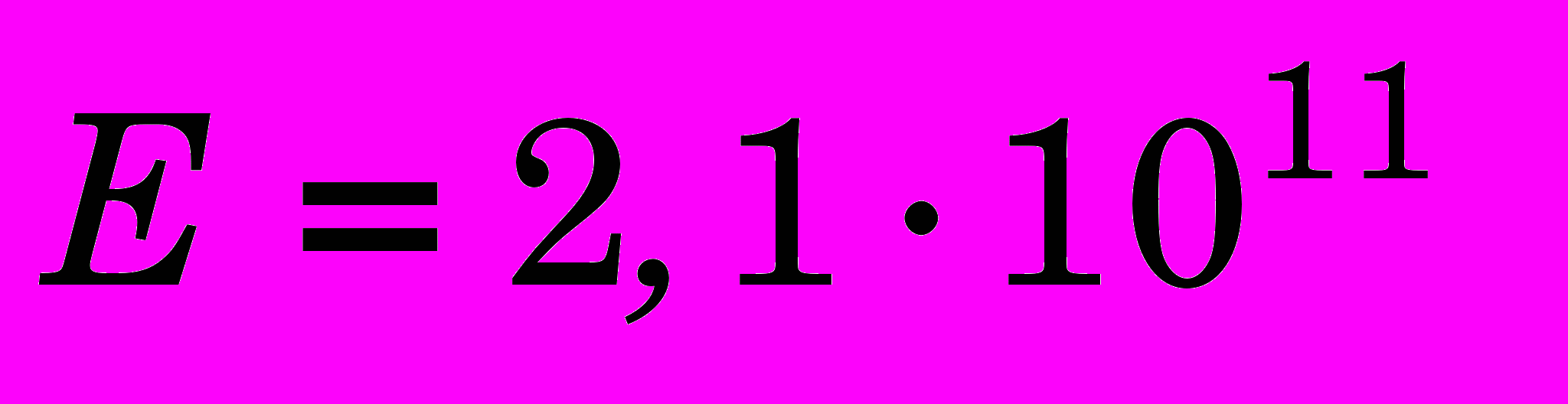 Па). Для указанных материалов, применяемых для данного процесса, показатель упрочнения материала изменяется в пределах
Па). Для указанных материалов, применяемых для данного процесса, показатель упрочнения материала изменяется в пределах 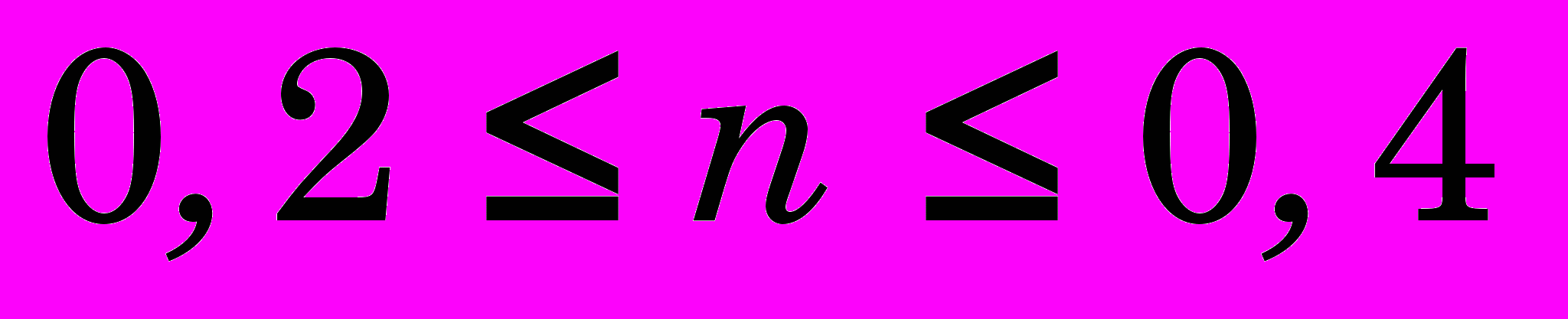 , а модуль упрочнения
, а модуль упрочнения 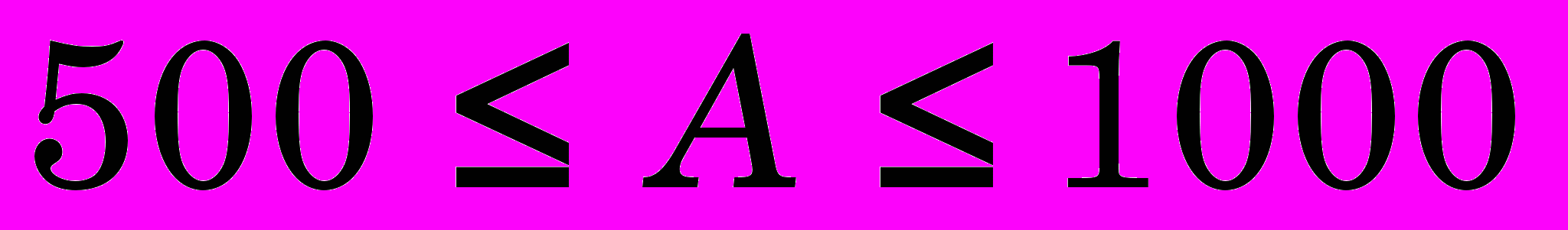 МПа.
МПа. Таким образом, пределы изменения рассматриваемых величин составляют:
- толщина стенки заготовки
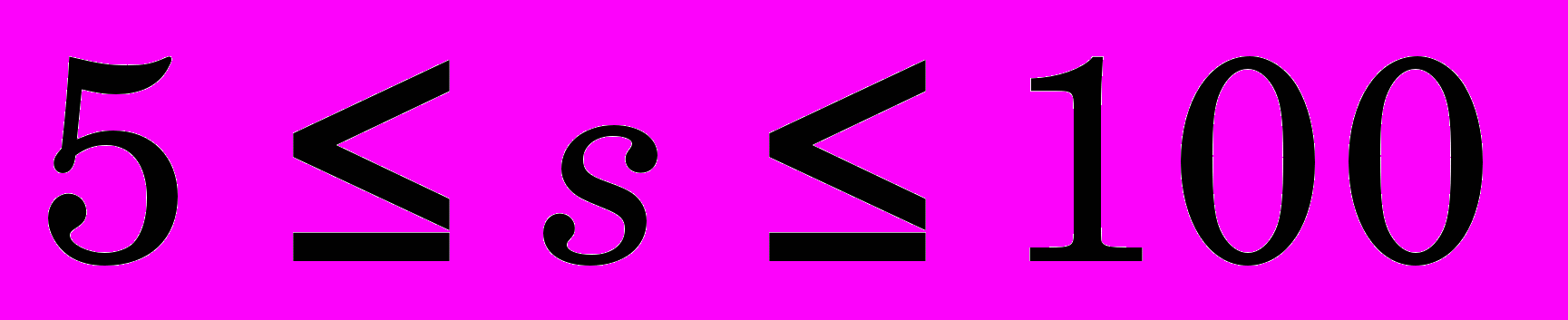 мм;
мм;
- натяг на сторону
 мм (относительный натяг
мм (относительный натяг 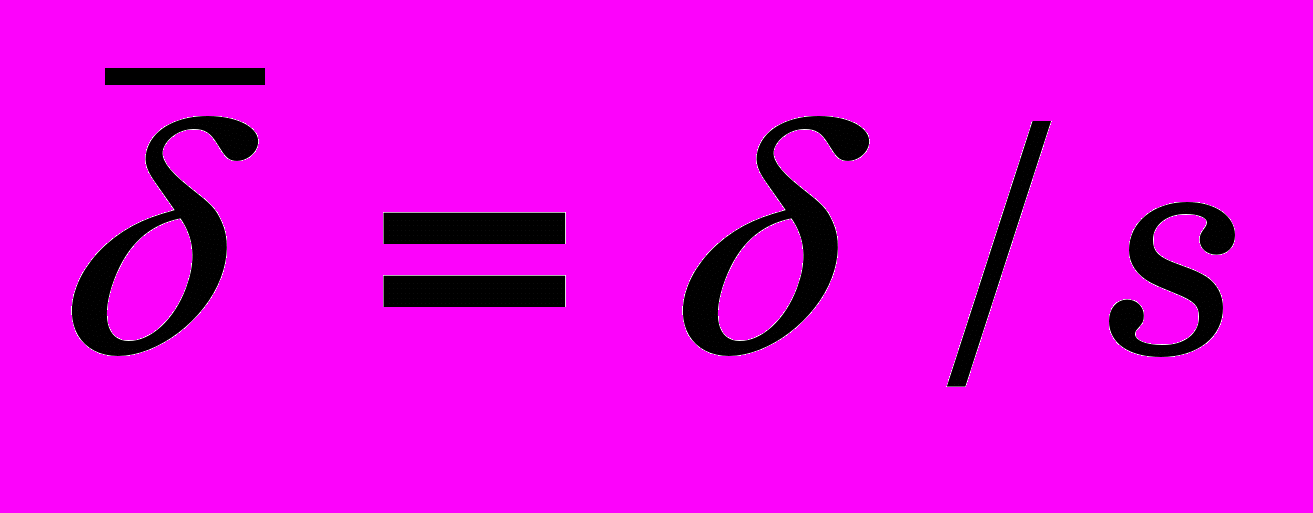 ,
, 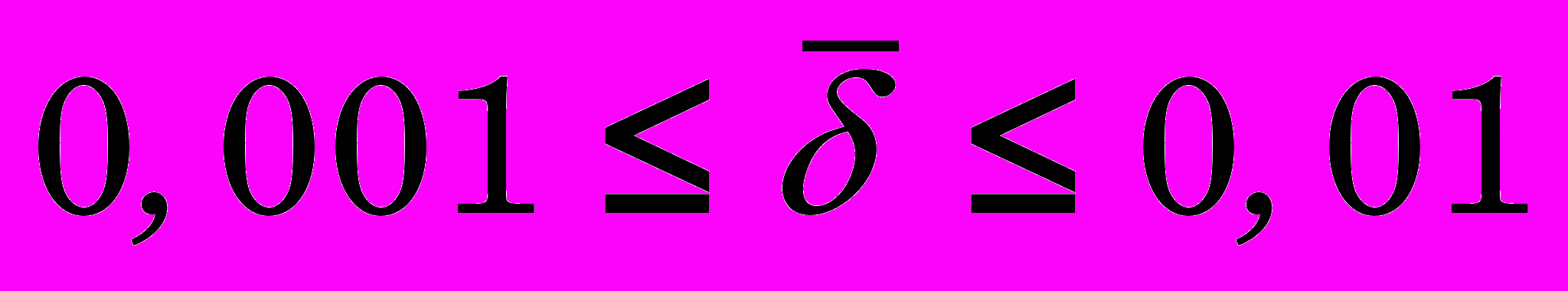 );
);
- внутренний диаметр заготовки
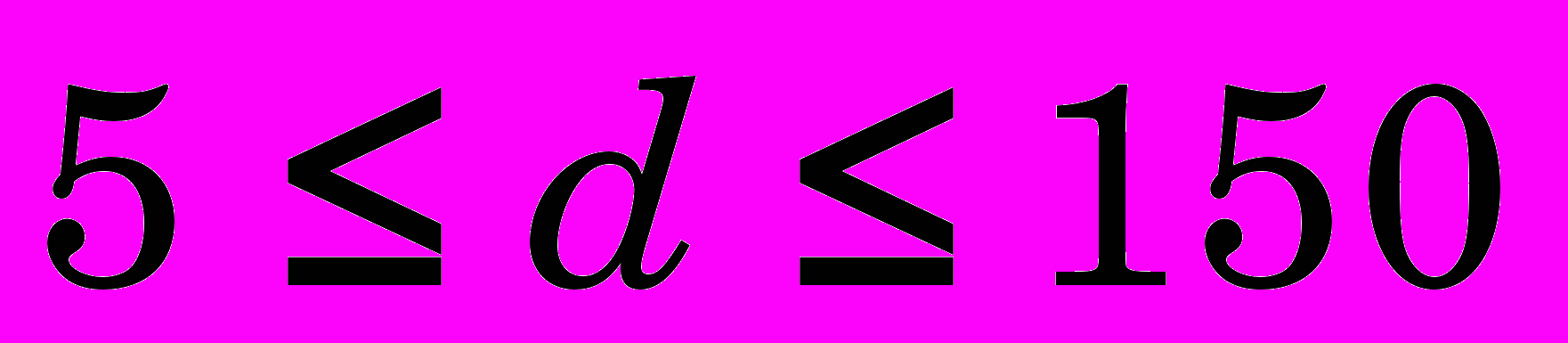 мм (относительный диаметр
мм (относительный диаметр 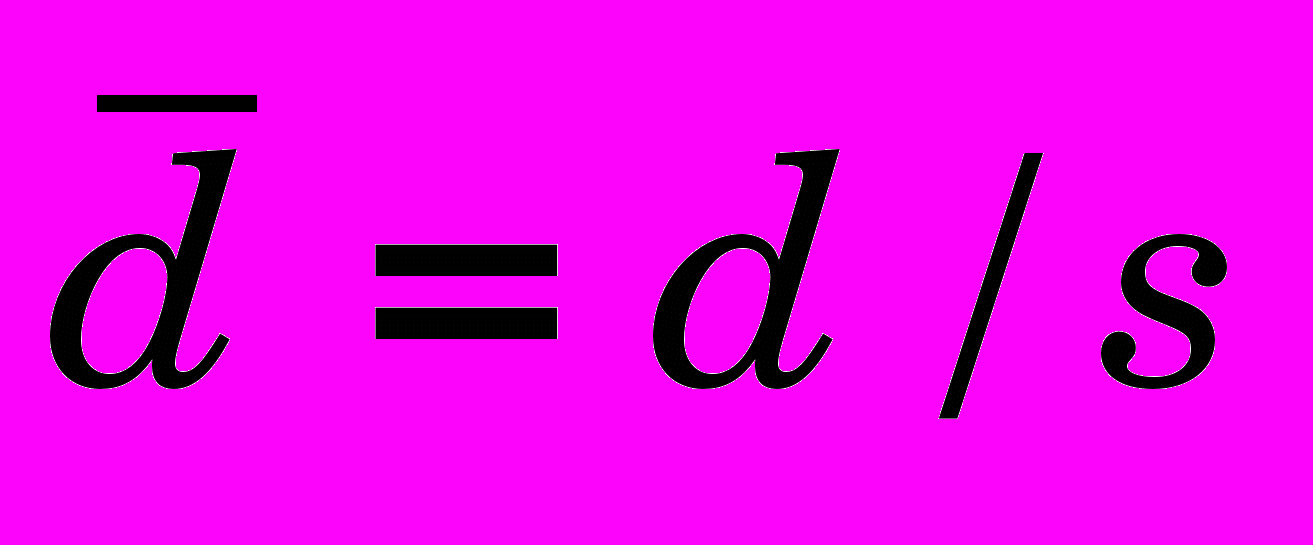 ,
, 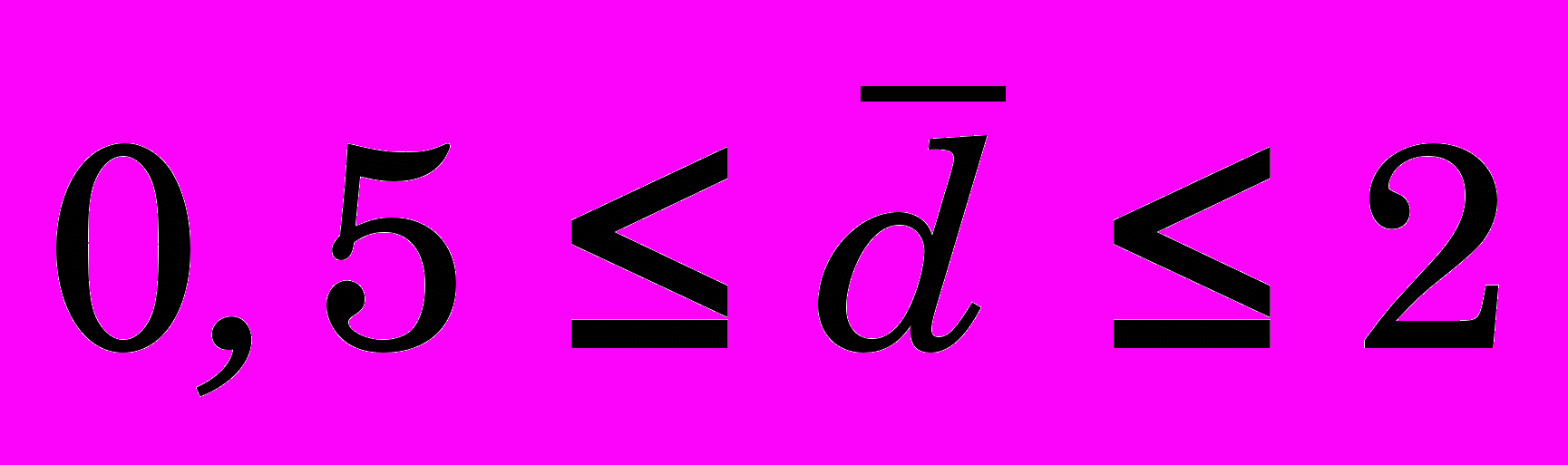 );
);
- угол конусности инструмента 4°<α<10°;
- коэффициент трения по Кулону
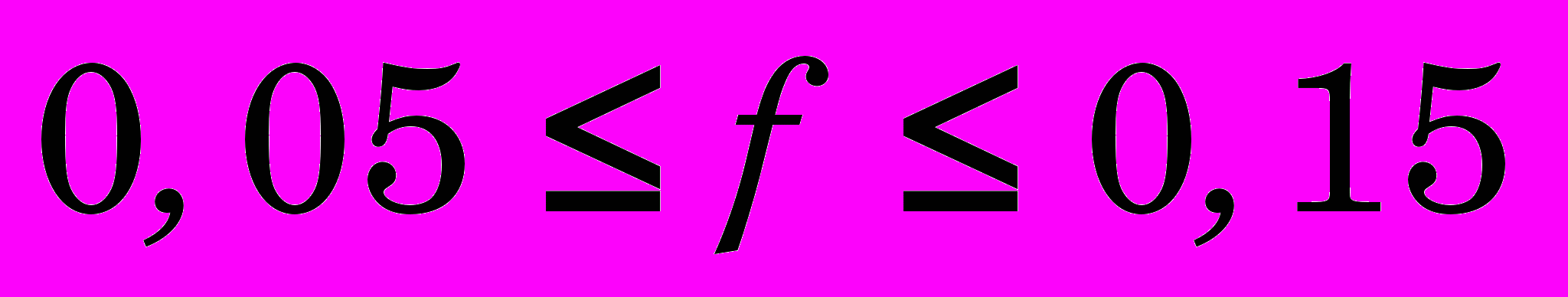 ;
;
- модуль упрочнения материала
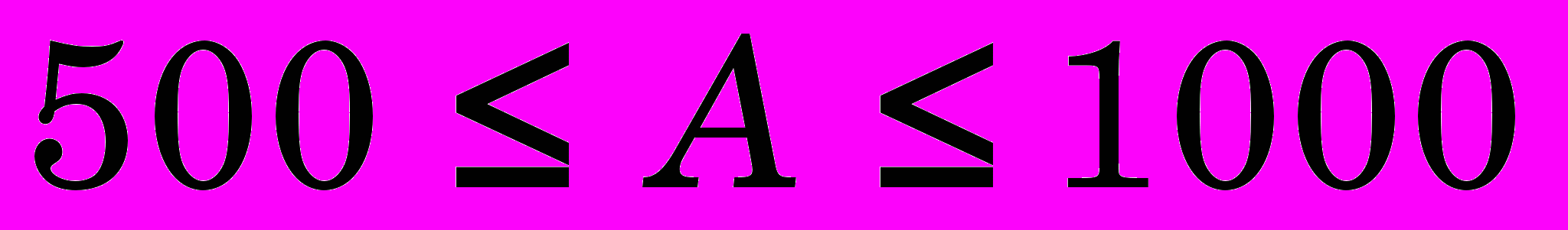 МПа;
МПа;
- показатель упрочнения материала
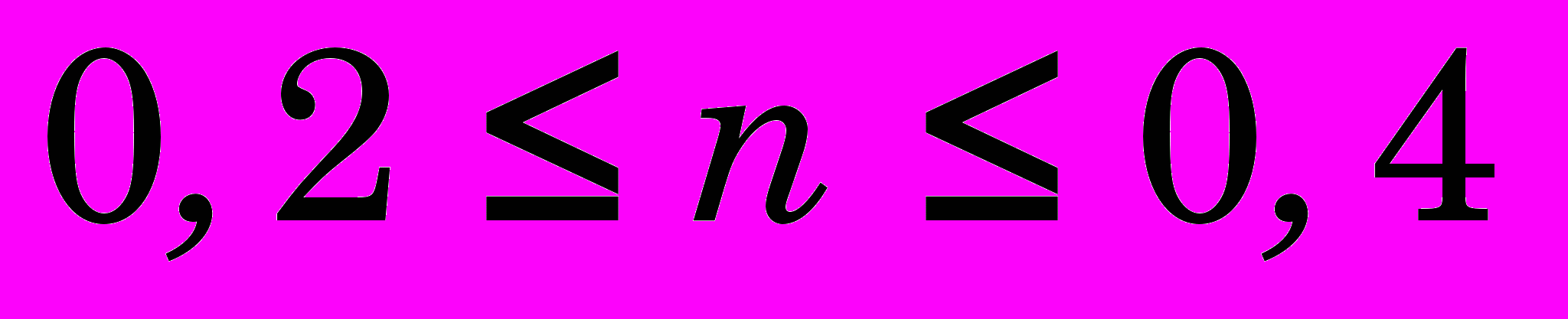 .
.
В результате планирования эксперимента было установлено влияние технологических параметров процесса деформирующего протягивания на параметры упрочнения:
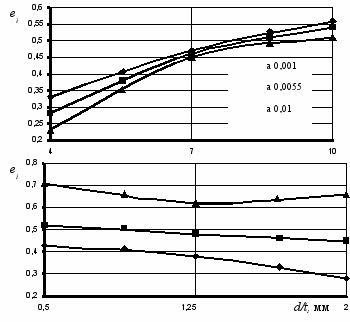
Рисунок 8 Влияние технологических параметров на интенсивность деформации: ♦ α=4°;■ – α=7°;▲ – α=10°
Следует отметить, что на установившуюся деформацию (X1/8) влияние имеет только натяг, остальные факторы имеют незначительное влияние. А вот остальные параметры упрочнения имеют связь с рассмотренными технологическими факторами. Проанализировав графики, представленные на рис. 9, были разработаны технологические рекомендации по определению степени упрочнения при обработке деформирующим инструментом.
В изученной области полученная модель не имеет экстремальных значений, что позволяет достигать максимальных (минимальных) деформаций, глубины распространения пластических деформаций и градиентов при граничных сочетаниях влияющих факторов.
Упрочнение на поверхности
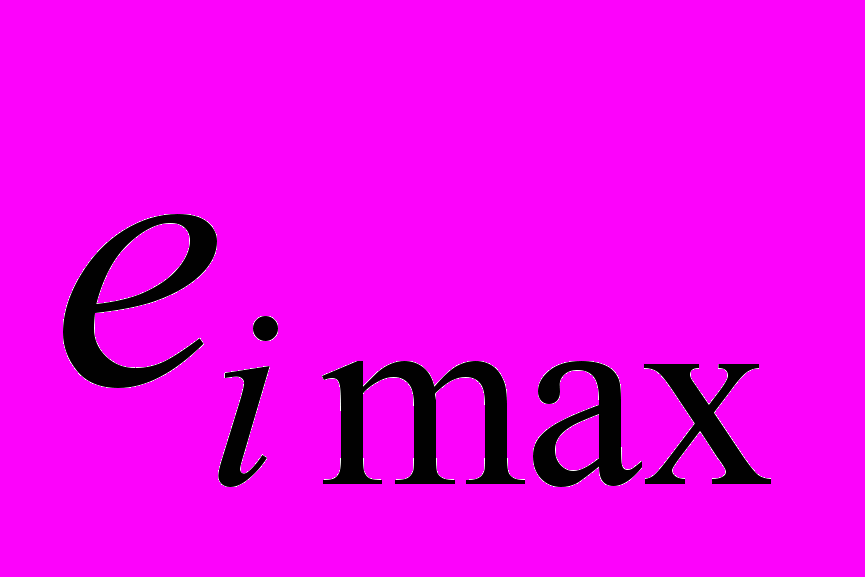 увеличивают угол конусности инструмента α (наиболее сильно влияющий фактор) и коэффициент трения
увеличивают угол конусности инструмента α (наиболее сильно влияющий фактор) и коэффициент трения 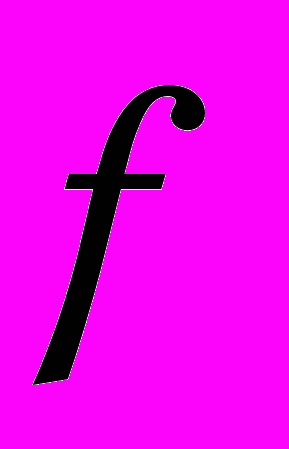 и уменьшает показатель упрочнения
и уменьшает показатель упрочнения 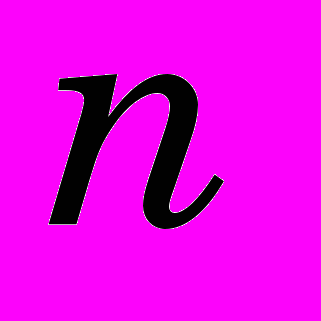 . Влияние иных факторов неоднозначно.
. Влияние иных факторов неоднозначно.К увеличению градиента деформаций
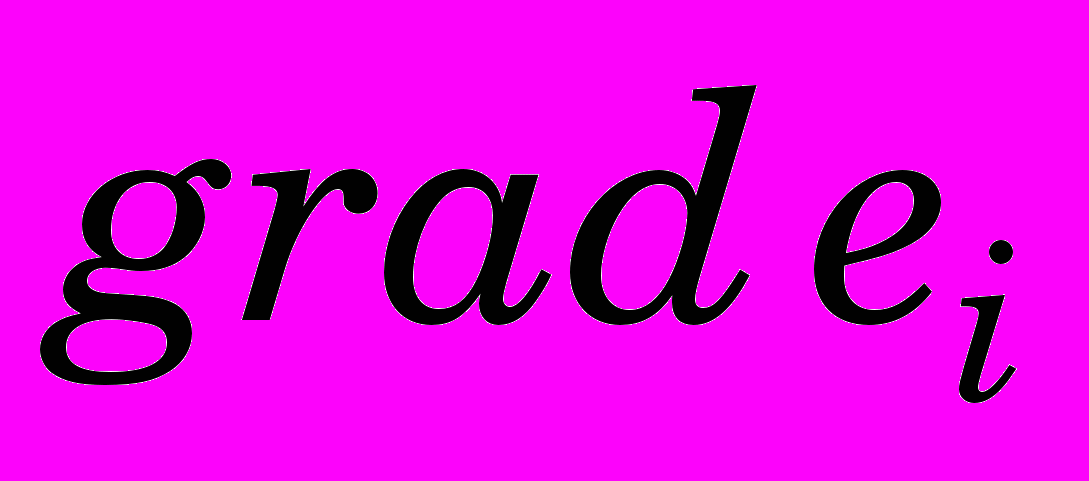 (или
(или 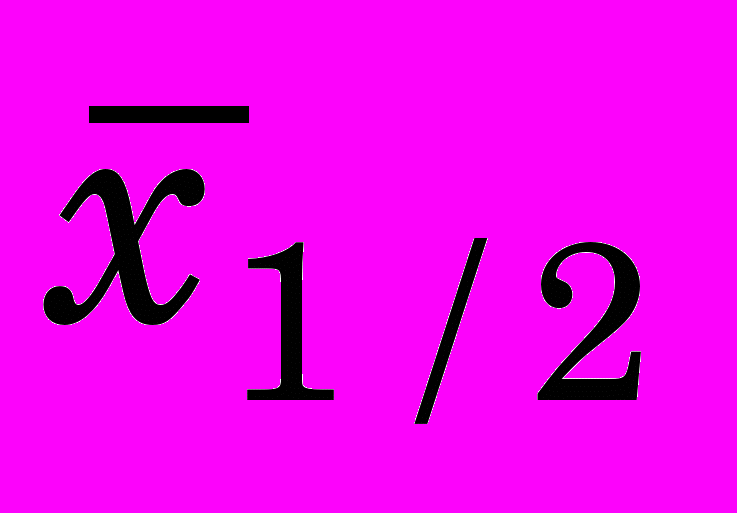 ) производит уменьшение натяга на сторону
) производит уменьшение натяга на сторону 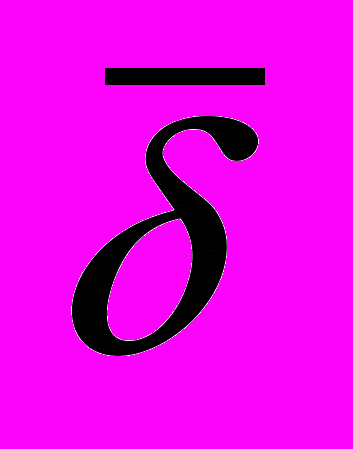 (наиболее сильно влияющий фактор), увеличение коэффициента трения
(наиболее сильно влияющий фактор), увеличение коэффициента трения 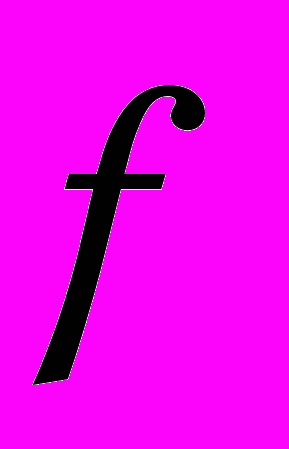 и увеличение угла конусности инструмента
и увеличение угла конусности инструмента 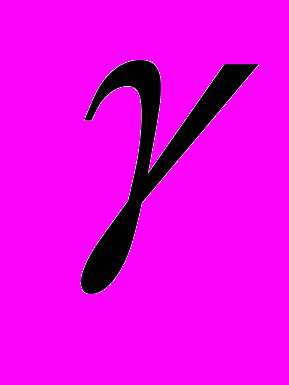 . Влияние иных факторов неоднозначно.
. Влияние иных факторов неоднозначно.К увеличению глубины деформированного слоя
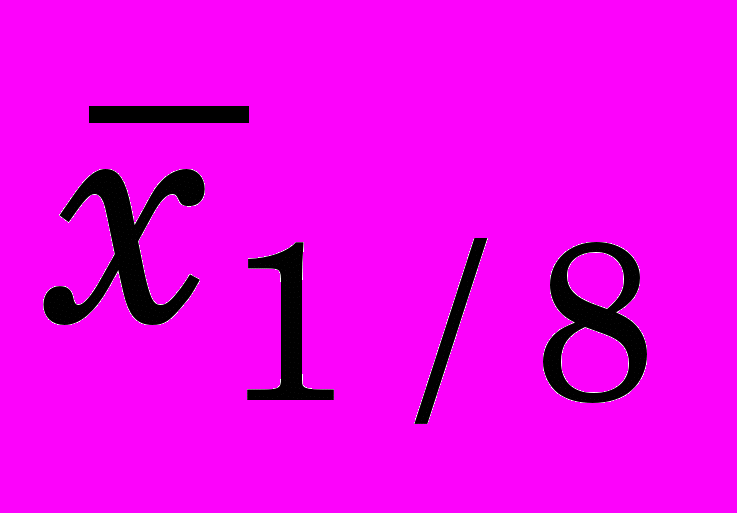 производит увеличение натяга на сторону
производит увеличение натяга на сторону 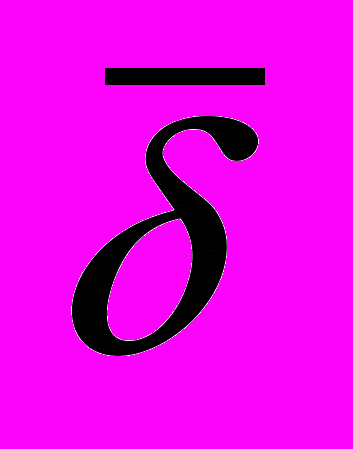 (наиболее сильно влияющий фактор) и уменьшение модуля упрочнения
(наиболее сильно влияющий фактор) и уменьшение модуля упрочнения  . Коэффициент трения практически не влияет на параметр
. Коэффициент трения практически не влияет на параметр 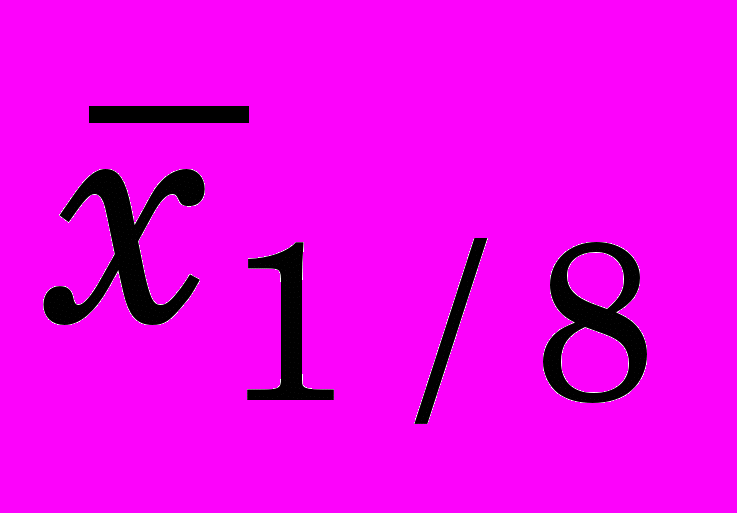 .
. 
0,14
0
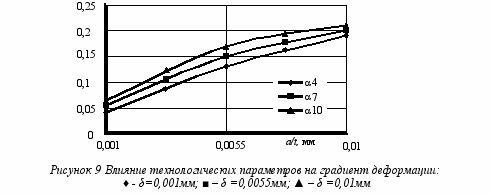
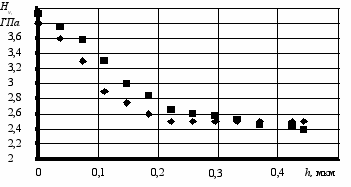
Рисунок 10 Зависимости микротвердости от глубины упроченного слоя, полученные в реальном эксперименте и при использовании разработанной модели ♦ экспериментальные значения; ■ – рассчитанные по МКЭ
ВЫВОДЫ
- Проанализировав графики, представленные на рис. 9, были разработаны технологические рекомендации по определению степени упрочнения при обработке деформирующим инструментом, а также граничные условия их применения.
- Впервые предложена методика определения связи параметров упрочнения с технологическими параметрами по характерным точкам. Благодаря этому получена более информативная картина влияния технологических факторов.
- На деформационное упрочнение оказывают такие параметры технологического процесса: натяг; толщина стенки заготовки; внутренний диаметр заготовки; угол конусности деформирующего инструмента; коэффициент трения по Кулону; модуль упрочнения материала; показатель упрочнения материала; модуль Юнга, коэффициент Пуассона и количество циклов деформирования.
- Глубина деформированного слоя и максимальное упрочнение
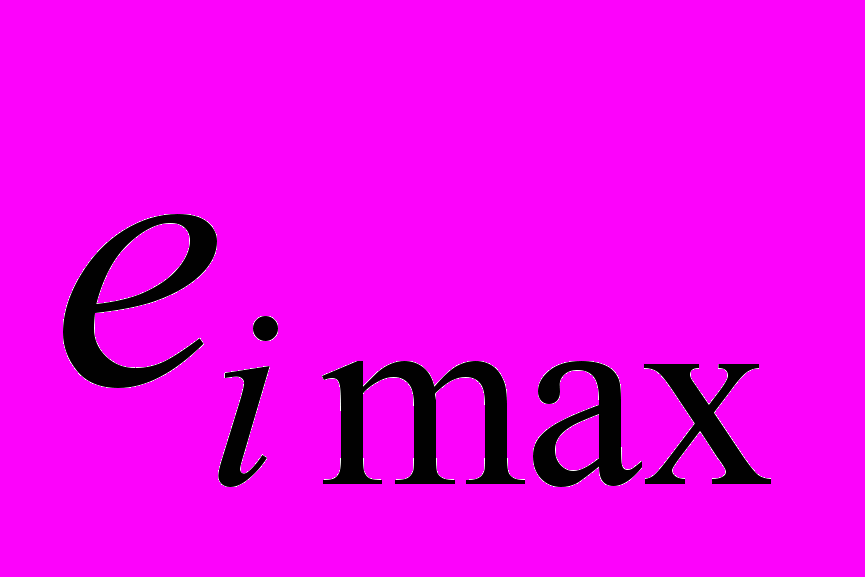 , согласно расчетов по МКЭ, не превышает 14% (рис.10), что позволяет достаточно точно спрогнозировать результаты обработки деформирующим протягиванием при проектировании технологических процессов.
, согласно расчетов по МКЭ, не превышает 14% (рис.10), что позволяет достаточно точно спрогнозировать результаты обработки деформирующим протягиванием при проектировании технологических процессов.
SUMMARY
The article is devoted to developing a mathematical model with which seems to predict the process of hardening the surface layer of machining by deforming broaching.
СПИСОК ЛИТЕРАТУРЫ
- Цеханов Ю.А. Технологическая механика деформирующего протягивания /
О. А. Розенберг, Ю.А. Цеханов, С.Е. Шейкин. – Воронеж : Воронеж. гос. технолог. акад. 2001. – 203 с.
- Розенберг О.А. Механика взаимодействия инструмента с изделием при деформирующем протягивании / О. А. Розенберг. – К.: Наук. думка, 1981. – 288 с.
- Цеханов Ю. А. Механика деформирующего протягивания как научная основа оценки качества деталей и работоспособности инструмента с износостойкими покрытиями: дис. … д-ра техн. наук: 05.02.08 / Юрий Александрович Цеханов. – Воронеж, 1993. –
385 с.– Бібліогр.: С. 365–383.
- Иванов К.М. Метод конечных элементов в технических задачах ОМД: учебное пособие / К.М. Иванов, В.С. Шевченко, Э.Е. Юргенсон. – СПб.: Институт машиностроения, 2000. – 217 с.
- Новик Ф.С. Оптимизация процессов технологии металлов методами планирования экспериментов / Ф.С. Новик, Я.Б. Арсов. – М.: Машиностроение; София: Техника, 1980. – 304 с.
- Дель Г.Д. Определение напряжений в пластической области по распределению твердости / Г.Д. Дель. – М.: Машиностроение, 1971. – 200 с.
- Огородников В.А. Энергия. Деформации. Разрушение (задачи автотехнической экспертизы) / Огородников В.А., Киселев В.Б., Сивак И.О. – Винница: УНІВЕРСУМ-Вінниця, 2005. – 204 с. – ISBN 966-641-117-2.
- Огородников В.А. Деформируемость и разрушение металлов при пластическом формоизменении / В.А. Огородников. – К. : УМК ВО, 1989. – 152 с.
- Дель Г.Д. Технологическая механика / Г.Д. Дель – М. : Машиностроение, 1978. – 174 с.
