Geum.ru

Національний педагогічний університет імені М. П. Драгоманова На правах рукопису cпірін олег Михайлович

Вид материалаДокументы
Лабораторна робота №3
Лабораторна робота №4
Подобный материал:
1   ...   10   11   12   13   14   15   16   17   18
Вимоги до захисту лабораторної роботи.

Звіт виконаної роботи повинен містити назву теми, текст програми, текст запитів мовою ПРОЛОГ та відповідей на них для завдань І-го рівня; текст модифікованої бази даних і модифікованого правила, запити для завдань ІІ-го рівня.
Лабораторна робота №3

Тема: “Арифметичні вирази у Пролог-програмах. Використання рекурсії”.

Мета: Одержати уміння та навички використання у програмах арифметичних операцій, операцій порівняння, логічних опера­цій, операцій перевірки типу. Розглянути та відпрацю­вати технологію використання рекурсії для розв'язування циклічних обчислювальних задач.
Теоретична частина: завдання та контрольні питання.

І рівень.
  1. За допомогою яких операндів конструюються арифметичні вирази? Який стандартний предикат обчислює їх?
  2. Які стандартні предикати реалізують операції порівняння?
  3. Описати стандартні предикати перевірки типу.
  4. Значення яких числових функцій дозволяють обчислити стандартні предикати?
  5. Означення рекурсії.
  6. Яка конструкція рекурсії?

ІІ рівень.
  1. У якому випадку виникає "нескінченна" рекурсія?
  2. Який процес називається "процедурою з усуненням хвостової рекурсії"?
  3. Який процес називається "процедурою з лівою рекурсією"?
  4. Описати рекурсивне виконання правила повторення.
  5. У чому полягає різниця між правилом та методом повторення?
Практична частина.

І рівень.

1-13 варіанти.

а) Скласти програму для визначення N-го числа ряду Фібоначчі: F1, F2,..., Fn, де F1=F2=1, Fi=Fi-1+Fi-2, i=3, 4, 5 ,…, n. Протестувати програму. Зберегти про­гра­му у файлі "LNN3_1а.pro", де NN – номер варіанту користувача.

б) Знайти факторіал числа N. Протестувати програму.

Зберегти програму у файлі "LNN3_1b.pro".

ІІ рівень.

Дано дійсне число x і натуральне n. Скласти програму, яка, використовуючи вихідну рекурсію, обчислює суму членів ряду (ряд указаний у варіанті). Програма повинна містити директиву include, за якою підключатиметься текст програми "LNN3_1b.pro". Протестувати та зберегти текст програми у файлі (ім'я файла програми вказано у варіанті).

1-3 варіанти. 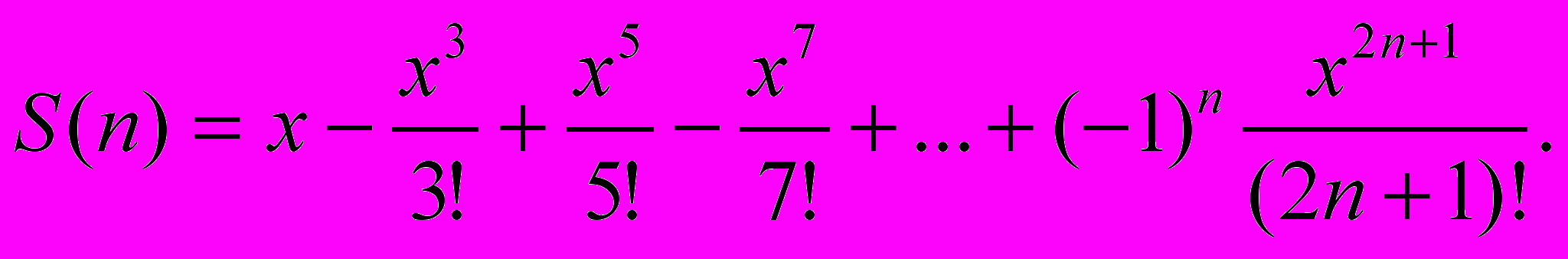Файл "LNN3_21.pro".

4-6 варіанти. 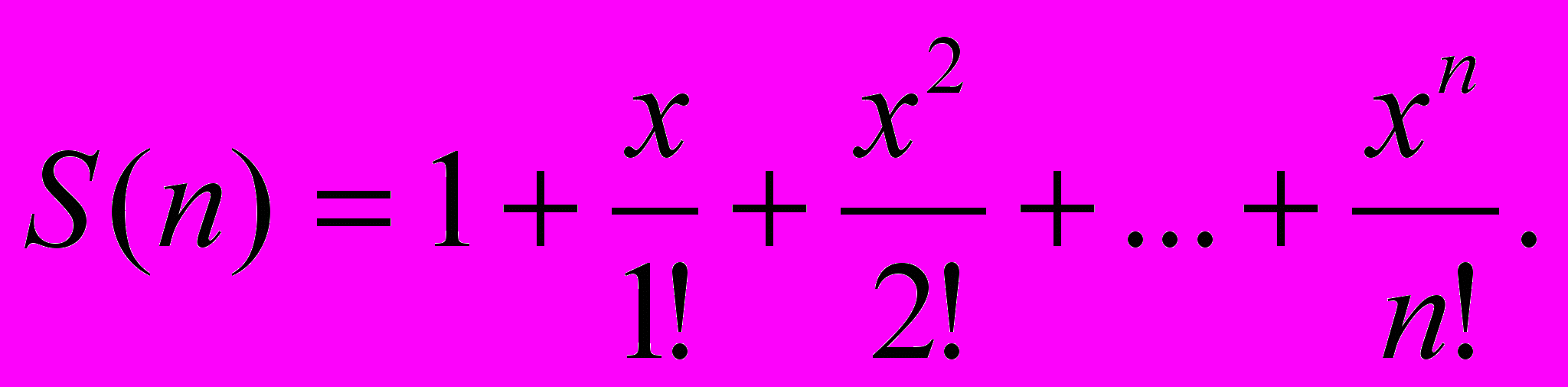Файл "LNN3_24.pro".

7-9 варіанти. 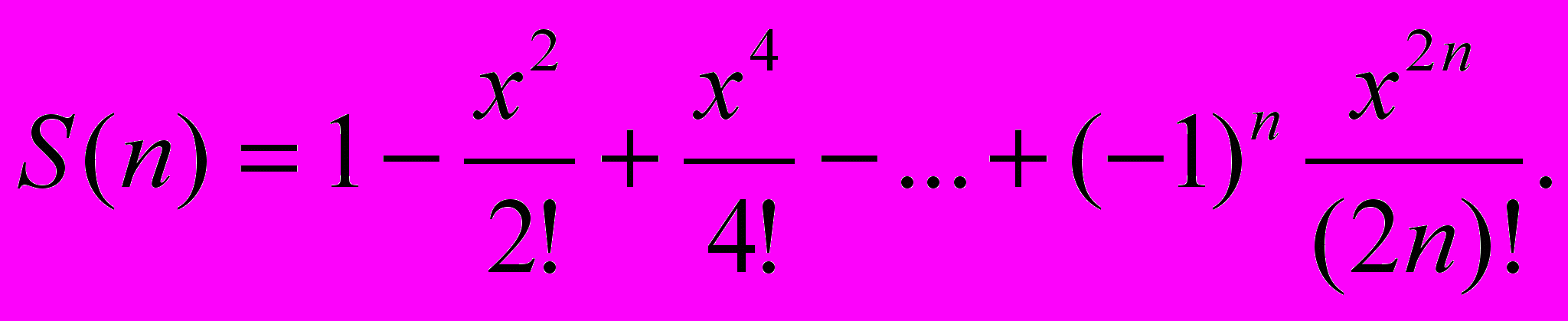Файл "LNN3_27.pro".

10-13 варіанти. 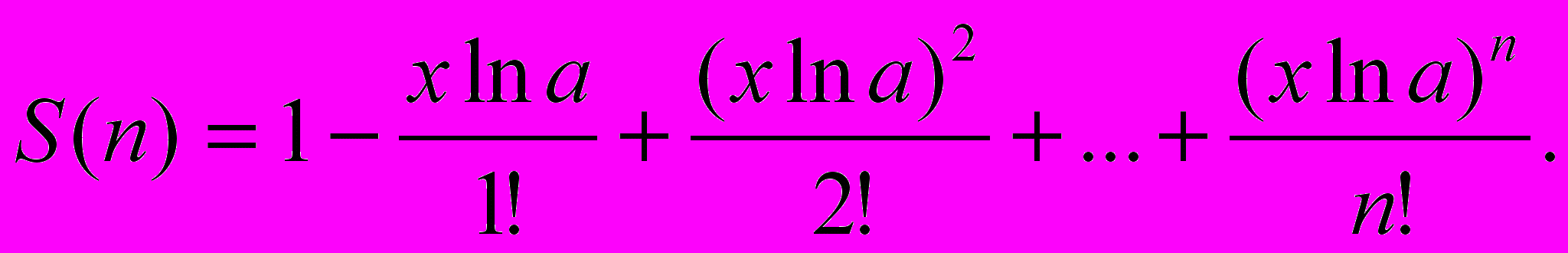Файл "LNN3_20.pro".
Вимоги до захисту лабораторної роботи.

Звіт виконаної роботи повинен містити назву теми, текст програм, текст запитів мовою ПРОЛОГ та відповіді для завдань І го, ІІ-го рівнів. Для рекурсії, використаної у програмах, необхідно вміти описувати природною мовою граничну умову та рекурсивне правило.
Лабораторна робота №4

Тема “Використання списків на ТУРБО-ПРОЛОЗІ”.

Мета: Закріпити поняття про списки. Одержати уміння та навички щодо використання процедур для роботи зі списками; використання процедур для роботи зі списками при розв’язуванні задач.
Теоретична частина: завдання та контрольні питання.

І рівень
  1. Дати означення списку як бінарної структури.
  2. Як рекурсивно означається список? Приклади списків.
  3. Які процедури найчастіше використовуються для роботи зі списками?
  4. Описати процедуру встановлення членства у списку.

ІІ рівень
  1. Описати процедуру об'єднання двох списків.
  2. Описати процедуру визначення довжини списку.
  3. Пояснити роботу предикату findall. Навести приклад.
Практична частина.

І рівень.

1-13 варіанти.

Скласти програму, що дозволяє у списку цілих чисел:
  • знайти максимальний елемент;
  • відшукати мінімальний елемент;
  • знайти кількість нульових елементів;
  • порахувати кількість додатних елементів;
  • впорядкувати елементи списку за зростанням.

Записати програму у файл "LNN4_1.pro", де NN – номер варіанту користувача. Сформулювати запити та протестувати програму.

ІІ рівень.

Є інформація про ділянки доріг певного регіону, що сполучають міста між собою. Ця інформація подана у вигляді таблиці:

Таблиця Б.2.

Дані про ділянки доріг регіону

№

ділянки
Міста, які між собою сполучає ділянка
Відстань між містами

1-ше місто
2-ге місто



Бердичів
Чуднiв
40


Бердичів
Житомир
45


Житомир
Чуднiв
55


Житомир
Червоноармiйськ
40


Житомир
Черняхiв
26


Житомир
Коростишiв
26


Коростишiв
Черняхiв
26


Коростишiв
Кочерiв
20


Кочерiв
Радомишль
20


Червоноармiйськ
Новоград
42


Червоноармiйськ
Черняхiв
30


Черняхiв
Коростень
91


Черняхiв
Потiєвка
29


Радомишль
Потiєвка
24


Радомишль
Малин
32


Потiєвка
Малин
38

Скласти програму, що містить факти "ділянка/4" на основі наведених даних. Використовуючи стандартний предикат findall/3, та підключивши директивою include текст програми І-го рівня, забезпечити виконання процедури (вказана у варіанті). Програму зберегти у файлі (ім'я файлу вказане у варіанті). Протестувати програму.

1-3 варіанти. Процедура: відшукати номер найкоротшої ділянки. Файл: "LNN4_21.pro".

4-6 варіанти. Процедура: відшукати міста, які зв’язані ділянкою найбільшої довжини. Файл: "LNN4_24.pro".

7-9 варіанти. Процедура: відшукати номера ділянок, які мають довжину, меншу за середнє арифметичне довжини всіх ділянок. Файл: "LNN4_27.pro".

10-13 варіанти. Процедура: Для кожної з тих ділянок, довжини яких перевищують середнє арифметичне довжини всіх ділянок, відшукати назву другого міста з пари міст. Файл: "LNN4_20.pro".