Зміст вступ 5
| Вид материала | Документы |
| § 7.3 Функції Юрко: Ця монета грецька і викарбувана в V столітті. Де і в якому столітті виготовлено монету. |
- Зміст, 429.02kb.
- Зміст, 329.83kb.
- Зміст вступ, 361.97kb.
- Зміст, 242.29kb.
- Зміст, 384.58kb.
- Зміст, 410.71kb.
- Зміст вступ, 388.95kb.
- Зміст перелік скорочень, 569.12kb.
- Зміст вступ, 540.64kb.
- Зміст Вступ, 574.44kb.
§ 7.3 Функції
Задача 149 Юрко, Сашко та Михайло знайшли в землі старовинну монету. Коли вони її відчистили від землі, то кожен з них висловив два припущення:
Юрко: Ця монета грецька і викарбувана в V столітті.
Сашко: Ця монета фінікійська і викарбувана в ІІІ столітті.
Михайло: Ця монета не грецька і викарбувана в ІV столітті.
Вчитель історії, який захоплювався нумізматикою, сказав дітям, що кожен з них був правий тільки в одному з двох припущень.
Де і в якому столітті виготовлено монету.
Розв’язання: Для розв’язку задачі згадаємо логічні операції, які ми розглядали раніше. З розглянутих операцій для розв’язку даної задані нам будуть потрібні операції not, and і or. Запишемо висловлення хлопчиків при допомозі цих операцій, ввівши попередньо наступні позначення:
А = {монета грецька},
B = {монета фінікійська},
C = {монету викарбувано в ІІІ столітті},
D = {монету викарбувано в ІV столітті },
E = {монету викарбувано в V столітті }.
Крім того використаємо для зменшення кількості записів такі позначення логічних операцій, які прийнято в алгебрі логіки, а саме:
- not (A) Û

- A and B Û A&B
- A or B Û AÚ B
Використовуючи домовленості, запишемо висловлювання юних нумізматів на мові алгебри логіки:
A&E – слова Юрка,
В &С – слова Сашка,
 Ú D – слова Михайла.
Ú D – слова Михайла.Зі слів вчителя історії випливає, що кожне з цих висловлень хибне, так як кожен з хлопчиків вірно висловив лише половину свого висловлення. Що це значить? Припустимо, що Юрко вірно вказав, що монета грецька (А = 1), але помилився в часі її виготовлення (Е = 0). Якщо ж він не правий в тому, що монета грецька (А = 0), то вірно вказав час виготовлення (Е = 1). Звідси випливає, що
А &
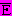 Ú
Ú  & Е = 1.
& Е = 1.Проводячи аналогічні міркування для висловлень Сашка та Михайла, отримаємо ще два істинних складних висловлення:
В &
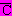 Ú
Ú  & C = 1
& C = 1 &
& 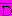 Ú A & D = 1.
Ú A & D = 1.Якщо ж ці висловлювання логічно перемножити, то отримаємо істинне складне висловлення:
(А &
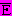 Ú
Ú  & Е) & (В &
& Е) & (В & 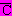 Ú
Ú  & C) & (
& C) & ( &
& 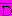 Ú A & D) = 1
Ú A & D) = 1Розкриваємо дужки, тобто спрощуємо отриманий складний вираз:
А &
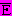 & B &
& B &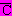 &
&  &
&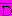 Ú A &
Ú A & 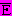 & B &
& B &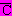 & A & D Ú
& A & D ÚА &
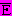 &
& & C &
& C &  &
&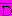 Ú A &
Ú A & 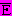 &
& & C & A & D Ú
& C & A & D Ú & E & B &
& E & B &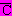 &
&  &
&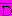 Ú
Ú  & E & B &
& E & B &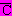 & A & D Ú
& A & D Ú & E &
& E &  &C &
&C &  &
&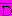 Ú
Ú  & E & B & C & A & D = 1.
& E & B & C & A & D = 1.Так як А &
 = 0 (монета не може бути одночасно і грецькою і не грецькою), то будуть рівні нулю (будуть хибними) і вирази:
= 0 (монета не може бути одночасно і грецькою і не грецькою), то будуть рівні нулю (будуть хибними) і вирази:А &
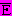 & B &
& B &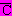 &
&  &
&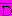 = 0
= 0А &
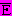 &
& & C &
& C &  &
&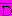 = 0
= 0 & E & B &
& E & B &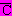 & A & D = 0
& A & D = 0 & E & B & C & A & D = 0
& E & B & C & A & D = 0Крім того, з умови випливає, що:
так як A & B = 0, то A &
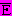 & B &
& B &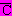 & A & D = 0,
& A & D = 0, C & D = 0, то A &
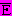 &
& & C & A & D = 0,
& C & A & D = 0,E & C = 0, то
 & E &
& E &  &C &
&C &  &
&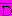 = 0.
= 0.(З яких даних умови це випливає?)
Тому залишається єдина відповідь:
 & E & B &
& E & B &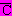 &
&  &
&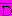 = 1, тобто істинними є висловлення В і Е.
= 1, тобто істинними є висловлення В і Е.Програмна реалізація даного розв’язку з виведенням станів всіх логічних змінних і відповідних повідомлень приведена нижче. Крім того під час виконання дана програма будує в пам’яті таблицю істинності для отриманого висловлення. Рекомендуємо Вам модифікувати дану програму для отримання значень таблиці істинності при всіх значеннях змінних.
program logic1;
uses crt;
const a1 = ‘ Монета грецька. ’;
b1 = ‘ Монета фiнiкiйська. ’;
c1 = ‘ Монету викарбувано в III столiттi. ’;
d1 = ‘ Монету викарбувано в IV столiттi. ’;
e1 = ‘ Монету викарбувано в V столiттi. ’;
var
a,b,c,d,e : boolean;
function answer: boolean;
begin
answer := (not (a)) and (e) and (b) and (not(c)) and (not a) and (not d);
end;
begin
clrscr;
for a := false to true do
for b := false to true do
for c := false to true do
for d := false to true do
for e := false to true do
begin
if answer = true then
begin
writeln(a,‘ ’,b,‘ ’,c,‘ ’,d,‘ ’,e,‘ ’,answer);
if a = true then writeln(a1);
if b = true then writeln(b1);
if c = true then writeln(c1);
if d = true then writeln(d1);
if e = true then writeln(e1);
end;
end;
writeln;
readln;
end.
Перед тим, як перейти до наступної задачі, спробуйте задати функцію answer таким чином, щоб в ній не було готового результату, а були лише дані, що отримуються на підставі аналізу умови задачі.
Розглянемо ще одну задачу такого типу. Вона буде цікавою ще й тим, що ми введемо нову логічну операцію, яка в мові Паскаль не визначена.
Задача 150 Повернувшись додому, комісар Мегре подзвонив на набережну Орфевр.
– Говорить Мегре. Є новини?
– Так, шеф. Надійшли повідомлення від інспекторів. Торранс встано-вив, що якщо Франсуа був напідпитку, то або Етьєн вбивця, або Франсуа каже неправду. Жусьє вважає, що або Етьєн вбивця, або Франсуа не був напідпитку і вбивство відбулось вночі. Інспектор Люка просив передати вам, що якщо вбивство відбулось вночі, то або Етьєн вбивця, або Франсуа каже неправду. Потім подзвонила...
– Гаразд. Дякую. Цього достатньо. – комісар поклав слухавку. Він знав, що тверезий Франсуа ніколи не каже неправду. Тепер він знав все.
Розв’язання: Задачі такого типу є досить цікавими, але рідко розглядаються в шкільному курсі інформатики. Для того, щоб постаратись зацікавити вас алгеброю логіки, при розв’язуванні даної задачі введемо ще одну логічну операцію, яку не реалізовано в мові Паскаль – imp (implementation).
Прості висловлення записані, як і в попередній задачі, у вигляді констант.
program logic2;
uses crt;
const a1 = ' Франсуа був не тверезим. ';
a2 = ' Етьен - вбивця. ';
a3 = ' Франсуа каже неправду. ';
a4 = ' Вбивство вiдбулось вночi. ';
var
a,b,c,d,m : boolean;
Операція imp призначена для реалізації наступної логічної операції над двома логічними змінними a,b: a imp b = false тоді і тільки тоді, коли a=true і b=false, у всіх інших випадках a imp b = true. В застосуванні до умови нашої задачі це звучить так: якщо Франсуа був напідпитку, то або Етьєн вбивця, або Франсуа каже неправду і записується на мові алгебри логіки так:
А Þ (В Ú С) = 1
Зверніть увагу, що ми примінили дану операцію до трьох змінних, об’єднавши дві з них у складне висловлення ( (В Ú С) = 1).
Тепер спробуйте самостійно записати на мові алгебри логіки умову задачі, якщо у вас виникнуть труднощі, то розберіться з функцією answer, в якій і записано повністю умову задачі, без жодних спрощень складних логічних виразів. Зверніть при аналізі розв’язку увагу саме на той факт, що використавши нову логічну операцію ми позбавились від необхідності виконувати логічні дії самостійно.
function imp(a,b:boolean):boolean;
begin
if (a=true) and (b=false) then imp:=false
else imp := true;
end;
function answer : boolean;
begin
m := b or c;
answer := ( (imp(a,m)) and (b or (not(a) and d)) and (imp(d,m)))
and (not (a) and (not (c)));
end;
begin
clrscr;
for a := false to true do
for b := false to true do
for c := false to true do
for d := false to true do
if answer = true then
begin
writeln(a,' ',b,' ',c,' ',d,' ',f);
if a = true then writeln(a1);
if b = true then writeln(a2);
if c = true then writeln(a3);
if d = true then writeln(a4);
end;
writeln;
readln;
end.
