Вопросы к вступительному экзамену в магистратуру для специальности
| Вид материала | Документы |
СодержаниеТеория вероятностей и математическая статистика |
- Экзаменационные вопросы к вступительному экзамену в магистратуру по программе «Менеджмент», 13.96kb.
- Программа подготовки к вступительному экзамену в магистратуру по направлению «Филология», 422.99kb.
- Творчество Михаила Пселла рассказ, 12.56kb.
- Программа вступительного экзамена в магистратуру по направлению, 321.1kb.
- Программа вступительного экзамена в магистратуру по направлению, 376.66kb.
- Планирование: сущность, виды, процесс. Организация как функция менеджмента. Централизация, 26.43kb.
- Программа вступительного экзамена в магистратуру по направлению, 664.35kb.
- Программа вступительного экзамена в аспирантуру по специальности 09. 00. 08 «философия, 272.94kb.
- Билеты к вступительному экзамену в магистратуру по специальности 071900 Билет, 55.17kb.
- Программа вступительного экзамена в магистратуру по направлению, 444.52kb.
Вопросы к вступительному экзамену в магистратуру для специальности
«6N0601-Математика»
Математический анализ
- Целая степень действительного числа и действительная степень положительного числа. Логарифм. Теорема о существовании логарифма. Свойства логарифма (точные формулировки, без доказательства).
- Полнота: существование предела монотонной последовательности. Определение числа е.
- Подпоследовательности и частичные пределы. Полнота: теорема Больцано - Вейерштрасса.
- Полнота: критерий Коши о сходимости последовательностей. Комментарии.
- Верхний и нижний пределы последовательности. Полнота: основная теорема о существовании наибольшего и наименьшего частичных пределов последовательности.
- О строении произвольной действительнозначной функции в окрестности каждой точки.
- Линейная функция. Дифференцирование в точке как локальная линеаризация. Дифференциал. Геометрическая интерпретация дифференциала.
- Формула Тейлора для многочленов. Формула Тейлора с остаточным членом в форме Шлемильха и Роша.
- Интеграл Римана. Классы интегрируемых по Риману функций: класс непрерывных и класс монотонных функций.
- Линейная числовая функция многих переменных и ее общий вид. Определение дифференцируемости функций многих переменных в точке. Дифференциал и частные производные. Достаточное условие дифференцируемости функции в точке.
- Определение неявной функции (двумерный случай). Существование и непрерывность неявной функции.
- Дифференцируемость неявной функции (двумерный случай). Вычисление производных неявных функций.
- Определение условного экстремума. Сведение задачи исследования функции на условный экстремум к исследованию на экстремум локальный. Необходимое условие условного экстремума. Метод множителей Лагранжа.
- Интегральный критерий сходимости ряда с неотрицательными членами. Следствия для рядов
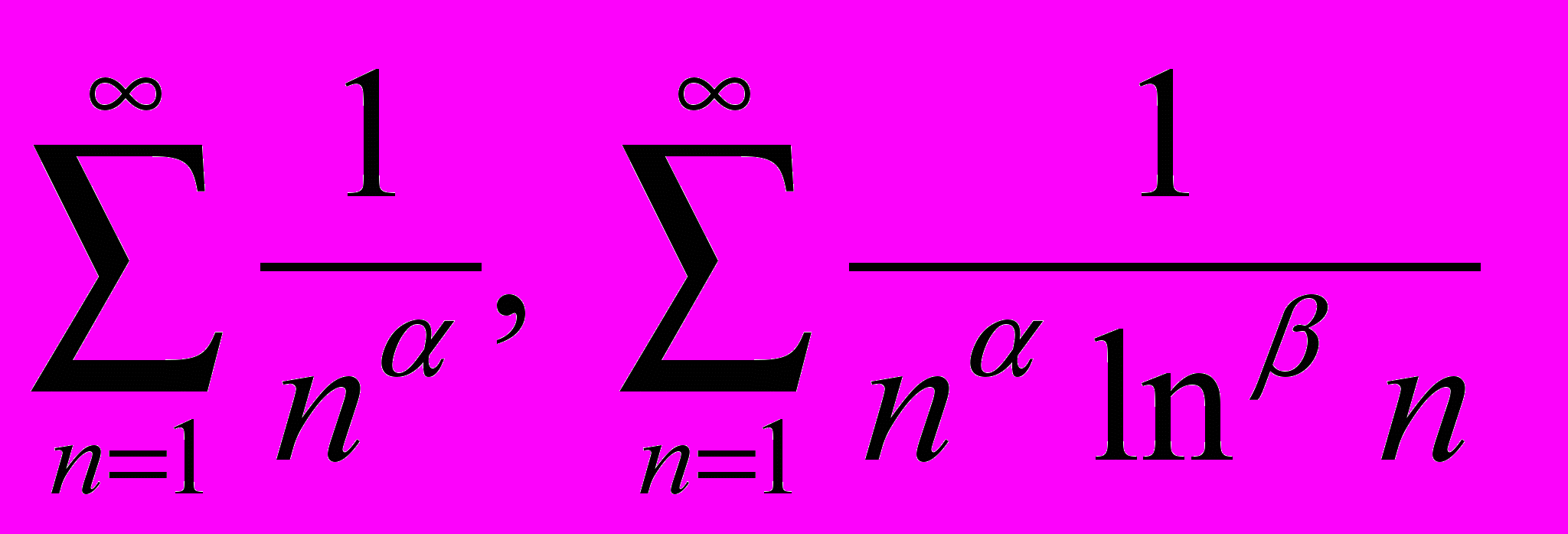 .
.
- Определение абсолютно сходящегося ряда и теорема о его сходимости. Произведение рядов по Коши. Теорема Мертенса.
- Перестановки рядов. Перестановки абсолютно сходящегося ряда. Теорема Римана - перестановки неабсолютно сходящегося ряда.
- Равномерная сходимость и непрерывность функциональных рядов. Равномерная сходимость и интегрирование функциональных рядов.
- Степенные ряды. Формула Коши-Адамара. Структура множества сходимости степенного ряда. Равномерная сходимость степенного ряда, непрерывность суммы.
- Критерий Лебега интегрируемости функции по Риману.
- Криволинейный интеграл первого рода как обобщение одномерного интеграла Римана: определение, достаточные условия существования.
- Интегрирование дифференциальной формы – криволинейный интеграл второго рода вдоль непрерывно дифференцируемой кривой: определения, достаточные условия существования, зависимость от направления обхода кривой, линейное свойство, аддитивность.
- Формула Грина. Аддитивное свойство формулы Грина.
- Критерий Коши сходимости несобственного интеграла. Абсолютная сходимость несобственного интеграла. Примеры: из сходимости интеграла от ½¦(x)½ не следует существование интеграла от ¦(x); сходящийся, но не абсолютно сходящийся интеграл.
- Равномерная сходимость интеграла, зависящего от параметра: определение, непрерывность и интегрирование по ограниченному промежутку.
- Ряд Фурье по ортогональной и тригонометрической системам. Ортогональный ряд и ряд Фурье. Полиномы по ортогональной системе. Минимальное свойство частичных сумм ряда Фурье. Неравенство Бесселя. Достаточное условие сходимости тригонометрического ряда Фурье в точке разрыва функции.
- Интегральный признак Дини сходимости в точке тригонометрического ряда. Сходимость ряда Фурье функции с односторонними производными в точке, непрерывно дифференцируемой функции, функции из классов Гельдера.
- Счетные множества. Счетные множества как наименьшие бесконечные множества. Определение бесконечного множества по Р. Дедекинду. Счетность не более чем счетного объединения счетных множеств.
- Несчетность сегмента [0, 1]. Определение множества мощности континуума. Мощность не более чем счетного объединения множеств мощности континуума.
- Сравнение мощностей. Теорема Кантора-Бернштейна. Существование множества мощности большей, чем мощность любого данного множества.
- Внешняя мера на R1, монотонность и счетная полуаддитивность внешней меры. Теорема об аппроксимации по внешней мере.
- Определение Каратеодори меры Лебега. Структура измеримых по Лебегу числовых множеств.
- Измеримые функции. Измеримость непрерывной функции. Применение арифметических действий к измеримым функциям сохраняет измеримость.
- Измеримость функции, предельной для последовательности измеримых функций, сходящейся всюду и почти всюду.
- Сходимость по мере сходящейся почти всюду последовательности измеримых функций (теорема Лебега).
- Теорема Н.Н. Лузина о структуре измеримых функций.
- Интегрируемость по Лебегу измеримой и ограниченной функции. Взаимоотношения между интегралами Римана и Лебега.
- Теорема Лебега о предельном переходе под знаком интеграла.
- Абсолютная непрерывность интеграла Лебега.
- Теорема Лебега о восстановлении абсолютно непрерывной функции по ее производной.
- Дифференцируемость в смысле R2 и в смысле С. Их связь: условия Коши – Римана. Производная и ее связь с дифференцируемостью. Геометрический смысл модуля и аргумента производной.
- Интегральная формула Коши (значения в области G голоморфной в
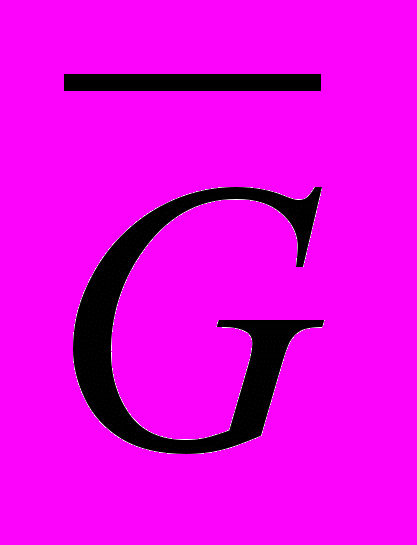 функции полностью определяются её значениями на границе
функции полностью определяются её значениями на границе 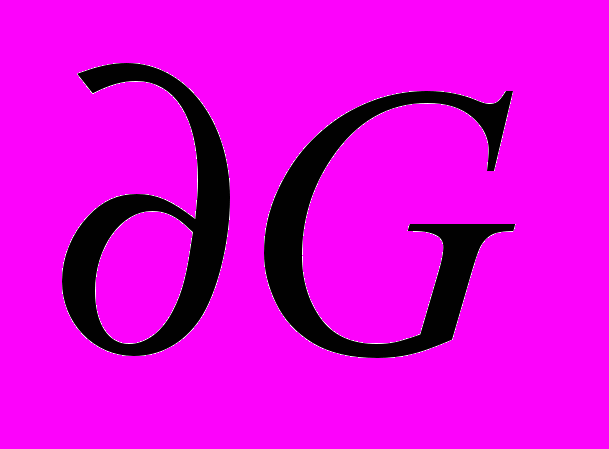 ).
).
- Теорема о представлении в окрестности каждой точки области своего определения голоморфной функции рядом Тейлора. Неравенство Коши. Теорема Лиувилля.
- Теорема о голоморфности суммы степенного ряда в своем круге сходимости. Бесконечная дифференцируемость голоморфных функций. Теорема Морера.
- Ряды Лорана, область сходимости. Теорема о разложении голоморфных в кольце функций в ряд Лорана. Единственность разложения.
- Изолированные особые точки голоморфных функций. Классификация изолированных особых точек на основе разложения функций в ряд Лорана.
- Выделение ветвей. Теорема о монодромии. Теорема Пуанкаре–Вольтерра. Элементарные функции: корень, логарифм, обратные тригонометрические функции, общая степенная функция, общая показательная функция.
- Римановы поверхности элементарных функций. Изолированные особые точки аналитических функций. Принцип аргумента. Теорема Руше.
Теория вероятностей и математическая статистика
- Теория вероятностей как аксиоматизируемая математическая дисциплина. Предмет теории вероятностей. Вероятностное пространство (, А, P) как математическая модель испытания. Аксиомы А.Н.Колмогорова.
- Теоретико-вероятностная (статистическая) независимость (независимость функции от чего-либо; независимость условной вероятности Р(А|В) от В, симметричность понятия независимости) и зависимость двух событий. Пример Бернштейна.
- Математическая модель, описывающая "n испытаний - независимых и повторяющихся при неизменных условиях". Важнейшие примеры: схема Бернулли и полиномиальная схема.
- Предельные теоремы (локальная и интегральная Муавра-Лапласа) для схемы Бернулли. Центральная предельная теорема.
- Математическое ожидание и дисперсия дискретной случайной величины. Математическое ожидание и дисперсия непрерывно распределенной случайной величины. Свойства математического ожидания и дисперсии.
- Теорема Чебышева. Следствия: теорема Бернулли. Закон больших чисел в форме Чебышева.
- Вероятностно-статистическая модель. Оценка вероятности "успеха" в схеме Бернулли: несмещенность, состоятельность. Эффективная оценка вероятности "успеха" в схеме Бернулли, информация Фишера, неравенство Рао-Крамера.
- Построение доверительного интервала для вероятности "успеха" в схеме Бернулли. Проверка статистических гипотез для вероятности "успеха" в схеме Бернулли.
- Оценка неизвестного параметра. Несмещенные и состоятельные оценки математического ожидания:
 n () и дисперсии -
n () и дисперсии - 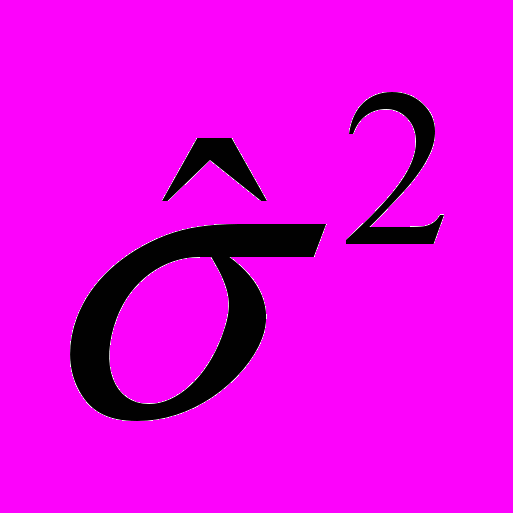 n().
n().
- Выбор из двух гипотез: статистический критерий, критическое множество, вероятности ошибок, уровень значимости критерия, наиболее мощный критерий. Критерий Пирсона (для проверки гипотезы о виде распределения).
Литература
- Г.И. Фихтенгольц. Курс дифференциального и интегрального исчисления. т. I, II, III, М.: Наука, 1969.
- У.Рудин. Основы математического анализа. М.: Мир, 1976.
- В.А.Ильин, В.А.Садовничий, Бл.Х.Сендов. Математический анализ. М.: 1979.
- Г.И.Архипов, В.А.Садовничий, В.Н.Чубариков. Лекции по математическому анализу. М.: Изд-во механико-математического факультета Московского университета, часть 1 - 1995; часть 2 - 1997; часть 3 - 1997; часть 4 - 1997.
- Н.Темiрғалиев. Математикалық анализ. Алматы: т.I, "Мектеп",1987; т.II, "Ана тiлi", 1991; т.III, "Бiлiм", 1997.
- Колмогоров А. Н., Фомин С. В. Элементы теории функции и функционального анализа. М.: Наука, 1972.
- Лузин Н.Н. Теория функций действительного переменного. М.: Учпедгиз, 1940.
- Натансон И. П. Теория функций вещественной переменной. М.: Наука, 1974.
- Титчмарш Е. Теория функций. М.: ГИТЛЛ, 1951.
- Ульянов П.Л., Бахвалов А.Н., Дьяченко М.И., Казарян К.С., Сифуэнтес П. Действительный анализ в задачах. М.: ФИЗМАТЛИТ, 2005.
- И.П.Привалов "Введение в теорию функций комплексного переменного".М.:Наука,1977.
- Б.В.Шабат "Введение в комплексный анализ" .М.:Наука,1985
- А.И.Маркушевич "Краткий курс теории аналитических функций".М.:Наука,1978.
- М.А.Лаврентьев, Б.В.Шабат "Методы теории функций комплексного переменного".М.:Наука,1973.
- М.А.Евграфов "Аналитические функции".М.:Наука,1991.
- Ю.В.Сидоров, М.В.Федорюк, М.И.Шабунин "Лекции по теории функций комплексного переменного".М.:Наука,1989.
- Колмогоров А.Н. Основные понятия теории вероятностей. M.:- «Наука», 1974.
- Феллер В. Введение в теорию вероятностей и ее приложения. т.1. M.: «Мир», 1969.
- Лоэв М. Теория вероятностей. M.: «ИЛ», 1962.
- Захаров В.К., Севастьянов Б.А., Чистяков В.П. Теория вероятностей. M.: «Наука», 1983.
- Смирнов Н.В., Дунин-Барковский И.В. Курс теории вероятностей и математической статистики. M.: «Наука», 1969.
- Розанов Ю.А. Теория вероятностей, случайные процессы и математическая статистика. M.: «Наука», 1989.
- Вентцель Е.С. Теория вероятностей. M.: «Наука», 1969.
- Ротарь В.И. Теория вероятностей. M.: «Высшая школа», 1992.
Алгебра и геометрия
- Скалярное и векторное произведение векторов, их свойства и приложения. Выражение скалярного и векторного произведения векторов через координаты векторов.
- Смешанное произведение векторов. Свойства и приложения. Необходимое и достаточное условие компланарности трех векторов.
- Взаимное расположение 2-х прямых в пространстве. Теорема о необходимых и достаточных условиях параллельности и перпендикулярности двух прямых.
- Определение векторного пространства. Основные свойства и примеры. Теорема о необходимом и достаточном условии линейной зависимости системы векторов.
- Понятие линейного преобразования векторного пространства. Матрица линейного преобразования. Матрица перехода от одного базиса к другому.
- Классификация кривых 2-го порядка.
- Системы линейных алгебраических уравнений. Теорема Кронекера-Капелли.
- Определители n-го порядка, их свойства. Теорема о разложении определителя по строке или столбцу.
- Правило Крамера для решения систем линейных алгебраических уравнений.
- Матрицы, действия над матрицами. Свойства операций над матрицами. Теорема о вычислении обратной матрицы.
- Построение поля комплексных чисел. Алгебраическая и тригонометрическая формы комплексных чисел. Операции над комплексными числами.
- Извлечение корней из комплексных чисел. Формула Муавра.
- Кольцо многочленов от одной переменной. Кратные корни многочлена.
- Сравнения и их основные свойства. Теорема Эйлера и Ферма.
- Кольцо классов вычетов по данному модулю.
Функциональный анализ
- Изоморфизм между всеми конечномерными пространствами данного числа измерений.
- Нормированные пространства Lp(а,в) (1р<). Неравенства Гельдера и Минковского.
- Гильбертовы (унитарные, евклидовы) пространства Н. Норма в Н. Пространства l2 и L2(а, b). Неравенство Шварца. Непрерывность скалярного произведения.
- Принцип вложенных шаров.
- Принцип сжимающих отображений.
- Теорема Бэра-Хаусдорфа о категориях. Множества меры 1 и первой категории, меры 0 и второй категории на [0,1].
- Теорема Арцела (критерий предкомпактности множества в С[а.b]).
- 0бщий вид линейных функционалов в С[0,1] [1, стр.182-185], Lp (0,1),(1
l
Литература
1. Люстерник. Л.А., Соболев В.И. Элементы функционального анализа. M.: Наука, 1965.
2. Садовничий В. А. Теория операторов. M.: изд. МГУ, 1986.
3. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. M.: Наука, 1972.
4. Натансон И. П. Теория функций вещественной переменной. M.: Наука, 1974.
5. Рудин У. Функциональный анализ. M.:Мир, 1975.
6. Иосида К. Функциональный анализ. M.:Мир, 1967.
7. Данфорд Н., Шварц Дж. Т. Линейные операторы (общая теория). M.: ИЛ, 1962.
8. Лузин Н. Н. Теория функции действительного переменного. M.:Учпедгиз,1949.
9. Партасарати К. Введение в теорию вероятностей и теорию меры. M.: Мир, 1952.
10. Темiргалиев Н. Математикалық анализ. Алматы:Ана тiлi, 1991, т. 2.
11. Вайнберг М . М. Функциональный анализ. - Просвещение, 1979.
12. Шилов Г. Е. Математический анализ. Специальный курс. M.:Физматгиз, 1961.
13. Шилов Г. Е. Математический анализ. Второй специальный курс. M.: Физматгиз, 1965.
14. Рисc Ф., Секевальфи-Надь Б. Лекции по Функциональному анализу. 1979.
15. Гелбаум Б., Олмстед Дж. Контрпримеры в анализе. M.: Мир, 1967.
16. Зигмунд А. Тригонометрические ряды. M.: Мир, 1965.
17. Никольский С.М. Курс математического анализа. т.2. M.: Наука, 1973.
Дифференциальные уравнения
- Теорема существования и единственности решения задачи Коши для обыкновенного дифференциального уравнения первого порядка
- Линейные обыкновенные дифференциальные уравнения (ОДУ). Общие свойства
- Однородные ОДУ. Фундаментальная система решений. Вронскиан-формула Лиувилля. Общее решение однородного ОДУ. Построение фундаментальной системы решений.
- Неоднородные линейные обыкновенные дифференциальные уравнения. Общее решение. Метод Лагранжа вариации постоянных.
- Однородная система линейных обыкновенных дифференциальных уравнений. Фундаментальная система решений и фундаментальная матрица-Вронскиан. Формула Лиувилля. Структура общего решения однородной системы ОДУ.
- Постановка краевых задач для линейного обыкновенного дифференциального уравнения второго порядка. Функция Грина и ее явные представления.
Литература.
- Айнс Э.Л. Обыкновенные дифференциальные уравнения М.: Факториал пресс, 2005.
- Матвеев Н.М. Методы интегрирования обыкновенные дифференциальных уравнений СПб.: Лань, 2003.
- Матвеев Н.М. Обыкновенные дифференциальные уравнения СПб.: Лань, 1996.
Заведующий кафедрой
математического анализа,
д.ф.-м.н., проф. Н. Темірғалиев
