Geum.ru

С. А. Вычислительные аспекты проблемы оценки устойчивости систем управления

Вид материалаДокументы
Подобный материал:
Давыдова А.П., Лупин С.А.

Вычислительные аспекты проблемы оценки устойчивости систем управления

Московский государственный институт электронной техники, Москва, e-mail: anastasia_19_88@mail.ru, lupin@miee.ru

Еще 50 лет назад писатели фантасты в своих романах рисовали мир будущего, в котором человек живет в окружении разного рода автоматов, которые призваны делать его жизнь комфортнее. Казалось, что до практической реализации их прогнозов еще очень и очень далеко. Но уже сегодня становятся обыденными не только мобильная связь с поддержкой видео, но и «умные дома» исполняющие малейшие прихоти своих хозяев. Что же позволило за очень короткий период, практически за время жизни одного поколения людей, сделать столь мощный технологический прорыв? Ответ прост – это современные микропроцессорные системы управления. Их вычислительные мощности позволили наделить даже такие простые устройства как микроволновая печь способностью запоминать рецепты приготовления различных блюд, а холодильник – следить за тем, чтобы наш любимый сыр всегда был в запасе. А ведь это только те устройства, с которыми мы соприкасаемся каждый день! Если же мы посмотрим на автоматические системы управления промышленными роботами, поезда метро, в которых нет машиниста, огромные промышленные установки, управляемые одним человеком, то мир из фантастических романов станет для нас гораздо более близким. Успехи в области автоматизации управления окружающим нас миром вещей очевидны, однако остались и очень серьезные нерешенные проблемы.

Одним из наиболее сложных, является вопрос о выборе алгоритма и стратегии управления устройством или системой. Действительно, доверяя жизнь пассажиров поезда метро автоматической системе управления, мы должны быть уверены не только в ее эффективности, но и в устойчивости, т.е. способности выполнять свои функции при всех возможных условиях. Для проверки технически сложных систем традиционно используются натурные испытания в сочетании с моделированием. Казалось бы, ошибок просто не может быть, но крупные техногенные катастрофы показывают, что это далеко не так.

Рассмотрим некоторую обобщенную схему управления (рис. 1). Пусть имеется объект управления (ОУ) и управляющее устройство (УУ), работающее по известному нам алгоритму. Информацию о состоянии окружающей среды УУ получает с помощью конечного числа датчиков 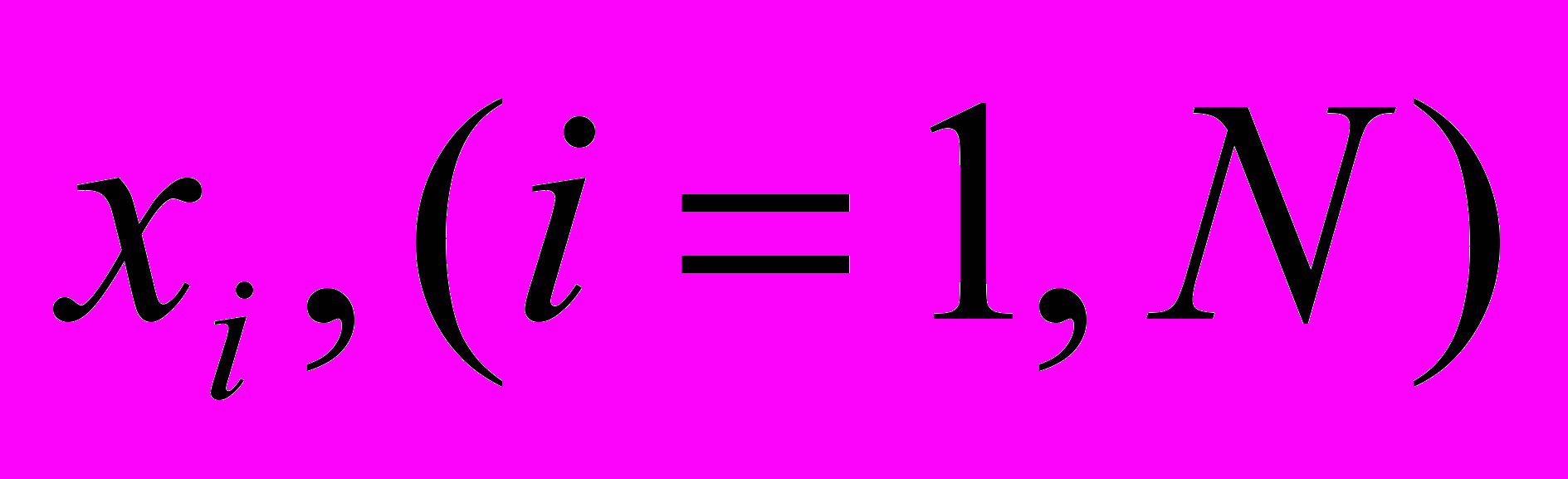. В общем случае, задачей устройства управления является достижение объектом управления состояния, при котором некоторая целевая функция будет равна величине 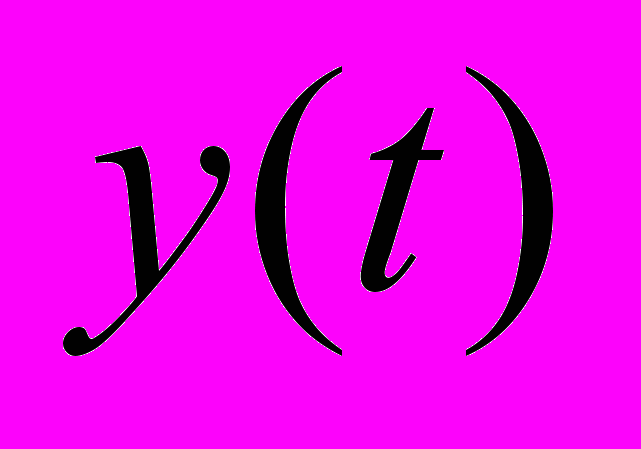[1]. При этом УУ может контролировать текущее значение целевой функции 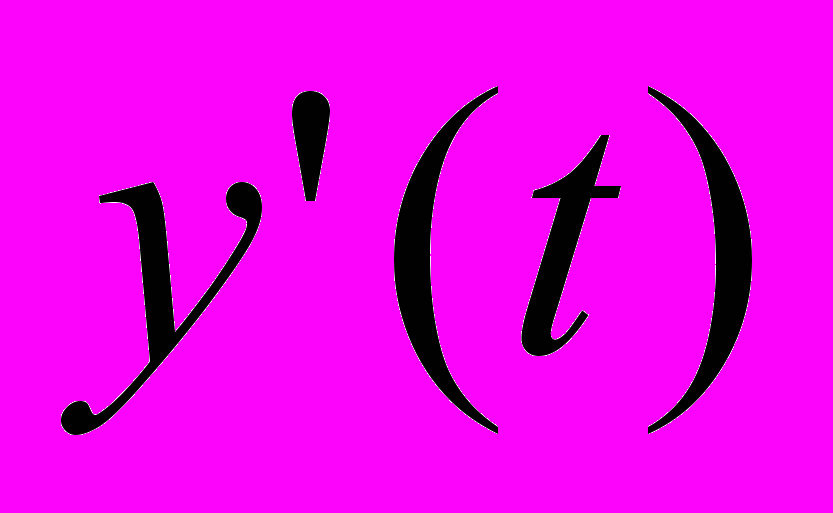и ее отклонение от идеала 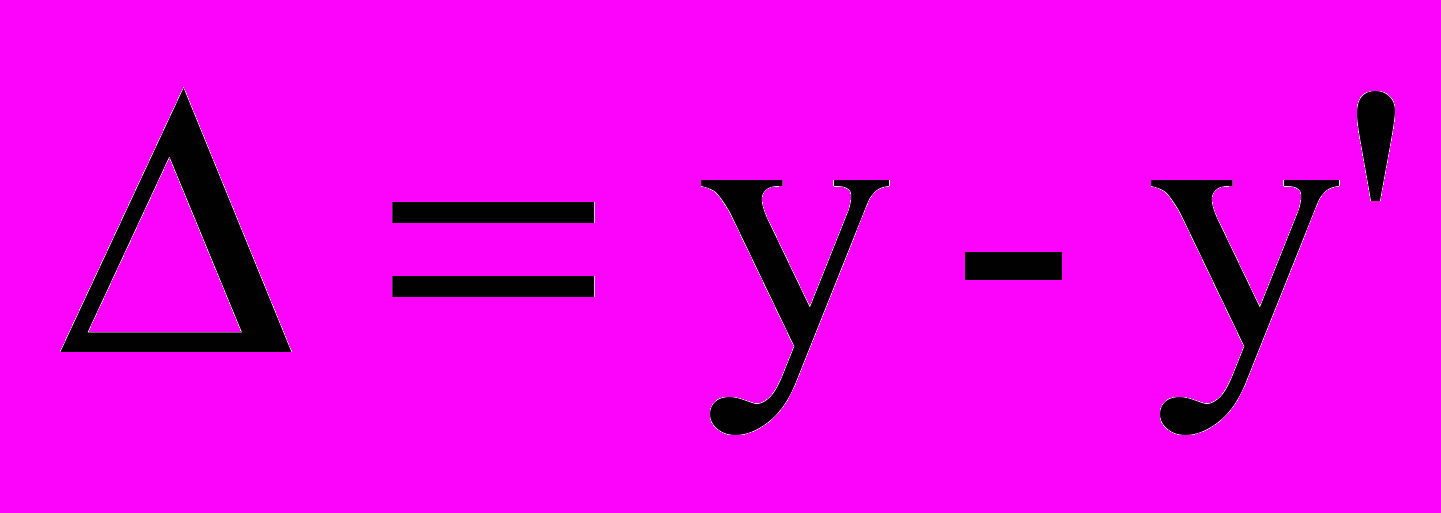. В реальных системах может быть задано несколько целевых и критериальных функций.






Рис.1. Система управления с обратной связью и входными параметрами на входах (получаемыми с датчиков)


Как оценить устойчивость подобной системы управления? Необходимо перебрать все возможные состояния датчиков. Для цифровых систем управления, сигнал на выходе каждого к-разрядного датчика может принимать 2к значений. Тогда возможное число состояний системы составит (2к)N. Задача анализа устойчивости становится вычислительно сложной уже при значениях к=10 и N>3. В реальных системах размерности этих параметров существенно выше. Особенность задачи состоит еще и в том, что подавляющее большинство из (2к)N состояний системы не может быть реализовано на практике, но может стать входной комбинацией сигналов для УУ. При традиционном подходе к проверке систем управления они проверяются только в физически реализуемом диапазоне сигналов датчиков (метод граничных испытаний). При этом предполагается, что показания датчиков корректно отображают состояние внешней среды и системы в целом. Учет неисправности датчиков при оценке устойчивости приведет к факториальному увеличению сложности задачи.

Другая особенность задачи связана с тем, что алгоритм, лежащий в основе работы УУ, использует для выработки управляющего воздействия не всю возможную информацию о состоянии системы. В нашем случае это означает, что есть еще группа из (N-M) датчиков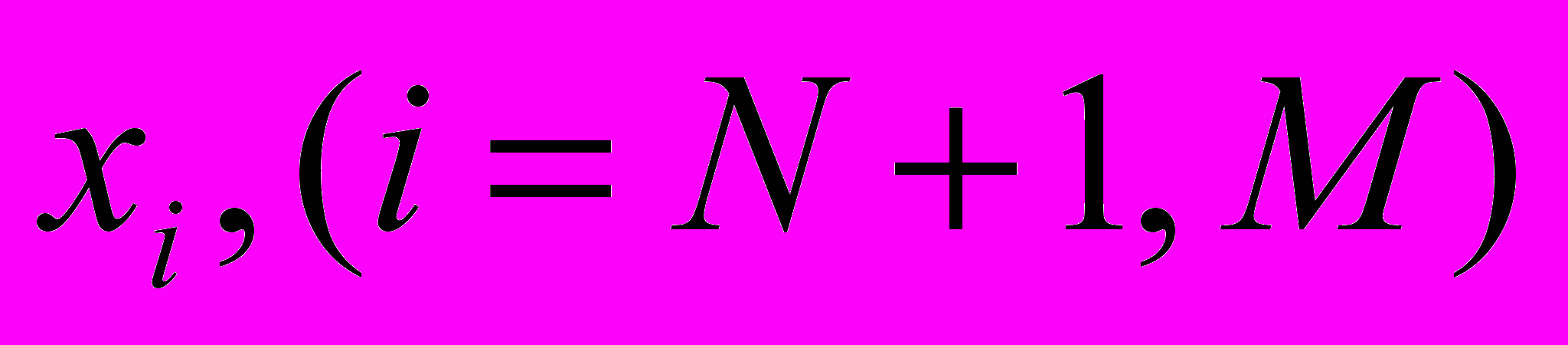, которые не используются УУ. Влияют ли их показания на устойчивость системы управления? Ответ очевиден, конечно, влияют. Можно привести такой пример. Операторы системы управления идентифицируют себя при входе в систему, однако алгоритм управления не учитывает их разный опыт работы, но он во многом определяет устойчивость системы! Как же можно оценивать устойчивость подобных систем? Современные суперкомпьютеры позволяют решать в некотором приближении подобные вычислительно сложные задачи.

В первую десятку суперкомпьютеров, входящих в последнюю редакцию списка TOP-500, входят вычислительные системы, состоящие из сотен тысяч ядер [2]. И уже сейчас, мы ясно понимаем, что находимся на пороге экзофлопной эры высокопроизводительных вычислений, а это значит, что самые мощные суперкомпьютеры мира будут насчитывать десятки миллионов ядер. Подобные вычислители можно использовать и для анализа устойчивости сложных систем. Для этого потребуется создать параллельную реализацию программного кода.

В нашем случае, природа задачи определяет естественный подход к распределению вычислительной нагрузки между ядрами системы - параметрический. Это предполагает репликацию кода и фрагментацию данных (состояний системы). В случае же поиска оптимальной стратегии управления можно говорить о реализации разных стратегий на узлах системы при одинаковых (реплицированных) внешних условиях.

Сведем вышеописанную задачу анализа системы автоматического управления к анализу поведения абстрактных объектов, обладающих определенных набором параметров. На начальном этапе разработки для простоты будем рассматривать взаимодействие двух объектов.

Предлагаемый подход был исследован на примере решения задачи типа «преступник-жертва» с расширенным набором параметров. При этом анализу подвергался фиксированный алгоритм поведения жертвы, а поведение преступника варьировалось [3]. Задачей жертвы является достижение заданной точки пространства, при этом она обладает способностью избегать опасностей на своем пути. Преступник стремится совершить нападение на жертву. Его поведение может отличаться разной степенью агрессивности. Поведение преступника и жертвы не является детерминированным, в модель введены элементы случайности. Каждый объект имеет свою зону обнаружения других сущностей. Объект жертва идет из точки A в точку B по самому кратчайшему пути до тех пор, пока в его зону обнаружения не попадет другой объект. В этом случае он меняет направление движения в зависимости от особенностей своего поведения. Объект преступник беспорядочно перемещается по полю до тех пор, пока не «увидит» жертву, тогда он меняет свое направлении и движется за ней для того чтобы совершить нападение.




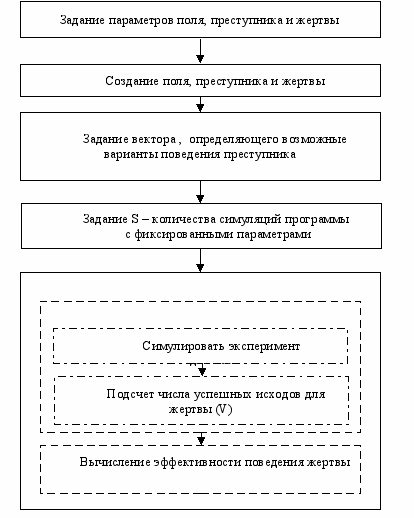
Рис. 2. Структурная схема моделирования


Алгоритм поведения жертвы будем считать эффективным, если он позволяет достичь цели и избежать при этом встречи с преступником и устойчивым, если он эффективен при различных вариантах поведения преступника и внешних условиях.

Структурная схема процесса моделирования приведена на рис. 2.

Программа моделирования реализована на языке программирования C++ на основе паттерна проектирования MVP (Model-View-Presenter), для построения интерфейса была использована библиотека Qt.

Программа позволяет оценить устойчивость алгоритма управления жертвы при вариации поведения преступника. Для этого задаем на отрезке 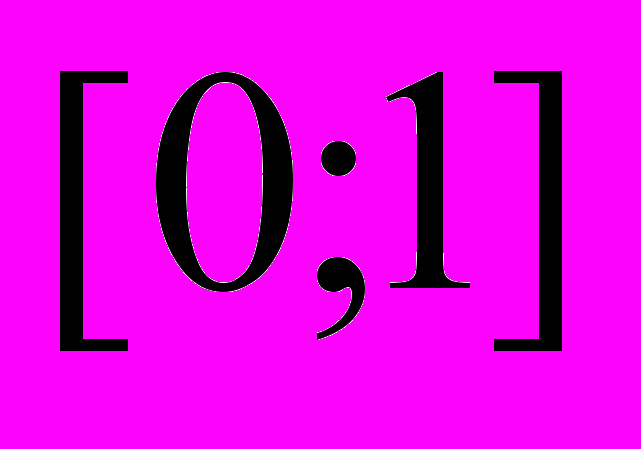некоторый упорядоченный по возрастанию вектор 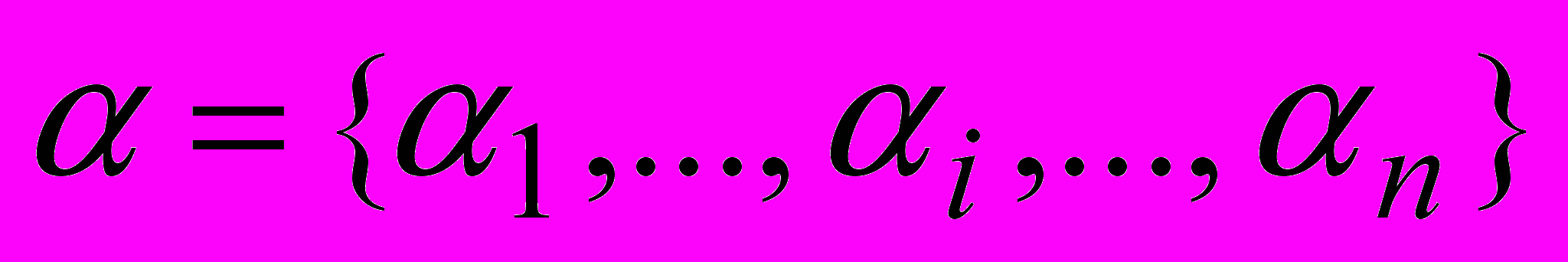, , , 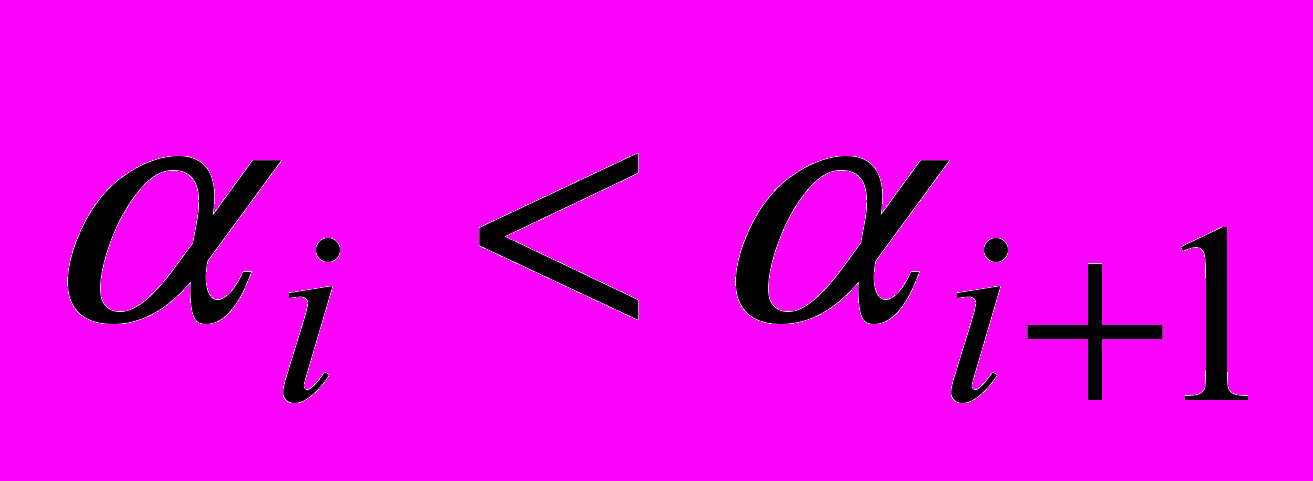который единственным образом определяет поведения объекта преступник. При этом коэффициент характеризует степень его агрессивности. Чем выше значение , тем больше преступник нацелен на уничтожение другого объекта. Далее мы проводим серию из S симуляций с фиксированными параметрами, суммируя при этом для каждого набора вариантов количество удачных для жертвы исходов. На основе полученных данных оцениваем математическое ожидание полученной выборки и вычисляем вероятность достижения жертвой цели или эффективность ее варианта поведения.

Результат работы последовательного варианта программы приведен в таблице 1.
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0



0.93
0.92
0.88
0.87
0.82
0.82
0.75
0.63
0.40
0.30
0.30


Табл. 1. Вероятность достижения жертвой цели при различных стратегиях поведения преступника,

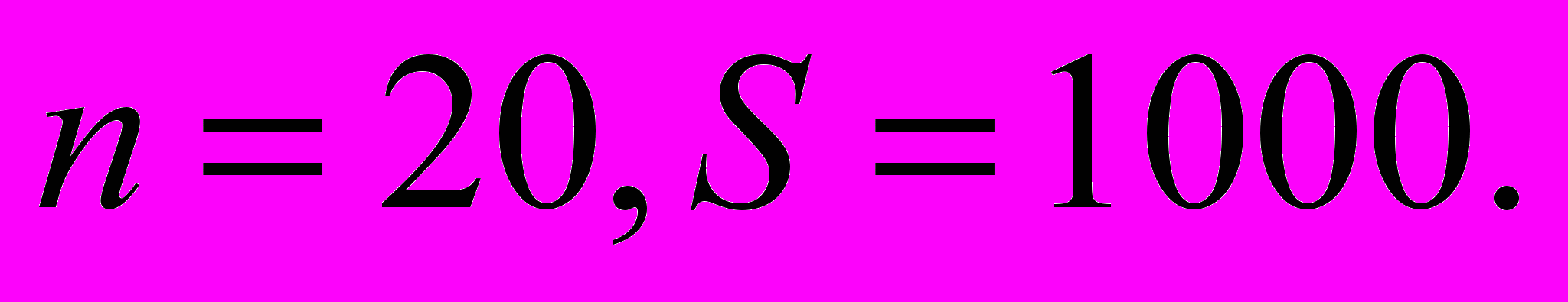
Из полученных результатов видно, что чем агрессивнее поведение объекта преступник, тем ниже вероятность выполнить поставленную задачу у жертвы. Таким образом, при и исследовании устойчивости алгоритма перемещений жертвы на поле только по одному параметру мы получили время вычисления одного элемента из результирующего вектора ,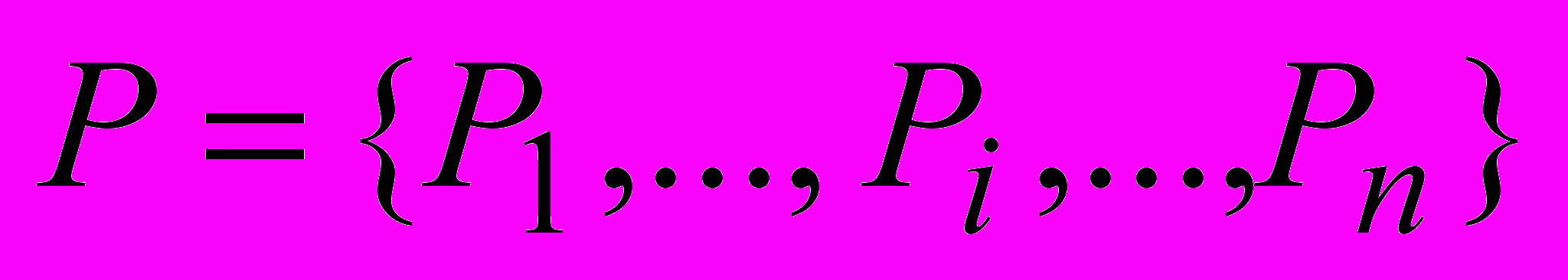

Проведенный эксперимент показал, что исследование систем управления с помощью последовательных алгоритмов занимает достаточно большое время, поэтому задачу необходимо реализовывать на многопроцессорной системе.

  1. Егоров А.И. Основы теории управления - Москва: Физматлит, 2007г.
  2. 0.org/list/2010/06/100
  3. Давыдова А.П. Моделирование устойчивости систем управления. Микроэлектроника и информатика – 2010: 17-я Всероссийская межвузовская научно-техническая конференция студентов и аспирантов, Москва, МИЭТ, 28-30 апреля 2010г.: Тезисы докладов. – М.: МИЭТ, 2010. – с. 196.