Конспект лекций по курсу тмм. Автор: Тарабарин В. Б. 22. 10. 1997г. Лекция 5

Вид материала

Конспект

Подобный материал:

• Конспект лекций по курсу тмм автор: Тарабарин В. Б. Лекция, 154.03kb.
• Конспект лекций по курсу тмм автор: Тарабарин В. Б. 10. 01. 1998г. Лекция, 312.16kb.
• Конспект лекций по курсу «Организация производства», 2034.84kb.
• Конспект лекций по курсу «Организация производства», 2032.47kb.
• Конспект лекций по курсу "Начертательная геометрия и инженерная графика" Кемерово 2002, 786.75kb.
• Конспект лекций по курсу «бизнес-планирование в условиях рынка», 461.46kb.
• Конспект лекций по курсу «Неорганическая и аналитическая химия», 18.21kb.
• Конспект лекций по курсу "Информатика и использование компьютерных технологий в образовании", 1797.24kb.
• Конспект лекций по курсу макроэкономика для студентов заочников факультета бухгалтерского, 2421.87kb.
• 2. Системный подход как метод управления, 2677.2kb.

₃ + m_B1.

Составляем уравнение статических моментов относительно точки А :

m _k1 l_k1 = m_В^*  l_АВ .

Задаемся величиной l_k1 и получаем корректирующую массу

m _k1 = m_В^*  l_АВ / l_k1.

Окончательно величины корректирующих масс для полного уравновешивания кривошипно-ползунного механизма


m _k2 = m _C  l_BC / l_k2 = ( m_С2 + m₃ )  l_BC / l_k2 ;


m _k1 = m_В^*  l_АВ / l_k1= (m₂ + m_k2 + m₃ + m_B1)  l_АВ / l_k1 .


Частичное статическое уравновешивание кривошипно-ползунного механизма.


1. Уравновешивание вертикальной составляющей главного вектора сил инерции.






m_B 2,l₂ 3

1,l₁ B

C,S₃

А S₁ S₂

m_A m_C

r_Sм S_м




m_k1 l_k1 0

Постановка задачи:


Дано: l_AB, l_BC, l_AS1, l_BS2, l_CS3=0,


m₁, m₂, m₃


___________________________


Определить: m_k1


Рис. 5.5


В этом случае необходимо добиться, чтобы центр масс механизма при движении перемещался вдоль направляющей ползуна (для схемы на рис. 5.5 по горизонтали). Для этого достаточно уравновесить только массу m_B . Составляем уравнение статических моментов относительно точки А : m _k1 l_k1 = m_В  l_АВ . Задаемся величиной l_k1 и получаем корректирующую массу m _k1 = m_В  l_АВ / l_k1. Окончательно величина корректирующей массы для уравновешивания вертикальной составляющей главного вектора сил инерции кривошипно-ползунного механизма


m _k1 = m_В  l_АВ / l_k1= (m_В2 + m_B1)  l_АВ / l_k1 .


2. Уравновешивание горизонтальной составляющей главного вектора сил инерции.





m_B 2,l₂ 3

1,l₁ B

C,S₃

А S₁ S₂

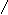
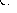m_A r_Sм^** m_C



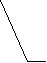
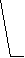
m_k1^* S_м^**

S_k y x 0

l_k1

Постановка задачи:


Дано: l_AB, l_BC, l_AS1, l_BS2,

l_CS3=0, m₁, m₂, m₃

_____________________


Определить: m_k1


Рис. 5.6


В этом случае необходимо добиться, чтобы центр масс механизма при движении перемещался по дуге окружности радиуса r_Sм^** (рис.5.6). Расчет корректирующей массы ведется в два этапа. В начале первой составляющей корректирующей массы m_k1^* уравновешивается масса m_B . Составляется, как и в предыдущем примере, уравнение статических моментов относительно точки А : m _k1^* l_k1 = m_В  l_АВ . Задается величина l_k1 и рассчитывается корректирующая масса m _k1^* = m_В  l_АВ / l_k1= (m_В2 + m_B1)  l_АВ / l_k1 . Затем с помощью второй составляющей корректирующей массы m_k1^**центр массы m_С. перемещается в точку S_м^**. Величина m_k1^** определяется следующим образом: центр шарнира С соединяется прямой с концом отрезка l_k1 точкой S_k . Радиус r_Sм^** проводится параллельно отрезку BС. Тогда

 S_kВС   S_kА S_м^** и x/y =. l_k1 / l_AB .

Статический момент относительно точки S_м ^**:

m_k1^** x = m_C  y, m_k1^** = m_C  y/x = m_C  l_AB / l_k1 .

Радиус-вектор r_Sм^** определяется из подобия треугольников из пропорций

x/ r_Sм^** = ( x + y )/ l_BC , x/( x + y ) = l_k1 / ( l_k1 + l_AB ),

откуда

r_Sм ^** = [ l_k1 / ( l_k1 + l_AB )]  l_BC = const.


Корректирующая масса, обеспечивающая уравновешивание горизонтальной составляющей главного вектора сил инерции кривошипо-ползунного механизма, размещается на первом звене механизма и равна сумме составляющих


m_k1 = m_k1^* + m_k1^** = ( m₂ + m₃ + m_B1 ) l_АВ / l_k1 .


Центр массы механизма при таком уравновешивании расположен в точке S_м, которая движется по дуге радиуса r_Sм


r_Sм = ( m_С2 + m₃ + m_k1^**) r_Sм ^** /( m₁ + m₂ + m₃ + m_k1 ).


(m₁ + m_C2 + m_k1^*)

A

S_м (m₃ + m_C2 +m_k1^**)




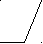r_Sм

r_Sм^** S_м^**


Рис. 5.7

Схема распределения масс в механизме после уравновешивания дана на рис. 5.7.


Балансировка роторов.

1. Общие сведения о балансировке. Ротор, неуравновешенность ротора и ее виды. Задачи балансировки. Ротором ( по гост 19534-74 ) называют звенья механизмов, совершающие вращательное движение и удерживаемые при этом своими несущими поверхностями в опорах. Если масса ротора распределена относительно оси вращения равномерно, то главная центральная ось инерции x-x совпадает с осью вращения и ротор является уравновешенным или идеальным. При несовпадении оси вращения с осью x-x, ротор будет неуравновешенным и в его опорах при вращении возникнут переменные реакции, вызванные действием инерционных сил и моментов ( точнее, движением центра масс с ускорением ).
   

В зависимости от взаимного расположения оси вращения и главной цетральной оси инерции x-x , по ГОСТ 19534-74, различают следующие виды неуравновешенности роторов (рис. 5.8): а - статическую, когда эти оси параллельны; б - моментную, когда оси пересекаются в центре масс ротора S ; в - динамическую, когда оси либо пересекаются вне центра масс, либо не пересекаются, а перекрещиваются в пространстве.





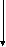
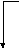
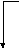а) e б) в) e

x x

М_и




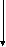
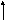x S x S S

x x

F_и F_и


Рис. 5.8

Как отмечено выше, неуравновешенность определяется конструктивными характеристиками ротора или механизма и не зависит от параметров движения. Поэтому при балансировке оперируют не инерционными силами, а дисбалансами. Дисбаланс - мера статической неуравновешенности ротора, векторная величина, равная произведению неуравновешенной массы