Молекулярная физика и основы термодинамики электронный учебник по физике кгту-кхти. Кафедра физики. Поливанов М. А., Старостина И. А., Кондратьева О. И
| Вид материала | Учебник |
- Рабочая программа Молекулярная физика Специальность 010400 физика, направление 510400-физика, 92.73kb.
- Молекулярная физика и термодинамика статистический и термодинамический методы Молекулярная, 12.67kb.
- Учебно-методический комплекс дисциплина «физика» Кафедра общей и экспериментальной, 611.05kb.
- Учебник " Открытая физика 5" (все разделы, от Механики до Физики атомного ядра). Интересен, 252.87kb.
- Программа по физике для 10-11 классов общеобразовательных, 75.87kb.
- Рабочая программа Физика атома и атомных явлений Кафедра общей физики Специальность, 228.56kb.
- Программа дисциплины дпп. Ф. 02 «Основы теоретической физики. Физика атомного ядра, 222.48kb.
- Рекомендация ответить на поставленные вопросы можно с помощью предложенной литературы., 1133.03kb.
- Урок-экскурсия Физика на весенней тропе (Тема "Тепловые явления"), 79.68kb.
- Учебно-методический комплекс по дисциплине Молекулярная физика для специальности 010701, 480.43kb.

Д
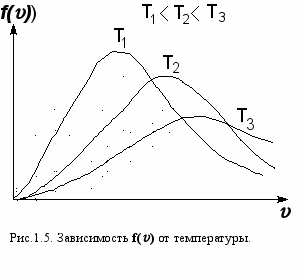 анное выражение - это закон о распределении молекул идеального газа по скоростям. Конкретный вид функции зависит от рода газа, массы его молекул и температуры (рис.1.5). Функция f()=0 при =0 и достигает максимума при некотором значении в, а затем асимптотически стремится к нулю. Кривая несимметрична относительно максимума. Относительное число молекул dN()/N, скорости которых лежат в интервале d и равное f()d, находится как площадь заштрихованной полоски основанием dv и высотой f(), показанной на рис.1.4. Вся площадь, ограниченная кривой f() и осью абсцисс равна единице, потому что, если просуммировать все доли молекул, имеющих всевозможные значения скорости, то получается единица. Как показано на рис.1.5, с ростом температуры кривая распределения смещается вправо, т.е. растет число быстрых молекул, но площадь под кривой остается постоянной, т.к. N = const.
анное выражение - это закон о распределении молекул идеального газа по скоростям. Конкретный вид функции зависит от рода газа, массы его молекул и температуры (рис.1.5). Функция f()=0 при =0 и достигает максимума при некотором значении в, а затем асимптотически стремится к нулю. Кривая несимметрична относительно максимума. Относительное число молекул dN()/N, скорости которых лежат в интервале d и равное f()d, находится как площадь заштрихованной полоски основанием dv и высотой f(), показанной на рис.1.4. Вся площадь, ограниченная кривой f() и осью абсцисс равна единице, потому что, если просуммировать все доли молекул, имеющих всевозможные значения скорости, то получается единица. Как показано на рис.1.5, с ростом температуры кривая распределения смещается вправо, т.е. растет число быстрых молекул, но площадь под кривой остается постоянной, т.к. N = const.Скорость в, при которой функция f() достигает максимума, называется наиболее вероятной скоростью. Из условия равенства нулю первой производной функции f(v) ′ = 0 следует, что
Н
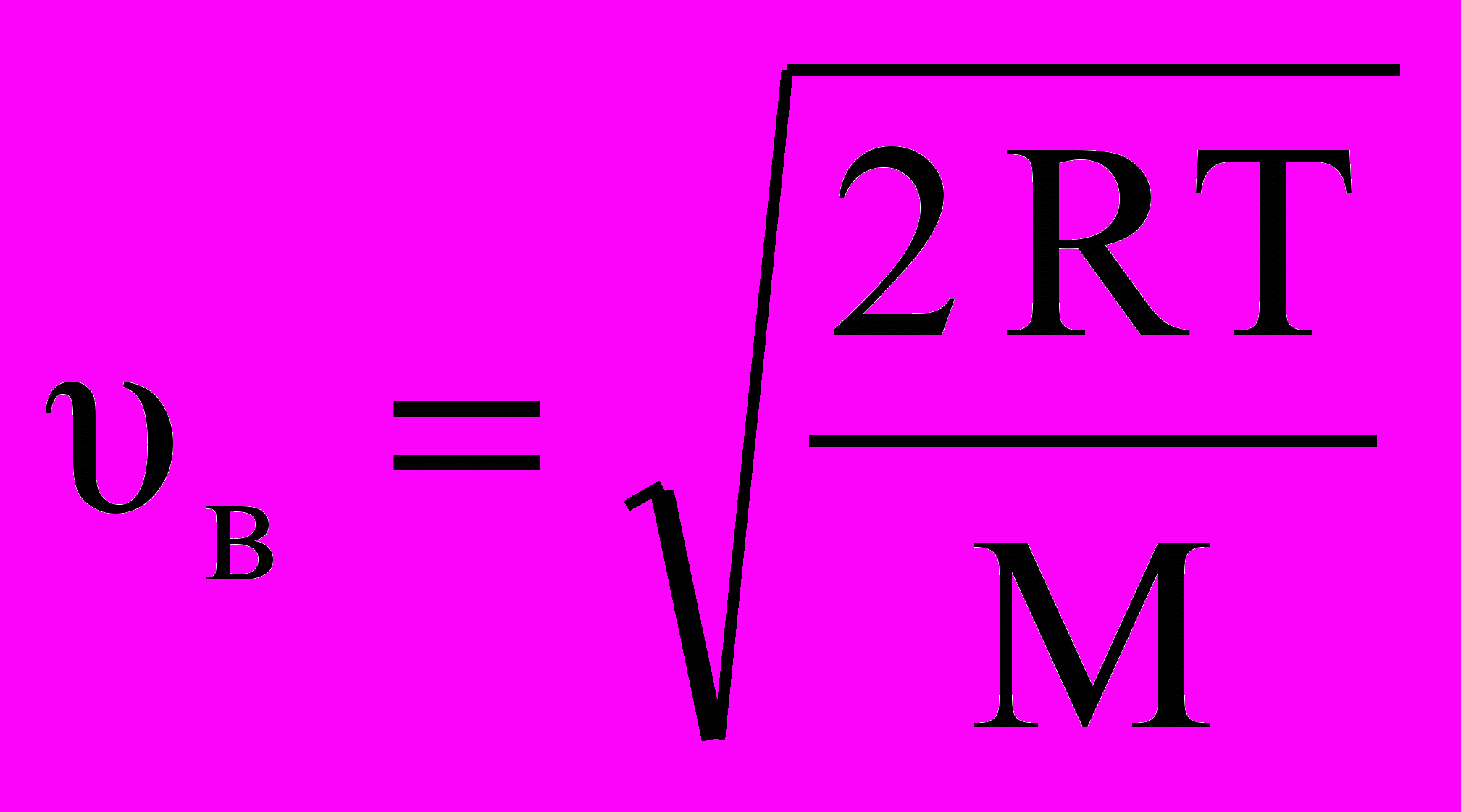
а рисунке 1.4. отмечена еще одна характеристика – средняя арифметическая скорость молекулы. Она определяется по формуле:
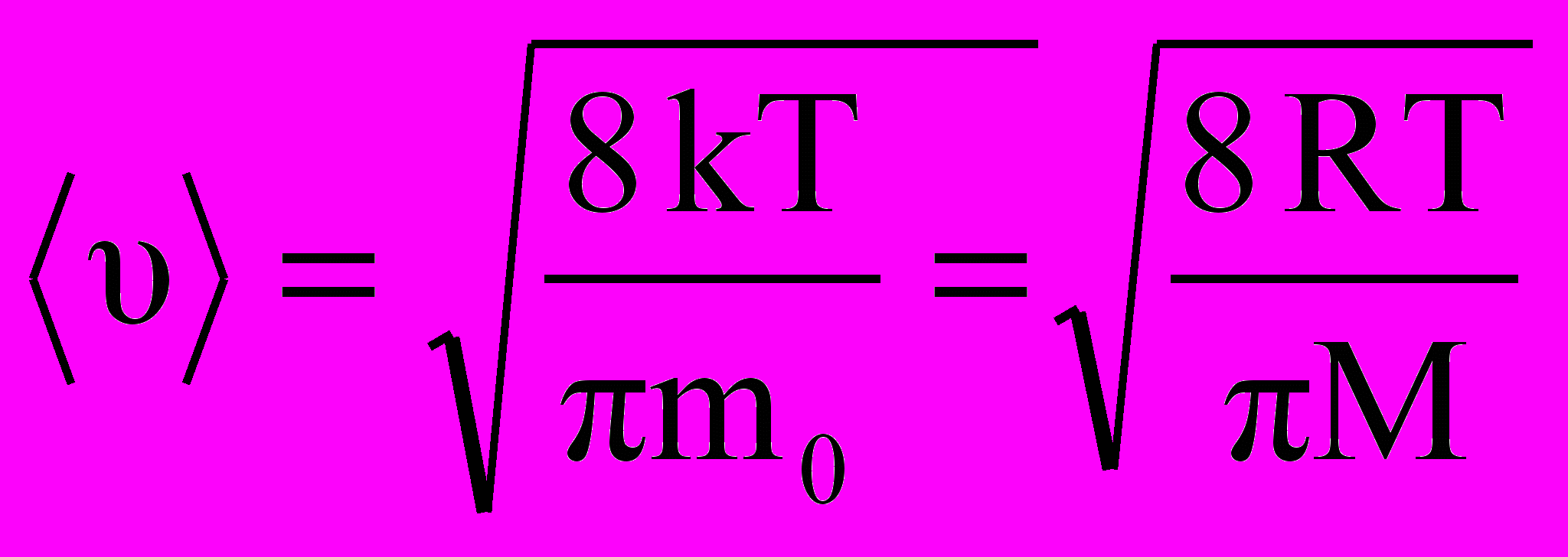
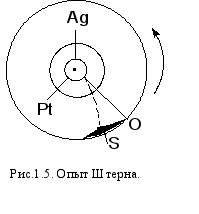 Опыт, проведенный немецким физиком О.Штерном, экспериментально подтвердил справедливость распределения Максвелла (рисунок 1.5.). Прибор Штерна состоит из двух коаксиальных цилиндров. Вдоль оси внутреннего цилиндра со щелью проходит платиновая проволока, покрытая слоем серебра. Если пропустить по проволоке ток,она нагревается и серебро испаряется. Атомы серебра, вылетая через щель, попадают на внутреннюю поверхность второго цилиндра. Если прибор будет вращаться, то атомы серебра осядут не против щели, а сместятся от точки О на некоторое расстояние. Исследование количество осадка позволяет оценить распределение молекул по скоростям. Оказалось, что распределение соответствует максвелловскому.
Опыт, проведенный немецким физиком О.Штерном, экспериментально подтвердил справедливость распределения Максвелла (рисунок 1.5.). Прибор Штерна состоит из двух коаксиальных цилиндров. Вдоль оси внутреннего цилиндра со щелью проходит платиновая проволока, покрытая слоем серебра. Если пропустить по проволоке ток,она нагревается и серебро испаряется. Атомы серебра, вылетая через щель, попадают на внутреннюю поверхность второго цилиндра. Если прибор будет вращаться, то атомы серебра осядут не против щели, а сместятся от точки О на некоторое расстояние. Исследование количество осадка позволяет оценить распределение молекул по скоростям. Оказалось, что распределение соответствует максвелловскому.2. ОСНОВЫ ТЕРМОДИНАМИКИ
2.1. Внутренняя энергия. @
Важной характеристикой любой термодинамической системы является ее внутренняя энергия – энергия хаотического теплового движения частиц системы - молекул, атомов и энергия их взаимодействия. К внутренней энергии не относится кинетическая энергия движения системы как целого и потенциальная энергия системы во внешних полях. Внутренняя энергия системы в определенном состоянии не зависит от того, как система пришла в это состояние (т.е. от пути перехода), а определяется только значениями термодинамических параметров в этих состояниях. В термодинамике имеются и другие функции, удовлетворяющие этим условиям, их называют функциями состояния системы. Таким образом, внутренняя энергия – это функция состояния.
Для дальнейших рассуждений нам понадобится понятие числа степеней свободы – это число независимых переменных (координат), полностью определяющих положение системы в пространстве. Например, молекулу одноатомного газа можно рассматривать как материальную точку, обладающую тремя степенями свободы поступательного движения (координаты x,y,z) (рис.2.1. а). Молекула двухатомного газа, рассматриваемая в классической механике как совокупность двух материальных точек, жестко связанных между собой, имеет уже 5 степеней свободы. У нее имеется 3 степени свободы поступательного движения центра масс и 2 степени вращательного, связанного с поворотами на углы и (рис. 2.1. б). Эти углы полярный угол θ и азимутальный угол φ, определяют ориентацию оси молекулы. В данном случае, на первый взгляд кажется, что необходимо также задавать угол поворота ψ молекулы относительно собственной оси. Но вращение двухатомной молекулы вокруг своей собственной оси ничего не меняет в положении молекулы, так как структуры у материальных точек атомов нет и, поэтому, этот угол не нужен для задания положения такой молекулы в пространстве. Трехатомные молекулы (рис. 2.1.в), в которых атомы связаны жестко между собой, имеют 6 степеней свободы, так как здесь уже необходим дополнительный угол ψ.
Если расстояния между атомами меняются, т.е. атомы в молекуле колеблются, то для задания этих расстояний необходимы дополнительные координаты - колебательные степени свободы и общее число степеней свободы будет больше 6. Для много-атомных молекул число степеней может быть намного больше 6.
Р
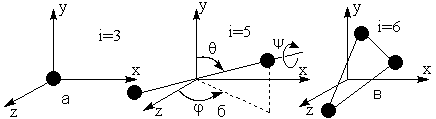 Рис.2.1. Степени свободы: а) одноатомной молекулы;б) двухатомной молекулы;в) трех- и многоатомной молекулы.
Рис.2.1. Степени свободы: а) одноатомной молекулы;б) двухатомной молекулы;в) трех- и многоатомной молекулы.анее мы получили формулу для средней кинетической энергии поступательного движения одно-атомной молекулы идеального газа следующее выражение: ‹ε0› = 3kT/2. Но у одно-атомной молекулы имеется 3 степени свободы поступательного движения и ни одна не имеет преимущества перед другими. Поэтому на каждую степень в среднем должна приходиться одинаковая энергия, равная 1/3 общей: ‹ε1› = kT/2. Так как, очевидно, что все степени свободы равноценны, то в классической статистической физике существует закон Больцмана о равномерном распределении энергии по степеням свободы. Он формулируется так: для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная кТ/2, а на каждую колебательную степень свободы – кТ. Колебательная степень свободы обладает вдвое большей энергией, так как на нее приходится не только кинетическая, но и потенциальная энергия взаимодействия. Таким образом, средняя энергия любой молекулы ‹ε› = ikT/2, где i - это сумма поступательных, вращательных и удвоенного числа колебательных степеней свободы.
Из этого закона получаем, что внутренняя энергия UМ одного моля идеального газа равна UМ=ikTNA/2 = iRT/2, а внутренняя энергия U газа массы m равна U = ikTN/2 = iRTm/2M (здесь мы учитываем, что потенциальная энергия взаимодействия молекул равна 0, общее число молекул в одном моле равно NA, N= mNA/M и kNA=R).
2.2. Первое начало термодинамики. @
Обмен энергией между термодинамической системой и внешней средой может осуществляться двумя качественно различными способами: путем совершения работы и путем теплообмена.
Изменение энергии системы, происходящее под действием сил измеряется работой. Если термодинамическая система совершает работу против внешних сил, то работа считается положительной (А>0). Если работу над системой совершают внешние силы, то она считается отрицательной (А< 0).
Изменение энергии системы, происходящее в результате теплообмена, определяется количеством переданной или отнятой теплоты Q. При теплообмене тела систем должны находится в тепловом контакте, т.е. молекулы этих систем должны иметь возможность сталкиваться при своем движении и обмениваться своей кинетической энергией. Если энергия (теплота) передается системе, то Q>0, если она от системы отнимается, то Q<0. Итак, работа и теплота – это две формы передачи энергии от одних тел другим. Поскольку внутренняя энергия - это механическая энергия всех молекул, то при всех ее изменениях должен соблюдаться закон сохранения энергии. Применительно к термодинамическим процессам этим законом является первое начало термодинамики, установленное в результате обобщения опытных данных. Опыт показал, что при любом способе перехода системы из состояния 1 в состояние 2 изменение внутренней энергии системы ΔU = U1 - U2 определяется количеством теплоты Q, полученной системой, и работой А, совершенной системой против внешних сил (получаемое тепло увеличивает энергию системы, а работа системы над внешней средой уменьшает ее) :
ΔU = Q – A или Q = ΔU + A
В дифференциальной форме (для малых изменений величин) это запишется следующим образом:
δQ = dU + δA ,
где δQ - бесконечно малое количество теплоты, dU – бесконечно малое изменение внутренней энергии, δA – элементарная работа. Это уравнение выражает первое начало термодинамики: теплота, подводимая к системе, расходуется на изменение ее внутренней энергии и на совершение работы против внешних сил. Знак δ в δQ и δА означают, что данные элементарные приращения не являются полными дифференциалами и, следовательно, А и Q не являются функциями состояния.
П
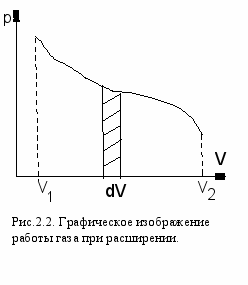 усть газ заключен в цилиндрический сосуд, закрытый легко скользящим поршнем площадью S. Найдем работу газа при расширении его объема δA = Fdl = pSdl =pdV, где F – сила, с которой газ действует на поршень, dl – перемещение поршня. Если зависимость р(V) изобразить графически, то общая работа при изменении объема от V1 доV2 равна площади фигуры, ограниченной кривой р(V), осью абсцисс и прямыми V= V1 и V= V2 (рис.2.2.). Графически можно изображать лишь равновесные процессы, и все количественные выводы термодинамики строго применимы только к равновесным процессам. При достаточно медленном протекании реальные процессы можно приближенно считать равновесными. Первое начало термодинамики выполняется во всех процессах, связанных с обменом энергией и совершением работы.
усть газ заключен в цилиндрический сосуд, закрытый легко скользящим поршнем площадью S. Найдем работу газа при расширении его объема δA = Fdl = pSdl =pdV, где F – сила, с которой газ действует на поршень, dl – перемещение поршня. Если зависимость р(V) изобразить графически, то общая работа при изменении объема от V1 доV2 равна площади фигуры, ограниченной кривой р(V), осью абсцисс и прямыми V= V1 и V= V2 (рис.2.2.). Графически можно изображать лишь равновесные процессы, и все количественные выводы термодинамики строго применимы только к равновесным процессам. При достаточно медленном протекании реальные процессы можно приближенно считать равновесными. Первое начало термодинамики выполняется во всех процессах, связанных с обменом энергией и совершением работы.2. 3. Теплоемкость. @
Одним из основных свойств тел, которое широко используется в термодинамике, является теплоемкость. Теплоемкостью тела называется физическая величина, численно равная отношению теплоты δQ, сообщаемой телу, к изменению температуры тела в рассматриваемом термодинамическом процессе. Теплоемкость тела зависит от его химического состава, массы и термодинамического состояния, а также от вида процесса, в котором поступает теплота. Тепловые свойства однородных тел характеризуются понятиями удельной и молярной теплоемкостей.
Удельная теплоемкость вещества – величина, численно равная количеству теплоты, необходимому для нагревания единицы массы вещества на 1 Кельвин при данном процессе, единица измерения – Дж/(кг∙К)
М
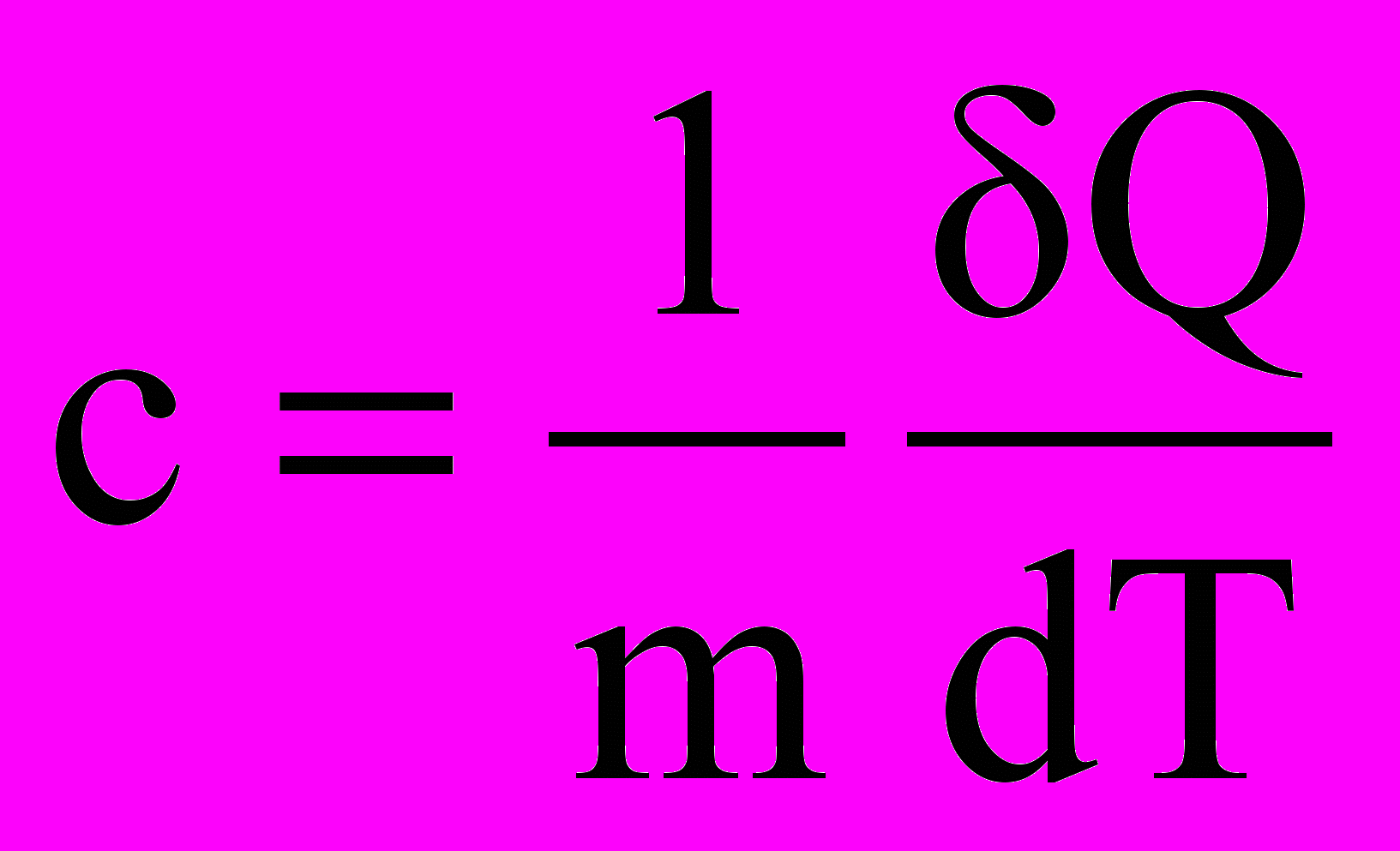
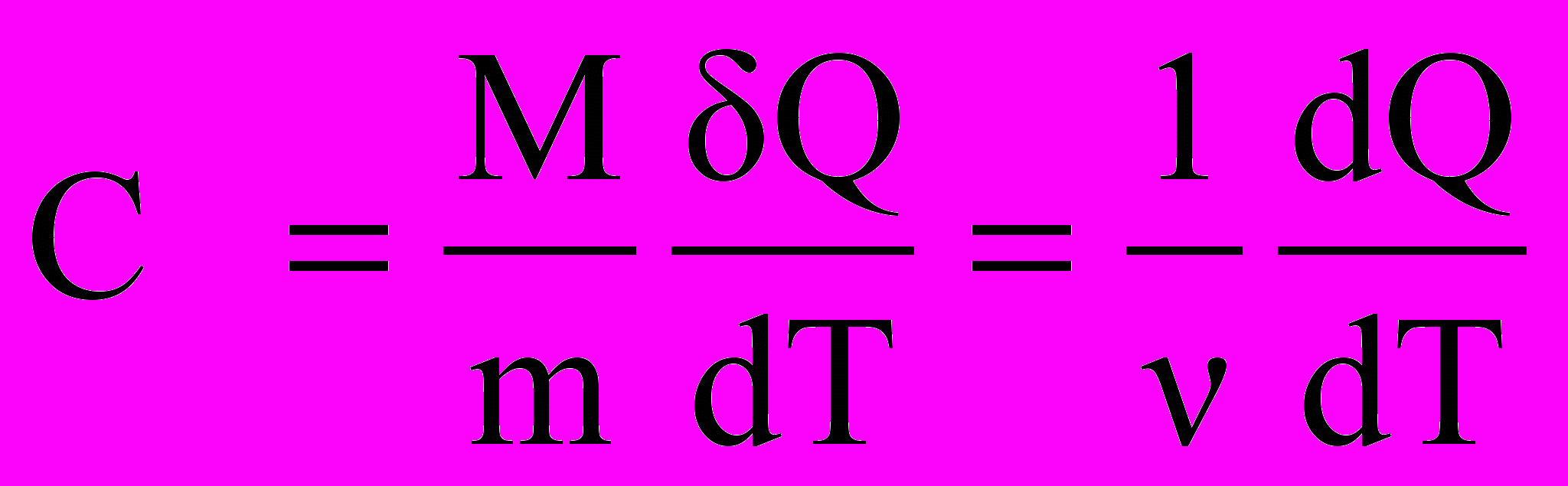
олярная теплоемкость – величина, равная количеству теплоты, необходимому для нагревания одного моля вещества на 1К , т.е. С =сМ, где М – молярная масса вещества. Теплоемкости одного и того же вещества при разных термодинамических процессах нагревания различаются.
Найдем молярную теплоемкость системы в изобарном процессе, для этого возьмем один моль газа и сообщим ему количество теплоты δQМ. Согласно определению молярной теплоемкости и первому началу термодинамики можем
записать (здесь δАМ - работа одного моля газа)
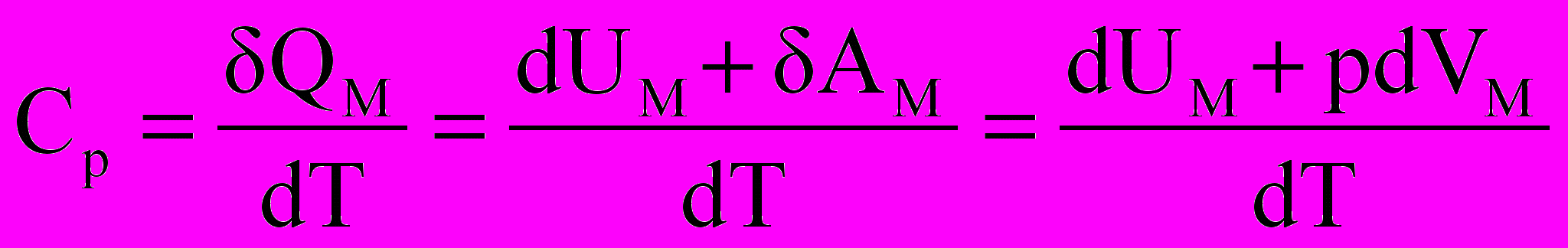
Если газ нагревается при постоянном объеме, то dV=0 и δАМ =0. Сообщаемая газу теплота идет только на увеличение его внутренней энергии и теплоемкость для изохорного процесса
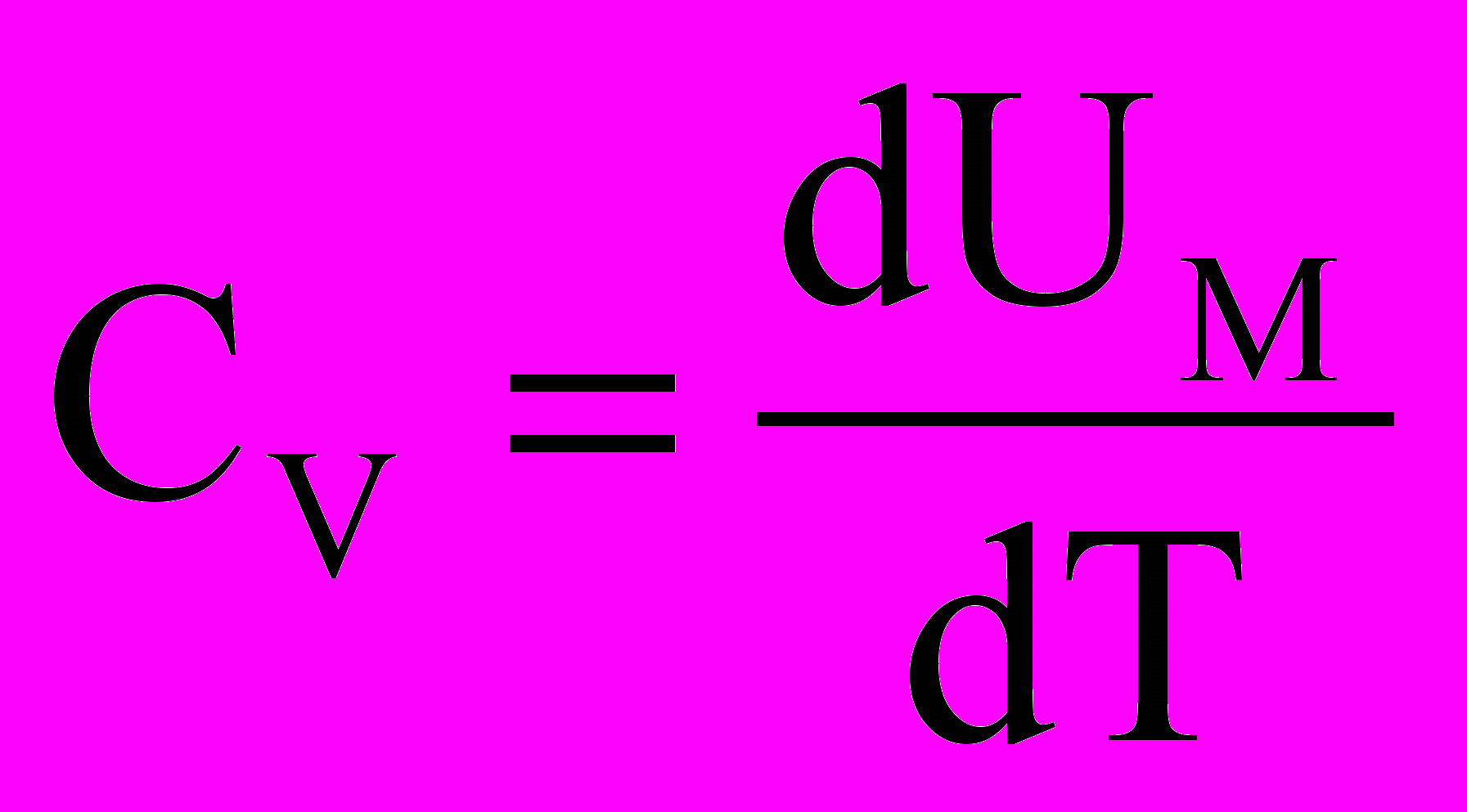
Откуда следует, что
И
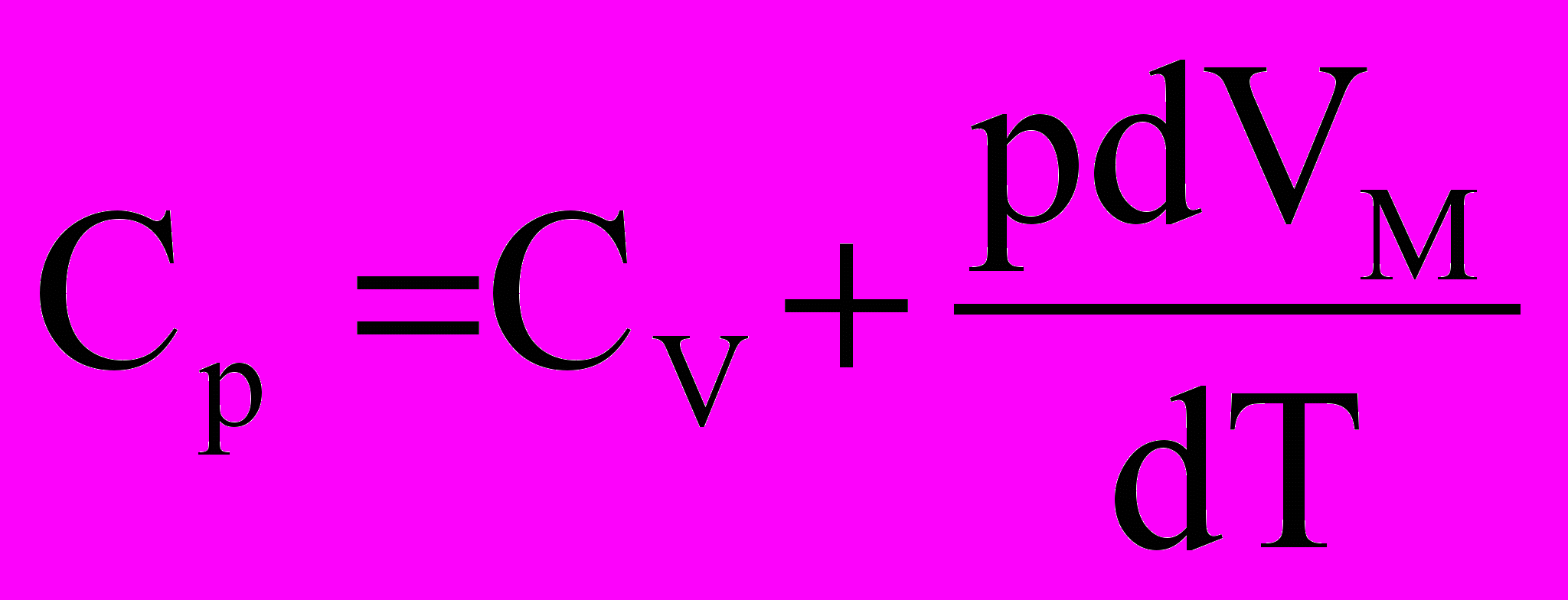
з уравнения Менделеева – Клапейрона для изобарного процесса можно получить pdVМ = RdT. Таким образом, pdVМ /dT = R. Из этой формулы следует физический смысл газовой постоянной: она численно равна работе (δАМ = pdVМ), совершаемой одним молем идеального газа, при его изобарном нагревании на 1 К. После замены получаем:
Э
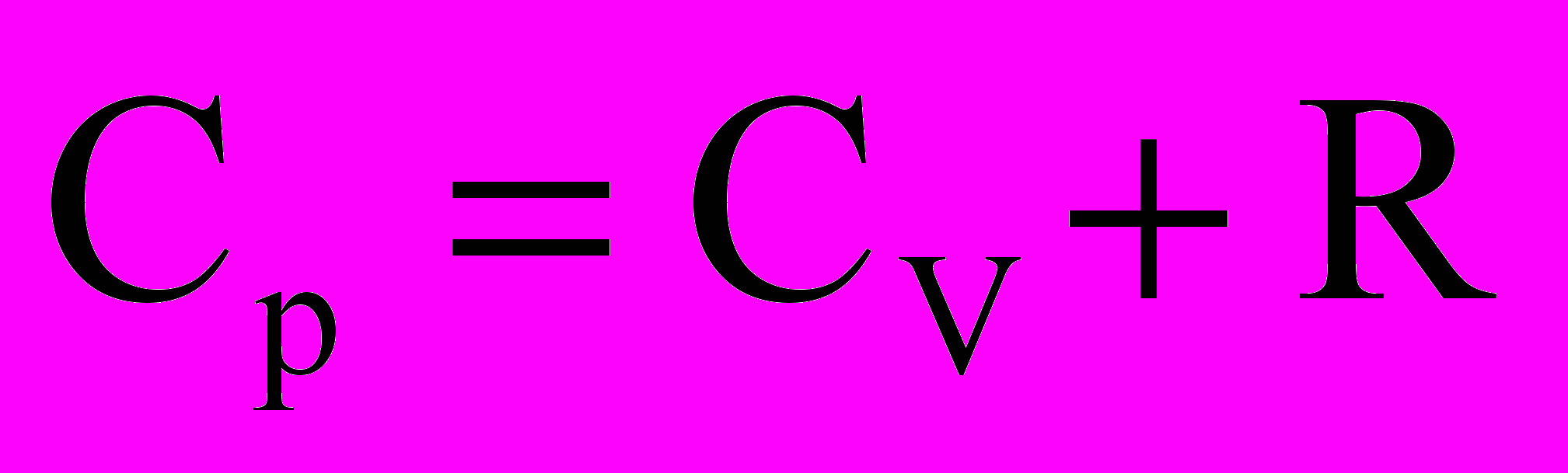
то выражение называется уравнением Майера, оно показывает, что молярная теплоемкость при постоянном давлении Ср всегда больше, чем теплоемкость при постоянном объеме Cv на величину, равную молярной газовой постоянной. Это объясняется тем, что при постоянном объеме все подводимое тепло идет только на увеличение внутренней энергии, т.е. повышение Т, а при постоянном давлении кроме этого требуется еще дополнительное количество теплоты на совершение работы газом против внешних сил при его расширении.
2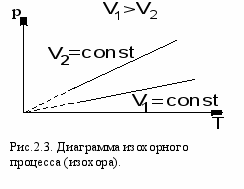 . 4. Применение первого начала термодинамики к изопроцессам. @
. 4. Применение первого начала термодинамики к изопроцессам. @
Различают следующие виды термодинамических процессов:
1. Изохорный - это процесс, протекающий при постоянном объеме. V=const. На диаграмме в координатах (р, Т) он изображается прямой, называемой изохорой (рис.2.3.). При изохорном процессе газ не совершает работы над внешними телами, так как dV=0. Вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии и отсюда I начало термодинамики для изохорного процесса δQ = dU. Для одного моля δQм=dUм , где dUм=СVdT. Изохорным является процесс сгорания топлива в карбюраторном двигателе.
2. Изобарный – это процесс, протекающий при постоянном давлении. Прямая, изображающая этот процесс в координатах (V,T), называется изобарой (рис.2.4.). Первое начало термодинамики для
изобарного процесса δQ = dU + δA. Так давление не меняется, то работа газа при увеличении объема от V1 до V2 равна
Т
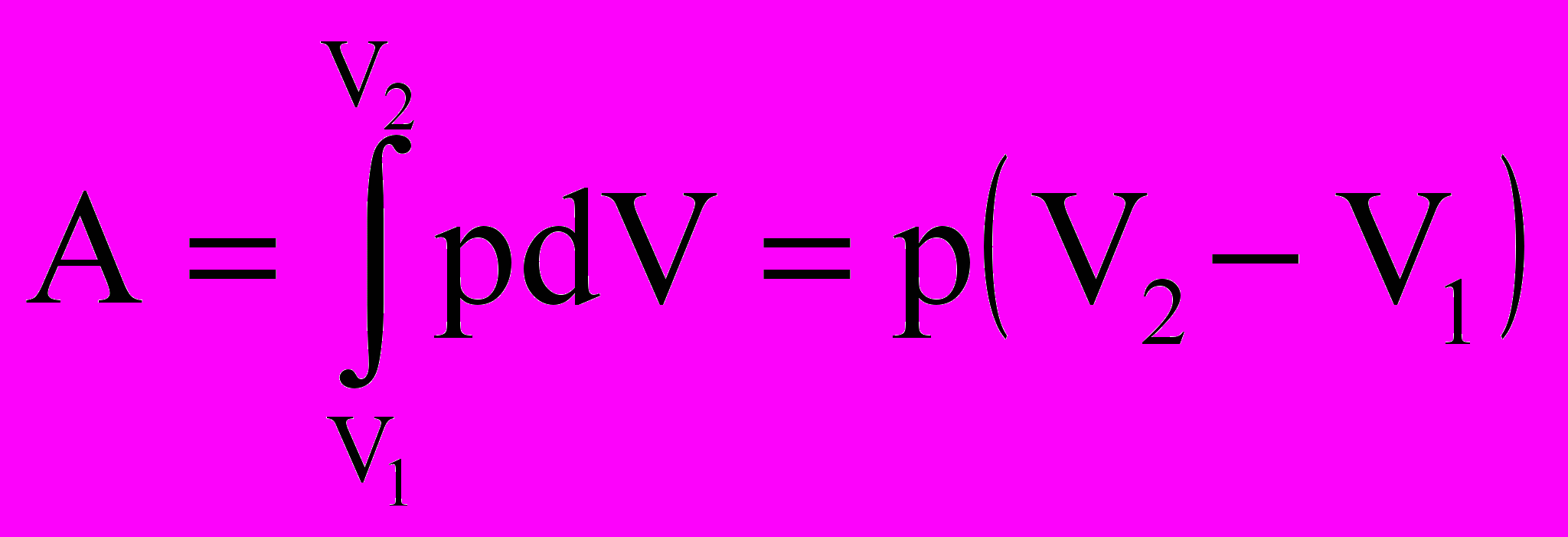
еплота, сообщаемая газу массой m в изобарном процессе
при этом его внутренняя энергия возрастает на величину
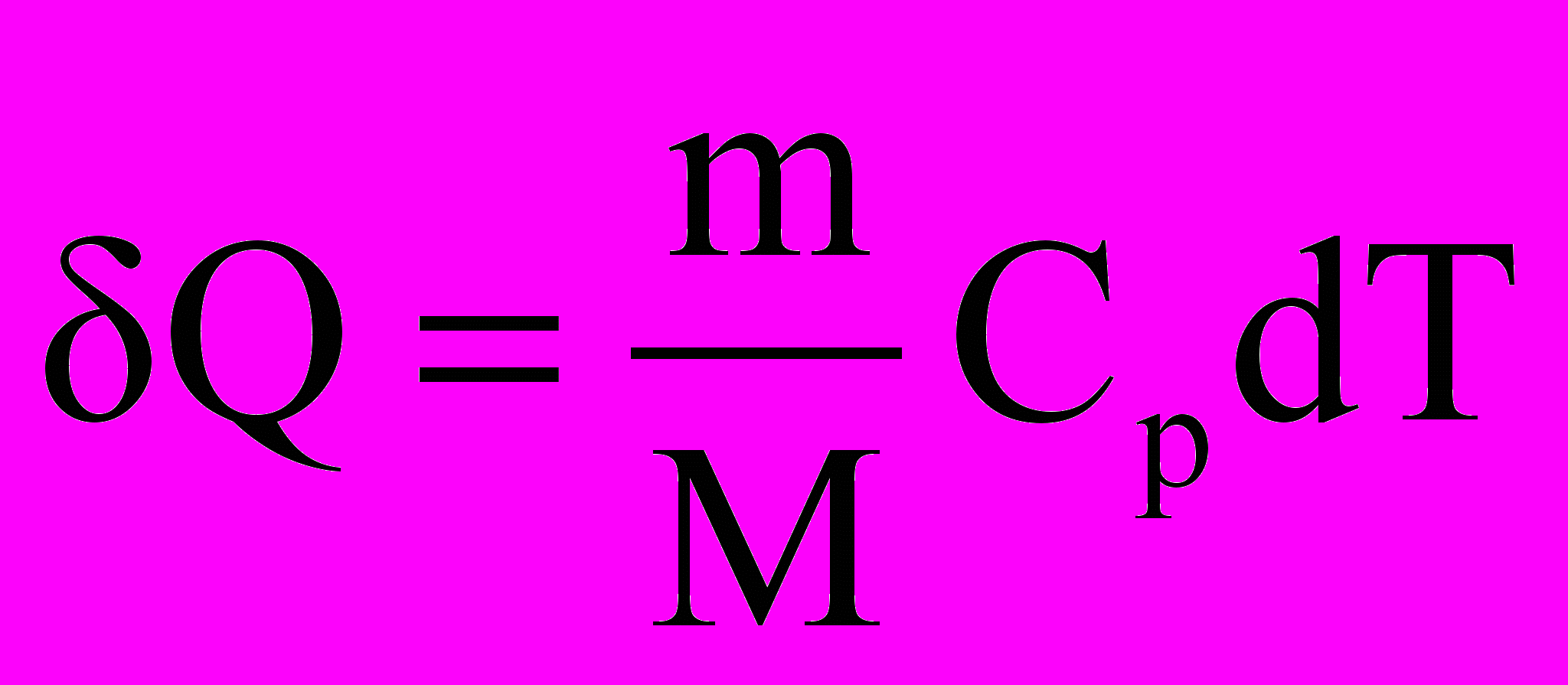
т
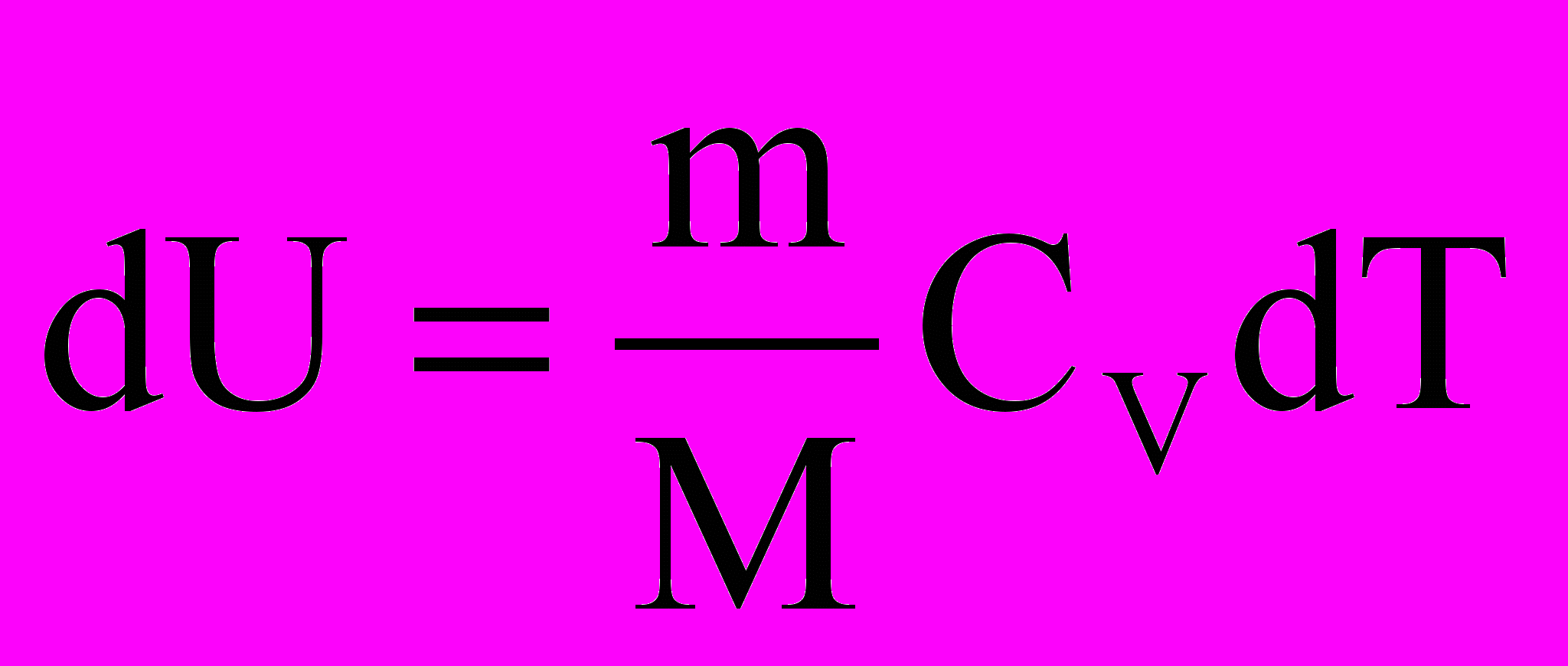
ак как внутренняя энергия идеального газа не зависит от давления и объема, а определяется лишь температурой. При изобарном нагревании к системе подводится тепло δQ >0 и δA >0, так как газ расширяется. При изобарном сжатии направление процесса меняется на противоположное и теперь тепло отводится от системы, т.е. δQ <0 и δA <0, так как работу над газом совершают внешние силы. dU также будет меньше нуля. Примером изобарного процесса может служить процесс образования пара в паровых котлах или сгорания топлива в воздушно-реактивных двигателях.
3. Изотермический – это процесс, протекающий при постоянной температуре. Кривая, построенная в координатах (р, V), называется изотермой. Она представляет собой гиперболу (
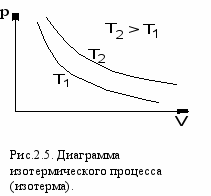 рис.2.5.), расположенную на диаграмме тем выше, чем выше температура, при которой происходит процесс. Так как при Т = const внутренняя энергия идеального газа не изменяется, то dU = 0 и первое начало термодинамики для изотермического процесса примет вид: δQ = δА. Теплоемкость при изотермическом процессе СТ =δQ/dT=δQ/0 = ∞ и не имеет смысла. Изотермический процесс осуществляется при наличии термостата (внешней среды или тела с большим запасом внутренней энергии, находящемся при той же температуре).
рис.2.5.), расположенную на диаграмме тем выше, чем выше температура, при которой происходит процесс. Так как при Т = const внутренняя энергия идеального газа не изменяется, то dU = 0 и первое начало термодинамики для изотермического процесса примет вид: δQ = δА. Теплоемкость при изотермическом процессе СТ =δQ/dT=δQ/0 = ∞ и не имеет смысла. Изотермический процесс осуществляется при наличии термостата (внешней среды или тела с большим запасом внутренней энергии, находящемся при той же температуре).Найдем работу изотермического расширения газа, учитывая, что все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил и не изменяет его температуру. Учитывая формулу для работы и уравнение Менделеева-Клайперона, получаем
П
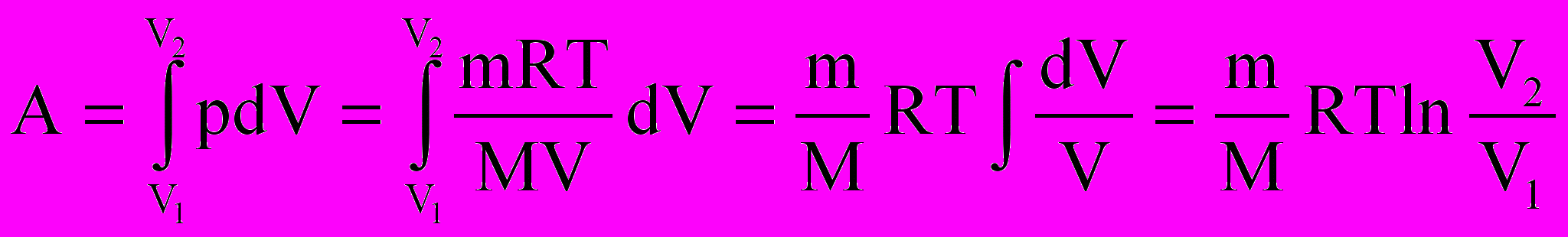
римерами изотермических процессов являются закалка и отжиг сталей в процессе их изготовления. Существуют автомобили и вагоны – рефрижераторы, служащие для перевозки скоропортящихся продуктов. Они имеют теплоизолированный кузов и холодильники для поддержания внутри постоянной температуры и поэтому процесс перевозки продуктов в таких условиях можно назвать изотермическим..
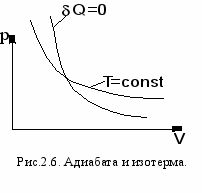
4. Адиабатический процесс. Адиабатическим называется процесс, при котором отсутствует теплообмен между системой и окружающей средой, т.е. δQ = 0, Q = const. Так как δQ = 0, первое начало термодинамики имеет вид: δА=-dU т.е. работа совершается за счет внутренней энергии газа. Если газ расширяется, то δА>0, dU<0 и температура газа уменьшается. Если происходит сжатие газа, то δА<0 и dU>0. Работу над газом совершают внешние силы, внутренняя энергия (а, значит, и температура) газа повышается. Реализовать адибатический процесс можно, если проводить его либо при хорошей теплоизоляции от окружающей среды, либо быстро за короткое время, при котором теплообмен будет мал.
Пуассона или показатель адиабаты. Уравнение адиабатического процесса (уравнение Пуассона) имеет вид: рVγ = const, где γ = Ср /Cv – коэффициент (показатель адиабаты).
Диаграмма адиабатического процесса (адиабата) в координатах (р,V) изображается гиперболой, более крутой, чем изотерма (рис.2.6.). Объясняется это тем, что при адиабатном сжатии увеличение давления происходит не только за счет уменьшения объема, как при изотермическом сжатии, но также связано с возрастанием температуры. Согласно уравнению р = nkT =NkT/V давление пропорционально T/V и в случае адиабатического сжатия его возрастание определяется одновременно и возрастанием температуры, и уменьшением объема. При адиабатном расширении газа его температура уменьшается и давление падает быстрее, чем при соответствующем изотермическом расширении, поскольку давление уменьшается пропорционально T/V и его падение определяется одновременно и понижением температуры, и увеличением объема. Теплоемкость при адиабатическом процессе СQ= Q/ΔT=0/ΔT=0, не имеет большого смысла. Адиабатические процессы широко распространены в технике, например, в двигателях внутреннего сгорания. Истечение газов через сопла реактивных двигателей также может считаться адиабатическим процессом, поскольку происходит очень быстро. Отчетливо выражен адиабатический характер процесса сжатия в дизеле, который не имеет зажигания: адиабатическое нагревание смеси при сжатии приводит к ее самовоспламенению. И, наконец, самый простой бытовой пример: сифон для газирования воды – в момент прокола газового баллончика, когда газ мгновенно его покидает, сам баллончик резко охлаждается (покрывается инеем).
- Второе начало термодинамики. @
Т
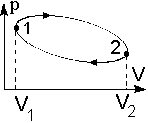
Рис.2.7. Круговой процесс (цикл).
ермодинамический процесс называется обратимым, если он может происходить как в прямом, так и в обратном направлении, а в окружающей среде и в системе при этом не происходит никаких изменений. Всякий процесс, не удовлетворяющий этим условиям, является необратимым.
Если система, пройдя через ряд состояний, возвращается в исходное, то такой процесс называется круговым процессом, или циклом. Циклы лежат в основе работы всех тепловых машин – двигателей внутреннего сгорания, паровых и газовых турбин, холодильников. На диаграмме процессов в координатах (р,V) цикл изображается замкнутой кривой, где процесс 1-2 – процесс расширения газа, а 2-1 – процесс сжатия (рис. 2.7.). В результате кругового процесса система может теплоту как получать, так и отдавать. Обозначим полученное количество теплоты Q1, а отданное - Q2. Работа, совершаемая газом за цикл, определяется площадью фигуры, ограниченной кривой 1-2-1. В результате цикла система возвращается в исходное состояние и, следовательно, полное изменение внутренней энергии газа равно нулю, а работа, совершаемая за цикл, равна полученной теплоте Q = Q1 Q2 = А.
2. 6. Энтропия. @
Для описания термодинамических процессов одного первого начала термодинамики недостаточно, потому что оно не позволяет определять направление протекания процессов. Например, процесс самопроизвольной передачи теплоты от холодного тела горячему первым началом не запрещен, однако опыты показывают, что он не происходит. Итак, необходимо определить условия, при которых возможны превращения энергии из одного вида в другой, что позволило бы узнать направления протекания процессов.
В термодинамике, кроме внутренней энергии, существует еще несколько функций состояния системы. Особое место среди них занимает энтропия S. Энтропия как раз и является той величиной, которая позволяет прогнозировать возможность и направление протекания процессов. Энтропия (от греч.entropia–поворот, превращение)- понятие, впервые введенное в термодинамике для определения меры необратимого рассеяния энергии немецким физиком Р.Клаузиусом в 1865г.
Пусть δQ – элементарное количество теплоты, сообщаемое системе каким-либо нагревателем с постоянной температурой Т. Если процесс равновесный (обратимый), то температура системы тоже равна Т. Отношение δQ/Т называется приведенным количеством теплоты и равно изменению энтропии при обратимом процессе: δQ/Т = dS. Поскольку Т всегда > 0, из 2-ого начала видно, что δQ и dS имеют один и тот же знак. Это позволяет по характеру изменения энтропии судить о направлении процесса теплообмена и прогнозировать его возможность. При нагревании тела δQ > 0 и его энтропия возрастает (dS > 0), при охлаждении энтропия убывает. Если δQ=0 (обратимый адиабатический процесс), то dS = 0 и S = const, то есть энтропия остается постоянной.
Энтропия, подобно внутренней энергии, является функцией состояния системы. Энтропия системы равна сумме энтропий всех тел, входящих в систему. Для изолированной системы энтропия в любом обратимом процессе не изменяется и S = const. В термодинамике доказывается, что в необратимом процессе энтропия системы может только возрастать: dS
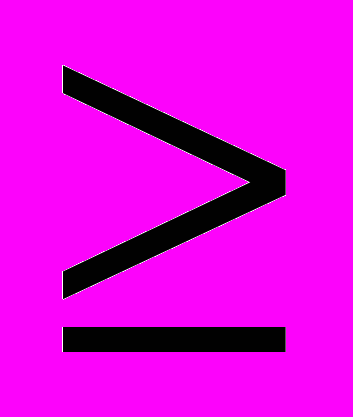 0. Объединяя два последних условия, мы получаем, что энтропия замкнутой системы может либо возрастать, либо оставаться постоянной: dS ≥ 0. Это неравенство Клаузиуса также является формулировкой второго начала термодинамики.
0. Объединяя два последних условия, мы получаем, что энтропия замкнутой системы может либо возрастать, либо оставаться постоянной: dS ≥ 0. Это неравенство Клаузиуса также является формулировкой второго начала термодинамики.С точки зрения молекулярной физики, энтропия является мерой разупорядоченности системы, т.е. чем система более хаотична, тем ее энтропия выше. С этой точки зрения второе начало термодинамики утверждает, что в замкнутой системе, при отсутствии внешних воздействий любая система стремится перейти в состоянии максимальной разупорядоченности. Такое состояние является наиболее вероятным, поэтому энтропию S можно связать с вероятностью W состояния системы соотношением Больцмана S=k lnW, а второе начало объяснять стремлением системы находиться в наиболее вероятном состоянии. Явление увеличения беспорядка можно легко наблюдать при добавлении в воду капли туши. Если не воздействовать на такую систему извне, то через небольшое время тушь полностью перемешается с водой, обратный процесс – процесс собирания частичек туши в каплю, хотя в принципе он и возможен, никогда не наблюдается.
3. ЯВЛЕНИЯ ПЕРЕНОСА
Беспорядочность теплового движения молекул газа или жидкости, непрерывные столкновения между ними приводят к постоянному перемешиванию частиц и к изменению их скоростей и энергий. Если в веществе имеется пространственная неоднородность плотности или температуры, то со временем, согласно второму началу термодинамики, происходит обязательное выравнивание этих неоднородностей. В среде возникают потоки энергии, вещества, а также импульса упорядоченного движения частиц. Эти потоки являются физической основой особых процессов, объединенных под общим названием явления переноса. К этим явлениям относится теплопроводность (обусловлена переносом энергии), диффузия (обусловлена переносом массы) и внутреннее трение (обусловлено переносом импульса).
3.1. Теплопроводность. @
Теплопроводность – это явление переноса внутренней энергии (теплоты) при наличии неоднородности в распределении температуры. Теплопроводность возникает, например, при наличии разности температур, вызванной какими-либо внешними причинами. При этом молекулы газа в разных местах его объема имеют разные средние кинетические энергии. В результате хаотического теплового движения молекулы, попавшие из нагретых частей газа в более холодные, отдают часть своей энергии окружающим частицам. Наоборот, медленно движущиеся молекулы, попадая из холодных частей объема газа в более нагретые, увеличивают свою энергию за счет соударений с молекулами, имеющими большие скорости и энергии. Это приводит к направленному переносу внутренней энергии газа.
В простейшем одномерном случае, когда температура газа меняется только в одном направлении, например, вдоль оси х, перенос внутренней энергии газа путем теплообмена описывается законом Фурье (1822 г.):
jE = -λdT/dx
где jE - это плотность теплового потока, т.е. величина, равная энергии, переносимой в форме теплоты в единицу времени через единичную площадку, перпендикулярную оси х. Величина λ называется теплопроводностью или коэффициентом теплопроводности, dT/dx – градиент температуры, показывающий, как изменяется температура на единицу длины х перпендикулярно рассматриваемой площадке. Знак «минус» показывает, что перенос энергии происходит в направлении убывания температуры. Теплопроводность λ численно равна плотности теплового потока при единичном градиенте температуры.
В общем случае закон Фурье имеет вид:
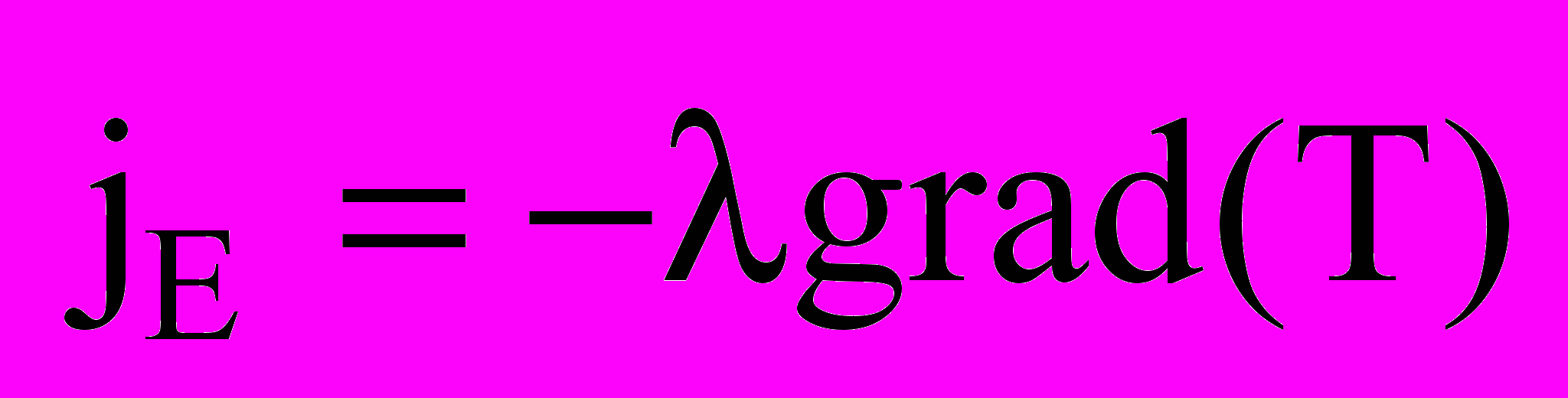 . Здесь
. Здесь  - вектор плотности теплового потока, направление которого совпадает с направлением переноса энергии. Согласно молекулярно-кинетической теории газов можно вывести выражение для теплопроводности газа λ ═ cV‹ℓ›ρ‹υ›/3, где cV – удельная теплоемкость при постоянном объеме, ρ – плотность газа, ‹υ› - средняя скорость теплового движения молекул, ‹ℓ› - средняя длина свободного пробега молекул (среднее расстояние, которое проходит молекула между двумя последовательными соударениями). Знание теплопроводности различных материалов очень важно, например, при расчете передачи тепла в котлах и нагревателях, а также при создании теплоизоляционных материалов. Например, для теплоизоляции систем от окружающей среды применяются материалы с низкой теплопроводностью – асбест, пенопласт, минеральная вата.
- вектор плотности теплового потока, направление которого совпадает с направлением переноса энергии. Согласно молекулярно-кинетической теории газов можно вывести выражение для теплопроводности газа λ ═ cV‹ℓ›ρ‹υ›/3, где cV – удельная теплоемкость при постоянном объеме, ρ – плотность газа, ‹υ› - средняя скорость теплового движения молекул, ‹ℓ› - средняя длина свободного пробега молекул (среднее расстояние, которое проходит молекула между двумя последовательными соударениями). Знание теплопроводности различных материалов очень важно, например, при расчете передачи тепла в котлах и нагревателях, а также при создании теплоизоляционных материалов. Например, для теплоизоляции систем от окружающей среды применяются материалы с низкой теплопроводностью – асбест, пенопласт, минеральная вата.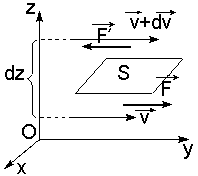
Рис.3.1. Силы внутреннего трения.
3. 2. Внутреннее трение (вязкость). @
Явление внутреннего трения заключается в ускорении и замедлении слоев газа или жидкости вследствие наличия неоднородности скорости. Между слоями, двигающимися параллельно друг другу с различными по величине скоростями, из-за хаотического теплового движения возникает обмен молекулами с разными импульсами. Это приводит к тому, что медленно перемещающиеся слои тормозят более быстро движущиеся слои и наоборот. При этом возникают силы трения или силы вязкости, направленные по касательной к поверхности соприкосновения слоев. В результате этого импульс слоя, движущегося быстрее, уменьшается, а движущегося медленнее – увеличивается, что и приводит к торможению быстрого слоя и ускорению медленного. По третьему эакону Ньютона эти силы равны по величине и противоположны по направлению. Формулу для силы внутреннего трения между двумя слоями газа или жидкости предложил также Ньютон:
З
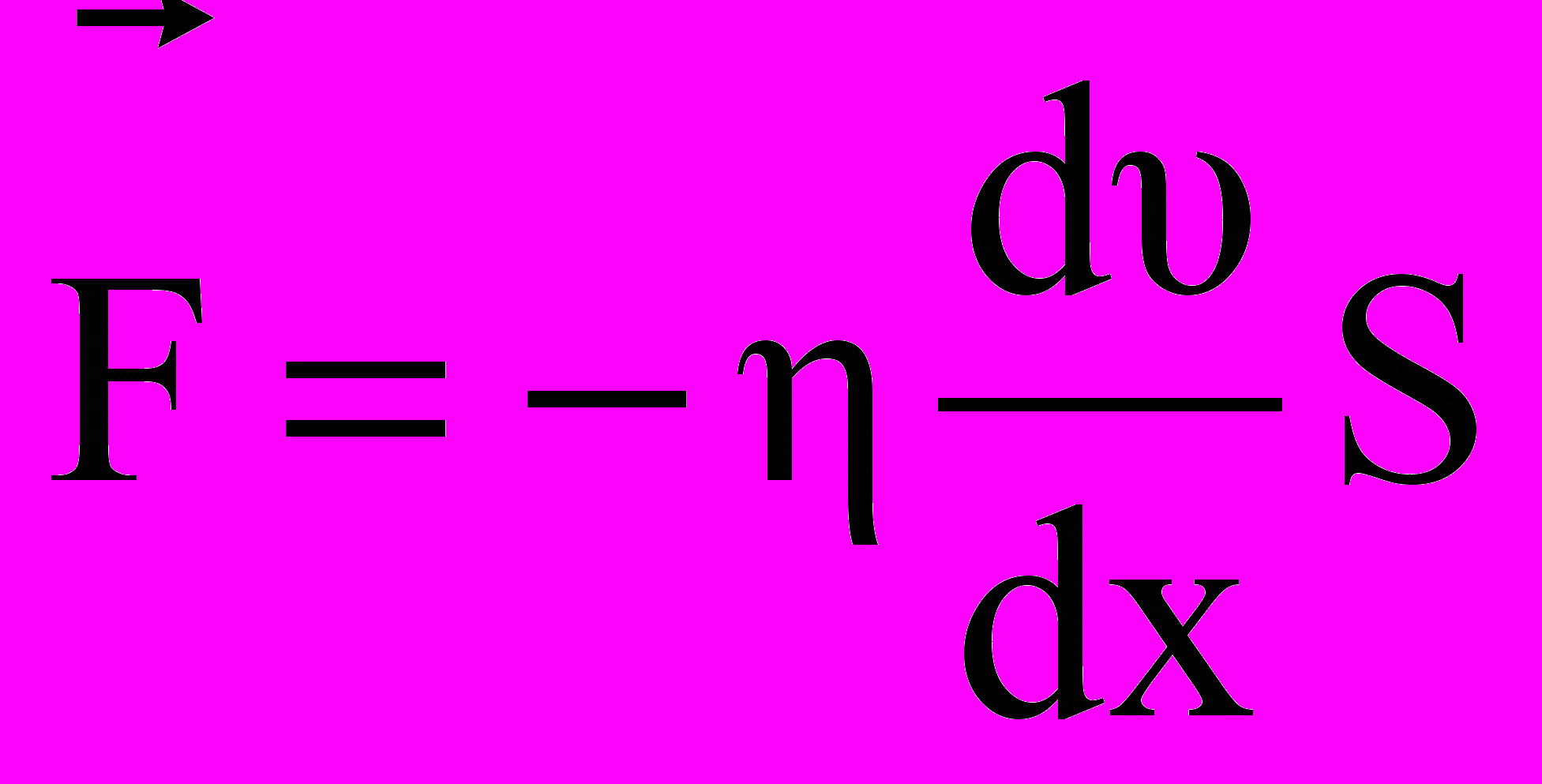
десь η - коэффициент динамической вязкости, dv/dx - градиент скорости, показывающий быстроту изменения скорости в направлении, перпендикулярном движению, S - площадь, на которую действует сила (рис. 3.1.). С другой стороны, согласно второму закону Ньютона
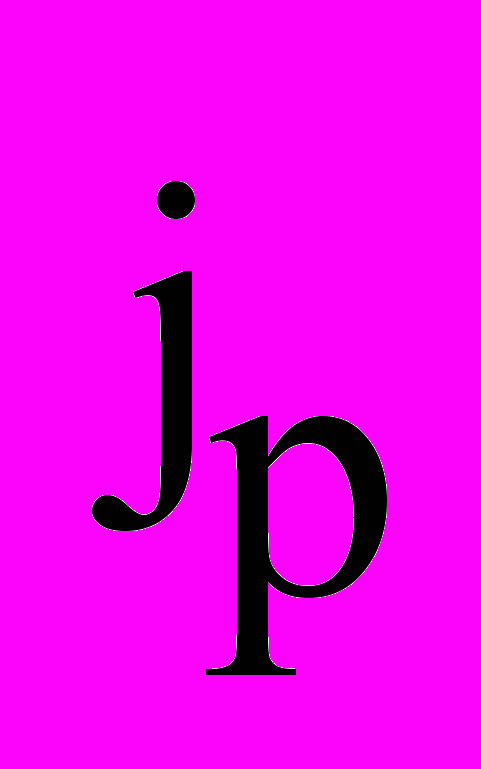
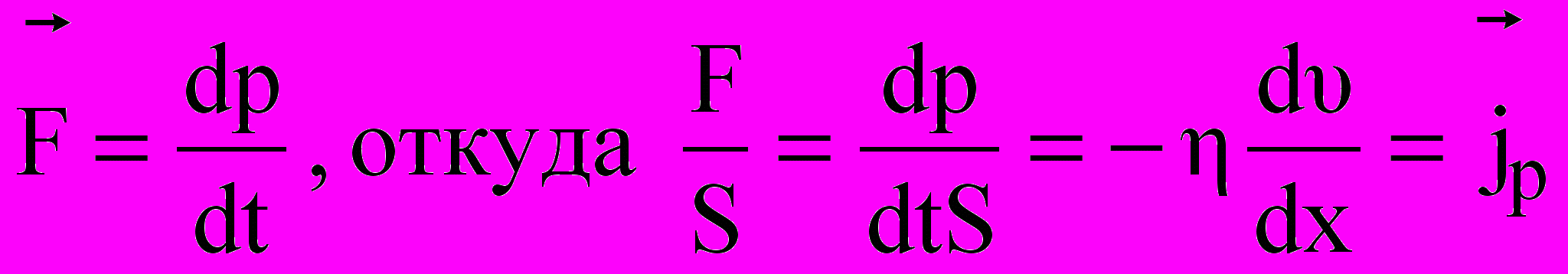
– это плотность потока импульса ( т.е. полный импульс, переносимый в единицу времени в положительном направлении оси х через единичную площадку, перпендикулярную оси ). Знак «минус» указывает, что импульс переносится в направлении убывания скорости. Из данной формулы видно, что динамическая вязкость численно равна плотности потока импульса при градиенте скорости, равном единице. Согласно молекулярно-кинетической теории газов вязкость газов можно вычислить по формуле: η═‹ℓ›ρ‹υ›/3. Коэффициент вязкости играет большую роль в различных технологических процессах, например, в производстве сахара, при уваривании густого сахарного сиропа в вакуумных аппаратах. Важнейшая характеристика полимеров – показатель текучести расплава (указываемый в марке полимера) – напрямую связан с вязкостью. Для выбора оптимальных режимов переработки полимеров (литье под давлением, экструзия) – необходимо управлять процессами плавления и вязкого течения, что невозможно без знаний коэффициентов вязкости.
3. 3. Диффузия. @
Диффузией называется явление самопроизвольного взаимного проникновения и перемешивания частиц соприкасающихся газов, жидкостей и даже твердых тел при наличии неоднородности распределения частиц разного сорта. В смесях диффузия вызывается наличием разных концентраций молекул компонентов смеси в разных частях объема. В химически чистых веществах она возникает вследствие неоднородности распределения в пространстве каких либо признаков молекул, не влияющих на их движение (например, радиоактивных меток), такой процесс носит название самодиффузии. В химически однородном газе явление диффузии подчиняется закону Фика (1855 г.):
jm = -Ddρ/dx
jm -плотность потока массы ( равна массе вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную оси х, т.е. jm=Δm/ΔtS), D - коэффициент диффузии, dρ/dx - градиент плотности, показывающий, как изменяется плотность на единицу длины х в направлении нормали к единичной площадке. Знак «минус» указывает, что перенос массы происходит в направлении убывания плотности. Коэффициент диффузии численно равен плотности потока массы при градиенте плотности, равном единице. Согласно кинетической теории газов D = ‹ℓ›‹υ›/3.
В общем случае трехмерной диффузии закон Фика имеет вид:
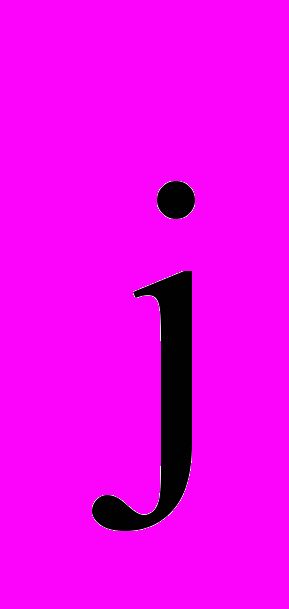 = - Dgrad(ρ). Явление диффузии широко распространено в окружающей нас действительности. Любой процесс приготовления пищи – варка варенья, консервирование (соление, маринование), копчение мяса и рыбы, словом, все явления, связанные с пропитыванием продуктов различными растворами, - подчиняются законам диффузии. Процессы диффузии имеют большое значение при модификации и окислительной деструкции в смесях и композиционных материалах на основе полимеров. В биологических мембранах, находящихся в клетках живых организмов, диффузия ионов играет очень важную роль. Широко используется это явление в процессах очистки питьевой воды от хлоридов, сульфатов, нитратов и т.п. с помощью искусственных мембран.
= - Dgrad(ρ). Явление диффузии широко распространено в окружающей нас действительности. Любой процесс приготовления пищи – варка варенья, консервирование (соление, маринование), копчение мяса и рыбы, словом, все явления, связанные с пропитыванием продуктов различными растворами, - подчиняются законам диффузии. Процессы диффузии имеют большое значение при модификации и окислительной деструкции в смесях и композиционных материалах на основе полимеров. В биологических мембранах, находящихся в клетках живых организмов, диффузия ионов играет очень важную роль. Широко используется это явление в процессах очистки питьевой воды от хлоридов, сульфатов, нитратов и т.п. с помощью искусственных мембран.Из сопоставления формул и законов, описывающих явления переноса, видно, что они во многом сходны между собой. Сходство математических выражений обусловлено общностью лежащего в основе всех этих явлений молекулярного механизма перемешивания молекул в процессе их хаотического движения и столкновений друг с другом.
4. РЕАЛЬНЫЕ ГАЗЫ
Модель идеального газа позволяет описывать поведение реальных газов при достаточно высоких температурах и низких давлениях, когда можно пренебречь размерами молекул и их взаимодействием друг с другом. Однако при повышении давления необходимо учитывать, что молекулы не являются материальными точками, а имеют определенный объем. Необходимо учитывать также силы межмолекулярного взаимодействия. Эти силы имеют электромагнитную и квантовую природу. Между молекулами вещества в любом агрегатном состоянии действуют силы взаимного притяжения, проявляющиеся в способности сопротивляться растяжению, образовывать капли и т.д. Кроме того, относительно малая сжимаемость плотных газов и способность жидких и твердых тел сопротивляться сжатию указывает на то, что между молекулами действуют также и силы отталкивания.
Н
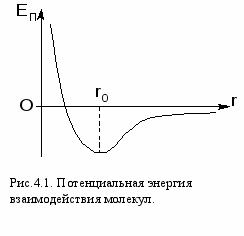 а рис.4.1. приведена качественная зависимость потенциальной энергии взаимодействия молекул от расстояния между ними. Потенциальная энергия равна нулю, когда молекулы находятся далеко друг от друга и силы межмолекулярного взаимодействия не действуют (r → ∞). При постепенном сближении между молекулами появляются силы взаимного притяжения и потенциальная энергия уменьшается, достигая минимума при r = r0. При r < r0 силы отталкивания возрастают и потенциальная энергия также начинает резко возрастать.
а рис.4.1. приведена качественная зависимость потенциальной энергии взаимодействия молекул от расстояния между ними. Потенциальная энергия равна нулю, когда молекулы находятся далеко друг от друга и силы межмолекулярного взаимодействия не действуют (r → ∞). При постепенном сближении между молекулами появляются силы взаимного притяжения и потенциальная энергия уменьшается, достигая минимума при r = r0. При r < r0 силы отталкивания возрастают и потенциальная энергия также начинает резко возрастать.4.1. Понятие фазы и фазовых переходов. @
Фазой называется совокупность всех частей системы, обладающих одинаковым химическим составом, находящихся в одинаковом состоянии и ограниченных поверхностями раздела. Понятие «фаза» шире, чем понятие «агрегатное состояние». В пределах одного агрегатного состояния вещество может находиться в нескольких фазах, отличающихся по свойствам, составу и строению. Лед, например, встречается более, чем в десяти различных фазах.
Переход вещества из одной фазы в другую называют фазовым переходом. Он всегда связан с качественными изменениями свойств вещества, различают фазовые переходы двух родов. Фазовый переход Ι рода сопровождается поглощением или выделением теплоты, называемой теплотой фазового перехода. Это плавление, кристаллизация и т.п. Фазовые переходы Ι рода характеризуются постоянством температуры (например, температура плавления льда постоянна и равна 0˚С) и сопровождаются изменением объема. Фазовые переходы, не связанные с выделением или поглощением теплоты и изменением объема, называются фазовыми переходами ΙΙ рода. Эти переходы характеризуются скачкообразным изменением теплоемкости (например, переход ферромагнитных веществ в парамагнитное состояние).
Фазовые переходы играют огромную роль в процессах плавления и кристаллизации полимеров при переработке их в изделия. Например, для улучшения физико-механических и диэлектрических свойств некоторые полимеры подвергают вытяжке, в результате чего полимер переходит из аморфного в кристаллическое состояние (фазовый переход I рода). Широкую известность имеют сформированные таким образом полимерные нити – орлон, лавсан и т.д.
4. 2. Уравнение Ван-дер-Ваальса. @
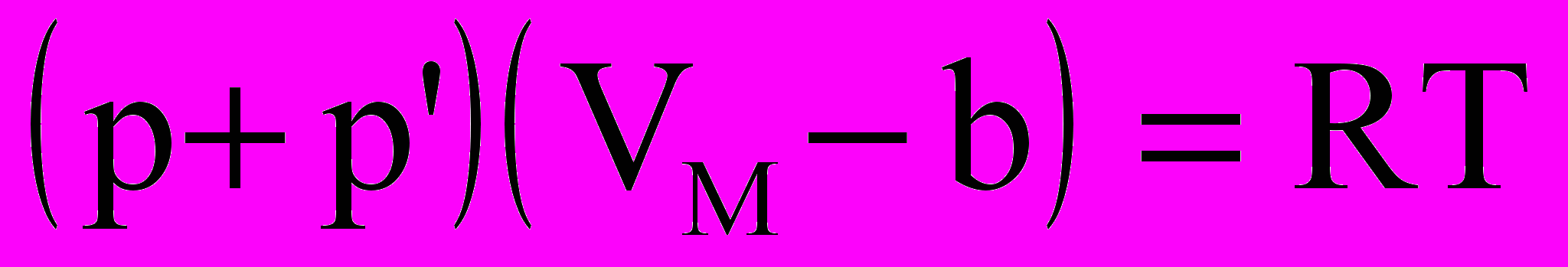
Реальные газы с повышением давления и уменьшением температуры уже не подчиняются уравнению Менделеева-Клапейрона. Ван-дер-Ваальс предположил, что в данном уравнении необходимо ввести поправки к объему и давлению. Так как молекулы реального газа имеют собственный объем, то для свободного их перемещения будет предоставлен не весь геометрический объем, занимаемый газом, а меньший - на величину той части объема, которую занимают сами молекулы.. Далее, благодаря силам притяжения молекулы находятся как бы под действием дополнительного давления р’, которое необходимо учитывать вместе с внешним. Скорректированное Ван-дер-Ваальсом уравнение для одного моля реального газа имеет вид:
Расчет показал, что добавочное давление р’= a/VМ2, где a – коэффициент Ван-дер-Ваальса, зависящий только от химической природы газа. Коэффициент b- поправка на собственный объем молекул, равная учетверенному объему молекул, н
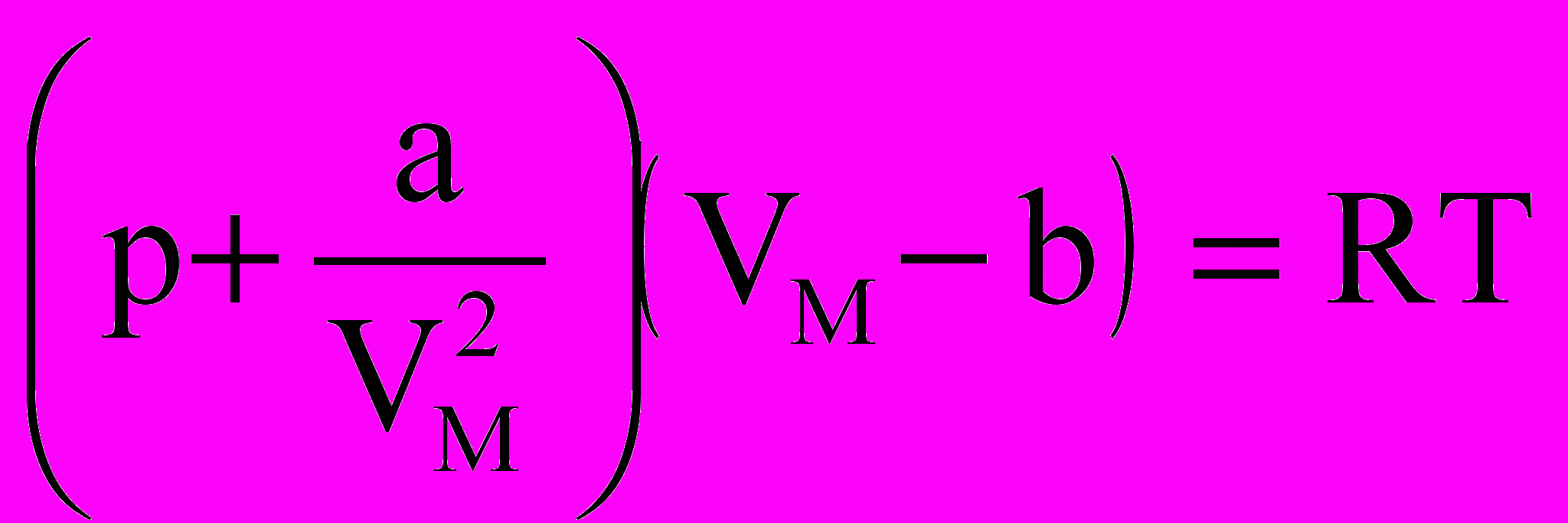
аходящихся в одном моле. Итак:
Д

ля произвольной массы газа уравнение Ван-дер-Ваальса с учетом равенства VМ = V/ν =VM/m принимает вид:
г

де V – это объем всей массы газа.
Если в уравнении Ван-дер-Ваальса для одного моля реального газа раскрыть скобки и привести уравнение к общему знаменателю, то получится уравнение третьей степени относительно VМ при заданных р и Т:
Д
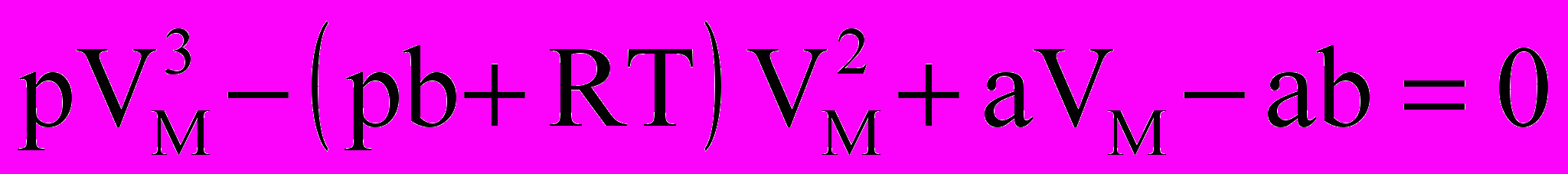
анное уравнение для конкретного давления р1 может иметь три вещественных корня VМ1, VМ2, VМ3. Зависимости р от VМ, построенные из данного уравнения при различных температурах - это изотермы Ван-дер-Ваальса. (рис.4.2).
М
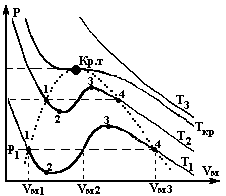 Рис.4.2. Изотермы Ван-дер-Ваальса.
Рис.4.2. Изотермы Ван-дер-Ваальса.ожно заметить, что пока температура не достигнет некоторого критического значения Ткр, в пространстве (р,V ) имеется область, где каждому значению давления соответствуют три точки изотермы с тремя различными VМ – три корня уравнения Ван-дер-Ваальса. По мере повышения температуры эти три точки сближаются и при Т=Ткр сливаются в одну точку, которая является точкой перегиба критической изотермы. При Т› Ткр изотермы Ван-дер-Ваальса близки к изотермам идеального газа.
4. 3. Изотермы реальных газов. @
Английский физик Т.Эндрюс в 1866 г. экспериментально исследовал зависимость молярного объема углекислого газа СО2 от давления при и
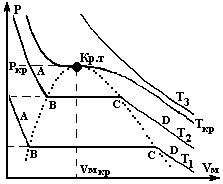 Рис.4.3. Изотермы углекислого газа СО2.
Рис.4.3. Изотермы углекислого газа СО2.зотермическом сжатии (рис.4.3). Было замечено, что при температурах, меньшей некоторой критической (Ткр=340 К) на изотермах имеется горизонтальный участок В С, на котором постоянно давление, а молярный объем возрастает от VВ до VС , причем, чем ниже Т, тем больше разностьVС –VВ. При приближении к Ткр эта разность стремится к нулю. Кривую, снятую при Ткр называют критической изотермой. На ней точки В и С сливаются в одну точку К, называемую критической точкой. Любую “докритическую” изотерму можно разбить на три характерных участка: АВ, ВС и СD. На участках АВ и СD при уменьшении объема давление возрастает, а на участке СВ – не меняется. Это своеобразие докритических изотерм связано с тем, что они охватывают различные агрегатные состояния СО2 : на участке АВ состояние системы характеризуется большой плотностью и малой сжимаемостью, что соответствует жидкости. На участке СD состояние системы характеризуется низкой плотностью и легкой сжимаемостью, что соответствует газообразному состоянию, а на участке ВС углекислота одновременно находится в 2-х агрегатных состояниях – жидком и газообразном. Если мы будем уменьшать объем газа, сжимая его, т.е. двигаться в направлении С →В, то точка С будет соответствовать началу конденсации СО2, а точка В – ее концу. Если же двигаться наоборот, от В к С (изотермическое расширение), то точка В будет соответствовать началу кипения, а точка С – его окончанию. Другими словами, точка В соответствует состоянию кипящей жидкости, а точка С – сухого насыщенного пара. В любой другой точке на участке ВС СО2 представляет собой смесь кипящей жидкости и сухого насыщенного пара. Такую смесь называют влажным паром. Он представляет собой, таким образом, двухфазную систему. С ростом Т прямолинейный участок сокращается по длине, точка В смещается вправо, С – влево. Объясняется это тем, что молярный объем жидкости, находящейся в равновесии с насыщенным паром, увеличивается с ростом температуры, так как при этом в жидкости ослабевают межмолекулярные силы сцепления. Молярный же объем насыщенного пара, напротив, уменьшается. При Т=Ткр, р=ркр, VM=VMкр точки В и С сливаются в одну и газ целиком переходит в жидкость, минуя двухфазное состояние.
Из сопоставления изотермы Ван-дер-Ваальса с реальной изотермой Эндрюса вытекает, что они примерно совпадают на участках, отвечающих однофазным состояниям вещества, но ведут себя совершенно различным образом в области расслоения на две фазы. Вместо S-образного завитка на изотерме Ван-дер-Ваальса реальная изотерма имеет в этой области прямолинейный горизонтальный участок.
Оказывается, что при некоторых условиях состояния, соответствующие участкам 1-2 и 3-4 (рис.4.2) могут осуществиться. Правда, они не вполне устойчивы. Такие состояния называются метастабильными. Вещество в состояниях 1-2 называется перегретой жидкостью, вещество в состояниях 3-4 называется пересыщенным (переохлажденным) паром. Участок кривой 2-3 практически воспроизведен быть не может, так как это состояние противоречит условию стабильности системы.
5. ЖИДКОСТИ
5. 1. Свойства и строение жидкостей. @
Жидкое состояние занимает промежуточное положение между газами и твердыми телами. В расположении частиц жидкости наблюдается так называемый ближний порядок. Это означает, что по отношению к любой частице расположение ближайших к ней соседей является упорядоченным. Однако по мере удаления от данной частицы порядок в расположении частиц довольно быстро исчезает.
Многие вопросы теории жидкого состояния были разработаны Я.И.Френкелем. Согласно Френкелю, тепловое движение в жидкостях имеет следующий характер: каждая молекула в течение некоторого времени (10-12–10-10с) колеблется около определенного положения равновесия, после чего она перескакивает в новое положение равновесия, отстоящее от прежнего примерно на расстояние, равное диаметру молекулы. Средняя длительность колебаний около одного и того же положения равновесия зависит от природы жидкости и убывает с повышением температуры.
Жидкости, как и газы, обладают текучестью: любая неуравновешенная сила вызывает их течение. Текучестью объясняется горизонтальность поверхности жидкости, находящейся в широком сосуде. Жидкость, сохраняя свой объем, под воздействием силы тяжести принимает форму сосуда. Если же жидкость освободить от действия силы тяжести, то, как показывает опыт, она принимает форму шара. Это явление наблюдается, например, в условиях невесомости (в кабинах космических кораблей).
Молекулы жидкости, в отличии от газов, интенсивно взаимодействуют между собой. Силы взаимодействия зависят от природы молекул и существенно различаются по величине для разных жидкостей.
Характерным свойством жидкостей является их очень малая изотермическая сжимаемость. Так, при увеличении внешнего давления на 105 Па объем жидкости уменьшается на тысячные доли процента. Это объясняется возникновением огромных сил отталкивания между молекулами жидкости при ее сжатии. Для жидкостей справедливо неравенство: pΔV<
Теплоемкости жидкостей зависят от их молекулярной массы, то есть от молекулярной структуры. Чем больше молекулярная масса жидкости, тем больше, как правило, ее значение теплоемкости. Особенно отчетливо это проявляется для органических жидкостей, молекулы которых состоят из большого числа атомов легких элементов Н, О, С, N, - следовательно, они обладают большим числом степеней свободы и теплоемкость их велика. Для жидкостей теплоемкость при постоянном давлении и постоянном объеме близки по значению: Ср ≈ Сv.
5. 2. Поверхностное натяжение жидкостей. @
Молекулы в жидкости располагаются настолько близко друг к другу, что силы притяжения между ними имеют значительную величину. Поскольку взаимодействие быстро убывает с расстоянием, начиная с некоторого расстояния силами притяжения между молекулами можно пренебречь. Это расстояние r называется радиусом молекулярного действия, а сфера радиуса r называется сферой молекулярного действия. Каждая молекула испытывает притяжение со стороны всех соседних с ней молекул, находящихся в пределах сферы молекулярного действия. Если молекула находится от поверхности жидкости на расстоянии, превышающем r, то равнодействующая всех сил притяжения для нее в среднем равна нулю. Если молекула находится на поверхности жидкости, равнодействующая сил притяжения не равна нулю, поскольку число соседей у такой молекулы уменьшается. Равнодействующая сил направлена внутрь жидкости перпендикулярно к ее поверхности и стремится втянуть эту молекулу во внутренние слои жидкости.
Переход молекулы из глубины жидкости в поверхностный слой возможен при совершении работы против сил в поверхностном слое. Эта работа совершается молекулой за счет запаса ее кинетической энергии и идет на увеличение потенциальной энергии молекулы. Итак, молекулы в поверхностном слое обладают дополнительной потенциальной энергией, которая называется поверхностной энергией. Поскольку положение равновесия соответствует минимуму потенциальной энергии, жидкость, свободная от внешних воздействий, как уже отмечалось, будет принимать форму шара, то есть форму с минимальной поверхностью. При заданном объеме жидкость должна иметь наименьшую площадь свободной поверхности.
Выделим мысленно часть поверхности жидкости, ограниченную замкнутым контуром. Тенденция этого участка к сокращению приводит к тому, что он действует на граничащие с ним участки с силами, распределенными по всему контуру. Эти силы называются силами поверхностного натяжения. Направлена сила поверхностного натяжения по касательной к поверхности жидкости и перпендикулярно к участку контура, на который она действует. Величина равная отношению силы поверхностного натяжения к длине контура, называется коэффициентом поверхностного натяжения, или просто поверхностным натяжением и обозначается σ. Единица поверхностного натяжения – ньютон на метр (Н/м) или джоуль на квадратный метр (Дж/м2). С повышением температуры σ уменьшается, так как увеличиваются средние расстояния между молекулами жидкости.
Поверхностное натяжение существенным образом зависит от примесей, имеющихся в жидкостях. Вещества, ослабляющие поверхностное натяжение жидкости, называются поверхностно-активными. Наиболее известным поверхностно-активным веществом по отношению, например, к воде является мыло. Существуют вещества (сахар, соль), которые увеличивают поверхностное натяжение жидкости благодаря тому, что их молекулы взаимодействуют с молекулами жидкости сильнее, чем молекулы жидкости между собой. Например, если посолить мыльный раствор, то в поверхностный слой жидкости выталкивается больше молекул мыла, чем в пресной воде. В мыловаренной технике мыло “высаливается” таким способом из раствора.
5. 3. Смачивание. Краевой угол. @
Если опустить стеклянную палочку в ртуть, а затем вынуть ее, то ртути на ней не окажется. Если же опыт повторить с водой, то палочка будет влажной и на ее конце останется капля воды. Это объясняется тем, что молекулы ртути притягиваются друг к другу сильнее, чем к молекулам стекла, а притяжение между молекулами воды слабее, чем между молекулами стекла. Говорят, что вода смачивает стекло, а ртуть – не смачивает. Явления смачивания и поверхностного натяжения взаимосвязаны.
П
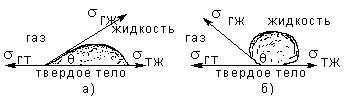
Рис.5.1. Капля жидкости на твердой поверхности
а) смачивание; б) несмачивание.
оверхностное натяжение свойственно не только жидкостям, но и твердым телам. В общем же случае поверхностное натяжение на границе двух сред 1 и 2 следует характеризовать величиной σ12, зависящей от свойств обеих сред. Если граничат друг с другом три различных вещества: твердое, жидкое и газообразное (рис.5.1), то система принимает конфигурацию, соответствующую минимуму поверхностной энергии. При этом равновесие для контура, ограничивающего жидкость на твердом теле, имеет место при выполнении условия σтг= σтж+ σжгcosθ, где σтг, σтж и σжг – поверхностные натяжения на границах: твердое тело – газ, твердое тело – жидкость и жидкость – газ.
Угол θ между касательными к поверхности твердого тела и к поверхности жидкости называется краевым углом. Этот угол может быть и острым, и тупым в зависимости от значений σтг и σтж. Если σтг > σтж, то cosθ>0 и угол θ острый, т.е. жидкость смачивает твердую поверхность (рис.5.1а). Если σтг <σтж, то cosθ<0 и угол θ тупой и жидкость не смачивает твердую поверхность (рис.5.1б). Если θ=0, то имеет место полное смачивание – жидкость растекается по поверхности твердого тела, покрывая его тонкой пленкой (как керосин на поверхности стекла). Полное несмачивание наблюдается, если жидкость образует на твердом теле шаровую каплю, имея с твердой поверхностью лишь одну точку соприкосновения (например, капля воды на поверхности парафина).
Смачивание и несмачивание являются понятиями относительными, т.е. жидкость может смачивать одну твердую поверхность и не смачивать другую. Ртуть, например, не смачивает стекло, но смачивает чистые поверхности металлов.
Явления смачивания и несмачивания широко используются в технике. Например, в процессе отделения руды от пустой породы ее, мелко раздробленную, взбалтывают в жидкости, смачивающей пустую породу и не смачивающей руду. Через эту смесь продувается воздух, а затем она отстаивается. При этом смоченные жидкостью частицы породы опускаются на дно, а крупинки руды “прилипают” к пузырькам воздуха и всплывают на поверхность.
5. 4. Поверхностное испарение и кипение жидкостей. @
При наличии свободной поверхности отдельные молекулы жидкости, обладающие избытком кинетической энергии, вырываются наружу и, таким образом, жидкость испаряется. Если ей не подводить тепло извне, внутренняя энергия молекул понижается и жидкость охлаждается. Над поверхностью жидкости образуется пар, часть молекул которого может переходить в жидкость. Равенство скорости испарения и скорости обратной конденсации пара соответствуют динамическому равновесию. При этом пар над поверхностью считается насыщенным и его давление зависит от температуры.
Жидкость испаряется с открытой поверхности при любой температуре, при этом испарение происходит на границе раздела жидкости и пара. Помимо поверхностного испарения жидкость может испытывать также объемное испарение, т.е. интенсивное образование при нагревании пузырьков насыщенного пара по всему объему, которое называется кипением. Кипение – это фазовый переход I рода.
Кипение начинается при равенстве внешнего давления и давления насыщенного пара в пузырьках внутри жидкости. При заданном постоянном внешнем давлении кипение происходит при определенной температуре Тк, называемой температурой кипения, при этом парообразование происходит во всем объеме жидкости. Для кипения жидкости необходимы два условия: 1). наличие в ней парогазовых пузырьков; 2). повышение температуры до Тк и сообщение жидкости при этой температуре теплоты. Если жидкость полностью лишена пузырьков (зародышей газовой фазы), в ней отсутствуют полости, где могли бы накапливаться пары и поэтому кипение не происходит. В процессе кипения ее температура Тк остается неизменной, поскольку подводимая теплота полностью идет на парообразование. Чем меньше внешнее давление, тем меньше Тк.
