Основы Pascal. Типы данных. Структура программы на языке Pascal

Вид материала

Теория множеств. Основные определения. Не совсем то возможно!
Понятие соответствия и функции. Композиция и способ задания функций.
Отношения и их виды.
Предикаты и кванторы.
Математическая логика: высказывания и алгебра высказываний, логические функции, суперпозиция функций, формулы. Булева алгебра.

Подобный материал:

1 2 3 4 5 6 7 8 9 ... 17

Основы C. Типы данных. Структура программы на языке С.

Си (англ. C) — стандартизированный процедурный язык программирования, разработанный в начале 1970-х годов сотрудниками Bell Labs Кеном Томпсоном и Денисом Ритчи как развитие языка Би. Си был создан для использования в операционной системе UNIX. С тех пор он был портирован на многие другие операционные системы и стал одним из самых используемых языков программирования. Си ценят за его эффективность. Он является самым популярным языком для создания системного программного обеспечения. Его также часто используют для создания прикладных программ. Несмотря на то, что Си не разрабатывался для новичков, он активно используется для обучения программированию. В дальнейшем синтаксис языка Си стал основой для многих других языков (см.: Си-подобный синтаксис).

Для языка Си характерны лаконичность, современный набор конструкций управления потоком выполнения, структур данных и обширный набор операций.

В языке Си предусмотрено несколько основных типов объектов:

Символьный.

- Объекты, описанные как символы (char), достаточно велики, чтобы хранить любой член из соответствующего данной реализации внутреннего набора символов, и если действительный символ из этого набора символов хранится в символьной переменной, то ее значение эквивалентно целому коду этого символа. В символьных переменных можно хранить и другие величины, но реализация будет машинно-зависимой. (На СМ ЭВМ значение символьных переменных изменяется от -0177 до 0177.)

Целый.

- Можно использовать до трех размеров целых, описываемых как short int, int и long int. Длинные целые

занимают не меньше памяти, чем короткие, но в конкретной реализации может оказаться, что либо короткие целые, либо длинные целые, либо те и другие будут эквивалентны простым целым. "Простые" целые имеют естественный размер, предусматриваемый архитектурой используемой машины; другие размеры вводятся для удовлетворения специальных потребностей.

Беззнаковый.

- Целые без знака, описываемые как unsigned, подчиняются законам арифметики по модулю 2**n, где n – число битов в их представлении. (На CM-ЭВМ длинные величины без знака не предусмотрены).

Вещественный.

- Вещественные одинарной точности (float) и вещественные двойной точности (double) в некоторых реализациях могут быть синонимами. (На СМ ЭВМ float занимает 32 бита памяти, а double - 64).

В языке нет логического типа данных, а в качестве логических значений используются целые "0" - "ложь" и "1" - "истина" (при проверках любое целое, не равное 0, трактуется как

"истина").

Поскольку объекты упомянутых выше типов могут быть разумно интерпретированы как числа, эти типы будут называться арифметическими. Типы char и int всех размеров совместно будут называться целочисленными. Типы float и double совместно будут называться вещественными типами. Кроме основных арифметических типов существует концептуально бесконечный класс производных типов, которые образу-

ются из основных типов следующим образом:

- массивы объектов большинства типов;

- функции, которые возвращают объекты заданного типа;

- указатели на объекты данного типа;

- структуры, содержащие последовательность объектов различных типов;

- объединения, способные содержать один из нескольких объектов различных типов.

Вообще говоря, эти методы построения объектов могут

применяться рекурсивно.

Структуры.

"Структура"-это набор логически связанных элементов данных различных типов.

-Создание структур.

При определении данных типа "структура" задаются элементы типов данных структуры и создается сама структура. Отдельные переменные в структуре называются "члены", а имя структуры называется "тэг" структуры. Данные типа structure описываются в следующей форме: struct structure-name { member-declarations }; Структура date,например, создается по следующему определению:

struct date

{

int month;

int day;

int year;

};

После того, как структура определена, вы можете описать переменную уже определенного типа. Тэг структуры должен следовать за ключевым словом struct.

Следующие ниже описания определяет переменную todayc date типа struct date:

struct date todays_date;

-Переменные в структурах.

Переменные, являющиеся элементом типа структуры, могут использоваться также, как и любые другие переменные. Оператор членства (.) определяет имя члена структуры и структуры, элементом которой он является. В приведенном ниже примере переменной month в структуре todays date присваивается значение 12:

todays date.month=12;

-Структура и указатели.

Указатели на структуры описываются также, как и на другие типы данных. Для ссылки на член структуры, адресуемой с помощью указателя, в языке СИ используется символ (->).

-Действия со структурами.

Для переменных-структур разрешены только три операции: вы можете получить ее адрес с помощью оператора адресации (&); вы можете получить доступ к одному из ее членов; вы можете присвоить одну структуру другой посредством операции присвоения.

Пример: Использования структур.

#include

#include

main()

{

struct ti *current_time;

time_t long_time; /* значение времени*/

time (&long time); /* получение количества секунд в long time */

/* преобразование в структуру времени */

current_time = localtime(&long_time);

/* использование оператора выборки члена структуры для доступа

к отдельному члену структуры */

printf ("hour: %d'n", current_time->tm_hour);

}

Приведенные выше программа использует оператор выборки члена структуры для доступа к отдельным элементам структуры tm, которая содержит информацию о времени. Затем распечатывается значение текущего часа. Функция localtime не содержится в библиотеке процедур Quick-C. В результате, вам понадобится для компиляции вашей программы в среде Quick-C воспользоваться программным списком. Использование программных списков описывается в Разделе 6.1.

Использование функций ввода/вывода языка СИ.

Стандартая библиотека процедур СИ содержит необходимый для программиста на языке СИ полный набор функций ввода/вывода (I/O). -Функции ввод/вывод одного символа (getchar, putchar). Функция getchar получает следующий по порядку символ с клавиатуры и возвращает его в качесве значения. Функция putchar выводит один символ на экран.

-Форматный вывод (printf).

Функция printf выводит на экран данные в заданном формате. В аргументы функции printf входит строка формата, заключенная в двойные кавычки, за которой следуют имена переменных, те, которые должны быть распечатаны. Литеральный текст в строке формата распечатывается в том же виде, в каком он находится в этой строке. Последовательности управляющих символов, находящиеся в строке формата, вставляют в вывод специальные символы. Ниже приведены некоторые наиболее часто используемые управляющие последовательности:

Управляющая последовательность Символ

\n сдвиг строки

\t табуляция

\' одинарная кавычка

\'' двойная кавычка

\\ обратный слэш

-Форматный ввод - scanf.

Функция scanf считывает с клавиатуры ввод в заданном формате. В аргументы функции scanf входит строка формата, заключенная в двойные кавычки, за которой следуют имена переменных, подлежащих считыванию. Аргументы, используемые функцией scanf, должны быть указателями на переменные, а не самими этими переменными. Это нужно для того,чтобы функция scanf могла изменять содержимое переменных.

-Спецификации строки формата.

В управляющей строке, в соответсвии с которой содержимое переменных будет считано или распечатано, помещаются спциальные знаки спецификаций преобразования. Первая переменная соответствует по своему местоположению первому символу процента (%) и т.д. по всему списку символов преобразования:

Спецификация Значение

преобразования

%d десятичное целое

%u десятичное без знака

%o восьмиричное без знака

%x шестнадцатеричное без знака

%e экспонента

%f число с плавающей точкойа

%c один символ

%s строка символов

-Пример: Использование функций ввода/вывода языка СИ.

#include

typedef char * string;

main()

{

char c, j;

int i;

string item1[10], item2[10];

float x;

printf ("please enter a single character:\n");

c = getchar();

printf ("\tthe character just input was -- %c\n",c);

printf ("nenter a digit, a string, a float, and a string: ");

scanf ("%d %s %f %s", &i, item1, &x, item2);

printf ("\n\ayou entered\n");

printf ("%d\n%s\n%f\n%s", i, item2, x, item2);

printf ("\n\nexample of conversion specifications:\n");

printf ("decimal\toctal\thex\tcharacter\n");

for (j = 65; j<=70; j++)

printf ("%d\t%o\t%x\t%c\n", j,j,j,j);

}

Графы и их виды. Матрицы инцидентности и смежности графа.

Граф — совокупность двух множеств V (точек) и E (линий), между элементами которых определено отношение инцидентности, причем каждый элемент еÎЕ инцидентен ровно двум элементам v, v"ÎV. Элементы множества V называются вершинами графа G, а элементы множества E - его ребрами. Если инцидентные ребру вершины рассматриваются в определенном порядке, то каждому ребру приписывается направление от первой из инцидентных вершин ко второй. Направленные ребра часто называют дугами, а содержащий их граф - ориентированным, в отличие от определенного ранее неориентированного графа. Первая по порядку вершина, инцидентная ребру ориентированного графа, называется его началом, вторая - его концом.

Множество ребер Е может быть пустым. Если же множество вершин V пусто, то пусто и Е. Такой граф называется пустым. Различные ребра могут быть инцидентны одной и той же паре вершин, в этом случае они называются кратными. Граф, содержащий кратные ребра, называется мультиграфом. Ребро может соединять некоторую вершину саму с собой. Такое ребро называется петлей. Если множества вершин и ребер графа конечны, то граф называется конечным.

Задать граф - значит описать множества его вершин и ребер, а также отношение инцидентности. Пусть v₁, v₂, ..., v_n - вершины графа G, а e₁, e₂, ..., e_m - его ребра. Отношение инцидентности можно определить матрицей инцидентности ïe_ijï, имеющей m строк и n столбцов. Столбцы соответствуют вершинам графа, строки - ребрам. Если ребро е_i инцидентно вершине v_j , то e_ij=1, в противном случае e_ij=0. В матрице инцидентности ïe_ijï ориентированного графа G, если вершина v_j - начало ребра e_i, то e_ij=-1; если v_j - конец e_i , то e_ij=1; если e_i - петля, а v_j - инцидентная ей вершина, то e_ij=a, где a - любое число, отличное от 1, 0 и -1. В остальных случаях e_ij=0.

Матрицей смежности графа называется квадратная матрица ïd_ijï, столбцам и строкам которой соответствуют вершины графа. Для неориентированного графа d_ij равно количеству ребер, инцидентных i-й и j-й вершинам, для ориентированного графа этот элемент матрицы смежности равен количеству ребер с началом в i-й вершине и концом в j-й. Таким образом, матрица смежности неориентированного графа симметрична (d_ij = d_ji).

Теория множеств. Основные определения. Не совсем то возможно!

Абстракцию, в результате которой некоторая часть мира признается предметом, будем называть абстракцией предмета. Математическое понятие множества, иллюстрациями которого в реальном мире являются различные собрания предметов, коллекции, совокупности, связано с еще одной абстракцией, которую будем называть абстракцией множества. Если предмет а входит в множество М, то говорят: "а является элементом М" или "элемент а принадлежит множеству М" и пишут аÎМ. Если множество А состоит из конечного числа элементов а₁, а₂,..., а_n, то пишут А={а₁,а₂,...,а_n}. Множество, не содержащее ни одного элемента, называют пустым и обозначают Æ. Число элементов в конечном множестве А называется мощностью А и обозначается ïАï. Если каждый элемент множества А является также элементом множества В, то А называют подмножеством множества В и пишут АÍВ.

Пусть А и В - два множества. Множество С тех элементов, которые принадлежат и А и В, называется пересечением или теоретико-множественным произведением множеств А и В. При этом пишут С=АÇВ={xïxÎА и xÎВ}. Операция построения АÇВ по заданным А и В называется теоретико-множественным умножением. Множество D всех элементов, каждый из которых принадлежит хотя бы одному из множеств А или В, называется объединением или теоретико-множественной суммой множеств А и В. При этом пишут D=АÈВ={xïxÎА или xÎВ}. Операция построения АÈВ по заданным А и В называется теоретико-множественным сложением. Множество Е тех элементов, принадлежащих А, которые не принадлежат В, называется теоретико-множественной разностью А и В. При этом пишут Е=А\В={xïxÎА и xÏВ}. Операция, позволяющая получить А\В по заданным А и В, называется теоретико-множественным вычитанием.

Множество пар, первая компонента в которых является элементом множества А, а вторая - элементом множества В, называется декартовым, геометрическим или прямым произведением множеств А и В и обозначается А´В. Если члены декартова произведения равны между собой, то декартово произведение называется декартовой степенью. Пары, являющиеся элементами множества А´В, обозначаются (а, b), где аÎА, bÎB. Элементами декартова произведения множеств А´В и С являются пары вида ((а,b),с)=(а,b,c), где сÎС. Если число множеств сомножителей равно n, то элементами их декартова произведения будут кортежи или векторы (упорядоченные наборы) по n элементов. Элементы, образующие кортеж (вектор), называются координатами или компонентами кортежа. Число координат называется длиной или размерностью кортежа. Проекцией вектора v на i-ю ось (обозначается пр_iv) называется его i-я компонента. Проекцией множества V векторов одинаковой длины на i-ю ось называется множество проекций всех векторов из V на i-ю ось: пр_iV={пр_ivïvÎV}.

Понятие соответствия и функции. Композиция и способ задания функций.

Соответствием между множествами А и В называется подмножество GÍАxВ. Если (а, b)ÎG, то говорят, что b соответствует а при соответствии G. Множество пр₁G называется областью определения соответствия, множество пр₂G - областью значений соответствия. Если пр₁G=А, то соответствие называется всюду определенным. В противном случае соответствие называется частичным. Если пр₂G=B, то соответствие называется сюръективным. Множество всех bÎB, соответствующих элементу аÎА, называется образом а в В при соответствии G. Множество всех а, которым соответствует b, называется прообразом b в А при соответствии G. Соответствие G называется функциональным (или однозначным), если образом любого элемента из пр₁G является единственный элемент из пр₂G. Соответствие G между А и В называется взаимно-однозначным, если оно всюду определено, сюръективно, функционально и, кроме того, прообразом любого элемента из пр₂G является единственный элемент из пр₁G.

Функцией называется функциональное соответствие. Если функция f устанавливает соответствие между множествами А и В, то говорят, что функция f имеет тип А→В и обозначают это f: А→В. Каждому элементу а из своей области определения функция f ставит в соответствие единственный элемент b из области значений. Это обозначается следующей записью: f(a)=b. Элемент a называется аргументом функции, b - значением функции на a. Функция типа А₁´А₂´...´А_n→В называется n-местной функцией. Пусть дано соответствие GÍA´B. Если соответствие HÍB´A таково, что (b, a) ÎH тогда и только тогда, когда (a, b)ÎG, то соответствие H называется обратным к G и обозначается G^-1. Если соответствие, обратное к функции f: А→B, является функциональным, то оно называется функцией, обратной к f и обозначается f^-1.

Пусть даны функции f: А→B и g: B→C. Функция h: A→C называется композицией функций f и g (обозначается f°g), если имеет место равенство h(x)=g(f(x)), где xÎA. Функция, полученная из f₁, ..., f_n некоторой подстановкой их друг в друга и переименованием аргументов, называется суперпозицией. f₁, ..., f_n. Выражение, описывающее эту суперпозицию и содержащее функциональные знаки и символы аргументов, называется формулой.

Наиболее простой способ задания функций - это таблицы, т.е. конечные списки пар (x, f(x)). Другим способом задания функций является формула, описывающая функцию как суперпозицию других функций. Еще одним способом задания функции является рекурсивная процедура, позволяющая вычислить значение функции на основе других, ранее определенных её значений.

Отношения и их виды.

Подмножество RÍМⁿ называется n-местным отношением на множестве М. Говорят, что а₁, ..., а_n находятся в отношении R, если (а₁, ..., а_n)ÎR. Одноместное отношение - это просто подмножество М. Такие отношения называются признаками. а обладает признаком R, если аÎR и RÍМ. Наиболее часто встречающимися и хорошо изученными являются двухместные (бинарные) отношения. Если а и b находятся в отношении R, это часто записывается как аRb. Для отношений на конечных множествах обычно используются матричный способ задания. Матрица бинарного отношения на множестве М={а₁, ..., а_m} - это квадратная матрица С размерности m, в которой элемент с_ij, стоящий на пересечении i-ой строки и j-го столбца, равен 1, если а_iRa_j, и 0 в противном случае.

Для любого множества М отношение Е, заданное матрицей, в которой по главной диагонали стоят единицы, а в остальных местах - нули, называется отношением равенства на М. Отношение называется обратным к отношению R (обозначается R^-1), если a_iRa_j тогда и только тогда, когда a_jR^-1a_i. Отношение R называется рефлексивным, если для любого аÎМ имеет место аRа. Главная диагональ его матрицы содержит только единицы. Отношение R называется антирефлексивным, если ни для какого aÎМ не выполняется аRа. Главная диагональ его матрицы содержит только нули. Отношение R называется симметричным, если для пары (а, b)ÎМ² из аRb следует bRа. Матрица симметричного отношения симметрична относительно главной диагонали, т.е. c_ij=c_ji для любых i и j. Отношение R симметрично тогда и только тогда, когда R=R^-1. Отношение R называется антисимметричным, если из аRb и bRа следует а=b. Отношение R называется транзитивным, если для любых а, b, с из аRb и bRс следует аRс. Отношение R называется отношением эквивалентности (или просто эквивалентностью), если оно рефлексивно, симметрично и транзитивно. Отношение R называется отношением нестрогого порядка, если оно рефлексивно, антисимметрично и транзитивно. Отношение R называется отношением строгого порядка, если оно антирефлексивно, антисимметрично и транзитивно.

Предикаты и кванторы.

Предикатом Р(х₁, ..., х_n) называется функция Р: М→В, где М - произвольное множество, а В - двоичное множество {0,1}. Иначе говоря, n-местный предикат, определенный на М, - это двузначная функция от n аргументов, принимающих значения в произвольном множестве М. М называется предметной областью предиката, а х₁, ..., х_n - предметными переменными. Для любых М и n существует взаимно-однозначное соответствие между n-местными отношениями и n-местными предикатами на М. Каждому n-местному отношению R соответствует предикат Р, такой, что Р(а₁,...,а_n)=1, если и только если (а₁,...,а_n)ÎR. Всякий предикат Р(a₁,...,a_n) определяет отношение R, такое, что (а₁,...,а_n)ÎR, если и только если Р(а₁,...,а_n)=1. При этом R задает область истинности предиката Р.

Пусть Р(х) - предикат, определенный на М. Высказывание "для всех х из М Р(х) истинно" обозначается "хР(х). Знак " называется квантором общности. Высказывание "существует такой х из М, что Р(х) истинно" обозначается $хР(х). Знак $ называется квантором существования. Переход от Р(х) к "хР(х) или к $хР(х) называется связыванием переменной х. Переменная, на которую навешен квантор, называется связанной; несвязанная переменная называется свободной. Навешивать кванторы можно на любые логические выражения, которые при этом заключаются в скобки. Выражение, на которое навешивается квантор, называется областью действия квантора; все вхождения переменной х в это выражение являются связанными.

Математическая логика: высказывания и алгебра высказываний, логические функции, суперпозиция функций, формулы. Булева алгебра.

Математическая логика представляет собой методику и теорию математических доказательств. Алгебра образованная множеством В={0,1} вместе со всеми возможными операциями на нем, называется алгеброй высказываний (алгеброй логики). Высказываниями называются 1) элементарные высказывания; 2) составные или сложные высказывания. Элементарным высказыванием называется символ, которому поставлено в соответствие логическое значение истина или ложь. Составные высказывания строятся с помощью логических связок Ø, Ù, Ú, ®, ~,

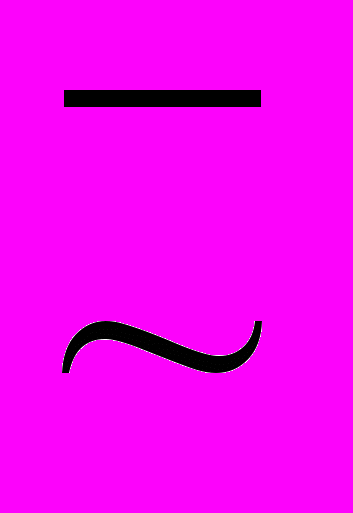(соответственно "не", "и", "или", "влечет", "эквивалентно", "неэквивалентно").

Логическая функция f(x₁,...,x_n) - это функция, принимающая значения 0 или 1, аргументы которой также принимают значения 0 или 1. Множество всех логических функций обозначается Р₂. Всякая логическая функция n переменных может быть задана таблицей, в левой части которой перечислены все 2ⁿ наборов значений переменных, а в правой части - значения функции на этих наборах.

Логические функции двух переменных

x₁	x₂	f₀	f₁	f₂	f₃	f₄	f₅	f₆	f₇	f₈	f₉	f₁₀	f₁₁	f₁₂	f₁₃	f₁₄
0	0	0	1	0	0	0	1	1	1	1	0	0	0	1	1	1
0	1	0	1	0	1	1	0	1	0	1	0	1	1	0	0	1
1	0	0	1	0	1	1	0	0	0	1	1	0	0	1	1	0
1	1	0	1	1	1	0	1	1	0	0	1	0	1	0	1	0

Функции f₀(х₁,х₂) и f₁(х₁,х₂) - константы. Функция f₂(х₁,х₂) называется конъюнкцией х₁ и х₂ (операция логического умножения или функция И). Её обозначения: х₁&х₂, х₁Ùх₂, х₁·х₂, х₁х₂. Функция f₃(х₁,х₂) называется дизъюнкцией х₁ и х₂ (операция логического сложения или функция ИЛИ). Её обозначения: х₁Úх₂, х₁+х₂. Функция f₄(х₁,х₂) - это сложение по модулю 2 (функция неравнозначности). Она равна 1, когда значения ее аргументов различны и равна 0, когда они равны. Её обозначения: х₁Åх₂, х₁Dх₂. Функция f₅(х₁,х₂) называется эквивалентностью или равнозначностью. Её обозначения: х₁~х₂, х₁ºх₂. Функция f₆(х₁,х₂) - импликация. Её обозначения: х₁®х₂, х₁Éх₂. Функция f₇(х₁,х₂) - стрелка Пирса. Её обозначение: х₁¯х₂. Функция f₈(х₁,х₂) - штрих Шеффера. Её обозначение: х₁ïх₂. Остальные функции специальных названий не имеют и легко выражаются через перечисленные ранее функции. Приведенные выше операции над логическими значениями известны под названием булевых операций.

Суперпозицией функций f1,...,fm называется функция f, полученная с помощью подстановок этих функций друг в друга и переименованием переменных, а формулой называется выражение, описывающее эту суперпозицию. Формулы, представляющие одну и ту же функцию, называются эквивалентными или равносильными.

Булева алгебра.

Алгебра (Р₂; Ú, &, Ø), основным множеством которой является все множество логических функций, а операциями - дизъюнкция, конъюнкция и отрицание, называется булевой алгеброй логических функций. Операции булевой алгебры также часто называют булевыми операциями. Они имеют следующие основные свойства.

Ассоциативность: а) х₁(х₂х₃)=(х₁х₂)х₃; б)(х₁Úх₂)Úх₃=х₁Ú(х₂Úх₃)

Коммутативность: а) х₁х₂=х₂х₁; б)х₁Úх₂=х₂Úх₁

Дистрибутивность конъюнкции относительно дизъюнкции: х₁(х₂Úх₃)=х₁х₂Úх₁х₃

Дистрибутивность дизъюнкции относительно конъюнкции: х₁Ú(х₂х₃)=(х₁Úх₂)(х₁Úх₃)

Идемпотентность (одинаковость): а) хх=х; б)хÚх=х.

Двойное отрицание:

.

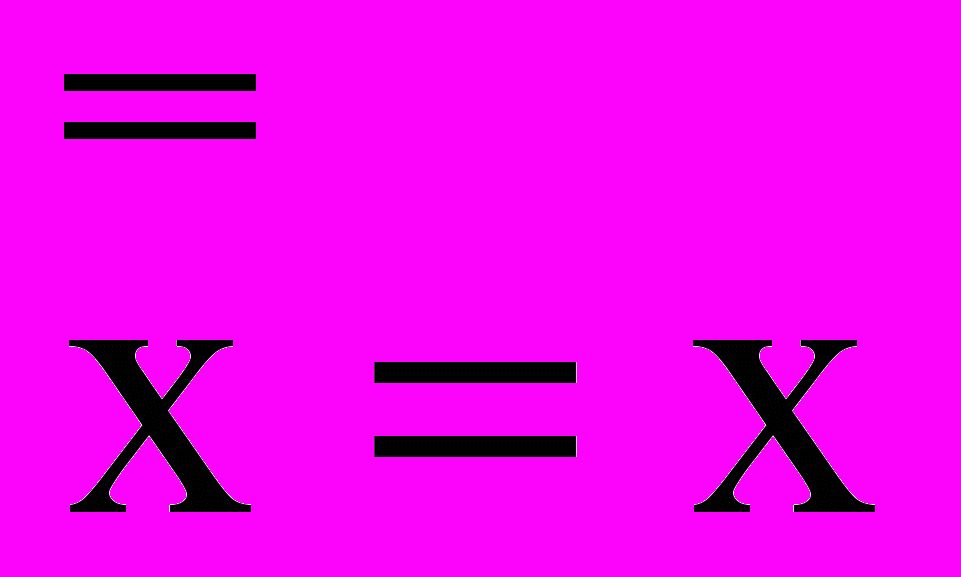Свойства констант: а) хÙ1=х; б) хÙ0=0; в) хÚ1=1; г) хÚ0=х; д)

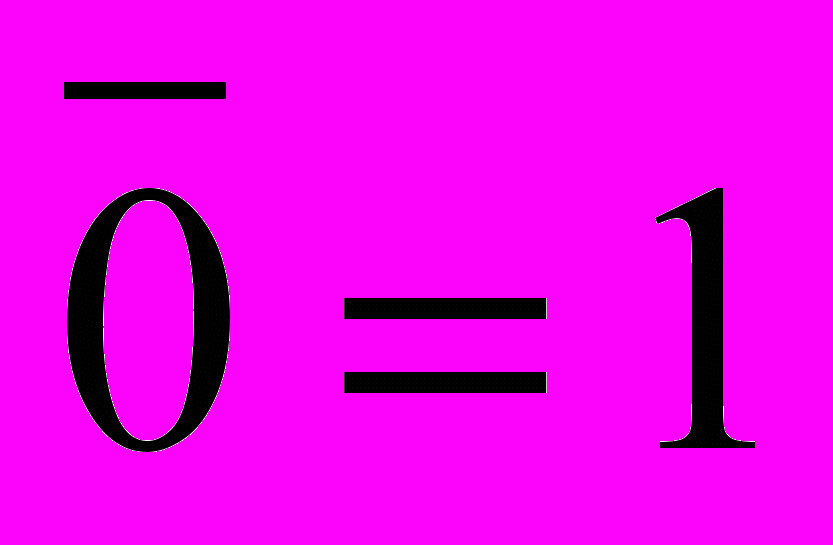; е)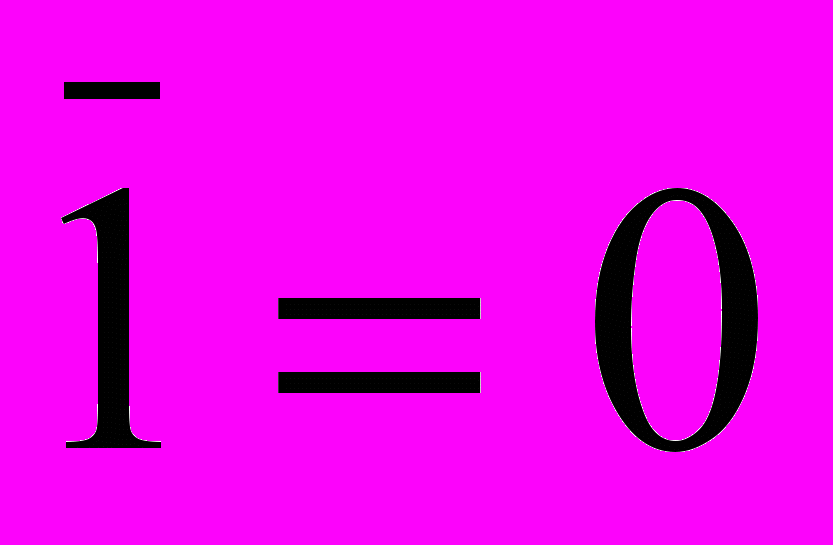

.

Правила де Моргана: а)

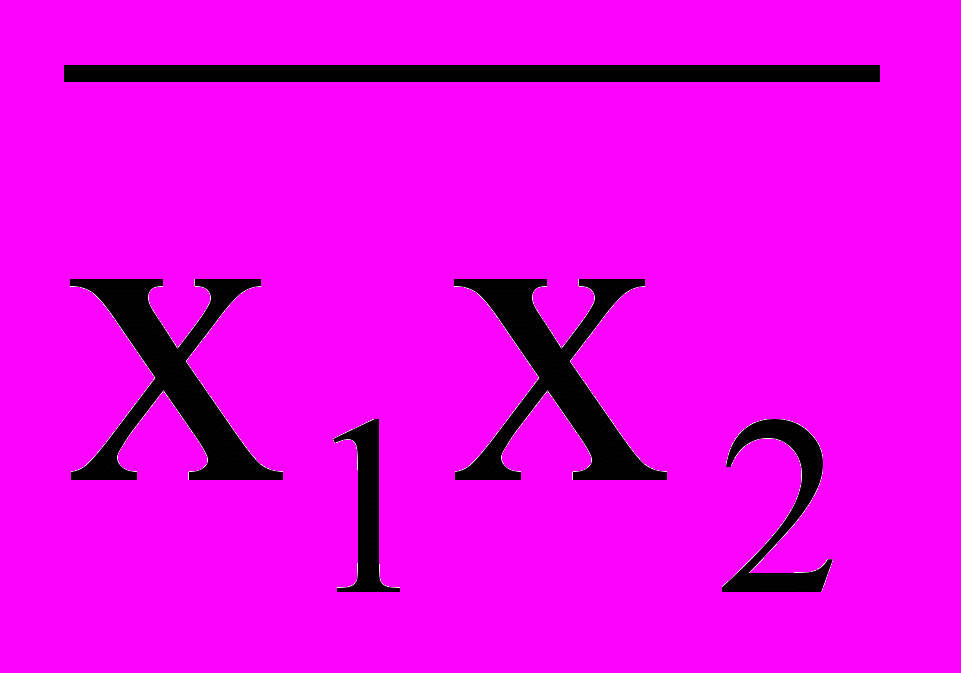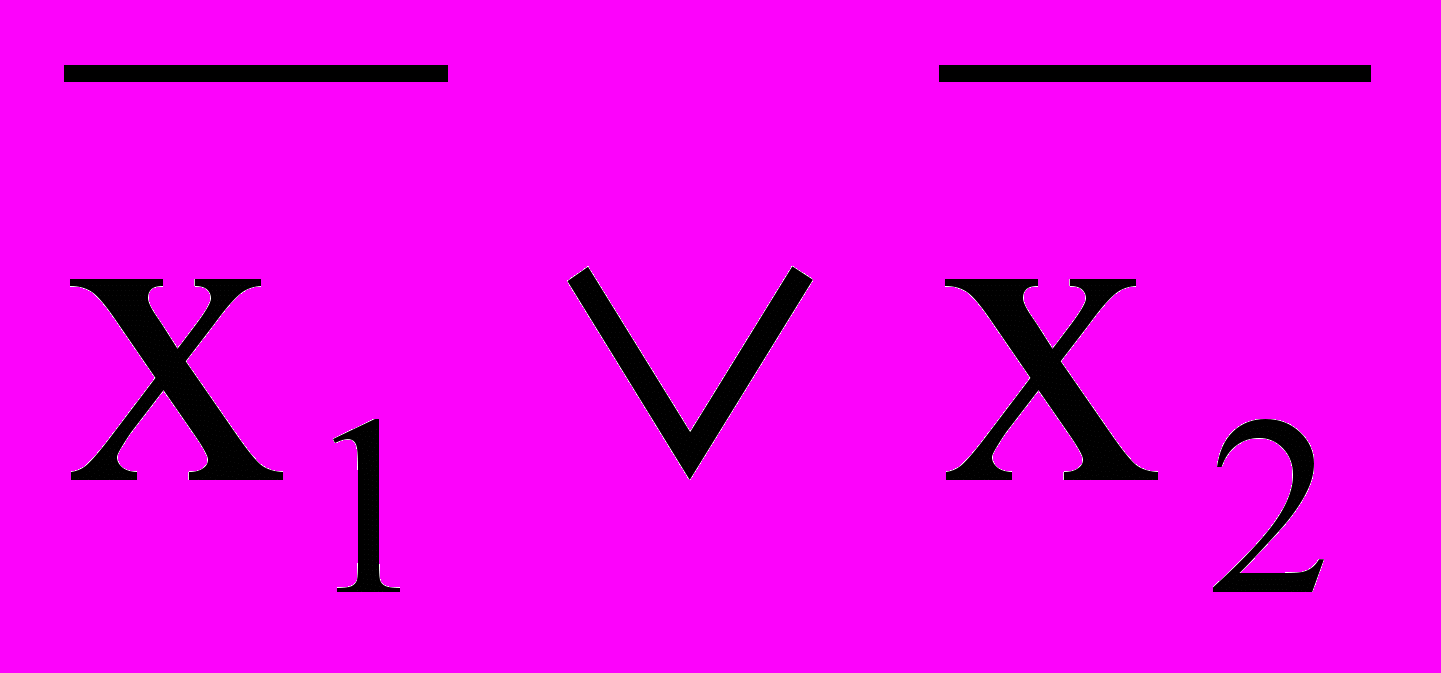; б)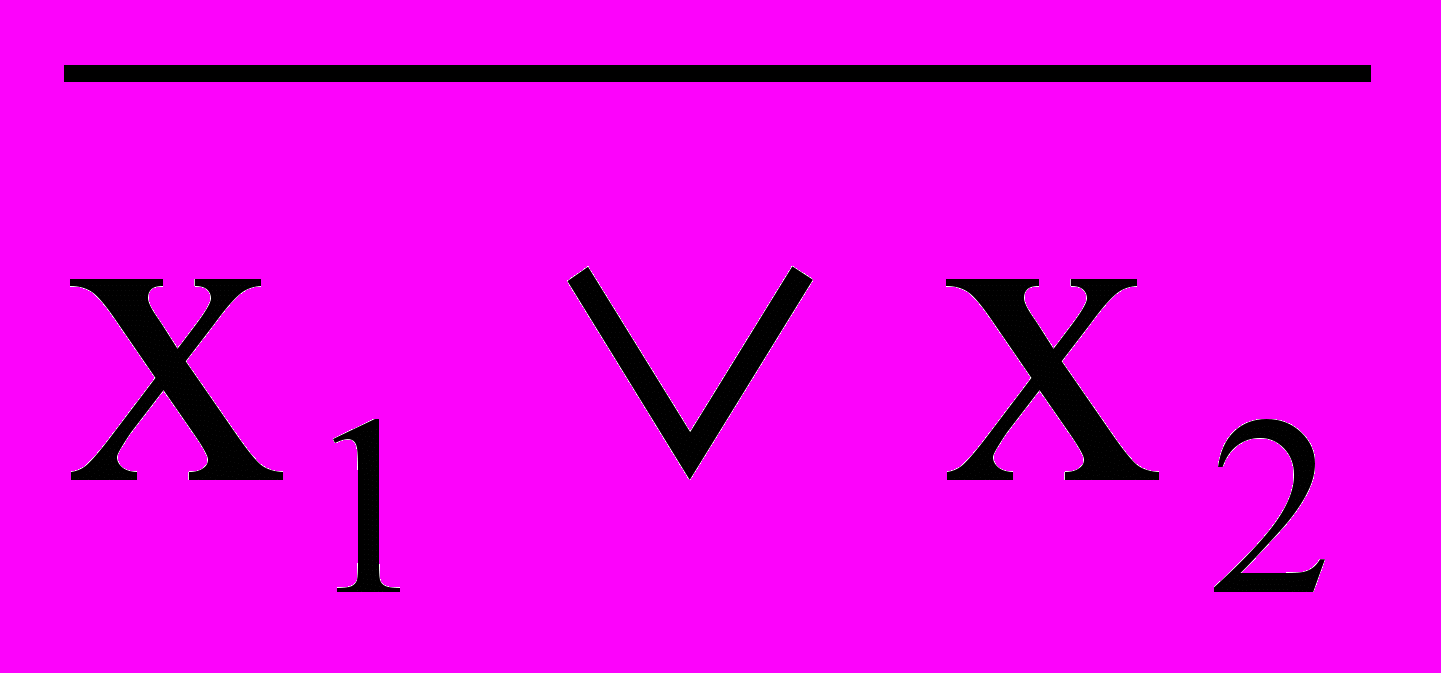

.

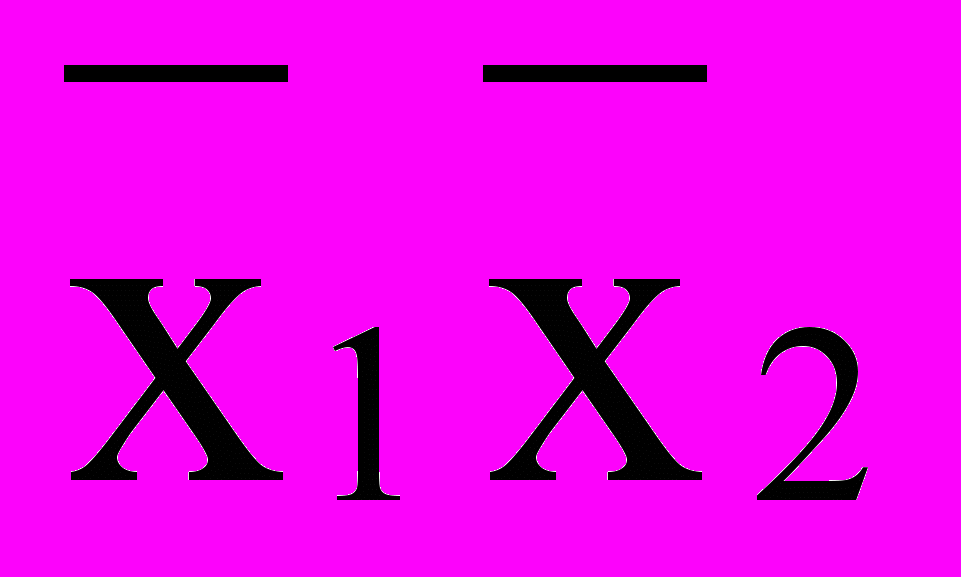Закон противоречия:

.

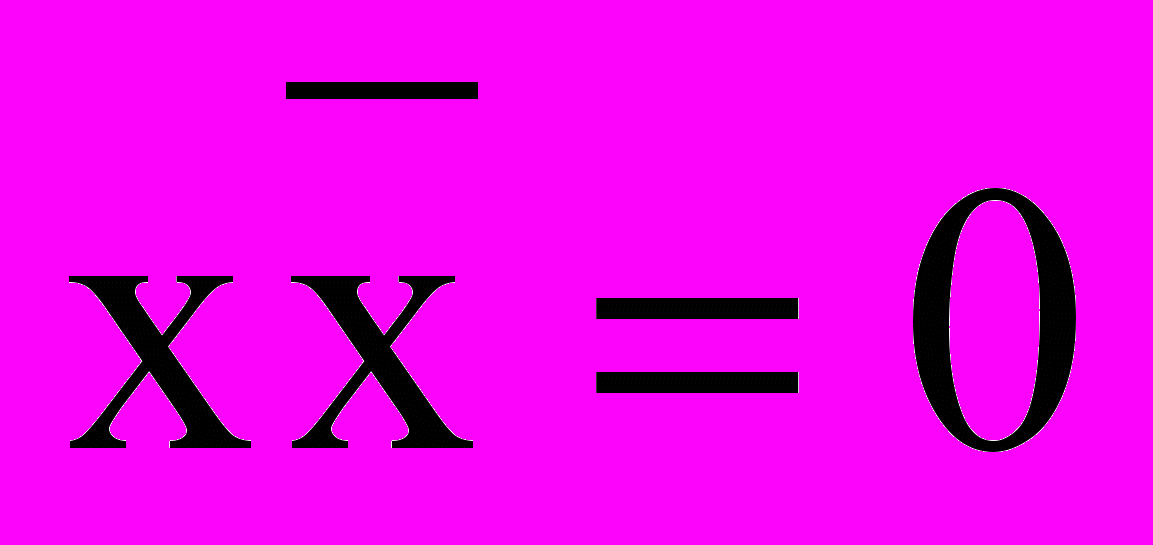Закон "исключенного третьего":

.

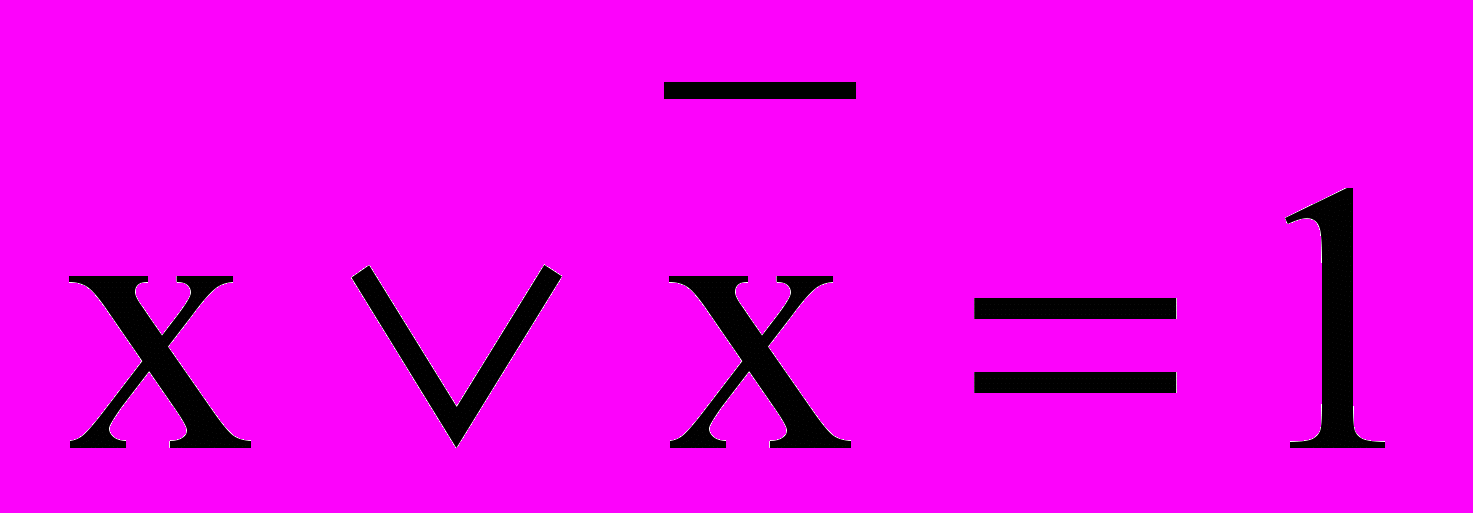Выделяют следующие эквивалентные преобразования в булевой алгебре: упрощение формул, приведение к дизъюнктивной и конъюнктивной нормальной форме. Упрощение формул, т.е. получение эквивалентных формул, содержащих меньшее число символов, включает:

Поглощение: xÚxy=x, x(xÚy)=x;

Склеивание:

;

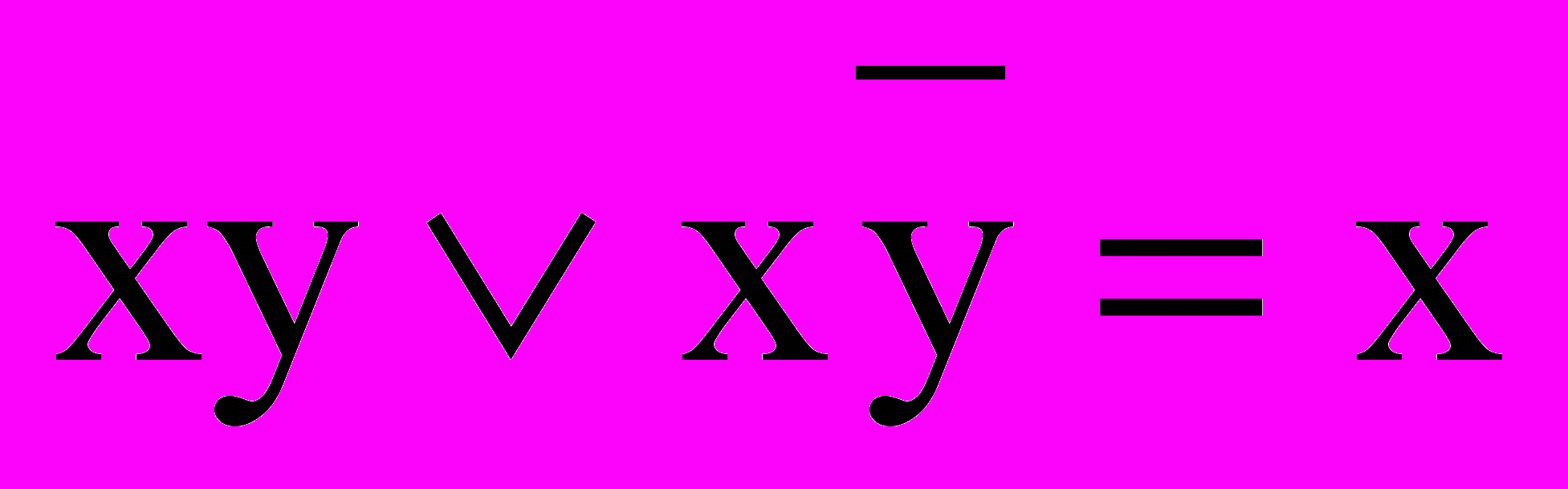Обобщенное склеивание:

;

Закон Блейка-Порецкого:

.

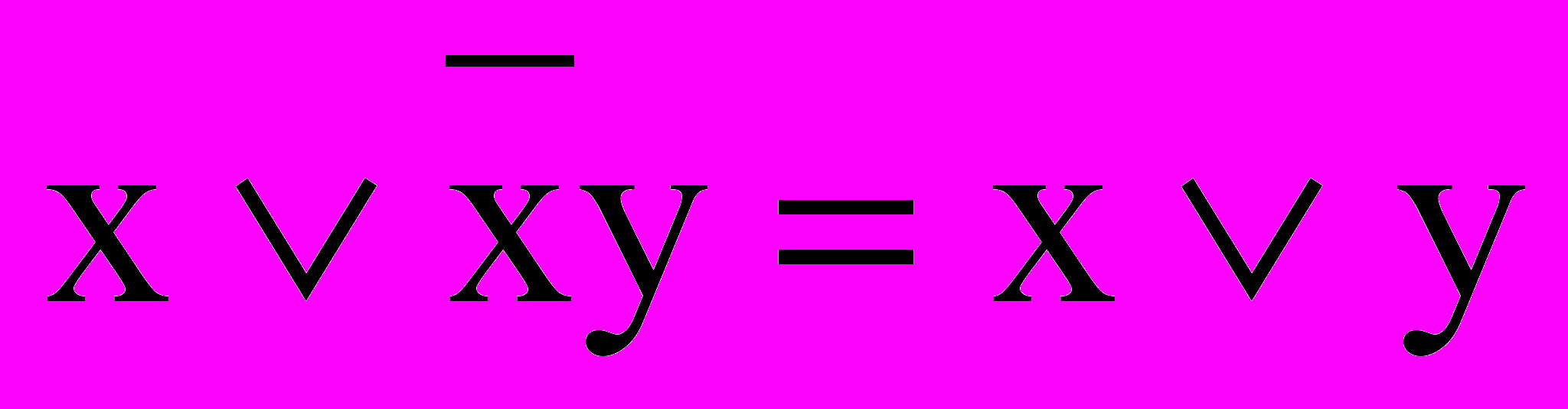Элементарными конъюнкциями называются конъюнкции переменных или их отрицаний, в которых каждая переменная встречается не более одного раза. Дизъюнктивной нормальной формой (ДНФ) называется формула, имеющая вид дизъюнкции элементарных конъюнкций. Приведение к ДНФ осуществляется следующим образом. Сначала с помощью двойного отрицания и правил де Моргана все отрицания "спускаются" до переменных. Затем раскрываются скобки, с помощью идемпотентности, законов противоречия и "исключенного третьего" удаляются лишние конъюнкции и повторения переменных в конъюнкциях, а также исключаются константы с помощью соответствующих соотношений. Совершенной дизъюнктивной нормальной формой (СДНФ) называется формула, имеющая дизъюнктивную нормальную форму, в которой каждая элементарная конъюнкция содержит все переменные.

Конъюнктивная нормальная форма (КНФ) определяется как конъюнкция элементарных дизъюнкций. Переход от ДНФ к КНФ можно выполнить с помощью двойного отрицания, “спуская” отрицания и используя упрощение формул и свойства булевых операций. Совершенной конъюнктивной нормальной формой (СКНФ) называется формула, имеющая конъюнктивную нормальную форму, в которой каждая элементарная дизъюнкция содержит все переменные.

Blog

Основы Pascal. Типы данных. Структура программы на языке Pascal