Физико-химические основы разделения биазеотропных смесей 05. 17. 04 Технология органических веществ
| Вид материала | Автореферат |
СодержаниеАфанасьев В.В. Общая характеристика работы Основное содержание диссертации Основные результаты диссертации отражены |
- А. Г. Морачевский профессор, д Х. н. Физико-химические основы процессов разделения, 39.16kb.
- Образовательная программа 240100 Химическая технология и биотехнология Дисциплина Химия, 54.66kb.
- Программа вступительного экзамена по специальным дисциплинам для магистрантов специальности, 87.1kb.
- Программа дисциплины "Технология органических веществ" Контрольная работа 1 по дисциплине, 1073.33kb.
- Физико-химические закономерности химического осаждения гидратированных оксидов металлов, 282.22kb.
- Гоу впо «Московский государственный открытый университет», 483.26kb.
- Контрольная работа По дисциплине физико-химические свойства и методы контроля качества, 77.41kb.
- Физико-химические основы процесса разделения «арсенита натрия гидролизного» на базовые, 258.81kb.
- Программа ХII международной конференции Физико-химические основы ионообменных процессов, 465.27kb.
- Программа ХI международной конференции Физико-химические основы ионообменных процессов, 195.73kb.
На правах рукописи
МЯГКОВА ТАТЬЯНА ОЛЕГОВНА
ФИЗИКО-ХИМИЧЕСКИЕ ОСНОВЫ
РАЗДЕЛЕНИЯ БИАЗЕОТРОПНЫХ СМЕСЕЙ
05.17.04 – Технология органических веществ
Автореферат
диссертации на соискание ученой степени
кандидата технических наук
Москва - 2007
Работа выполнена на кафедре химии и технологии основного органического синтеза государственного образовательного учреждения высшего профессионального образования «Московская государственная академия тонкой химической технологии им. М.В. Ломоносова»
| Научный руководитель: | доктор технических наук, профессор Фролкова А.К. |
| Официальные оппоненты: | доктор технических наук, профессор Тойкка А.М. |
| кандидат технических наук Афанасьев В.В. | |
| Ведущая организация: | ГОУ ВТО «Российский химико-технологический университет им. Д.И.Менделеева» |
Защита состоится 13 ноября 2007 года в 14.30 в аудитории М-119 на заседании диссертационного совета Д 212.120.02 при Московской государственной академии тонкой химической технологии им. М.В.Ломоносова по адресу: 119571, г. Москва, пр. Вернадского, 86.
С диссертацией и авторефератом можно ознакомиться в библиотеке Московской государственной академии тонкой химической технологии им. М.В.Ломоносова по адресу: 119571, г. Москва, пр. Вернадского, 86.
Автореферат размещен на сайте МИТХТ им. М.В. Ломоносова www.mitht.ru и разослан _____ октября 2007года.
Ученый секретарь
диссертационного совета, к.т.н. Е.А. Анохина
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы:
Явление биазеотропии сегодня является достаточно уникальным (изучено 12 систем) и представляет особый интерес при изучении термодинамики фазовых равновесий. Диаграммы парожидкостного равновесия (ПЖР) таких систем характеризуются близкими температурами кипения во всем концентрационном симплексе, малой разницей между составами равновесных фаз и, как следствие, относительной летучестью компонентов (α), близкой к единице. По этим причинам возникают трудности: 1) при постановке физического эксперимента, качество которого определяет надежность оценки параметров математических моделей; 2) при моделировании фазовых равновесий и процессов разделения; 3) при разделении биазеотропных смесей.
Исследование биазеотропии несомненно актуально, поскольку в ряде случаев она является необходимым элементом преобразования структур фазовых диаграмм, а имеющиеся сведения о биазеотропном поведении составляющих промышленных смесей, в частности, в производстве высших жирных спиртов придают этим исследованиям и практическую значимость.
Цель работы:
Создание физико-химических основ разделения бинарных и многокомпонентных биазеотропных смесей.
Для достижения поставленной цели необходимо решить следующие задачи:
- синтезировать структуры диаграмм фазового равновесия биазеотропных систем на основе заданного граничного контура диаграммы и выбрать из полученного множества объекты для дальнейшего исследования;
- оценить возможности использования сложного фазового поведения как критерия адекватности моделей и получить термодинамически согласованные математические модели ПЖР исследуемых систем;
- исследовать эволюцию биазеотропных систем при варьировании давления и при добавлении тяжелокипящих разделяющих агентов (РА);
- предложить схемы разделения смесей заданного состава на основе термодинамико-топологического анализа базовых (исходных) и производных (в присутствии РА) диаграмм;
- исследовать закономерности разделения биазеотропных смесей и определить статические параметры работы колонн схемы.
Научная новизна:
1. Для заданного граничного контура тройной системы с одной биазеотропной и двумя моноазеотропными составляющими (контур 3.4) синтезировано 158 новых структур диаграмм хода дистилляционных линий классов 3.4.0, 3.4.1, 3.4.2 и 264 соответствующих им структур диаграмм хода единичных К-линий.
2. Впервые получены математические модели (параметры уравнения Вильсона), термодинамически непротиворечиво описывающие ПЖР биазеотропных систем бутилпропионат (БП) – пропионовая кислота (ПК), бензол (Б) - перфторбензол (ПФБ) – метилпропионат (МП), бензол – перфторбензол - третичный амиловый спирт (ТАС); сформулированы рекомендации к выбору математической модели.
3. На основе полученных в вычислительном эксперименте полных данных ПЖР в тройных системах с двумя тройными азеотропами локализованы составы азеотропов и показана эволюция структур диаграмм при варьировании давления, протекающая через стадию образования внутреннего тройного тангенциального азеотропа.
4. На основе полных данных ПЖР в четырехкомпонентных системах проведен анализ поведения тройных биазеотропных составляющих Б-ПФБ-МП, Б-ПФБ-ТАС в присутствии потенциального разделяющего агента (ДМСО). Выявлен сложный характер вложения единичных α – многообразий в концентрационный тетраэдр, осуществлен прогноз возможных продуктов экстрактивной ректификации биазеотропных смесей.
Практическая значимость:
1. Предложены принципиальные технологические схемы полного разделения тройных биазеотропных смесей Б-ПФБ-МП, Б-ПФБ-ТАС эквимолярного состава, сочетающие комплекс экстрактивной ректификации с комплексом, основанным на варьировании давления в колоннах. Определены оптимальные параметры работы колонн ЭР.
2. При наличии в системе двух единичных α – многообразий одноименных пар компонентов показана возможность управления составами продуктов ЭР за счет инверсии летучестей азеотропообразующих компонентов при различных концентрациях РА.
3. Показана принципиальная возможность разделения биазеотропной смеси бутилпропионат - пропионовая кислота, являющейся первым представителем ряда промышленных биазеотропных систем, экстрактивной ректификацией.
Апробация работы и публикации:
По материалам диссертации опубликовано две статьи в изданиях, рекомендованных ВАК, и тезисы четырех докладов на международных научно-технических конференциях. Подана заявка № 2007117782/04 от 16 мая 2007г. на изобретение.
Работа выполнялась в рамках госбюджетной темы № 1Б-1-353 и гранта РФФИ № 05-03-32958.
Объем работы:
Диссертация состоит из введения, четырех глав, списка литературы и приложения. Работа представлена на _____ страницах машинописного текста, содержит _____ рисунков, _____ таблиц. Библиография включает _____ наименования.
ОСНОВНОЕ СОДЕРЖАНИЕ ДИССЕРТАЦИИ
Во введении обоснована актуальность изучаемой проблемы, сформулированы цель и задачи исследования, представлена структура диссертации и основные выводы работы.
Первая глава посвящена обзору литературы по вопросам фазового поведения азеотропных систем, математического моделирования ПЖР и современным проблемам разделения сложных многокомпонентных смесей. Азеотропы разного типа и сепаратрисы (границы областей развития процесса) накладывают ограничения на процесс ректификационного разделения. Рассмотрены термодинамические особенности фазового равновесия жидкость-пар моно- и биазеотропных систем, в том числе и при варьировании внешних параметров (давление Р, температура Т), описаны все известные в настоящее время биазеотропные системы. Приведены условия возникновения биазеотропии. На основе анализа специальных приемов разделения азеотропных смесей сделан вывод о перспективности экстрактивной ректификации.
Рассмотрены математические модели парожидкостного равновесия, которые используются при описании зеотропных и моноазеотропных систем. Примеры моделирования биазеотропии в литературе, за редким исключением, отсутствуют.
На основании анализа литературных источников, патентов, научно - технической документации сформулированы цель и конкретные задачи диссертационной работы.
Во второй главе представлен выбор методов и объектов исследования. Для решения поставленных задач в работе используются: термодинамико - топологический анализ фазовых диаграмм, компьютерный эксперимент с использованием проблемно-ориентированного комплекса ChemCad 5.2.0. Для интерпретации полученных результатов привлекаются экспериментальные данные разных авторов.
Для выбора исходных объектов в теоретической части второй главы проведен синтез всего множества диаграмм ПЖР биазеотропных систем с заданным граничным контуром. Как уже отмечалось, при разделении смесей со сложной структурой равновесной диаграммы, которые характерны для моно-, а тем более биазеотропных систем, перспективным является метод экстрактивной ректификации. Для того, чтобы показать явные преимущества экстрактивной ректификации, выбран более сложный граничный контур (3.4), который содержит 2 моно- и одну биазеотропную составляющие, и далее соответствующие ему диаграммы трехкомпонентных систем, характеризующиеся в том числе наличием тройной биазеотропии.
С помощью метода, ранее примененного Л.А Серафимовым к моноазеотропным системам, осуществлен синтез возможных диаграмм дистилляционных и К - линий в тройных системах с заданным граничным контуром (3.4). Здесь под заданным контуром мы понимаем закрепленное количество граничных особых точек (семь) и разное чередование типов граничных особых точек при обходе контура в одном направлении. Рассмотрены два вида граничных контуров (1 и 2), представленных в табл. 1.
На рис. 1 показаны примеры диаграмм с обычным и нетривиальным ходом дистилляционных линий в тройных диаграммах с разными наборами граничных особых точек.
Таблица 1
Количество структур диаграмм дистилляционных линий
и единичных К-линий в системах с заданным граничным контуром 3.4.
| Граничный контур | Класс диаграммы | Количество диаграмм | |
| дистилляционных линий | единичных К-линий | ||
| Контур 1 N+1N2-C1N2+N1-N2+N2- | 3.4.0 | 7 | 12 |
| 3.4.1 | 11 | 21 | |
| 3.4.2 | 46 | 84 | |
| ВСЕГО | 64 | 117 | |
| Контур 2 N+1N2-N+1N2-C1N2+N2- | 3.4.0 | 7 | 8 |
| 3.4.1 | 16 | 26 | |
| 3.4.2 | 21 | 53 | |
| ВСЕГО | 94 | 147 | |
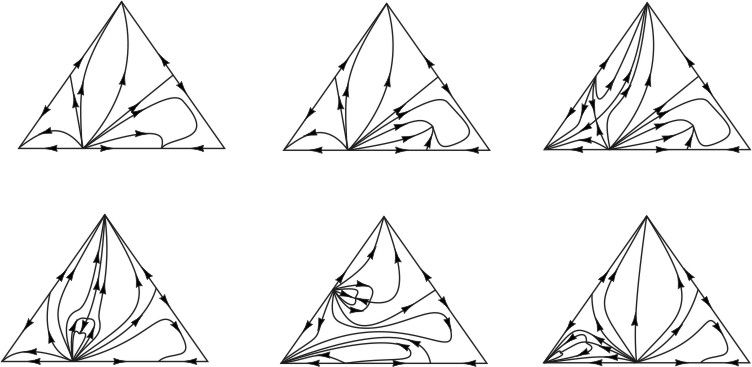
3.4.0
3.4.1
3.4.2
3.4.2
3.4.2
3.4.2
Рис. 1. Примеры хода дистилляционных линий в тройных диаграммах
с разными наборами граничных особых точек
Проведенный нами синтез структур позволил дополнить существующую классификацию тройных систем 155 новыми диаграммами хода дистилляционных линий и 288 диаграммами единичных К-линий.
В качестве исходных систем для дальнейшего исследования выбраны бинарные и тройные системы (исходные и составляющие с разделяющим агентом), которые принадлежат полученным множествам диаграмм:
- базовая бинарная биазеотропная система бензол - перфторбензол, наиболее полно изученная при различных условиях и тем ценная в качестве теста для оценки адекватности математической модели и в целом надежности вычислительного эксперимента;
- бинарная биазеотропная система бутилпропионат – пропионовая кислота, имеющая промышленное значение;
- тройные системы, включающие две моно- и биазеотропную бинарную составляющую бензол – перфторбензол – метилпропионат, бензол - перфторбензол – третичный амиловый спирт;
- тройные системы с потенциальным разделяющим агентом (бензол – перфторбензол - ДМСО, бутилпропионат – пропионовая кислота - ДМСО).
ДМСО - полярный растворитель, наиболее часто применяемый в промышленных процессах экстракции и ЭР - выбран в качестве разделяющего агента на основе литературных данных и качественных представлений о межмолекулярных взаимодействиях.
Третья глава посвящена моделированию парожидкостного равновесия в исследуемых системах и, прежде всего, в биазеотропных.
Применение ЭВМ в исследовательской практике, методов математического моделирования и вычислительного эксперимента способствует ускорению предпроектной стадии разработки технологий; снижению затрат на проведение натурных экспериментов; позволяет изучать поведение систем в широких диапазонах внешних параметров. Активно используемые в настоящее время специализированные программные продукты (различные версии проблемно-ориентированного комплекса ChemCad, PRO-II, Hysys) ориентированы в основном на решение прикладных химико - технологических задач, что требует определенной осторожности при их использовании как средств научного поиска.
Основным при организации вычислительного эксперимента остается вопрос выбора математической модели, способной качественно и количественно воспроизводить, используя минимум экспериментальных данных, термодинамические особенности фазового поведения системы. Методически важен и выбор объекта исследования, который, с одной стороны, представляет интерес с точки зрения дальнейшего развития теории и практики разделения сложных смесей, а с другой, – может выступать тестом для оценки термодинамической согласованности выбранной модели. К таким объектам и относятся выбранные нами биазеотропные системы.
При оценке параметров модели (выбрано уравнение Вильсона) по немногочисленным экспериментальным и псведоэкспериментальным данным (UNIFAC) для бинарных систем особое внимание нами уделялось выбору при закрепленном давлении тех из них, которые:
- дают удовлетворительное количественное описание азеотропных параметров в биазеотропной системе;
- моделируют логически непротиворечивую картину эволюции обоих азеотропов при варьировании внешних условий (в соответствии со 2-м законом Вревского);
- дают знакопеременную концентрационную зависимость избыточного потенциала Гиббса ∆gЕ(х);
- воспроизводят биазеотропию хотя бы на качественном уровне.
Важен также выбор уравнения, описывающего зависимость упругостей паров индивидуальных компонентов и азеотропов от температуры, которые воспроизводят условия реализации биазеотропии: наличие точек Банкрофта разного рода, в частности, точек третьего рода (r22) в тройной системе Б-ПФБ-МП между двумя бинарными положительными и двумя бинарными отрицательными азеотропами; в тройной системе Б-ПФБ-ТАС между бинарным положительным азеотропом ПФБ-Б и двумя положительными азеотропами ПФБ-ТАС, Б-ТАС. Для описания зависимости Р(Т) нами используется уравнение Library, содержащееся в базе данных ChemCad и имеющее вид:
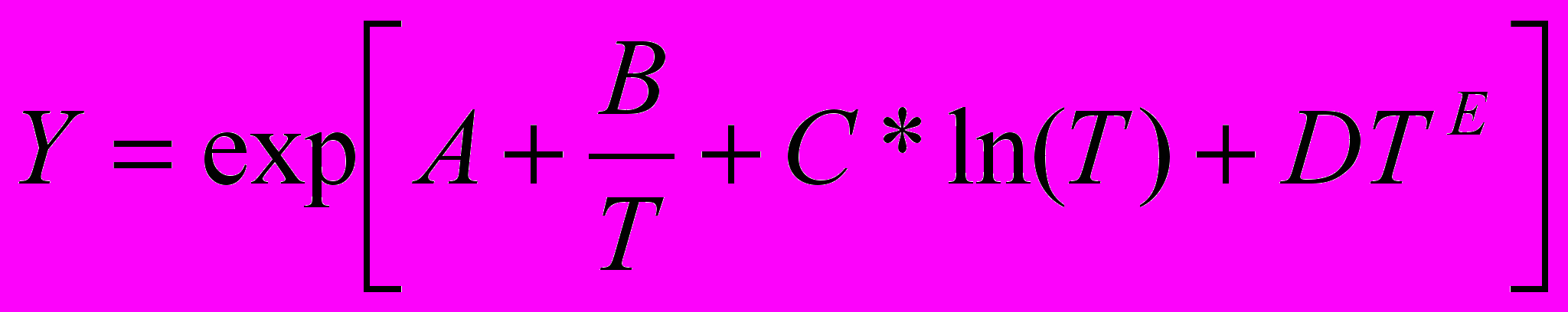 .
.Были получены малые параметры уравнения Вильсона, отвечающие п.п. 1-4 (табл.2), что обеспечивает корректность вычислительного эксперимента. Отмечено, что биазеотропия моделируется с параметрами разного знака, что иллюстрируется в работе и на примере других систем (диэтиламин-метанол, изобутилацетат-уксусная кислота, пентафторэтан - аммиак).
В табл. 3 приведены температуры кипения индивидуальных компонентов и азеотропов, а также составы азеотропов при закрепленном давлении. Для сравнения представлены характеристики азеотропов, полученные экспериментально или расчетом по модели UNIFAC (псевдоэкспериментальные данные).
В ряде случаев экспериментальные составы азеотропов, полученные разными авторами, различаются весьма значительно (на ~4-6%), что затрудняет оценку параметров модели. Отмечено также, что групповая модель значительно уступает по качеству описания и может применяться как источник псевдоэкспериментальных данных для модельных систем.
При моделировании ПЖР в тройных системах выбор составов жидкой фазы проводили по методу секущих и сечений. Данные представлены в концентрационном треугольнике ходом единичных К- и α-линий (рис. 2), что позволило локализовать составы тройных азеотропов. На рисунках также показан ход дистилляционных линий. Полученные структуры диаграмм фазового равновесия тройных систем Б-ПФБ-МП и Б-ПФБ-ТАС принадлежат к классу 3.4.2 синтезированного множества.
Таблица 2
Малые параметры уравнения Вильсона
| Система 1 – 2 | Давление, мм рт.ст. | Параметры | |
| λ12 | λ21 | ||
| Бензол – перфторбензол | 760 | -445,561 | 1218,177 |
| 300 | -455.8238 | 1164.119 | |
| Бензол – метилпропионат | 760 | 7,033 | 98,176 |
| Перфторбензол – МП | 760 | 7,854 | -35,152 |
| Бензол - ТАС | 300 | 121.5741 | 982.5173 |
| Перфторбензол – ТАС | 300 | 433.4386 | 1190.528 |
| Бутилпропионат – пропионовая кислота | 104,9 | -853.8698 | 1527.496 |
| Бензол – ДМСО | 760 | 108,137 | 871,833 |
| 300 | 147.5312 | 846.3485 | |
| Перфторбензол – ДМСО | 760 | 218,430 | 30,217 |
| 300 | 47.83627 | 92.66113 | |
| Метилпропионат – ДМСО | 760 | 150,048 | 780,254 |
| ТАС – ДМСО | 300 | 1917.484 | -568.6025 |
| Бутилпропионат – ДМСО | 104,9 | 787.5041 | 1350.729 |
| Пропионовая к-та -.ДМСО | 104,9 | -999.8604 | -906.4543 |
Изучена эволюция структур фазовых диаграмм тройных систем при варьировании давления. На рис. 3 представлена цепь преобразования диаграмм системы Б-ПФБ-ТАС, в которой неотъемлемым элементом являются биазеотропная система (рис. 3,б) и тонкая система с тройным внутренним тангенциальным азеотропом (рис. 3,в).
Таблица 3
Свойства индивидуальных компонентов и параметры бинарных азеотропов
| Система 1-2 | Давление | Т1, 0С | Т2, 0С | Параметры азеотропа | |||
| Трасч, 0С | Храсч, м.д. | Тэксп, 0С | Хэксп, м.д. | ||||
| Б-ПФБ | 760 | 80,13 | 80,24 | 80,4 | 0,21 | 80,45 | 0,24 |
| 79,85 | 0,83 | 79,35 | 0,8168 | ||||
| Б-ПФБ | 500 | 67,13 | 67,85 | 67,91 | 0,15 | 68,61 | 0,2248 |
| 66,39 | 0,85 | 66,85 | 0,845 | ||||
| Б-ПФБ | 300 | 52,73 | 54,08 | 54,17 | 0,16 | 54,55 | 0,2 |
| 52,39 | 0,91 | 52,5 | 0,89 | ||||
| Б-МП | 760 | 80,13 | 79,46 | 78,71 | 0,45 | 79.45 | 0.49 |
| 500 | 67,13 | 67,18 | 66,19 | 0,53 | 66,18 | 0,53 | |
| ПФБ-МП | 760 | 79,46 | 80,24 | 80,39 | 0,70 | 80,39* | 0,65* |
| 500 | 67,85 | 67,18 | 68,07 | 0,65 | 68,05* | 0,65* | |
| Б-ТАС | 760 | 80,13 | 101,84 | 78,89 | 0,88 | 80,00 | 0,865 |
| 500 | 67,13 | 90,62 | 66,35 | 0,9 | 66,47* | 0,9* | |
| 300 | 52,73 | 78,16 | 52,35 | 0,95 | 52,41* | 0,95* | |
| ПФБ-ТАС | 760 | 80,24 | 101,84 | 76,69 | 0,79 | 76,98* | 0,79* |
| 500 | 67,85 | 90,62 | 65,11 | 0,82 | 65,29* | 0,80* | |
| 300 | 54,08 | 78,16 | 52,11 | 0,85 | 52,25* | 0,84* | |
| БП-ПК | 104,9 | 87,04 | 87,43 | 88,06 | 0,279 | 88,44 | 0,305 |
| 87,02 | 0,945 | 88,06 | 0,876 | ||||
| БП-ДМСО | 104,9 | 87,04 | 127,62 | 86,96 | 0,95 | 86.95* | 0,95* |
| ПК-ДМСО | 104,9 | 87,43 | 127,62 | 136,57 | 0,32 | 136.6* | 0,32* |
* - псевдоэкспериментальные данные (UNIFAC)

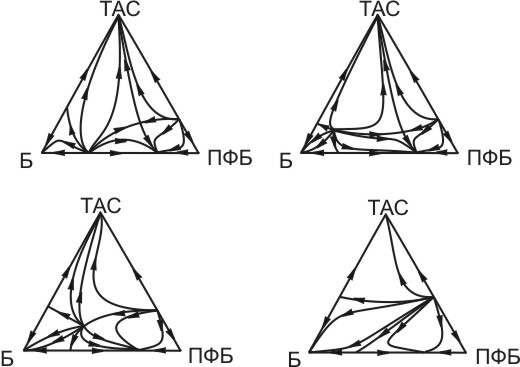
а)
б)
в)
г)
Рис. 3. Эволюция структуры фазовой диаграммы системы Б-ПФБ-ТАС
при варьировании давления а) 100; б) 300; в) 500; г) 760 мм рт.ст.
Таким образом, нами впервые получены математические модели, термодинамически непротиворечиво описывающие ПЖР биазеотропных бинарных и тройных систем.
В четвертой главе рассматриваются поведение исходных биазеотропных систем в присутствии ДМСО (РА) и закономерности ЭР. Роль РА в экстрактивной ректификации состоит в направленном изменении относительной летучести азеотропообразующих компонентов. Однако, достаточно сложный ход большего числа (по сравнению с моноазеотропными системами) единичных α-линий в базовой тройной диаграмме приводит к формированию единичных α-поверхностей в производной диаграмме четырехкомпонентной системы, которые разбивают концентрационный симплекс (тэтраэдр) на области с разным характером изменения α азеотропообразующих компонентов.
Наличие биазеотропии приводит к поливариантности диаграмм α – многообразий, в том числе в присутствии РА, что может вызывать инверсию летучестей исходных компонентов при разных концентрациях РА и влиять на состав продуктов разделения. Ранее инверсию летучести связывали с заменой РА.
Характерным является пример ЭР смеси бензол-перфторбензол с использованием ДМСО. В отсутствие достаточного количества экспериментальных данных по ПЖР в производной системе Б-ПФБ-ДМСО в литературе приводятся диаметрально противоположные сведения о влиянии РА на летучесть пары Б-ПФБ. Исходя из условия непрерывного изменения свойств в концентрационном симплексе, можно привести по крайней мере четыре диаграммы хода единичных α – линий в системе Б-ПФБ-РА (рис.4).
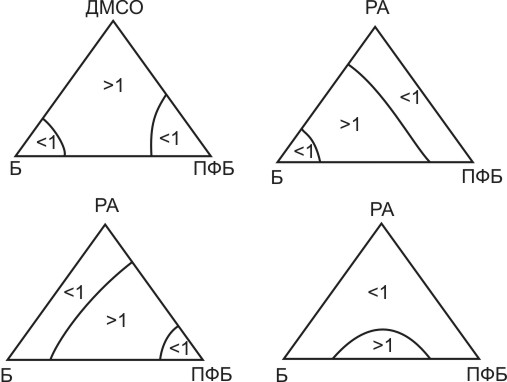
а)
б)
в)
г)
Рис 4. Возможные диаграммы хода единичных α – линий в системе Б-ПФБ-ДМСО (показано изменение относительно 1 величины α пары Б-ПФБ)
Первая из диаграмм (рис. 4а) получена нами при моделировании ПЖР, косвенно подтверждена квантовохимическими расчетами (по программе Priroda, созданной в МГУ им. Ломоносова) и используется для изучения закономерностей ЭР. Доказательств иного хода α-линий в рассматриваемой системе в литературе не приведено. В пользу оставшихся диаграмм могут свидетельствовать экспериментальные значения относительной летучести пары перфторбензол-бензол, полученные для составов, обогащенных ДМСО (М.И.Зарецкий с сотр.).
Для изучения особенностей формирования α-многообразий в системах Б-ПФБ-МП-ДМСО (Система I) и Б-ПФБ-ТАС-ДМСО (Система II) был проведен обширный вычислительный эксперимент (около 150 точек в каждой системе) по моделированию ПЖР в четырехкомпонентных системах и тройных составляющих. Качественный ход дистилляционных линий на развертке тетраэдра представлен на рис.5.
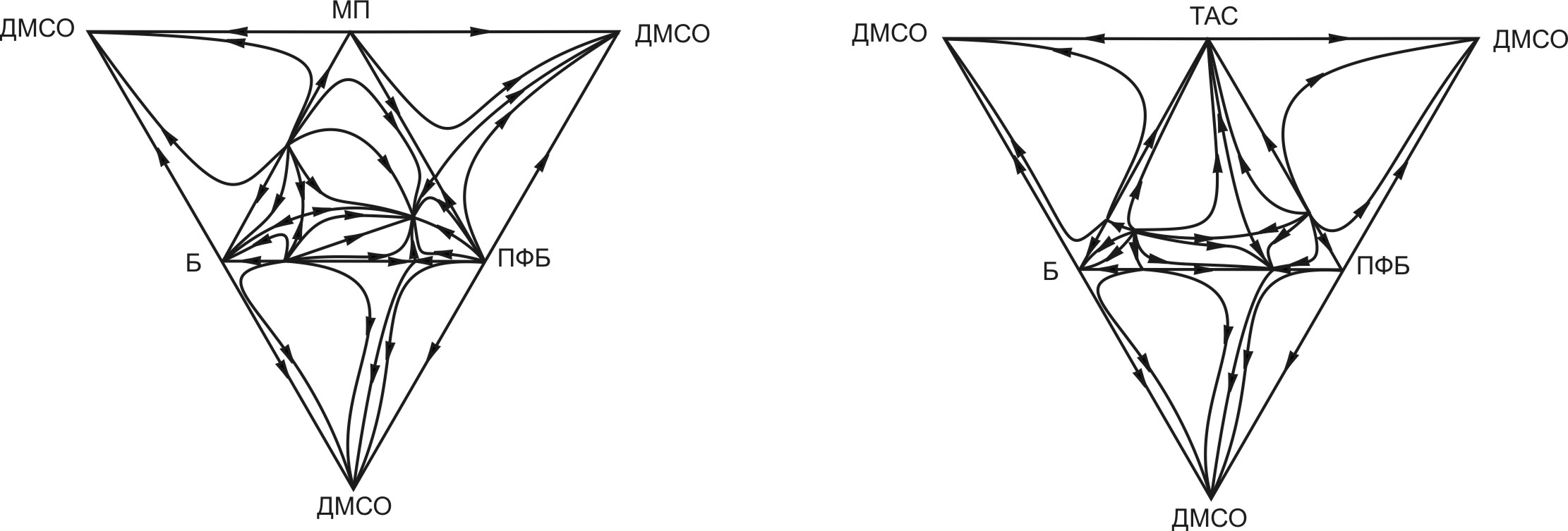
Рис.5. Ход дистилляционных линий в тройных составляющих
четырехкомпонентных систем
Четырехкомпонентные азеотропы в системах отсутствуют, на что указывают концентрационные зависимости температур кипения. Сепаратрическими поверхностями концентрационные симплексы разбиваются на 3 области дистилляции (Система I) и 2 области дистилляции (Система II), что подтверждается в работе соответствием диаграмм балансу индексов особых точек относительно границы и относительно тетраэдра. Общая картина вложения α-поверхностей в тетраэдр представлена на рис. 6.
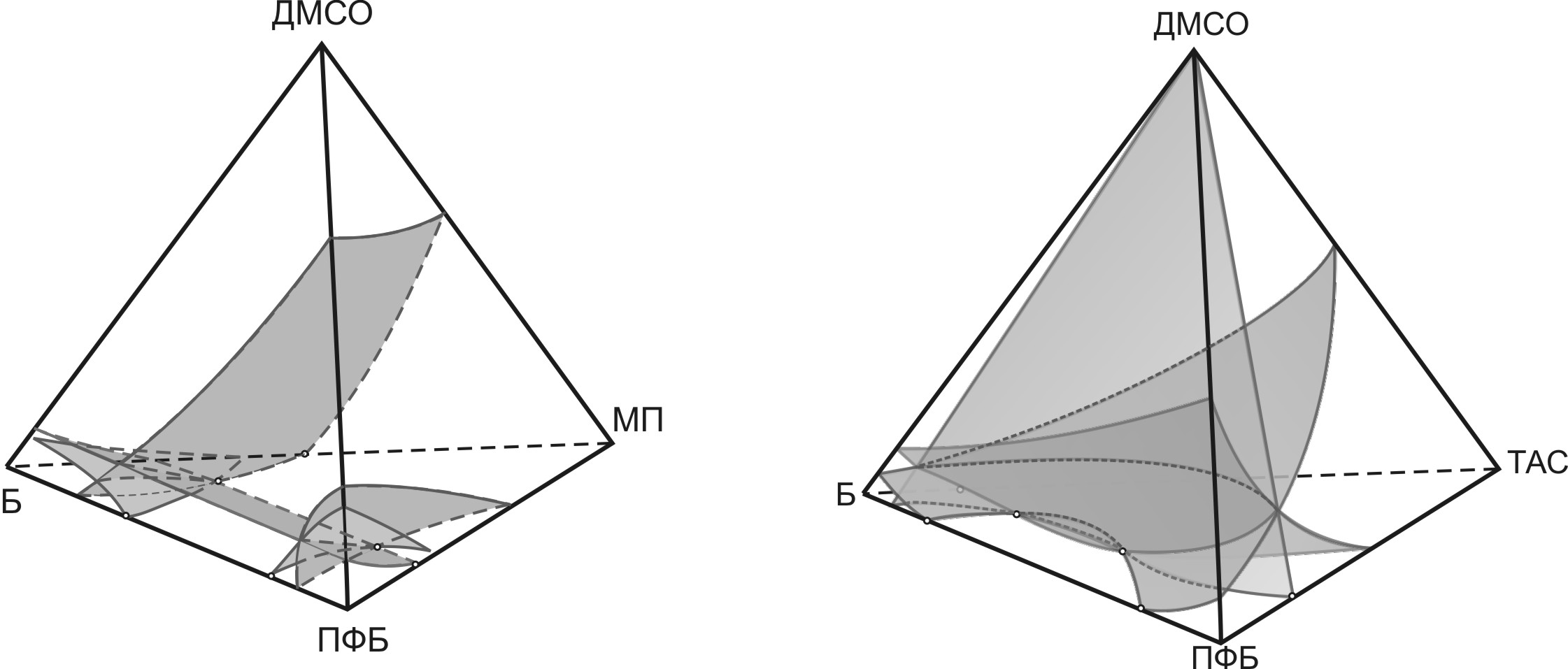
Рис. 6. Общая картина расположение единичных α – многообразий
в концентрационном симплексе
Количественно следы единичных α-поверхностей можно показать на развертке тетраэдра (рис. 7). Для их построения получены массивы данных по ПЖР для составов, в которых концентрация одного или нескольких компонентов стремится к нулю (бесконечное разбавление).
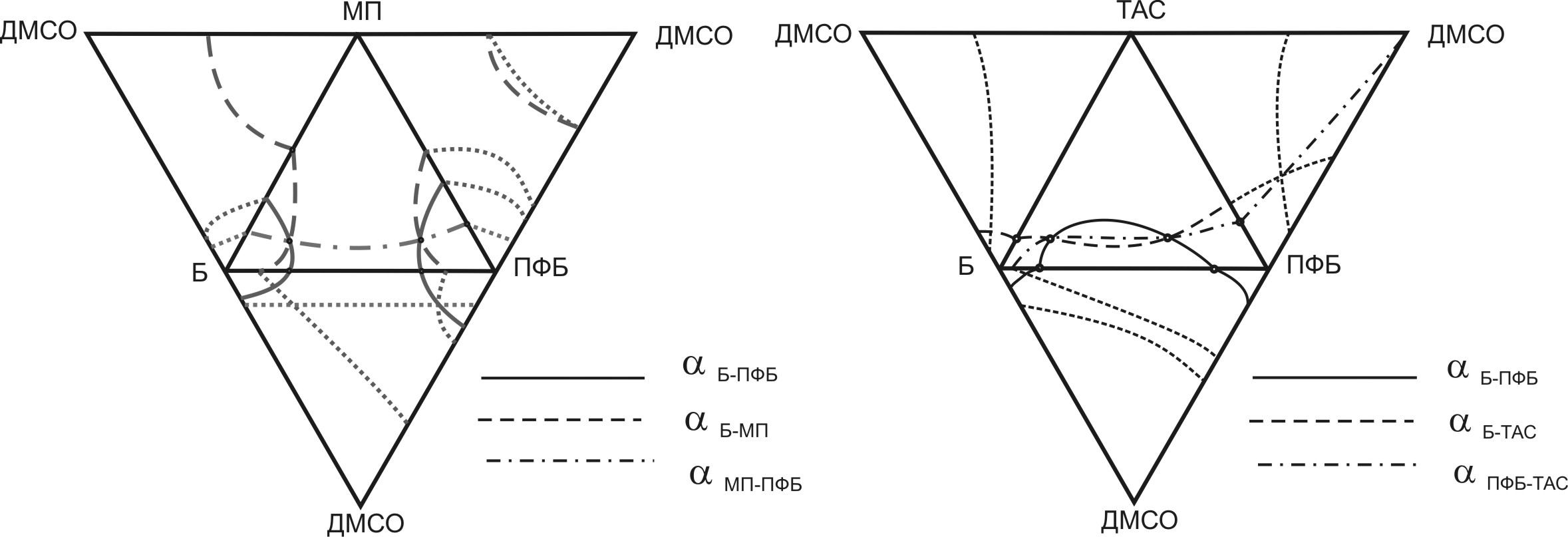
Рис. 7. Ход следов единичных α-поверхностей на развертке тэтраэдра
Эволюцию свойств тройной биазеотропной системы 123 (азеотропия, экстремумы температуры и др.) в присутствии четвертого компонента (ДМСО) можно наглядно представить в сечении с постоянной концентрацией нелетучего РА. Это сечение имеет вид концентрационного треугольника и для выражения состава жидкой фазы в этом случае удобно использовать относительные доли распределенных между фазами компонентов (1-3). При переходе от сечения к сечению наблюдается трансформация структуры диаграммы, которая зависит от того, пересекает ли сечение все единичные -многообразия или только часть их. На рис. 8 показана эволюция диаграмм дистилляционных линий тройных биазеотропных систем Б-ПФБ-МП и Б-ПФБ-ТАС при добавлении ДМСО (в сечениях с концентрацией ДМСО 0,4 и 0,8 м.д.).
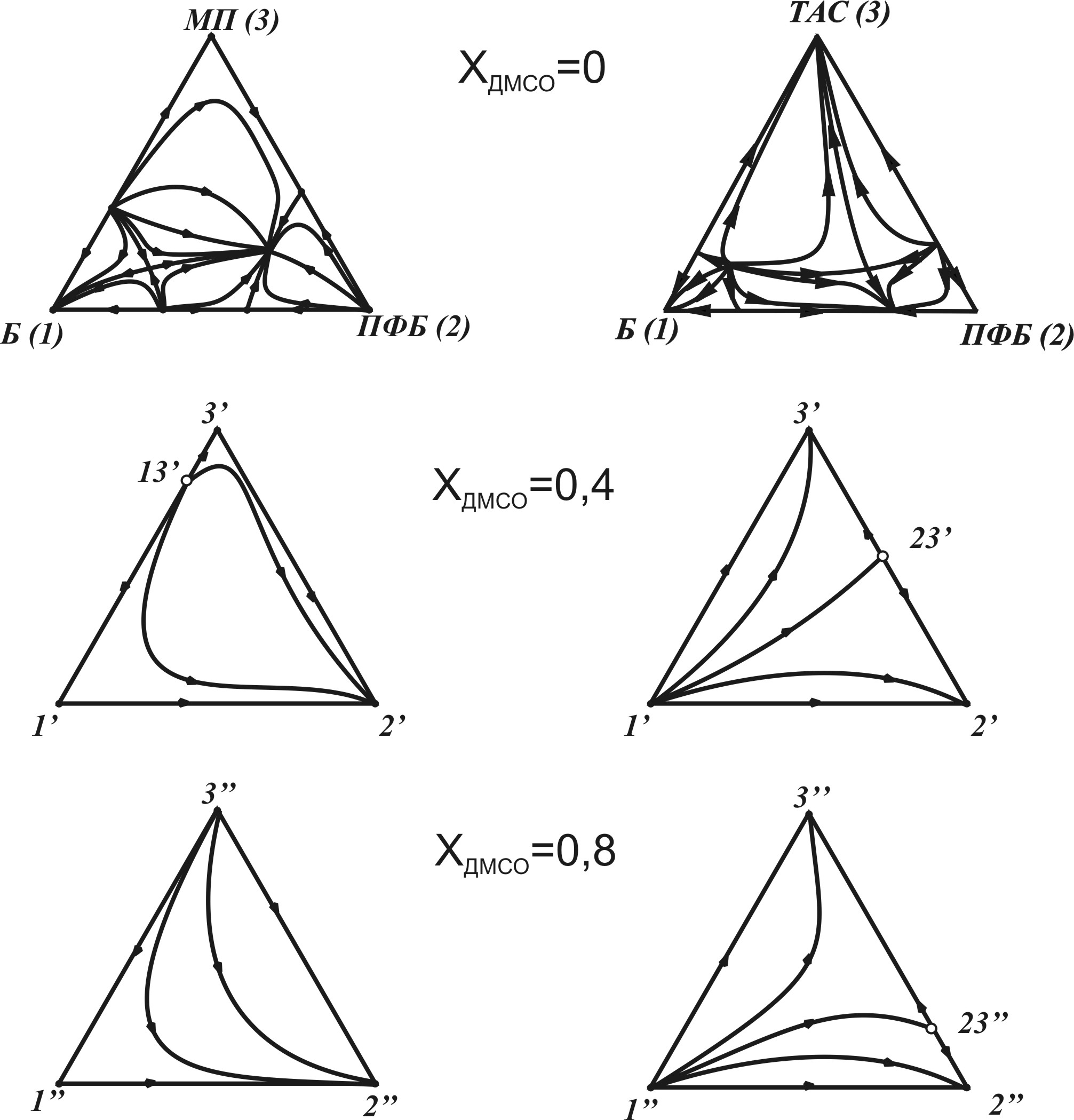
Рис.8. Эволюция диаграмм хода дистилляционных линий в сечениях
с постоянной концентрацией РА (1’-3’, 1”-3” – точки псевдокомпонентов,
(13)’, (23)’, (23)” - точки псевдоазеотропов)
На ребрах сечений появляются точки псевдоазеотропов и точки локальных экстремумов температуры (на рисунке не показаны в силу сложности изотермо - изобарических многообразий), которым отвечают разные составы. Это свидетельствует о невыполнении в различных сечениях и на их границах закона Гиббса - Коновалова, согласно которому особые точки векторного поля нод жидкость-пар и скалярного поля равновесных температур должны совпадать. С практической точки зрения этот вывод важен для объяснения экстремальных профилей температуры по высоте колонны экстрактивной ректификации.
Приведенный анализ диаграмм четырехкомпонентных систем необходим для оценки возможности реализации ЭР и прогноза результата процесса разделения (оценка расхода, определение трудноразделимых пар компонентов). α-Поверхности в тетраэдре, порождаемые биазеотропией, дают две бифуркационные концентрации, которые определяют разный расход РА и разные результаты разделения (за счет инверсии летучестей). В моноазеотропных системах связь этих показателей процесса ЭР с ходом α-многообразий однозначна: чем меньше хбиф, тем легче пара для разделения и тем меньший расход РА требуется и наоборот.
Анализ диаграммы хода α - многообразий показывает, что в ЭР смеси Б-ПФБ-МП трудно разделимой является пара бензол - метилпропионат, поскольку эти компоненты обладают примерно одинаковой летучестью относительно перфторбензола и поэтому возможно выделение фракции Б-МП в дистиллате колонны ЭР. В системе Б-ПФБ-ТАС заметной летучестью в присутствии ДМСО обладает бензол, в то время как трудно разделимой является пара ПФБ-ТАС, выделение которой можно ожидать в кубе.
Проведено компьютерное исследование более 100 режимов экстрактивной ректификации тройных смесей эквимолярного состава, в которых варьировались: соотношение количеств исходной смеси и РА (F/PA), флегмовое число (R), эффективность колонны (N, т.т.), уровни подачи исходной смеси и РА.
В табл. 4 приведены результаты экстрактивной ректификации смесей Б-ПФБ-МП и Б-ПФБ-ТАС, которые подтверждают сделанный прогноз. Пониженное давление в колоннах ЭР выбрано с целью предотвращения разложения ДМСО, которое происходит при температурах более 150 оС.
С учетом полученных результатов предложены принципиальные схемы разделения исходных тройных биазеотропных смесей в присутствии селективного РА, которые сочетают комплекс ЭР (колонны 1 и 2) и комплекс колонн (3,4), работающих под разными давлениями (рис. 9). Определены статические параметры работы всех колонн при достижении чистоты получаемых продуктов не менее 99,5%.
Таблица 4
Результаты разделения и параметры колонны ЭР
тройных смесей эквимолярного состава
| Система | Р | F/PA | R | Xd, м.д. | Td 0С | Xw, м.д. | Tw 0С |
| Б-ПФБ-МП | 500 | N=50, NF=30, NPA=10, температура подачи РА =66 0С | |||||
| 1:5 | 3 | МП = 0.4999 Б = 0.4990 ПФБ = 0.0011 | 66.20 | ДМСО=0.9259 ПФБ = 0.0740 Б = 0.0001 | 144.56 | ||
| Б-ПФБ-ТАС | 300 | N=50, NF=30, NPA=10, температура подачи РА =52 0С | |||||
| 1:7 | 1,5 | Б = 0.9980 ПФБ = 0.0020 | 52.70 | ПФБ = 0.0431 ТАС = 0.0431 ДМСО=0.9138 | 125.04 | ||
Примечание: XW,D – состав кубового остатка и дистиллата, м.д., TW,D – температура кубового остатка и дистиллата, оС


Рис. 9. Принципиальные технологические схемы разделения тройных смесей Б-ПФБ-МП и Б-ПФБ-ТАС с использованием ДМСО (1,2 – комплекс ЭР, 3,4 – комплекс колонн, работающих под разными давлениями)
Бинарная система бутилпропионат – пропионовая кислота является первым представителем ряда промышленных биазеотропных систем. Проблема разделения таких смесей в производстве высших жирных спиртов весьма актуальна, т.к. используемый на данный момент метод энергоемок и неэкологичен. На рис. 10 приведены диаграммы хода дистилляционных линий и a–линий всех пар компонентов в тройной системе БП-ПК- ДМСО.
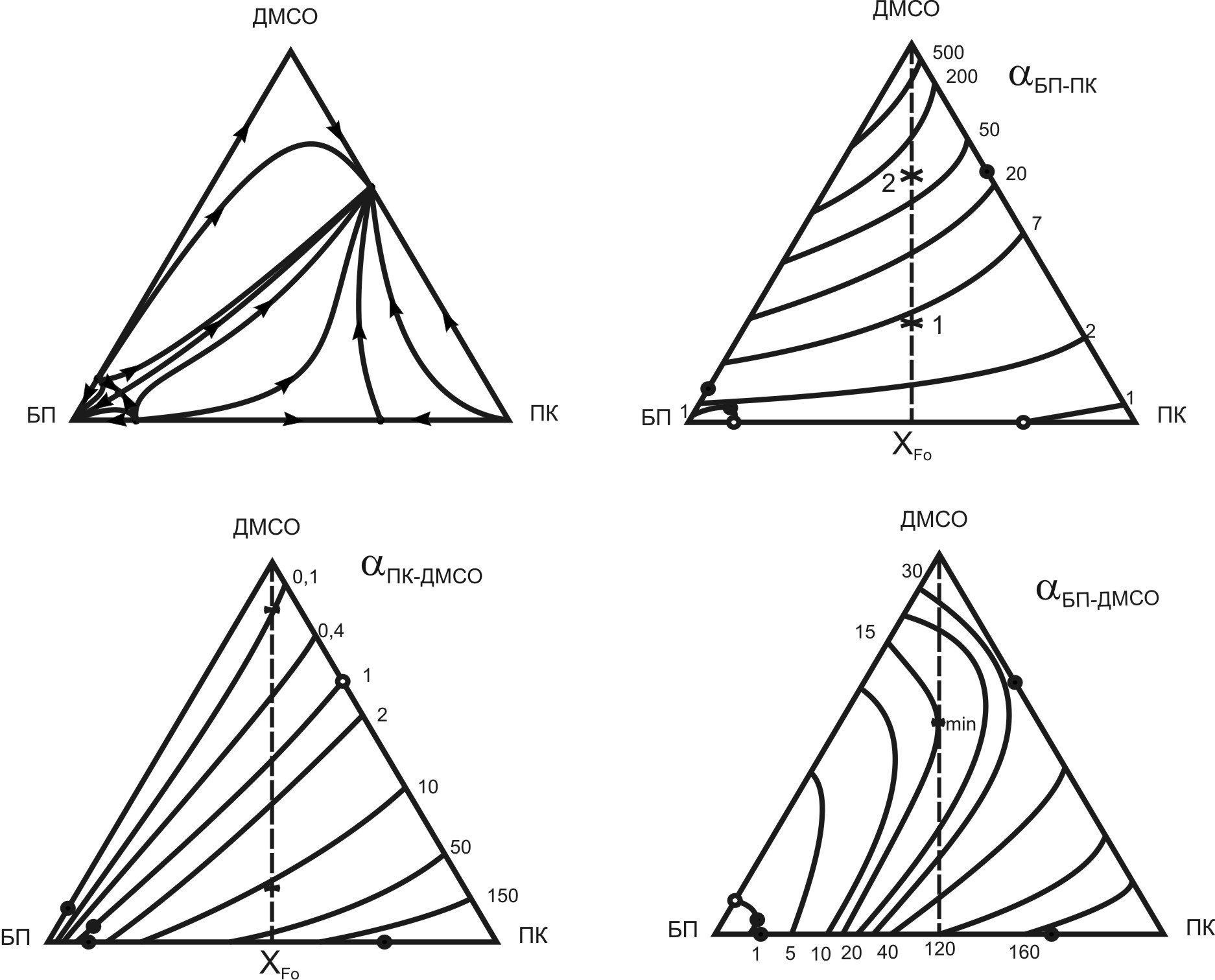
Рис. 10. Диаграммы хода дистилляционных и a–линий
в системе БП-ПК-ДМСО
Как видно из рис. 10, увеличение концентрации ДМСО повышает летучесть эфира относительно кислоты и, соответственно, селективность ДМСО как разделяющего агента. Это свидетельствует о возможности выделения в дистиллате колонны ЭР бутилпропионата. В то же время анализ диаграммы хода α-линий пары ПК-ДМСО показал, что в условиях ЭР при заметных расходах РА происходит инверсия летучестей и можно ожидать нежелательное присутствие в дистиллате колонны в заметных количествах РА. Это потребует дополнительной очистки целевого продукта (бутилпропионата) от разделяющего агента.
Для пары БП-ДМСО наблюдается экстремальный характер (проходит через минимум) зависимости α от концентрации ДМСО на линии смешения. При высоких концентрациях ДМСО летучесть БП понижается по сравнению с исходной смесью, что так же нежелательно, поскольку может привести к появлению БП в кубе колонны экстрактивной ректификации. Выводы, полученные нами при анализе диаграмм хода α-линий для каждой пары компонентов, подтвердились расчетами экстрактивной ректификации. Так, в дистиллате колонны ЭР выделился целевой продукт (БП) и ДМСО. В кубе колонны помимо диметилсульфоксида и пропионовой кислоты присутствовал бутилпропионат. Для разделения данной смеси в дальнейшем следует подобрать другой РА, в том числе легкокипящий (для процесса реэкстрактивной ректификации) или с помощью специальных методов отделить бутилпропионат от диметилсульфоксида.
ВЫВОДЫ
- Для заданного граничного контура тройной системы с одной биазеотропной и двумя моноазеотропными составляющими (контур 3.4) синтезировано 158 новых структур диаграмм хода дистилляционных линий классов 3.4.0, 3.4.1, 3.4.2 и 264 соответствующих им структур диаграмм хода единичных К-линий.
- Впервые получены математические модели, термодинамически непротиворечиво описывающие ПЖР (в том числе при варьировании давления) сложных биазеотропных систем БП-ПК, Б-ПФБ-МП, Б-ПФБ-ТАС; получены полные данные ПЖР в тройных системах с двумя тройными азеотропами; сформулированы рекомендации к выбору математической модели.
- Впервые получены данные по ПЖР в четырехкомпонентных системах Б-ПФБ-МП-ДМСО, Б-ПФБ-ТАС-ДМСО и проведен термодинамико-топологический анализ фазовых диаграмм;
- Выявлен сложный характер вложения единичных α – многообразий в концентрационный тетраэдр, осуществлен прогноз возможных продуктов разделения тройных смесей с использованием селективного РА.
- C использованием вычислительного эксперимента подтверждена возможность разделения биазеотропных смесей Б-ПФБ, Б-ПФБ-МП, Б-ПФБ-ТАС экстрактивной ректификацией в присутствии ДМСО и определены оптимальные параметры работы колонн ЭР.
- Предложены принципиальные схемы полного разделения тройных биазеотропных смесей Б-ПФБ-МП, Б-ПФБ-ТАС эквимолярного состава, сочетающие комплекс ЭР с комплексом, основанным на варьировании давления в колоннах.
- Показана принципиальная возможность разделения биазеотропной смеси БП-ПК, являющейся первым представителем ряда промышленных биазеотропных систем, экстрактивной ректификацией.
Основные результаты диссертации отражены
в следующих публикациях:
- Мягкова Т.О., Челюскина Т.В., Фролкова А.К. Исследование особенностей фазового поведения многокомпонентных биазеотропных систем // ЖФХ. – 2007. – Т.81, № 6. - C. 971-977.
- Мягкова Т.О., Челюскина Т.В., Фролкова А.К. Разделение экстрактивной ректификацией тройной системы с двумя тройными азеотропами // Журн. «Химическая технология». – 2007, № 10. - C. 476-481.
- Челюскина Т.В., Мягкова Т.О., Фролкова А.К. Разделение биазеотропной смеси бензол-перфторбензол экстрактивной ректификацией // «Наукоемкие химические технологии – 2002»: Материалы восьмой междунар. научн.-техн. конф. по проблемам наукоемких химических технологий. – Уфа: Гос. издат. научн.-техн. литературы «Реактив», 2002.
- Мягкова Т.О.,Челюскина Т.В., Фролкова А.К. Компьютерное исследование закономерностей экстрактивной ректификации биазеотропной трехкомпонентной смеси // Ученые записки МИТХТ, 1-ая научно-техническая конф. молодых ученых «Наукоемкие химические технологии». - 13-14 октября 2005 г. Тезисы докладов. Т.1. - М.: 2005. – С. 711-12.
- Мягкова Т.О., Челюскина Т.В., Фролкова А.К. Компьютерное исследование экстрактивной ректификации биазеотропной трехкомпонентной смеси // XI Международная научно-техническая конференция «Наукоемкие химические технологии – 2006»: Тезисы докладов. Самара, 16-20 октября 2006, Том 2, с.188.
6) Myagkova T.O., Chelyuskina T.V. The phase behavior of multicomponent biazeotropic systems XVI International Conference on Chemical Thermodynamics in Russia (RCCT-2007), Suzdal, 1-6 July, 2007, с.333-334.
Сдано в печать 10.2007
Формат 60×90 1/16. Отпечатано на ризографе.
Тираж 100 экз. Заказ №
ИПЦ МИТХТ имени М.В. Ломоносова
119571, Москва, пр. Вернадского, 86
