Краткое содержание: Виброзащита машин и механизмов. Методы виброзащиты. Взаимодействие двух подвижных звеньев. Подрессоривание и виброизоляция.

Вид материала

Краткое содержание

Содержание Постановка задачи

Подобный материал:

• Примерная программа дисциплины теория механизмов и машин Рекомендуется Минобразованием, 326.52kb.
• Программа дисциплины по кафедре Детали машин детали машин и механизмов, 575.22kb.
• Памятка для студентов группы пкм- по изучению дисциплины " Теория механизмов и машин, 72.92kb.
• Краткое содержание: Классификация кинематических пар. Модели машин. Методы исследования, 258.21kb.
• Закономерности проектирования механизмов для передачи и преобразования, 19.17kb.
• Рабочая программа по дисциплине опд. Ф. 04 Теория механизмов и машин для направления, 252.07kb.
• «Теория машин и механизмов и проектирование текстильных машин», 240.94kb.
• Задачи изучения дисциплины: освоение кинетостатического метода анализа механизмов, 124.17kb.
• Моу верхнетойденская сош, 396.04kb.
• Методические указания Аннотация. Приводится краткое содержание курсового проекта, 143.6kb.

A_i система A_j

с КПД < 1

 _i u _ij  _j




 = | A_j /A_i | = | А_i - A_пот | / | A_i | ,


 = 1 - | A_пот/ | A_i | = 1 -  ,


где A_i - работа движущих сил, A_j - работа сил полезного сопротивления,  - коэффициент полезного действия,  - коэффициент потерь.

Рис. 9.10


Работа движущих сил за цикл

_in

А_i =  М_д  d_i  М_дср  (_in - _i0 )  М_дср  _i ,

^i0

работа сил полезного сопротивления за цикл

_jn

А_j =  М_с  d_j  М_cср  (_jn - _j0 )  М_cср  _j ,

^j0

где М_дср и М_cср - среднеинтегральные значения движущего момента и момента сил сопротивления,

_in ,_jn и _i0 , _j0 - значения угловых координат звеньев i и j ,соответственно в начале и в конце цикла.

Подставим эти выражения в формулу для КПД и получим


 = | A_j /A_i | = | М_cср  _j | / | М_дср  _i | = | М_cср  | / | М_дср | ,


где u_ji - передаточное отношение механизма.


КПД механической системы при последовательном

и параллельном соединении механизмов.

• 
  
  
  Механизм i Механизм j
  
  A_вхi _i _j А_выхi
  
  А_выхi = А_вхj
  
  
  при последовательном соединении (рис. 9.11) весь поток механической энергии проходит последовательно через каждый из механизмов
  

Рис. 9.11


 = | A_j /A_i | = | А_выхj /A_вхi |


А_выхj = А_вхj   _j = А_выхj  _j , 

  А_выхj = A_вхi  _i  _j ,

А_выхi = A_вхi  _i , 






 =  _i  _j

• при параллельном соединении механизмов i и j (рис. 9.12) поток механической энергии делится на две части: часть проходящую через механизм i обозначим , а часть проходящую через механизм j  , причем  + = 1.
  

A_вх Механизм i _i А_вх

_i

А_вх А_вых




Механизм j

 А_вх _j _j А_вх





Рис. 9.12


 = | А_вых /A_вх | , где А_вых = _i А_вх + _j А_вх = ( _i + _j ) А_вх





 = ( _i + _j )


Литература к лекции 9:


1. Теория механизмов и машин. Под ред. К.В.Фролова. М.: Высшая школа, 1987.

2. Левитский Н.И. Колебания в машинах: Учебное пособие для втузов. - М: Наука. Гл. ред. физ. - мат. лит., 1988. - 336 с.
   
3. Штейнвольф Л.И. Динамические расчеты машин и механизмов. - Москва - Киев: Машгиз., 1961. - 340 с.
   
4. Вибрации в технике: Справочник. В 6-ти т./ Ред. совет: В.Н.Челомей и др.,- М.: Машиностроение, 1981. - Т.6, Защита от вибрации и ударов/ Под ред. К.В.Фролова, 1981. - 456с.
   
5. Силовой расчет, уравновешивание, проектирование механизмов и механика манипуляторов: Учебное пособие. Под ред. А.К.Мусатова. М.: Изд. МГТУ, 1990.
   

Приложение к лекции 4: Метод планов положений, скоростей и ускорений подробно рассматривается на упражнениях и осваивается студентами при выполнении домашнего задания и курсовой работы. Здесь кратко рассматривается кинематическое исследование методом планов скоростей и ускорений простейшего кулисного механизма (механизм подъемника с приводом от гидроцилиндра).

Постановка задачи: Дано: Кинематическая схема механизма - l_AB, l_AC, l_BS2, l_AS1; ₁ , ₁ , _{1 .}

________________________________________________


Определить: V_j , a_j ,  _i ,  _i  ?


Построим кинематическую схему механизма в заданном положении в масштабе _l, мм/м . По другой терминологии схема называется планом положений звеньев и точек механизма (рис. 9.13).




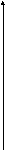
y _l, мм/м 1 s₁




V_S1

S₁ _V, мм/мс^-1

₁ ₁ B

₁ V_CB

A s₂ b

x d V_B

c₂

0 2 S₂ V_C = V_{C 2C0} V_S2

S₃ ₂ = ₃

S₂ ₂ = ₃ V_D

V_S3 s₃

 D

2 D p_v ,a,c₀

3

С c’₂

C a^t_CB a^t_C2C0



d’ a_CB

3

a_C2 = a_C2C0

n’_CB s’₂ a_S2

aⁿ_CB n’_C2

a_S1 a_B

s’₁ a^k_C2C0

b’ a^t_B a_S3 p_a,a’,c’₀

_a, мм/мс^-2 n’_B aⁿ_B

n’_S3



Рис. 9.13


При кинематическом исследовании схему механизма гидроцилиндра удобнее представить в виде штока 2 и втулки 3. Движения звеньев механизма: 1 и 3 вращательное, 2 - плоское. План скоростей строится в масштабе _V, мм/мс^-1 на основании

следующих уравнений:

вращательное движение 1-го звена

V_B = ₁ l_AB ; V_B  l_AB ;

плоское движение звена 2

V_C2 = V_B + V_C2B ;

AB BC

сложное движение звена 2 (вращение совместно со звеном 3 и поступательное движение звена 2 относительно звена 3)

V_C2 = V_С3 + V_C2С3 ;

0 BC

скорости точек D и S₂ определяются пропорциональным делением отрезков плана скоростей

BD/BC = bd/bc  bc = (BC/BD)bd;


BD/BS₂ = bs₂/bc  bs₂ = (BC/BS₂)bd;

угловая скорость звеньев 2 и 3

₃ = ₂ = V_BC2/l_BC;

скорость точки S₃

V_S3 = ₃ l_CS3 ; V_S3  l_CS3 .

План ускорений строится в масштабе _a, мм/мс^-2 на основании следующих уравнений:

вращательное движение 1-го звена

a_B = aⁿ_B + a^t_B ,

где aⁿ_B = ²₁ l_AB , aⁿ_B  l_AB , a^t_B = ₁ l_AB , a^t_B  l_AB ;

плоское движение звена 2

a_C2 = a_B + a ⁿ_C2B + a ^t_C2B ,

 BC BC

где aⁿ _C2B = ²₂ l_BC , aⁿ _C2B  l_BC ,

сложное движение звена 2

a_C2 = a_С3 + a ⁿ_C2С3 + a ^k_C2С3;

0 BC

где a ^k_C2С3 - ускорение Кариолиса, возникающее при изменении направления вектора относительной скорости при совместном вращении звеньев 2 и 3, и равное скалярному произведению вектора относительной скорости и вектора угловой скорости ₂ , модуль этого вектора равен

a ^k_C2С3 = 2 ₂ V_C2С3 ,

а направление определяется направлением вектора относительной скорости V_C2С3 повернутого на 90 градусов в направлении ₂;

ускорения точек D и S₂ определяются пропорциональным делением отрезков плана ускорений

BD/BC = bd/bc  bc = (BC/BD)bd;


BD/BS₂ = bs₂/bc  bs₂ = (BC/BS₂)bd;

угловое ускорение скорость звеньев 2 и 3

₃ = ₂ = a ^t_BC2 / l_BC;

ускорение точки S₃, определяется вращательным движением звена 3

a_S3 = aⁿ_S3 + a^t_S3 ,

где aⁿ_S3 = ²₃ l_CS3 , aⁿ_S3  l_CS3 , a^t_S3 = ₃ l_CS3 , a^t_S3  l_CS3 .