Методика определения расчетных величин пожарного риска в объектах защиты на основе полевого метода моделирования пожаров Общие положения

Вид материала

Документы

Содержание Основные расчетные величины и зависимости, используемые для оценки индивидуального пожарного риска PЭ — вероятность эвакуации людей; P N1 – число людей на первом участке, чел; f Расчет социального пожарного риска. Основные расчетные величины и зависимости, используемые для оценки социального пожарного рис Дополнительные противопожарные мероприятия при расчете пожарного риска

Подобный материал:

• Методика определения расчетных величин пожарного риска в зданиях, сооружениях и строениях, 132.13kb.
• Правительства Российской Федерации от 31 марта 2009 года n 272 "О порядке проведения, 1211.45kb.
• Приказ от 10 июля 2009 г. N 404 об утверждении методики определения расчетных величин, 924.4kb.
• О внесении изменений в приказ мчс россии от 10. 07. 2009 №404, 222.16kb.
• Приказ мчс РФ от 10 июля 2009 г. N 404 "Об утверждении методики определения расчетных, 735kb.
• Приказ от 30 июня 2009 г. №382 об утверждении методики определения расчетных величин, 140.81kb.
• Применение ионометрического метода определения йодид-ионов для мониторинга йоддефицитных, 31.31kb.
• Административный регламент, 909.59kb.
• 1. Общие положения, 501.61kb.
• Вычисление числа  с помощью метода Монте-Карло, 15.1kb.

МЕТОДИКА

определения расчетных величин пожарного риска в объектах защиты на основе полевого метода моделирования пожаров

1. Общие положения
   

1.1 Настоящая методика определяет порядок получения расчетных величин пожарного риска на основе методов компьютерного моделирования для зданий, сооружений, производственных объектов, строений (далее – объект защиты), которые соответствует Ф1 – Ф5 классам функциональной пожарной опасности. Данная методика может применяться для определения расчетных величин пожарного риска при проектировании, реконструкции, реставрации, капитальном ремонте и эксплуатации объекта защиты. Использование данной методики рекомендуется совместно со специализированным пакетом программ для компьютерного моделирования пожаров «σFire».

Применение данной методики не предполагается использовать для проведения расчетов пожарного риска объектов защиты специального назначения, в том числе объектов военного назначения, объектов производства, переработки, хранения радиоактивных и взрывчатых веществ и материалов, объектов уничтожения и хранения химического оружия и средств взрывания, наземных космических объектов и стартовых комплексов, горных выработок, объектов, расположенных в лесах.

1.2 В соответствии с постановлением Правительства РФ от 31 марта 2009 г. №272 «О порядке проведения расчетов по оценке пожарного риска» расчеты по оценке пожарного риска проводятся путем сопоставления расчетных величин пожарного риска с соответствующими нормативными значениями пожарных рисков, установленными Федеральным законом "Технический регламент о требованиях пожарной безопасности" (далее – Технический регламент).

Определение расчетных величин пожарного риска осуществляется на основании:

а) анализа пожарной опасности зданий;

б) определения частоты реализации пожароопасных ситуаций;

в) построения полей опасных факторов пожара для различных сценариев его развития;

г) оценки последствий воздействия опасных факторов пожара на людей для различных сценариев его развития;

д) наличия систем обеспечения пожарной безопасности зданий.

1.3. Расчетные величины пожарного риска являются количественной мерой возможности реализации пожарной опасности объекта защиты и ее последствий для людей.

Определение расчетных величин пожарного риска основывается на расчете индивидуального пожарного риска для людей находящихся внутри объекта защиты. Индивидуальный пожарный риск определяется как частота воздействия опасных факторов пожара (ОФП) на человека. Для определения частоты воздействия ОФП выбирается сценарий развития пожара наиболее опасного для жизни и здоровья людей.

1.4. Расчеты пожарного риска оформляются в виде отчета, в который включаются:

а) наименование использованной методики;

б) описание объекта защиты, в отношении которого проведен расчет по оценке пожарного риска;

в) результаты проведения расчетов по оценке пожарного риска;

г) перечень исходных данных и используемых справочных источников информации;

д) вывод об условиях соответствия (несоответствия) объекта защиты требованиям пожарной безопасности.

1.5. В данной методике используются основные понятия, установленные статьей 2 Технического регламента о требованиях пожарной безопасности.

2. Математическая модель развития пожара
   

На данный момент в мире все большее распространение получает подход оценки пожарной опасности строительных и технологических объектов при помощи математического моделирования.

Строительные сооружения или технологические объекты могут быть уникальными, поэтому типовые решения по обеспечению их противопожарной защиты не всегда могут быть приемлемыми. Выбор того или иного способа защиты от пожара зависит от наличия и размещения исполнительных элементов системы противопожарной защиты, а также от возможных вариантов возникновения и развития опасных факторов пожара.

Полевые модели являются наиболее мощным и универсальным инструментом компьютерного моделирования. В полевых моделях выделяется расчетная область делится на большое количество контрольных объемов. Для каждого из этих объемов с помощью численных методов решается система уравнений в частных производных, выражающих принципы локального сохранения массы, импульса, энергии и масс компонентов. С его помощью можно рассчитать температуры, скорости, концентрации компонентов смеси, тепловые потоки и т.д. в каждой точке расчетной области. Использую полевые модели можно провести расчет пожара на объекте практически любой геометрической формы с учетом основных физико-химических процессов.

Для использования полевых моделей требуются значительно большие вычислительные ресурсы по сравнению с другими менее универсальными подходами (интегральным или зональным). Однако, в настоящее время появились достаточно мощные и доступные вычислительные системы, расширились познания в области физики и химии процессов, происходящих при горении, созданы эффективные методы расчета турбулентной аэродинамики, сложного теплообмена и химического реагирования, созданы компьютерные программы, позволяющих с достаточной для практической деятельности точностью моделировать процессы, происходящие при пожарах. Проведение вычислительного эксперимента с помощью этих программ характеризуется низкими затратами и возможностью получения максимально полной информации об исследуемом объекте. В своей основе полевой метод не содержит никаких априорных допущений о структуре течения, и в связи с этим принципиально применим для рассмотрения любого сценария развития пожара.

Представленные ниже математические модели реализованы в специализированном программном комплексе σFire, созданном для компьютерного моделирования развития пожара. В программном комплексе σFire реализована поддержка многоядерной архитектуры ЭВМ, что позволяет эффективно использовать суперкомпьютеры (кластер СФУ).


2.1. Математическая модель процессов переноса

2.1.1. Уравнения для ламинарного режима течения.

Уравнение сохранения массы или уравнение неразрывности имеет вид:

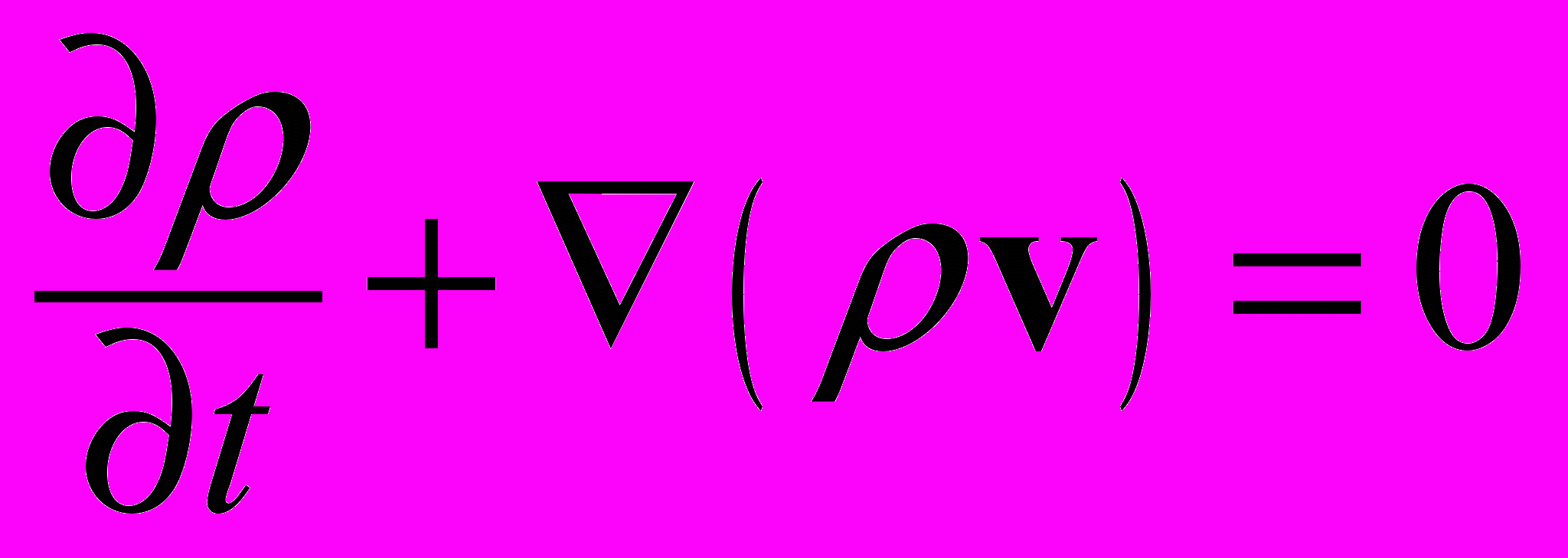(2.1.1.1)

Уравнения сохранения количества движения:

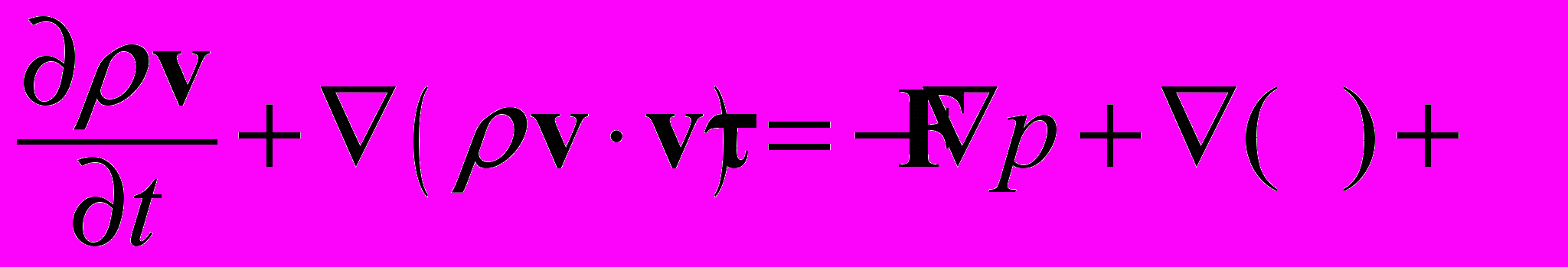(2.1.1.2)

где -тензор вязких напряжений, - вектор объемных сил.

Составляющие тензора вязких напряжений определяются как: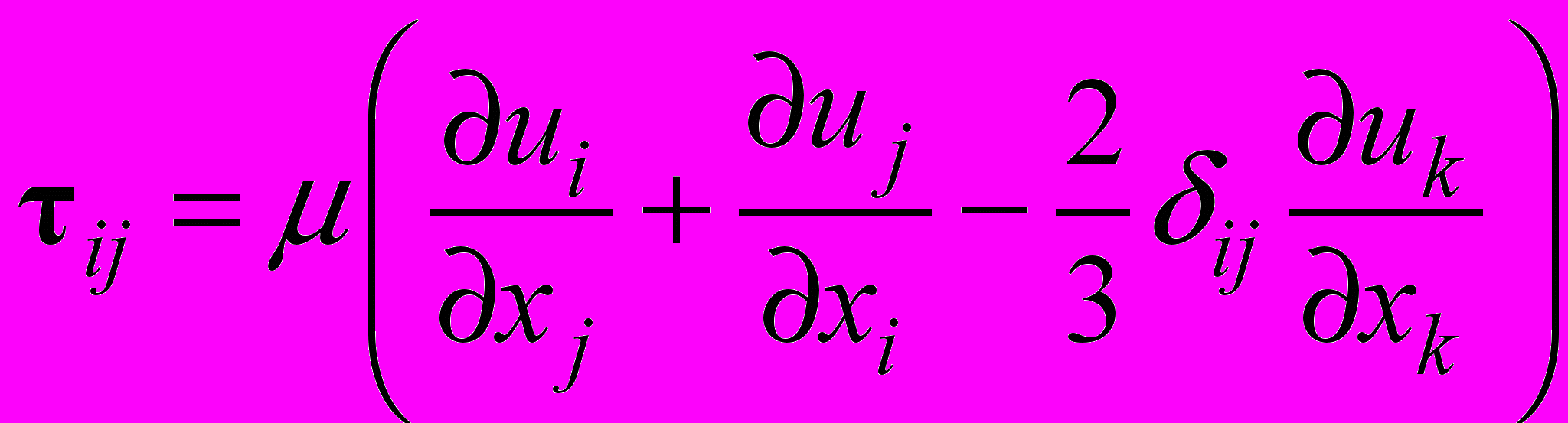

(2.1.1.3)

где - динамическая (молекулярная) вязкость, 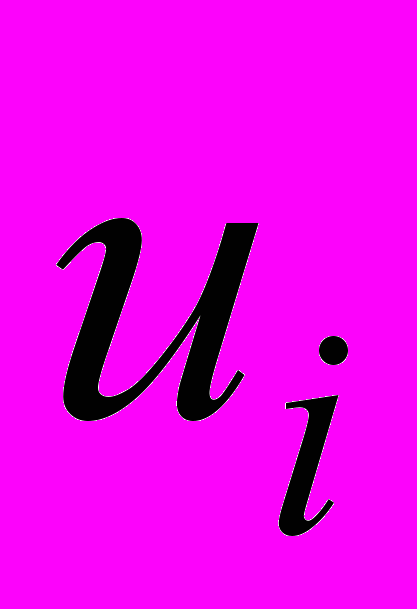- компоненты вектора скорости.


2.1.2. Уравнение энергии

В пакете “Fire” уравнение сохранения энергии рассматривается в следующем виде:

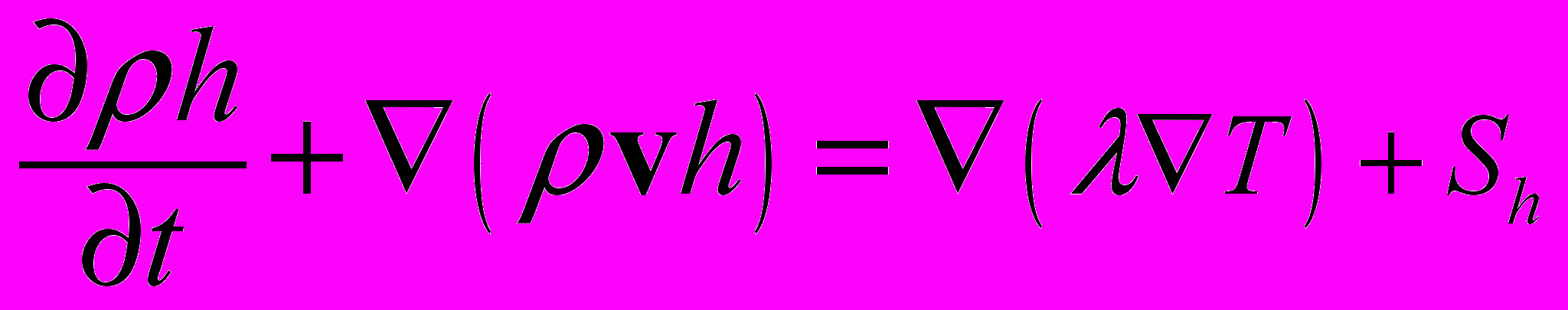(2.1.2.1)

где 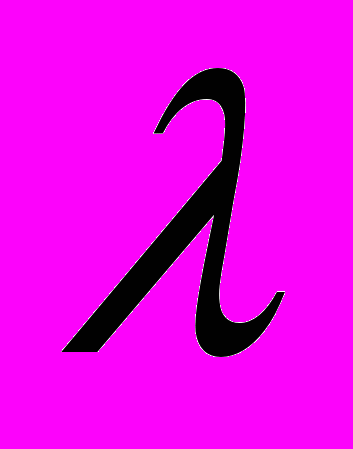- коэффициент теплопроводности, 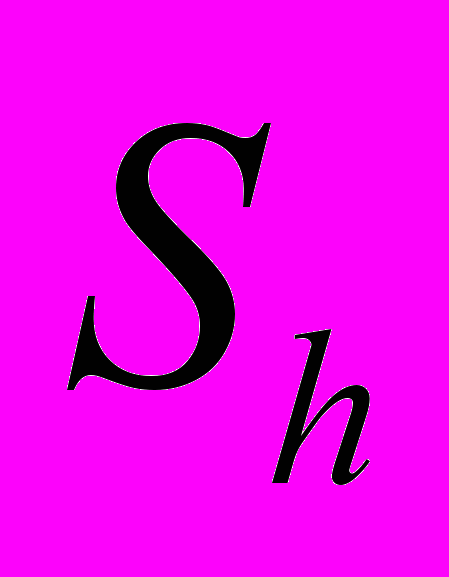– источниковый член, отвечающий за приток (отток) энергии в процессе химического реагирования, излучения, или каких-либо других процессах.

Энтальпия многокомпонентной среды определяется по правилу смеси

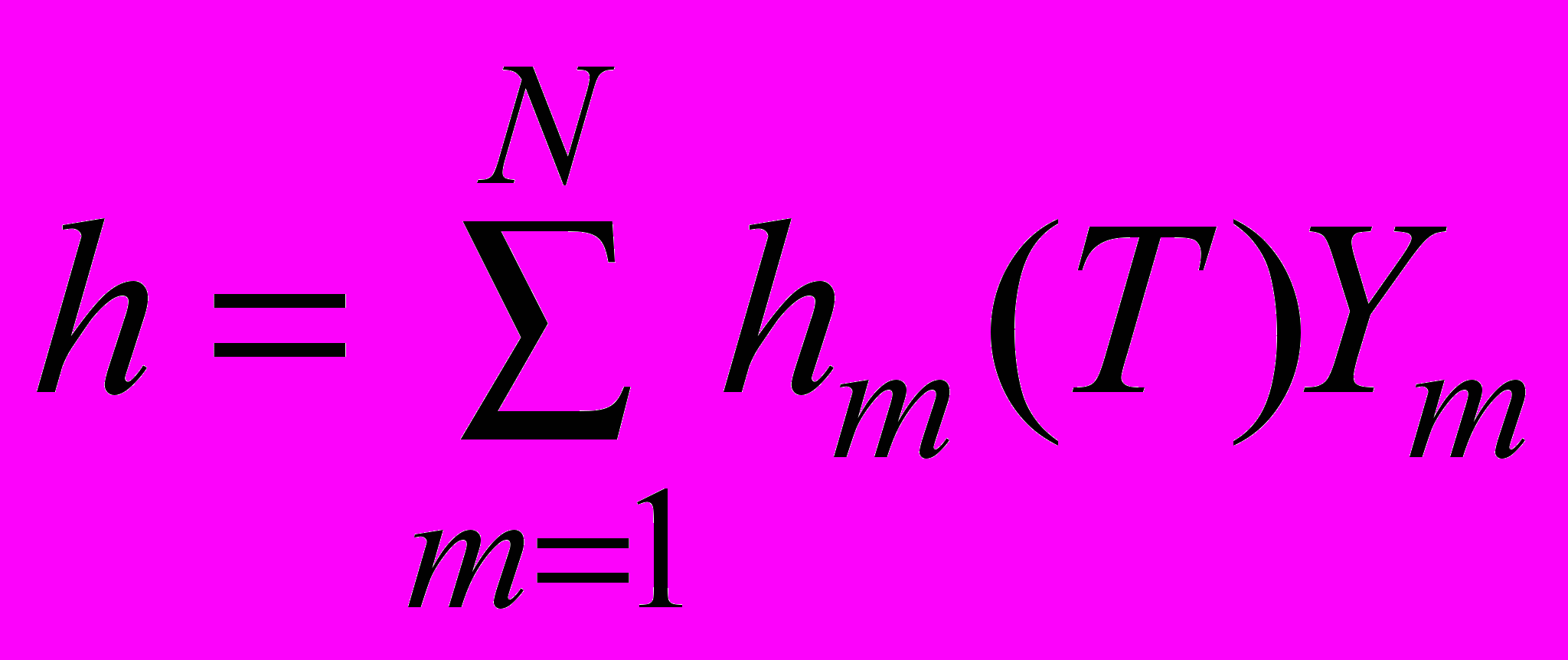(2.1.2.2)

где энтальпия компонент h_m(T) вычисляется как

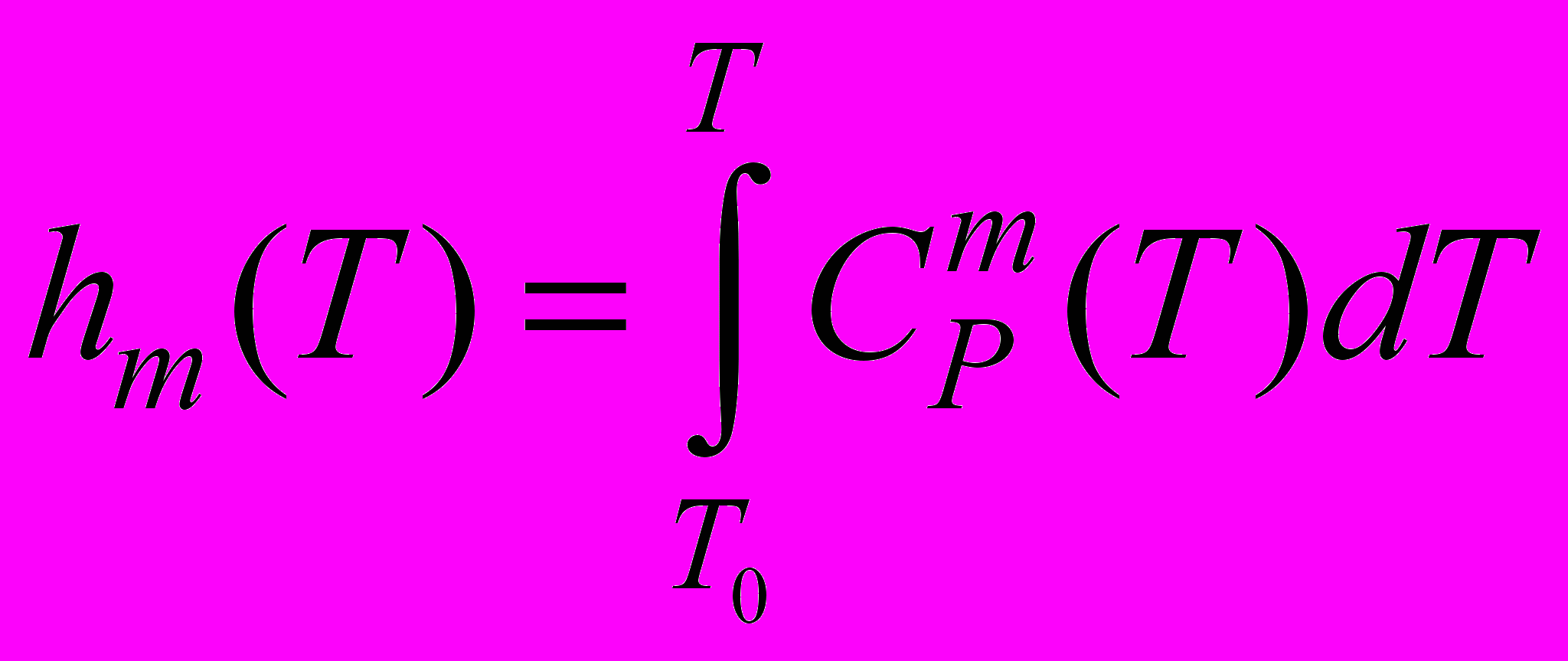(2.1.2.3)

Удельная теплоемкость компонент задается в виде полинома 4-ой степени от температуры

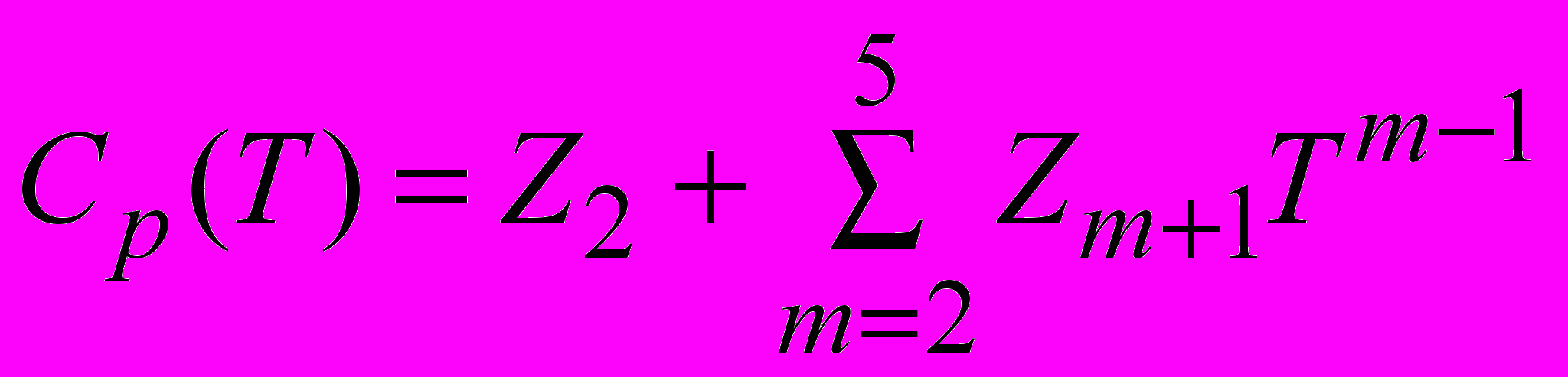(2.1.2.4)

Температура смеси Т в каждой точке рассчитывается по вычисленному из уравнения (2.1.3.1) значению энтальпии h и составу смеси Y_m.


2.1.3. Уравнение переноса компонент среды

Уравнение переноса концентрации компонент:

(2.1.3.1)

где 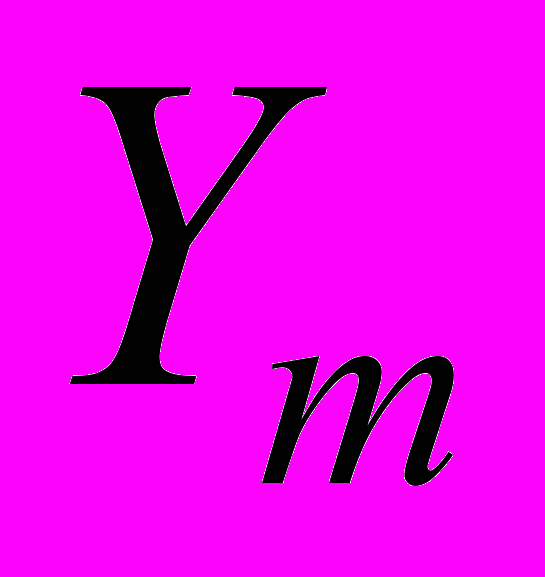- массовая доля m-той компоненты,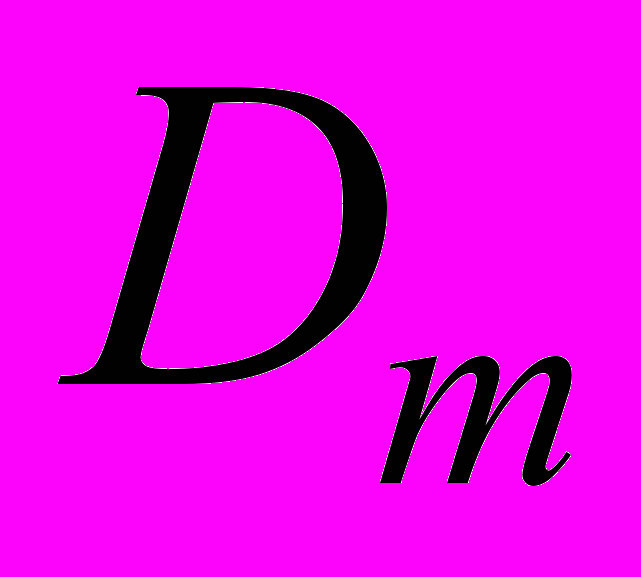- коэффициент диффузии компонента m, 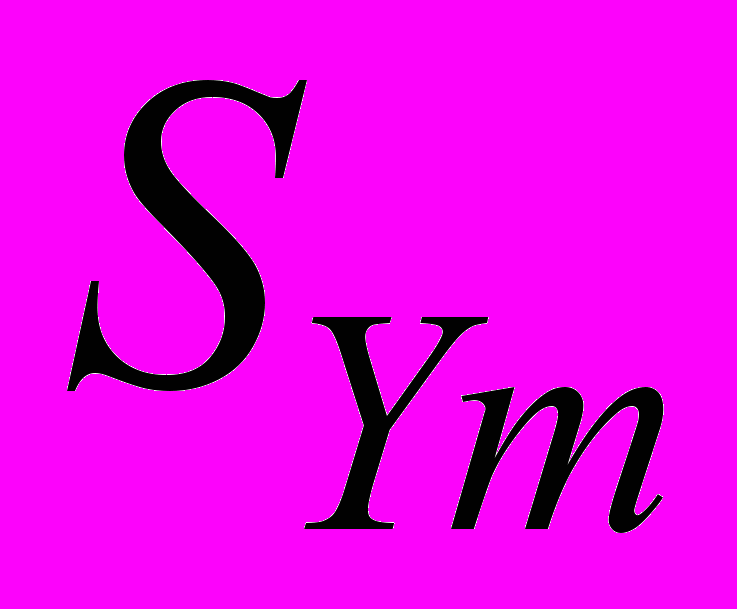– источниковый член, отвечающий за изменение компоненты в процессах химического реагирования или в каких-либо других процессах.


2.1.4. Термодинамические свойства среды

Уравнения состояния

1). Несжимаемая жидкость

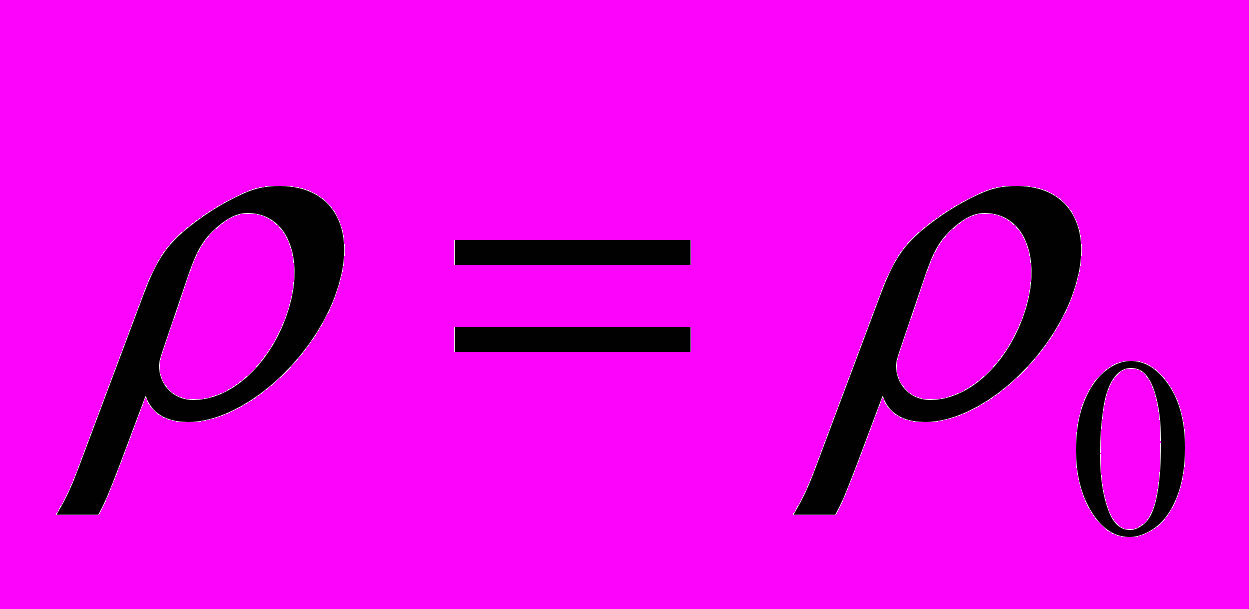(2.1.4.1)

где -константа.

2). Модель термического расширения

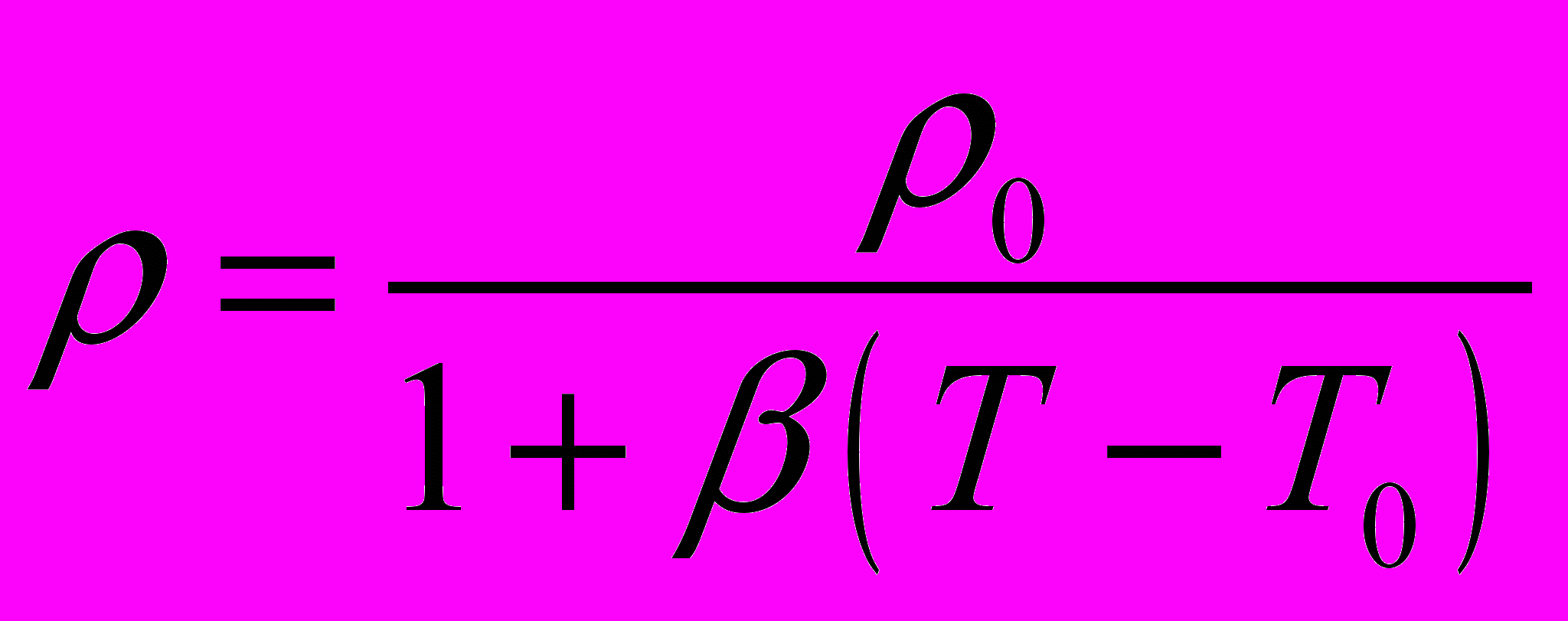(2.1.4.2)

где 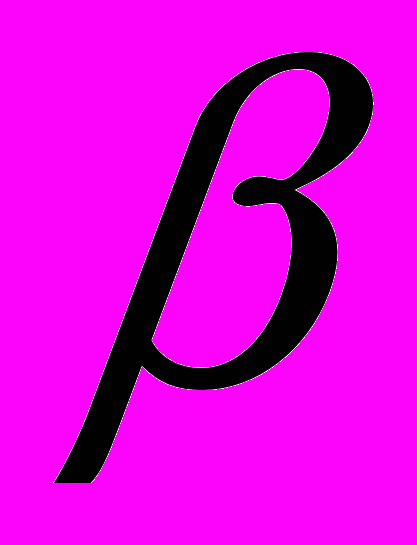- коэффициент термического расширения, 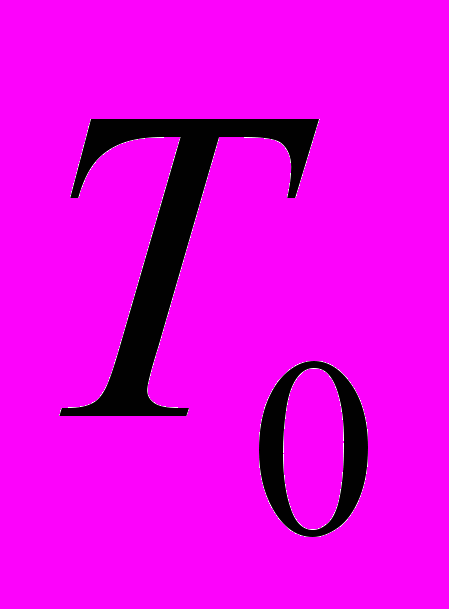-опорная температура, -опорная плотность.

3). Модель идеального газа

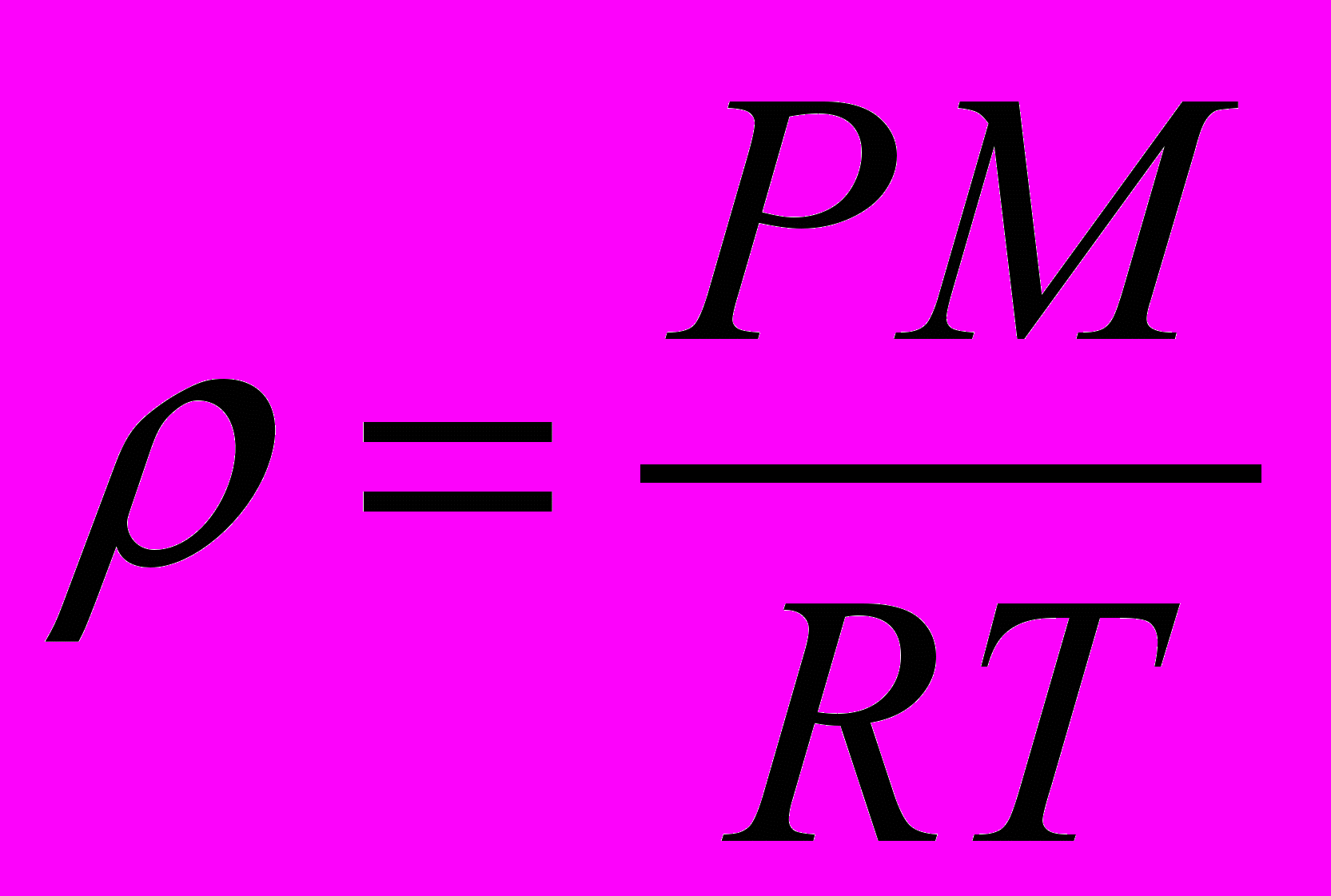(2.1.4.3)

где P статическое давление, M - молярная масса газа, R - универсальная газовая постоянная, T - температура газа.


Свойства смеси

В программе “Fire” свойства смеси определяются через массовые доли ее компонент .

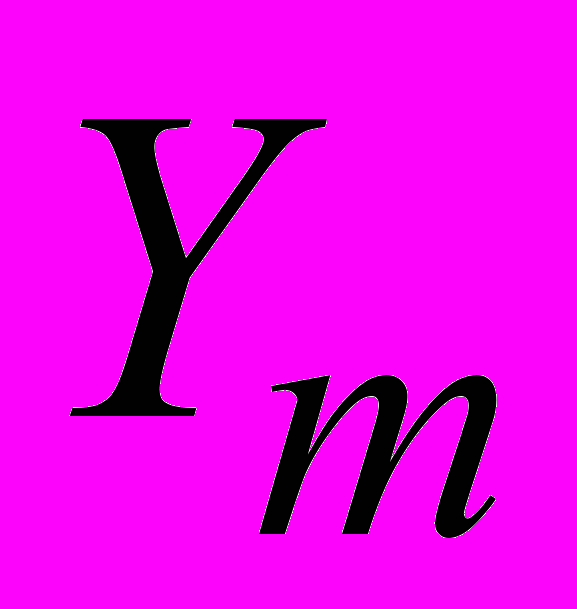Теплопроводность смеси

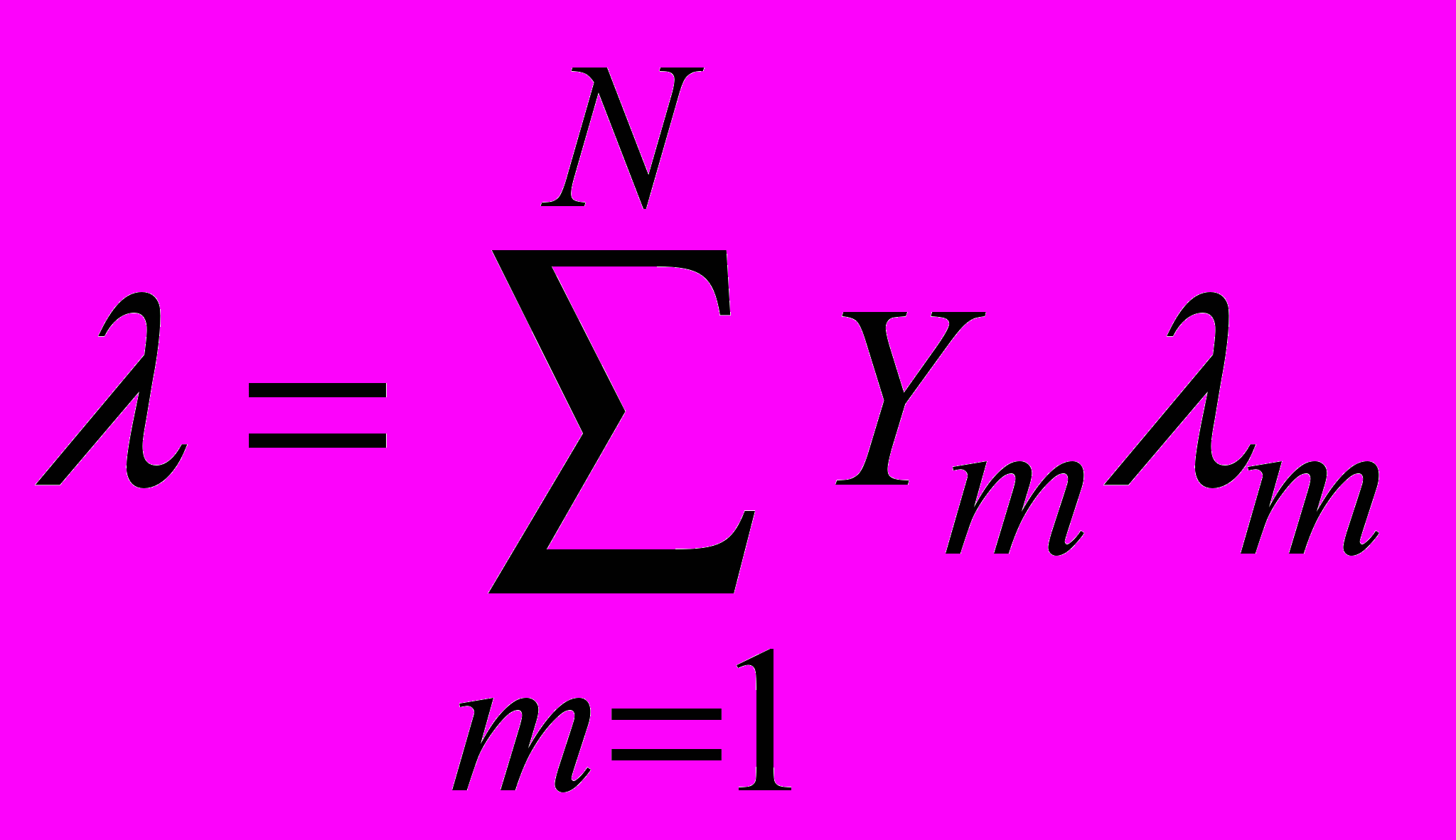(2.1.4.4)

Плотность смеси

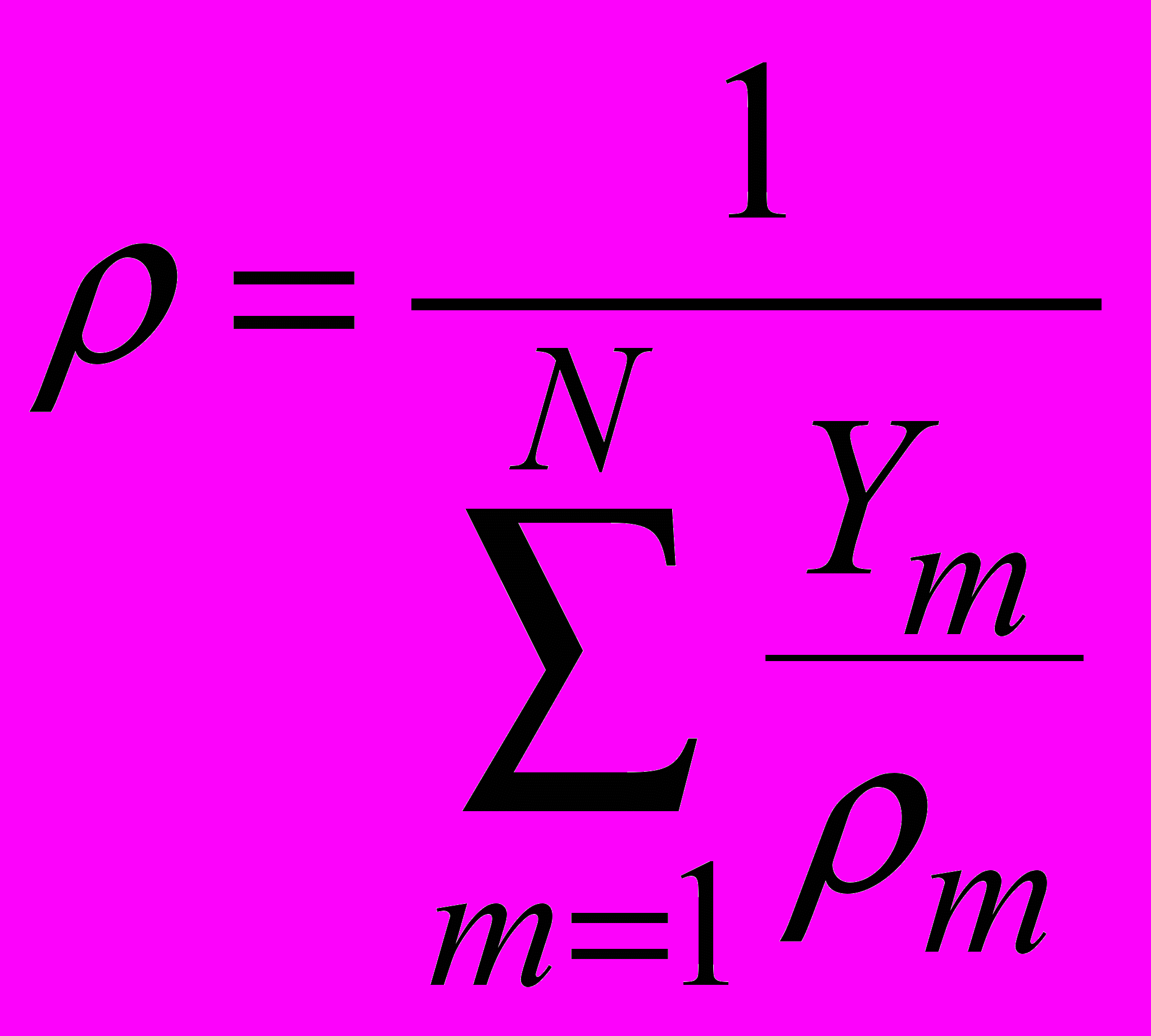(2.1.4.5)

Удельная теплоемкость смеси

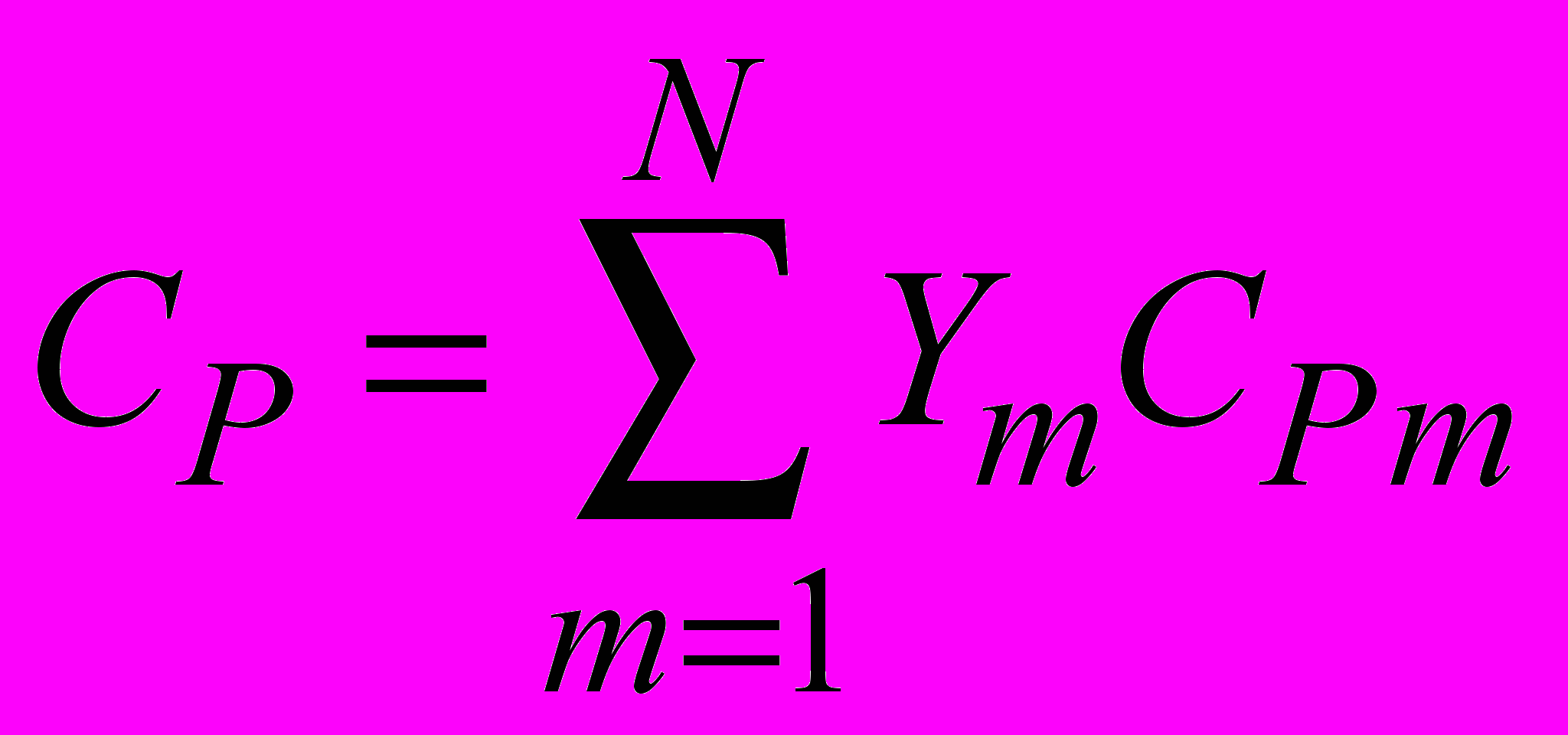(2.1.4.6)

Энтальпия смеси

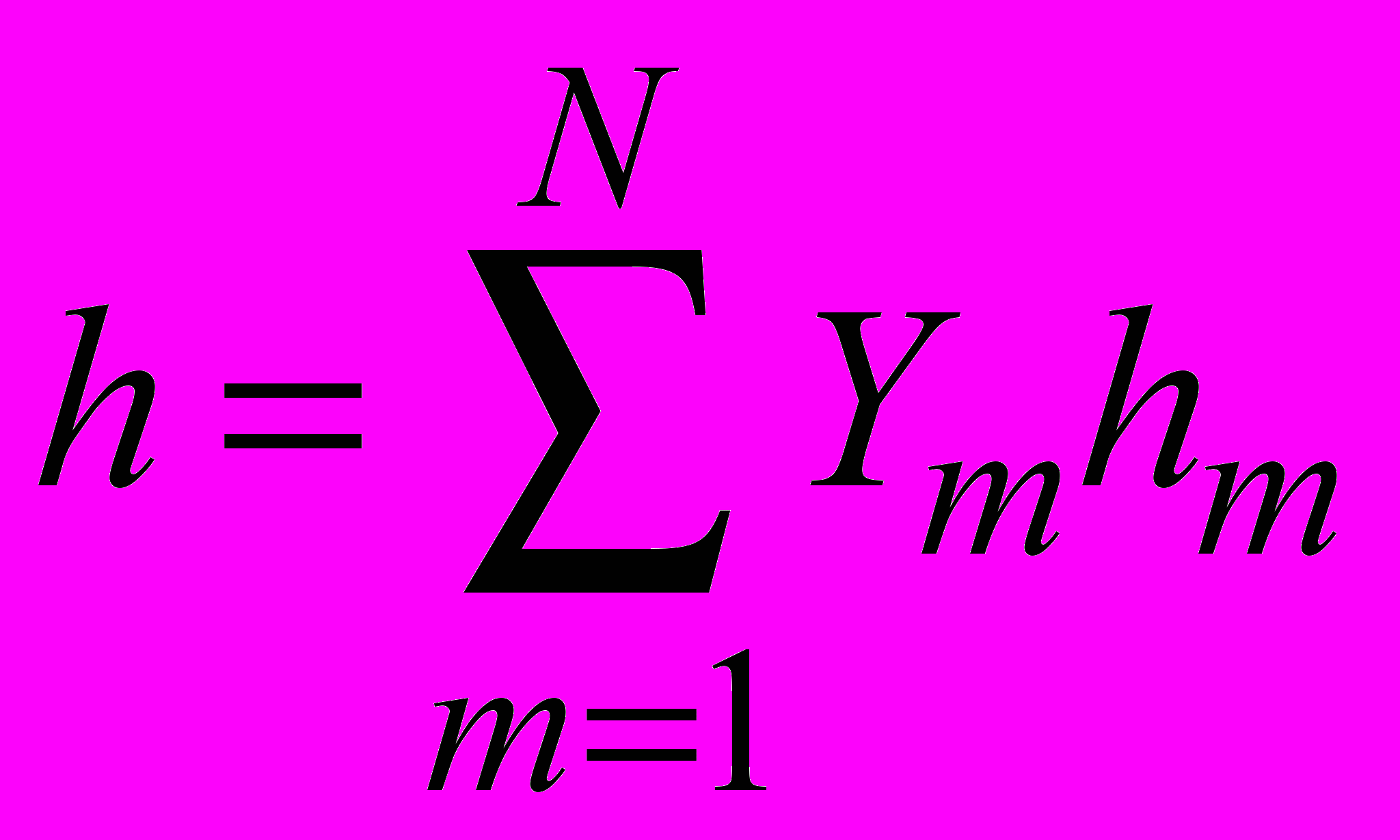(2.1.4.7)

Динамическая вязкость смеси

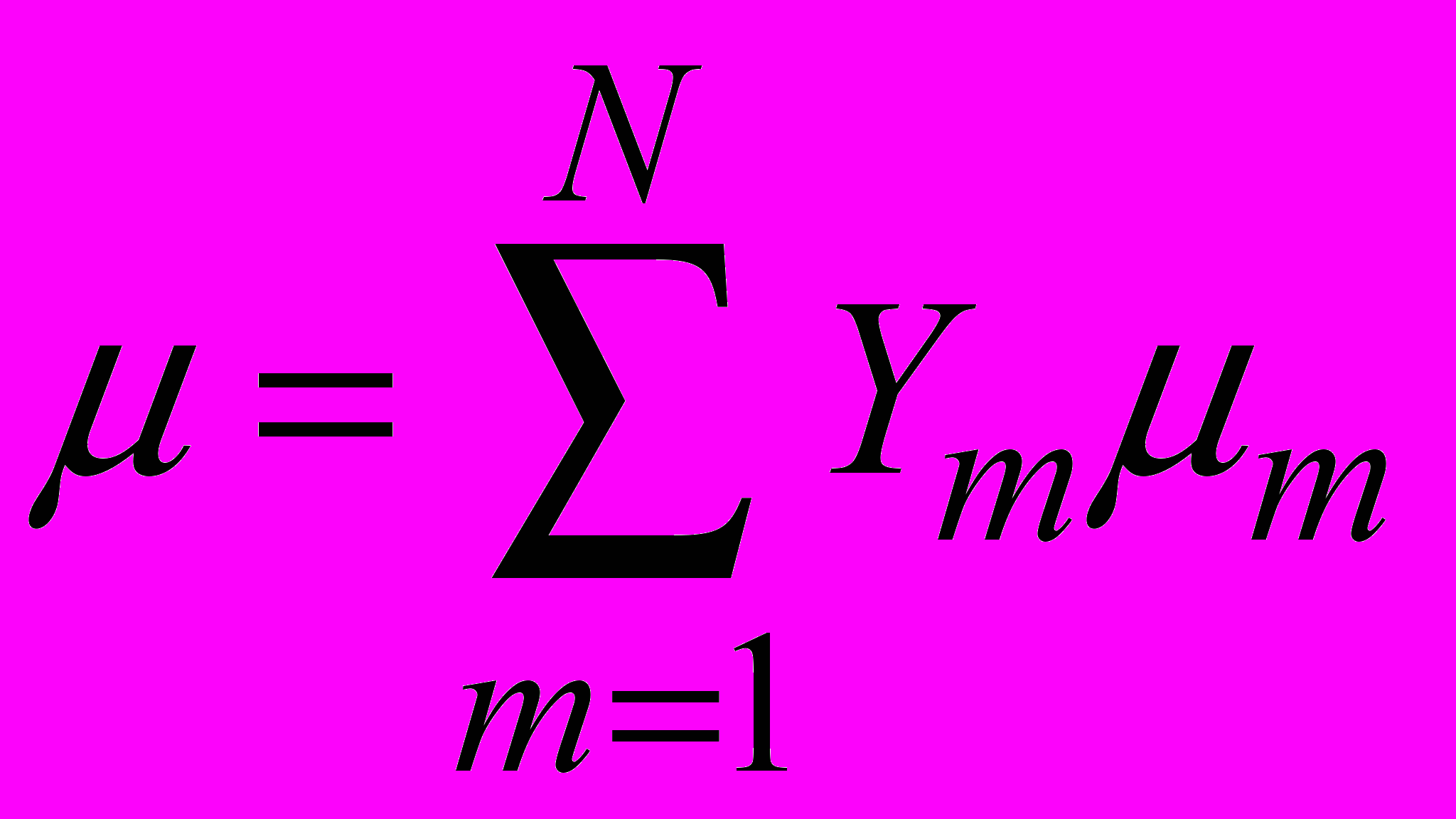(2.1.4.8)

Молярная масса смеси

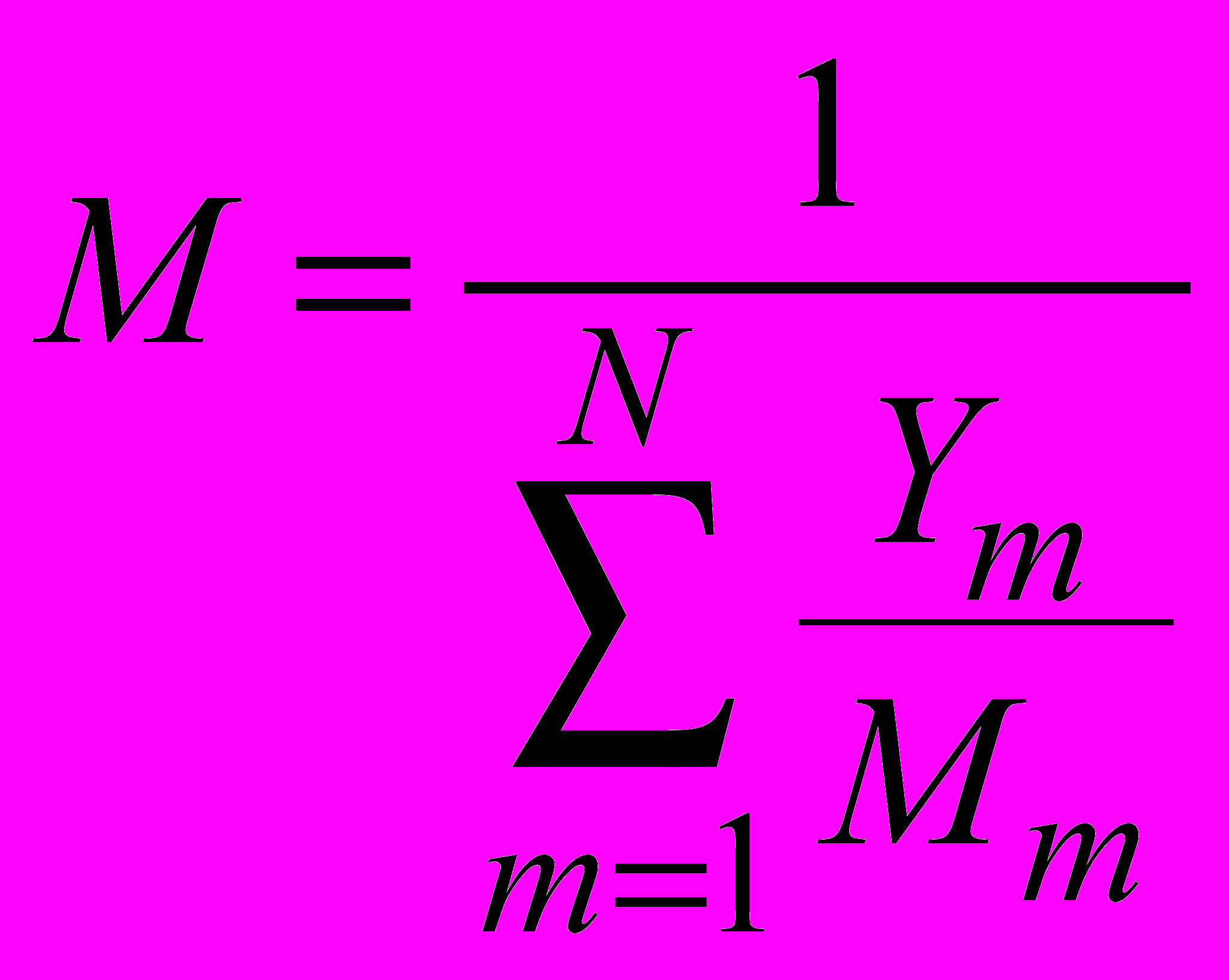(2.1.4.9)

2.2. Моделирование турбулентности

Считается, что при помощи уравнения Навье-Стокса можно описать как ламинарное так и турбулентное течение (Ландау Л.Д., Лифшиц Е.М., 1986), практически же реальные достижения в расчетах турбулентных потоков связаны с использованием полуэмпирических моделей турбулентности использующих подход Рейнольдса. Обоснованием необходимости применения такого подхода может служить приведенная в ряде работ оценка, согласно которой отношение характерных размеров энергосодержащих (крупных) вихрей и мелкомасштабных вихрей, определяющих «турбулентный фон», имеет порядок Re^3/4. Естественно, что, ориентируясь на возможности современных ЭВМ, решить поставленные задачи в практически важном диапазоне Re  10³ в настоящее время маловероятно.

Применим операцию осреднения по времени к уравнениям (2.1.1.1) и (2.1.1.2) получим уравнения движения в форме Рейнольдса (RANS).

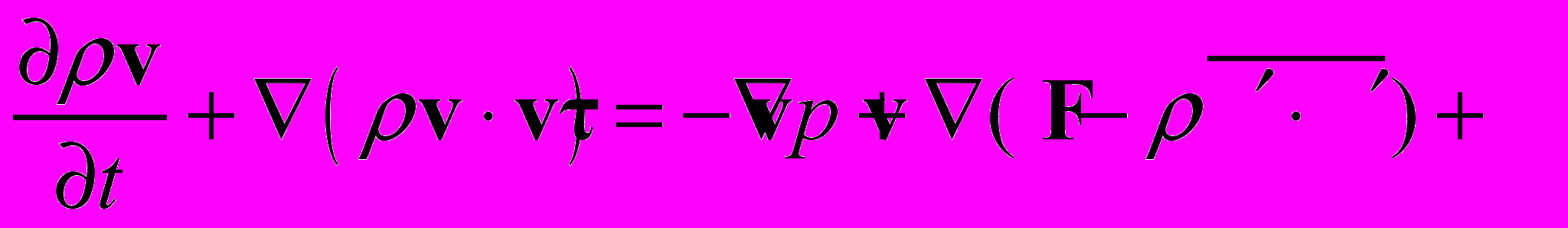(2.2.1)

где 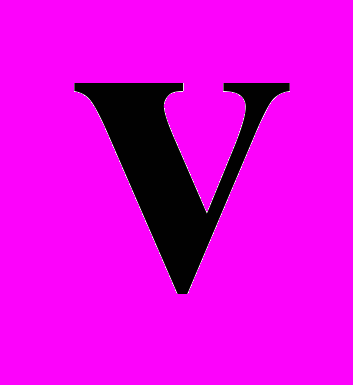- усредненное по времени поле скоростей, 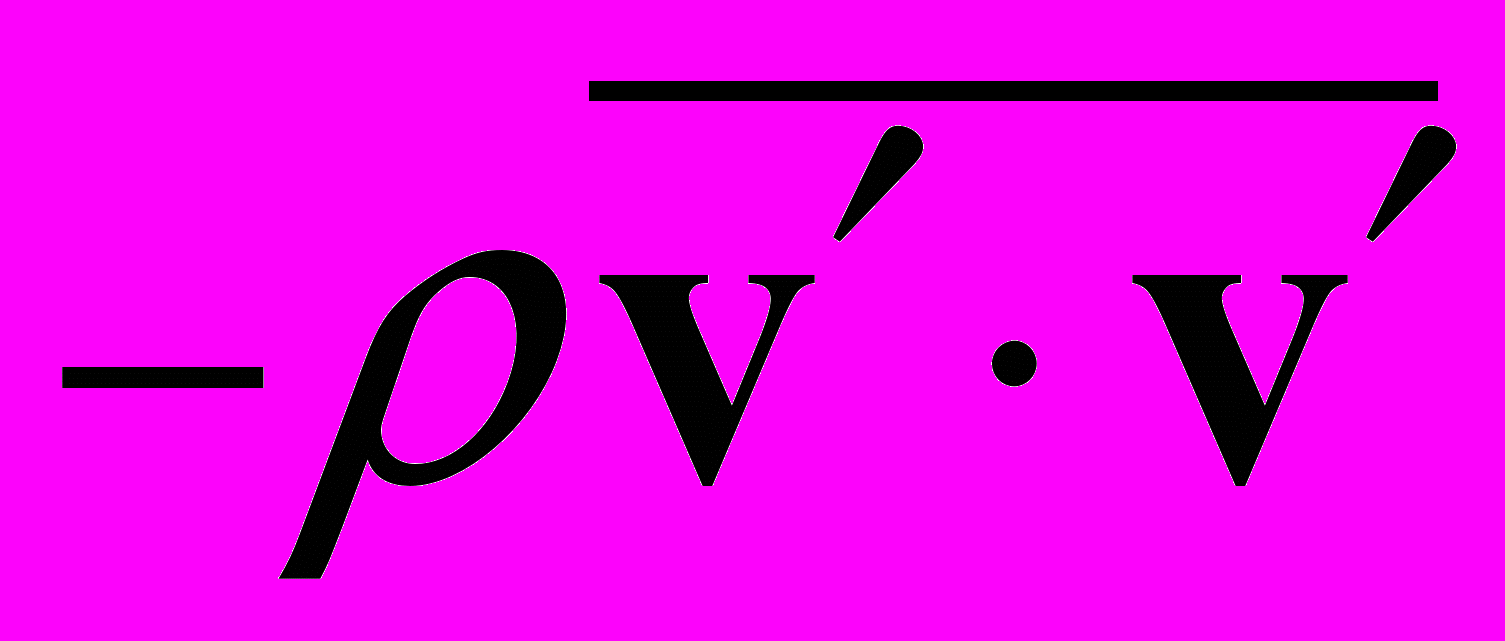- тензор рейнольдсовых напряжений, - символ Кронекера.

Для определения компонент тензора рейнольдсовых напряжений используем гипотезу Буссинеска

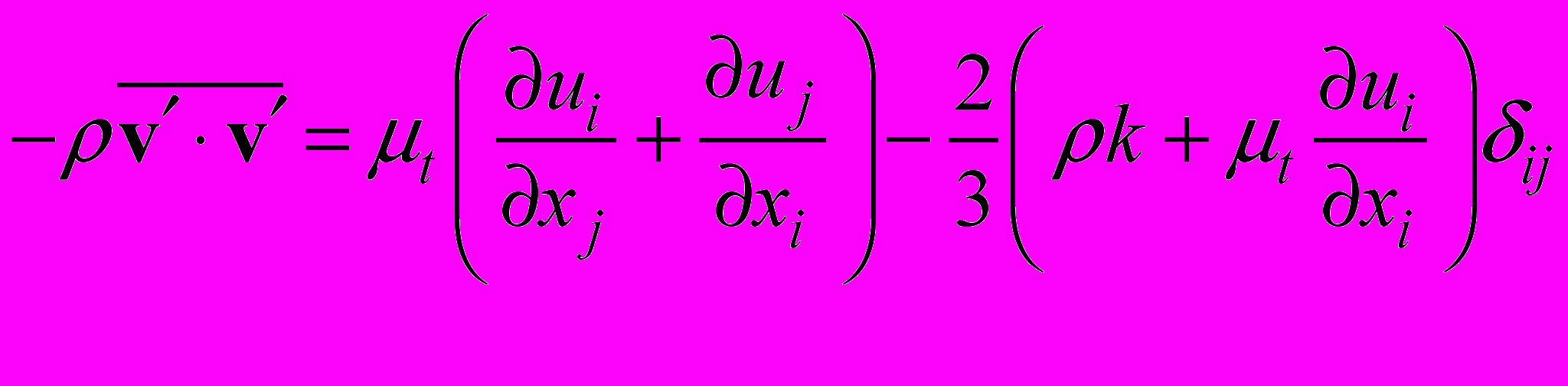(2.2.2)

где 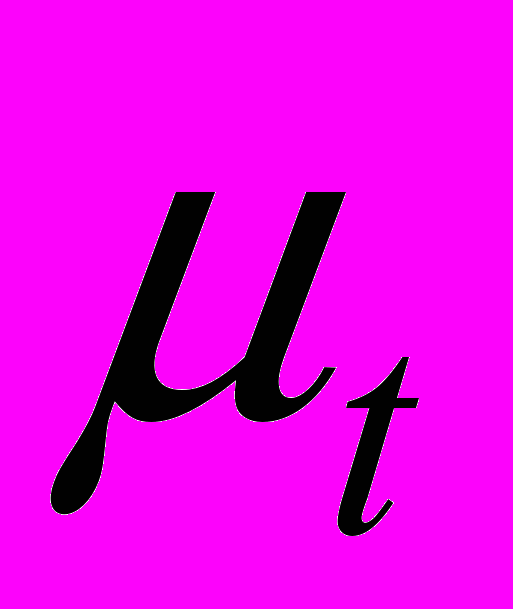- турбулентная вязкость, 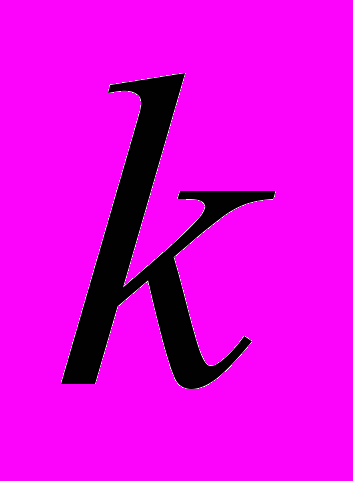- кинетическая энергия турбулентных пульсаций.

Система уравнении (2.2.1)-( 2.2.2) является не замкнутой поэтому для ее замыкания применяются различные полуэмпирические модели турбулентности которые описаны ниже.


2.2.1. Модели турбулентности

Стандартная k- модель (Launder and Spalding, 1972)

Уравнения стандартной высоко-рейнольдсовой k- модели:

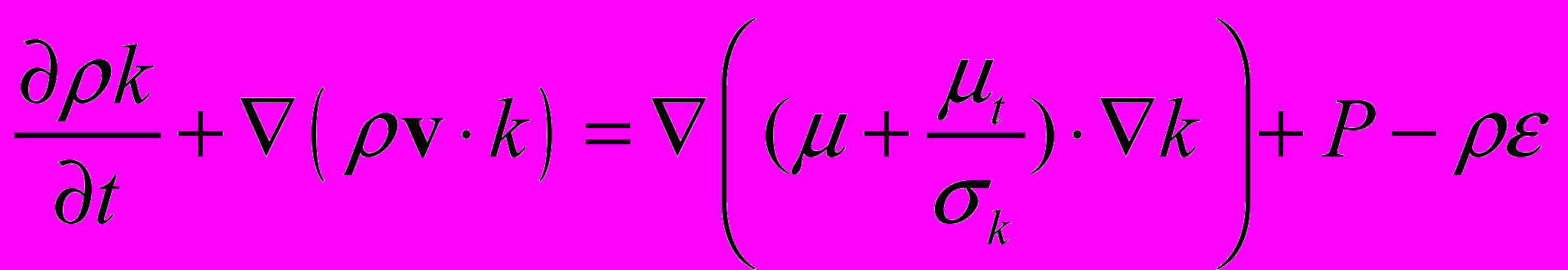(2.2.1.1)

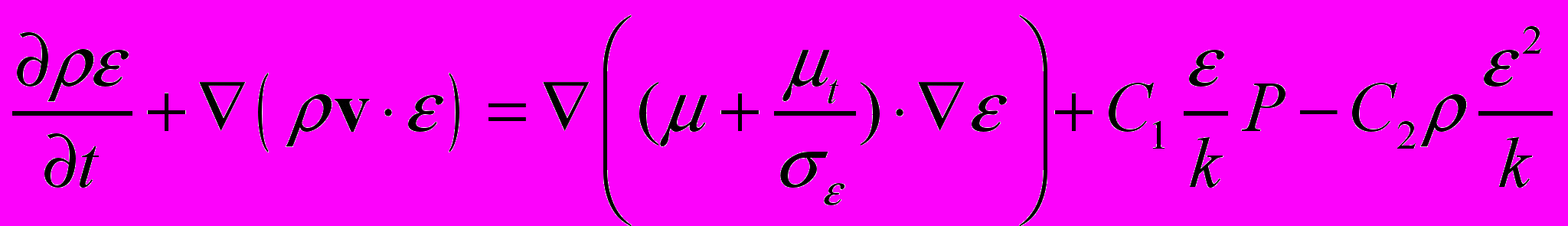(2.2.1.2)

где P - скорость генерации турбулентности:

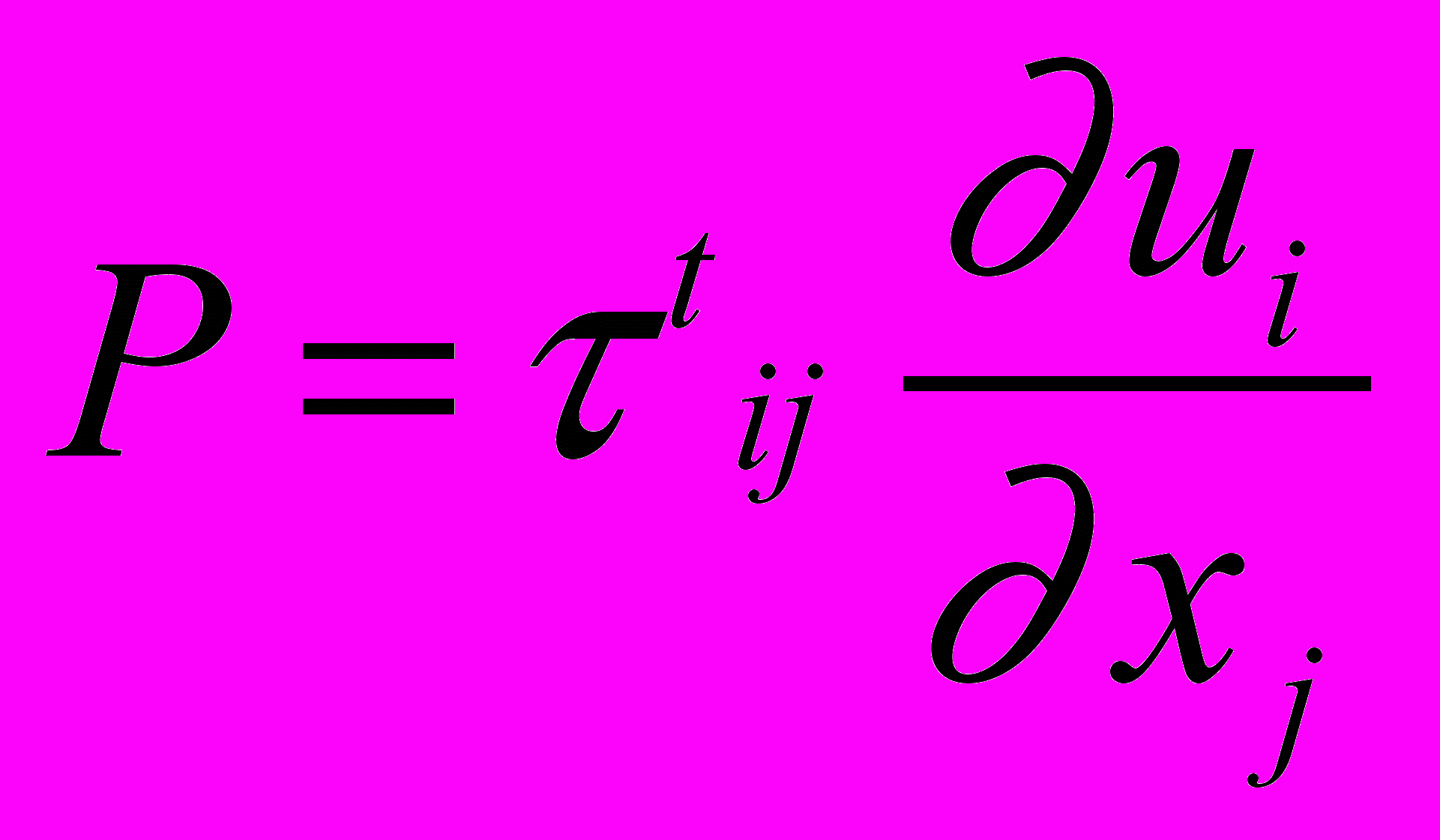(2.2.1.3)

турбулентная вязкость:

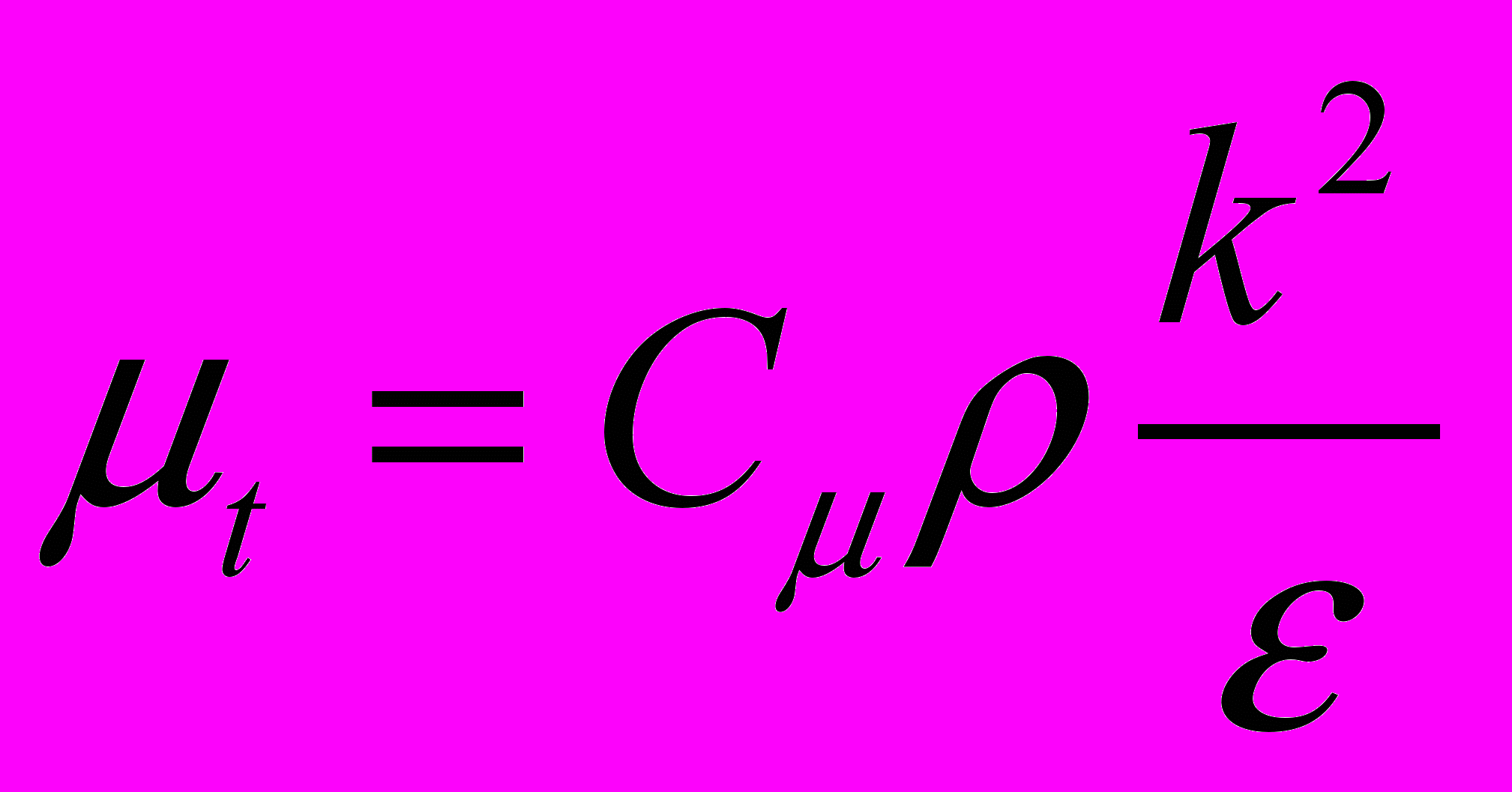(2.2.1.4)

Тензор Рейнольдсовых напряжений принимает форму:

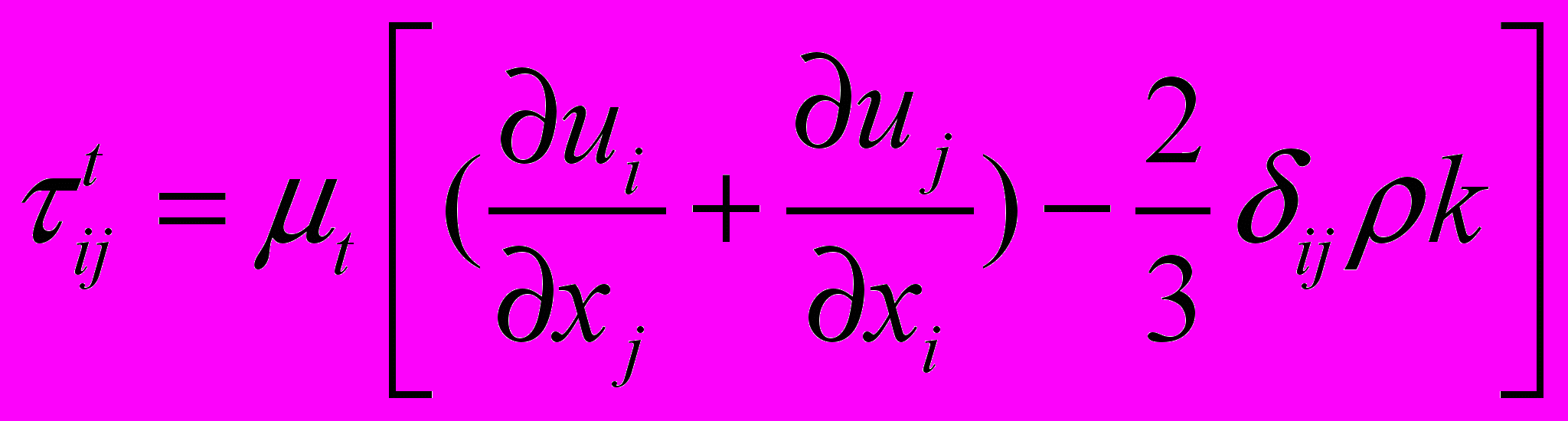. (2.2.1.5)

Константы замыкания стандартной модели (Launder and Spalding, 1972):

C=0,09, k=1,0, =1,3, С1=1,44, C2=1,92.


Chen k- модель

Уравнения для модификации k- модели Chen, которые определяют кинетическую энергию турбулентности и скорость ее диссипации для k- модели, имеют вид (Chen and Kim, 1987):

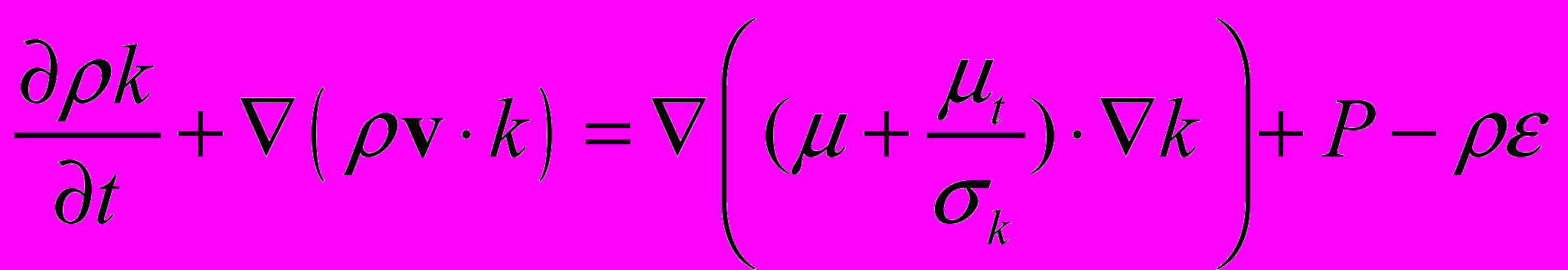(2.2.1.6)

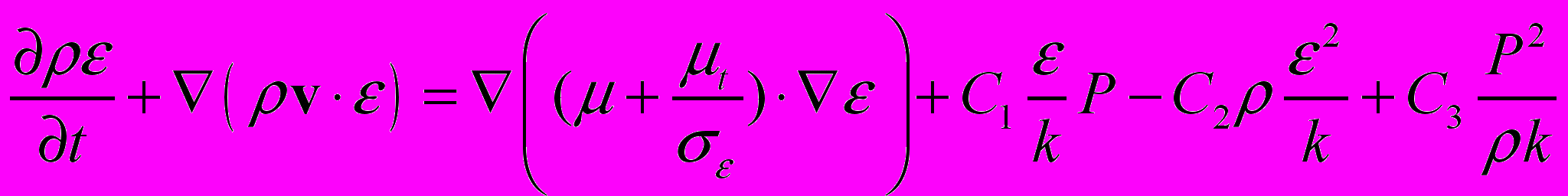(2.2.1.7)

Эмпирические константы C=0,09, k=0,8, _=1,15, С₁=1,15, C₂=1,9, C₃=0,25 взяты из работы (Chen and Kim, 1987).


M-SST модель турбулентности

Модель Ментера записывается путем суперпозиции моделей k- и k-, основанной на том, что модели типа k- лучше описывают свойства свободных сдвиговых течений, в модели - имеют преимущество при моделировании пристеночных течений. Плавный переход от k- модели в пристеночной области к k- модели вдали от твердых стенок обеспечивается введением весовой эмпирической функцией F₁ .

Вторая важная деталь модели состоит в изменении стандартной связи между k,  и турбулентной вязкостью. Модификация этой связи состоит во введении перехода к формуле Бредшоу в пристеночной области. Согласно предположению Бредшоу напряжение сдвига в пограничном слое пропорционально энергии турбулентных пульсаций.

Уравнения M-SST модели [M-SST]:

Транспортные уравнения для k и 

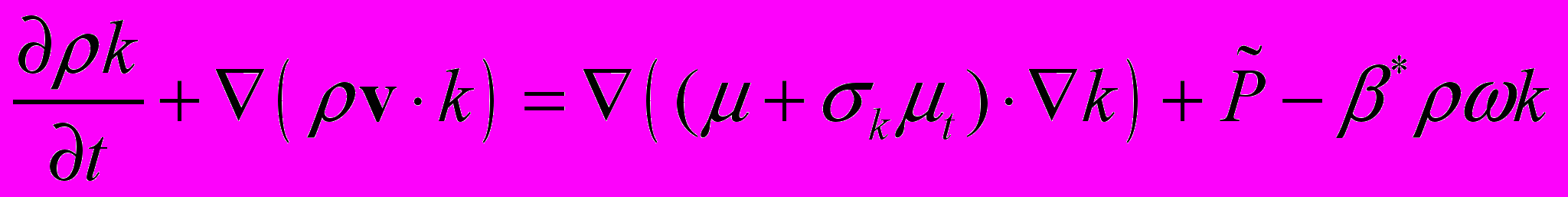(2.2.1.8)

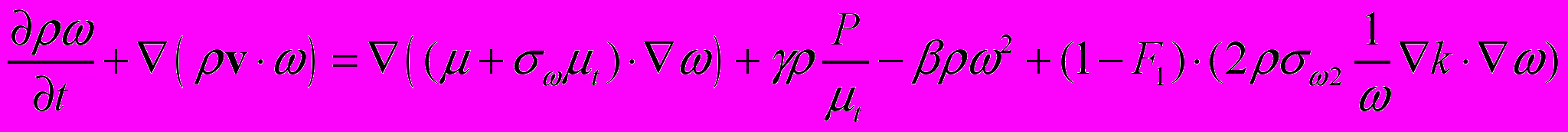(2.2.1.9)


В члене генерации турбулентной энергии введен ограничитель:

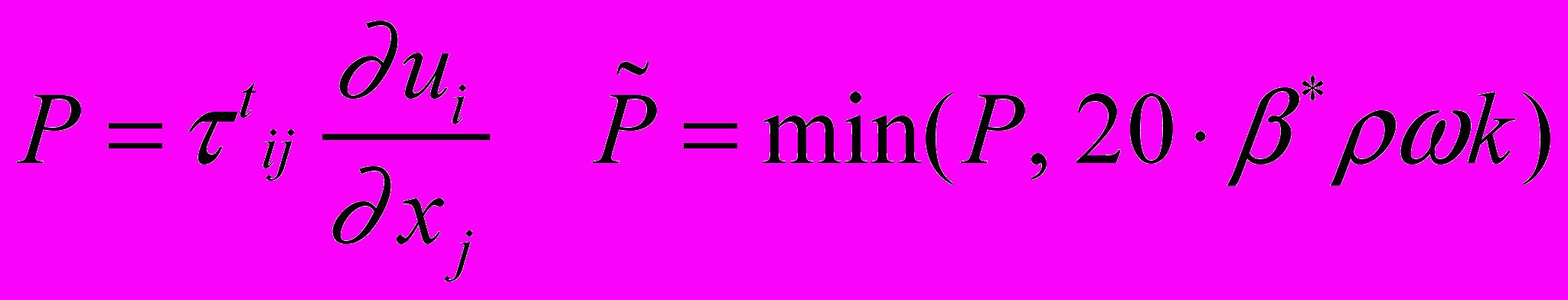(2.2.1.10)

Весовая функция и ее аргумент

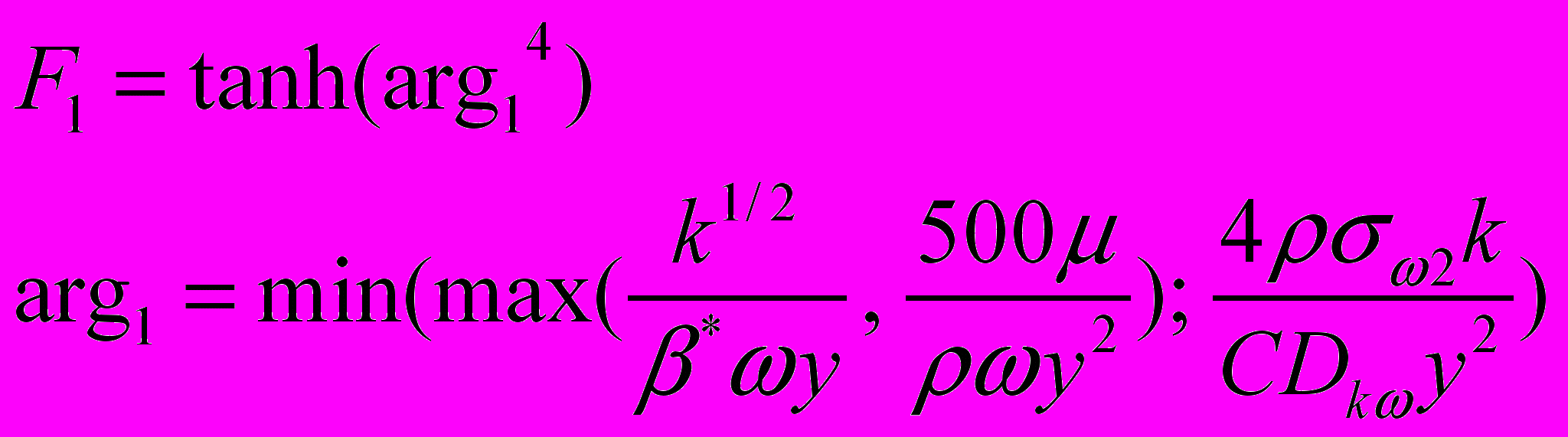, (2.2.1.11)

где положительная часть перекрестных диффузионных членов в уравнении переноса 

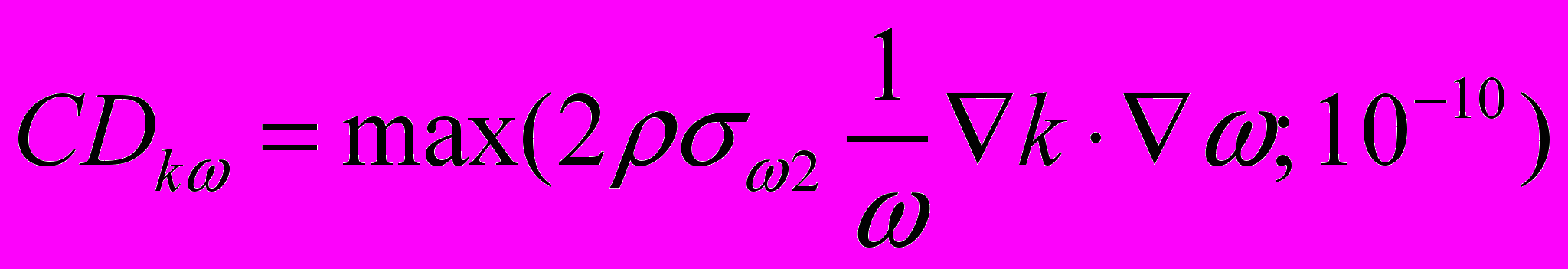. (2.2.1.12)


Выражения для вихревой вязкости с учетом гипотезы Бредшоу:

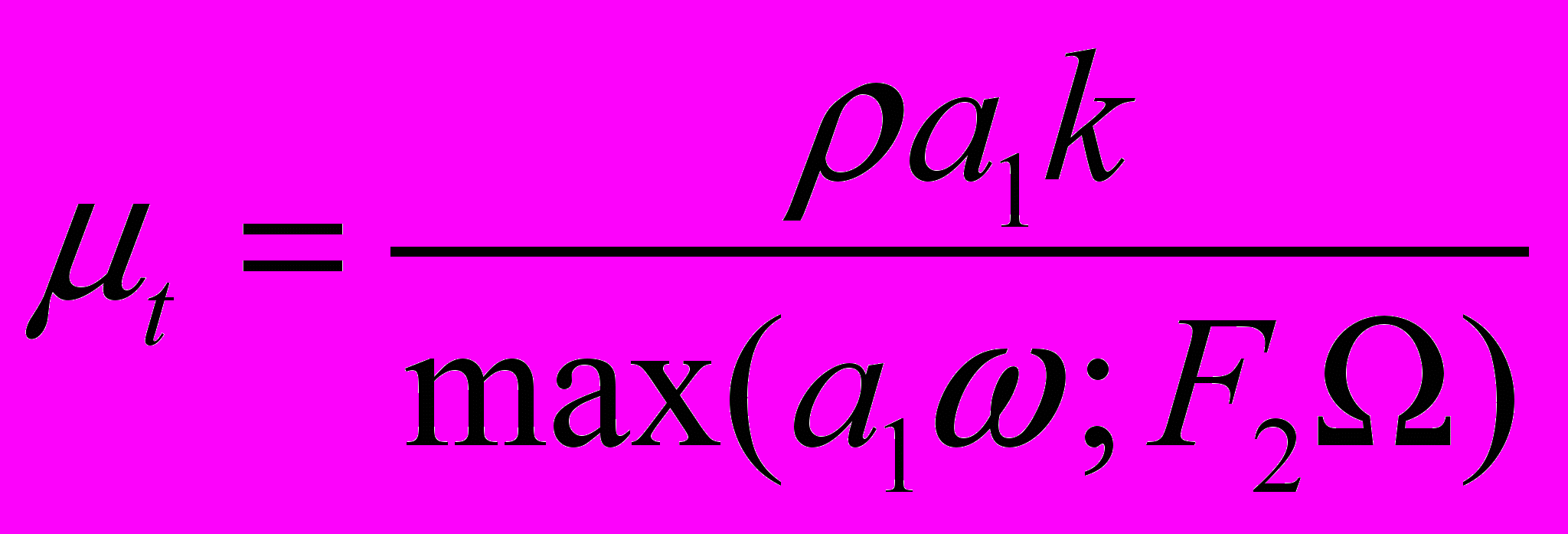, (2.2.1.13)

где величина завихренности

. (2.2.1.14)

Функция переключения F₂ определяется подобно F₁ :

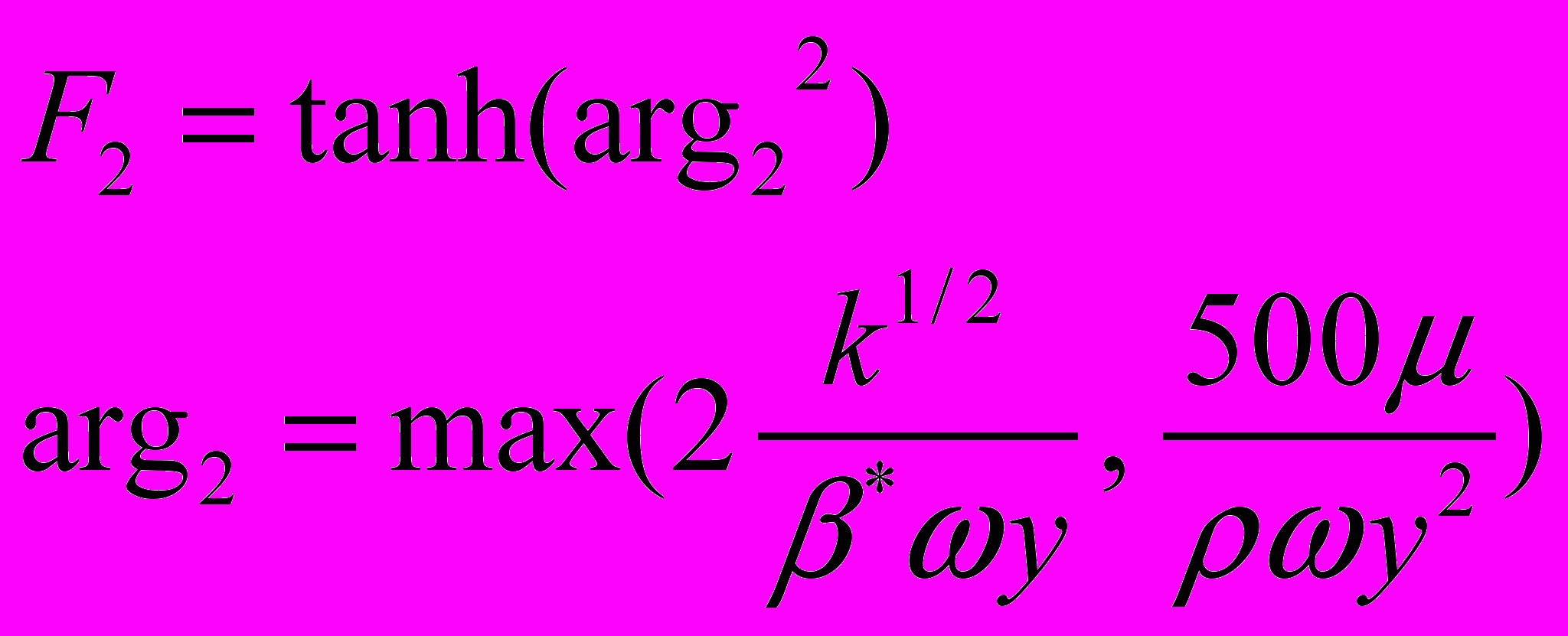. (2.2.1.15)

Константы в уравнениях переноса записываются путем суперпозиции констант для модели k- модели (Wilcox) и констант стандартной k- модели:

константы:

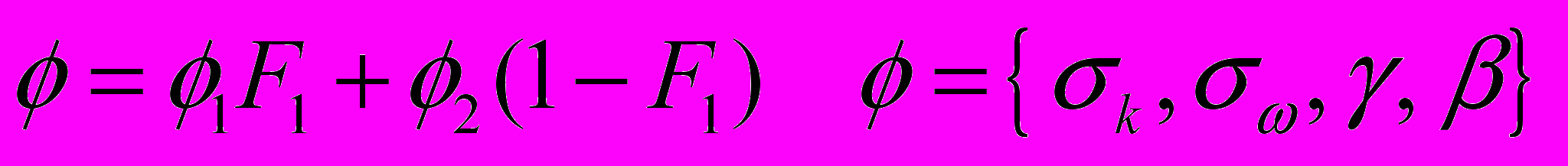(2.2.1.16)


Набор констант для пристеночного слоя SST модели:

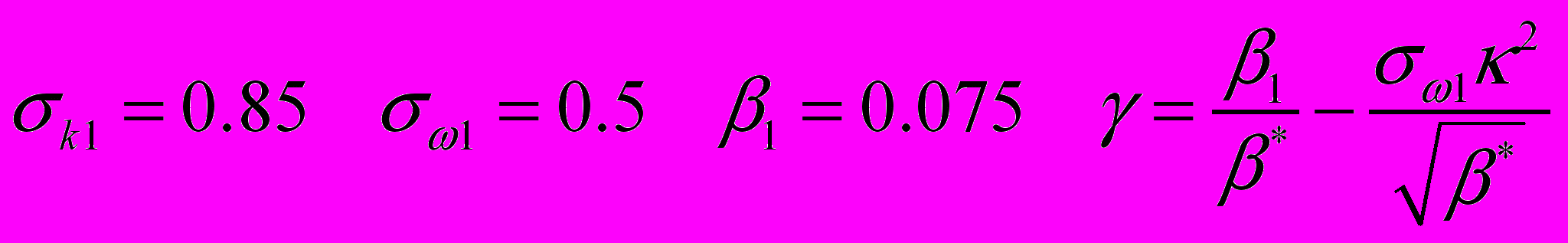. (2.2.1.17)

Набор констант для свободных сдвиговых слоев:


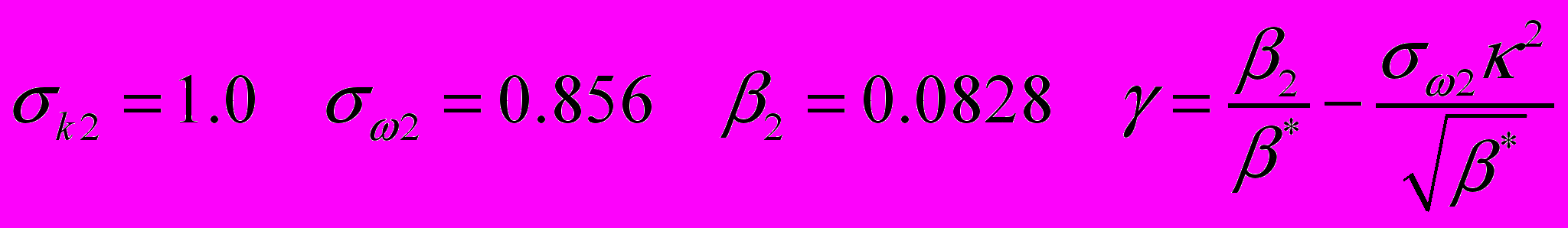. (2.2.1.18)


Другие константы, использующиеся в модели:



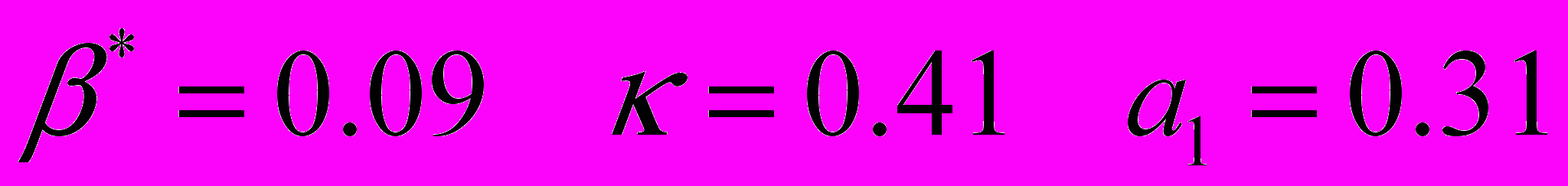
2.2.2. Метод пристеночных функций

Вблизи стенок турбулентный поток имеет сложную структуру со значительными градиентами. Во внутренней области, занимающей порядка 20% толщины пограничного слоя, генерируется около 80% всей энергии турбулентности. Для моделирования пристеночных течений часто применяется метод пристеночных функций, который позволяет экономить вычислительные ресурсы и учитывать влияния различных факторов (шероховатости стенки, градиента давления вблизи стенки, вдув-отсос с поверхности тела) за счет введения эмпирической информации. Метод пристеночных функций, связывающий параметры течения с расстоянием до стенки, представляет собой аналитическое решение упрощенных решений турбулентного течения.

В основе упрощения лежат следующие предположения:

1) локальное равновесие энергии турбулентных пульсаций (локальная скорость производства турбулентности уравновешивается скоростью вязкой диссипации);

2) постоянство касательного напряжения вдоль слоя;

3) пренебрежимо малый градиент давления вдоль потока;

4) локальная изотропность диссипирующих вихрей;

5) универсальность профиля скорости (слабая зависимость от числа Рейнольдса).

Следует отметить, что этот метод является в основном эмпирическим. Метод пристеночных функций, основанный на обобщении экспериментальных данных для развитых турбулентных течений, достаточно хорошо описывает пристеночные течения при значительных турбулентных числах Рейнольдса с пренебрежимо малой областью вязкого слоя. В случае не выполнения гипотез, лежащих в основе пристеночных функций, требуется модификация соотношений метода или использование низкорейнольдсовых диссипативных моделей.

2.3. Дискретизация уравнений переноса

Для решения уравнения переноса энергии используется широко известный метод контрольного объема, суть которого заключается в разбиении расчетной области на контрольные объемы (рис. 2.3.1) и интегрировании исходных уравнений сохранения по каждому контрольному объему для получения конечно разностных соотношении. Метод и его свойства достаточно подробно описаны в литературе (Белов и др., 1989), (Ferziger and Peric, 2002).

В пакете «Fire» используются многоблочные структурированные криволинейные сетки.




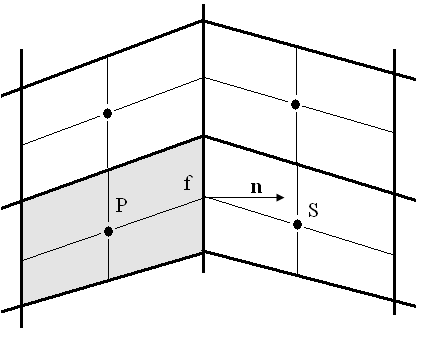
Рис. 2.3.1. К вычислению потоков через грань контрольного объема.


В расчетном алгоритме применяется подход стыковки отдельных сеток с различной плотностью расчетных узлов вдоль выделенной поверхности раздела, при этом сетки не пересекаются. В этом случае граничный контрольный объем может соприкасаться с несколькими контрольными объемами из соседнего блока. Соответственно граничная грань ячейки разбивается на несколько подобластей. Для каждой области пересечения строится полный поток. Рассчитанные потоки разбиваются на явную и неявную части и заносятся в правую часть и матрицу коэффициентов системы уравнений соответственно. Использование значения величины из соседнего блока с предыдущей итерации для вычисления потока через общую грань несколько снижает скорость сходимости по сравнению с одноблочной техникой. Но многоблочная технология позволяет существенно снизить вычислительные затраты для построения сетки и проведения расчетов тепловых и гидродинамических процессов в многосвязных областях сложной геометрии.


2.4. Граничные условия.


Условия на входе потока

В пакете «Fire» существует возможность задавать на входе либо фиксированное значение скорости, либо массовый расход. При этом если задан расход то компоненты скорости u, v, w в каждом входе рассчитываются по заданному массовому расходу, углу наклона оси входного потока к осям координат и по доли потока, заданное для данного входного «окна». Например, компонента u на входе определяется следующим образом:

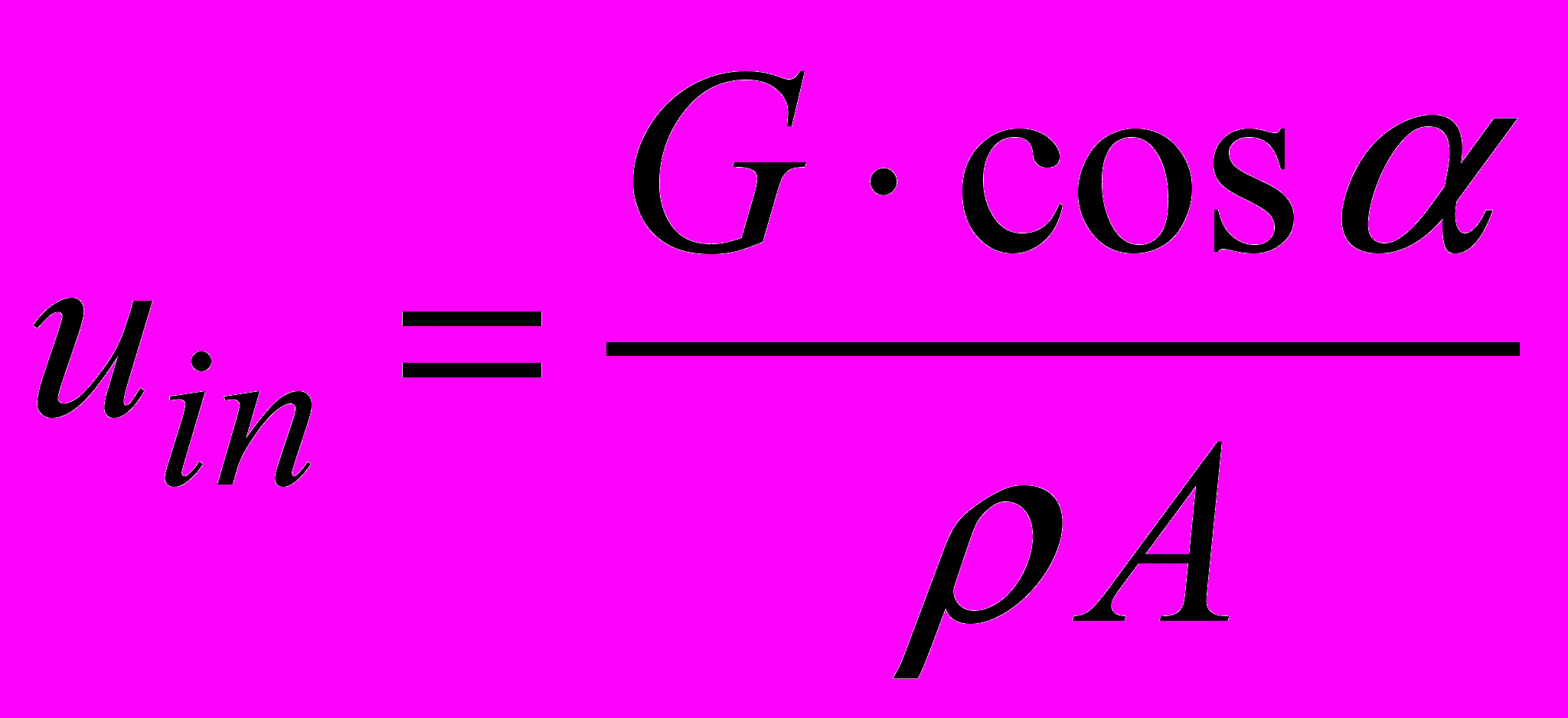(2.4.1)

где G - массовый расход жидкости на входе,  - суммарная плотность, А-площадь сечения входного окна,  - угол между осью OX и осью входного потока.

Кинетическая энергия турбулентности k и скорость диссипации турбулентности  на входе оцениваются по соотношениям вида:

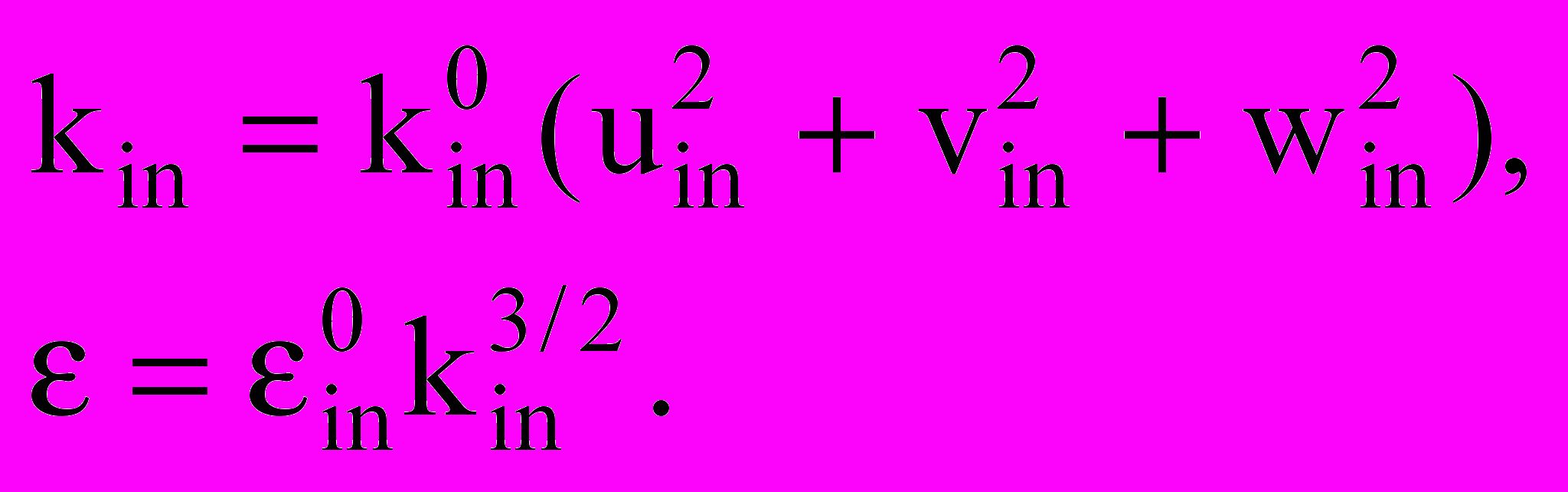(2.4.2)

где константы k^o_in, ^o_in подбираются эмпирически.

Обычно для развитых турбулентных потоков на входе уровень турбулентных пульсации составляет порядка 1%, поэтому k^o_in=0,01, а ^o_in =C_/L, где L - характерный размер энергосодержащих вихрей.

Энтальпия на входе вычисляется по заданным температуре входа и составу газов или жидкости.

Граничные условия для Y_m задаются в виде массовых долей компонентов на входе.


Условия на выходе потока

На выходной границе при решении уравнений для u, v, w, k, , h, Y_m ставятся условия отсутствия градиентов (так называемые «мягкие условия»):

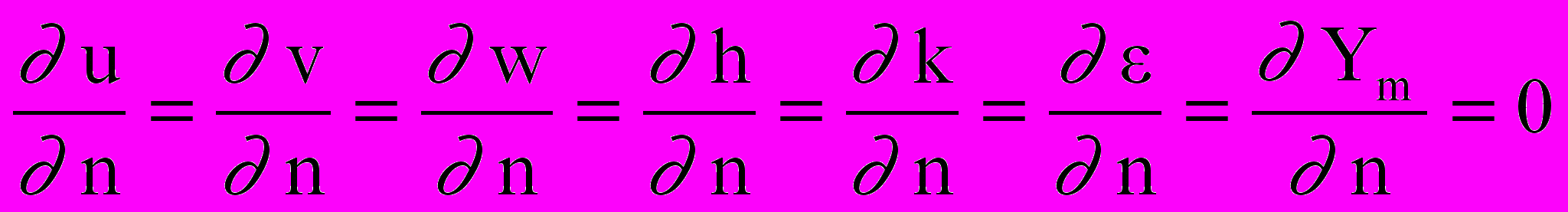, (2.4.3)

где n - вектор внешней нормали к расчетной области.


Условие симметрии (скольжение)


На плоскости симметрии ставятся условия равенства нулю: производной по нормали к плоскости симметрии всех скалярных величин и тангенциальной составляющей скорости , нормальной к плоскости составляющая скорости .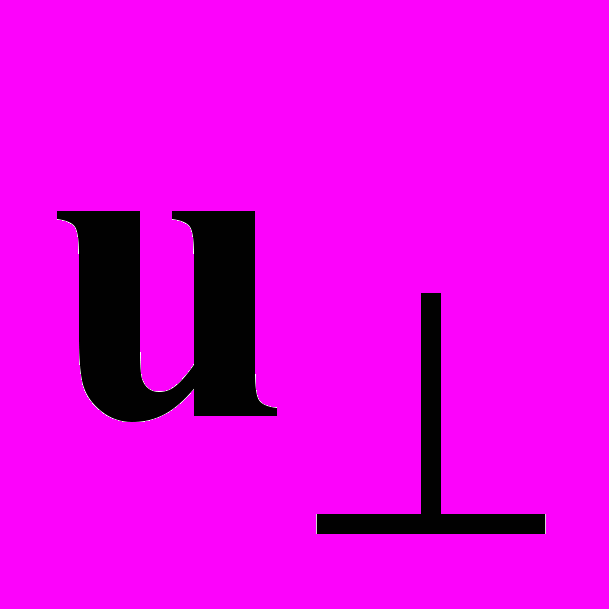

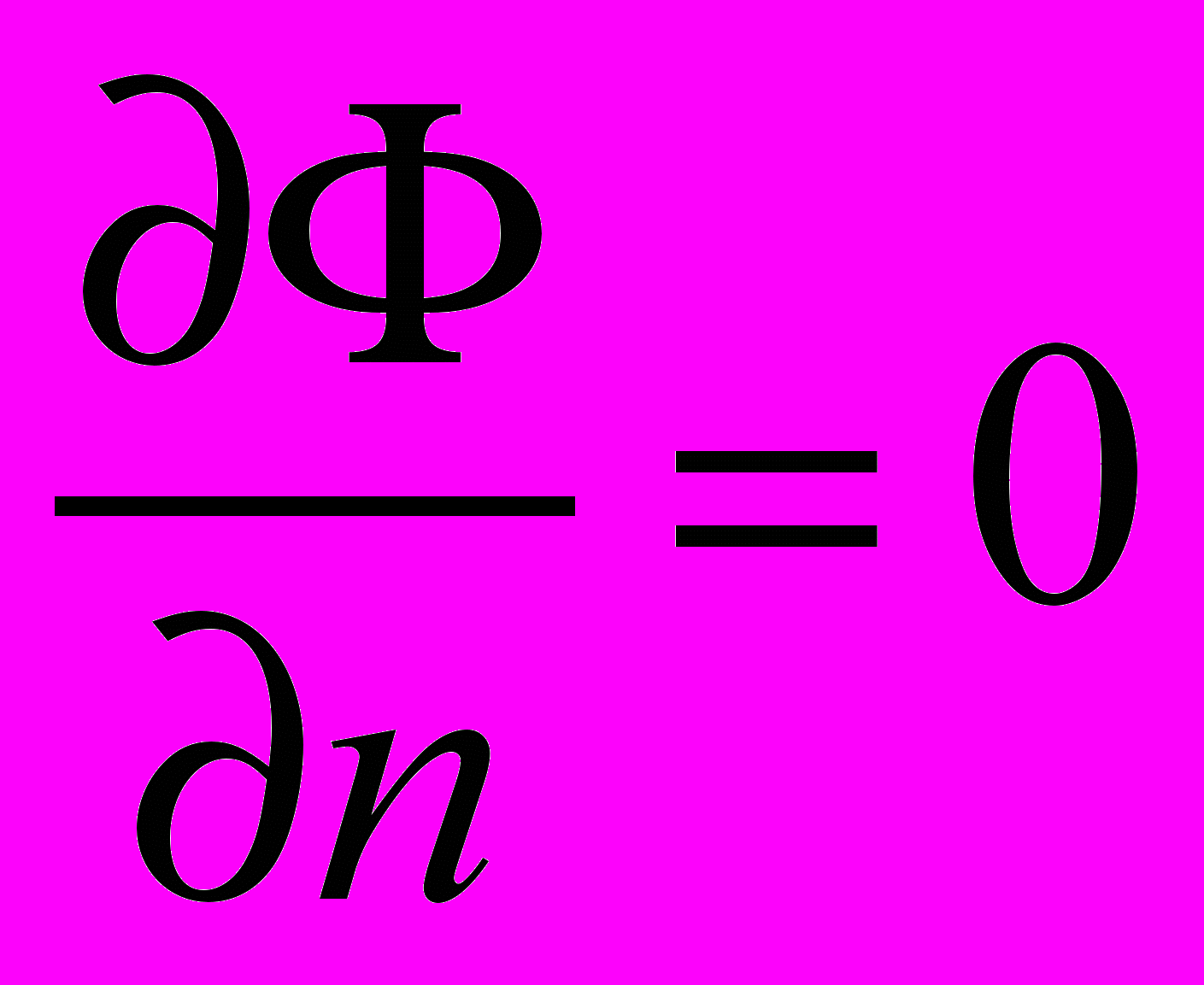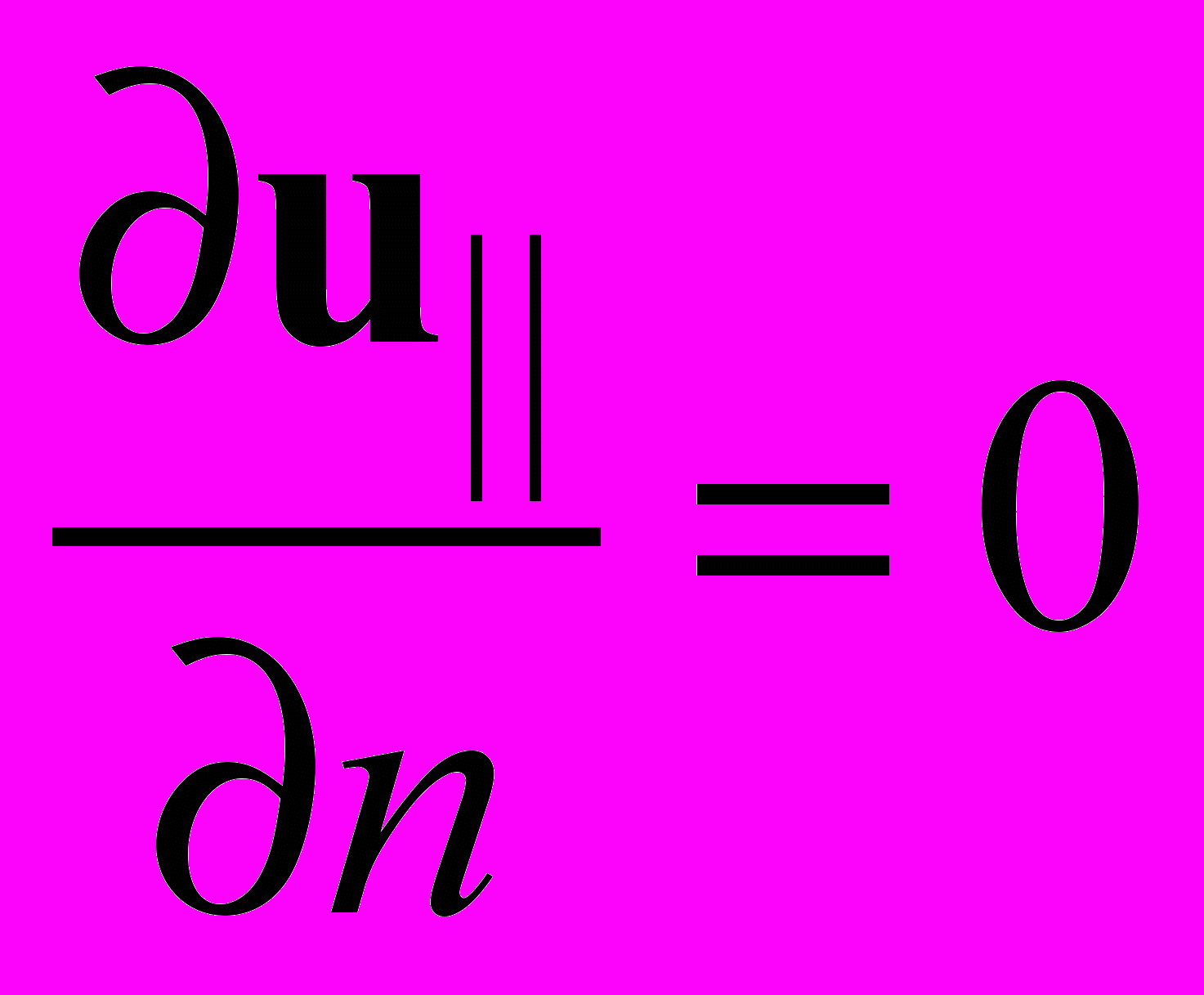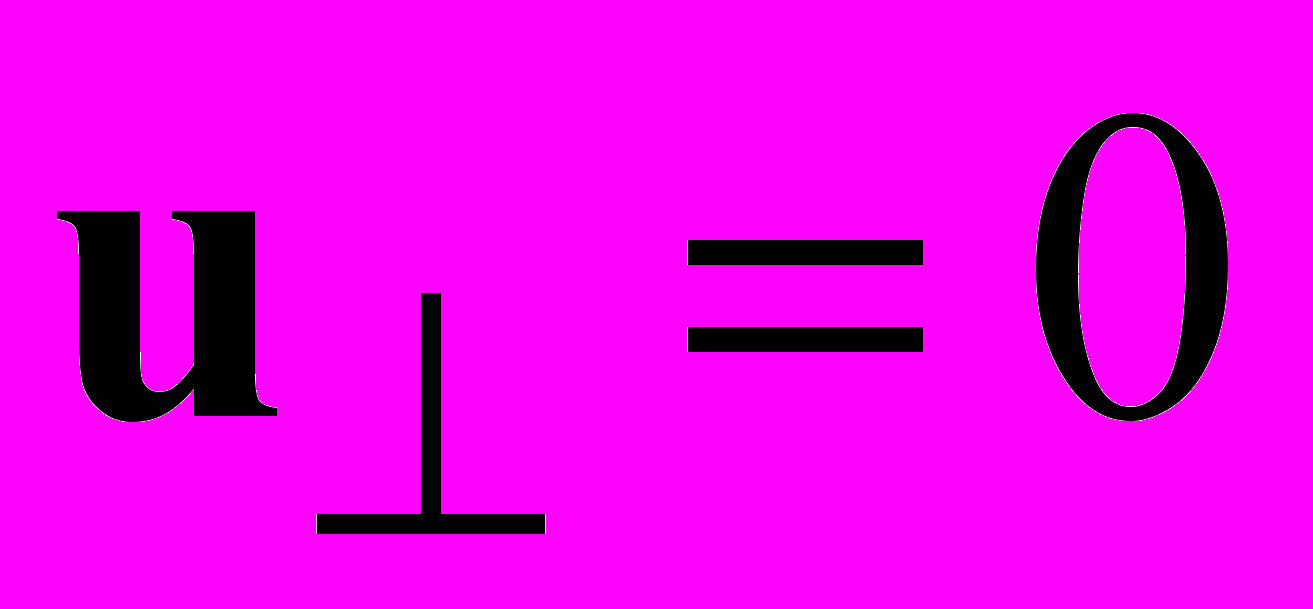, , (2.4.4)

где n- вектор нормали к плоскости симметрии.


Твердая стенка

Нормальную и тангенциальную компоненты скорости на стенках полагаем равными нулю, что моделирует соответственно непротекание и прилипание.

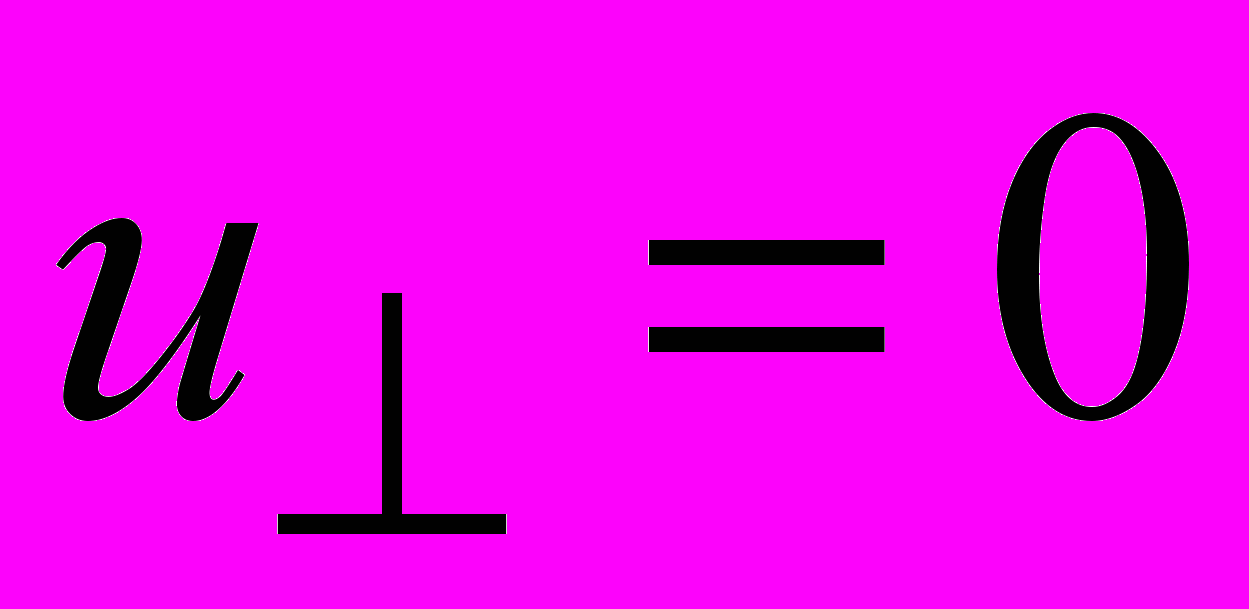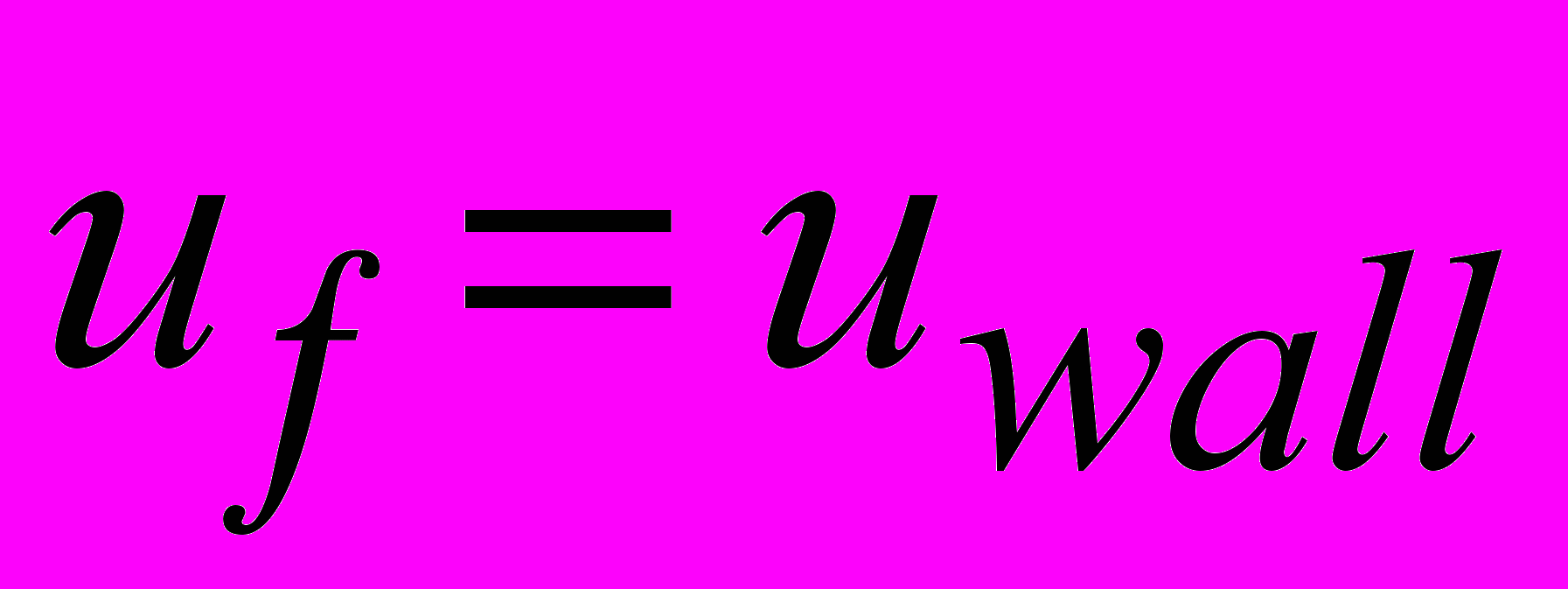, (2.4.5)

Для определения турбулентных характеристик вблизи стенки используется метод пристеночных функций.

Для массовых долей задаются условия отсутствия диффузионных потоков через стенку (конвективные потоки отсутствуют в силу (2.4.5))

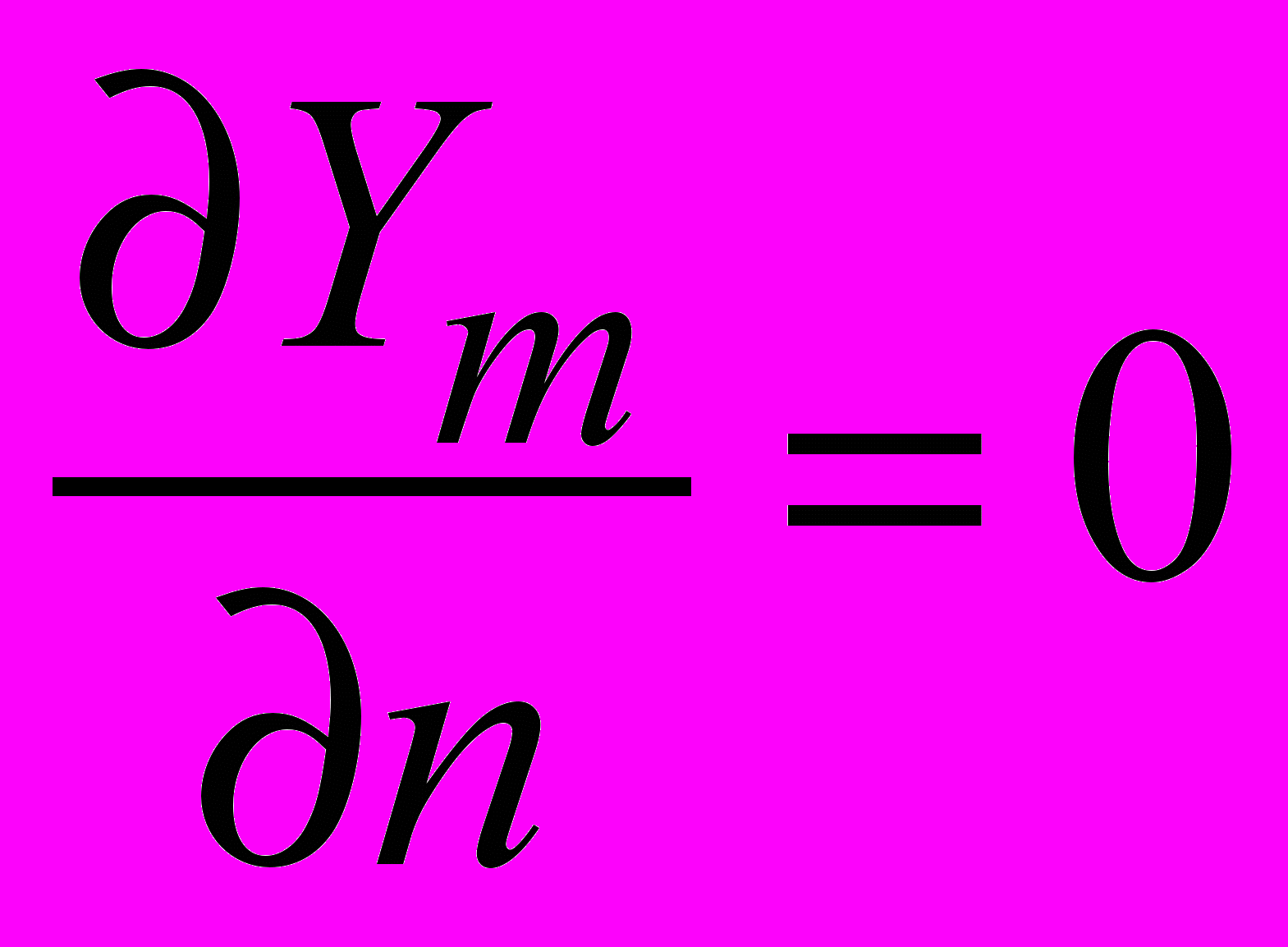(2.4.6)

где n- вектор нормали к стенки.


Теплоотдача на стенках


Граничные условия для уравнения на энтальпию можно задать двумя способами:

1) Задание постоянной температуры на стенке

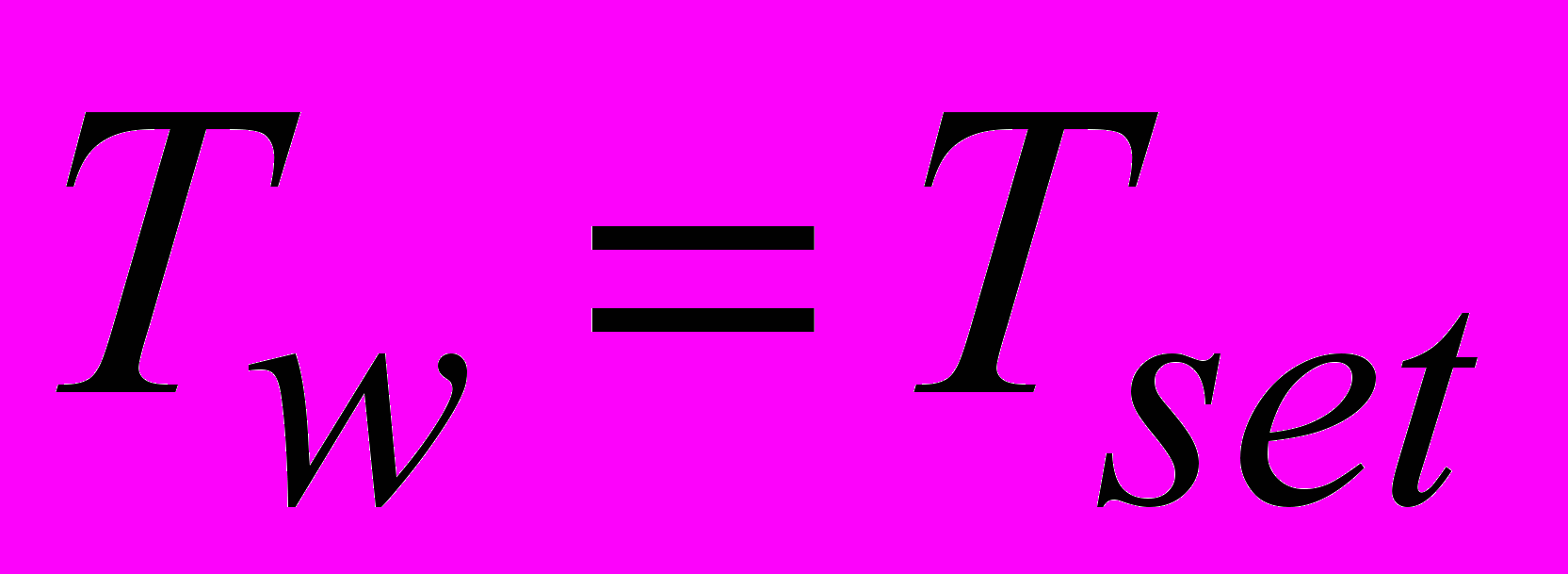(2.4.7)

2) Задание теплового потока и теплоотдачи на стенке

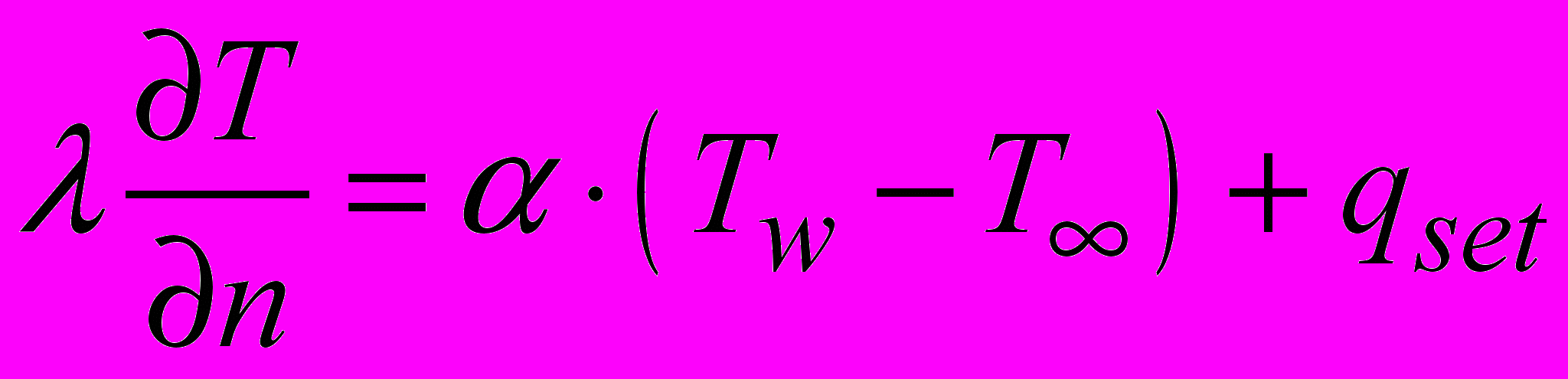(2.4.8)

где 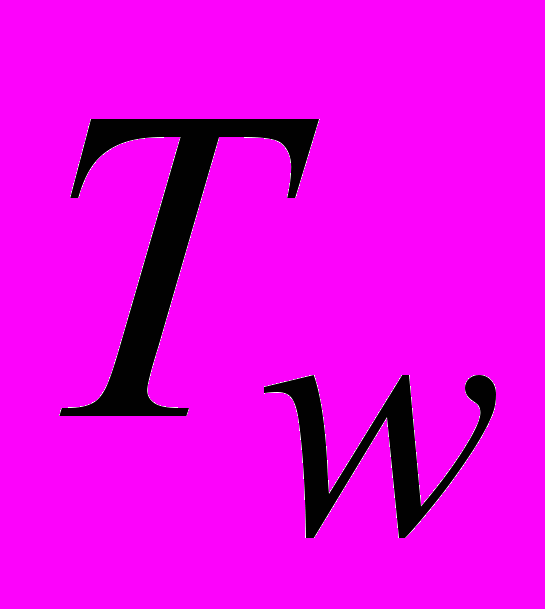- температура на стенке, 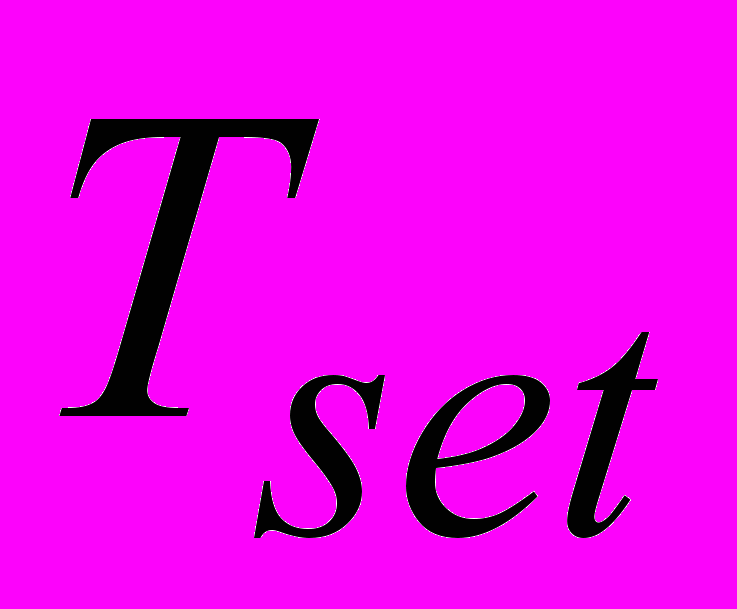- заданная температура, 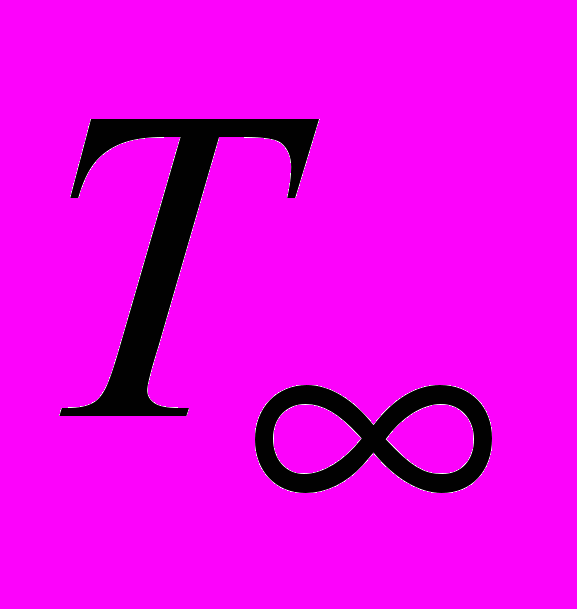- температура внешней среды, 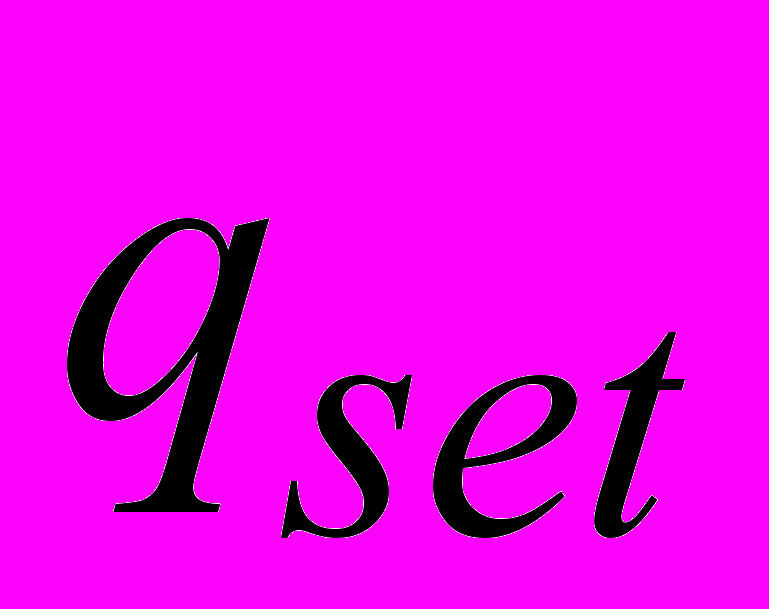-заданный тепловой поток через стенку, -коэффициент теплоотдачи.


2.5. Методы решения систем линейных алгебраических уравнений


После дискретизации исходных уравнении по времени и пространству получаем системы линейных алгебраических уравнений:



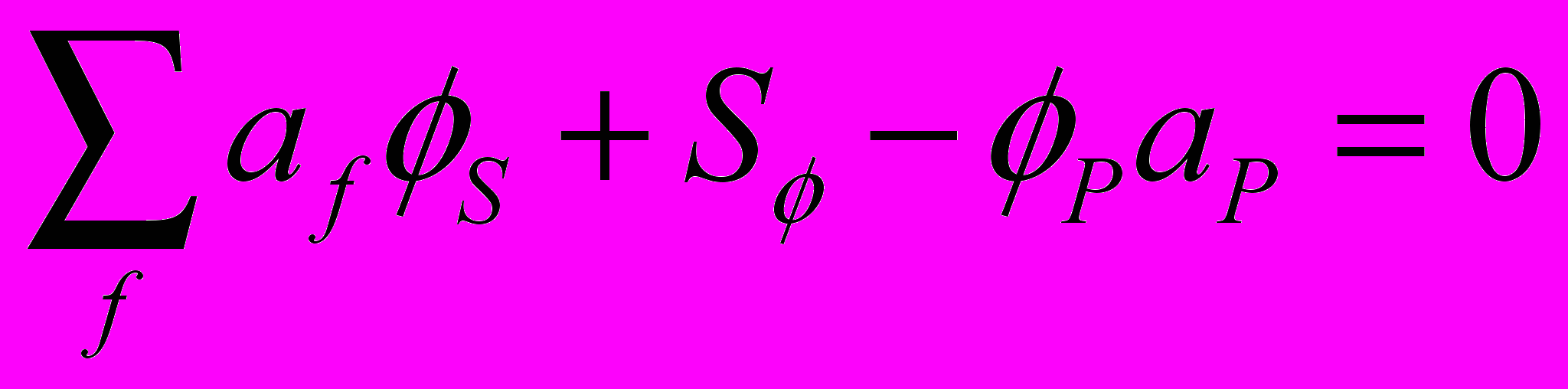
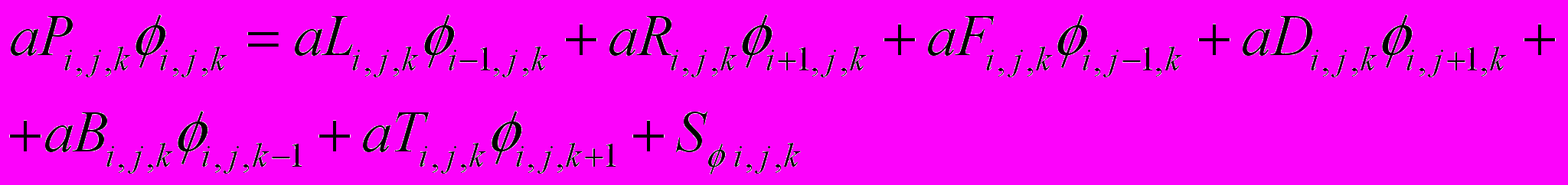(2.5.1)

Для решения систем линейных алгебраических уравнений в пакете реализовано несколько методов, описание которых можно найти в соответствующей литературе:

• полинейный,
  
• переменных направлений,
  
• неполной факторизации Булеева (Булев Н.И., 1989),
  
• метод сопряженных невязок с факторизацией по Булееву (Булев Н.И., 1989)
  

2.6. Радиационный перенос энергии.


Моделирование процесса радиационного теплообмена является очень сложной и ресурсоемкой задачей, т.к. в отличие от остальных процессов тепломассопереноса каждый элементарный объем среды находится в непосредственном взаимодействии со всеми другими элементарными объемами и решение интегро-дифференциальных уравнений, описывающих это явление, очень трудоемко. Вычислительные затраты на решение уравнения радиационного теплопереноса (УРТ) (ур. 2.6.1) может существенно превосходить затраты на решение всех остальных процессов.

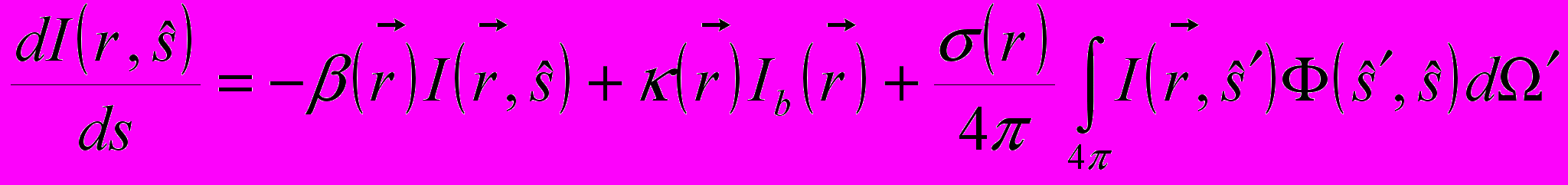(2.6.1)

Граничные условия на УРТ для случая диффузионного отражения

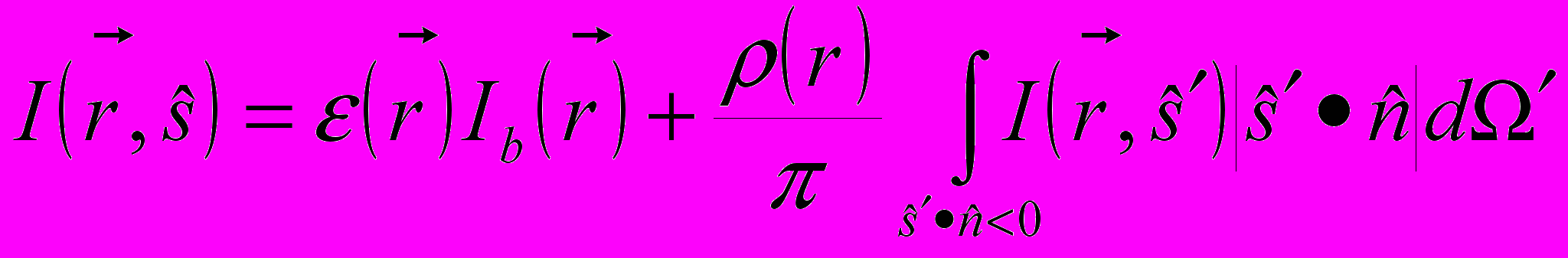(2.6.2)

Радиационный источниковый член в уравнении энергии

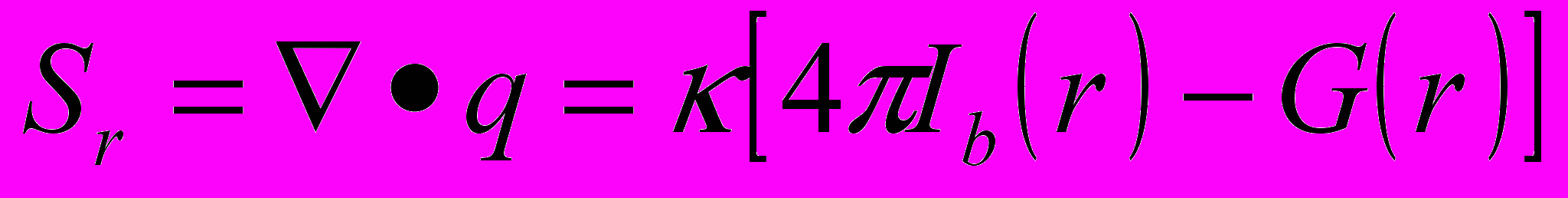(2.6.3)

где

где I – интенсивность (Вт/(ср*м²)); Ib – интенсивность абсолютно черного тела, s коэффициент рассеивания, м^-1; к – коэффициент поглощения, м^-1; b - коэффициент затухания (b = к + s), м^-1; W - телесный угол, рад; r – радиус-вектор, м; s – угловое направление, м; Ф – функция рассеивания.

Коэффициенты поглощения газа к вычисляются по модели суммы серых газов (WSGG модели), коэффициенты поглощения рассчитываются через оптическую плотность дыма.

Для задачи радиационного обмена в разработан ряд подходов. Это методы имитационного моделирования, в которых прослеживается движение отдельных лучей и фиксируется изменение их энергии вдоль траектории. К ним относятся различные варианты метода Монте-Карло и методы дискретных направлений.

Ряд других методов основан на представлении исходного интегро-дифференциального уравнения переноса излучения в форме дифференциальных уравнений второго порядка. Наиболее простой из этих методов - это диффузионный метод, который получается интегрированием уравнения переноса излучения по всему телесному углу. Диффузионный метод плохо работает в оптически тонких средах, а метод Монте-Карло достаточно требователен к вычислительным затратам, поэтому здесь представлены два метода дискретных направлений: конечно-объемный метод (КОМ) и дискретно-ординтный метод (ДОМ)

Конечно-объемный метод

КОМ – лучевой метод. Лучевые методы не имеют ограничений по применению, их точность зависит, прежде всего, от дискретизации углового пространства, однако, требуют существенных вычислительных ресурсов. В КОМ переход к разностному аналогу ур. 2.6.1 происходит интегрированием по контрольному объему и угловому пространству (ур. 2.6.1).

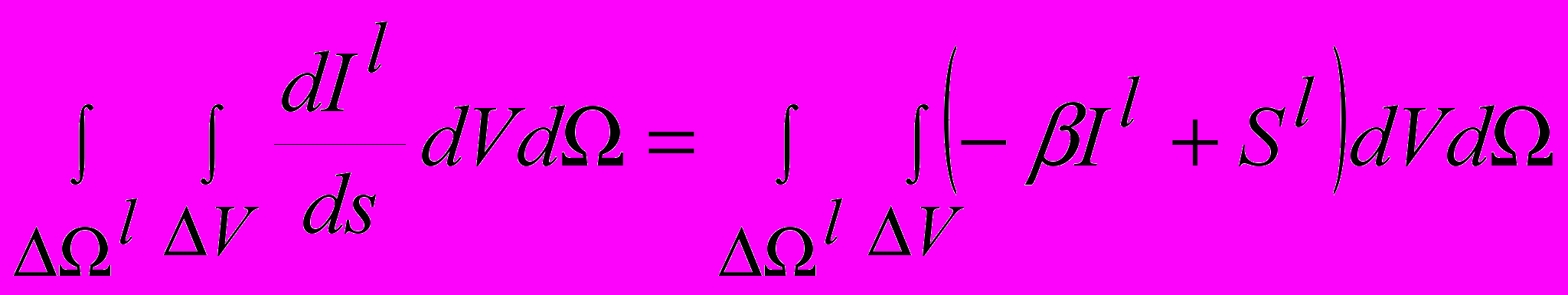(2.6.4)

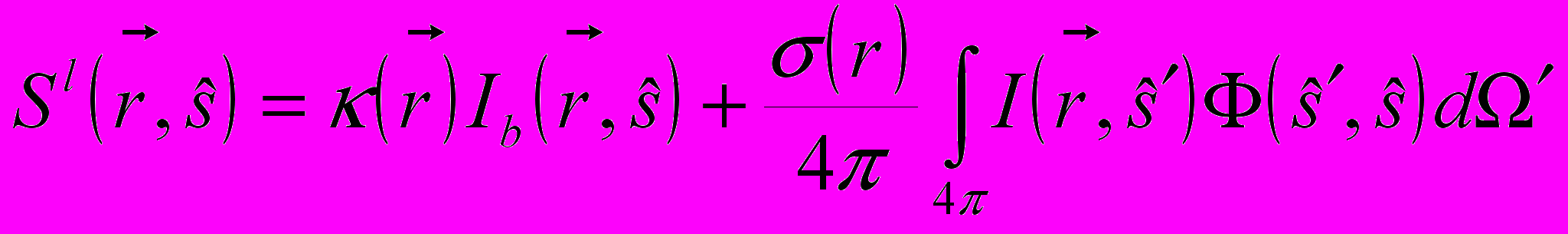(2.6.5)

где l - l–ый контрольный телесный угол для КОМ.

Разностный аналог УРТ для КОМ

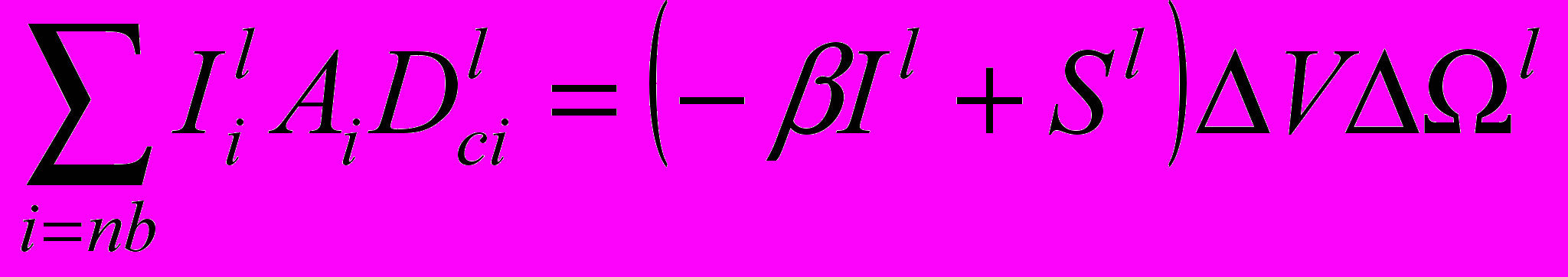(2.6.6)

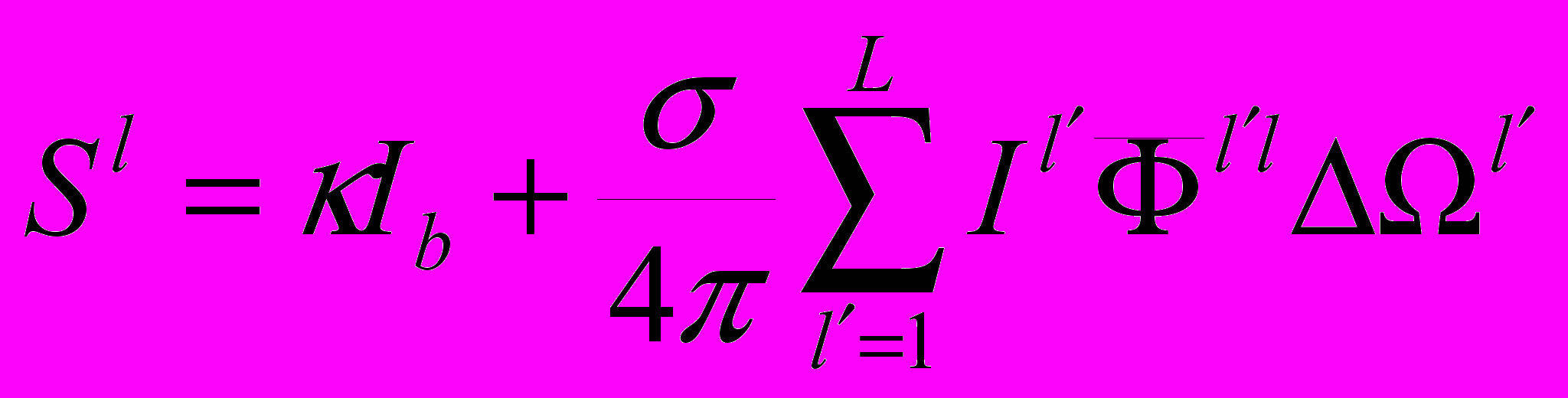(2.6.7)

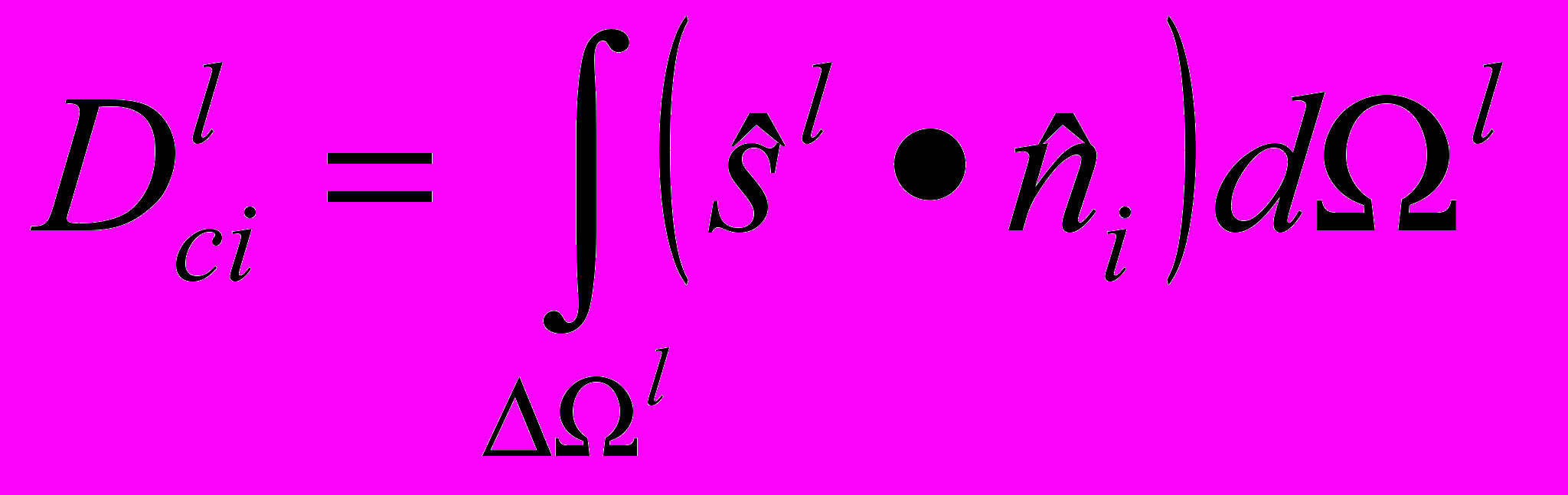(2.6.8)

где i – грань контрольной ячейки, а l – контрольный телесный угол

Дискретно-ординтный метод

В ДОМ переход к разностному аналогу ур. 2.6.1 происходит интегрированием по контрольному объему (ур. 2.6.1).

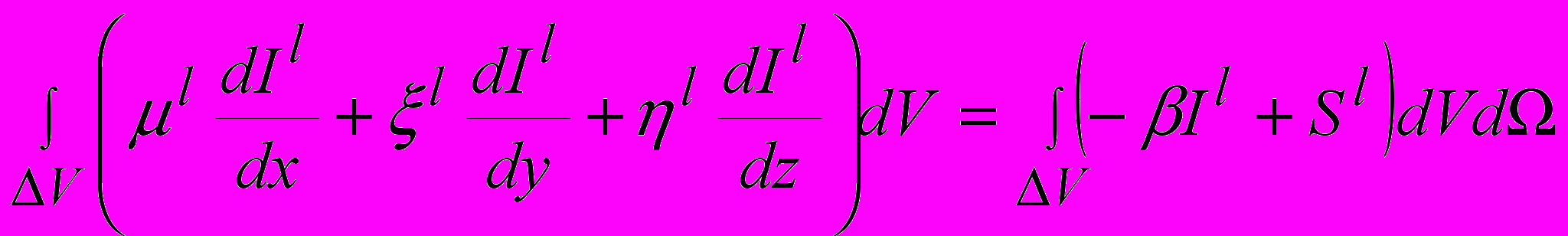(2.6.9) где где μ, ,  - направляющие косинусы; l - l–ое угловое направление для ДОМ.

И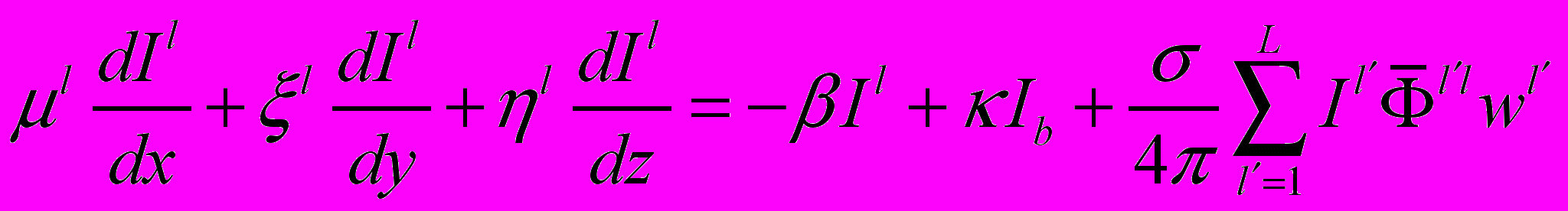нтегралы по телесному пространству в (6.1) заменяются квадратурами, суммируемыми по ординатным направлениям

(2.6.10)




где на квадратуры накладывается следующее условие:

Разностный аналог УРТ для ДОМ




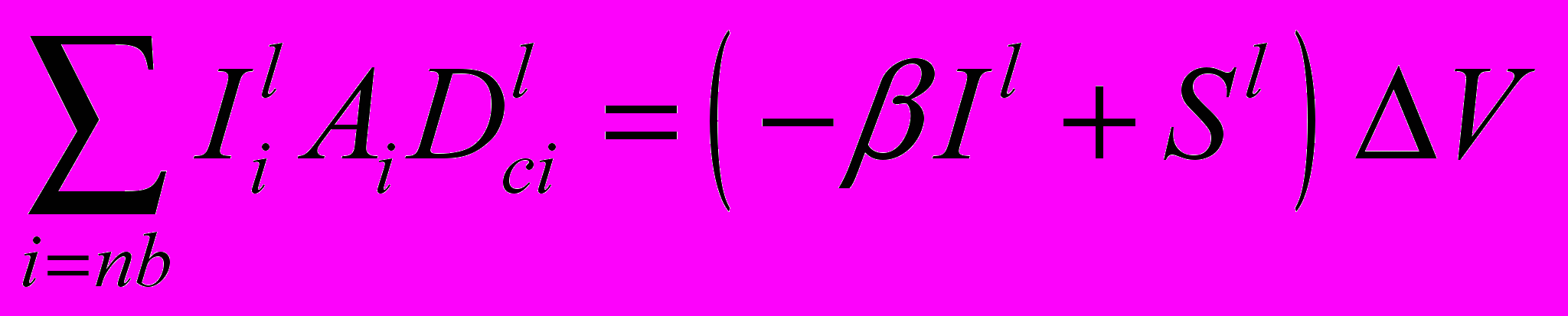
(2.6.11)

г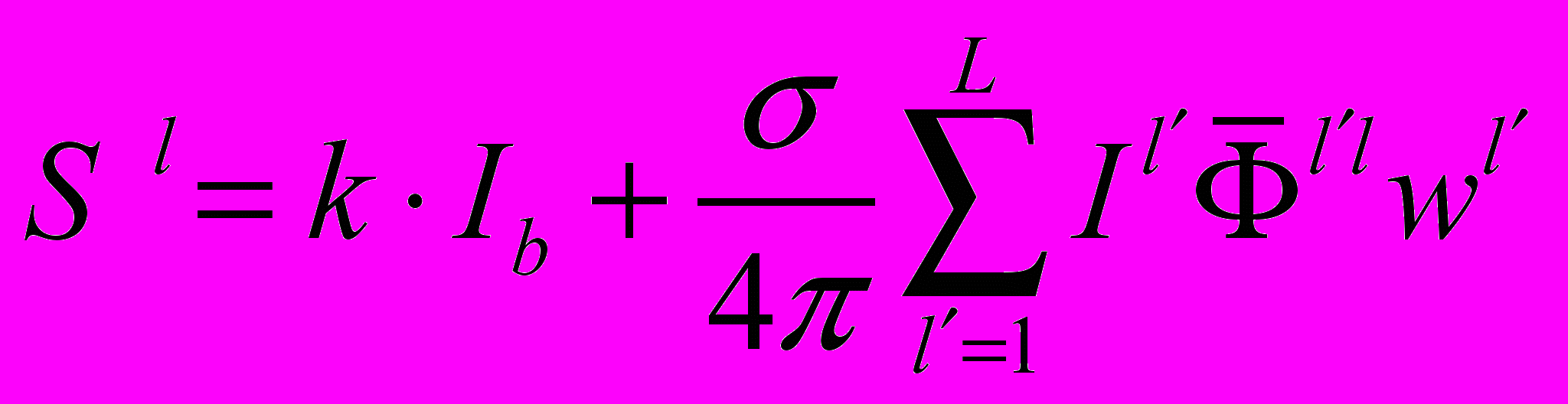де:

(2.6.12)

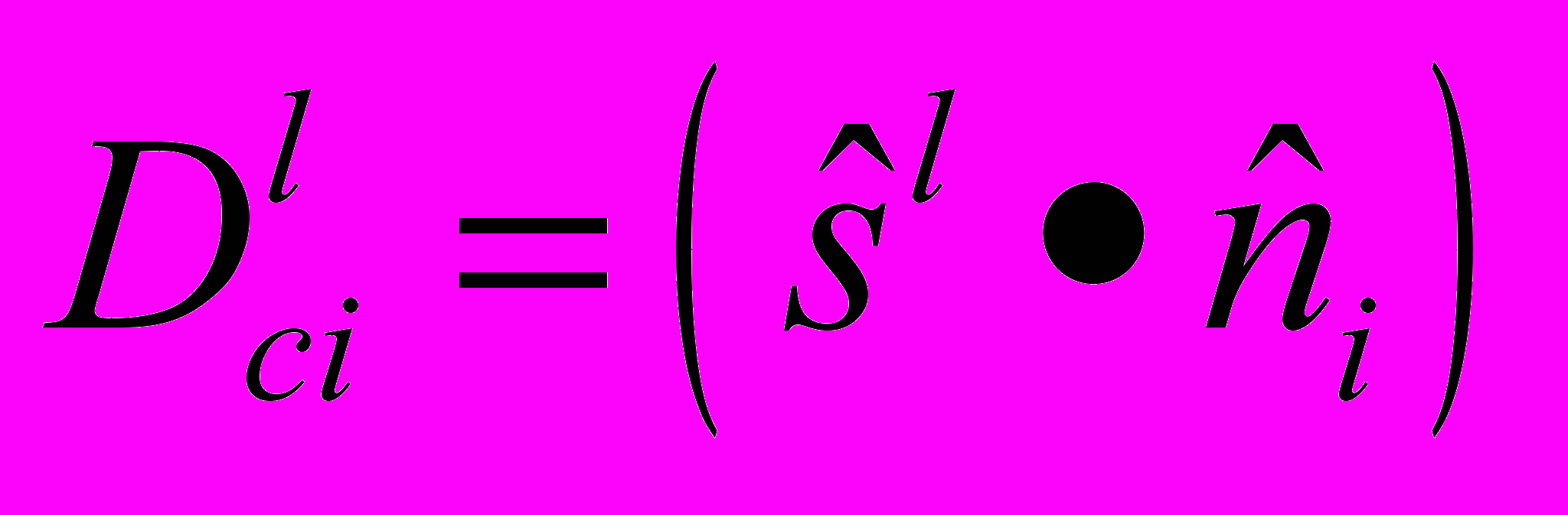(2.6.13)

2.7. Химическое реагирование и горение.

2.7.1. Модели горения газообразного топлива

Расчет химической кинетики горения газового топлива основан на использовании глобальных необратимых реакцией между реагентами (горючими и окислителем) с образованием продуктов реакции.





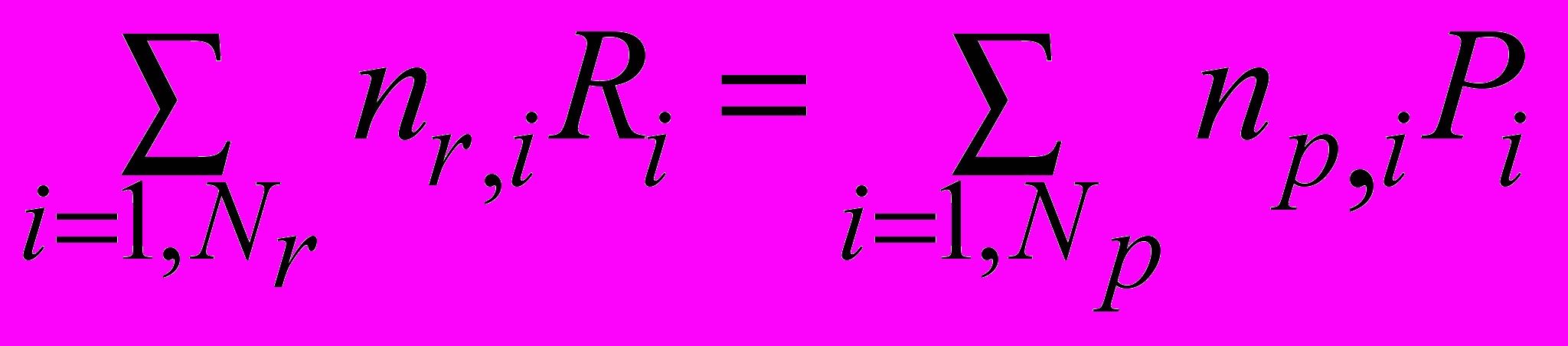
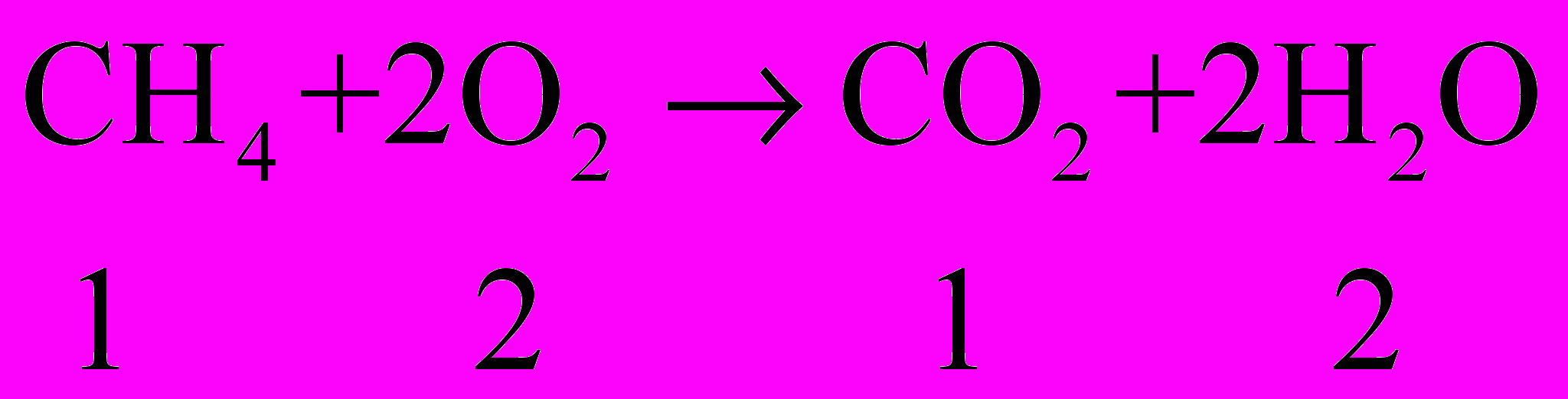
сохранение массы:



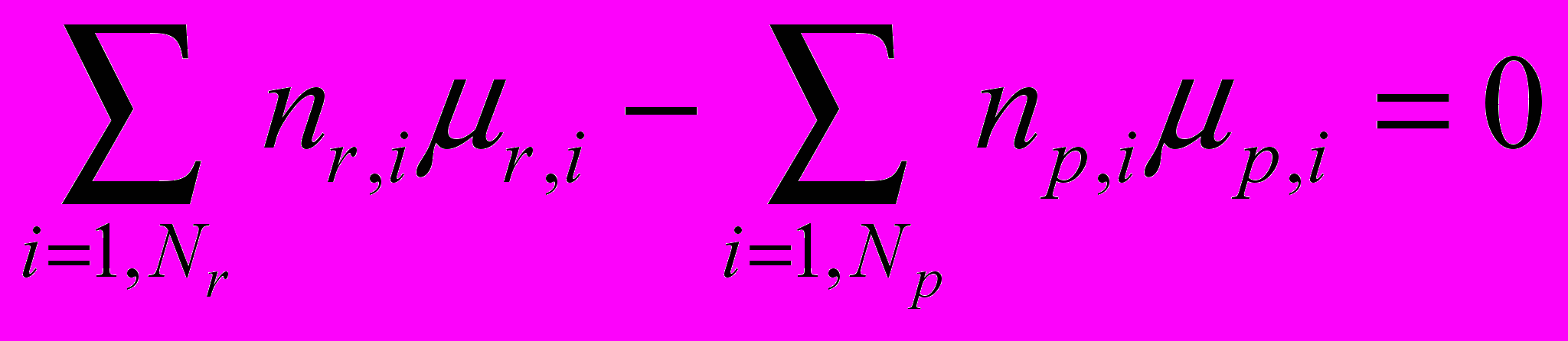
изменение концентрации за счет реагирования:

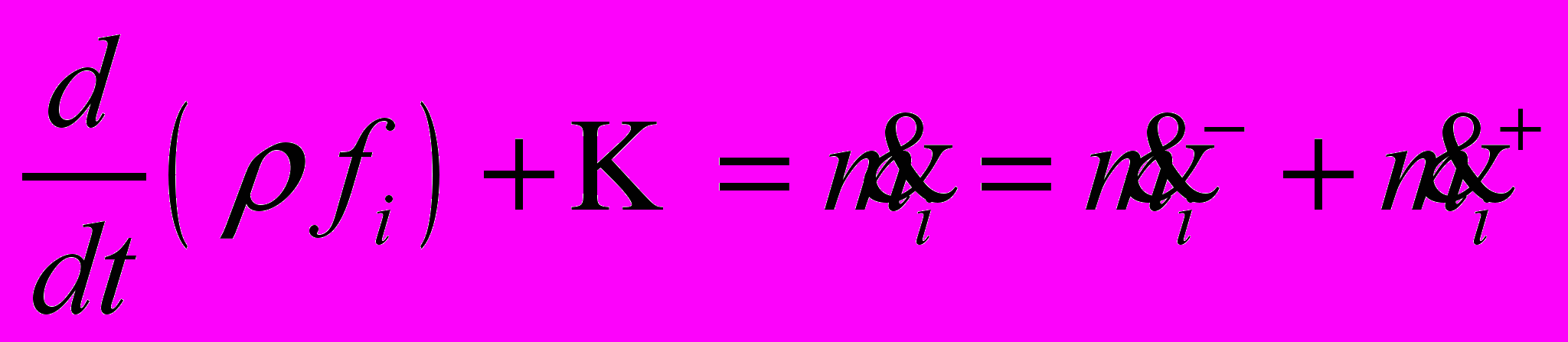(2.7.1.1)

сток, (компонент является реагентом):

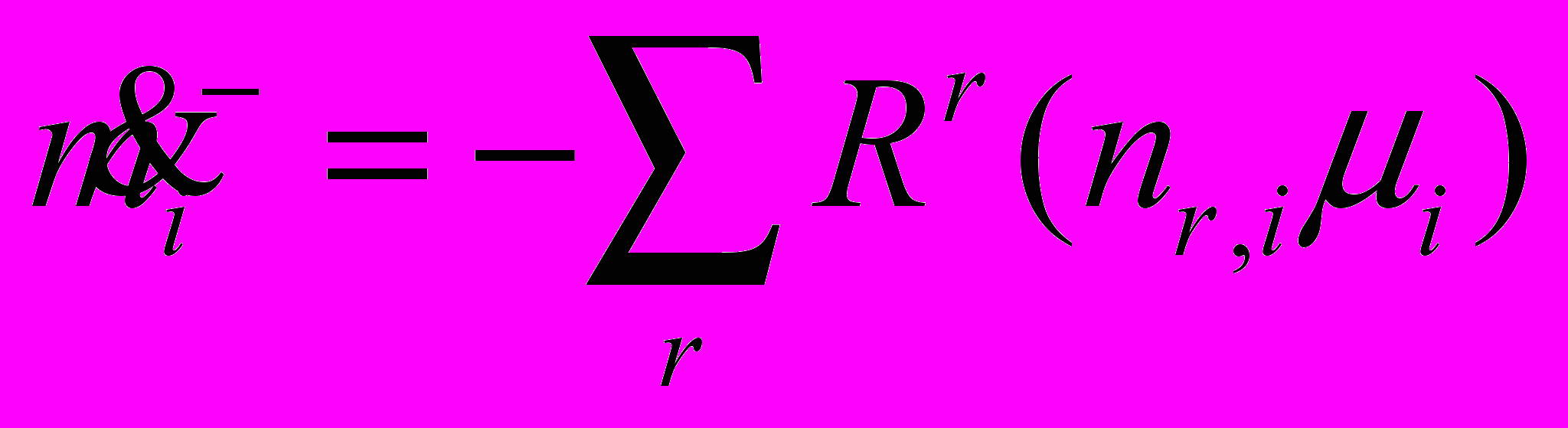(2.7.1.2)

источник, (компонент является продуктом реакции):



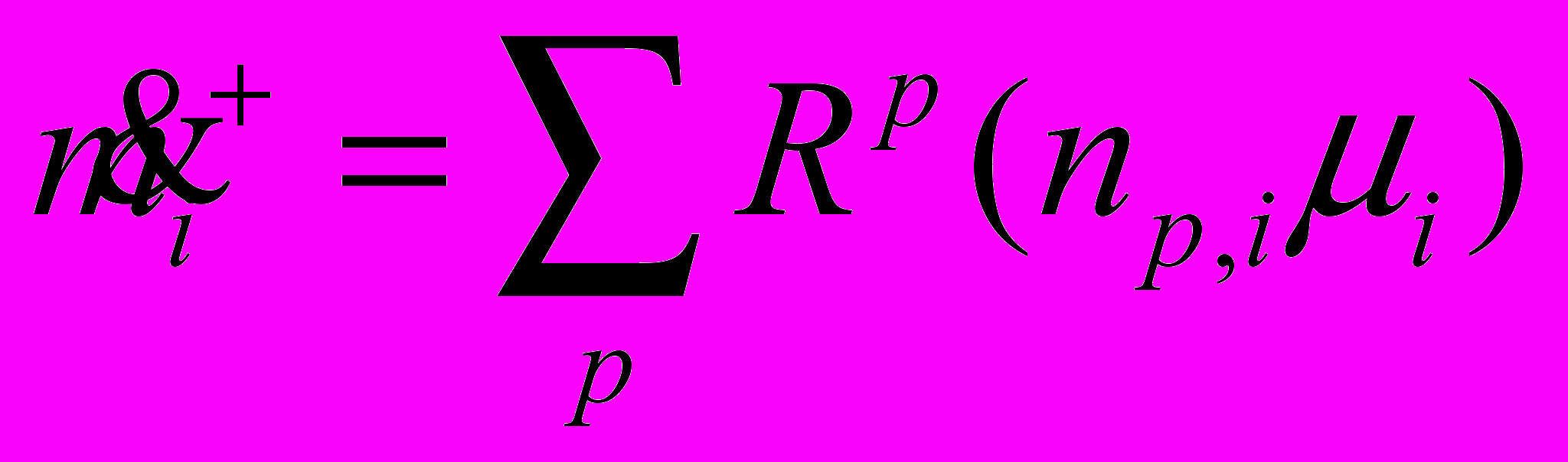
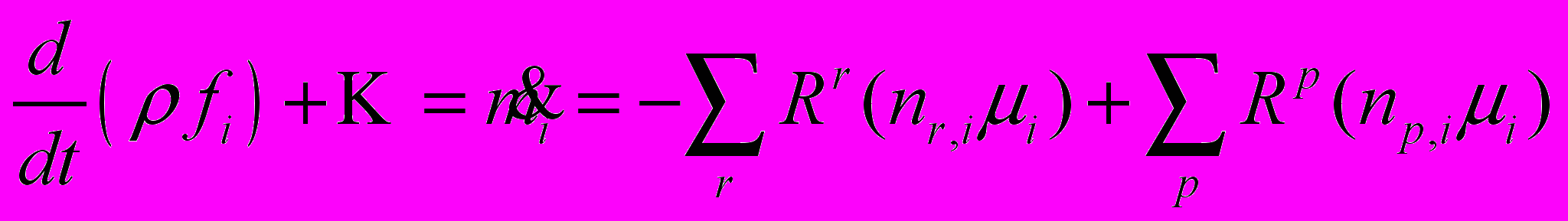(2.7.1.3)

где скорость реагирования

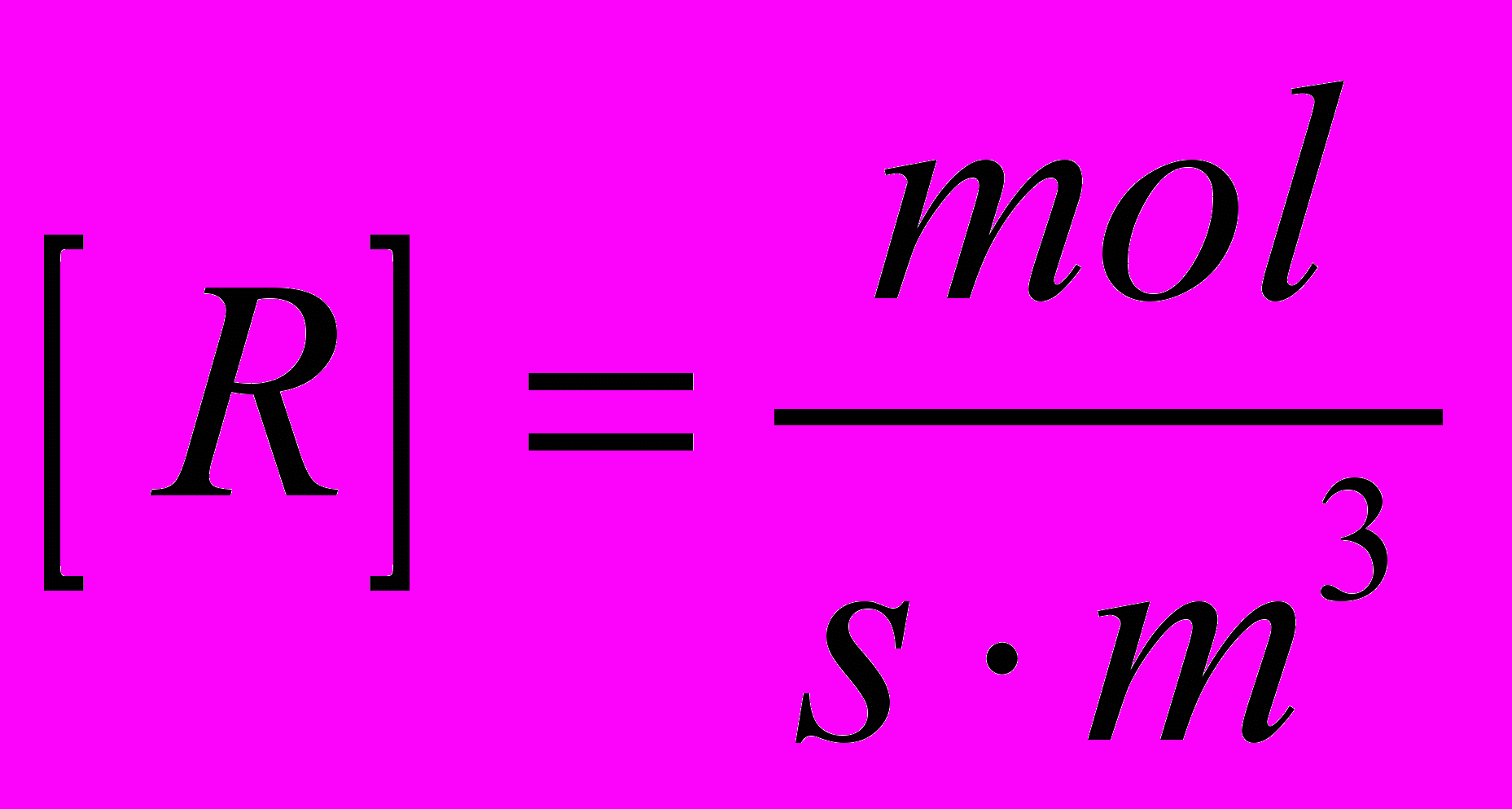
изменение энтальпии:



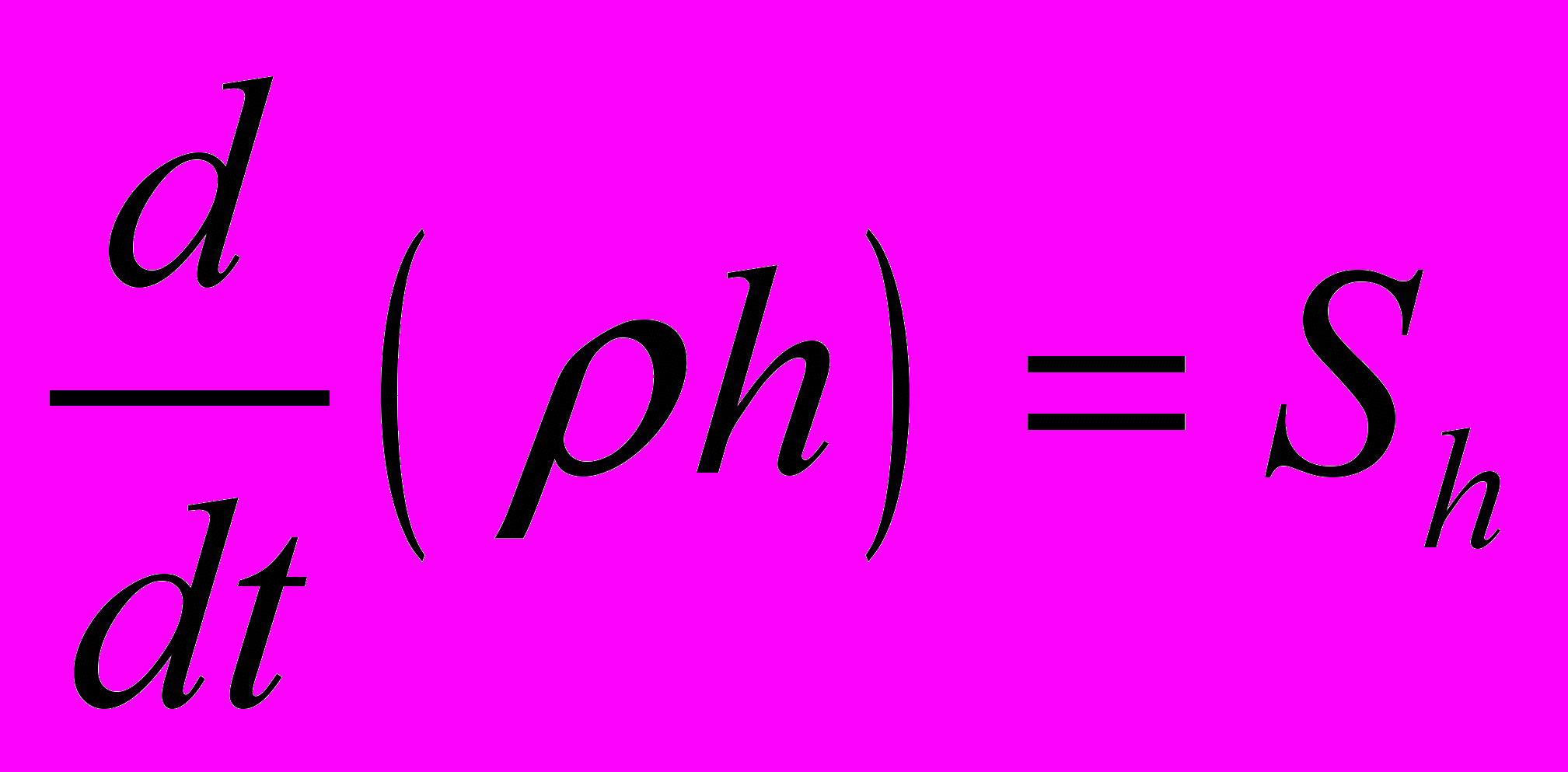
изменение термической энтальпии:



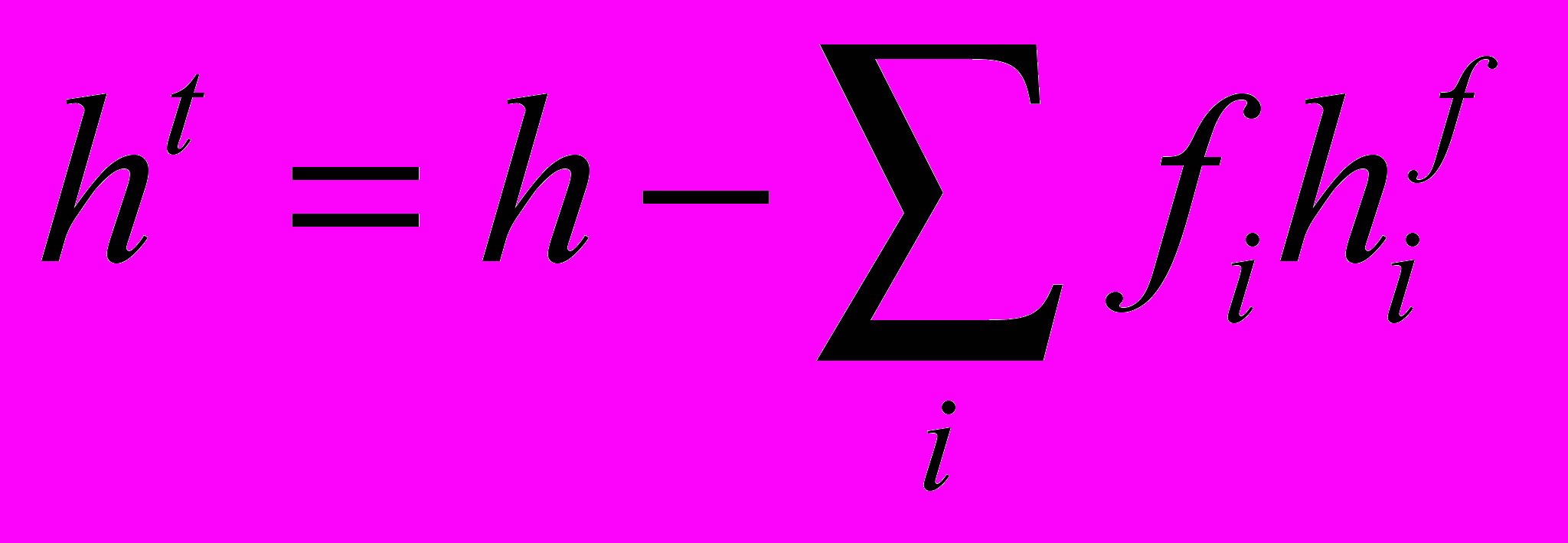
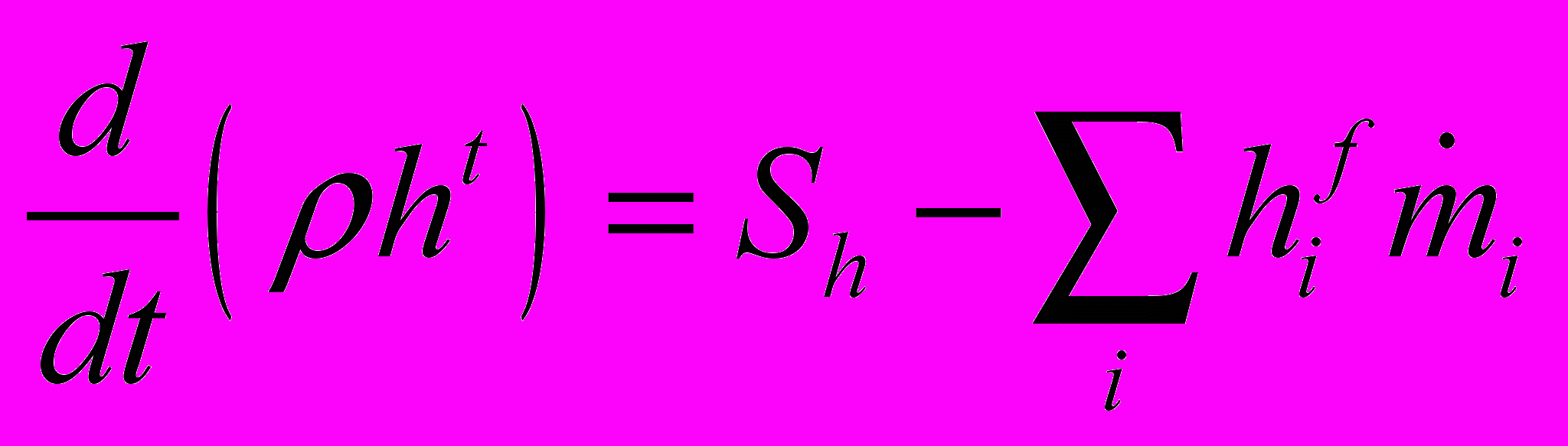(2.7.1.4)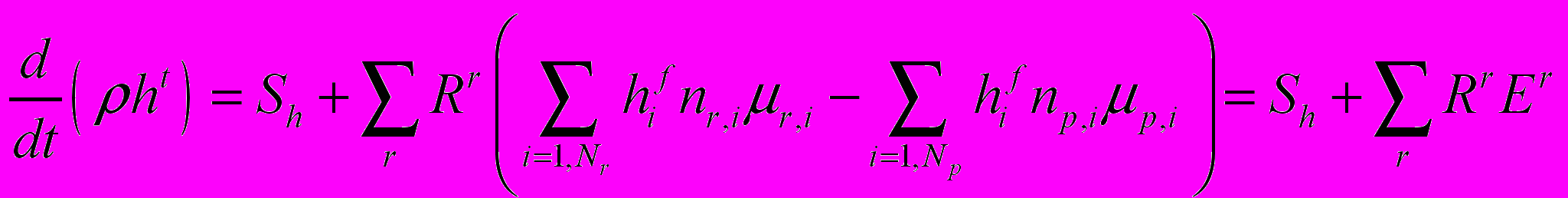




2.7.2. Модели скоростей реакции.

Кинетическая модель.

Скорость горения i-го реагента в этой модели определяется соотношением Аррениусовского типа:


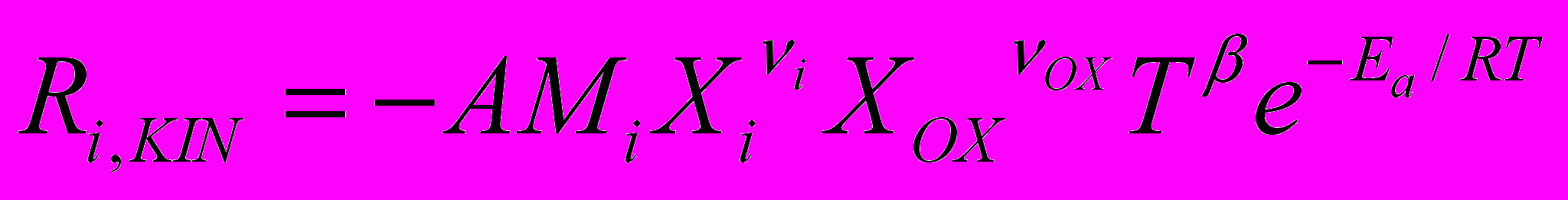, (2.7.2.1)

где 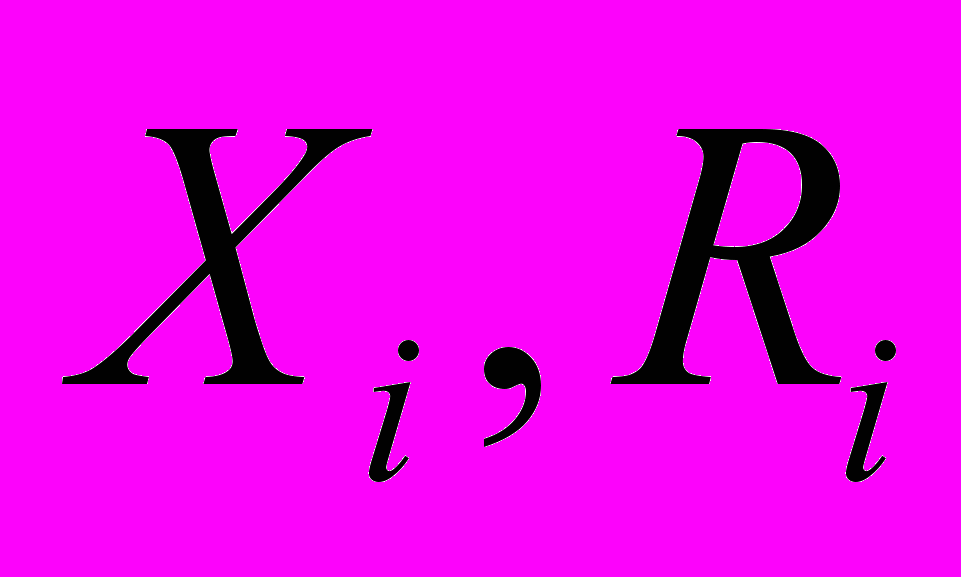- молярная концентрация и скорость реакции i-го реагента, 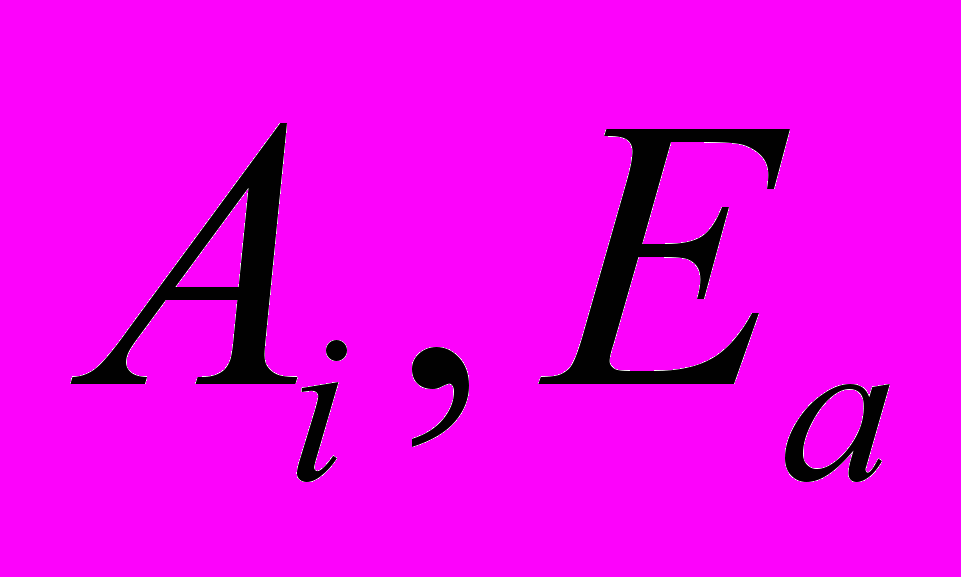- предэкспоненциальный множитель и энергия активации реакции соответственно, 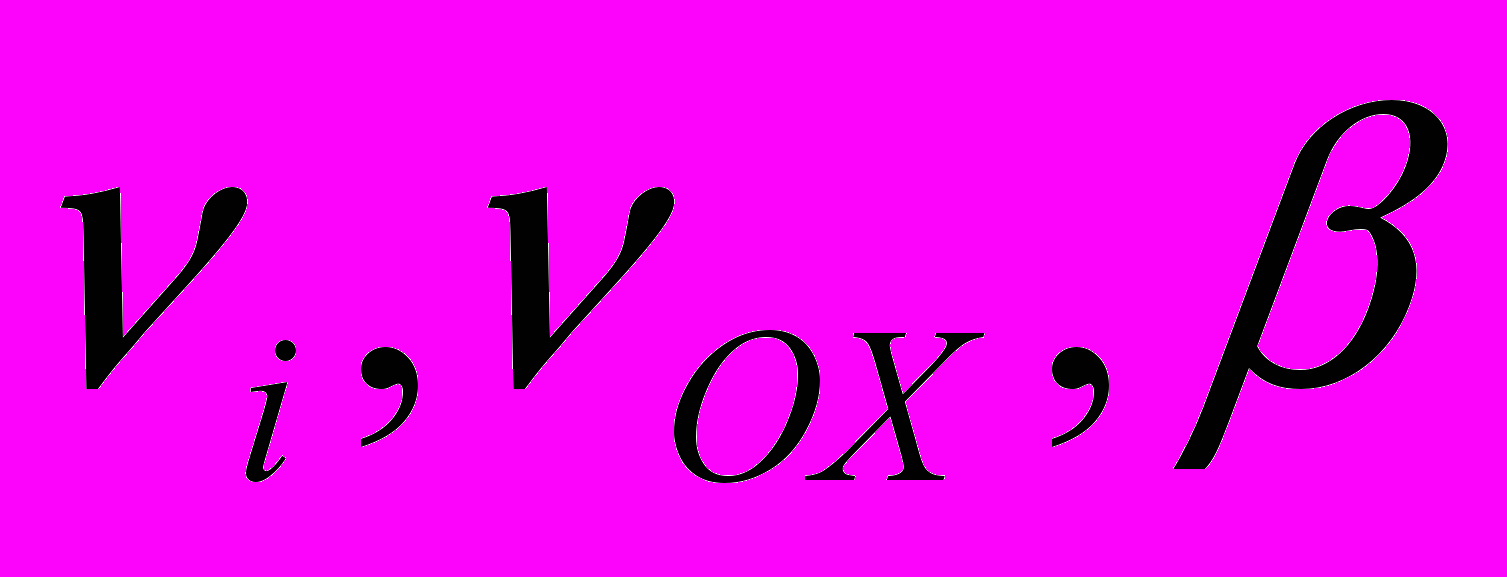эмпирические константы, X_OX – молярная концентрация окислителя (кислорода).


Модель "обрыва вихря" (eddy break up model).

Скорость горения в этой модели ограничивается скоростью турбулентного перемешивания топлива и окислителя (Magnussen, B.F., and Hjertager, B.W., 1981):


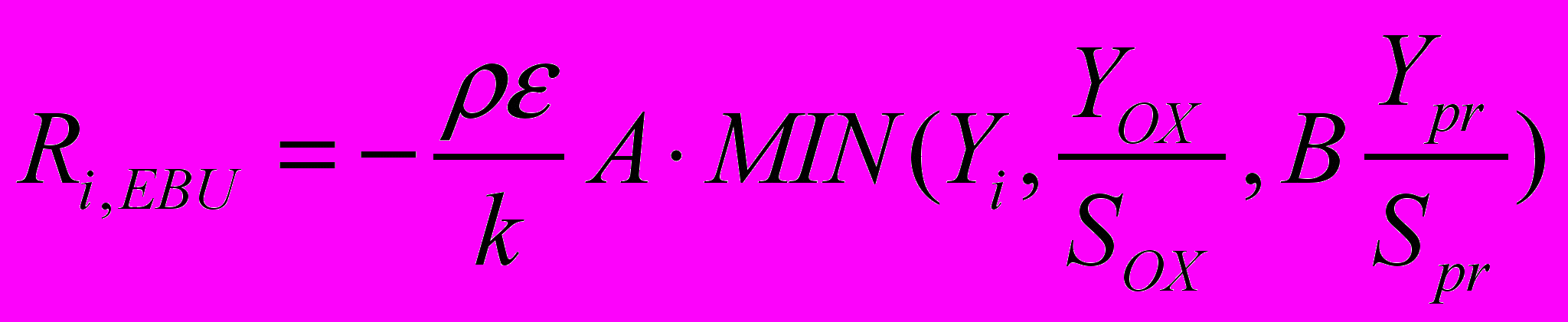(2.7.2.2)

где A и В - эмпирические константы равные соответственно 4,0 и 0,5;

Y_i, Y_OX, Y_PR - концентрации (массовые доли) реагента, окислителя и продуктов сгорания;

S_OX, S_PR - стехиометрические коэффициенты в реакции горения.


Гибридная модель (кинетика/обрыв вихря)

Для описания реагирования в турбулентных течениях с большим временем перемешивания применяется гибридная модель, использующая оба вышеприведенных механизма определения скорости реакции. По этой модели в качестве результирующей скорости выбирается наименьшая из скоростей (2.7.2.1, 2.7.2.2):


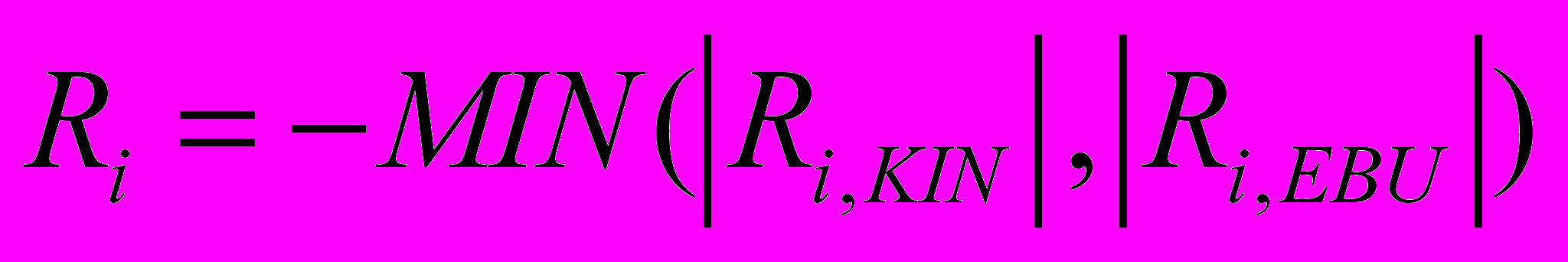. (2.7.2.3)

Модель комбинированного временного масштаба

Модель "обрыва вихря" дает завышенную скорость горения в пристеночных областях. Эту проблему удается избежать путем добавления времени, определяемого кинетическим механизмом горения, к времени турбулентного перемешивания:



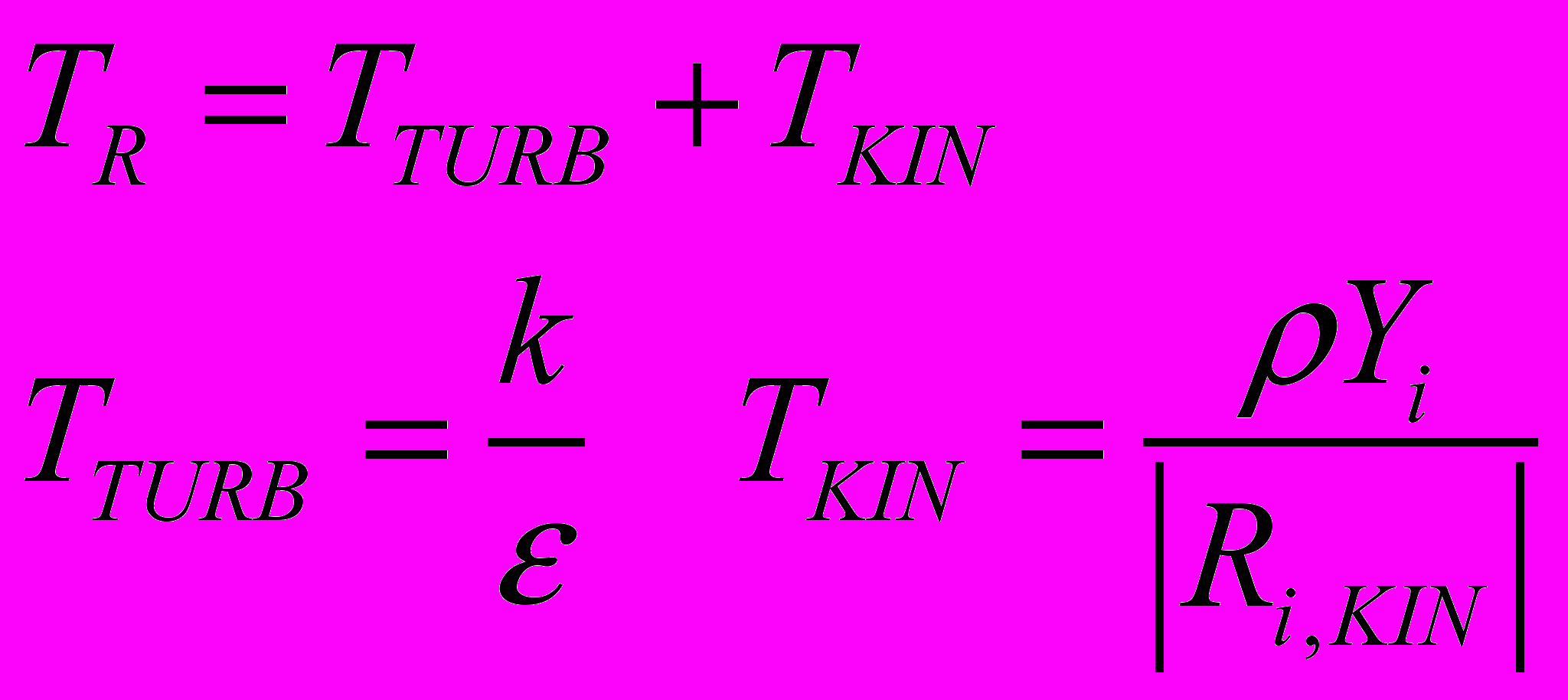
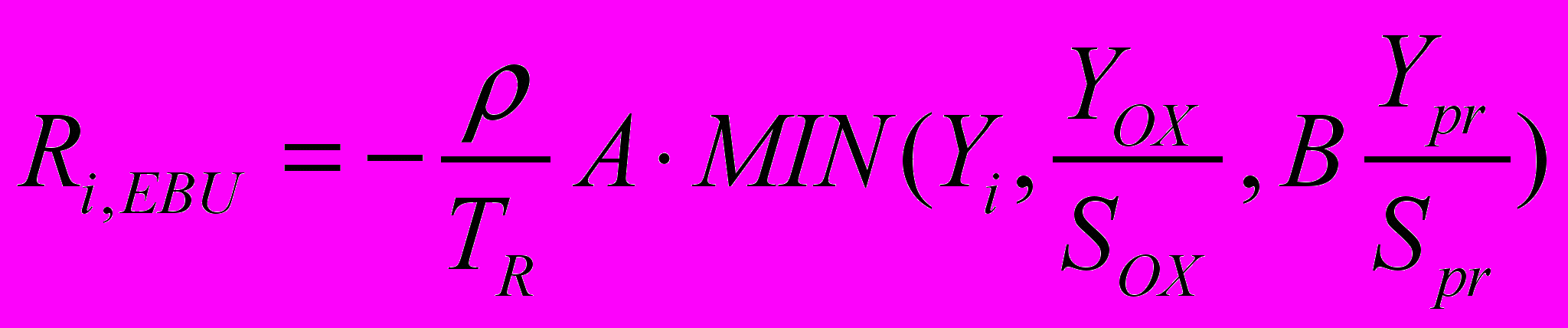(2.7.2.4)

3.