В (рэк) является одной из важнейших задач конструирования радиоэлектронных средств (рэс), которая решается после выполнения компоновки всех конструктивных узлов

Вид материала

Документы

Подобный материал:

• Рабочая программа учебной дисциплины основы компьютерного проектирования рэс направление, 193.97kb.
• Ые способы и последовательность выполнения важнейших оперативных задач, порядок взаимодействия,, 27.45kb.
• Решение задач управления и оптимизации на основе гибридных интеллектуальных методов*, 142.81kb.
• Холодная штамповка является одним из прогрессивных методов получения узлов и деталей, 263.85kb.
• Осрб 1-39 02 02-2007, 761.48kb.
• 1 Схема электрическая принципиальная, 90.35kb.
• Реферат привести методы и алгоритмы решения задач компоновки, размещения и трассировки,, 272.23kb.
• Сная промышленность является одной из важнейших отраслей народного хозяйства, которая, 327.52kb.
• Боли в животе у детей, 275.98kb.
• Задание на проект 3 Схема принципиальная электрическая, 191.7kb.

УДК 62-50


ОПТИМИЗАЦИЯ РАЗМЕЩЕНИЯ РАДИОЭЛЕКТРОННЫХ КОМПОНЕНТОВ

НА ПЕЧАТНЫХ ПЛАТАХ В ПРОЦЕССЕ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ПРИНЦИПИАЛЬНЫХ ЭЛЕКТРИЧЕСКИХ СХЕМ


Шандриков А.С.


Размещение радиоэлектронных компонентов (РЭК) является одной из важнейших задач конструирования радиоэлектронных средств (РЭС), которая решается после выполнения компоновки всех конструктивных узлов. В результате размещения должно быть определено наилучшее расположение модулей в пределах коммутационного пространства, при котором обеспечиваются наиболее благоприятные условия для последующей трассировки всех соединений в соответствии с принципиальной электрической схемой. Качественное решение этой задачи способствует снижению искажений и задержек сигналов, взаимных наводок, конструктивных размеров узлов и блоков, повышению надёжности проектируемых РЭС.

Автоматизированное решение задачи размещения осуществляется с использованием математической модели в виде графа G = (X, U), у которого множество вершин X обозначает множество РЭК, подлежащих размещению, а множество рёбер U – электрические цепи в соответствии с принципиальной электрической схемой. Исходной информацией для решения данной задачи являются:

1) количество позиций, полученное в результате решения задачи компоновки (распределения РЭК по узлам и блокам);

2) расположение посадочных мест.

На коммутационное пространство накладывается декартова система координат с осями s и t, определяющая координатную решётку G_r (рис. 1).





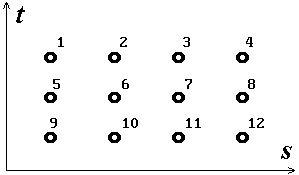
Рис. 1

Шаг решётки, т.е. расстояние между двумя соседними позициями принимается равным единице, а расстояние d_ij между любыми двумя позициями i и j координатной решётки определяется по формуле


d_ij = | s_i – s_j | + | t_i – t_j | (1)

где s_i, s_j, t_i, t_j – координаты позиций решётки по осям s и t.

Расположение посадочных мест задаётся в виде размеров координатной решётки n × m, где n – количество позиций по оси s, а m – по оси t. Всё решение задачи размещения сводится к отображению подграфа проектируемого узла в решётку заданных размеров. Критерием качественного размещения является минимальная суммарная длина соединений (МСД).

Для размещения вершин подграфа в позициях координатной решётки используется большое количество алгоритмов, ориентированных на обеспечение критерия МСД. Однако предпосылки для минимизации суммарной длины соединений могут быть заложены ещё на этапе построения исходного графа принципиальной электрической схемы. Формирование графа как математической модели принципиальной электрической схемы можно условно разделить на четыре этапа:

1 этап – развязка электрических узлов.

2 этап – построение связывающих деревьев.

3 этап – объединение полученных связывающих деревьев.

4 этап – проведение рёбер, обозначающих связи между последовательно соединёнными РЭК во всех отдельных ветвях принципиальной электрической схемы.

На первом этапе каждый электрический узел (соединение трёх и более ветвей) принципиальной электрической схемы заменяется подграфом. Поскольку электрический узел рассматривается как место соединения нескольких РЭК, то в результате развязки узлов будут построены полные подграфы, у которых каждая вершина соединена со всеми остальными вершинами подграфа, что соответствует правилам дискретной математики. Полученные подграфы как модели электрических узлов содержат избыточные рёбра, интерпретирующие не существующие в схеме связи. Наличие избыточных рёбер отрицательно сказывается на результатах решения конструкторских задач компоновки и размещения. Для технической реализации электрических соединений в узлах принципиальной электрической схемы достаточно иметь вместо полных подграфов их связывающие деревья.

Построение связывающих деревьев выполняется на втором этапе и представляет собой удаление из каждого полного подграфа «лишних рёбер», количество которых определяется цикломатическим числом подграфа по формуле


γ(G) = r – n + p (2)


где r – количество рёбер в полном подграфе;

n – количество вершин подграфа;

p – компонента связности. Для полного подграфа (графа) компонента связности всегда равна единице.

В результате выполнения описанных действий каждый полный подграф должен быть заменён связывающим деревом, то есть связным подграфом, не содержащим ни одного цикла.

Операции, выполняемые на третьем и четвёртом этапах, в дальнейших пояснениях не нуждаются.

Оптимальность конструкторских решений, в частности, размещение РЭК, зависит от принятых конфигураций связывающих деревьев на втором этапе формирования графа принципиальной электрической схемы. Для получения связывающего дерева в каждом полном подграфе удаляются любые «лишние» ребра, количество которых определяется по формуле (2). Известно, что таким путём для полного подграфа можно получить d = n^{n – 2} вариантов связывающих деревьев. Правила дискретной математики не накладывают каких-либо ограничений, указывающих, какие именно рёбра следует удалять. По этой причине выбор конкретного варианта связывающего дерева чаще всего осуществляется произвольно, без предварительной оценки последующих результатов размещения РЭК с точки зрения критерия МСД. Объяснить это можно неочевидностью влияния выбранного варианта связывающего дерева на получение оптимальных размещения графа и отсутствием пояснений по данному вопросу в литературных источниках.

В большинстве случаев принципиальная электрическая схема РЭС содержит некоторое количество групп РЭК, имеющих между собой более одной связи в разных узловых точках, например, в случае параллельного соединения и т.п. Очевидно, что оптимальным размещением РЭК будет то, в результате которого параллельно соединённые РЭК окажутся в соседних позициях коммутационного пространства печатной платы. Для оптимизации результатов решения задач разрезания и размещения графа необходимо анализировать возможные варианты связывающих деревьев и выбирать наиболее подходящий вариант в каждой конкретной ситуации.

Рассмотрим зависимость результатов отображения графа в решётку заданных размеров от выбранного варианта конфигурации связывающих деревьев в узлах параллельного соединения РЭК.

В качестве примера на рис. 2 представлена принципиальная электрическая схема электромегафона.



Рис. 2


В данной принципиальной электрической схеме можно выделить группы РЭК, имеющие соединения между собой более чем в одном узле. К таким РЭК относятся: резистор R2 и транзистор VT2, имеющие соединение в узлах c и e; транзисторы VT2 и VT4 (соединяются в узлах e и f), транзисторы VT3 и VT5 (соединяются в узлах g и h); резистор R3 и транзистор VT4 (соединяются в узлах f и g); резистор R4 и транзистор VT5 (соединяются в узлах b и h). Для всех узлов данной схемы выполним развязку и построим по два варианта связывающих деревьев. В первом варианте учёт связей между параллельно соединёнными РЭК будет сведён к минимуму, т.е. из полного подграфа каждого узла будет удалено ребро, связывающее параллельно соединённые РЭК. Второй вариант связывающих деревьев будет построен с сохранением в каждом узле ребер, связывающих параллельно соединённые РЭК. Так, например, резистор R4 и транзистор VT5 имеют соединения в узлах b и h. Для связывающих деревьев подграфов этих узлов могут быть выбраны крайние варианты: с сохранением рёбер u(r₄, vt₅) в обоих узлах и без сохранения этих рёбер.

Результаты построения первого и второго вариантов связывающих деревьев для каждого узла схемы представлены в таблице 1.

Таблица 1

Узел	Полный подграф	Связывающее дерево
		1 вариант	2 вариант
a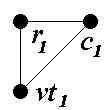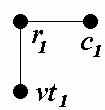
b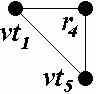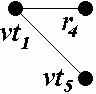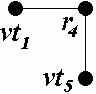
c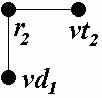
d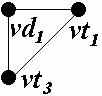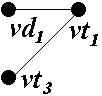
e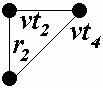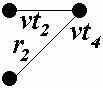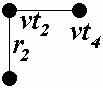
f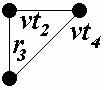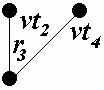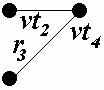
g
h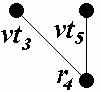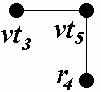

Для узлов a и d построение второго варианта связывающего дерева не предусматривался, так как в этих узлах соединены РЭК, не связанные между собой в других узлах и в такой ситуации все возможные варианты равноценны.

При построении связывающих деревьев не учитывалось наличие разъёма XS1, так как его место на плате уже определено техническими требованиями.

По результатам построения первого варианта связывающих деревьев для каждого электрического узла схемы был сформирован граф G⁽¹⁾, представленный на рис. 3. На рис. 4 представлен граф G⁽²⁾, сформированный из связывающих деревьев второго варианта.

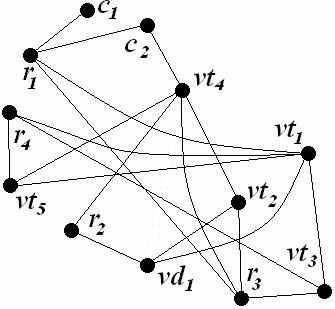Рис. 3. Граф G(1)

Рис. 4. Граф G(2)

Как видно из рис. 4, выбор варианта связывающего дерева с сохранением связи между параллельно соединёнными РЭК в каждом электрическом узле приводит к получению мультиграфа.

На рис. 5 и 6 представлены результаты отображения графов G⁽¹⁾ и G⁽²⁾ в решётку G_r с размерами 4 × 3.

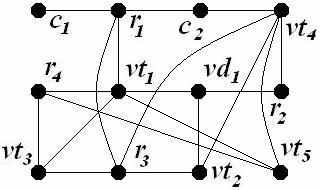Рис. 5. Результат размещения графа G(1)

Рис. 6. Результат размещения графа G(2)

Размещение вершин графов G⁽¹⁾ и G⁽²⁾ в позициях коммутационного пространства выполнялось последовательным методом и факторизация графов с целью оптимизации размещения РЭК по критерию МСД не производилось. Суммарная длина соединений отображенного в решётку графа G⁽¹⁾ составляет 32 шага, а графа G⁽²⁾ – 23 шага, что на девять шагов меньше. Следует заметить, что граф G⁽²⁾ является планарным. Планарность размещённого на коммутационном пространстве графа G(2) позволит выполнить трассировку соединений печатной платы в пределах одного слоя и тем самым повысить качество РЭС при одновременном снижении их стоимости.

Полученные результаты, а также результаты ранее проведённых исследований позволяют сделать следующие выводы:

1) суммарная длина соединений зависит от выбранных вариантов связывающих деревьев для подграфов, интерпретирующих электрические узлы принципиальной электрической схемы;

2) аналитический подход к выбору варианта связывающего дерева для каждого узла с учётом особенностей соединений РЭК позволяет минимизировать суммарную длину соединений печатной платы и во многих случаях (в зависимости от сложности принципиальной электрической схемы) обеспечить планарность отображённого в решётку графа.

Литература


1. Мелихов А.Н. Применение графов для проектирования дискретных устройств /А.Н. Мелихов, Л.С. Бернштейн, В.М. Курейчик – М. : Наука, 1974 – 304 с.

2. Абрайтис Л.Б. Автоматизация проектирования ЭВМ. / Л.Б. Абрайтис, Р.И. Шейнаускас, В.А. Жилевичюс; под ред. Л.Б. Абрайтиса – М. : Сов. радио, 1978 – 272 с.

3. Шандриков А.С. Особенности построения графа принципиальной электрической схемы, влияющие на результаты компоновки РЭС / А.С. Шандриков // Современная радиоэлектроника: научные исследования, подготовка кадров: материалы международной научно-практической конференции: в 3 ч. Ч 1, Минск, 20- 21 апреля 2006 г. / Минский государственный высший радиотехнический колледж. – Минск. : 2006. – С. 354-358.