Сти и полноты предпочтений, которые вместе с непрерывностью обеспечивают существование аналитического представления предпочтений в виде функ­ции полезности [13]

Вид материала

Документы

Подобный материал:

• Задачи: познакомить с результатами диагностики профессиональных предпочтений; познакомить, 161.54kb.
• Примерный план лекций для финансового потока (2010-2011 уч г.) Дата и тема, 77.52kb.
• Задачи управления персоналом. Оптимизация затрат на содержание рабочей силы, 580.86kb.
• Лекция Проведение маркетинговых исследований по проекту, 225.3kb.
• Справочник «Клиенты», 1818.27kb.
• Обзор новостей рекламного рынка за 08. 08 – 12., 491.65kb.
• Анализ потребительских предпочтений в отношении пива, 63.08kb.
• Результаты исследования, 1098.61kb.
• Литература, 435.79kb.
• Программа: Отделение менеджмента предприятий питания Данные о преподавателе: фио, 119.84kb.

В.К. Горбунов, А.Г.Ледовских

Ульяновский государственный университет

Построение поля потребительских предпочтений по торговой статистике: параметрический метод¹

1. Многие зарубежные исследователи в последние десятилетия предпринимают попытки пересмотра классической теории потребительского спроса (ПС) на основе отказа от свойств транзитивности и полноты предпочтений, которые вместе с непрерывностью обеспечивают существование аналитического представления предпочтений в виде функ­ции полезности [13]. Большинство из них ограничивается теоретико-множественным уровнем без построения аналитического аппарата, позволяющего вычислять спрос (см., например, [11, 12, 15]). Построению аналитических обобщений классической модели на основе отказа от транзитивности предпочтений посвящены работы Р.Аллена [6], развитие этой работы [9] и работа Шафера [14].

Аллен предложил теорию локального потребительского выбора на основе представления потребительских предпочтений через «направление предпочтения» (preference direction), определенное в каждой точке пространства товаров 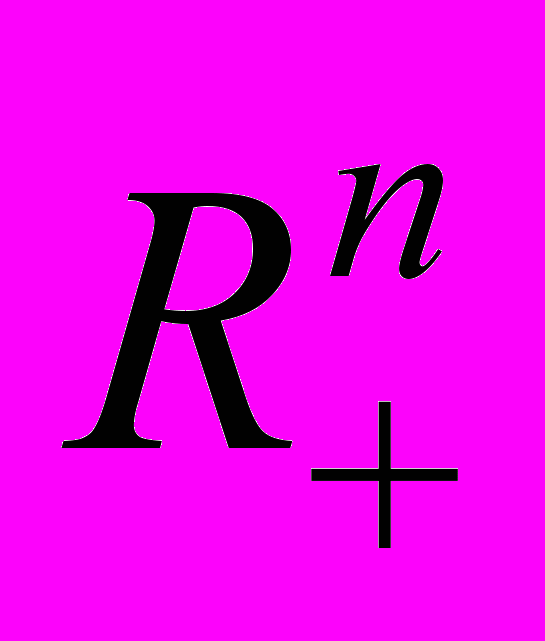. Это представление фактически является векторным полем 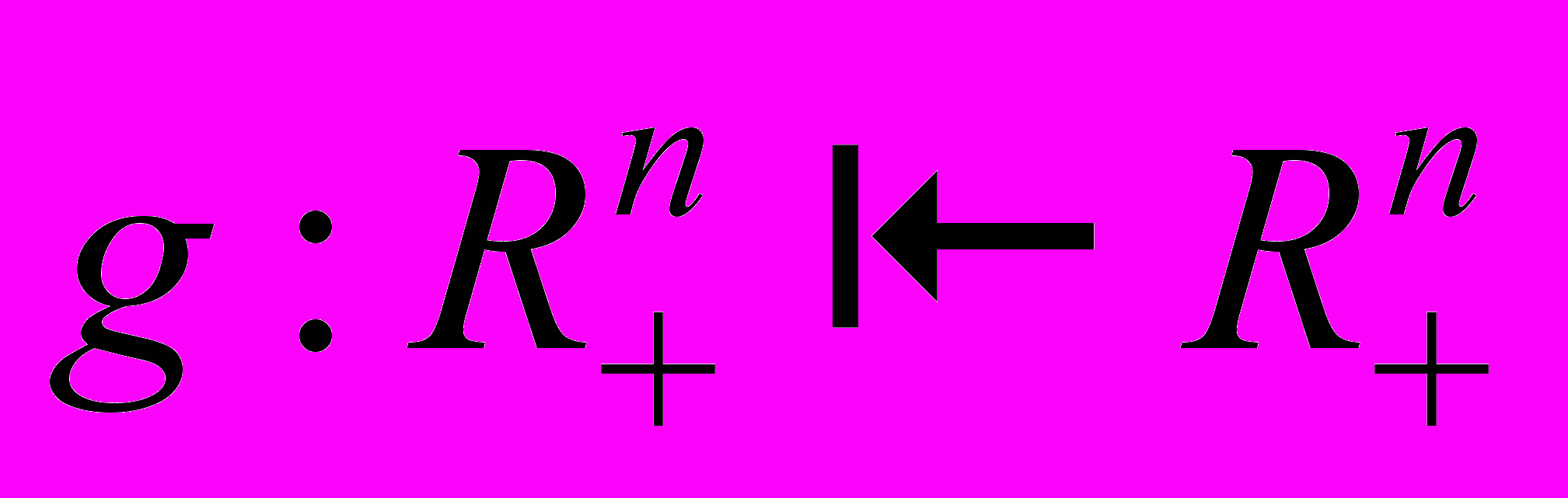, однако Аллен и его последователи не использовали теорию векторных полей и не построили содержательную теорию спроса (сравнительную статику), аналогичную классической теории, основанной на модели максимизации полезности.

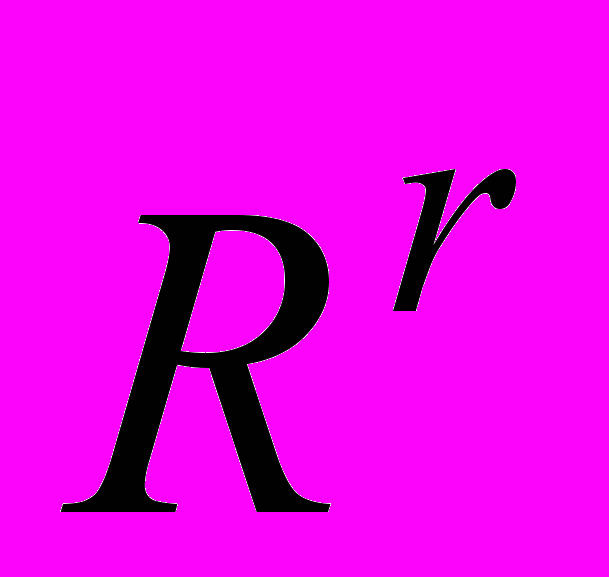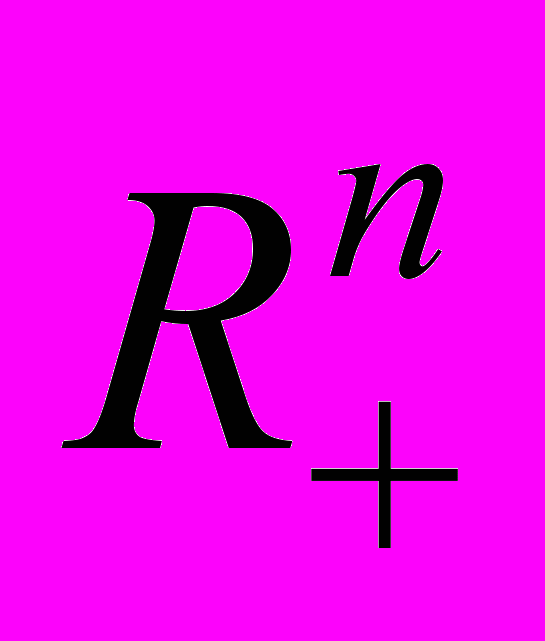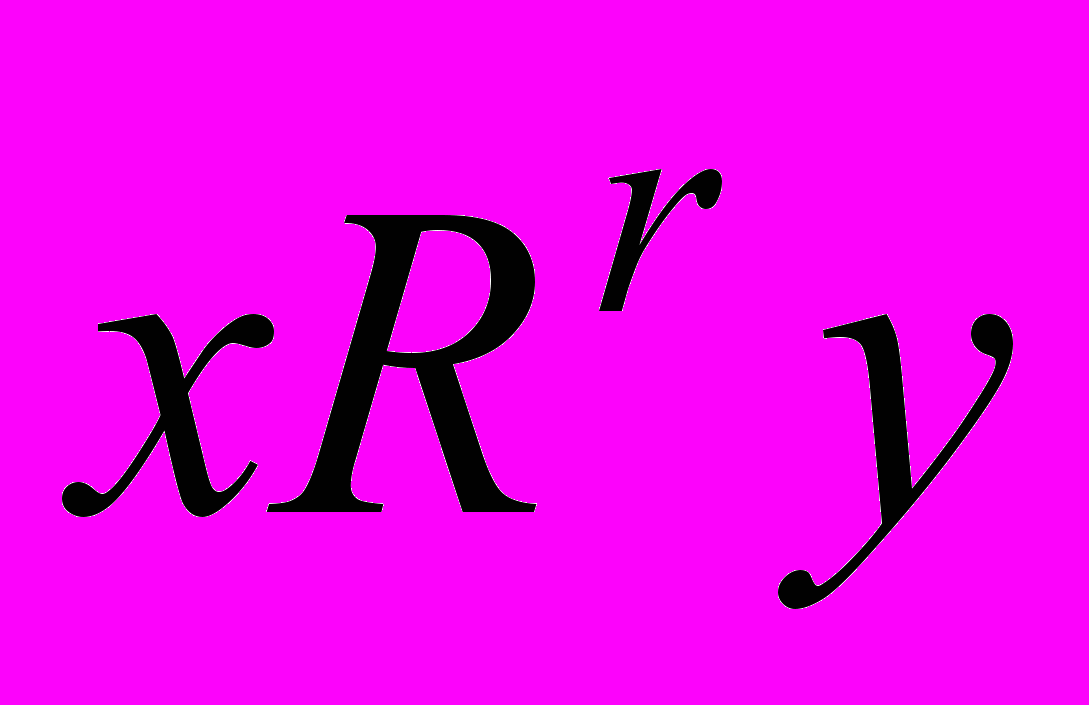
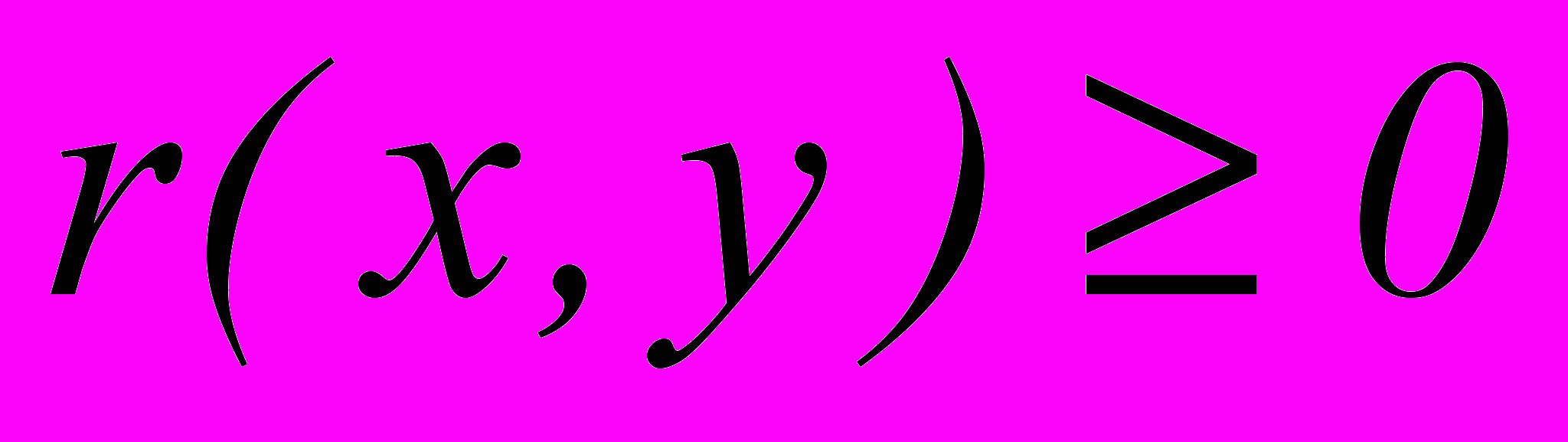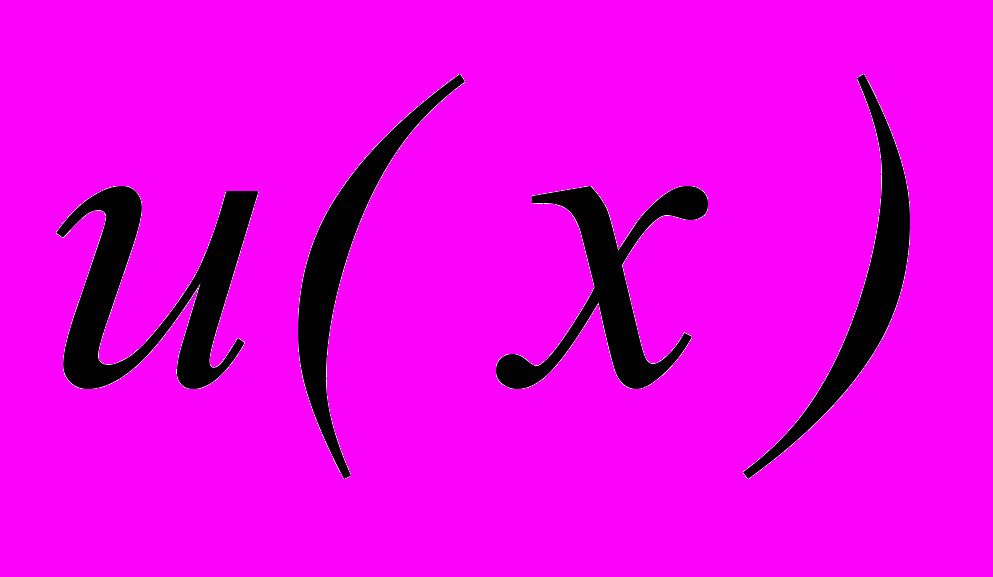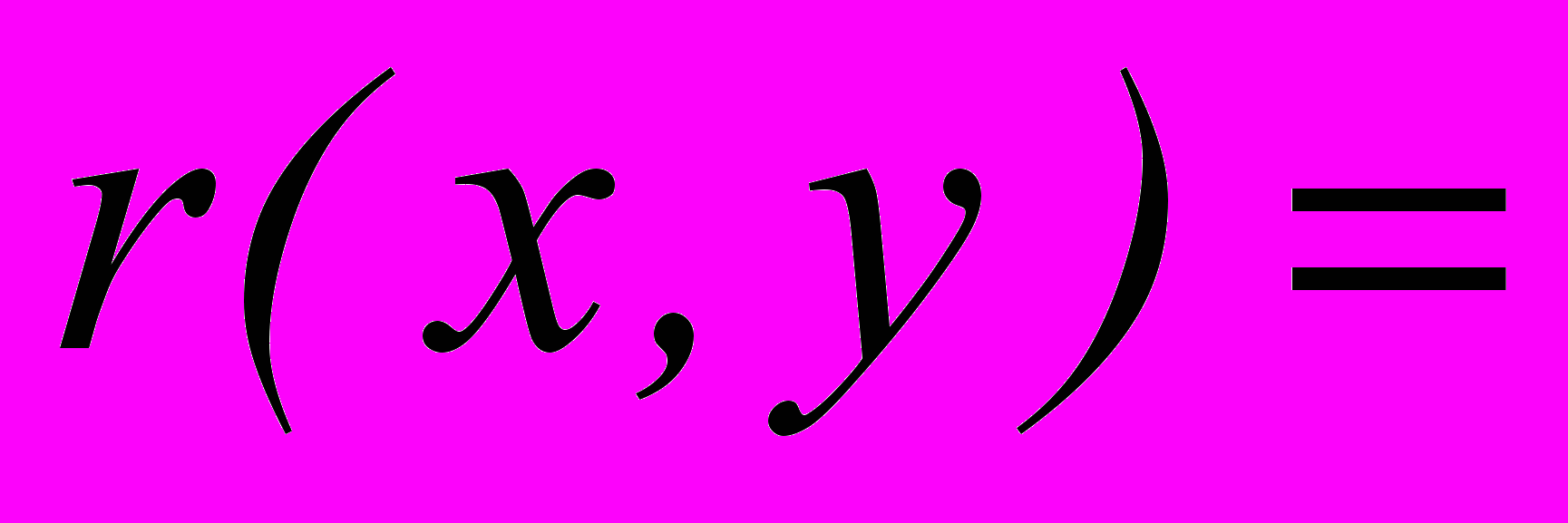
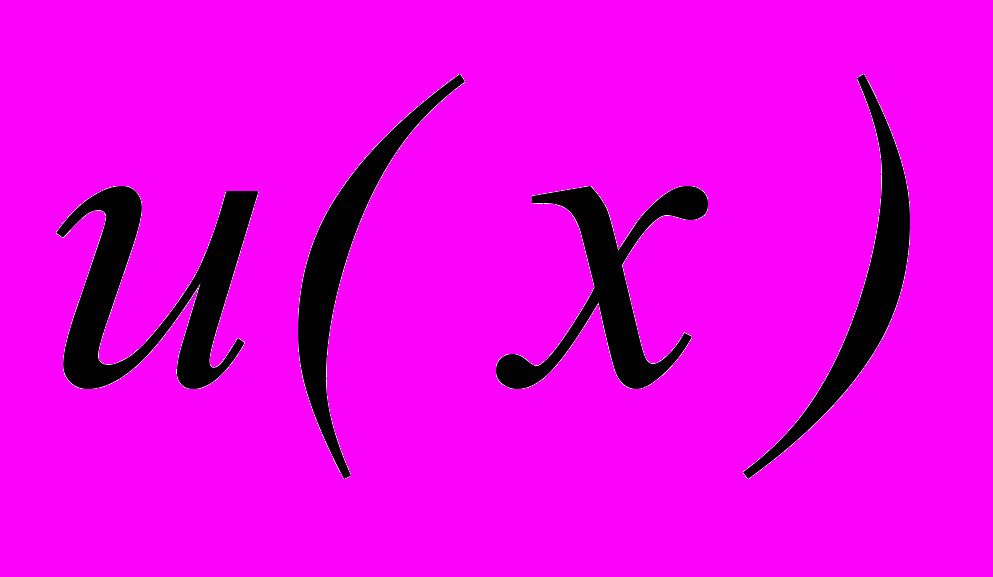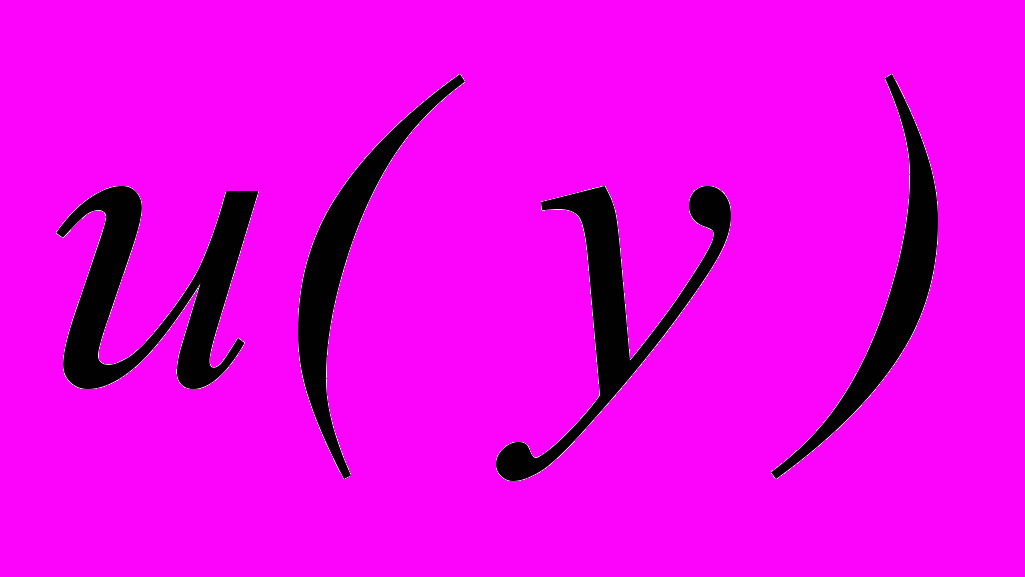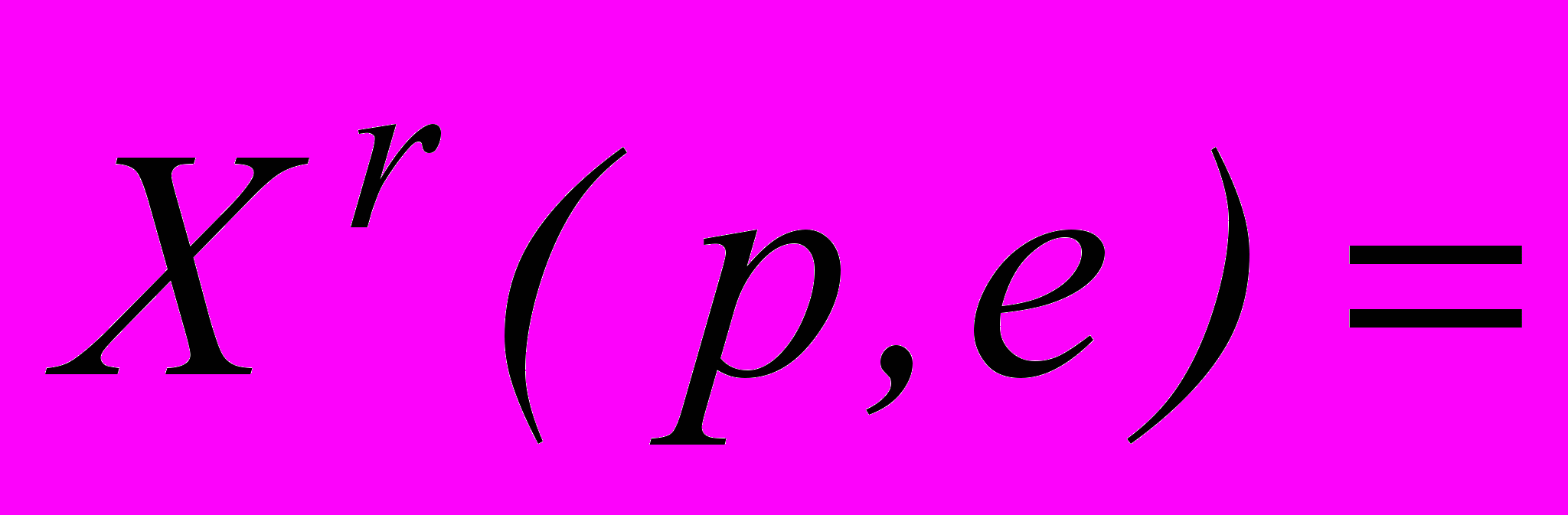
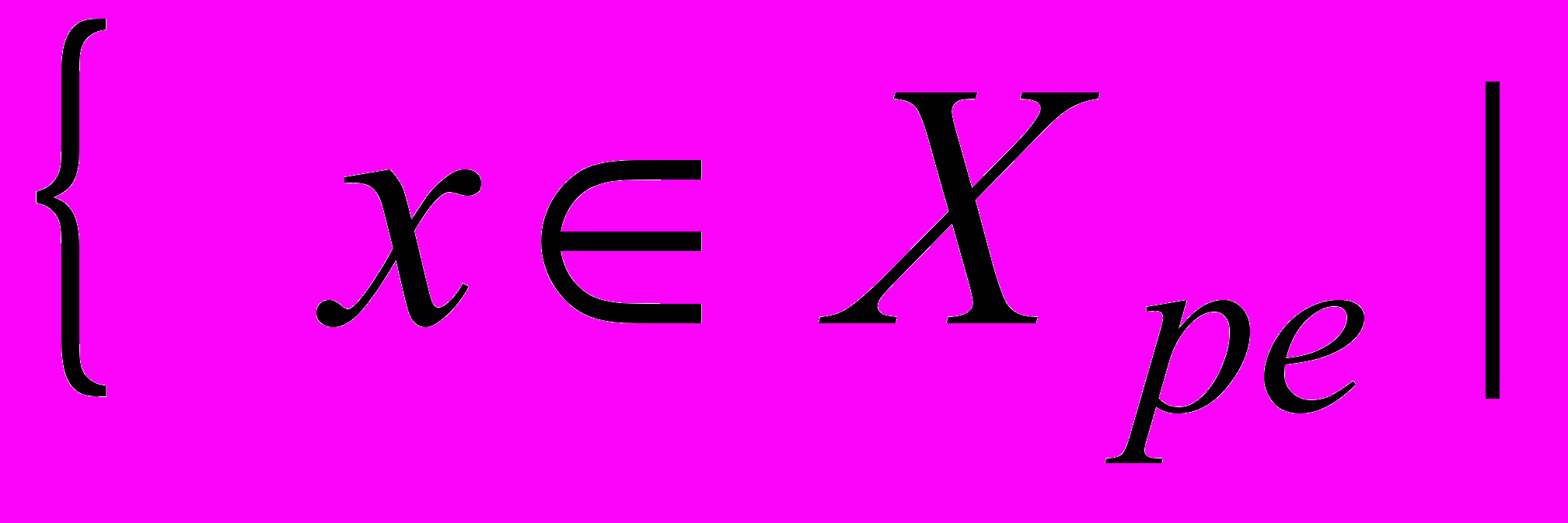
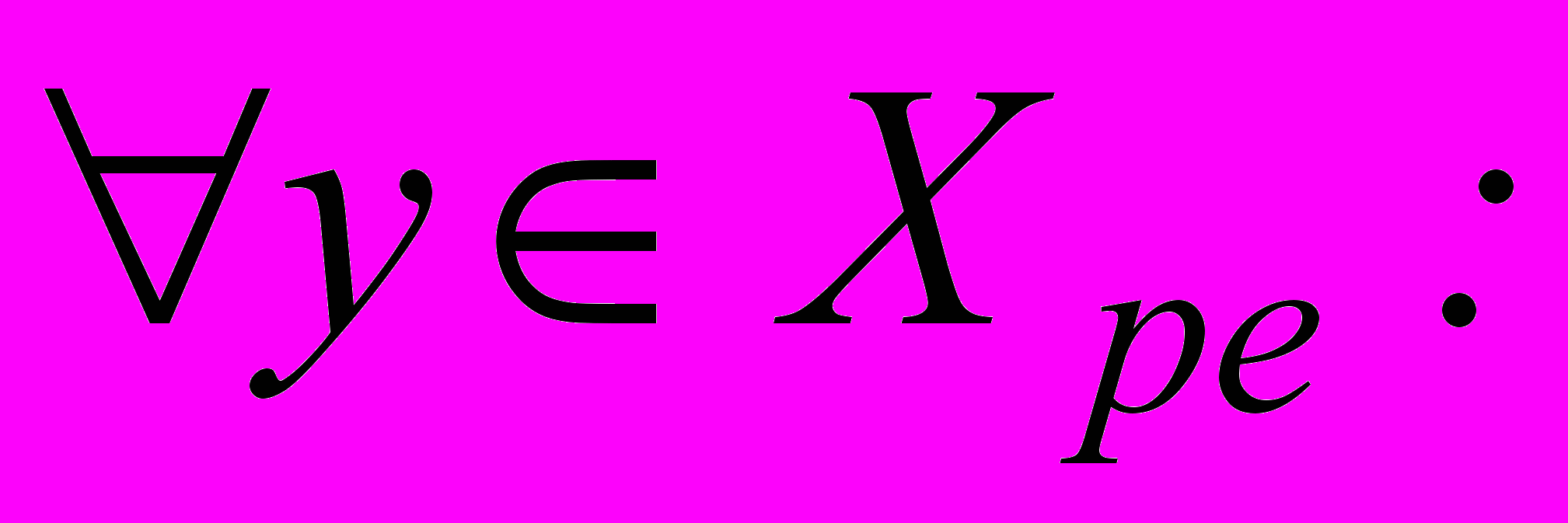
Шафер предложил теорию «нетранзитивного потребителя» на основе полного, но не обязательно транзитивного бинарного отношения предпочтений на , представляемого непрерывной и кососимметричной вещественной функцией r, т.е. . В транзитивном случае существует такая функция полезности , что –. Спрос Шафера определяется вариационным неравенством: 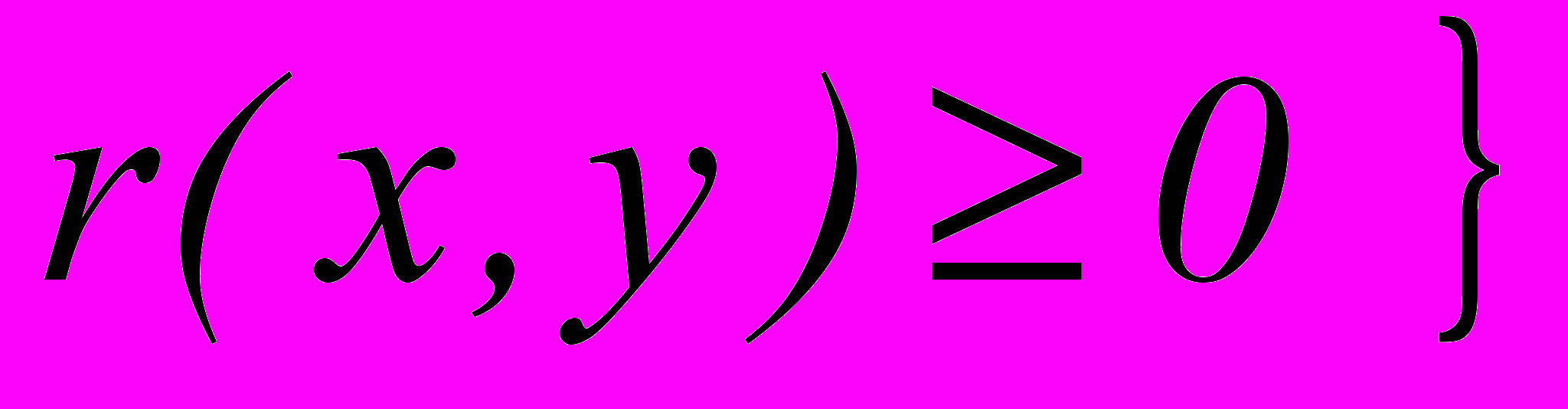, где 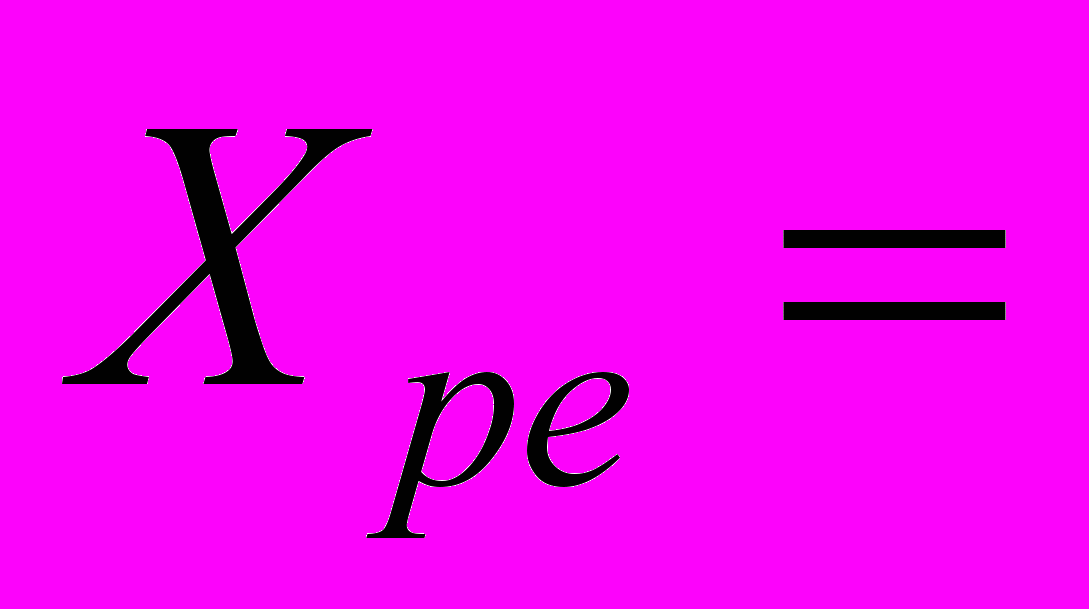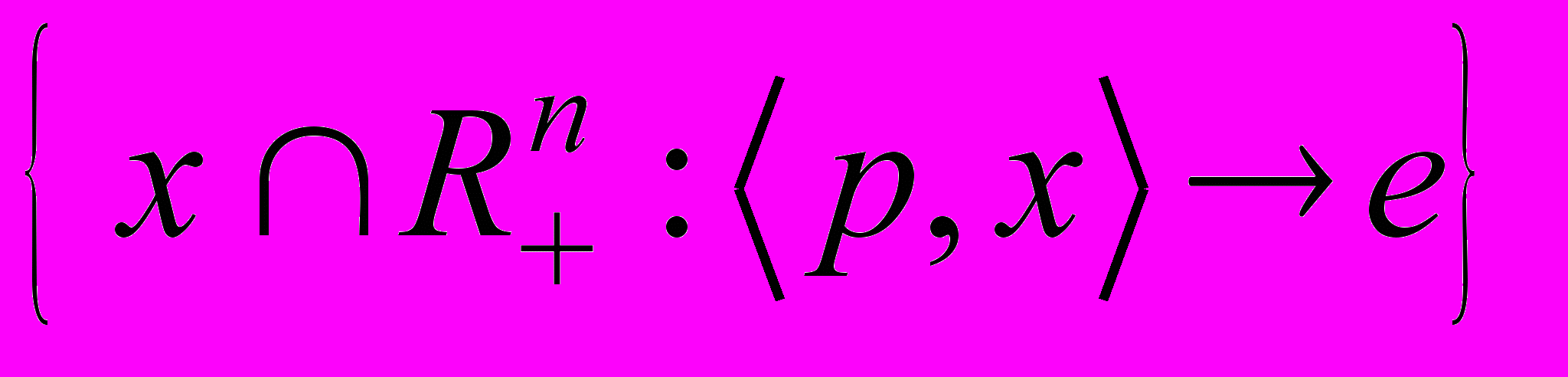– множество товаров, доступных при ценах 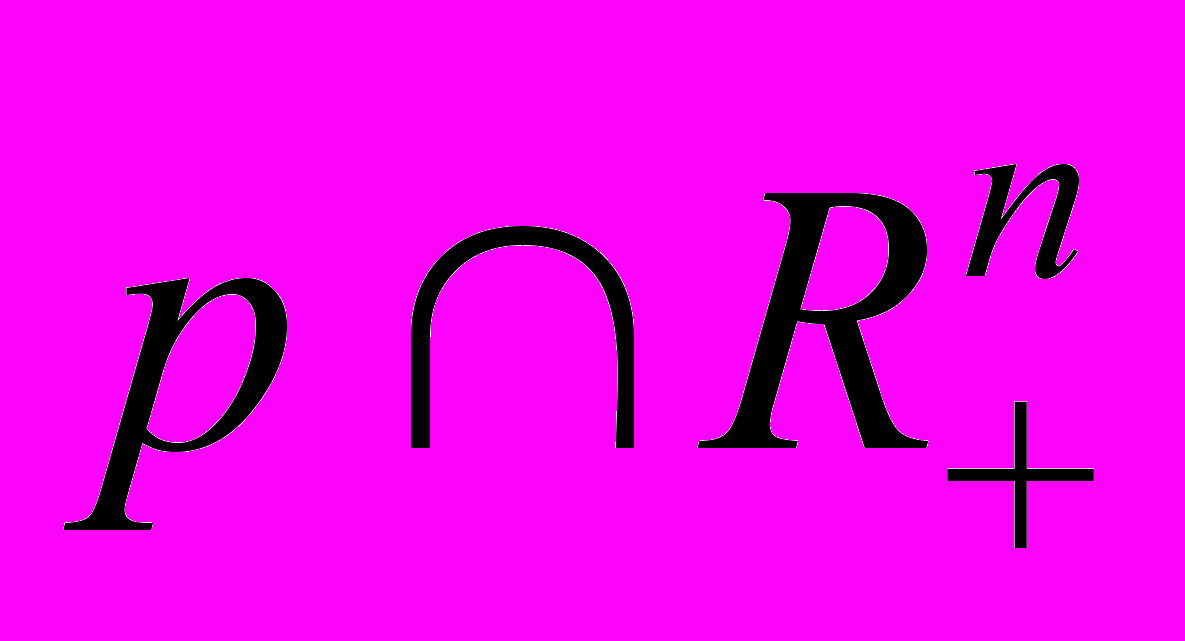и расходах e. Содержательная теория этого спроса также не известна.

В недавней статье [7] анализируются теории Аллена и Шафера. Здесь для модели Аллена введено бинарное отношение предпочтения 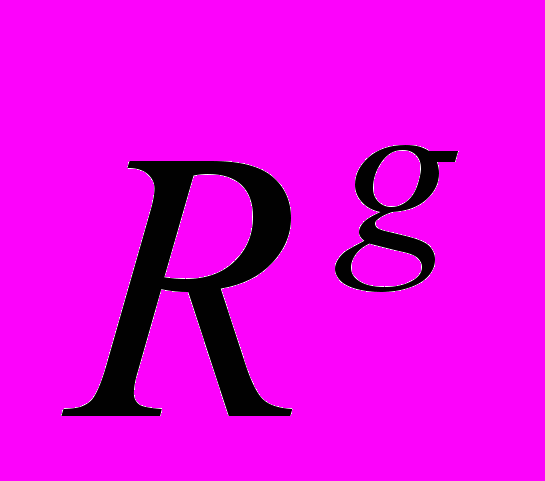так, что набор y из некоторой окрестности набора x считается лучше, чем x, т.е. 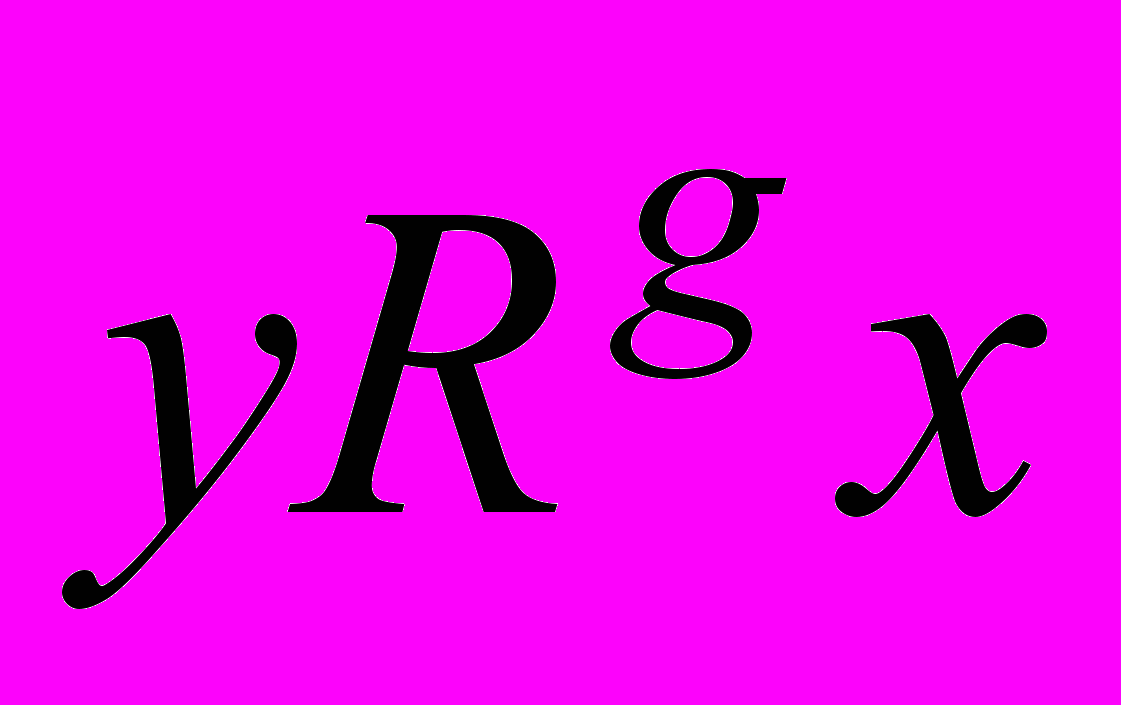, тогда и только тогда, когда 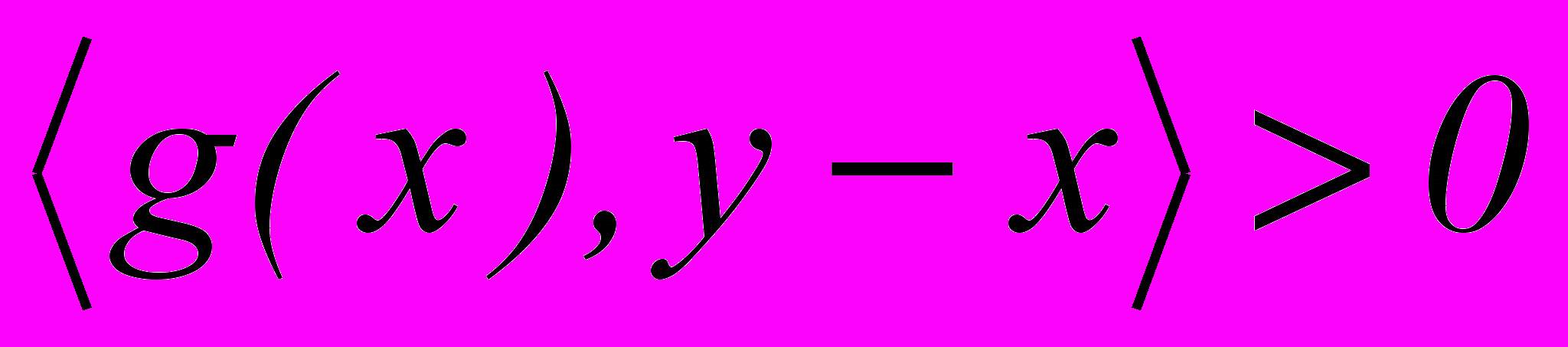. Утверждается, что теории Аллена (локальная) и Шафера (глобальная) эквивалентны.

Предлагаемый доклад представляет обратную задачу для новой аналитической модели рационального потребительского выбора В.К.Горбунова [2, 3], основанной на понятии векторного поля потребительских предпочтений. В общем случае это поле непотенциальное, положительное и монотонно невозрастающее. Эта модель свободна от стеснительных предположений классической модели о полноте и транзитивности предпочтений. В случае потенциальности поля новая модель совпадает с классической². Новая модель, как и классическая, является аналитической и позволяет вычислять и анализировать регулярные функции спроса. Она может считаться развитием модели Аллена на основе использования метода сравнительной статики (анализ Слуцкого) и теории векторных полей. Обратная задача заключается в построении поля предпочтений по статистическим данным о спросе.

2. Обобщенная аналитическая модель потребительского спроса [2, 3] описывает рациональный выбор ансамбля потребителей некоторого рынка конечных продуктов, рассматриваемого как априорный объект моделирования [5]. Такой подход позволяет избежать известные противоречия современной теории потребительского спроса (парадоксы агрегирования покупателей Гормана, Зонненшейна, Дебре и Мантеля [18]). Здесь система предпочтений ансамбля потребителей представляется с помощью векторного поля 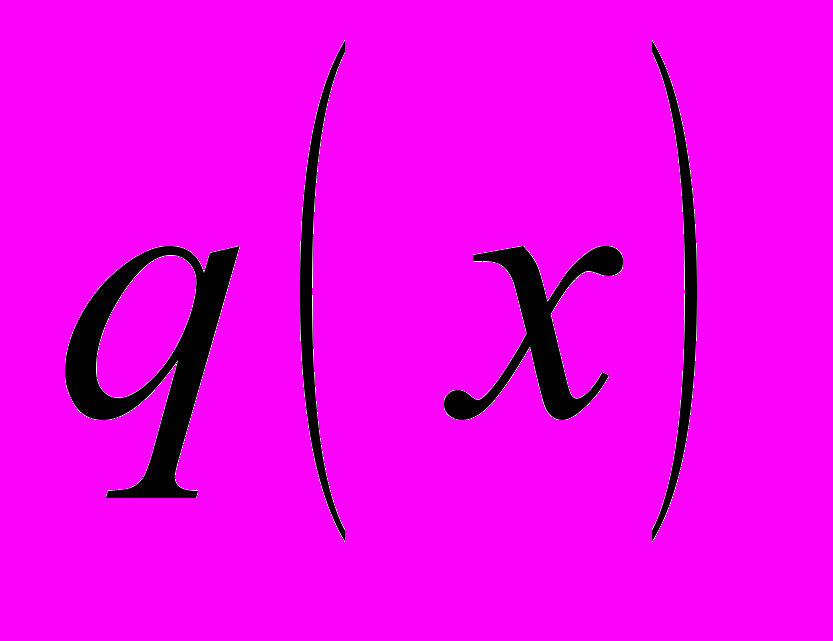в пространстве товаров 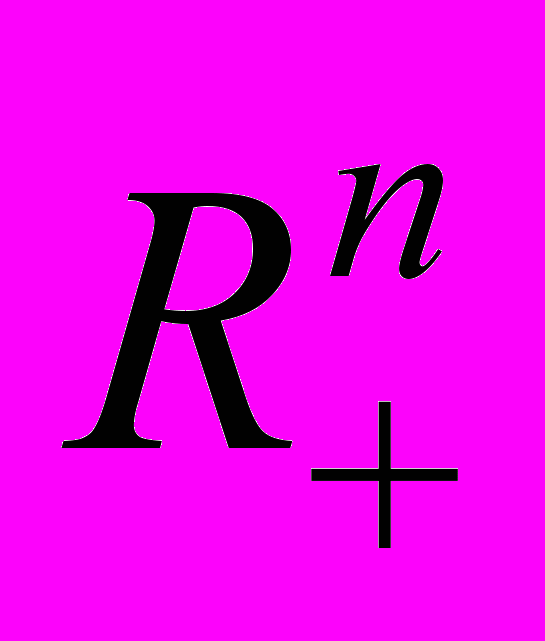. Поле 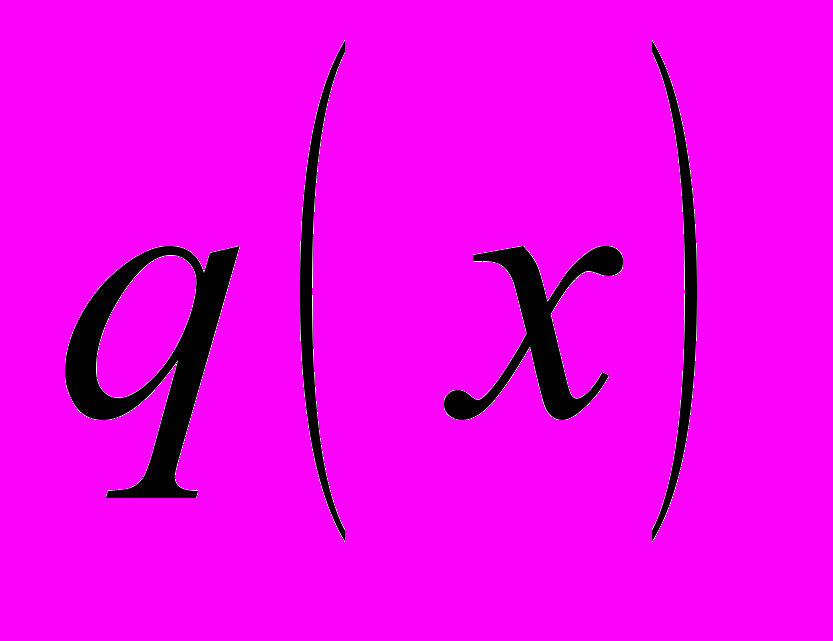называется потенциальным, если существует такая скалярная дифференцируемая функция 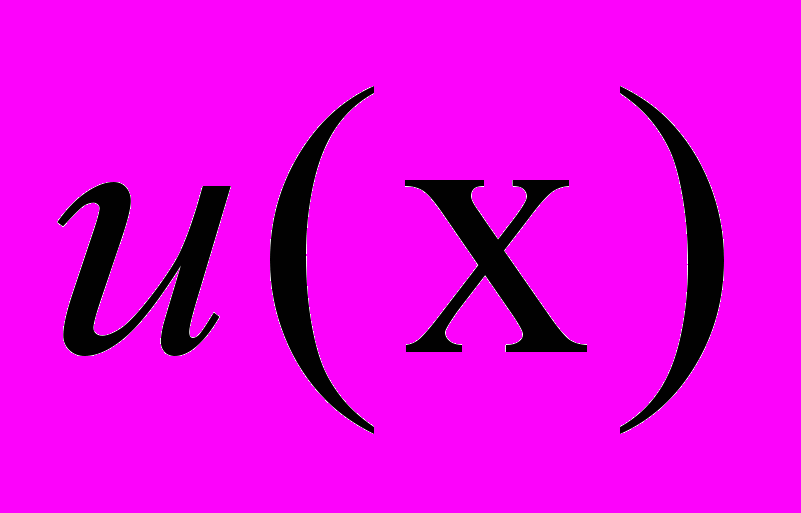, называемая потенциалом поля, что 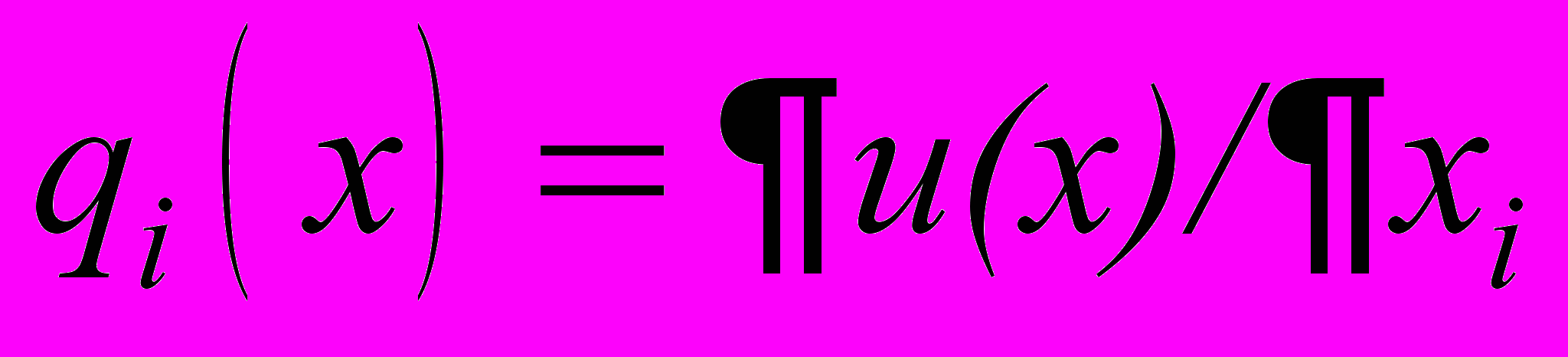. Потенциал монотонно невозрастающего поля 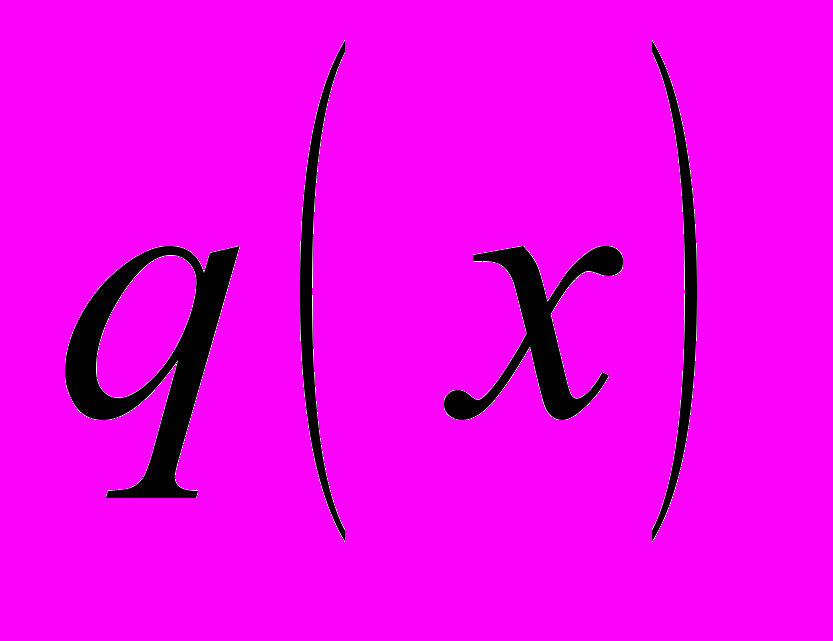является вогнутой функцией. Неотрицательность компонент 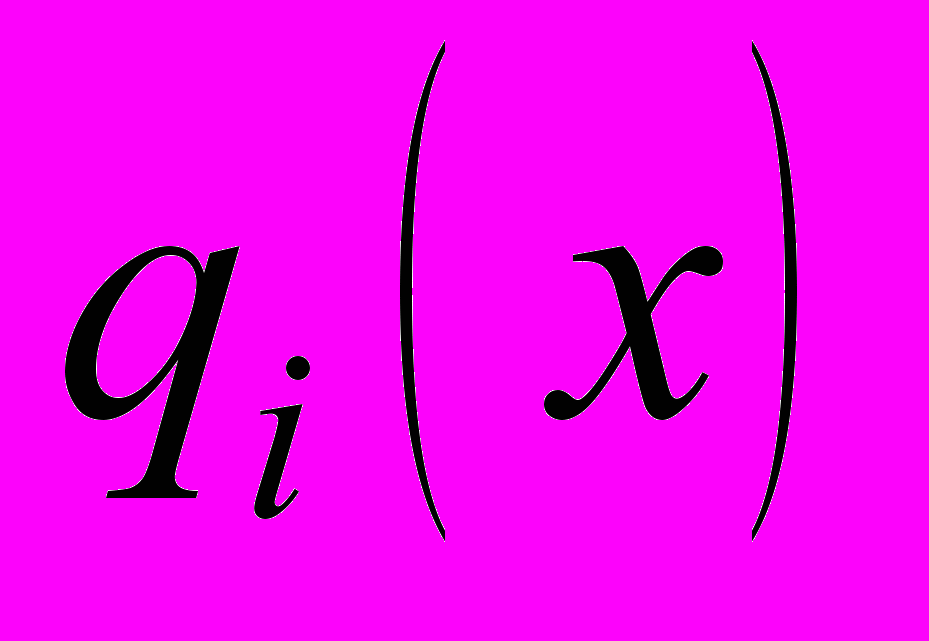означает неубывание потенциала. Поле 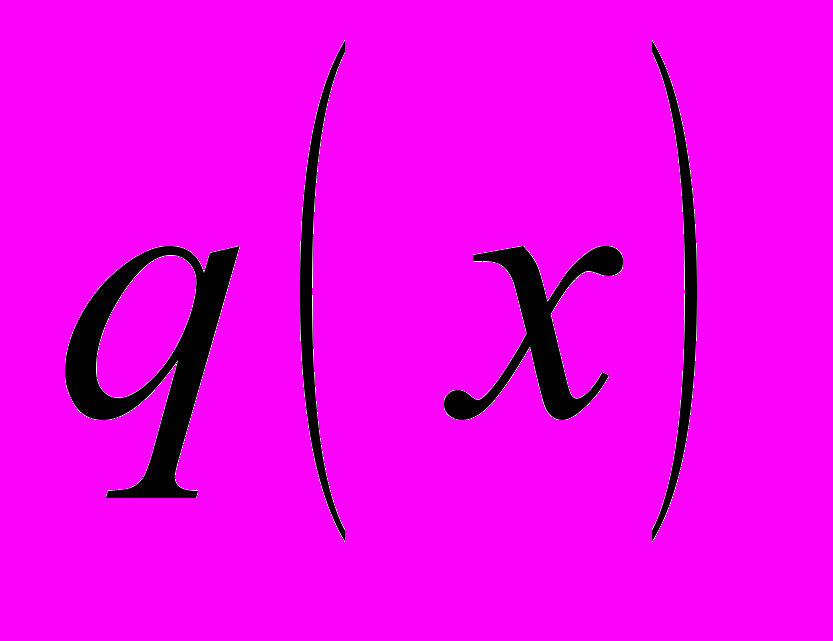называется монотонно невозрастающим, если для любых точек x и y выполняется неравенство

.

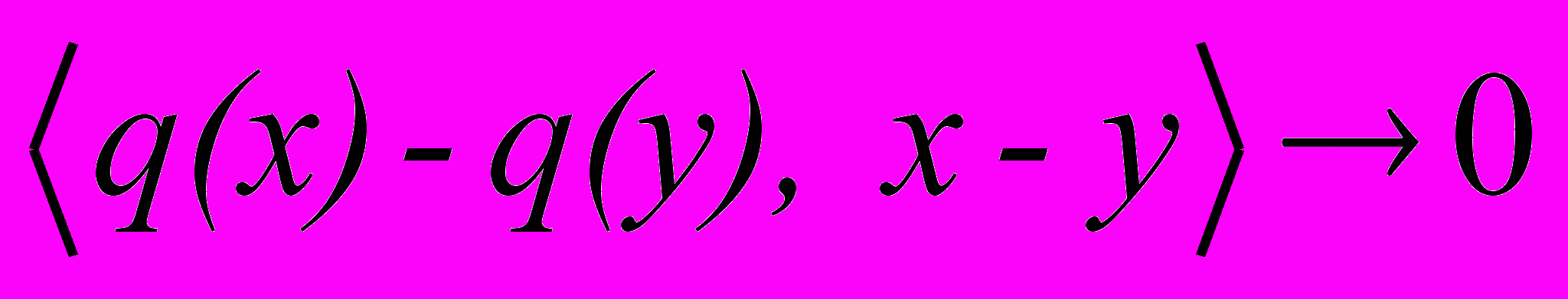Если это неравенство для 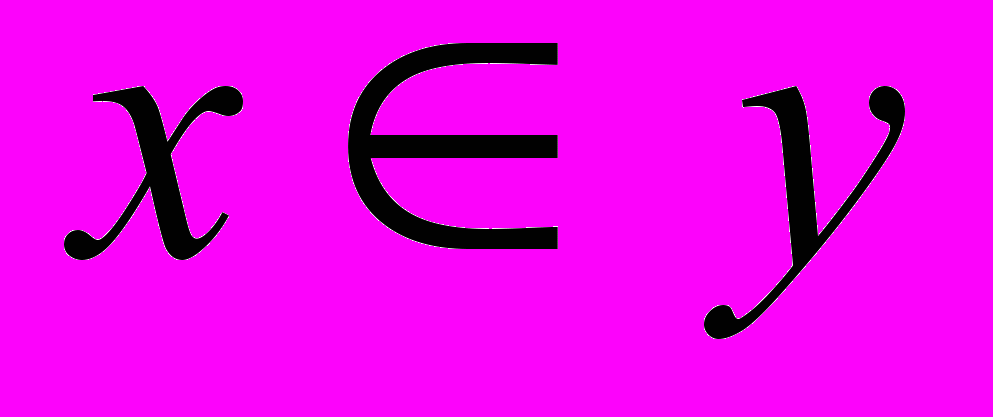строгое, то поле называется монотонно убывающим. В общем случае поле предпочтений может быть непотенциальным. Отношение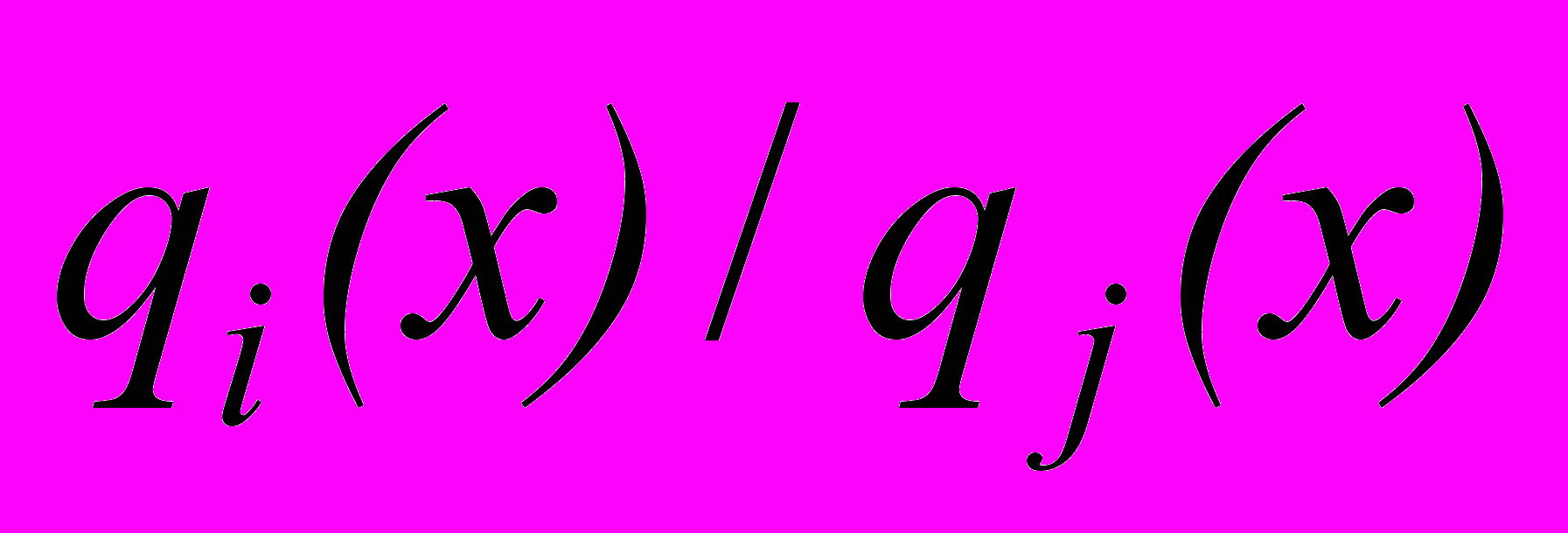

является предельной нормой замещения товара i товаром j.

Если поле предпочтений 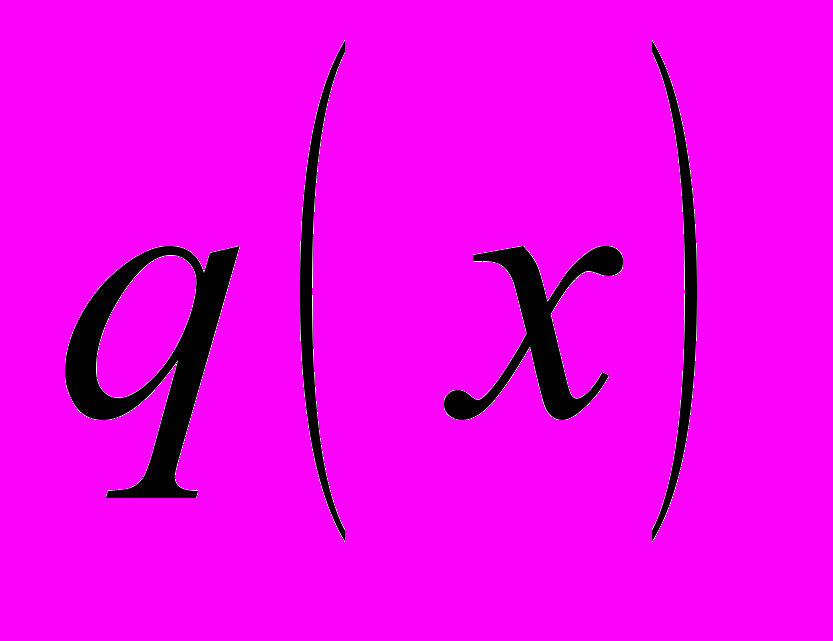потенциальное, то его потенциал 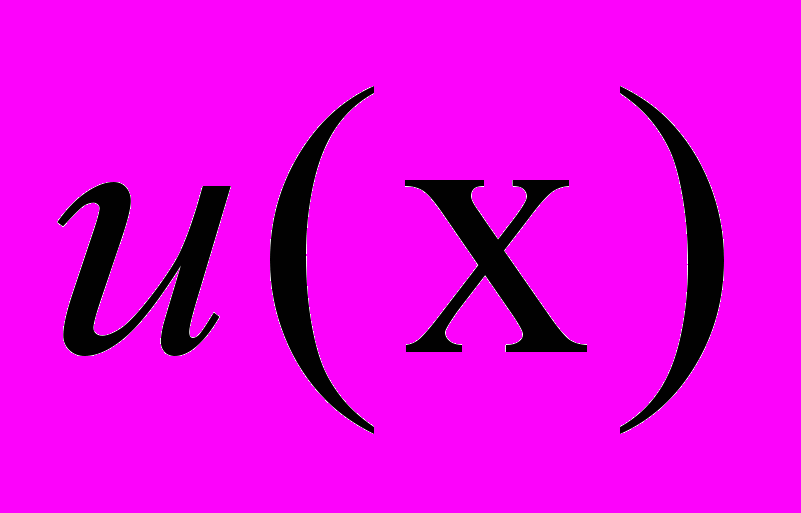можно считать порядковой функцией полезности. Соответственно, компоненты 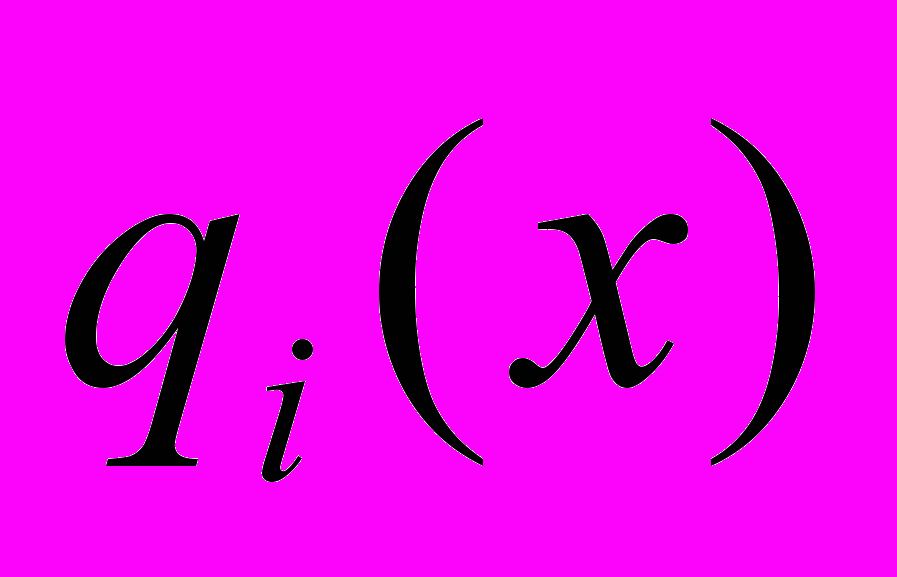принимают смысл классических предельных полезностей, и свойство монотонного убывания поля соответствует первому закону Госсена классической теории – закону убывания предельной полезности.

Рациональный выбор ансамбля потребителей, имеющих поле предпочтений 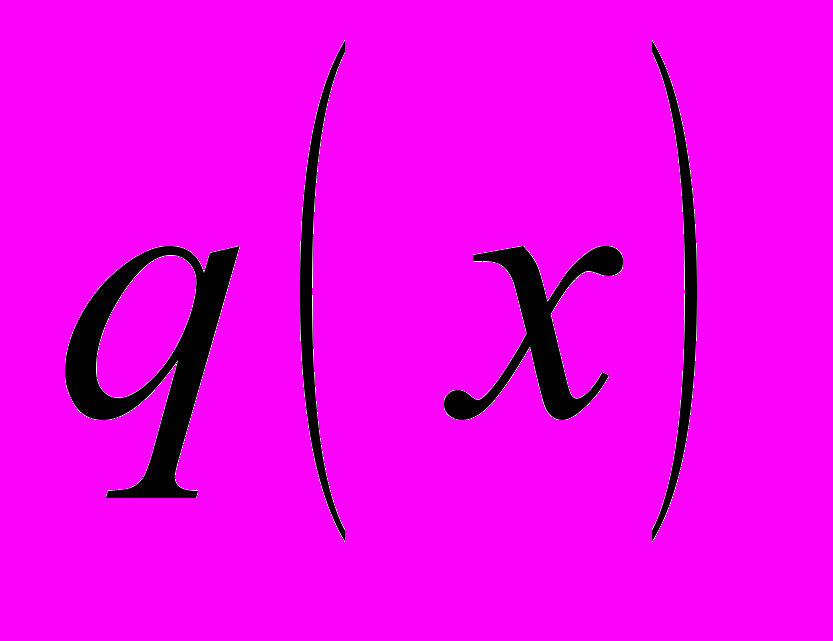и расходующих на данном рынке в ценовой ситуации p суммарное количество денег e, т.е. рыночный спрос 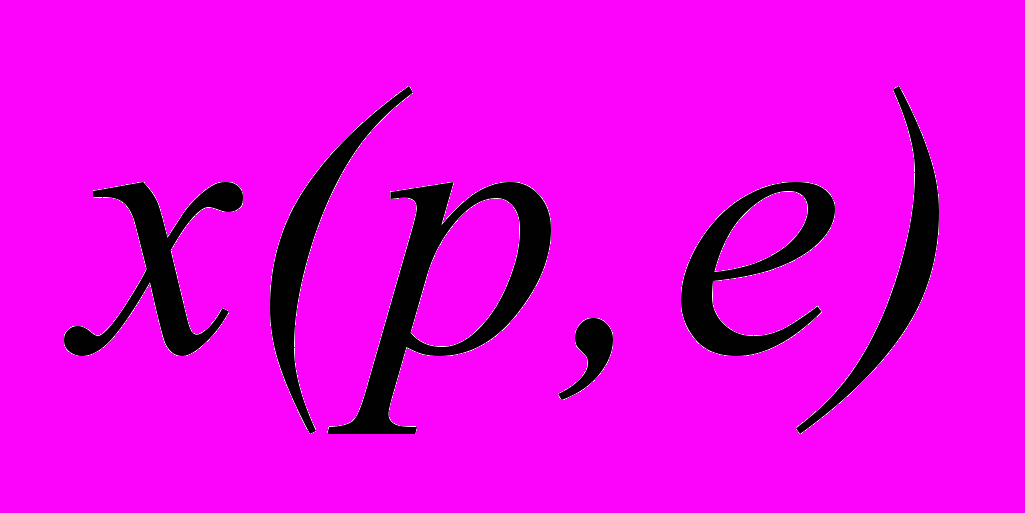, определяется вместе с множителем 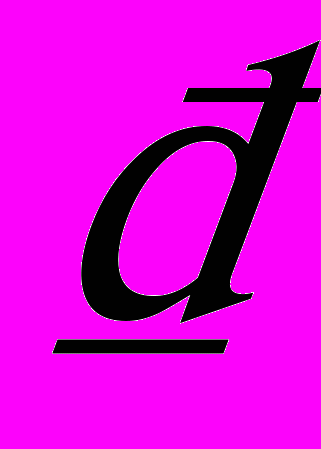системой нелинейных уравнений

(1)

В случае потенциальности поля система (1) совпадает с характеристической системой классической модели [1, 13].

В [2, 3] доказано, что в случае дифференцируемости и строгого убывания поля 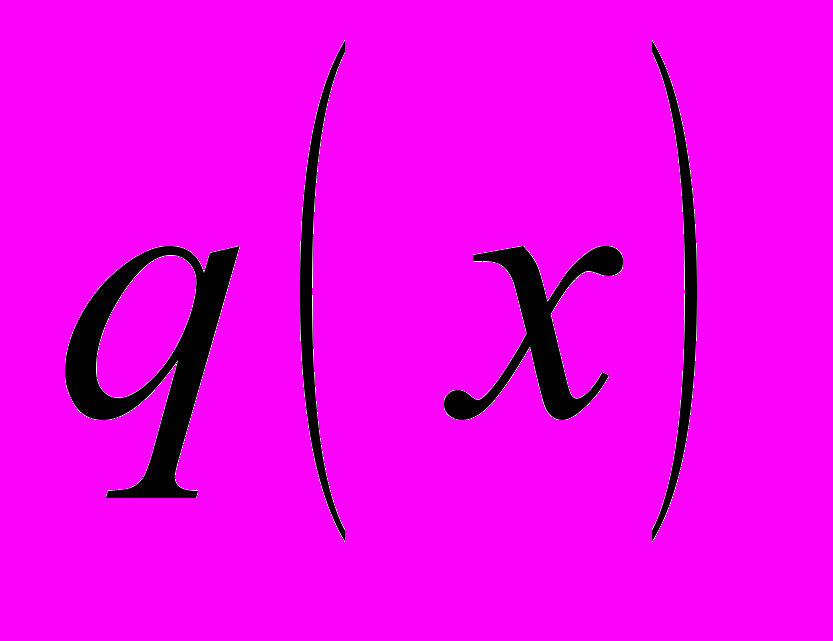система (1) определяет регулярный (однозначный и непрерывно дифференцируемый) спрос 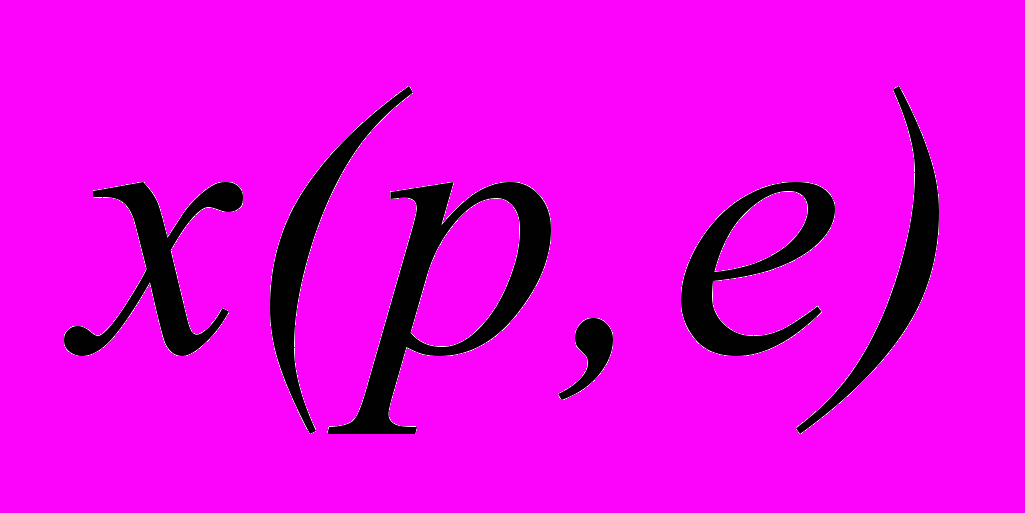, матрица Слуцкого которого обладает всеми свойствами классической теории (отрицательная полуопределённость, структура нуль-пространства), кроме симметричности. В соответствии с условиями интегрируемости Гурвица-Узавы [8] при этом в общем случае функция полезности, рационализирующая этот спрос, не существует, а в соответствии с результатами [10], спрос модели (1) удовлетворяет Слабой Аксиоме Выявленного Предпочтения.

3. Обратной задачей для модели (1) будем понимать задачу нахождения поля предпочтений 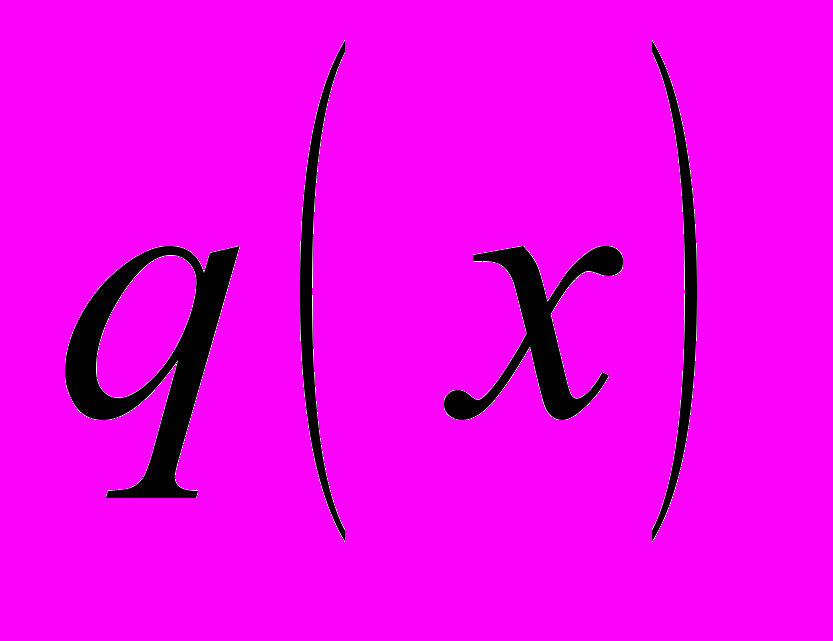, наиболее адекватного торговой статистике 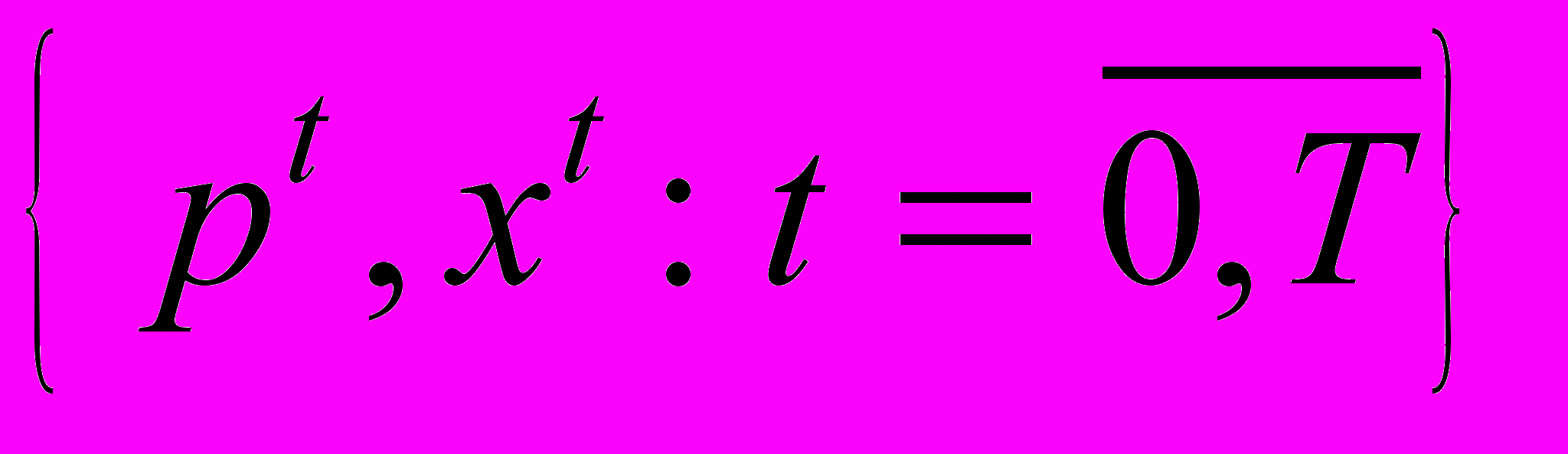в смысле метода наименьших квадратов (МНК). Она может быть решена как параметрическим, так и непараметрическим методом.

Параметрический метод заключается в выборе некоторого параметрического класса поля 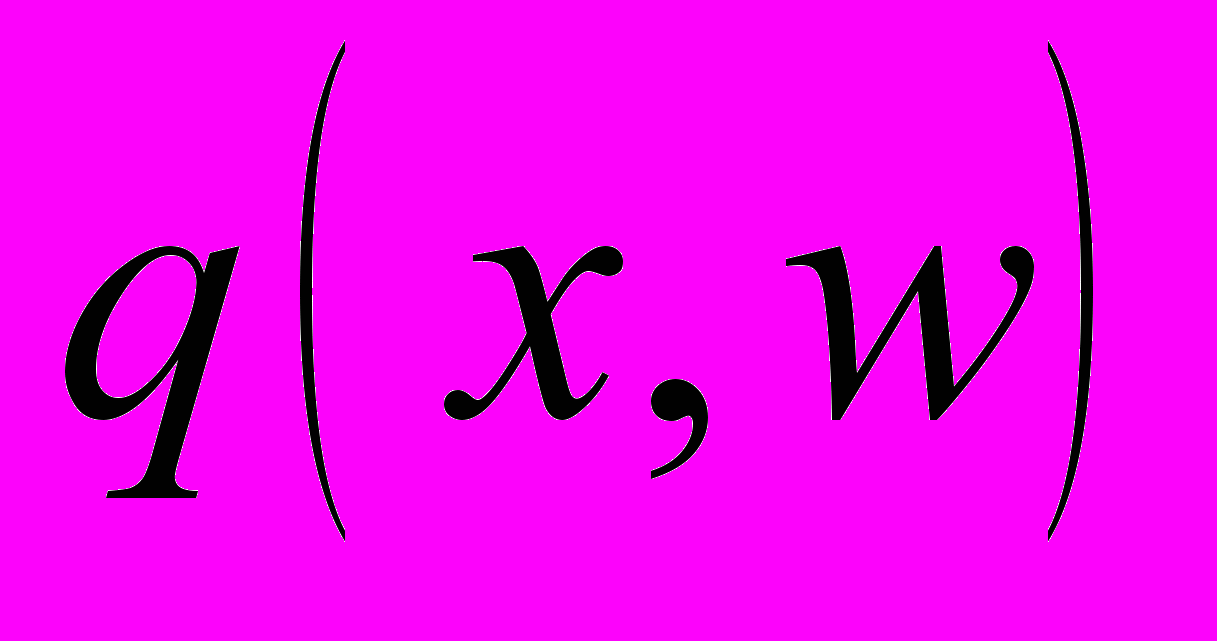, где 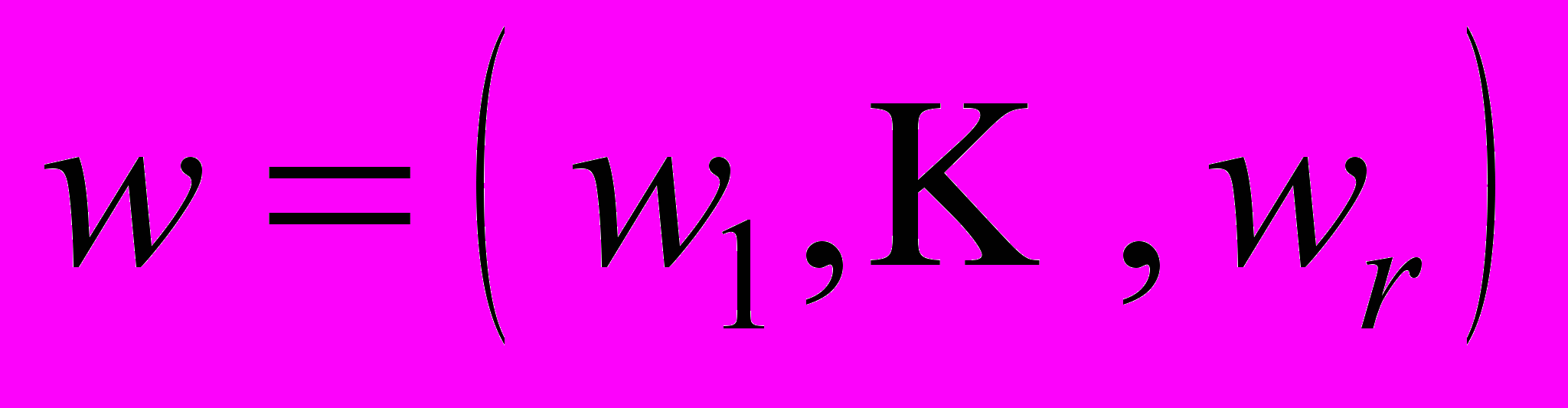- вектор параметров и последующим определении оценок параметров посредством МНК. При этом на параметры накладываются ограничения, обеспечивающие положительность и монотонность искомого поля.

На данном этапе мы используем два класса полей:

1. линейное поле
   

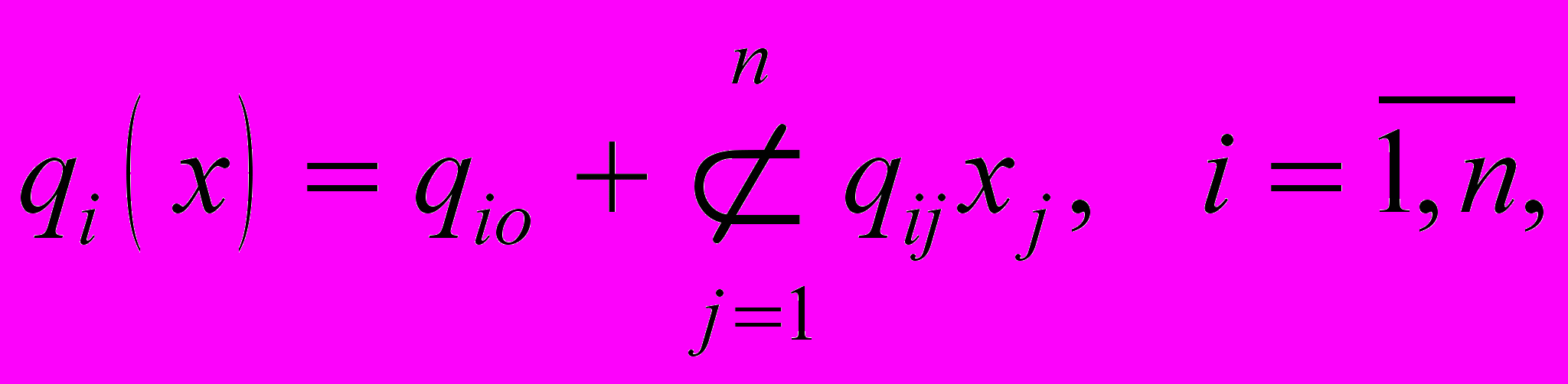(2)

где и матрица 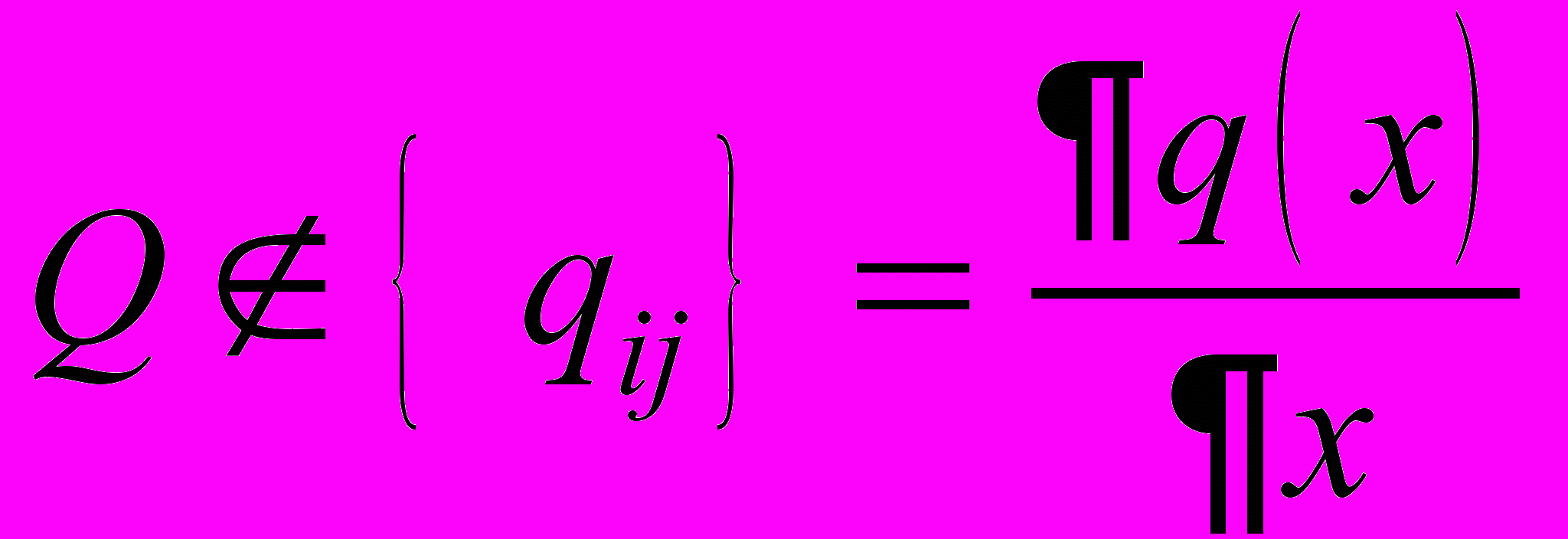отрицательно определена;

2. обобщённо-гиперболическое поле
   

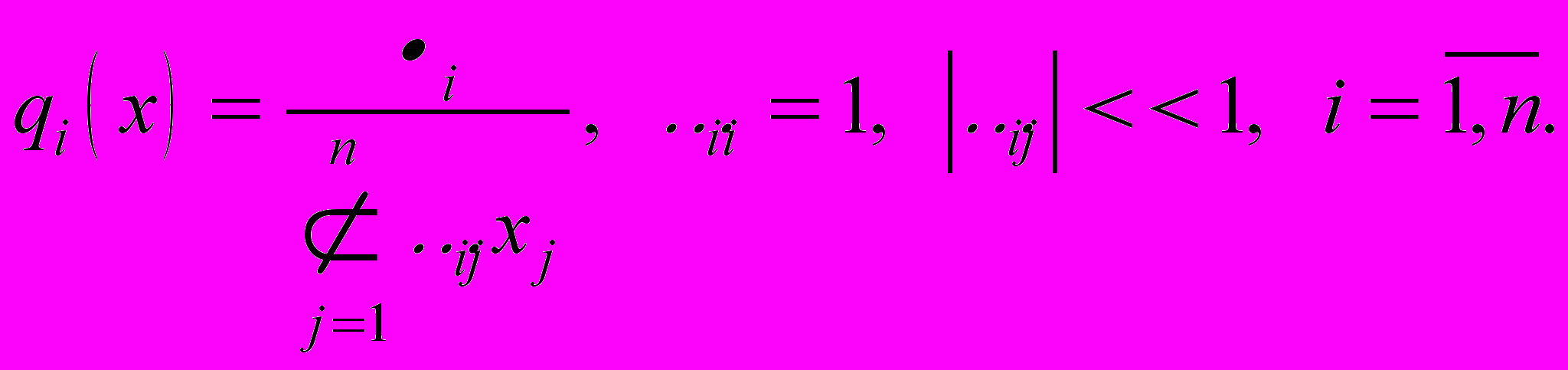(3)

Поле (2) является наиболее простым классом. Поле (3) при , совпадает с градиентным полем классической функции Кобба-Дугласа. Следовательно, при и малых значениях параметров 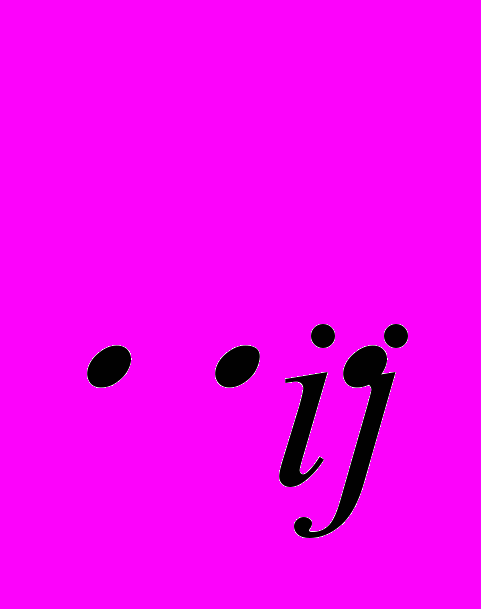поле (3) сохранит монотонное убывание.

В докладе будут приведены примеры построения полей предпочтений для модельных статистик, в частности, представляющих неинтегрируемые функции спроса, построенные в [9, 14].


Список литературы

1. Горбунов В.К. Математическая модель потребительского спроса: Теория и прикладной потенциал. – М.: Экономика, 2004.
   
2. Горбунов В.К. Модель потребительского спроса без функции полезности // Труды Средневол. матем. общества. 2005. Т.7. Вып.1.
   
3. Горбунов В.К. Модель потребительского спроса, основанная на векторном поле предпочтений // Вестн. Моск. ун-та. Сер. 6. Экономика. 2009. №1.
   
4. Горбунов В.К. Особенности агрегирования потребительского спроса // ЖЭТ. 2009. № 1.
   
5. Afriat S.N. The construction of utility functions from expenditure data // International Economic Review. 1967. No 1. V.8.
   
6. Allen R.G.D. The foundation of a mathematical theory of exchange // Economica. 1932. V.12.
   
7. John R. Local and Global Consumer Preferences // Generalized Convexity and Relative Topics. LN in Econ. Math. Syst. – Berlin: Springer, 2007.
   
8. Hurwic, L., Uzawa H. On the integrability of demand functions / In: Chipman J.S. et al. (Eds). Preference, Utility and Demand. – New York: Harcourt Brace, 1971.
   
9. Katzner D.W. Demand and exchange analysis in the absence of integrability conditions / Preference, Utility and Demand. Ed. by J.S. Chipman et al. New York: Harcourt, Brace, Jovanovich, 1971.
   
10. Kihlstrom R., Mas-Colell A., Sonnenschein H. The Demand Theory of the Weak Axiom of Revealed Preference // Econometrica. 1976. No 5. V.44.
    
11. Mariotti M. What kind of preference maximization does the weak axiom of reveald preference characterize? // Economic theory. 2008. V.35.
    
12. Mas-Colell A. An equilibrium existence theorem without complete and transi­tive preferences // J. Math. Economics. 1974. V.1.
    
13. Mas-Colell A., Whinston M., Green J. Microeconomic Theory. – New York: Ox­ford University Press, 1995.
    
14. Shafer W.J. The nontransitive consumer // Econometrica. 1974. V.42.
    
15. Quah J. K-H. Weak axiomatic demand theory // Economic theory. 2006. V.29.
    
16. Varian H. The nonparametric approach to demand analysis // Econometrica. 1982. No 4. V.50.