Методика количественного оценивания качества инвестиционных проектов, позволяющая учитывать как объективные, так и субъективные критерии. Неформальное введение

Вид материала

Документы

Содержание 3. Математическая формализация частных критериев качества проекта Определение коэффициентов относительной важности частных критериев 4. Формирование обобщенного показателя качества проекта Список литературы

Подобный материал:

• Конференция 'Роль аналитика в управлении предприятием' Критерии выбора ставки дисконтирования, 130.93kb.
• Методика выполнения творческих проектов, 116.13kb.
• А. В. Голубев Предложена методика, позволяющая делать расчеты денежных потоков инвестиционных, 125.96kb.
• Вопросы к экзамену по курсу «Теория антикризисного управления предприятием», 27.71kb.
• Вопросы к экзамену по курсу «Теория антикризисного управления предприятием», 27.84kb.
• Основные причины современного кризиса цивилизации и возможные пути выхода из него Галкин, 20.47kb.
• «Ядерная энергетика и здоровье», 301.05kb.
• Объективные и субъективные факторы при организации конкурентоспособного производства, 55.47kb.
• Компетентность докладчика /ответы на вопросы, 49.5kb.
• Долгожданный третий урок (час) физической культуры на государственном уровне утвержден, 815.92kb.

СРАВНИТЕЛЬНАЯ ОЦЕНКА КАЧЕСВА ИНВЕСТИЦИОННЫХ ПРОЕКТОВ


Методика количественного оценивания качества инвестиционных проектов, позволяющая учитывать как объективные, так и субъективные критерии.

1. Неформальное введение
   

Не секрет, что «неформальные введения» чаще всего используются, чтобы замаскировать нежелание или невозможность строгой, и, что еще страшнее, математически формализованной постановки задачи. Честно признаемся, что в данном случае речь идет скорее о нежелании сразу формализовать задачу, чем о недостаточной математической подкованности авторов. Желающим рассматривать проблемы инвестирования исключительно с математической точки зрения, предлагаем наши ранние работы [1-3], в которых любители могут обнаружить весьма удачные практические приложения одного из наиболее замысловатых (даже по названию) разделов современной математики- теории нечетких множеств.

Дело в том, что в широком смысле под инвестициями можно понимать чуть ли не все, что мы привыкли делать в обыденной жизни. Как ни странно, мы обычно не задумываемся о математической обоснованности (и, вообще, об обоснованности) принимаемых нами инвестиционных решений. Например, в жаркий летний полдень мы легкомысленно покупаем мороженое, хотя должны были бы всерьез задуматься о преимуществах альтернативной инвестиции в улучшение нашего самочувствия- покупки кружки холодного кваса. Все это, конечно, несерьезно, скажет “серьезный” читатель. Настоящие инвестиции - это вложение капитала в солидное дело и получение ощутимых доходов. Однако, что может быть серьезнее и ответственнее, чем вложение интеллектуальной собственности, например, своего математического таланта. Можно «вложить» его в наиважнейшее и благороднейшее дело– в разрешение шестой проблемы Гильберта и даже разрешить ее. Экономический эффект такой инвестиции весьма сомнителен ввиду отсутствия Нобелевской премии за достижения в математике. Однако вложение математического таланта в, скажем прямо, нечестные карточные игры с высокими ставками может всерьез обогатить инвестора.

Все эти не очень научные рассуждения должны были осторожно подготовить читателя к восприятию печальной мысли о невозможности выработки единого универсального рецепта для оценки инвестиций.

Собственно, на этой грустной ноте можно было бы и закончить статью, если бы не бескорыстное научное любопытство: на какой основе люди все же принимают инвестиционные решения? (и не слишком бескорыстное любопытство: как, инвестируя немножко денег, а лучше какую-нибудь виртуальную собственность, вроде интеллектуальной, получить в результате как можно больше (всего) и, по возможности, без риска?).

Поскольку «нельзя объять необъятное», несколько сузим проблему до рассмотрения «нормальных» инвестиционных проектов, с которыми имеют дело инвестиционные фонды, банки, крупные и не очень фирмы, и другие солидные организации.

2. Введение
   

Критерии оценивания проекта определяются позицией оценивающего по отношению к инвестируемым средствам. Если судьбу проекта решает банкир, то его интересуют, в основном, срок окупаемости, проценты и риски. Если оценивает преставитель государственного сектора, то могут оказаться очень важными критерии экологичности, технологической новизны, занятости населения и пр. При этом, может быть отвергнут совершенно революционный и суперприбыльный проект реструктуризации градообразующего предприятия, реализация которого оставит половину населения города без работы.

Ясно, что в такой вызывающе неупорядоченной ситуации первое, что приходит в голову серьезному теретику- это идея создания “стройной” универсальной системы критериев оценки инвестиций. Идея со всех сторон привлекательна и может послужить предметом весьма занимательной научной дискуссии. Однако ее воплощение в жизнь, особенно в виде обязательной для выполнения инструкции с приложением большой круглой печати, небезопасно для общества, поскольку может нанести существенный урон экономике.

Все это вовсе не означает, что люди не используют при оценке проектов каких-либо систем критериев. Как раз наоборот.

Например, в США при конкурсном отборе инвестиционных проектов на федеральном уровне используется до 40 различных критериев. Ясно, что часть из них может быть объективно представлена к количественной форме (приведенные доход, срок окупаемости и пр.), а часть -лишь в качественной форме экспертных оценок (степень влияния на экологию региона, степень политического риска). Кроме того критерии имеют различную значимость в оценке проектов.

В работе [4] представлена некоторая “рамочная” система критериев, достоинствами которой является отсутствие претензий на “стройность” и всеобщность, а также то, что она является научным обобщением практики бизнес-инновационных и технологических центров Германии. Совокупность возможных критериев предлагается условно разбить на следующие основные группы: критерии, характеризующие соответствие проекта экономическому развитию региона, его экологическим особенностям и научно-технологической направленности инновационной структуры; критерии оценки коммерческого успеха нововведения; критерии оценки научно-технического уровня; критерии финансовой эфективности; критерии оценки вероятности производственной реализации проекта; критерии оценки различных видов риска.

Даже весьма повехностный анализ предложенной систематики критериев позволяет сделать вывод, что задача оценки качества инвестиционных и инновационных проектов осложняется следующими обстоятельствами:

• частные критерии могут основываться на количественных характеристиках (финансовые парметры), а также на оценках экспертов ( критерии научно-технического уровня), которые чтобы не ошибиться, предпочитают давать советы на качественном уровне и весьма неопределенно. Поскольку в этом случае в игру вступают опыт и интуиция, неизбежны проявления неопределенности субъективной, нечеткой природы, которая не может быть описана в привычном вероятностном смысле. Со школьных времен известно: то, что не объективно- не научно, интуиция- от лукавого. Поэтому, опираясь на непримиримо-строгие традиционные научные представления, можно было бы с облегчением забыть о критериях, заданных на качественном, вербальном уровне описания. Однако на практике именно такие критерии часто играют решающую роль;
  
• часть критериев находятся в антагонистических отношениях, т.е. улучшение по одним критериям неизбежно ведет к ухудшению по другим и классическая формула “кто не рискует, тот не пьет шампанского” не стареет;
  
• критерии явно неравноценны, т.е. вносят разный вклад в интегральную оценку качества проекта.
  

Кроме того, критериев много. Сложность в том, что люди плохо воспринимают излишне детализированные шкалы значений признаков или критериев. Согласно данным психофизических исследований, человек уверенно различает не более 7-9 градаций на шкале некоторого признака. Если же она содержит большее число градаций, то соседние уровни начинают сливаться и уже не могут быть с уверенностью разграничены [5].

Список проблем можно продолжить, однако устрашение читателя не является целью статьи.

Умудренный читатель, конечно, понимает, что чем страшнее во введении описаны трудности, тем изящнее и проще будут предложенные авторами способы их преодоления.

Название следующего раздела начинается со слова “математическая”. К сожалению, совсем обойтись без математики при оценивании инвестиционных проектов не удается: речь идет о деньгах, а они счет любят.

Однако, хорошо понимая вполне оправданное, сформированное жизненным опытом многих читателей, отвращение и недоверие к математике, постараемся, по возможности, использовать математику в картинках. При этом будем опираться на несложный пример и его реализацию с помощью разработанного авторами программного обеспечния.

3. Математическая формализация частных критериев качества проекта

Для того, чтобы оценивать проекты, необходимо иметь матаматический аппарат для приведения характеризующих их разнокачественных частных критериев к некоторой общей норме. Для этого воспользуемся аппаратом теории нечетких множеств [6,7]. Рассмотрим для примера такой важный количественный показатель, как внутренний коэффициент окупаемости IRR. Ясно, что существует некая нижняя допустимая граница IRR, обычно примерно равная учетной банковской ставке в стране инвестора -r. Далее существует довольно широкий интервал r < IRR < IRRm, в котором эффективность проекта растет и одновременно растет вероятность вложения инвестиций. Предполагается, что при IRR>IRRm эффективность проекта с точки зрения параметра IRR настолько высока, что при прочих равных условиях инвестирование гарантировано.

Для формализации таких описаний в теории нечетких множеств используется аппарат функций принадлежности, которые в контексте нашей задачи удобнее называть функциями желательности, изменяющиеся от 0 в области недопустимых значений до максимального значения, равного 1 в области наилучших значений анализируемого показателя качества.

Общий вид функции желательности для нашего примера, представлен на рис.1а. Сразу отметим, что линейный характер возрастания функций желательности не является догмой и употребляется чаще всего в тех случаях, когда о различных значениях показателей качества можно лишь сказать, что одно из них предпочтительнее другого. Аналогично строятся функции желательности и для других количественных показателей. Наиболее часто функции желательности строятся в виде нечетких ( рис. 1б - рис.1г ) или четких (рис. 1д ) интервалов.



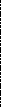
1

a)


0.5


0

IRR


IRRm

IRR1


б)

1

в)

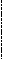
1

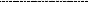
г)

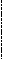
1

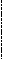
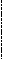
д)

1




0

0

0

0




1

е)


(IRR)


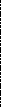
0.5

IRR


0 1 2 3 4 5 6 7 8 9

Рис. 1. Основные способы построения функций желательности частных критериев: а) функция желательности IRR. б), в), г), д) - типичные формы функций желательности частных показателей;е) - функция желательности качественно заданного показателя: 0 - не выражено; 1 - немного выражено; 2 - заметно выражено и т.д.


Формализация показателей качества, задаваемых на качественном уровне, может быть также проведена с помощью функций желательности. При этом удобно пользоваться лингвистическими оценками степени выраженности показателя. Например, степень выраженности показателя “воздействие на экологию региона” может быть оценена по вербальной шкале : “не выражен” ,”слабо выражен”,“заметно выражен” и т.д. (не более 9 градаций, как будет показано ниже). Способ построения соответствующей функции желательности представлен на рис. 1е.

В итоге все качественные и количественные показатели представляются в единой безразмерной шкале функций желательности.

Теперь можно перейти к рассмотрению примера. Допустим, что необходимо провести сравнительную оценку четырех проектов, по параметрам, представленным на рис.2.





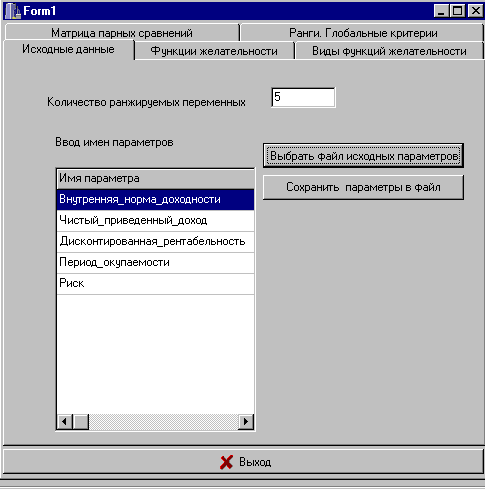
Рис.2. Параметры оценки проектов.


В реальной ситуации параметров может быть значительно больше, однако без внутренней нормы доходности (IRR), чистого приведенного дохода (NPV), дисконтированной рентабельности (PI) и периода окупаемости (PB) проекты обычно не оцениваются. Это наиболее важные количественные параметры. Риск проекта (R) является, вообще говоря, сложной агрегированной характеристикой, в определении которой могут использоваться как количественные данные, так и качественные оценки экспертов. Тонкости в [1]. В нашем простом примере примем, что в итоге риск каким-либо способом оценивается в интервале от 0 до 1.

Численные значения параметров для нашего примера представлены в табл. 1.

Таблица 1.

Параметры сравниваемых проектов

Номер проекта	IRR, %	NPV, $тыс	PI	PB, месяцы	R,
1	25	2500	0.70	18	0.25
2	40	4000	0.85	48	0.60
3	32	3800	0.75	24	0.30
4	37	3000-	0.80	36	0.50

Теперь можно постоить функции желательности критериев. В меню (рис.3) следует выбрать подходящий тип функции и задать соответсявующие опорные точки (x1-x4).

Рис.3. Типы функций желательности частных критериев.


Опорные точки могут быть заданы на основе экспертных оценок, анализа состояния дел в отрасли, на основании строгих (например, банковских) нормативов и т.д. Поскольку в нашем примере нужно всего-лишь выбрать лучший из четырех проктов, поступаем проще. Например, наихудшее среди всех проектов значение NPV равно 2500, наилучшее 4000. Поэтому (рис.4) принимаем x1=2000 (меньше 2500, поскольку мы не хотим сразу отвергать проект № 1), x2=4000 и , попросту, для определенности x3=4000. Аналогично, интерактивным образом, строим остальные функции желательности (рис.4).




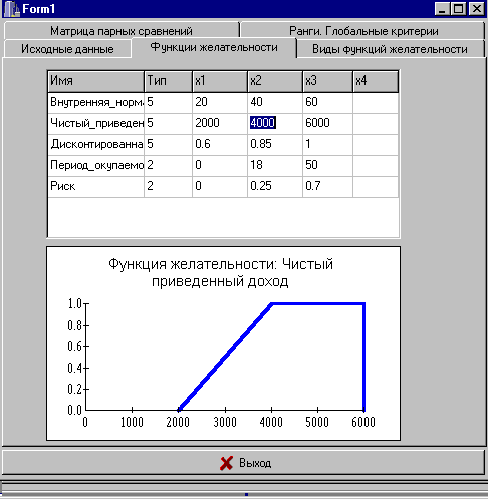
Рис. 4. Построение функций желательности частных критериев.

3. Определение коэффициентов относительной важности частных критериев

Существенные методические проблемы возникают при ранжировке большого количества критериев на основе мнений экспертов. Выше уже указывалось на ограниченные возможности человека при оценке многокритериальной ситуации. Однако, при сравнении двух альтернатив он обычно способен адекватно определить, у какой из них рассматриваемый признак (важность) выражен сильнее, а в ряде случаев - и грубо оценить (вербально), насколько велика разница между наблюдаемыми у двух альтернатив значениями [8]. Поэтому разработанная нами методика ранжировки критериев обеспечивает получение количественных значений коэффициентов относительной значимости на основе их попарного сравнения, выраженного в вербальной форме. Основой методики является построение матрицы лингвистических парных сравнений, предложенной Т. Саати [8]. Способ ее заполнения для нашего примера показан на рис. 5.





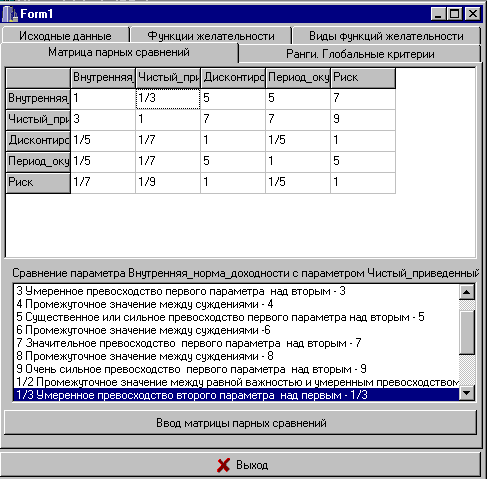
Рис. 5. Формирование матрицы парных сравнений.


Как видно из рис. 5, используется только 9 базовых словесных оценок. Последнее не случайно и связано с тем, что в естественных языках большинства народов используются также не более 9 лингвистических градаций значимости. Формулировки оценок могут быть иными, но число их практически постоянно- таковы особенности нашего мышления [9] . Словесным оценкам парной важности поставлены в соответствие числа натурального ряда. Это понятно, иначе как же проводить расчеты рангов. Однако числа на рис . 5 приведены исключительно из дидактических соображений. На практике не рекомендуем даже просто показывать экспертам какие –либо числа. Пусть оценивают на основе лингвистической шкалы.. Дело в том, что если предложить группе специалистом оценить известные им объекты, то вербальные оценки окажутся весьма близкими. Иначе и быть не может: Люди учились по одним и тем же учебникам, читают одни и те же статьи, работают в общей для них отрасли. Однако, если удастся уговорить их использовать для оценок цифры (только за очень отдельные деньги: цифры никто не любит) , то никакого единодушия уже не будет [10 ]. Дело в том, что “в начале было слово”, цифры появились значительно позже. За микроскопический в историческом масштабе период времени (всего несколько тысячелетий) люди просто не научились как следует пользоваться числами. И, слава Богу, до сих пор думаем мы словами, а не цифрами и даже упорно стараемся научит этому фокусу компьютеры.

Поскольку было обещано не раздражать читателя математикой укажем только, что итоговые ранги критериев из матрицы парных сравнений лучше всего получаются при использовании методов нелинейного программирования. Подробности в [11,12 ].

4. Формирование обобщенного показателя качества проекта

Итак мы имеем частные критерии, их ранги. Хорошо еще, что нашем примере имеем только пять критериев, а если –55, как в реальности. Задача оценки проекта выглядит пока не намного проще, чем в начале статьи. Для решения проблемы необходимо выработать способы агрегирования всей

этой разнородной информации в некоторые итоговые количественные оценки. В итоге нужно получить одно число- значение обобщенного показателя качества проекта. Далее немного математики, иначе не будет ясно о чем идет речь.

Пусть m1(x1),m2(x2),...,mn(xn) - функции желательности частных критериев качества проекта; {xi}, i=1,...,n - количественные и качественные показатели качества проекта; а1,...,an - коэффициенты относительной важности критериев (ранги).

В литературе [12-15] наиболее часто встречаются следующие варианты построения свертки неравнозначимых частных критериев в обобщенный показатель:


DD1 = min ( m1(x1)^a1, m2(x2)^a2 ,..., mn(xn)^an); DD2 =  ( ai *mi(xi) ) ;

DD3 =  mi(xi)^ai ; DD4 = min ( a1*m1(x1), a2*m2(x2),..., an*mn(xn)).


Существуют различные мнения о сравнительной эффективности приведенных способов формирования обобщенного показателя. Варианты DD2 и DD3 обладают свойством компенсации малых значений одних критериев за счет других, что не всегда желательно.

Варианты DD1 и DD4 от этого недостатка свободны, но приводят к очень жесткой оценке ситуации, в связи с чем их иногда называют критериями максимального пессимизма. Более строгую оценку относительной предпочтительности вариантов DD1-DD4, можно провести следующим образом.

Предположим, что мы рассматриваем более общую задачу- задачу оптимизации. При этом целью является отыскание таких значений показателей {xi}опт , i=1,...,n , которые максимизируют выбранный обобщенный показатель качества проекта, например DD1:


{x1,...,xn}опт = arg( max DD1(x1,...,xn)).


В сущности, ставится задача отыскания параметров некого оптимального для заданных критериев и ограничений проекта.

Следует отметить, что ввиду антагонистичности частных критериев, решение этой задачи далеко не тривиально и может быть найдено лишь в компромиссной форме.

В работе [12] со строгим доказательством соответствующих теорем показано, что на практике использование сверток типа DD2-DD4 для решения рассмотренной оптимизационной задачи приводит к абсурдным результатам и единственным разумным вариантом является DD1. Однако практика всегда богаче теории. Поэтому в задачах оценки проектов целесообразно использовать одновременно три первых способа формирования обобщенного критерия (рис.6). Все они обеспечивают получение численных оценок качества проекта в интервале от 0 (совсем непригодный проект) до 1 (проект-мечта инвестора). Качественное совпадение итоговых результатов, полученных по эти критериям, повышает доверие в к выводам, несовпадение будет способствовать полезным дополнительным размышлениям.

Ясно, чем выше значение глобального критерия, тем предпочтительнее анализируемый праект. Из рис. 6 следут, что в рассматриваемой примере наилучщим следун признать третий проект, поскольку именно для этого проекта получены максимильные значения глобальных критериев для двух разных вариантов их построения.





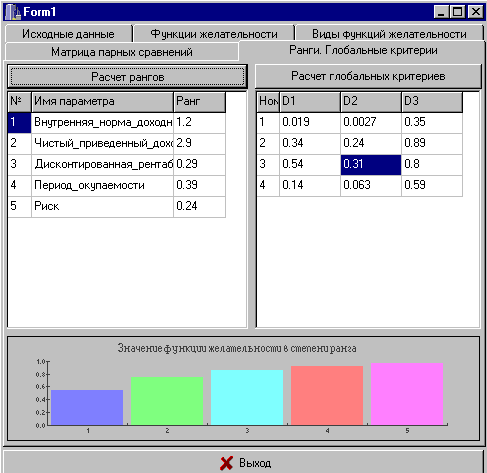
Рис. 6. Итоговые результаты.


Разработанная методика позволяет не только одним числом (но на строго научной основе) оценить качество проекта, но как видно из рис. 6, выяснить какой вклад в итоговую оценку вносит каждый из частных критериев вместе со своим рангом.

В заключение отметим, что на практике задачи оценки качества инвестиционных (и прочих) проектов являются не только многокритериальными, но и многоуровневыми (иерархическими). Наша методика позволяет решать и такие задачи. Но об этом в следующей статье.


СПИСОК ЛИТЕРАТУРЫ

1. Севастьянов П.В., Севастьянов Д.П. Оценка финансовых параметров и риска инвестиций с позиций теории нечетких множеств. Надежные программы, 1997, № 1, с. 10-18.
   
2. Севастьянов П.В, Севастьянов Д.В. Извлечение максимума. Риск., 1998, №
   

5-6, с. 71-75.

3. Dymova L.,Sevastjanov D., Sevastjanov P. Application of fuzzy sets theory methods for the evaluation of investment efficiency parameters// Fuzzy economic review. 2000, Vol. V, N 1, P. 34-48 .

4. Нехорошева Л.Н. Проблемы формирования инновационной структуры.

//Тезисы международной конф. “Инновационные центры Беларуси: общие подходы, текущая ситуация и перспективы развития. Могилев, 1995 г.- с. 200-216.

5. Миллер Дж. Магическое число семь. плюс или минус два. О некоторых пределах нашей способности перерабатывать информацию// Инженерная психология.- М: Прогресс,1964.- с. 192- 225.

6. Zadeh L.A. Fuzzy sets//Inf. Contr.-1965.-vol. 8.-p.338-358.

7. Орловский С.А. Проблемы принятия решений при нечеткой исходной информации.- М: Наука, 1981.-208с.
   
8. Saaty T. A Scaling Method for Priorities in Hierarhical Structures//J. of Mathematical Psychology.-1977.-vol. 15.-No 3.-p.234-281.
   

9. Борисов.А.Н., Корнеева Г.В. Лингвистический подход к построению моделей принятия решений в условиях неопределенности//Методы принятия решений в условиях неопределенности.- Рига, 1980., No 7.- с. 4-6

10. Zollo G., Iandoli L., Cannavacciuolo A. The performance requirements analysis with fuzzy logic// Fuzzy economic review. 1999, Vol. IV, N 1, P. 35-69.

11. Chu A., Kalaba R.,. Springarn R. A Comparison of Two Methods for Determining the weight of Belonging to Fuzzy Sets//J. of Optimisation theory and applications.-1979.-vol. 27.-No 4.- p. 531-538.

12..Севастьянов П.В, Туманов Н.В.. Многокритериальная идентификация и оптимизация технологических процессов.-Мн.: Навука i тэхнiка, 1990.- 224с.

13. Dubois, H. Prade. Fuzzy sets and systems. Theory and applications.- New York: Akad. Press,1980.-344p.

14. Yager R. Multiple objectiv decision-making using fuzzy sets//Int. J. Man-Mach. Stud.-1979.- vol.9.-No 4.-p. 375-382.

15.Bellman R., Zadeh L.A. Decision- making in fuzzy invironment//Management Science. - 1970.- vol.17.- p. 141-164.