Статистика вопросов за два года вопросы повторяемость

Вид материала

Документы

Содержание Дифференциальный и интегральный законы распределения. Дифференциальный закон Мера положения и мера рассеивания (численно-вероятностные характеристики) Мера рассеивания Входной контроль

Подобный материал:

• Вопросы к зачету по курсу «Финансово-банковская статистика», 27.1kb.
• Контрольные вопросы по дисциплине Статистика коммерческой деятельности в целом (вопросы, 33.99kb.
• Открытая конференция ап кит. 23 мая 2002г, 18.87kb.
• Вопросы по программе курса «Экономика предприятия», 28.16kb.
• Контрольные вопросы по дисциплине «Юридическая статистика», 180.99kb.
• + [5] вопросов мкм + [3] вопросов чгк + [61] вопросы + [1] вопросы (что? где? когда?), 339.65kb.
• Экзаменационные вопросы по дисциплине «Статистика», 22.97kb.
• Экзаменационные вопросы по дисциплине «Статистика», 46.14kb.
• Курсовая работа по дисциплине «Статистика», 354.39kb.
• «Ранетки», 67.54kb.

Дифференциальный и интегральный законы распределения.

Случайной величиной называется переменная, которая может принимать в зависимости от исходов испытания те или иные случайные значения.

Если при этом переменная принимает последовательные различные значения и известны вероятности каждого из них; то она называется дискретной случайной величиной.

Функция распределения плотности вероятности дискретного закона представляет собой ряд распределения, ставящий в соответствие значения дискретной случайной величины и вероятности появления этих значений.

Функция распределения вероятностей, или интегральный закон распределения вероятностей, показывает вероятность попадания значений случайной величины X в интервал




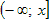
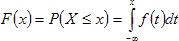
где f - функция распределения плотности вероятности, X - одномерная случайная величина, x - граничное значение одномерной случайной величины, F - интегральный закон распределения случайной величины.


Дифференциальный закон, или функция распределения плотности вероятности непрерывного закона, является непрерывной функцией и определяется как производная от интегрального закона распределения:




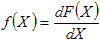
Мера положения и мера рассеивания (численно-вероятностные характеристики)


Мера положения – это математическое ожидание (1й момент).

М. о. характеризует расположение значений случайной величины

а) для дискретной случайной величины:

,

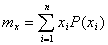где n – число возможных значений случайной величины x;

б) для непрерывной случайной величины:

,

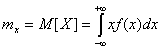где 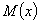– характеристика теоретического распределения случайной величины.

.

Мера рассеивания – среднее квадратичное отклонение и дисперсия (2й момент). Характеристикой рассеяния значений случайной величины около центра группирования 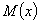является дисперсия. Однако чаще используют не саму дисперсию, а положительный квадратный корень из нее, называемый средним квадратичным отклонением:

а) дисперсия и среднее квадратичное отклонение дискретной случайной величины

;

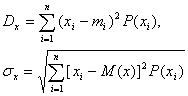б) дисперсия и среднее квадратичное отклонение непрерывной случайной величины

.


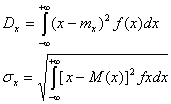Закон нормального распределения (закон Гаусса)

Плотность вероятности или дифференциальная функция распределения:

,

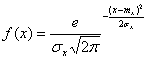где 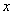– переменная случайная величина; 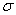x – среднее квадратичное отклонение 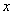от ;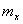

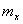– математическое ожидание величины .

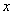Функция или интегральный закон нормального распределения в общем виде можно записать:

.

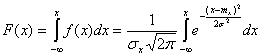Входной контроль

В процессе изготовления проводят с целью:

1. Проверки на соответствие ТУ ЭРЭ и сб.ед. (комплектующие).
   
2. Отбраковка изделий и ЭРЭ с дефектами.
   
3. Выявление скрытых дефектов (если эта задача может быть решена).
   

Дефекты, обнаруживаемые при входном контроле можно классифицировать следующим образом:

1. Дефекты комплектации (перепутывание типов, номиналов и т.д.);
   
2. Дефекты, связанные с низким качеством упаковки (трещины, сколы и т.д);
   
3. Дефекты по внешнему виду;
   
4. Отказы при проверке на работоспособность.
   
5. Отказы на проверку дестабилизирующих факторов.
   

По охвату:

1. Выборочный
   
2. Сплошной
   

Выборочный

1. Одноступенчатый (однократной выборки)
   
2. Двухступенчатый (двухкратной выборки)
   
3. Многоступенчатый
   
4. Последовательный
   

Одноступенчатый

Заключается в том, что при входном контроле случайным образом берётся выборка, подвергается статистическим испытаниям (проверка), полученные результаты обрабатываются статистически. По анализу полученных результатов делается вывод о приёмке либо браковке генеральной партии.

Двухступенчатый

Берётся первая выборка, подвергается статистическим испытаниям. По анализам полученных результатов предлагается взять вторую выборку.

Многоступенчатый

Берётся ряд выборок, подвергаются статистическим испытаниям и по результатам анализа делается вывод о приёмке или браковке всей генеральной партии.

Последовательный

Берутся выборки через определённый интервал времени. Каждая выборка подвергается статистическим испытаниям и по результатам делается вывод о годности или браковки генеральной партии.