Оптимизация режимов работы синхронных двигателей в узлах нагрузки систем электроснабжения компрессорных станций магистральных газопроводов
| Вид материала | Автореферат |
- Схемы возможного импортозамещения контроллеров в системах асу тп компрессорных станций, 2357.31kb.
- Программа подготовки: Оптимизация структур, параметров и режимов систем электроснабжения, 149.78kb.
- Программа подготовки: Оптимизация структур, параметров и режимов систем электроснабжения, 173.18kb.
- Программа подготовки: Оптимизация структур, параметров и режимов систем электроснабжения, 146.95kb.
- Магистерская программа: Оптимизация структур, параметров и режимов систем электроснабжения, 134.24kb.
- Программа подготовки: Оптимизация структур, параметров и режимов систем электроснабжения, 109.45kb.
- Программа подготовки: Оптимизация структур, параметров и режимов систем электроснабжения, 145.75kb.
- Оптимизация технологий строительства для обеспечения нормативных требований к сварным, 358.73kb.
- Программа вступительных испытаний для поступающих в магистратуру по направлению 140400, 76.6kb.
- Повышение устойчивости синхронных генераторов в системе внутризаводского электроснабжения, 247.3kb.
На правах рукописи
ГОЛУБОВСКИЙ Александр Владимирович
ОПТИМИЗАЦИЯ РЕЖИМОВ РАБОТЫ СИНХРОННЫХ ДВИГАТЕЛЕЙ
В УЗЛАХ НАГРУЗКИ СИСТЕМ ЭЛЕКТРОСНАБЖЕНИЯ КОМПРЕССОРНЫХ СТАНЦИЙ МАГИСТРАЛЬНЫХ ГАЗОПРОВОДОВ
Специальность 05.09.03 – Электротехнические комплексы и системы
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата технических наук
Самара – 2008
Работа выполнена в Государственном образовательном учреждении высшего профессионального образования «Самарский государственный технический университет» на кафедре «Электропривод и промышленная автоматика»
| Научный руководитель | доктор технических наук, профессорРассказов Федор Николаевич |
| Официальные оппоненты: | доктор технических наук, профессор Абакумов Александр Михайлович кандидат технических наук Горюнов Олег Алексеевич |
| Ведущая организация | Российский государственный университет нефти и газа им. И.М. Губкина, г. Москва |
Защита состоится «26» июня 2008 года в 1100 часов на заседании диссертационного совета Д 212.217.04 при Государственном образовательном учреждении высшего профессионального образования "Самарский государственный технический университет" по адресу: 443100, г. Самара, ул. Молодогвардейская, 244, ауд. 200.
С диссертацией можно ознакомиться в научной библиотеке СамГТУ, а с авторефератом диссертации на официальном сайте: www.samgtu.ru/disertac/d4.php
Отзывы на автореферат (в двух экземплярах, заверенные печатью) просим направлять по адресу: 443100, г. Самара, ул. Молодогвардейская, 244, СамГТУ, Главный корпус, учёному секретарю диссертационного совета Д 212.217.04 ; факс (8462) 278-44-00; E-mail: aees@samgtu.ru
Автореферат разослан «__» мая 2008 г.
Ученый секретарь
диссертационного совета, к.т.н., доцент Е.А. Кротков
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы. Повышение энергетической эффективности и надёжности электропривода компрессорных станций (КС) магистральных газопроводов (МГ) связано с оптимизацией систем автоматического регулирования возбуждения (АРВ) синхронных двигателей (СД) газоперекачивающих агрегатов (ГПА). Задачи автоматического регулирования возбуждения синхронных машин и оптимизации режимов узлов нагрузки систем электроснабжения отражены в работах многих авторов: Д.П. Петелина, И.Д. Сыромятникова, Б.Н. Абрамовича, И.Д. Лищенко, В.А. Веникова, Ф.Г. Гусейнова, Н.И. Воропая и других учёных. В работах Н.Д. Абдуллаева, В.Ф. Шумилова, Г.Р. Шварца и др. рассмотрены вопросы синтеза оптимальных систем АРВ при случайных изменениях нагрузки. Тем не менее, задача оптимизации систем АРВ СД, синтеза оптимальных и гарантирующих АРВ с учётом специфики приложения случайных возмущающих воздействий остаются открытыми. Также актуальным является построение цифровых возбудителей СД ГПА.
Цель и задачи исследований. Основной целью работы является повышение эффективности функционирования, устойчивости узлов нагрузки систем электроснабжения газоперекачивающих агрегатов компрессорных станций магистральных газопроводов с синхронными электродвигателями путём оптимизации алгоритмов автоматического регулирования возбуждения.
Исходя из указанной цели, в диссертационной работе решаются следующие научные и практические задачи:
1. Формирование математической модели синхронного электропривода ГПА.
2. Разработка методики оптимизации режимов работы СД ГПА.
3. Исследование гарантирующих управлений возбуждением СД ГПА.
4. Определение областей динамической устойчивости СД ГПА при различных законах регулирования возбуждения.
5. Практическая реализация алгоритмов оптимальных и гарантирующих АРВ в цифровых системах регулирования возбуждения.
Основные методы научных исследований. При выполнении работы использовались основные положения теории электропривода, аппарат передаточных функций и метод пространства состояний, теория оптимального управления, теория случайных процессов, методы синтеза оптимального регулятора, алгоритмы математического моделирования на ЭВМ и др.
Научная новизна работы.
1. Разработана математическая модель синхронного электропривода ГПА с учётом вероятностных характеристик регулируемых координат.
2. С использованием метода пространства состояний разработана методика синтеза оптимальных систем АРВ при случайных возмущениях.
3. Поставлена и решена задача синтеза гарантирующих управлений СД ГПА.
4. Разработана вычислительная процедура для определения областей динамической устойчивости СД ГПА при различных законах регулирования возбуждения.
Практическая ценность.
1. Разработаны инженерные методики синтеза оптимальных и гарантирующих систем АРВ при возмущениях случайного характера.
2. Получены оптимальный регулятор напряжения и гарантирующий регулятор внутреннего угла СД, которые реализованы в цифровых системах регулирования возбуждения.
3. Показана практическая реализуемость этих регуляторов, эффективность оптимальных систем регулирования возбуждения по сравнению с традиционными.
Достоверность полученных результатов определяется корректным использованием соответствующего математического аппарата, модельных исследований, и подтверждается удовлетворительным совпадением результатов расчёта и экспериментальных данных.
Реализация результатов работы. Поставленные в диссертационной работе задачи решались в соответствии с «Концепцией энергосбережения в ОАО «Газпром» в 2001-2010 гг.». Цифровые системы регулирования возбуждения внедрены на ряде ЛПУ МГ ООО «Волготрансгаз». Проведена замена аналоговых возбудителей ВТЕ 320/230 на цифровые ВТЦ 320/230 в четырёх из шести филиалов с ЭП ГПА. Установлены ВТЦ 320/230 в: Починовском ЛПУ МГ, Сееповском ЛПУ МГ, Волжском ЛПУ МГ, Чебоксарском ЛПУ МГ. Замена возбудителей производилась согласно договора представителями ОАО «НИПОМ» г. Дзержинск совместно КТИ ВТ СО РАН г. Новосибирска и Починовского филиала ООО «Волготрансгаз».
Разработанные в диссертации методики также внедрены в учебный процесс Самарского государственного технического университета и используются при подготовке специалистов предприятий ОАО «Газпром» в Сервис-центре САМГТУ МИЭИ.
Основные положения, выносимые на защиту.
1. Математическая модель синхронного электропривода ГПА с учётом вероятностных характеристик регулируемых координат.
2. Методика синтеза оптимальных систем АРВ СД ГПА при случайных возмущениях.
3. Алгоритмы синтеза гарантирующих управлений возбуждением СД ГПА.
4. Методика определения областей динамической устойчивости СД ГПА при различных законах регулирования возбуждения.
5. Конкретная реализация микропроцессорной системы регулирования возбуждения СД.
Апробация работы. Основные положения и результаты работы докладывались и были одобрены на отраслевой конференции «Новые техники и технологии в энергетике ОАО «Газпром» (г. Москва, 1999 г), на заседании НТС ОАО «Газпром» по теме «Энергосбережение и энергосберегающие технологии в энергетика газовой промышленности» (г. Москва, 2000 г), на заседании НТС ОАО «Газпром» по теме «Концепция применения электропривода газоперекачивающих агрегатов» (г. Нижний Новгород, 2002 г), на заседании НТС ОАО «Газпром» по теме «Обеспечение надёжности работы энергетического оборудования» (г. Нижний Новгород, 2006 г), отраслевой конференции «Энергетическое оборудование нового поколения для ОАО «Газпром» (г. С.-Петербург, 2004 г), отраслевых конференциях ОАО «НИПОМ» (г. Дзержинск, 2001-2007 гг), отраслевых конференцях в Сервис-центр САМГТУ МИЭИ (г. Самара, 2001-2008 гг.), расширенных заседаниях НТС кафедры «Электропривод и промышленная автоматика» СамГТУ (г. Самара, 2003-2008 гг), на Всероссийской научно-технической конференции «Проблемы электротехники, электроэнергетики, электротехнологии» (г. Тольятти, 2004 г), Второй Всероссийской научной конференции «Математическое моделирование и краевые задачи» (г. Самара, 2005 г).
Публикации. По теме диссертации опубликовано 10 печатных работ, в том числе 3 – в изданиях, включённых в перечень ведущих рецензируемых научных журналов и изданий, рекомендованных ВАК РФ [1-3].
Объем и структура и работы. Диссертация состоит из введения, пяти глав, заключения, списка использованной литературы, приложения и содержит 164 страницы основного текста, включая 52 рисунка. Список литературы включает 122 наименования. Общий объём работы 183 страницы машинописного текста.
СОДЕРЖАНИЕ РАБОТЫ
Во введении обосновывается актуальность темы диссертационной работы, сформулированы цели и задачи исследования, показаны научная новизна и практическая значимость полученных результатов, сформулированы основные положения, выносимые на защиту.
Краткий обзор работ проведён в двух направлениях:
1. По алгоритмам и системам регулирования возбуждения синхронных машин.
2. По методам синтеза оптимального регулятора при случайных возмущениях.
Обзор работ по первому направлению говорит о том, что проблеме автоматического регулирования возбуждения СД целью оптимизации режимов его работы и работы узлов нагрузки СЭС посвящено значительное количество исследований, среди которых следует выделить фундаментальные работы И.А. Сыромятникова, Д.П. Петелина, И.А. Глебова, А.И. Лишенко, Б.Н. Абрамовича, А.А. Круглого и др. Вопросами идентификации и управления режимами регулируемых узлов нагрузки энергосистем посвящены работы В.А. Веникова, Ф.Г. Гусейнова, Н.И. Воропая, Ю.Е. Гуревича, Л.Е. Либовой, З.А. Хачатрян и др. В известных исследованиях подробно рассмотрены вопросы автоматического управления возбуждением СД с точки зрения повышения их динамической устойчивости и улучшения технико-экономических показателей питающей сети, получены математические модели СД как объекта управления, изучены рациональные законы регулирования возбуждения СД, учитывающие разнообразие условий их работы, рассмотрены особенности исследования динамики систем АРВ, отражающие существенные нелинейности, присущие объекту управления, дано описание и сравнительный анализ различных схем систем управления возбуждением СД.
Задачи синтеза оптимальных систем АРВ при случайных изменениях нагрузки, отражены в работах Н.Д. Абдуллаева, В.Ф. Шумилова, Г.Р. Шварца. При этом были использованы частотные методы синтеза оптимальных систем. Тем не менее задачи оптимизации систем АРВ СД, синтеза оптимальных и гарантирующих АРВ в пространстве состояний с учётом специфики случайных возмущающих воздействий остаются актуальными.
Обзор работ по второму направлению говорит о том, что при синтезе систем управления до недавнего времени игнорировался случайный характер возмущающих сил, что не имело логического обоснования. Традиционными методами синтезировались системы с хорошим протеканием переходных процессов (быстрым затуханием, малой колебательностью и перерегулированием и т.п.) при детерминированных, чаще всего скачкообразных, воздействиях. В реальных условиях работы такие системы управления не обеспечивали требуемых показателей качества. Поэтому в настоящее время большое внимание уделяется методам синтеза систем управления при наличии возмущающих сил, имеющих вероятностный характер. При этом для широкого класса объектов управления критерий оптимальности может быть представлен в виде среднеквадратичной формы от фазовых координат системы и управляющих воздействий. Указанные подходы к синтезу систем управления базируются на корреляционной и спектральной теории случайных процессов, разработанных в середине 20 века на основе работ А.Н. Колмогорова и Н.В. Винера.
Определился ряд методов, позволяющих решать задачу оптимального синтеза линейных систем управления с учетом случайных возмущений. Фундаментальные результаты получены в трудах B.C. Пугачева, Н.А. Лившица, Р.А. Полуэктова, В.Б. Ларина, В.Н. Сунцева, К.И. Науменко, а также Р. Калмана, Р. Бьюси, Дж. Кушнера, М. Уонема, других советских и зарубежных ученых. При этом синтез оптимальных регуляторов производится или в частотной области - Винеровская фильтрация, или во временной области - в области пространства состояний, что связано с теорией аналитического конструирования регуляторов A.M. Летова, теорией оптимальной фильтрации Р. Калмана.
Однако, при конкретной реализации этих методов возникают проблемы, связанные с определением весовых коэффициентов среднеквадратичного критерия качества управления, учета ограничений на модуль управляющего воздействия, сохранением устойчивости при неизбежных на практике вариациях параметров объекта управления и статистических характеристик возмущающих воздействий, проблема реализуемости регуляторов без "идеальных" дифференцирующих звеньев, хорошей стабильности системы, определения эффективности измерения дополнительных фазовых координат системы и др. Решению указанных проблем посвящен цикл работ, выполненных в Государственном Санкт-Петербургском университете под руководством профессора Ю.П. Петрова.
Применение этих методов при оптимизации систем управления электротехническими комплексами отражено в работах Н.Д. Абдуллаева, В.Ф Шумилова, Н.И. Шумиловой, Ф.Н. Рассказова, А.М. Абакумова и др.
В настоящей диссертационной работе используются алгоритмы синтеза оптимальных систем управления, разработанные М.А. Галактионовым, Ф.Н. Рассказовым в научной школе профессора Ю.П. Петрова.
В первой главе разработаны математические модели синхронного электропривода газоперекачивающих агрегатов с учётом вероятностных характеристик возмущающих воздействий. На рис. 1 представлена схема узла нагрузки.
Рис. 1 Схема замещения узла нагрузки с синхронными двигателями ГПА
VC - напряжение в периферийной точке электрической системы; ZC - эквивалентное сопротивление питающей линии и трансформаторов; V - напряжение в узле нагрузки (напряжение питания синхронных двигателей).
Наиболее полной математической моделью синхронного двигателя является система уравнений Парка-Горева. Данная система уравнений является нелинейной, где независимыми переменными являются входная величина VB- напряжение возбуждения, возмущающее воздействие MН - момент на валу двигателя. Используя принцип линеаризации, переходя к изображению по Лапласу в системе уравнений, можно получить передаточные функции СД по управляющему и возмущающему воздействиям
(1)При этом указанные передаточные функции, полученные для полной системы уравнений Парка-Горева будут иметь 7 порядок. В большинстве случаев при анализе переходных процессов в СД можно пренебречь электромагнитными переходными процессами в статорной цепи, а также не учитывать активное сопротивление обмотки статора, величина которого значительно меньше индуктивного. С учётом указанных допущений передаточные функции (1) будут иметь 3-й порядок.
Синхронный двигатель приводит во вращение центробежный нагнетатель (ЦН) газоперекачивающего агрегата. При этом нагрузка ЦН зависит от скорости. В статических режимах характеристика нагрузки является вентиляторной. Проведена линеаризация нелинейной характеристики ЦН. Получена структурная схема СД с учетом характеристики ЦН и внутреннего контура регулирования тока возбуждения, рис 2.
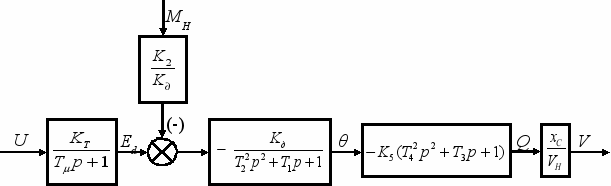
Рис. 2 Структурная схема СД
U – управляющее воздействие, Ed – э.д.с. обмотки статора, θ – внутренний угол, Q – реактивная мощность, V – напряжение в узле
Параметры передаточных функций определяются через паспортные данные СД и характеристику ЦН. На основании структурной схемы получена система уравнений состояния синхронного электропривода в виде
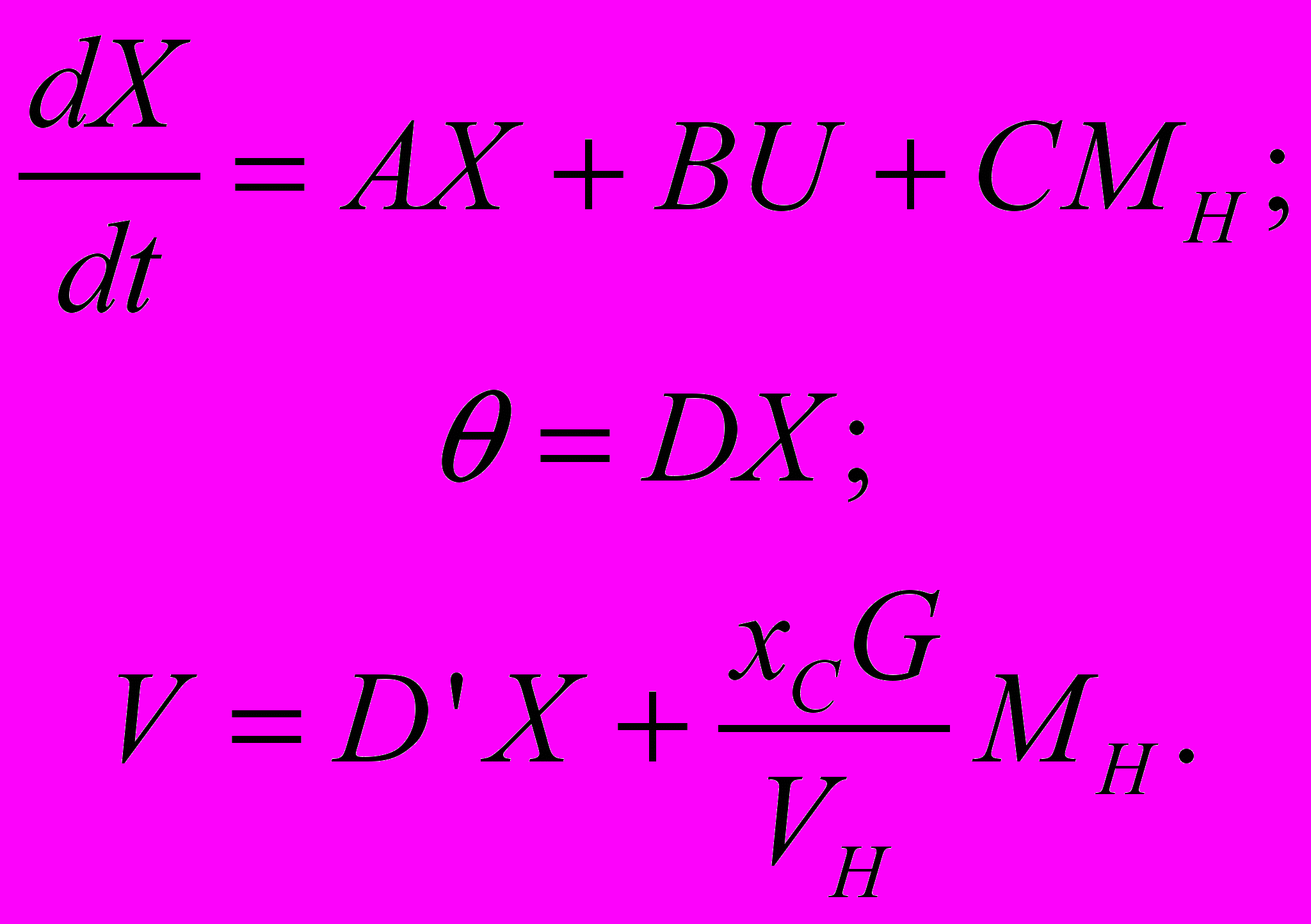(2)Определены матрицы A, B, C, D, D', G.
Электропривод ГПА работает в условиях многочисленных случайных возмущений, таких как изменение нагрузки на валу, колебания напряжения в системе энергоснабжения, изменение мощности смежных электроприемников, подключенных к узлу нагрузки и т.д. В большинстве случаев возмущающие воздействия недоступны измерению и, следовательно, нельзя снять их реализации и тем самым рассчитать их вероятностные характеристики.
Измерению подлежит выходная, регулируемая координата объекта управления, т.е. напряжение в узле нагрузки V. В этом случае все возмущения приводятся к выходу объекта. При этом эквивалентное возмущающее воздействие φЭ = ΔV можно определить записав реализацию V в узле нагрузки в разомкнутой системе, т.е. при U = 0 (рис. 3). На рис. 4 приведена автокорреляционная функция случайного процесса изменения напряжения, а на рис. 5 – спектральная плотность мощности.
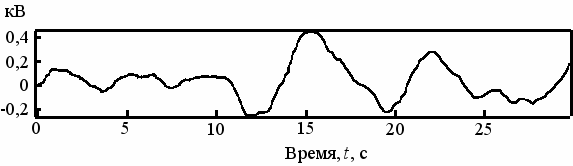
Рис. 3 Реализация изменения напряжения
Рис. 4 Автокорреляционная функция Рис. 5 Спектральная плотность мощности
В большинстве случаев корреляционная функция отклонения напряжения в узле нагрузки аппроксимируется выражением
; (3)и соответствующее уравнение формирующего фильтра для возмущающего воздействия будет иметь вид
(4)
где ξ – «белый шум».
Объединяя систему уравнений объекта управления (2) с системой уравнений формирующего фильтра (4), получим следующую систему матричных уравнений
(5)
(6)где Х0 = [XXФ]T – расширенный вектор переменных состояния,
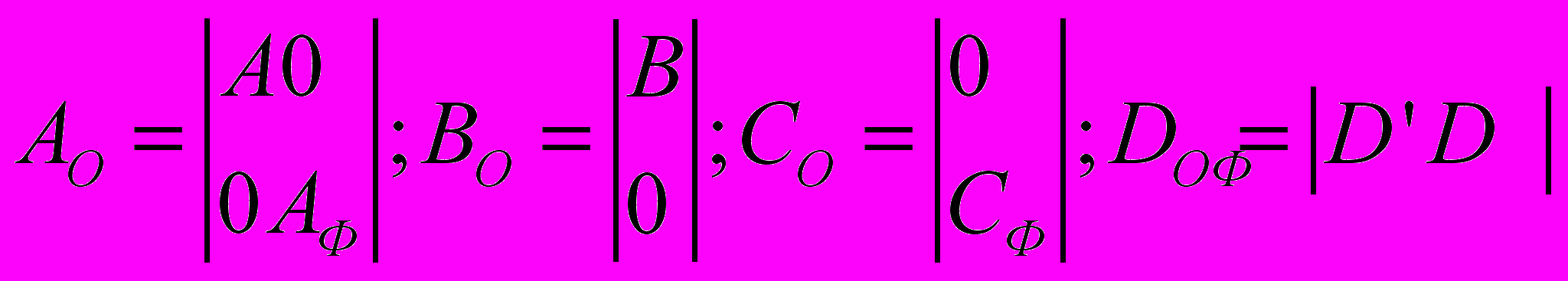– расширенные матрицы соответствующих размерностей. Уравнения (5),(6) являются нормальной формой записи системы стохастических уравнений синхронного электропривода.Во второй главе проведена оптимизация систем регулирования возбуждения синхронных двигателей с обратной связью по напряжению. При решении задач регулирования напряжения узла нагрузки целевая функция может быть представлена в виде приведенных затрат
(7)где К - капиталовложения при данном режиме работы; ЕН - нормативный коэффициент эффективности; а0- коэффициент эксплуатационных отчислений; И - затраты на возмещение потерь электроэнергии; У - ущерб от некачественной электроэнергии. Ущерб от некачественной электроэнергии является нелинейной функцией от отклонения напряжения. При этом определяющей будет являться квадратичная составляющая. Потери электроэнергии в сети также зависят от квадрата узловых напряжений. Поэтому, учитывая нормальный закон распределения отклонения напряжения у потребителей, за критерий оптимальности регулирования напряжения может быть взят средний квадрат
(8)Заметим, что на основании правила «трех сигма» будем также обеспечивать заданную малость отклонения напряжения |ΔV|. При синтезе оптимальных систем необходимо учитывать ограничение на управление, которое препятствует сведению к нулю критерия качества (8). Обычно задается ограничение на модуль управляющего воздействия
(9)Далее выполняется переход к ограничению на средний квадрат, мощность управляющего воздействия
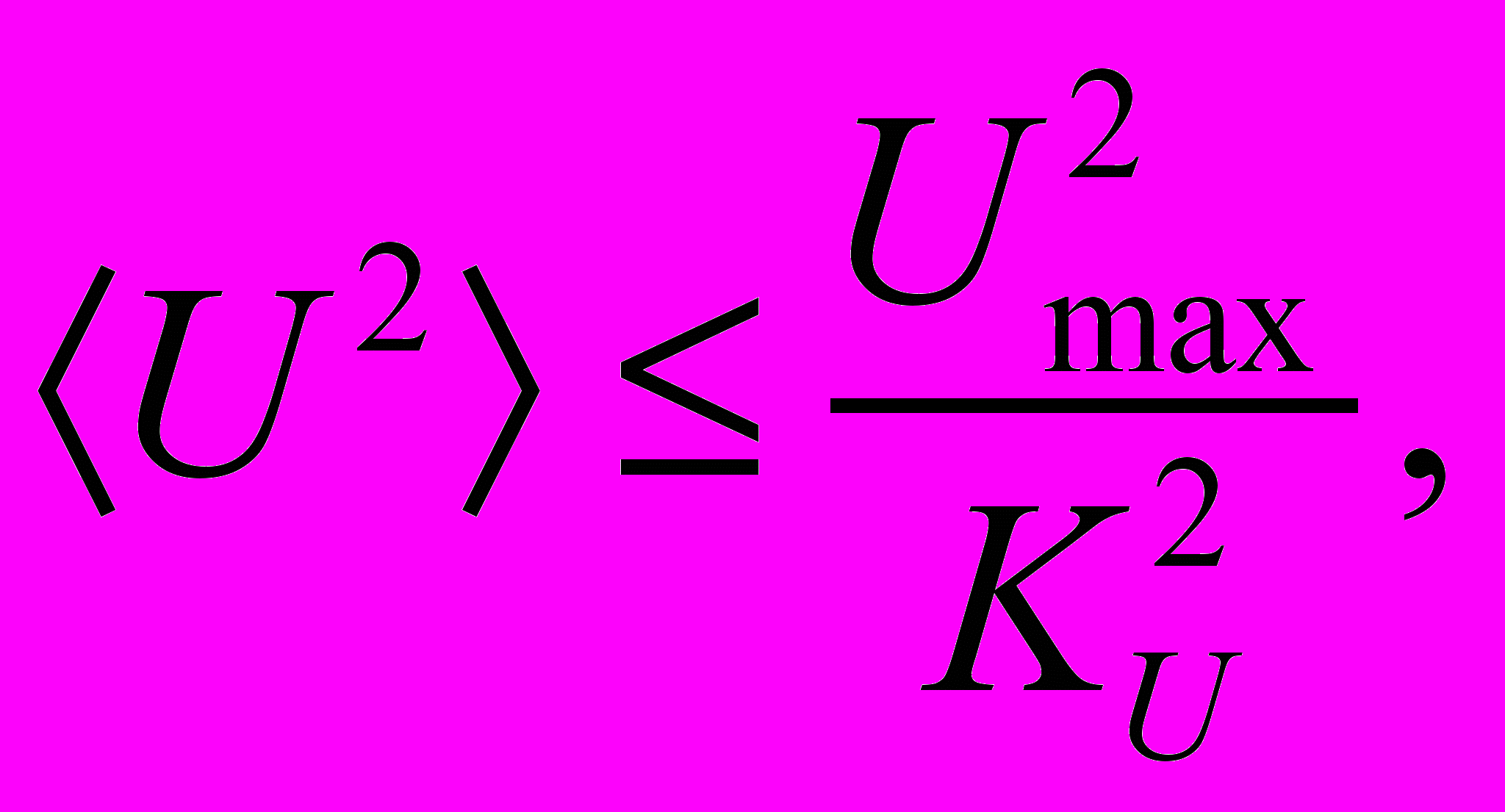(10)где для KU берется обоснованное значение KU = 1,645.
Ограничение (10) учитывается согласно решению изопериметрических задач вариационного исчисления путем дополнения функционала (8) мощностью управляющего воздействия
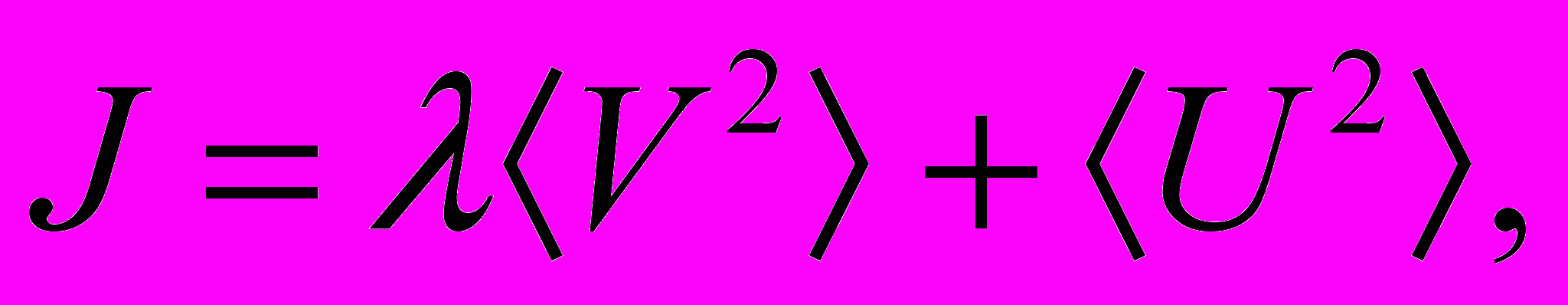(11)где
множитель Лагранжа, подлежащий в дальнейшем определению.С учетом (6) функционал (11) можно представить в следующем виде
(12)где
Далее проведён синтез оптимального регулятора напряжения узла нагрузки с использованием вероятностных характеристик регулируемой координаты. Задачу оптимального управления можно сформулировать следующим образом: для объекта управления (5), (6) требуется определить передаточную функцию оптимального регулятора, доставляющего минимум функционалу (12). Разработана методика синтеза оптимального регулятора. Продифференцируем (6) с учётом (5)
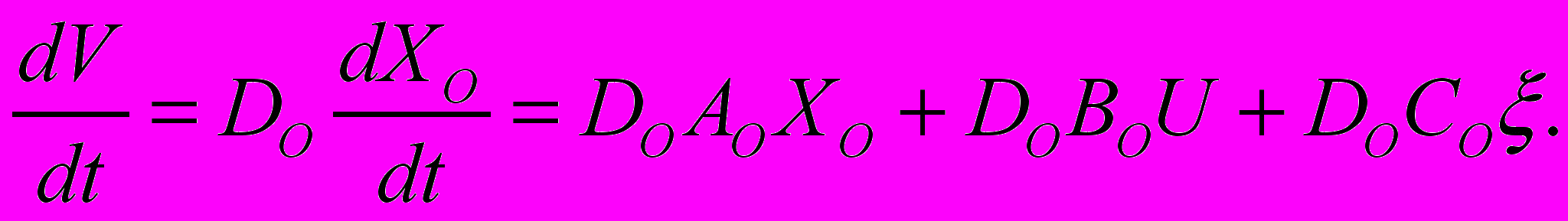(13)При этом DО,CО ≠ 0. Тогда задача синтеза оптимального регулятора, согласно теоремы разделения, будет состоять из определения оптимальных оценок вектора Х0 и самой задачи оптимального управления при среднеквадратичном критерии качества (12). Для этого введем обозначение в соотношении (13)
(14)тогда (13) примет следующий вид
(15)Оптимальная оценка вектора состояния системы
по V1 производится фильтром Калмана
(16)где N – матрица, полученная в результате решения уравнения Риккати.
Оптимальное управление, доставляющее минимум функционалу (12), имеет вид
(17)где К =
; М – квадратная матрица, являющаяся решением алгебраического уравнения РиккатиПереходя к изображению по Лапласу в выражениях (14),(16),(17), получим передаточную функцию оптимального регулятора
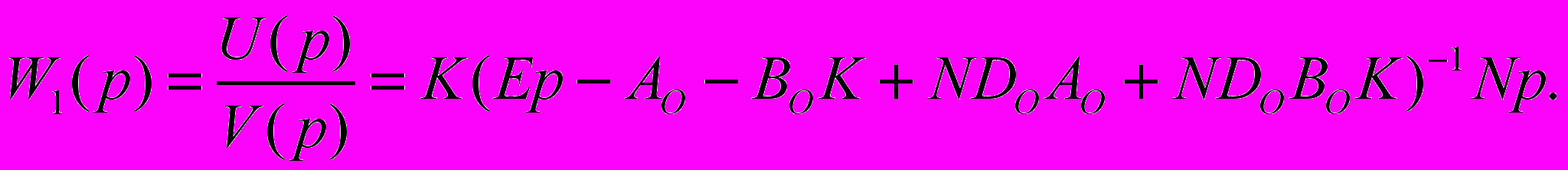(18)где Е – единичная матрица.
Здесь возможна модификация рассматриваемого алгоритма синтеза. В этом случае наряду с уравнением
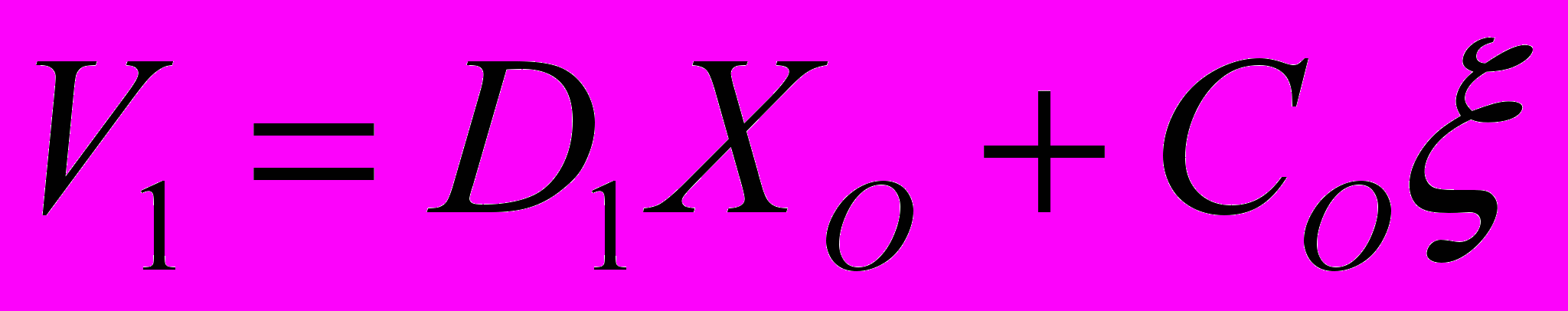используется незашумленное матричное уравнение (6) 
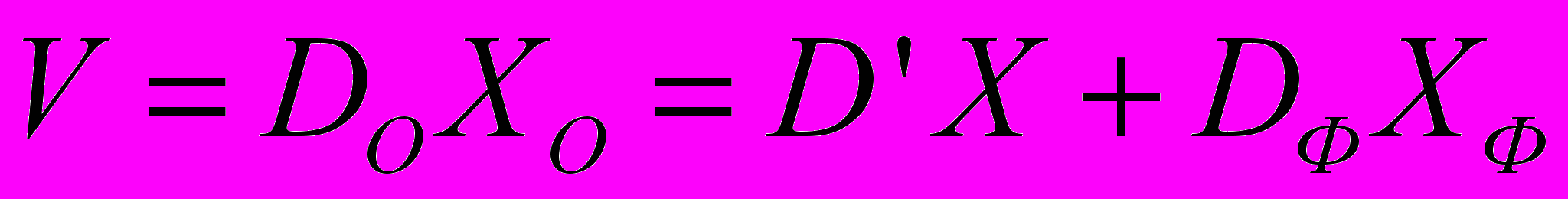.В этом случае передаточная функция оптимального регулятора напряжения узла нагрузки может быть представлено в виде
(19)Такой регулятор не содержит «идеальных» дифференцирующих звеньев, что обеспечивает его техническую реализацию и защищенность системы к помехам в каналах измерения. Показано, что система с регулятором (19) является стабильной, т.е., сохраняет устойчивость при сколь угодно малом отклонении действительных параметров от расчетных. Разработана процедура определения среднего квадрата отклонения напряжения в узле нагрузки, мощности управляющего воздействия, а также множителя Лагранжа λ.
Анализ реализаций отклонения напряжения в разомкнутой и замкнутой системе регулирования показывает, что использование оптимальных стохастических законов управления позволяет снизить среднеквадратичное отклонение напряжения в 4,5 раза. Это свидетельствует об эффективности разработанной методики синтеза оптимального регулятора. Дальнейшее уменьшение отклонения напряжения связано с повышением мощности управляющего воздействия. Отметим, что синтез оптимального регулятора напряжения проведён для центрированных случайных процессов (возмущающих воздействий), т.е. переменной составляющей. В результате реализуется быстрый канал регулирования напряжения. Однако возмущающее воздействие содержит и постоянную составляющую. Поэтому для обеспечения нулевой статической ошибки (придание астатизма системе регулирования) оптимальный регулятор (19) дополняется интегрирующим звеном (И регулятором) с небольшим коэффициентом передачи. В результате получим медленный канал регулирования напряжения.
Система автоматического регулирования возбуждения СД, замкнутая по напряжению узла нагрузки, предназначена не только для стабилизации напряжения, но также для обеспечения устойчивости синхронных режимов работы СД при действии возмущений. При этом возможная потеря устойчивости синхронного режима определяется величиной внутреннего угла θ. Поэтому для обеспечения требуемых запасов устойчивости синхронной машины необходимо обеспечить заданную величину внутреннего угла
(20)Учитывая нормальный закон распределения, переходим от ограничения на модуль к ограничению на средний квадрат
(21)На основании «принципа практической уверенности» (правило «трех сигма») выбираем Kθ = 3 и можем утверждать, что неравенство (20) будет выполнено.
Тогда при оптимальном регулировании возбуждения необходимо выполнить условие
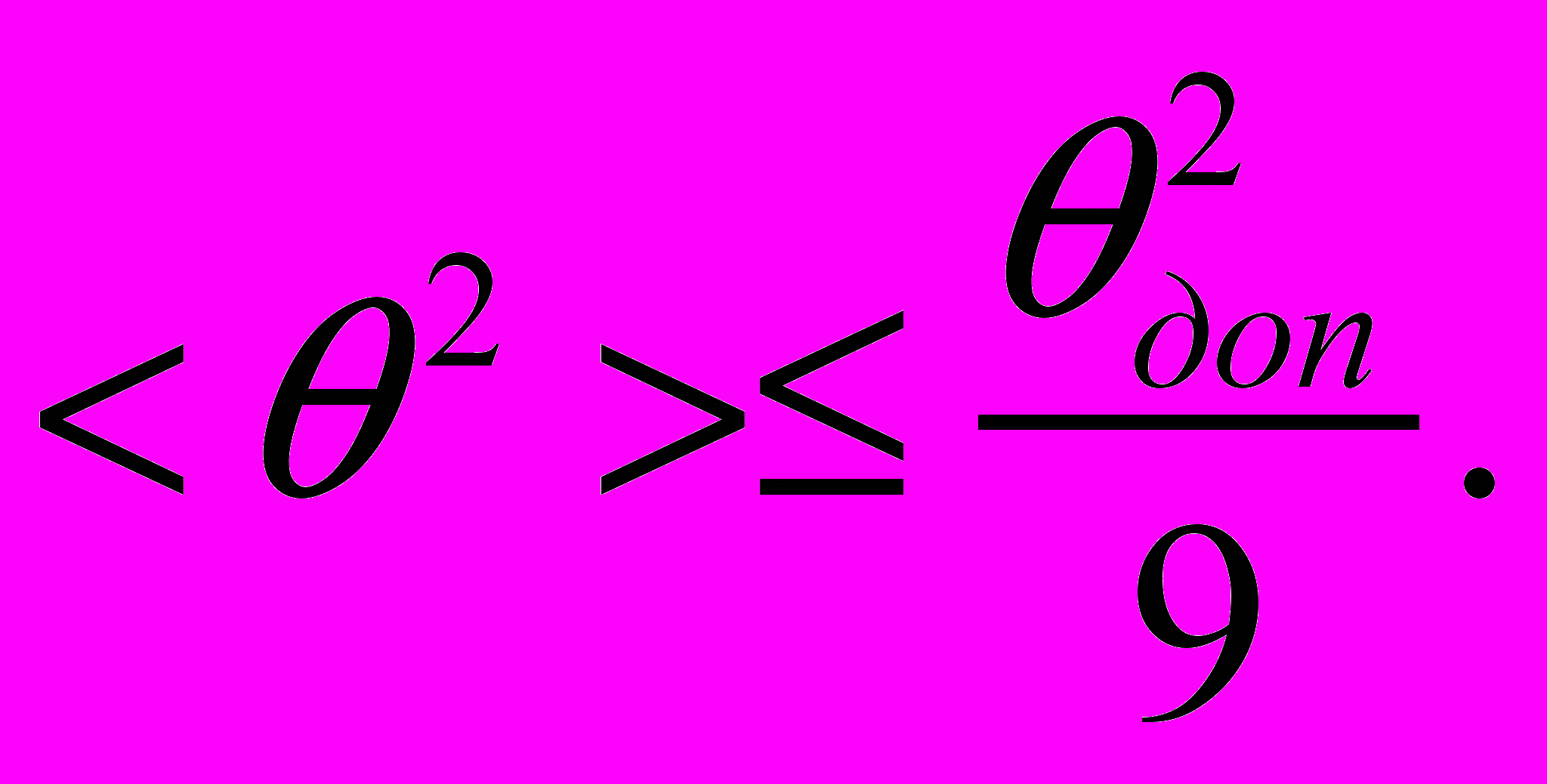(22)Критерий качества регулирования примет вид
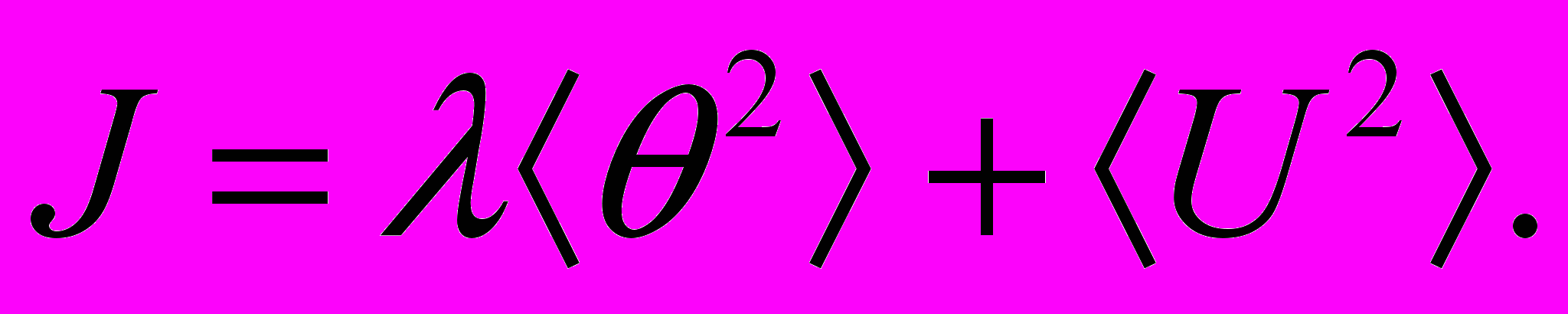(23)В качестве основного возмущающего воздействия в этом случае будем рассматривать изменение момента нагрузки MH(t). Причем будем полагать, что MH(t) - случайный процесс типа «белый шум», функцией - представителем которого является случайная последовательность δ - функций. В реальной системе электропривода это соответствует ударам по лопаткам рабочего колеса центробежного нагнетателя ГПА. Разработана методика синтеза оптимального регулятора. Особенностью данного варианта синтеза является то обстоятельство, что регулируемой координатой является угол нагрузки θ, а измеряемой является напряжение в узле нагрузки V, т.е. регулируемая координата не совпадает с измеряемой. Построение систем АРВ с обратной связью по напряжению узла нагрузки с целью повышения устойчивости синхронных машин, регулирования внутреннего угла θ широко используется в электрических системах. При этом передаточная функция оптимального регулятора может быть представлена в виде
(24)В цифровых системах регулирования возбуждения обычно реализуется медленный канал регулирования напряжения с И – регулятором с передаточной функцией
и быстрый канал регулирования угла θ с передаточной функцией W2(p) (24). Тогда обеспечивается заданный уровень напряжения узла нагрузки и демпфирование колебаний ротора СД (стабилизация угла θ). Заметим, что регулятор (24) относится к так называемым «регуляторам сильного действия», поскольку содержит 2 реальных производных. Проведены компьютерные исследования оптимальных систем регулирования возбуждения синхронных двигателей газоперекачивающих агрегатов. На рис. 6 приведена реализация изменения угла θ в разомкнутой системе, а на рис. 7 – в замкнутой.
Рис. 6 Реализация изменения угла θ в разомкнутой системе
Рис. 7 Реализация изменения угла θ в замкнутой системе
Сравнительный анализ реализаций регулируемой координаты в разомкнутой и замкнутой системах, показал, что при замыкании системы оптимальным регулятором, среднеквадратичное отклонение внутреннего угла синхронного двигателя уменьшаются в 5,1 раз. Дальнейшее уменьшение отклонения угла связано с повышением мощности управляющего воздействия.
В третьей главе выполнен синтез гарантирующих управлений возбуждением синхронных двигателей газоперекачивающих агрегатов. При синтезе оптимальных стохастических систем управления электроприводами полагали, что корреляционные функции (или, что тоже самое, спектральные плотности мощности) возмущающих воздействий известны. Однако спектральные плотности мощности возмущений могут быть либо неизвестны, либо существенно изменяться с течением времени. При неизвестных спектральных плотностях возмущающих воздействий нужно ставить вопрос о синтезе гарантирующего управления, т.е. такого управления, которое должно гарантировать, что для любого спектра возмущений критерий качества не превысит некоторого (наименьшего из всех возможных) гарантированного уровня.
Будем рассматривать задачу стабилизации внутреннего угла θ. Согласно структурной схеме можно записать следующее уравнение для выходной координаты
. (25)Возмущающее воздействие МН(t) имеет конечную мощность, т.е. конечный средний квадрат
. (26)Спектр SМН() изменения момента МН нагрузки неизвестен, можно только записать, что
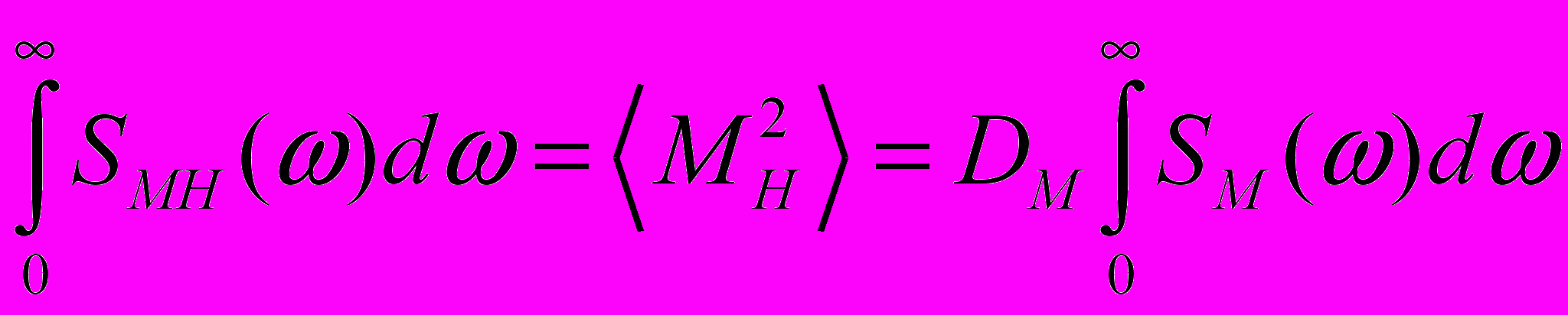. (27)Критерием качества является интегральный среднеквадратичный функционал
. (28)Вариационными методами определяется минимальное значение критерия качества (29)
. (29)Теперь можно определить наихудший спектр возмущающего воздействия МН(t) при учете изопериметрического условия (26). Показано, что наихудшим спектром будет спектр в виде обобщенной -функции Дирака
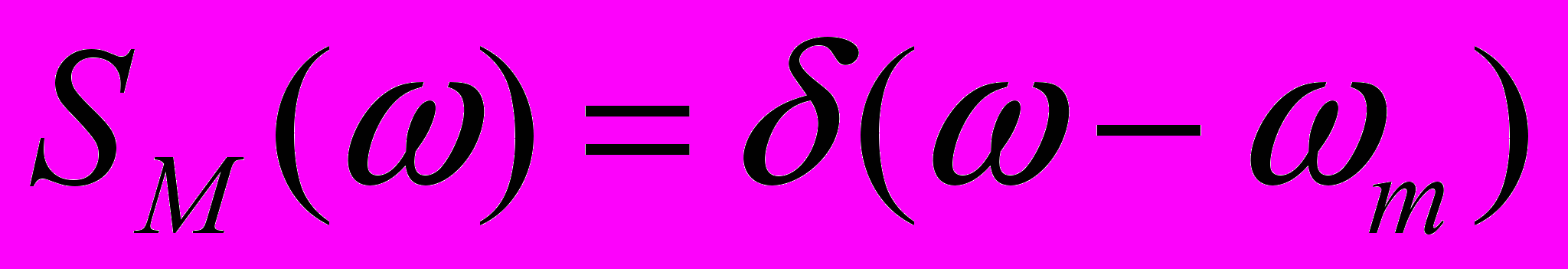. (30)Доказано, что при произвольном спектре МН(t) с учётом (26) величина критерия качества (29) не превысит своего минимального значения (29). Наихудший спектр возмущающего воздействия (30) аппроксимируется соответствующим выражением. При синтезе гарантирующего регулятора исключаются звенья «идеального» дифференцирования, в результате чего передаточная функция будет равна
(31)На рис. 8 приведены разделяющие кривые, которые дают решение задачи о гарантированных показателях качества управления при строго гарантирующем регуляторе (кривая 1) и квазигарантирующем регуляторе (кривая 2).
Ниже разделяющей кривой лежат значения θ, которые заведомо не могут быть гарантированы для произвольного спектра возмущающего воздействия. Разделяющая кривая существенно облегчает задачу проектирования системы управления, поскольку для каждого ресурса управления U становится известно, какую точность управления θ можно гарантировать и, обратно, - для каждой точности управления θ известно, какой ресурс управления U необходим для ее реализации. С помощью разделяющей кривой легко определяется значение множителя Лагранжа в критерии качества управления (28). В рассматриваемом случае для обеспечения синхронного режима работы электродвигателей центробежных нагнетателей необходимо гарантировать такой режим, чтобы при известном интервале изменения момента нагрузки отклонение угла θ не превышало заданного максимального значения
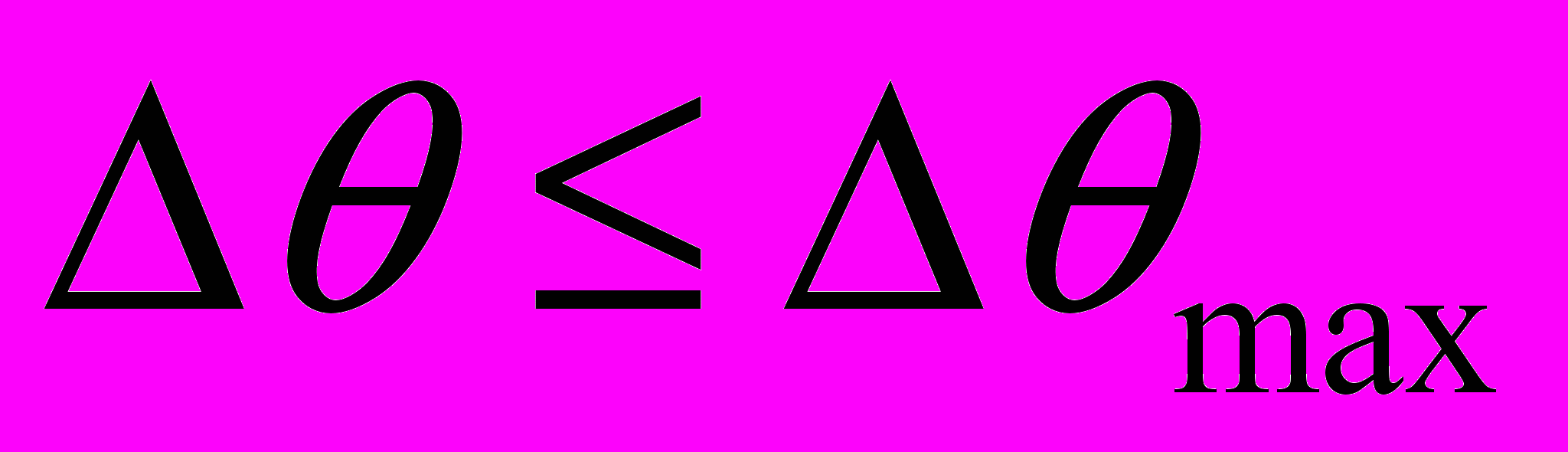. Тогда на основании «принципа практической уверенности» (правило трех сигма) необходимо обеспечить для среднеквадратичного отклонения угла θ выполнение следующего условия 
. (32)Далее с помощью разделяющей кривой легко определяем требуемое для выполнения условия (32) максимальное среднеквадратичное отклонение управляющего воздействия U max на входе регулятора тока возбуждения синхронного двигателя. В этом случае необходимое максимальное значение управляющего воздействия будет равно
.Также разработаны алгоритмы синтеза гарантирующего регулятора без учёта инерционности контура тока возбуждения и с учётом возмущающих воздействий, приведённых к выходу объекта управления.
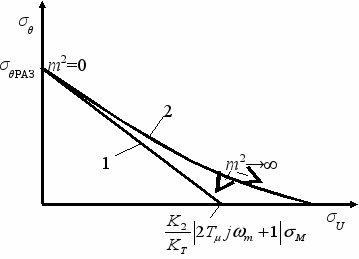
Рис. 8 Зависимость среднеквадратичных отклонений угла θ от управляющего воздействия при гарантирующем управлении
В четвёртой главе определены области динамической устойчивости синхронного двигателя газоперекачивающего агрегата при различных законах регулирования возбуждения. При аварийных режимах, связанных с помпажом ГПА, отключением части питающих линий и т.д., отклонение внутреннего угла синхронного двигателя может быть значительным относительно установившегося значения. Это вызывает необходимость рассмотрения переходного процесса «в большом» и в первую очередь возникает необходимость исследования устойчивости положения равновесия системы с учетом нелинейности характеристик. При анализе системы АРВ «в большом» математическую модель СД будем описывать полной нелинейной системой уравнений Парка-Горева. Для определения области устойчивости запишем уравнение движения в отклонениях относительно положения равновесия (уравнение возмущенного движения). В этом случае приращение вектора Х будет равно
, где X0 – вектор установившихся значений переменных состояния системы (положение равновесия). В результате преобразования (исключения алгебраических уравнений связи), система уравнений Парка-Горева в отклонениях в матричном виде может быть записана следующим образом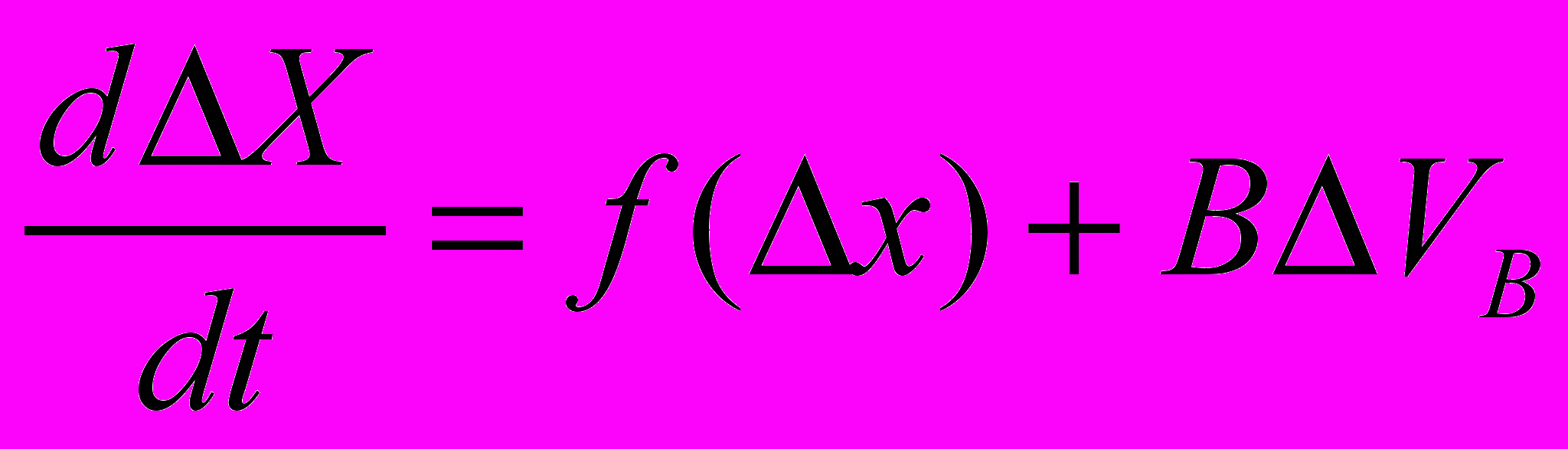
, (33)где
вектор отклонения переменных состояния; ƒ(Δx) - вектор-функция; В - матрица соответствующей размерности. Области устойчивости рассчитываются в плоскости двух переменных: Δθ и Δω. Величина области устойчивости зависит от закона регулирования возбуждения СД. Для систем нелинейных уравнений одним из наиболее распространенных и строгих методов анализа устойчивости с определенной областью притяжения является аппарат построения, исследования функций Ляпунова и прямой метод Ляпунова. Однако не существует общего метода построения функций Ляпунова для нелинейных систем. Причем функции Ляпунова конструируются не единственным способом, что не позволяет достаточно точно (а иногда очень приближенно) оценить область притяжения. Поэтому при определении областей динамической устойчивости ограничимся расчетом на ЭВМ численными методами с использованием стандартных программ при различных законах управления. Определена область устойчивости при гарантирующем управлении возбуждением СД, рис. 10 (область 1). Далее приведен расчет областей устойчивости СД с системой регулирования возбуждения с обратной связью по напряжению узла нагрузки. Структурную схему системы регулирования возбуждения СД в векторно-скалярной форме можно представить в следующем виде (рис. 9). В структурной схеме присутствуют нелинейные звенья типа «зона насыщения», ограничивающие соответственно напряжение на обмотке возбуждения и ток возбуждения. 
Рис. 9 Структурная схема системы регулирования возбуждения в векторно-скалярной форме. П, П1, П2, П3,
- матрицы преобразований; Δψ – вектор отклонения потокосцепления; ΔI – вектор отклонения токов.Запишем уравнения замкнутой системы регулирования возбуждения с учетом уравнений регулятора напряжения (19). Для этого введем в рассмотрение обобщенный вектор переменных состояния
.Напомним, что ΔX, ΔXР – векторы, а ΔEТП, ΔXРТВ - скалярные величины, где ΔXР – отклонение вектора переменных состояния регулятора.
Тогда систему регулирования возбуждения в отклонениях можно записать следующим образом
(34)где F'(ΔX0) – вектор-функция.
На основании (34) была рассчитана область притяжения, которая показана на рис. 10 (область 3). Аналогично была сформирована система уравнений состояния для регулятора напряжения с передаточной функцией (24) и рассчитана область притяжения, рис 10 (область 2). На этом же рисунке приведена область устойчивости (область 4) при традиционных настройках системы регулирования возбуждения (регулятора сильного действия – ПД-регулятора). Использование систем регулирования возбуждения расширяет естественную область устойчивости, что позволяет обеспечивать асимптотическую устойчивость положения равновесия при углах нагрузки
больших 90˚, 
- так называемая «искусственная» устойчивость за внутренним естественным пределом мощности. С ростом максимального напряжения на обмотке возбуждения Vmax указанные области устойчивости будут расширяться. 
Рис.10. Области динамической устойчивости
В пятой главе выполнена практическая реализация и экспериментальное исследование цифровой системы регулирования возбуждения синхронных двигателей газоперекачивающих агрегатов.
Статические системы возбуждения двигателей ЭГПА газоперекачивающих станций с двигателями типа СТД укомплектованы в настоящее время в основном возбудителями типов ТЕ-320, ВТЕ-320, которые морально устарели, их технические и эксплуатационные возможности не соответствуют современным требованиям. Отсутствует техническая возможность интеграции возбудителей в САУ ЭГПА и другие системы управления верхнего уровня, создаваемые на объектах ОАО «Газпром». Преодоление вышеперечисленных недостатков, несомненно, лежит на пути перехода на современную элементную базу, применение микропроцессорной техники, позволяющей реализовать более сложные и эффективные законы управления возбуждением, основанные на большем количестве непосредственно измеряемых и вычисляемых параметров состояния СД, обеспечение статической и динамической устойчивости СД при более низком уровне энергопотребления. Начато промышленное производство отечественных цифровых систем возбуждения. Выпускаемый предприятием ОАО НИПОМ цифровой тиристорный возбудитель ВТЦ-СД-320 разработан с участием автора по заданию управления энергетики ОАО «Газпром» для двигателей типа СТД электропривода ЭГПА. ВТЦ-СД-320 сертифицирован Госстандартом РФ. Общий вид цифрового возбудителя приведён на рис. 11. Базовая конфигурация представлена на рис. 12.
С использованием преобразования Тустена осуществлён переход от непрерывных передаточных функций оптимальных регуляторов к дискретным передаточным функциям, а затем к разностным уравнениям, удобным для программирования. Цифровой регулятор выполнен на базе промышленного контроллера Octagon Systems с процессором типа 5066-586-133 MHz или CPU Fastwell 686e и осуществляет функции пуска, останова, защиты двигателя, высокоэффективного цифрового регулирования возбуждения (реализует оптимальный и гарантирующий регулятор возбуждения). Функционирует регулятор под управлением мощной операционной системы реального времени типа QNX 4.25.
 Рис. 11 Общий вид цифрового возбудителя |  Рис. 12 Конфигурация блоков и узлов возбудителя |
Экономическая эффективность от использования оптимальных алгоритмов регулирования возбуждения СД ГПА для двигателей мощностью до 12,5 МВт заключается в уменьшение потребления реактивной мощности на 1,12-1,27 МВар, что эквивалентно экономии средств, измеряемой в миллионах руб. в год. Также повышается качество напряжения в узле нагрузки и тем самым снижается ущерб от некачественной электроэнергии, повышаются запасы устойчивости синхронных режимов СД. Срок окупаемости составляет менее 1 года. Экспериментальные исследования проводились на СТД-12500 при возбуждении от ВТЦ-320/230 с использованием оптимального регулятора. Результаты экспериментальных исследований с удовлетворительной точностью совпадают с расчетными. Цифровые системы возбуждения внедрены на ряде ЛПУ МГ объектов ОАО «Газпром».
Заключение.
Существенные научные и практические результаты диссертационной работы состоят в следующем:
1. Разработаны математические модели синхронного электропривода газоперекачивающих агрегатов с учётом вероятностных характеристик возмущающих воздействий. С использованием уравнений Парка-Горева проведено математическое описание динамических процессов в синхронном двигателе. Получена структурная схема и уравнения состояния синхронного электропривода ГПА с учётом характеристик центробежного нагнетателя. Получены корреляционные функции и спектральные плотности мощности возмущений. С использованием формирующего фильтра получены уравнения состояния возмущающих воздействий.
2. С использованием метода пространства состояния разработана методика синтеза оптимальной системы регулирования возбуждения СД ГПА. Получена передаточная функция оптимального регулятора напряжения узла нагрузки и угла θ. Показано, что оптимальный регулятор удовлетворяет комплексу технических требований к системе регулирования.
3. Разработана методика синтеза гарантирующего регулятора внутреннего угла синхронного двигателя. В результате получены разделяющие кривые – зависимости среднеквадратичного отклонения угла θ от мощности управляющего воздействия. Модельные исследования гарантирующей системы управления возбуждением СД ГПА показали её эффективность по сравнению с традиционными системами регулирования с П- и ПИД-регуляторами.
4. С использованием ЭВМ разработана методика определения областей динамической устойчивости нелинейной системы регулирования возбуждения СД ГПА. Рассчитаны области динамической устойчивости при различных законах управления возбуждением СД ГПА.
5. Осуществлена микропроцессорная реализация оптимального регулятора в цифровых возбудителях ВТЦ-СД-320. Проведены экспериментальные исследования и отражён опыт эксплуатации цифровой системы возбуждения ВТЦ-320/230 для синхронного двигателя СТД-12500-2. Показано, что результаты экспериментальных исследований с удовлетворительной точностью совпадают с рассчётными. Цифровые системы возбуждения внедрены на ряде ЛПУ МГ объектов ОАО «Газпром», определена технико-экономическая эффективность применения оптимальных цифровых систем возбуждения.
Достоверность научных положений, теоретических выводов, основных результатов и рекомендаций диссертационной работы подтверждена экспериментальной проверкой на действующем газоперекачивающем агрегате с синхронным электроприводом.
Основные положения и результаты диссертации опубликованы в следующих работах:
- Голубовский, А.В. Оптимизация и повышение энергоэффективности электроприводных КС МГ / Г.Р. Шварц, А.В. Голубовский, Л.А. Мигачёва, Ф.Н. Рассказов // Газовая промышленность. 2005. № 12. С. 76-77.
- Голубовский, А.В. Синтез гарантирующих систем регулирования возбуждения синхронных двигателей газоперекачивающих агрегатов / Ф.Н. Рассказов, Г.Р. Шварц, Л.А. Мигачёва, А.В. Голубовский // Вестник Самарского государственного технического университета, Технические науки. 2004. № 20. С. 144-151.
- Голубовский, А.В. Оптимизация систем управления электроприводами газоперекачивающих агрегатов / Г.Р. Шварц, А.В. Голубовский, Л.А. Мигачёва, Ф.Н. Рассказов, П.К. Кузнецов // Вестник Самарского государственного технического университета, Технические науки. № 37 – 2005. С. 171-176.
- Голубовский, А.В. Оптимизация систем управления электроприводами при случайных изменениях нагрузки / Ф.Н. Рассказов, М.В. Божьев, А.В. Голубовский // Проблемы электротехники, электроэнергетики, электротехнологии: тр. Всеросс. научно-технической конф. Тольятти, 2004. – C. 73-75.
- Голубовский, А.В. Синтез оптимального регулятора возбуждения синхронного двигателя газоперекачивающего агрегата / Ф.Н. Рассказов, С.А. Сенин, А.В. Голубовский // Математическое моделирование и краевые задачи: тр. второй Всеросс. научной конференции. Самара, 2005. – С. 215-217.
- Голубовский, А.В. Опыт эксплуатации, разработка организационных и технических мероприятий, модернизация и реконструкция энергетического оборудования в ООО «Волготрансгаз» / А.В. Голубовский // Материалы научно-технического совета ОАО «Газпром». – М.: ООО «ИРЦ Газпром», 2007. – С. 32-39.
- Голубовский, А.В. Опыт эксплуатации цифровой системы возбуждения ВТЦ-320/230 для синхронного двигателя СТД-12500-2 / А.В. Голубовский // Материалы научно-технического совета ОАО «Газпром». – М.: ООО «ИРЦ Газпром», 2002. – Т.1. – С. 49-55.
- Голубовский, А.В. Цифровые возбудители синхронных двигателей ЭГПА / А.В. Голубовский, И.В. Леонтьев // НефтегазЭкспо. - №4.- 2005. – С. 88-89.
- Патент 2239936 Российская Федерация МПК Н 02 Р1/46 5/40 7/36. Способ управления током возбуждения синхронного электродвигателя / Кислов Е.А., Голубовский А.В., Леонтьев И.В., Левичев Ю.Д.; заявитель и патентообладатель ОАО «Научно-исследовательское предприятие общего машиностроения» – № 2002130177; заявл. 11.11.2002 ; опубл. 10.11.2004, Бюл. № 31. – 1 с.
- Патент 53611 Российская Федерация. Возбудитель тиристорный цифровой синхронного двигателя / Леонтьев И.В., Шварц Г.Р., Великий С.Н., Щеголев И.Л., Голубовский А.В., Кислов Е.А., Левичев Ю.Д.; заявитель и патентообладатель ОАО «Научно-исследовательское предприятие общего машиностроения» – № 2002500722; заявл. 29.04.2002. – 1 с.
Личный вклад автора. 2 статьи написаны лично автором. В работах написанных в соавторстве автору принадлежат: разработка математических моделей синхронного электропривода ГПА [1, 4], методика синтеза оптимального регулятора возбуждения [3, 4, 5], алгоритмы синтеза гарантирующего управления [2].
Разрешено к печати диссертационным советом Д 212.217.04.
Протокол № 5 от 13.05.2008.
Подписано в печать 13.05.2008
Бумага типографская № 1. Печать офсетная.
Формат 60х84 1/16 Усл. печ. л. 1.Тираж 100 экз. Заказ № ____
ГОУ ВПО Самарский государственный технический
университет. Типография СамГТУ.
443100, г. Самара, ул. Молодогвардейская, 244