Geum.ru

Методическое письмо «Об использовании результатов единого государственного экзамена 2006 года в преподавании математики в средней школе»

Вид материалаМетодическое письмо

Содержание


Методическое письмо
Методическое письмо
Структура КИМ. Основные результаты ЕГЭ по математике в 2006 году
Ниже в отдельности приведены результаты, показанные при выполнении заданий по курсу алгебры и начал анализа и по курсам геометри
Курс геометрии основной и старшей школы
Рекомендации по совершенствованию преподавания математики Курс алгебры и начал анализа
Описание алгебраической подготовки участников экзамена в соответствии
Курс геометрии
Произвольный остроугольный или тупоугольный треугольник
Прямоугольный треугольник
Равнобедренный треугольник
Правильный треугольник
Параллелограмм и его виды (прямоугольник, ромб, квадрат)
Подобный материал:





Федеральная служба по надзору в сфере образования и науки

Федеральный институт педагогических измерений



согласовано:


Председатель научно-методического совета ФИПИ по математике,

к.ф.-м.н., профессор Г.Г.Канторович


подпись

_________________________ 2006 г.
УТВЕРЖДЕНО:

Ученым советом ФИПИ (протокол №4 от 15.12.06)

Председатель Ученого совета ФИПИ, директор ФИПИ

к.философ. н. А.Г.Ершов


подпись

__________________________ 2006 г.



Методическое письмо

«Об использовании результатов единого государственного экзамена

2006 года в преподавании математики в средней школе»


Научный руководитель: Г.С. Ковалева, к. п. н., заместитель директора ФИПИ.


Письмо подготовлено членами федеральной предметной комиссии по математике к. п. н. Л.О. Денищевой, к. п. н. Н.Б. Мельниковой, к. п. н. К.А. Краснянской на основе аналитического отчета «Результаты единого государственного экзамена 2006 года», размещенного на сайте ФИПИ (ru).



Методическое письмо

«Об использовании результатов единого государственного экзамена

2006 года в преподавании математики в средней школе»


Единый государственный экзамен (ЕГЭ) по математике проводится в течение 6 лет и является одним из направлений модернизации образования. Анализ результатов этого экзамена позволяет выявить те положительные тенденции в организации процесса обучения математике, которые можно считать непосредственным следствием введения ЕГЭ.

В ходе разработки контрольных измерительных материалов (КИМ) по математике конкретизируются требования утвержденного в 2004 году стандарта математического образования. Результаты выполнения заданий позволяют получать объективную и достоверную информацию об овладении контролируемыми элементами содержания учащимися, продемонстрировавшими разные уровни математической подготовки. Выявлены элементы содержания, контролируемые на базовом уровне, которые усваивает большинство выпускников, а также те элементы, которыми большинство выпускников не овладевает.

Полученная информация о состоянии подготовки выпускников, доступная математическому сообществу, имеет практическое значение для разработчиков стандартов математического образования и других нормативных документов, для авторов школьных учебников и различной методической литературы.

В условиях обязательной для всех выпускников сдачи экзамена по математике постепенное и поэтапное введение ЕГЭ дало возможность учителям по-новому подходить к подготовке и проведению уроков, учитывая необходимость обеспечить овладение всеми школьниками учебного материала на базовом уровне, а также возможность мотивированным учащимся, заинтересованным в получении высоких баллов для поступления в вуз, динамичного продвижения в овладении материалом на повышенном и высоком уровне.

В ходе расширения эксперимента по введению ЕГЭ совершенствуется система непрерывного образования и система переподготовки педагогических кадров: обновляются не только программы общеобразовательных дисциплин, но вводятся курсы, раскрывающие основы дифференцированного и индивидуального обучения и др. Эти нововведения в целом направлены на развитие профессиональных умений и профессионального мастерства учителя математики.

Рассмотрим особенности вариантов КИМ 2006 г. и результаты их выполнения участниками экзамена.

Структура КИМ. Основные результаты ЕГЭ по математике в 2006 году

Единый государственный экзамен является одной из форм (в ряде регионов эта форма является основной) единовременной сдачи двух экзаменов: выпускного экзамена за среднюю (полную) школу и вступительного в вузы. По своему назначению ЕГЭ должен обеспечить итоговую аттестацию выпускников средней (полной) школы по курсу алгебры и начал анализа 10-11 классов курс В) и дифференциацию выпускников по уровню общей математической подготовки для отбора в вузы. Согласно поставленным целям при сдаче ЕГЭ содержательная область контрольных измерительных материалов включает материал указанного выше курса, который дополняется материалом курса стереометрии, а также некоторыми вопросами курса математики основной школы, усвоение которых, как правило, проверяется на вступительных экзаменах в вузы (например, проценты, прогрессии, сведения из курса планиметрии).

При разработке вариантов КИМ 2006 г. была использована та же модель, что и в 2005 году, т.е. в структуру, назначение частей работы, число и сложность включаемых в них заданий не было внесено никаких изменений по сравнению с 2005 годом. На выполнение работы отводилось 4 часа. Модель ЕГЭ по математике была прокомментирована в методическом письме «О преподавании математики в средней школе с учетом результатов единого государственного экзамена 2005 года», направленном в органы управления образованием субъектов Российской Федерации письмом Департамента государственной политики Минобрнауки России от 20.03.06 N 03-302. Познакомиться с документами, регламентирующими разработку ЕГЭ по математике 2007 г., можно на портале информационной поддержки проекта «Единый государственный экзамен» ссылка скрыта, а также на сайте Федерального института педагогических измерений ссылка скрыта.


В 2006 году ЕГЭ по математике сдавали 623493 выпускника из 73 регионов России. По сравнению с 2005 годом (680154 выпускника из 69 регионов) на 4 увеличилось количество регионов, но при этом уменьшилось общее число участников экзамена. Одной из причин уменьшения числа участников является увеличение числа регионов, в которых выпускники могли по желанию выбрать другую форму сдачи выпускного и вступительного экзаменов. Число участников экзамена в регионах варьировалось от 213 (Чукотский АО) до 39801 (Краснодарский край).

Как и в предыдущие годы, основную часть участников экзамена составили выпускники общеобразовательных школ – около 96% (среди них гимназии – 6%, лицеи – 6%, школы-интернаты – 0,6% и кадетские школы – 0,1%), выпускники вечерних школ – около 0,8 % (в 2005 г. их было 1,7%), около 0,4% приходятся на выпускников начальных (0,13%) и средних (0,24%) профессиональных училищ. При этом важно отметить, что более четверти участников ЕГЭ 2006 г. (26,9%) составили выпускники сельских школ (в 2005 г. – 29,1%) и выпускники поселков городского типа – 8,7% (в 2005 г. – 8,7%).

Экзамен в форме ЕГЭ сдавала значительная часть (около 48%) выпускников 2006 года в 73 регионах страны, что позволило получить достоверную информацию как о положительных качествах, так и о недочетах, присущих математической подготовке этой совокупности учащихся.

О состоянии общей математической подготовки1 участников экзамена можно судить по данным, представленным в таблице 1.

Таблица 1


Процент участников экзамена, показавших различные уровни общей математической подготовки в 2005 и 2006 г.г.

Годы
Неудовлетв.

(0–37

баллов)

«2»
Удовлетв.

(38–53 балла)

«3»
Хороший

(54–71 балл)

«4»
Отличный

(72–100 баллов)

«5»
100

баллов
Число

участников

2005
21,6 % .
40,2 %
31,3%
6,9%
0,02%

(163 чел.)
680154

2006
19,4%
39,5%
34,0%
7,1%
0,017%

(109 чел.)
623493


В 2006 г. немного снизился процент учащихся, показавших низкий и удовлетворительный уровни подготовки, и соответственно на столько же увеличился процент учащихся, показавших хороший и высокий уровни подготовки. Таким образом, по сравнению с 2005 годом, в 2006 году наблюдается тенденция некоторого повышения уровня математической подготовки участников экзамена, хотя различия в распределении учащихся по выделенным уровням подготовки в эти годы невелики.

Ниже в отдельности приведены результаты, показанные при выполнении заданий по курсу алгебры и начал анализа и по курсам геометрии старшей и основной школы.

Курс алгебры и начал анализа


В 2006 году участники экзамена, продемонстрировавшие различные уровни подготовки2 по данному курсу, распределились в процентном отношении следующим образом: «неудовлетворительный» – 19,6% (2005 год – 22,1 %); «удовлетворительный» – 34,1% (2005 г. –35,0%); «хороший» –34,3% (2005 г. – 32,1%); «отличный» – 12,0% (2005 г. –10,9%). Таким образом, наблюдается тенденция некоторого улучшения состояния подготовки по курсу алгебры и начал анализа в целом.

Результаты 2006 года, как и в 2001 – 2005 г.г., показали значительные различия в достижении проверявшихся требований стандарта 2004 года. Так, с подавляющим большинством заданий, характеризующих достижение обязательных требований стандарта по курсу алгебры и начал анализа, в 2006 г. справились – 32%-90% участников экзамена (2005 г. – 42%-89%). При выполнении большинства алгебраических заданий повышенного уровня с кратким ответом в 2006 году результаты были примерно такие же, как и 2005 году – справились 8%-44% (в 2005 году – 10% - 48%).

С большинством алгебраических задач повышенного уровня (С1 и С2) и высокого уровня (С3 и С5), требующих записи решения, справились:

С1 – 19% -29% участников экзамена (2005 г. – 13%-21%);

С2 – 7% -13% (2005 г. – 20%-25%);

С3 – 0,7% -2,3% (2005 г. – 1,3%-2,3%);

С5 – 0,2%- 1,0% (2005 г. – 0,26%-0,81%).


Более высокие результаты выполнения задания С1 объясняются целенаправленным снижением сложности этого задания по сравнению с 2005 годом, чтобы с ним могли справиться не только «отличники», но и твердые «хорошисты». Более низкие результаты выполнения задания С2 связаны с целенаправленным повышением его сложности по сравнению с 2005 годом, чтобы обеспечить последующую более тонкую дифференциацию хорошо подготовленных выпускников. При выполнении заданий С3 и С5 значительных изменений в результатах не произошло.

Результаты выполнения алгебраических заданий С1, С2, С3 показывают, что с их введением в варианты КИМ 2006 г. удалось осуществить более плавный переход от заданий повышенной сложности к заданиям высокой и самой высокой сложности.

Повышение верхней границы процента выполнения самого сложного задания С5 по сравнению с 2005 годом показывает, что в 2006 году к этому заданию приступало больше учащихся с высоким уровнем подготовки и справлялось с ним. Этот результат свидетельствует о правильном направлении совершенствования подходов к разработке подобных заданий, позволяющем сделать данное задание более привлекательным для самых подготовленных учащихся.

Курс геометрии основной и старшей школы


Согласно спецификации вариантов КИМ в каждый вариант работы включалось три задания по геометрии: два повышенного уровня и одно высокого уровня сложности.

С большинством геометрических задач повышенного уровня по планиметрии в 2006 году по вариантам КИМ справились 7,5%–11,7% выпускников (2005 г. 6,8%–8,6%), по стереометрии результаты несколько лучше – 8,5%-18,3% (2005 г. 10,9%-14,3%). По сравнению с 2005 годом наблюдается тенденция некоторого повышения результатов.

Тем не менее, как и в предыдущие годы, участники экзамена 2006 года показали невысокие результаты при решении геометрических задач повышенного уровня сложности. При интерпретации этих результатов следует иметь в виду, что часть учащихся, не заинтересованных в получении свидетельства о сдаче ЕГЭ по математике для поступления в вузы или ссузы, скорее всего, просто пропустили эти задания. Это обстоятельство не позволяет с достаточным основанием распространять полученные результаты на всю совокупность выпускников российских школ.

Стереометрические задачи высокого уровня (С4), рассчитанные на способных и очень хорошо подготовленных учащихся, в 2006 году по вариантам КИМ выполнили в целом 0,1%-1,0% участников экзамена (2005 г. – 0,93% -1,05%). При сравнении итогов 2006 и 2005 г.г. наблюдается некоторое снижение результатов выполнения стереометрической задачи высокого уровня. Это объясняется более высоким уровнем сложности задачи С4 в 2006 году.

Учащиеся с удовлетворительным уровнем математической подготовки не справляются с задачами по геометрии повышенного и, тем более, высокого уровня. Невысоки результаты у учащихся, показавших «хороший» уровень подготовки. Только 8%-15% из них продемонстрировали возможность справляться с задачами по курсу планиметрии, и 10%-20% – по курсу стереометрии. Совсем небольшой процент этой группы выпускников (не более 0,1%) показал возможность справиться с задачами высокого уровня сложности.

По сравнению с остальными выпускниками группа учащихся, продемонстрировавших «высокий» уровень математической подготовки, выделяется и более высоким уровнем геометрической подготовки: 47%-66% этих учащихся справились с задачами повышенного уровня по стереометрии и несколько меньше – 40%-56% показали возможность решать задачи по курсу планиметрии, с задачей высокого уровня, сумели справиться 1%-3,2% (в 2005 г. – 0,6%-0,8%). Они продемонстрировали способность самостоятельно разработать способ решения достаточно сложной стереометрической задачи с нестандартной конфигурацией, применив знания из различных разделов школьного курса геометрии, и математически грамотно записать свое решение, приводя обоснования ключевых моментов решения.


Рекомендации по совершенствованию преподавания математики




Курс алгебры и начал анализа


Анализ результатов выполнения заданий КИМ позволил описать состояние алгебраической подготовки выпускников, продемонстрировавших различные уровни общей математической подготовки.

Таблица 2


Описание алгебраической подготовки участников экзамена в соответствии

с показанным ими уровнем общей математической подготовки

Уровень математической подготовки участника экзамена
Описание подготовки выпускников по алгебре

НЕУДОВЛЕТВОРИТЕЛЬНЫЙ

Тестовый балл 1 – 37;

Оценка «2»
Выпускники этой группы не овладели ни одним из проверяемых элементов содержания на базовом уровне

УДОВЛЕТВОРИТЕЛЬНЫЙ

Тестовый балл 38 – 55;

Оценка «3»

Процент выпускников – 39,5%
Выпускники этой группы овладели 6 – 8 элементами содержания из 13, которые контролировались с помощью заданий базового уровня сложности в каждом варианте КИМ.

Овладели на базовом уровне умением проводить преобразования радикалов и степеней, преобразования логарифмов и тригонометрических выражений с использованием ограниченного набора формул. Эта категория выпускников умеет решать простейшие показательные и логарифмические уравнения, дробно-рациональные неравенства, а также читать по графику некоторые свойства функции

ХОРОШИЙ

Тестовый балл 54 – 71;

Оценка «4»

Процент выпускников – 34,0%
Выпускники этой группы овладели всеми элементами содержания, проверяемыми на базовом уровне: они умеют преобразовывать все изученные виды выражений, решать все проверявшиеся виды уравнений и неравенств, исследовать свойства функций.

Овладели (выполняют задания более 50% учащихся данной группы) 3-4 элементами содержания из семи, освоение которых проверялось на повышенном уровне. Они умеют преобразовывать выражения, включающие различные их виды; исследовать свойства функций элементарными методами и с помощью производной; решать комбинированные уравнения

ОТЛИЧНЫЙ

Тестовый балл 72 – 100;

Оценка «5»

Процент выпускников – 7,1%
Выпускники этой группы успешно овладели всеми элементами содержания, проверяемыми на базовом и повышенном уровнях.

Овладели не только методами решения всех математических задач при выполнении заданий с выбором ответа и кратким ответом, но и показали умение грамотно и обоснованно записать свое решение при выполнении заданий с развернутым ответом



Анализ результатов экзамена позволил выделить проблемы в обучении математике, которые явно проявляются при сдаче ЕГЭ выпускниками, которые продемонстрировали «удовлетворительный» уровень математической подготовки.

1) Выделяются разделы, темы, вопросы, усвоение которых вызывает серьезные затруднения учащихся. Они допускают грубые ошибки при выполнении заданий базового уровня сложности по следующим темам:
  • преобразование тригонометрических выражений3, преобразование логарифмических выражений;
  • решение иррациональных уравнений;
  • решение логарифмических и показательных неравенств с основанием 0<а<1;
  • исследование свойств функций элементарными методами (нахождение области определения, множества значений, распознавание четности (нечетности).

2) Анализ ответов на задания базового уровня сложности выявил, что учащимися не усвоены стандартные алгоритмы выполнения изученных преобразований, основных методов решения уравнений и неравенств, элементарных методов исследования свойств функций. Так, например, допускаются следующие ошибки в преобразовании разности логарифмов в логарифм частного: до 25% участников экзамена пишут в ответе логарифм разности, до 10% – разность чисел, стоящих под знаком логарифма, до 15% – частное чисел, стоящих под знаком логарифма уменьшаемого и вычитаемого.

При решении простейших логарифмических неравенств положение еще более плачевное. Около трети учащихся не учитывают область определения логарифма, еще треть учащихся не меняет знак неравенства на противоположный, когда основание логарифма 0
Учащиеся затрудняются в нахождении области определения функции (например 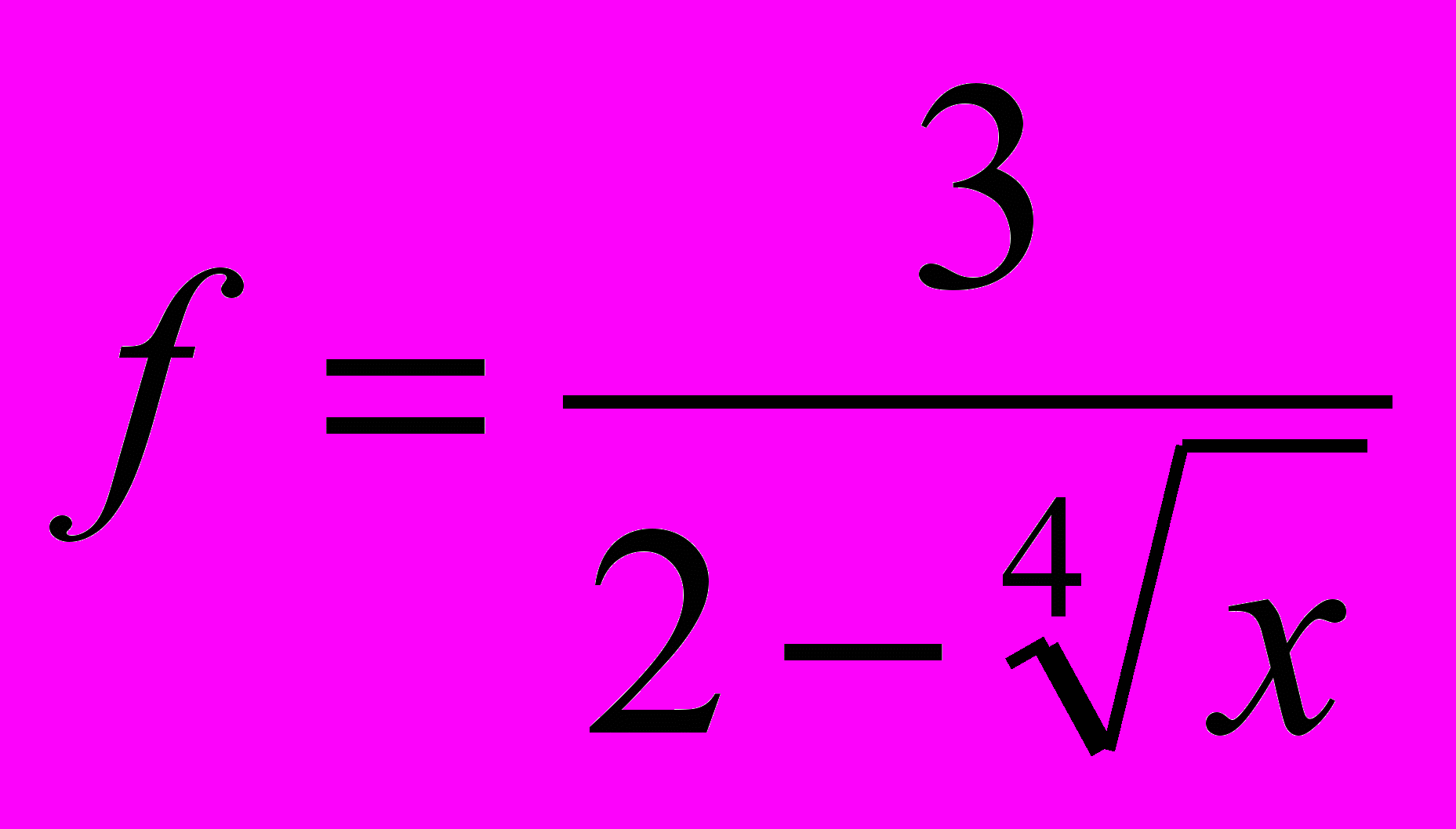). Около четверти выпускников за область определения заданной функции принимают область определения корня четной степени, пятая часть экзаменуемых исключает из множества всех действительных чисел только те значения аргумента, при которых знаменатель обращается в ноль.

При выполнении заданий базового и повышенного уровня выпускники допускают много вычислительных ошибок.

3) Очень небольшой процент участников экзамена, получивших оценку «3», справляется только с отдельными заданиями повышенного уровня сложности. Обычно для решения таких задач нужно применить не одну формулу или одно свойство, а две формулы или два свойства, или применить изученные знания (формулы, свойства) в несколько измененной ситуации.

С описанными заданиями повышенного уровня сложности справляются лишь около половины выпускников, получивших оценку «4». Им оказываются под силу лишь те задания, где требуется выполнить более сложные вычисления или преобразования, но школьные «хорошисты» испытывают затруднения в тех заданиях, где нужно изменить стандартный алгоритм решения, согласуясь с данными задачи. Так, при нахождении наибольшего и наименьшего значений сложной функции на заданном отрезке (например, «Найдите разность между наибольшим и наименьшим значениями функции y = log 0,1(10-x2) на отрезке [-3; 1]») условие задачи провоцирует выпускника на применение стандартного алгоритма исследования функции с помощью производной. Однако анализ условия показывает, что в силу монотонности логарифмической функции и с учетом значений функции y=10-x2 на отрезке [-3;1] задачу можно решить элементарным методами, найдя разность y(– 3) – y(0). Очевидно, что школьный «хорошист» имеет теоретическую базу, достаточную, чтобы справиться с этой ситуацией. В ходе обучения необходимо ставить перед учениками такие проблемы, решение которых выходило бы за рамки стандартных алгоритмов, но ученики могли бы с ними справиться, применяя самостоятельно изученный ими материал.

4) Особое беспокойство вызывают проблемы, о которых свидетельствует перепроверка4 ответов учащихся на задания с развернутым ответом повышенного уровня сложности, выполнение которых оценивается максимально 2 баллами. При записи решений этих заданий не требуется каких-либо объяснений, т.к. обычно проверяются известные методы решений. Но вместе с тем выполнение этих заданий требует определенной внимательности выпускников, т.к. в одних случаях нужно учесть область определения выражения, в других - сделать проверку найденных корней уравнения – следствия или отобрать значения, исходя из ограничений данных в условии задачи.

Согласно критериям проверки этих заданий, положительно оцениваются (выставляется 1 или 2 балла) те работы, в которых очевидно показано владение методом, проверка выполнения дополнительных ограничений, внесенных в ходе решения, учет условий задачи и т.п. Различие в выставлении 1 или 2 баллов состоит в том, что на оценку в 1 балл допускается вычислительная ошибка или описка, не влияющая на дальнейший ход решения задачи. Однако при перепроверке работ выпускников обнаруживается, что эксперты (а это учителя школ) к опискам относят неверно выполненные отдельные действия, входящие в состав стандартных алгоритмов; отсутствие отдельных шагов стандартных алгоритмов и пр. Например, отсутствие исследования на пригодность корней уравнения-следствия; отсутствие указания числового промежутка при раскрытии знака модуля, приводящее к появлению посторонних корней и пр. Наличие указанных недочетов в решениях выпускников сигнализирует нам о необходимости обращения внимания к математически грамотному оформлению записи решения математических задач. Не нужно давать и разучивать с учащимися образцы решений, не нужно «канонизировать» какие-то эталоны, решения у разных учеников могут и, по-видимому, должны быть различными, единственным критерием их оценки должна быть математическая грамотность записи решения.

Нельзя не заметить, что указанные проблемы не являются новыми, возникшими только в ходе ЕГЭ 2006 г. О большинстве из них уже говорилось в методических письмах, подготовленных на основе итогов ЕГЭ 2003 и 2005 г.г. Напомним, что в этих письмах указывались направления совершенствования преподавания: активнее включать в учебный процесс идеи дифференцированного обучения (дифференциация требований в процессе обучения, разноуровневый контроль); использовать практические разработки по индивидуализации обучения (создание индивидуальных модулей обучения); учитывать рекомендации психологов по организации усвоения и пр.

Хотя болевые точки выявлены и рекомендации предложены, но, как показывает опыт, положительных результатов трудно ожидать в течение двух и даже трех лет, т.к. математика является таким предметом, где невероятно сильна преемственность в обучении. Чтобы получить высокие результаты в средней школе, нужно добиться успешного овладения теми результатами, которые формируются в основной школе.

К таким важным результатам обучения математике в 5-6 классах и алгебре в 7-9 классах относятся умения:
  • выполнять вычисления с обыкновенными и десятичными дробями,
  • преобразовывать многочлены, алгебраические дроби, степени с целыми показателями и квадратные корни,
  • решать линейные, квадратные и дробно-рациональные уравнения и неравенства,
  • читать свойства функций по их графикам, исследовать отдельные свойства функций аналитически.

Учителям математики, начинающим работу в 10 классе и готовящим выпускников к итоговой аттестации, необходимо в начале учебного года получить достоверную информацию об уровне подготовки десятиклассников по основным разделам курса алгебры основной школы и своевременно организовать работу по ликвидации пробелов в знаниях учащихся. Этой цели служит организация вводного повторения материала курса алгебры 7-9 классов. Исходя из результатов, получаемых ежегодно на едином экзамене по математике, можно предложить следующую тематику вводного повторения.


Основные вопросы повторения
Вспомогательный материал

Преобразования одночленов, многочленов, алгебраических дробей и арифметических квадратных корней
– свойства степеней с одинаковыми основаниями,

– формулы сокращенного умножения,

– правила сложения (вычитания), умножения многочленов,

– свойства арифметического квадратного корня,

– действия с десятичными и обыкновенными дробями

Решение линейных и квадратных уравнений и неравенств. Решение дробно-рациональных уравнений

– теоремы о равносильных преобразованиях уравнений и неравенств,

– формула корней квадратного уравнения,

– действия с десятичными и обыкновенными дробями

Линейная и квадратичная функции, их свойства и графики

Функции вида 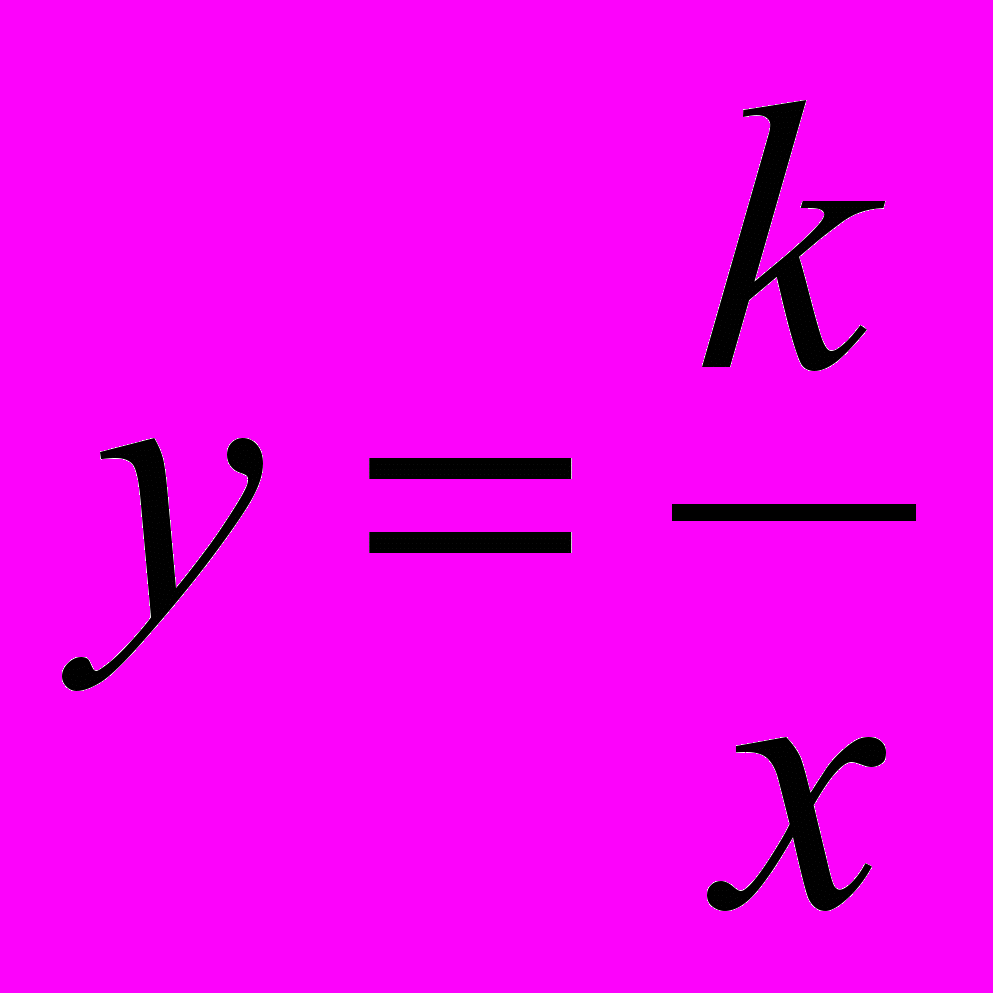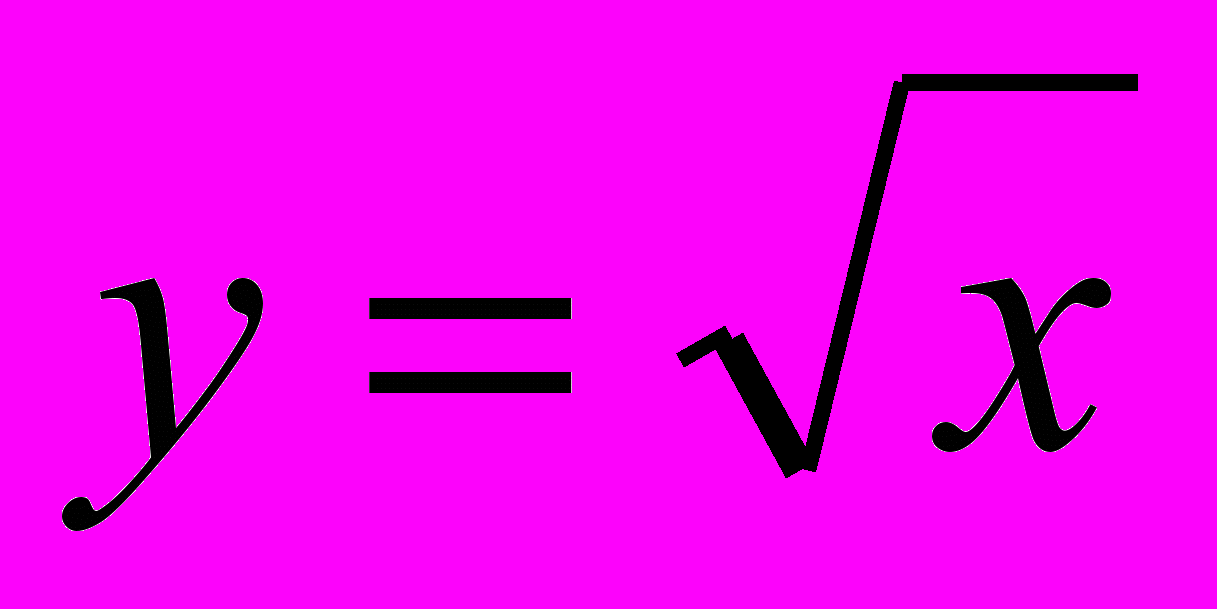и , их свойства и графики
– нахождение значений функции, нулей функции, промежутков знакопостоянства (аналитически и графически),

– чтение по графику свойств функций,

– действия с десятичными и обыкновенными дробями


Вполне понятно, что решить проблему ликвидации пробелов в знаниях десятиклассников по курсу алгебры основной школы только с помощью организации вводного повторения не удастся. Поэтому целесообразно организовать еще и индивидуальное повторение, учитывающее пробелы в знаниях и умениях конкретного ученика, и с помощью диагностических работ систематически фиксировать продвижение старшеклассника по пути достижения уровня запланированных требований.

Итак, для успешной подготовки к итоговой аттестации в старших классах необходимо целенаправленное вводное повторение разделов курса алгебры 7-9 классов (математики 5-6 классов) и систематический мониторинг продвижения отдельных учеников по ликвидации пробелов за основную школу.

Вместе с тем не стоит забывать, что курс алгебры и начал анализа отличается не только преемственностью с курсом математики 5-6 классов и курсом алгебры 7-9 классов, но и преемственными связями между различными разделами внутри самого курса. Поэтому для обеспечения прочного овладения всеми выпускниками основными элементами содержания, изучаемыми в старшей школе не только на базовом, но и на повышенном уровне, нужно проводить систематическое повторение пройденного. Во многих учебниках, входящих в федеральный комплект учебников, такое повторение обеспечивается системой упражнений, рекомендованных для домашней работы. Обычно эти упражнения достаточно объемны, трудоемки и требуют письменного выполнения. Одним из возможных альтернативных путей организации текущего повторения может быть использование в ходе обучения устных упражнений.

Устные упражнения традиционно включаются в учебный процесс на уроках математики в основной школе, но, как показывает практика, недостаточно используются в старших классах. Устные упражнения, проводимые обычно в начале урока, имеют своей основной целью актуализацию знаний, необходимых для последующего объяснения учителя. Вместе с тем они могут выполнять и другие функции, например, использоваться для первичного закреплении материала, при опросе (фронтальном и индивидуальном).

При разработке содержания и формы представления устных упражнений следует позаботиться об обеспечении простоты «технических» преобразований и вычислений, необходимых для их выполнения. Этот подход позволит сосредоточить внимание учащихся на смысловой стороне их выполнения, то есть на определении метода их решения. Кроме того, простота технической стороны устных упражнений позволяет с их помощью моделировать различные нестандартные ситуации применения тех или иных знаний (теоретического материала)5, в которых центр тяжести сосредоточен на конструировании нового метода и не осложнен сопутствующими (второстепенными) деталями. Так, подводя учащихся к поиску решения нестандартного уравнения6, можно в устных упражнениях обсудить сущность соответствующего метода решения, например, на заданиях типа:

– решите уравнение

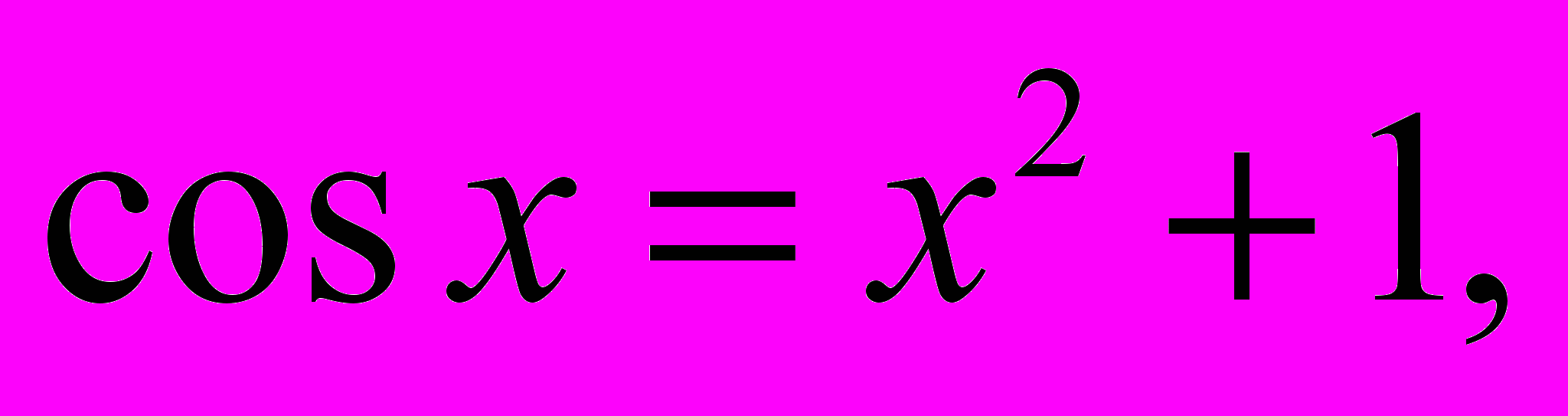
– решите уравнение .

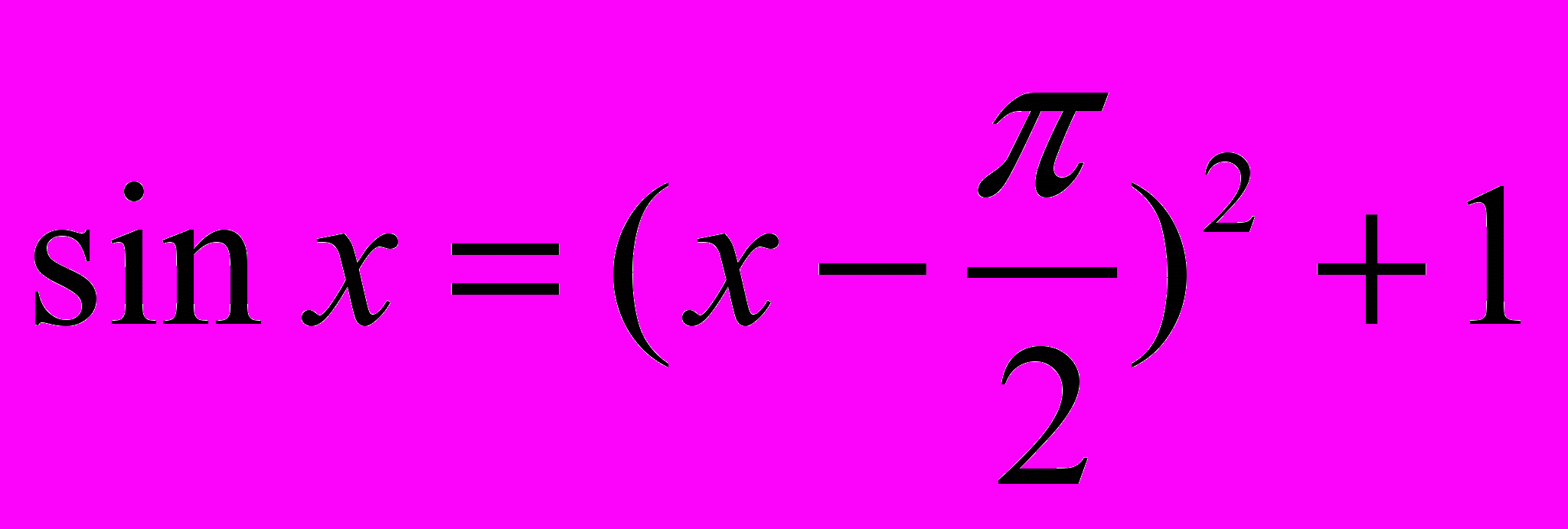Таким образом, учитель сможет связать учебный материал из различных разделов курса, обеспечивая, с одной стороны, систематическое повторение, а с другой стороны, мотивируя более подготовленных учащихся к решению задач повышенной сложности.

Отдавая должное вводному и систематическому текущему повторению, нельзя переоценить важность и значение итогового повторения, в ходе которого осуществляется систематизация знаний по мере изучения всего курса.

Курс геометрии


Количество геометрических задач среди заданий в вариантах экзаменационной работы в течение трех последних лет проведения ЕГЭ остается постоянным. В каждый вариант включается одна планиметрическая задача (повышенного уровня сложности) и две стереометрические задачи (повышенного и высокого уровня сложности). Обе задачи повышенного уровня – это задания с кратким ответом, то есть учащийся должен записать только полученный им ответ. При выполнении стереометрической задачи высокого уровня требуется записать и само решение.

Как уже отмечалось выше участники экзамена 2006 года, как и в предыдущие годы, показали невысокие результаты при решении геометрических задач. При этом большое число учащихся либо не дали никакого ответа к задачам повышенного и высокого уровня, либо вообще не приступали к их выполнению. При интерпретации этого факта следует иметь в виду, что задания по геометрии в вариантах КИМ не только отражают повышенный уровень требований к математической подготовке выпускников, но и относятся к «абитуриентским» заданиям, выполнение которых не учитывается при выставлении аттестационных отметок по курсу алгебры и начал анализа. Поэтому значительное число учащихся, которые вообще не дали никакого ответа на геометрические задания7, объясняется двумя причинами. Во-первых, результаты экзамена показывают, что некоторые учащиеся, приступившие к решению, не смогли довести его до получения ответа. Во-вторых, многие выпускники вообще не приступают к решению, если они не предполагают поступать в вузы, в которых нужно сдавать экзамен по математике, и участвуют в ЕГЭ с целью получения аттестационной отметки по алгебре.

Кроме того, часть учащихся получила при решении задач неверный ответ. Заметим, что пытаются решить геометрическую задачу, как правило, достаточно сильные выпускники. Однако многим из них не хватает знаний или умений применить свои знания. Так, со многими геометрическими задачами повышенного уровня справились меньше половины даже среди учеников с «хорошей» и «высокой» подготовкой по математике.

Задачи по планиметрии, которые используются на вступительных испытаниях в вузы, как правило, требуют применения сведений из разных разделов курса. Таким образом, для их решения нужно ориентироваться во всей совокупности свойств рассматриваемой фигуры, которые могли изучаться и в разных классах основной и старшей школы. Это характерно для задач, включаемых в варианты ЕГЭ, решение которых состоит из небольшого числа вычислительных шагов, но требует применения 2-3 геометрических фактов из разных разделов курса. Например, в 2006 году предлагались задачи такого типа: «В параллелограмме ABCD биссектриса угла D пересекает сторону АВ в точке К и прямую ВС в точке Р. Найдите периметр треугольника CDP, если DК = 18, РК = 24, AD = 15». Для решения такой задачи «на параллелограмм» нужно было применить признак подобия треугольников, свойство углов при параллельных прямых и секущей и признак равнобедренного треугольника. Такие задачи отличаются от большинства обычных учебных задач, направленных на отработку материала темы, изучающейся в данный момент.

Кроме того, абитуриентские задания выбираются из задач, в которых ситуация применения геометрических фактов не является для учащихся привычной и отработанной в ходе обучения. Поэтому даже при небольшом числе шагов решения они трудны для многих учащихся.

В связи с этим представляется важным формировать у учащихся системные знания о свойствах фигур. Конечно, при изучении каждой конкретной темы основное внимание уделяется вновь изучаемому материалу. Но вместе с тем очень важно установить взаимосвязи нового материала с тем материалом, который изучался ранее в связи с рассматриваемой фигурой. Например, при изучении окружностей, вписанных в треугольник или описанных около треугольника, рассматривается вопрос о положении центров таких окружностей: в первом случае в точке пересечения биссектрис треугольника, во втором – в точке пересечения серединных перпендикуляров к сторонам. Если при этом вспомнить изучавшиеся до этого свойства равнобедренных и равносторонних треугольников, то они пополнятся фактом о расположении центров вписанной и описанной окружностей на высоте, проведенной к основанию.

Кроме того, при совместном с учащимися решении задач в классе необходимо помнить, что цель этой работы состоит не в том, чтобы решить конкретную задачу, а в том, чтобы сформировать умения решать подобные задачи. Поэтому, рассматривая данную конфигурацию, нужно обращать внимание учащихся на то, какие геометрические факты можно было бы применить для решения задачи и на выбор способа решения.

Особая роль в формировании системных знаний об изученных в курсе фигурах отводится повторению материала. Именно при повторении, когда нет необходимости рассматривать материал в том порядке, который обусловлен логикой построения теоретической линии курса, можно выстроить последовательность рассмотрения материала, группируя его вокруг определенных фигур (треугольник, параллелограмм, трапеция, окружность и т.п.). Ниже приводятся примерные темы такого повторения и связанный с ними материал.


Тема
Основное содержание

Окружность
Свойства касательных, положение центра по отношению к пересекающимся касательным, свойство хорды, перпендикулярной радиусу, положение центра по отношению к хорде, свойства пересекающихся хорд и секущих, вписанные и центральные углы, длина окружности и дуги окружности, площадь круга и площади сектора и сегмента

Треугольники

Произвольный остроугольный или тупоугольный треугольник
Равенство треугольников, сумма углов треугольника, свойство точки пересечения медиан, свойство биссектрисы треугольника, высота в остроугольном и в тупоугольном треугольнике, подобие треугольников, площадь треугольника (формулы для вычисления площади треугольника, площади подобных треугольников и треугольников с общей высотой, метод площадей), решение косоугольных треугольников, вписанные и описанные треугольники (положение центра окружности, формулы, связанные с радиусами вписанной и описанной окружностей)

Прямоугольный треугольник
Равенство прямоугольных треугольников, решение прямоугольных треугольников (теорема Пифагора и определения тригонометрических функций острого угла прямоугольного треугольника), пропорциональные отрезки в прямоугольном треугольнике, свойство медианы, проведенной к гипотенузе.

Сумма углов в прямоугольном треугольнике, подобие прямоугольных треугольников, формулы для вычисления площади, вписанные и описанные прямоугольные треугольники (положение центра окружности, формулы, связанные с радиусами вписанной и описанной окружностей)

Равнобедренный треугольник
Свойство углов при основании, свойство медианы, биссектрисы и высоты, проведенных к основанию, равенство двух медиан (биссектрис, высот), проведенных к боковым сторонам. Положение центров вписанной и описанной окружности, решение косоугольных и прямоугольных треугольников для вычисления элементов равнобедренного треугольника, подобие треугольников Свойства равнобедренного прямоугольного треугольника

Правильный треугольник
Углы правильного треугольника, медианы, биссектрисы и высоты, положение центра правильного треугольника и вычисление его элементов и площади

Четырехугольники

Параллелограмм и его виды (прямоугольник, ромб, квадрат)8
Свойства сторон и углов параллелограмма, его признаки. Свойство диагоналей. Соотношение между квадратами диагоналей и сторон параллелограмма, метод удвоения медианы треугольника. Формулы площади параллелограмма. Свойство биссектрисы угла параллелограмма. Свойство диагоналей прямоугольника, признаки прямоугольника. Свойство диагоналей ромба, признаки ромба. Формулы для вычисления площади ромба. Свойства и признаки квадрата. Вписанные в окружность и описанные около окружности виды параллелограммов

Трапеция
Свойства средней линии трапеции, формула площади трапеции, равнобедренная трапеция и ее свойства. Трапеция, вписанная в окружность и описанная около окружности и их свойства

Многоугольники
Сумма углов многоугольника, сумма его внешних углов. Свойства правильных многоугольников9


Как известно, в современных учебниках к теоретическим фактам (теоремам) отнесены в основном только те утверждения, которые необходимы для построения теории. При этом многие утверждения, весьма полезные для решения большого числа задач, даются как задачи на доказательство, а это приводит к тому, что учащиеся не помнят сформулированные в них факты. Вместе с тем владение этими фактами значительно сокращает время, необходимое для решения задачи. Поэтому в ходе повторения, кроме «законных» теорем, нужно повторить и такого рода дополняющие их утверждения. Так, например, о равнобедренной трапеции в качестве задач формулируются очень важные для решения задач свойства.

1) В равнобедренной трапеции углы при основании равны.

2) В равнобедренной трапеции ABCD с основаниями AD = а и ВС = b основание высоты ВН делит основание AD на отрезки: АН = 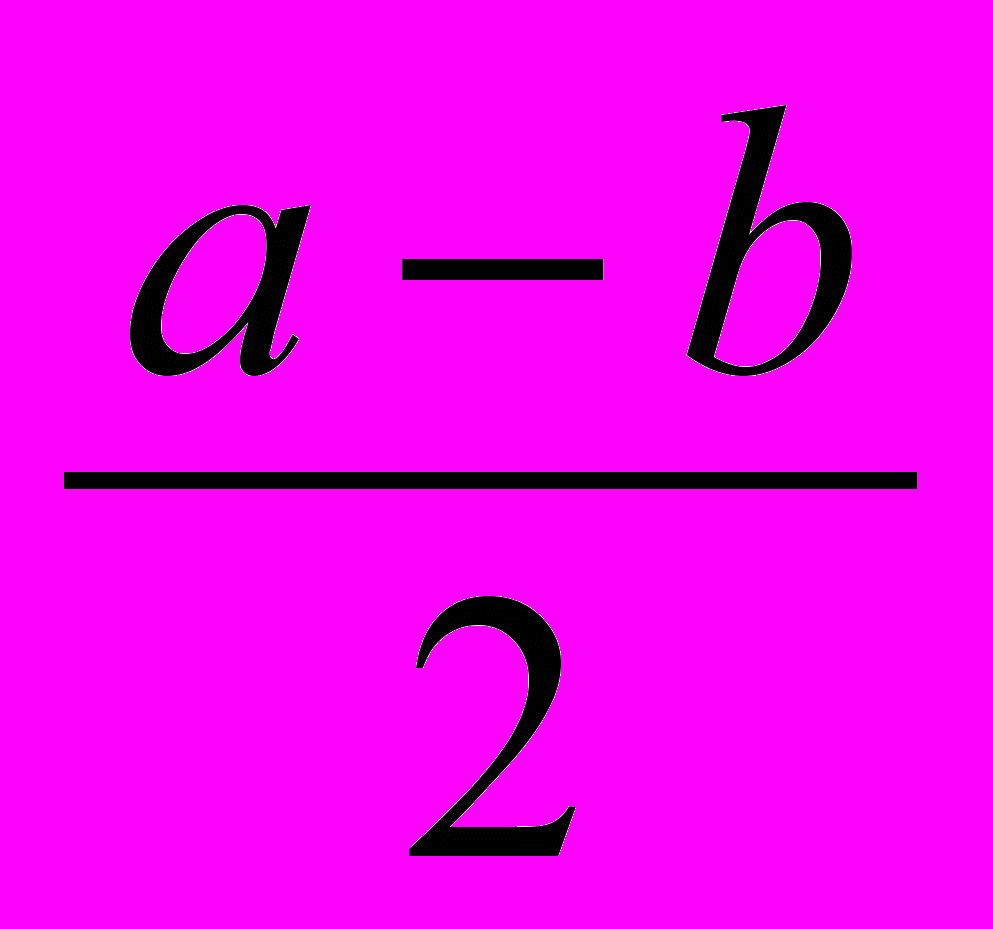, DH = 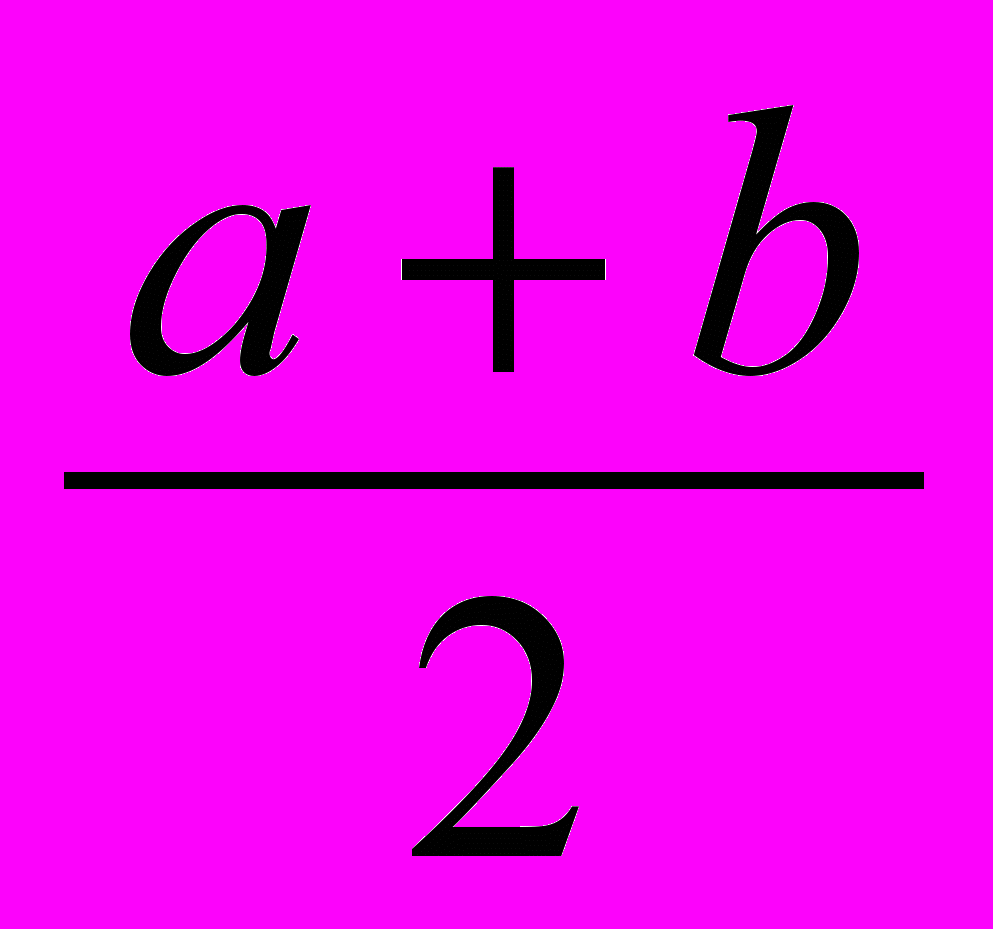= m, где m – средняя линия трапеции.


При повторении курса стереометрии тоже полезно группировать материал вокруг определенных фигур (пирамиды, призмы, конуса и т.п.). Рассматривая те или иные фигуры, необходимо не только вспомнить свойства фигуры и формулы боковой поверхности и объема, но также повторить те геометрические факты, которые используются для определения элементов данной фигуры.


Тема
Основное содержание

Многогранники

Призма (правильная, прямая, наклонная)
Сечение призмы плоскостью. Площадь боковой и полной поверхностей призмы. Объем призмы.

Угол между прямой и плоскостью (диагональю призмы или грани и плоскостью основания, ребром основания и боковой гранью); угол между плоскостями (плоскостью сечения и плоскостью основания, плоскостью диагонального сечения и плоскостью боковой грани); угол и расстояние между скрещивающимися прямыми (ребрами оснований, ребром основания и диагональю грани)

Пирамида (правильная, с равными ребрами, с одинаковыми углами между плоскостями боковых граней и плоскостью основания)

Сечение пирамиды плоскостью. Усеченная пирамида. Площадь боковой и полной поверхностей пирамиды. Объем пирамиды.

Угол между прямой и плоскостью (боковым ребром или высотой боковой грани и плоскостью основания, ребром основания и плоскостью боковой грани); угол между плоскостями (боковых граней и основания, сечения и основания, двух боковых граней с общим ребром); угол и расстояние между скрещивающимися прямыми (боковым ребром или высотой пирамиды и ребром или диагональю основания)

Тела вращения

Прямой круговой цилиндр
Сечение цилиндра плоскостью. Площадь боковой и полной поверхностей цилиндра. Объем цилиндра.

Угол между прямой и плоскостью (прямой в секущей плоскости и плоскостью основания); угол между плоскостями (сечения и основания); угол и расстояние между скрещивающимися прямыми (хордами двух оснований)

Прямой круговой конус
Сечение плоскостью. Усеченный конус. Площадь боковой и полной поверхностей конуса. Объем конуса.

Угол между прямой и плоскостью (образующей и плоскостью основания); угол между плоскостями (сечения и основания); угол и расстояние между скрещивающимися прямыми (образующей и хордой основания)

Шар и сфера
Сечение плоскостью. Площадь поверхности. Объем шара. Свойства фигуры, вписанной в сферу. Касательная плоскость


Особого внимания требуют вопросы, связанные с вычислением расстояний и углов в пространстве применительно к конкретной фигуре. Они остаются трудными для большинства учащихся, причем, даже в тех достаточно типичных ситуациях, которые используются в задачах повышенного уровня. Так, если в задачах высокого уровня сложности рассматривается угол между двумя плоскостями, которые зачастую являются плоскостями боковых граней или плоскостями проведенных сечений, то в задачах повышенного уровня это угол между плоскостью основания и плоскостью боковой грани пирамиды или плоскостью типичного сечения призмы. Задачи, связанные с такими ситуациями, из года в год присутствуют в вариантах ЕГЭ (как и в вариантах многих вступительных экзаменов в вузы), тем не менее, процент их верного решения невысок. Это объясняется двумя причинами. Первая причина связана с тем, что углы между плоскостями (а также другие вопросы, связанные с углами и расстояниями в пространстве) в учебниках часто рассматриваются и проходят первичное закрепление до изучения многогранников и тел вращения. Поэтому еще раз подчеркнем высказанную ранее мысль: очень важно при изучении каждого вида многогранников и тел вращения, а также при повторении материала обращать внимание учащихся на использование изученных ранее геометрических фактов для вычисления элементов рассматриваемой фигуры.

Вторая причина связана с задачами, в которых рассматриваются углы между прямой и плоскостью или между плоскостями, где необходимо применять планиметрический материал, нередко усвоенный непрочно. В данном случае речь идет о решении прямоугольных (реже – косоугольных) треугольников. Поэтому необходимо наиболее часто используемые сведения из планиметрии восстанавливать в памяти учащихся при изучении стереометрии. При этом более продуктивным является постепенное (и возможно, неоднократное) повторение тех вопросов, которые актуальны для изучаемого стереометрического материала. Например, при изучении параллельности прямых и плоскостей целесообразно повторить; свойства углов при параллельных прямых и секущей, свойства средних линий треугольника и трапеции, признаки подобия треугольников, а при изучении перпендикулярности прямых и плоскостей – определения тригонометрических функций острого угла прямоугольного треугольника, свойства треугольников и четырехугольников, связанные с перпендикулярностью. В дальнейшем часть из этих сведений, наиболее важную для решения задач, полезно повторять при изучении многогранников и тел вращения.

Вполне возможно, что часть учащихся, потенциально обладающих уровнем подготовки, достаточным для решения геометрических задач, помещаемых в варианты ЕГЭ, просто не доверяет своим знаниям и умениям и, предполагая, что задачи очень трудные, не пытаются их решить. Здесь, видимо, могло бы помочь более активное ознакомление учащихся с задачами, которые использовались в вариантах прошлых лет. Такие задачи представлены в сборниках, содержащих задания и варианты контрольных измерительных материалов, использованных при проведении ЕГЭ10. Знакомясь с ними, учащиеся не только повторят некоторые геометрические сведения и приемы решения, но также увидят, что задачи по планиметрии при рациональном способе решения не требуют длинной цепочки рассуждений и выкладок, а стереометрические задачи повышенного уровня построены на достаточно типичных ситуациях и тоже решаются в 2-3 действия.

Следует отметить, что в методической литературе в настоящее время имеется очень много пособий, предназначенных для подготовки к сдаче ЕГЭ. При этом довольно часто предлагаемые в них задания отражают взгляд автора на то, какие задачи должен уметь решать выпускник, чтобы сдать этот экзамен11. Не обсуждая вопрос о правильности авторской позиции, отметим, что с точки зрения информирования учащихся об уровне сложности задач и широте используемого содержания в процессе обучения целесообразно рассматривать задачи, непосредственно использовавшиеся в вариантах ЕГЭ.

Поскольку речь идет о задачах повышенного и высокого уровня сложности, то, естественно, на уроках геометрии в массовой общеобразовательной школе нет возможности рассматривать большое число таких задач. Поэтому можно некоторую их часть использовать для работы со всем классом, но, кроме того, предусмотреть их включение в индивидуальные задания (в классе и для домашней работы) для более подготовленных или просто желающих учащихся.


Итоги ЕГЭ 2006 г. позволяют высказать некоторые общие рекомендации, направленные на совершенствование процесса преподавания и подготовки учащихся средней школы.

1) Сравнительный анализ результатов выполнения базовых заданий одинаковой тематики в 2002 –2006 г.г. показал наличие повторяющихся из года в год типичных ошибок учащихся, о которых сообщается в ежегодных отчетах по результатам проведения ЕГЭ по математике, в сборниках по подготовке к ЕГЭ, опубликованных в открытой печати. Следует обратить внимание учителей, авторов учебников и разработчиков методических пособий на необходимость совершенствования методики формирования базовых умений, составляющих основу математической подготовки выпускников средней школы.

2) Анализ результатов выполнения базовых заданий по курсу алгебры и начал анализа показал наличие положительной динамики в овладении материалом раздела «тригонометрия», о существенных недочетах в усвоении которого говорилось в отчетах по результатам ЕГЭ в прошлые годы. В настоящее время вызывают тревогу низкие результаты выполнения заданий на решение иррациональных уравнений и логарифмических неравенств. Учителям в процессе обучения следует обратить внимание на обеспечение более прочного усвоения учащимися стандартных алгоритмов решения этих уравнений и неравенств.

3) Геометрическая подготовка выпускников школы продолжает оставаться невысокой, поэтому по-прежнему необходимо усиленное внимание учителей к преподаванию курса геометрии в основной и старшей школе, чтобы в процессе обучения учащиеся не только овладевали теоретическими фактами курса, но и приобретали умения проводить обоснованные рассуждения при решении геометрических задач и математически грамотно записывать полученное решение.

Письмо подготовлено

членами Федеральной предметной

комиссии по математике

к. п. н. Л.О. Денищевой,

к. п. н. Н.Б. Мельниковой,

к. п. н. К.А. Краснянской

на основе аналитического отчета

«Результаты единого государственного

экзамена 2006 года)»


1 Состояние общей математической подготовки учащихся оценивается на основе результатов выполнения ими всех заданий работы.

2 Состояние алгебраической подготовки учащихся по курсу алгебры и начал анализа оценивается на основе результатов выполнения алгебраических заданий работы. При этом не учитываются результаты выполнения четырех заданий: текстовой задачи (В9) и трех заданий по геометрии (В10, В11 и С4).

3 Имеется положительная динамика в овладении этим материалом ( при проверке ограниченного набора формул).

4 Перепроверка части работ участников ЕГЭ проводится ежегодно. В 2006 г. были также перепроверены работы всех учащихся, получивших максимальную тестовую оценку 100 баллов.

5 В КИМ для ЕГЭ такие задания относят к повышенному уровню сложности.

6 В КИМ 2006 г. предлагались уравнения типа

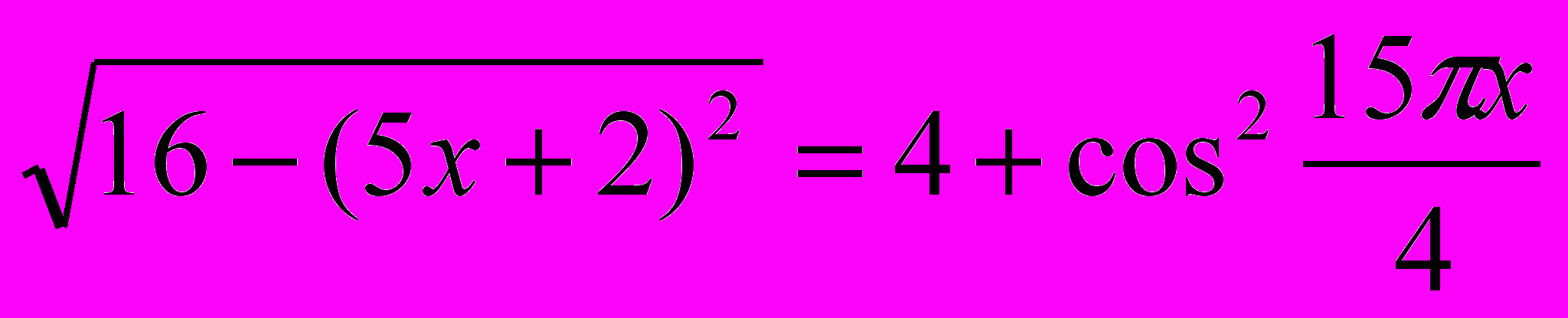
7 Так, к планиметрическим задачам в 2005 и 2006 годах не указывали ответ соответственно 50-82% и 54-79% участников ЕГЭ, к стереометрическим задачам – 45-76% и 55%-78%.

8 Помимо свойств параллелограмма и его разновидностей рассматриваются конфигурации, связанные с треугольниками. Поскольку любая диагональ делит параллелограмм на два равных треугольника, а высота выделяет прямоугольный треугольник, то все задачи на треугольники могут быть сформулированы и для параллелограммов. На эту возможность перехода от параллелограмма к треугольникам нужно обратить внимание учащихся.


9 Основные проблемы, связанные с решением задач на правильные многоугольники, возникают из-за слишком формального подхода к изучению этого материала. О том, как с этим бороться, можно прочитать в книге: Единый государственный экзамен: математика: методика подгот.: книга для учителя / [Л.О. Денищева, Ю.А Глазков, К.А. Краснянская и др.] М.:Просвещение, 2005.

10 Единый государственный экзамен: математика: Сборник заданий / [Л.О.Денищева, Г.К Безрукова, Е.М.Бойченко и др.] М-во образования и науки Рос.Федерации, Федерал. служба по надзору в сфере образования и науки – М.:Просвещение, 2005, 2006.


Единый государственный экзамен: математика: Контрольные измерительные материалы / [Л.О.Денищева, Г.К Безрукова, Е.М.Бойченко и др.] М-во образования и науки Рос.Федерации, Федерал. служба по надзору в сфере образования и науки – М.:Просвещение, 2005, 2006.


11 При работе с учебными материалами, связанными с подготовкой к ЕГЭ по любому предмету, обратите внимание на наличие грифа Федерального института педагогических измерений (ФИПИ), который занимается разработкой КИМ. Этот гриф учебное пособие может получить при прохождении экспертизы в ФИПИ.