Учебно-методический комплекс по циклу дисциплин ен. Ф. 02 Для студентов очной и заочной формы обучения по специальности 030501. 65 «Юриспруденция»

Вид материала

Учебно-методический комплекс

Содержание 1.Учебно-тематические планы Наименование темы Итого по дисциплине Контрольная работа Учебно-тематический план занятий Наименование темы Итого по дисциплине Контрольная работа 2. Программа дисциплины Тема 2. Элементы высшей алгебры Тема 3. Дифференцирование и интегрирование функций Тема 4. Теория множеств Тема 5. Математическая логика Тема 6. Комбинаторика Тема 7. Теория вероятностей Тема 8. Математическая статистика Тема 9. Математическое моделирование и принятие решений 3. Список литературы Дополнительная литература 4. Планы практических занятий ... Полное содержание

Подобный материал:

• Учебно-методический комплекс по циклу дисциплин гсэ. Н-р. 04 Для студентов очной, 211.12kb.
• Учебно-методический комплекс по циклу дисциплин опд. Ф. 08 для студентов очной и заочной, 904.8kb.
• Учебно-методический комплекс по циклу дисциплин ен. Ф. 03 Для студентов очной и заочной, 506.68kb.
• Учебно-методический комплекс по циклу дисциплин опд. В. 01а для студентов очной (заочной), 614.11kb.
• Учебно-методический комплекс по циклу дисциплин опд. Н-р. 02 Для студентов очной (заочной), 546.9kb.
• Учебно-методический комплекс по циклу дисциплин опд. Н-р. 01 для студентов очной, 1693.75kb.
• Учебно-методический комплекс по циклу дисциплин дс. 03 для студентов очной формы обучения, 248.01kb.
• Учебно-методический комплекс по циклу дисциплин опд. Ф. 11 для студентов заочной формы, 668.86kb.
• Учебно-методический комплекс по циклу дисциплин опд. Ф. 03 Для студентов очной формы, 560.05kb.
• Учебно-методический комплекс по циклу дисциплин опд. Ф. 23 для студентов очной формы, 441.02kb.

НЕГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

КУЗБАССКИЙ ИНСТИТУТ ЭКОНОМИКИ И ПРАВА

ЭКОНОМИЧЕСКИЙ ФАКУЛЬТЕТ

КАФЕДРА МАТЕМАТИЧЕСКИХ И ЕСТЕСТВЕННО-НАУЧНЫХ ДИСЦИПЛИН

МАТЕМАТИКА

УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС

по циклу дисциплин ЕН.Ф.02

ДЛЯ СТУДЕНТОВ ОЧНОЙ И ЗАОЧНОЙ ФОРМЫ ОБУЧЕНИЯ

по специальности

030501.65 – «Юриспруденция»

КЕМЕРОВО 2007

Математика: учебно-методический комплекс для студентов очной и заочной формы обучения / сост. Т. Д. Чекменева, Л.А.Андреева; Кузбас. ин-т экон. и права. – Кемерово, 2007. – 22 с.


Настоящий учебно-методический комплекс разработан в соответствии с Государственным образовательным стандартом высшего профессионального образования по специальности – 021100 (030501.65) «Юриспруденция» (утв. Министерством образования РФ от 27 марта 2000 г.).

УМКд содержит все необходимые для изучения и преподавания курса «Математика» учебно-методические материалы.

Предназначен для студентов первого курса очной и заочной формы обучения юридического факультета института.


Утвержден на заседании кафедры математических и естественно-научных дисциплин

Протокол № ____ от « ____ » ________________ 2007г.


И.О. Зав. кафедрой ________________ Ан.И. Щербаков


Рекомендован для издания методической комиссией института

Протокол № _____ от «____ » ______________ 2007 г.

Секретарь комиссии ________________О.Ю. Сиялко


Утвержден

Проректор по учебной работе

_______________ Г.А. Мартынов

«____» _____________ 2007 г.


Зарегистрирован в методкабинете «_____» ________________ 2007г.


регистрационный номер _______

СОДЕРЖАНИЕ

Введение 4

1. Учебно-тематические планы 6

1.1.Учебно-тематический план занятий

для студентов очной формы обучения 6

1.2. Учебно-тематический план занятий

для студентов заочной формы обучения 7

2. Программа дисциплины 8

3. Список литературы 10

4. Планы практических занятий 11

4.1 Планы практических занятий для студентов

очной формы обучения 11

4.2 Планы практических занятий для студентов

заочной формы обучения 14

5. Методические указания по выбору и выполнению

контрольной работы для студентов заочной формы обучения 15

6. Задания для контрольной работы 16

7. Контрольные вопросы для самостоятельной проверки знаний 19

8. Примерные вопросы зачету 21

ВВЕДЕНИЕ

Предметом учебной дисциплины «Математика» являются количественные отношения между величинами и пространственными формами, отражающие отношения как между реальными, так и между абстрактными объектами (математическими структурами).

Математика имеет дело с возможными мирами структур, упорядоченными совокупностями объектов различной (любой) природы. Тем самым математика раздвигает область своего приложения и актуализирует ее. Математизация гуманитарных наук способствует познанию, управлению, прогнозированию изучаемых объектов, явлений, процессов.

Математика обладает исключительно эффективными методами и инструментами познания, которые помогают моделировать и анализировать различные варианты (сценарии) поведения, определять цели и условия их достижения, принимать оптимальные в данных условиях решения.

Изучение основ математики позволит будущим юристам расширить профессиональные возможности, сформировать качественное профессиональное мышление.

Цель преподавания данной дисциплины заключается в подготовке специалистов, знакомых с основными методами и подходами, инструментами и разделами современной математики; умеющих пользоваться ее языком и терминологией; понимающих ее методологические основы. Математизация гуманитарного образования ориентирована на обучение математическому мышлению, а также на развитие с помощью математики профессионального мышления будущих специалистов. Этой цели соответствуют содержание и структура курса, а также стоящие перед ним задачи.

Задачи изучения дисциплины.

В результате изучения математики студенты должны знать: основные понятия и термины языка математики; методы изучения абстрактных математических объектов; разделы (теории) математической науки, наиболее важные для применения.

Студенты должны уметь пользоваться основными понятиями и методами важнейших математических теорий, формулировать задачи в соответствующих терминах, интерпретировать результаты применения математического аппарата.

К основным видам занятий относятся: лекционные и практические занятия, а также самостоятельная работа студентов. Для студентов заочной формы обучения юридического факультета обязательным является выполнение контрольной работы.

Приступая к изучению курса «Математика» студенты должны ознакомиться с данным учебно-методическим комплексом, чтобы получить общее представление о курсе в целом, его системе, содержании, круге вопросов по каждой теме, последовательности изложения материала.


Практические занятия по изучаемой дисциплине призваны:

- закрепить полученные на лекционных занятиях знания;

- выработать умения пользоваться основными понятиями и методами важнейших математических теорий, решать поставленные задачи;

- закрепить навыки.

В результате изучения дисциплины студенты должны:

— иметь представление об основных методах и подходах, инструментах и разделах современной математики;

— знать основные понятия и термины языка математики; методы изучения абстрактных математических объектов; разделы (теории) математической науки, наиболее важные для применения;

— уметь применять полученные знания при решении математических задач.


1.УЧЕБНО-ТЕМАТИЧЕСКИЕ ПЛАНЫ

1. УЧЕБНО-ТЕМАТИЧЕСКИЙ ПЛАН ЗАНЯТИЙ
   

для студентов очной формы обучения

№ п\п		Наименование темы	Количество часов
			Аудиторные занятия			Сам. работа	Всего
			всего аудит.	лек- ции	практ.занят.
1		2	3	4	5	6	7
1-й семестр
1	Предмет математики, основные математические структуры		4	2	2	4	8
2	Элементы высшей алгебры		5	4	1	6	11
3	Дифференцирование и интегрирование функций		8	6	2	6	14
4	Теория множеств		3	2	1	4	7
5	Математическая логика		3	2	1	4	7
6	Комбинаторика		3	2	1	4	7
7	Теория вероятностей		6	4	2	10	16
8	Математическая статистика		12	8	4	6	18
9	Математическое моделирование и принятие решений		6	4	2	6	12
	Итого по дисциплине:		50	34	16	50	100
	Форма итогового контроля		Зачет		Контрольная работа
			1 семестр		-

Примечание. Самостоятельная работа студентов включает в себя изучение студентами некоторых тем курса, подготовку к практическим занятиям, тестированию, зачету, выполнение домашнего задания.

2. УЧЕБНО-ТЕМАТИЧЕСКИЙ ПЛАН ЗАНЯТИЙ
   

для студентов заочной формы обучения

№ п/п	Наименование темы	Количество часов
		Аудиторные занятия			Сам. работа	Всего
		всего аудит.	лек- ции	практ.занят.
1	2	3	4	5	6	7
1-й семестр
1	Предмет математики, основные математические структуры	1	1	-	6	7
2	Элементы высшей алгебры	3	2	1	10	13
3	Дифференцирование и интегрирование функций	4	2	2	12	16
4	Теория множеств	-	-	-	10	10
5	Математическая логика	-	-	-	10	10
6	Комбинаторика	-	-	-	12	12
7	Теория вероятностей	2	1	1	10	12
8	Математическая статистика	-	-	-	10	10
9	Математическое моделирование и принятие решений	-	-	-	10	10
	Итого по дисциплине:	10	6	4	90	100
	Форма итогового контроля	Зачет		Контрольная работа
		1 семестр		+

Примечание. Самостоятельная работа студентов включает в себя изучение студентами некоторых тем курса, подготовку к практическим занятиям, тестированию, зачету, выполнение контрольной работы.


2. ПРОГРАММА ДИСЦИПЛИНЫ


Тема 1. Предмет математики, основные математические структуры


История развития математики, основные этапы. Содержание понятия «математика». Предмет математики как науки. Математический язык, его особенности и применение. Аксиоматический метод. Место и роль математики в современном мире. Основные математические структуры: алгебраические структуры, структуры порядка, топологические структуры. Важные разделы математики, их методы и инструменты.


Тема 2. Элементы высшей алгебры


Матрицы. Свойства матриц. Понятие обратной матрицы. Определители. Свойства определителей. Решение и исследование системы трех уравнений первой степени с тремя неизвестными.


Тема 3. Дифференцирование и интегрирование функций


Понятие производной. Понятие дифференциала. Связь дифференциала и производной функции. Правила дифференцирования суммы, разности, произведения и частного. Теорема о производной сложной функции. Применение производной к исследованию функций. Понятие первообразной и неопределенного интеграла. Свойства неопределенного интеграла. Основные методы интегрирования. Понятие определенного интеграла и его свойства. Некоторые физические и геометрические приложения определенного интеграла.


Тема 4. Теория множеств


Теория множеств как язык математики. Основные понятия теории множеств. Операции над множествами и их обозначения. Диаграммы Венна.


Тема 5. Математическая логика


Логика – наука о законах мышления. Математическая (символическая) логика как основа и язык научной теории. Двузначная логика, логические высказывания. Логические операции и их обозначения. Правила логических выводов, истинностные таблицы.


Тема 6. Комбинаторика


Комбинаторика – раздел дискретной математики. Задачи комбинаторики. Основные правила комбинаторики: правило сложения, правило умножения. Основные формулы комбинаторики: перестановки, сочетания, размещения.


Тема 7. Теория вероятностей


Понятие о случайных событиях и их вероятностях. Виды событий, операции над случайными событиями. Классическое определение вероятности, геометрические вероятности. Относительная частота и вероятность. Аксиомы теории вероятностей. Пространство элементарных событий, алгебра событий. Теоремы сложения и умножения, схема испытаний Бернулли.

Понятие о случайной величине и законе распределения. Нормальный закон распределения, его таблицы. Дискретные и непрерывные величины, их числовые характеристики. Правило «трех сигм». Понятие о законе больших чисел и центральной предельной теореме.


Тема 8. Математическая статистика


Основные задачи и понятия математической статистики. Ряды распределения, их иллюстрация. Статистические оценки числовых характеристик распределения. Изучение зависимостей: корреляция, регрессия, взаимосвязь неколичественных признаков, анализ дисперсий. Изучение динамики явлений. Понятие динамических (временных) рядов, их классификация, правила построения. Показатели анализа рядов динамики (показатели интенсивности изменения, средние показатели динамики). Изучение тенденции временного ряда (тренда), методы выделения тренда. Автокорреляция временного ряда, коррелограмма, ее применение.


Тема 9. Математическое моделирование и принятие решений


Математическое моделирование как необходимое условие обоснованного принятия решений. Основные классы математических моделей (теорий). Исследование операций как наука применения математических методов и моделей для выбора и обоснования решений, его основные разделы. Теория игр – теория математических моделей конфликтов. Антагонистическая игра, принцип минимакса. Понятие смешанной стратегии. Биматричная игра, принцип равновесия. Понятие о коалиционных играх многих лиц и принципах оптимальности. Игры с «природой», принципы оптимальности. Понятие риска. Принятие решений в условиях риска и неопределенности.


3. СПИСОК ЛИТЕРАТУРЫ


ОСНОВНАЯ ЛИТЕРАТУРА

1. Гмурман В. Е. Теория вероятностей и математическая статистика: учебное пособие для студентов вузов.- 4-е изд. - М.: Высш. шк., 1997. – 400 с.
   
2. Рассолов М.М. Элементы высшей математики для юристов / М.М. Рассолов, С.Г. Чубукова, В.Д. Элькин. – М.: Юристъ, 1999.
   
3. Тихомиров Н.Б. Математика: учебный курс для юристов / Н.Б. Тихомиров, А.М. Шелехов. – М.: Юрайт, 1999. – 223 с.
   
4. Шипачев В.С. Курс высшей математики: учебник / под ред. А.Н.Тихонова. – М,: ПБОЮЛ М.А.Захаров, 2002. – 600 с.
   

ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА

5. Вентцель Е. С. Исследование операций: задачи, принципы, методология. – М.: Наука, 1980.
   
6. Гнеденко Б. В. Математика и математическое образование в современном мире. – М., 1985.
   
7. Горелик В. А. Исследование операций: учебник / В.А. Горелик, И.А. Ушаков. – М.: Машиностроение, 1986. – 288 с.
   
8. Грес П. В. Математика для гуманитариев: учебное пособие. – М.: Логос, 2003. – 120 с.
   
9. Гусаров В. М. Статистика: учебное пособие для вузов – М.: ЮНИТИ-ДАНА, 2002.
   
10. Дубров А. М. Моделирование рисковых ситуаций в экономике и бизнесе: учебное пособие / А.М. Дубров, Б.А. Лагоша, Е.Ю. Хрусталев; под ред. Б. А. Лагоши. – М.: Финансы и статистика, 1999. – 176 с.
    
11. Математический энциклопедический словарь / под ред. Ю. В. Прохорова. – М.: Сов.энцикл., 1988. – 847 с.
    
12. Москинова Г. И. Дискретная математика. Математика для менеджера в примерах и упражнениях. – М.: Логос, 2000.
    
13. Мышкис А. Д. Элементы теории математических моделей. – М.: Физматлит, 1994.
    
14. Очерки по истории математики / под ред. Б. В. Гнеденко. – М.: Изд-во МГУ, 1997.
    
15. Юшкевич А. П. Математика и ее история. – М.: Янус, 1996.
    

4. ПЛАНЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ


4.1.ПЛАНЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ

для студентов очной формы


Тема 1. Предмет математики, основные математические структуры

Время -2 часа


Основные математические структуры: алгебраические структуры, структуры порядка, топологические структуры (числовые множества, векторы, матрицы, ряды и др.).

Решение заданий и задач.


Литература: [1, 2, 3, 6]


Тема 2. Элементы высшей алгебры

Время – 1 час


Свойства матриц. Понятие обратной матрицы. Свойства определителей.

Решение и исследование системы трех уравнений первой степени с тремя неизвестными.

Решение заданий и задач.


Литература: [3, 4, 8]


Тема 3. Дифференцирование и интегрирование функции

одной переменной

Время – 2 часа


Производная. Дифференциал. Правила дифференцирования суммы, разности, произведения и частного. Теорема о производной сложной функции. Применение производной к исследованию функций.

Первообразная и неопределенный интеграл. Основные методы интегрирования. Определенный интеграл и его свойства. Методы интегрирования определенного интеграла.

Решение заданий и задач.


Литература: [3, 4, 8]


Тема 4. Теория множеств

Время -1 час


Основные понятия теории множеств. Операции над множествами. Диаграммы Венна.

Решение задания и задач.


Литература: [1, 2, 8]


Тема 5. Математическая логика

Время -1 час


Логические высказывания, логические операции. Правила логических выводов, истинностные таблицы.

Решение заданий и задач.


Литература: [1, 2, 8]


Тема 6. Комбинаторика

Время – 1 час


Правила комбинаторики: правило сложения, правило умножения. Факториалы. Формулы комбинаторики: число перестановок, сочетаний, размещений.

Решение заданий и задач.


Литература: [1, 8]


Тема 7. Теория вероятностей

Время – 2 часа


Классическое определение вероятности, геометрические вероятности. Пространство элементарных событий, алгебра событий. Теоремы сложения и умножения, схема испытаний Бернулли. Закон распределения дискретной случайной величины, ее числовые характеристики. Правило «трех сигм». Самостоятельная работа.

Решение заданий и задач.


Литература: [1, 2, 8]


Тема 8. Математическая статистика

Время – 4 часа


Ряды распределения, их иллюстрация. Числовые характеристики распределения. Корреляция, парная линейная регрессия. Показатели анализа динамики. Определение линейного тренда, прогнозирование. Самостоятельная работа.

Решение заданий и задач.


Литература: [2, 8, 9]


Тема 9. Математическое моделирование и принятие решений

Время – 2 часа


Антагонистическая игра, принцип минимакса. Биматричная игра, принцип равновесия. Игры с «природой», принципы оптимальности. Понятие риска. Принятие решений в условиях риска и неопределенности.

Решение заданий и задач.


Литература: [1, 3, 8, 13]


4.2. ПЛАНЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ

для студентов заочной формы


Тема 1. Элементы высшей алгебры

Время – 1 час


Свойства матриц. Понятие обратной матрицы. Свойства определителей. Решение и исследование системы трех уравнений первой степени с тремя неизвестными.

Решение заданий и задач.


Литература: [3, 4, 8]


Тема 2. Дифференцирование и интегрирование функции

одной переменной

Время – 2 часа


Производная. Дифференциал. Правила дифференцирования суммы, разности, произведения и частного. Теорема о производной сложной функции. Применение производной к исследованию функций. Первообразная и неопределенный интеграл. Основные методы интегрирования. Определенный интеграл и его свойства. Методы интегрирования определенного интеграла.

Решение заданий и задач.


Литература: [3, 4, 8]


Тема 3. Теория вероятностей

Время – 1 час


Классическое определение вероятности, геометрические вероятности. Пространство элементарных событий, алгебра событий. Теоремы сложения и умножения, схема испытаний Бернулли. Закон распределения дискретной случайной величины, ее числовые характеристики. Правило «трех сигм». Самостоятельная работа.

Решение заданий и задач.


Литература: [1, 2, 8]


5. Методические указания по выбору

и выполнению контрольной работы

для студентов заочной формы обучения

В контрольной работе внимание уделяется вопросам подготовленности студентов к самостоятельному и эффективному использованию полученных знаний по дисциплине для решения поставленных задач.

Лекции для студентов заочного отделения выполняют в большей степени ориентирующую функцию, поэтому в качестве «отчета» об освоении курса им предстоит выполнить контрольную работу.

После выбора варианта контрольной работы требуется подобрать, изучить необходимую для ее выполнения литературу. Определяя перечень литературы и других материалов, важно руководствоваться списком источников, которые представлены в УМКд.

Если в процессе изучения материала или при решении той или иной задачи у студента возникают трудности, то можно обратиться к преподавателю кафедры математических и естественно-научных дисциплин для получения консультации. При выполнении контрольной работы студент должен руководствоваться следующими указаниями:

- контрольную работу следует выполнять в отдельной тетради, на внешней обложке которой должны быть указаны ФИО студента, номер зачетной книжки;

- решение всех задач и пояснения к ним должны быть достаточно подробными. Рекомендуется делать соответствующие ссылки на вопросы теории с указанием формул, теорем, выводов, которые используются при решении;

- все вычисления должны быть приведены полностью;

- для удобства рецензирования преподавателем контрольной работы следует оставлять на каждой странице широкие поля.

В случае незачета контрольной работы студент должен в кратчайшие сроки выполнить все требования рецензента и представить работу на повторное рецензирование, приложив при этом первоначальный (с замечаниями) вариант работы. Контрольная работа должна выполняться самостоятельно. На зачете студент обязан представить зачтенную контрольную работу и по требованию преподавателя дать устные пояснения ко всем задачам, содержащимся в работе.

Контрольная работа включает в себя 5 заданий. В задании пример или задача выбираются в соответствии со своим вариантом. Вариант соответствует последней цифре номера зачетной книжки.

6. Задания для контрольной работы

для студентов заочной формы обучения


Задание 1. Проверить, совместна ли система, и решить ее методом Крамера


Вариант 1, 6 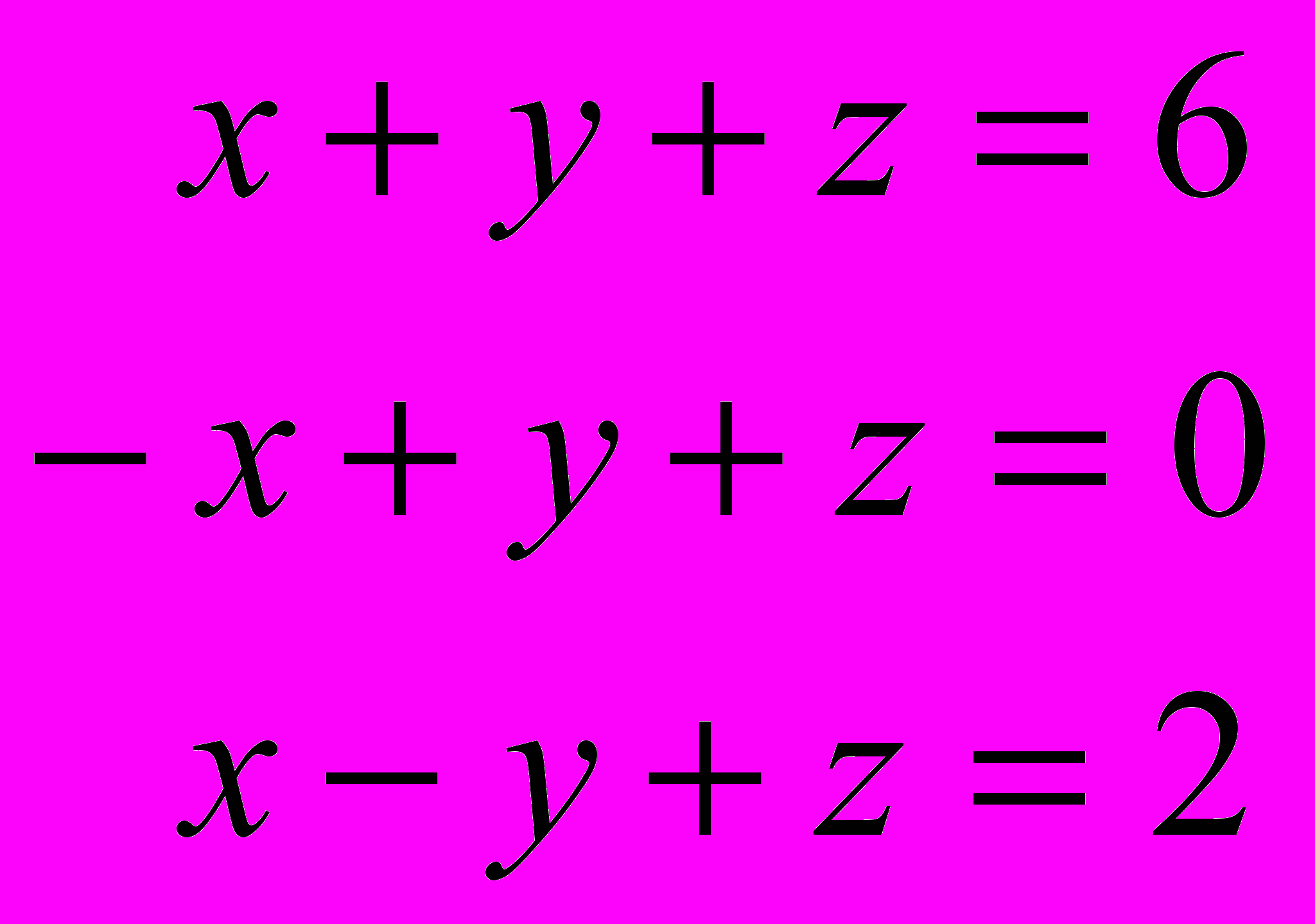Вариант 3, 8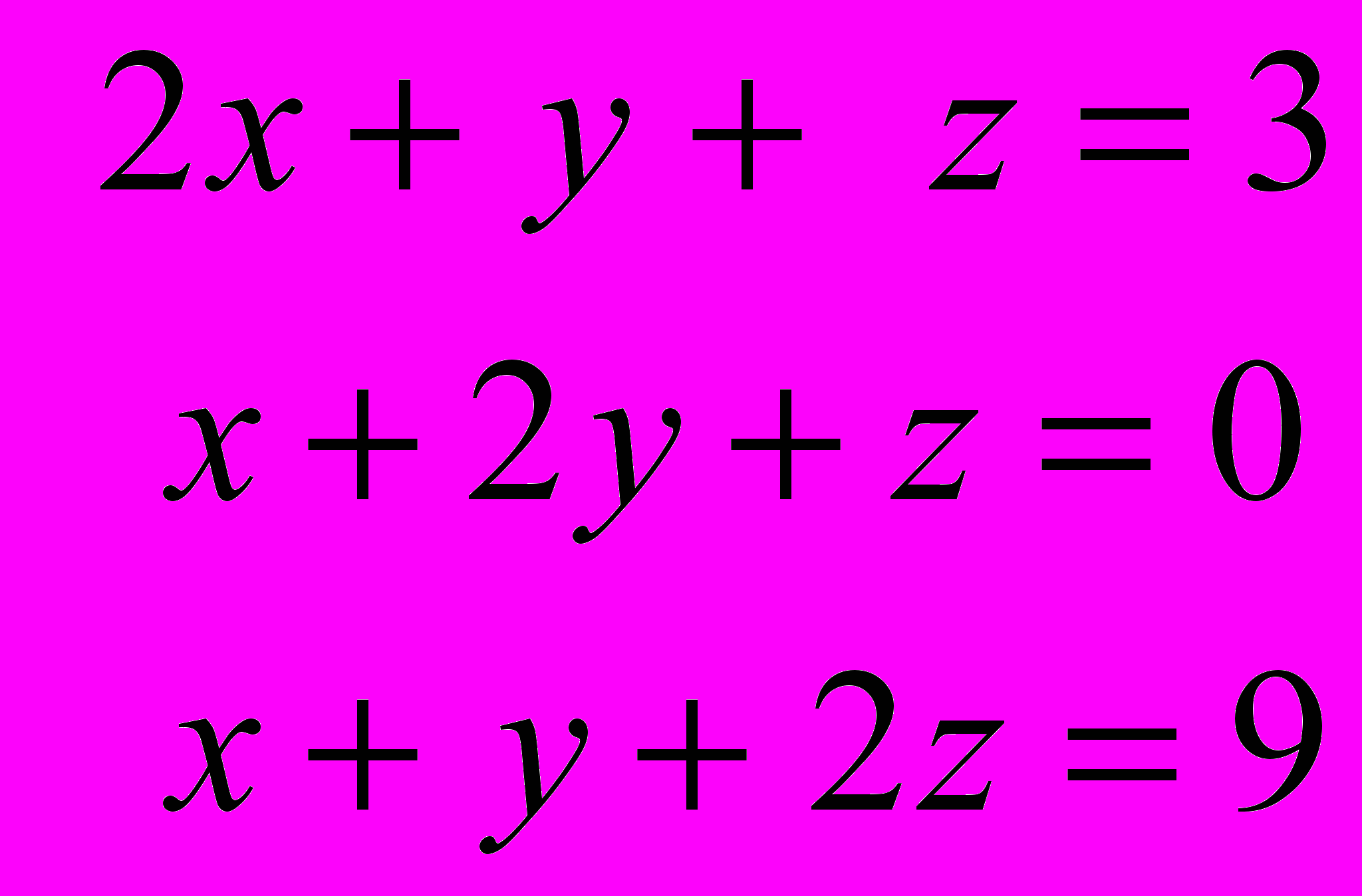

Вариант 2, 7 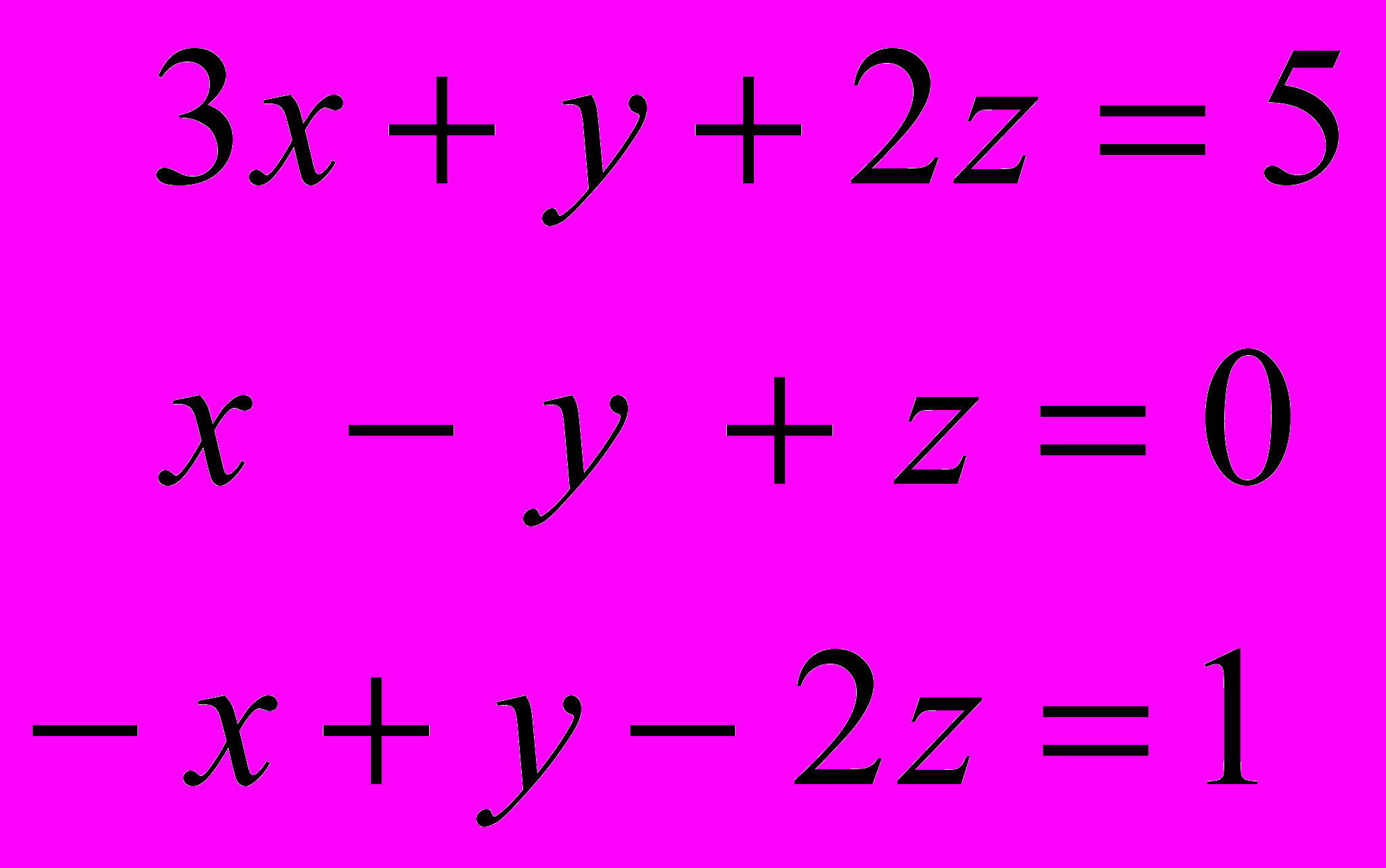Вариант 4, 9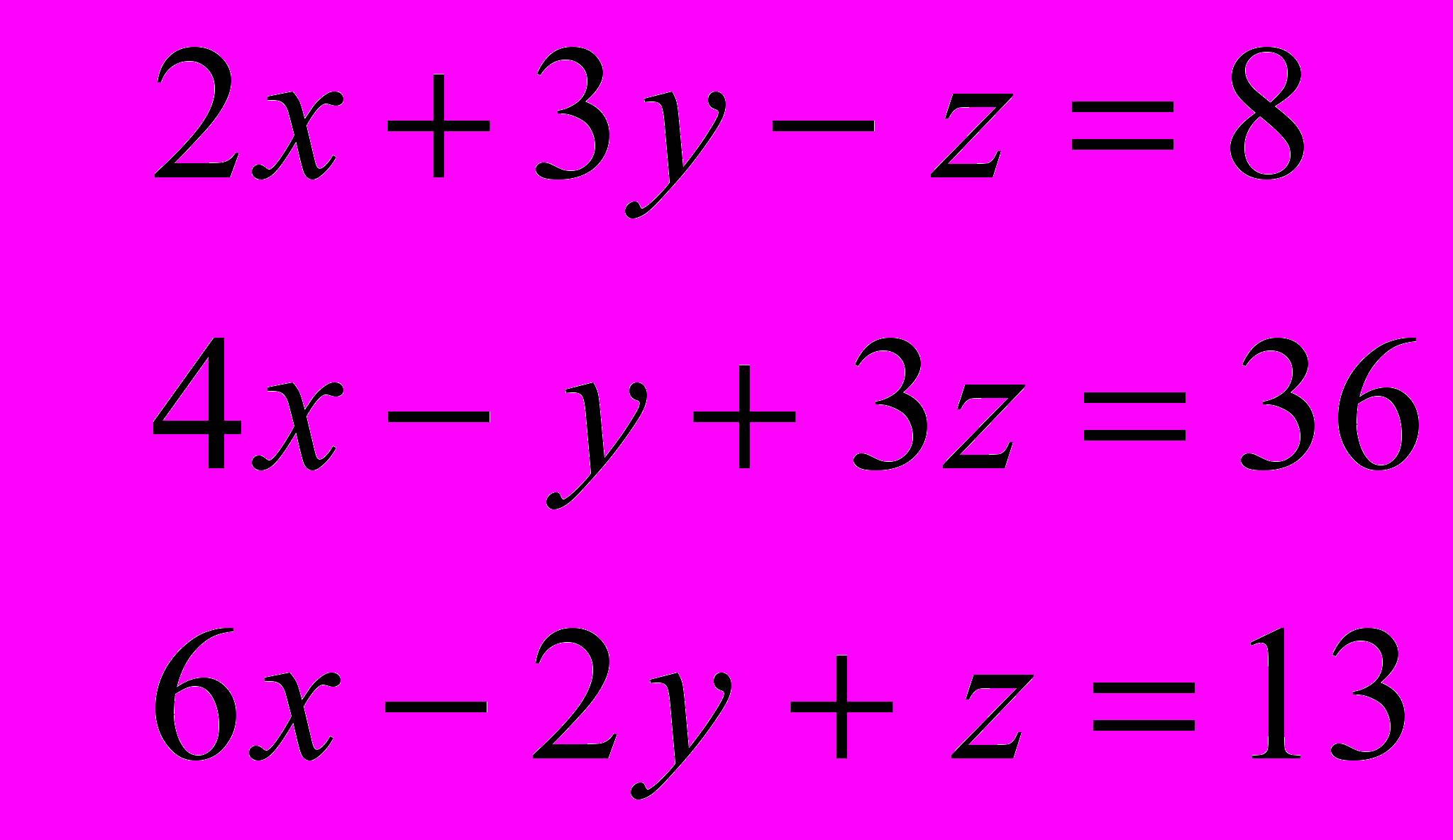


Вариант 5, 0

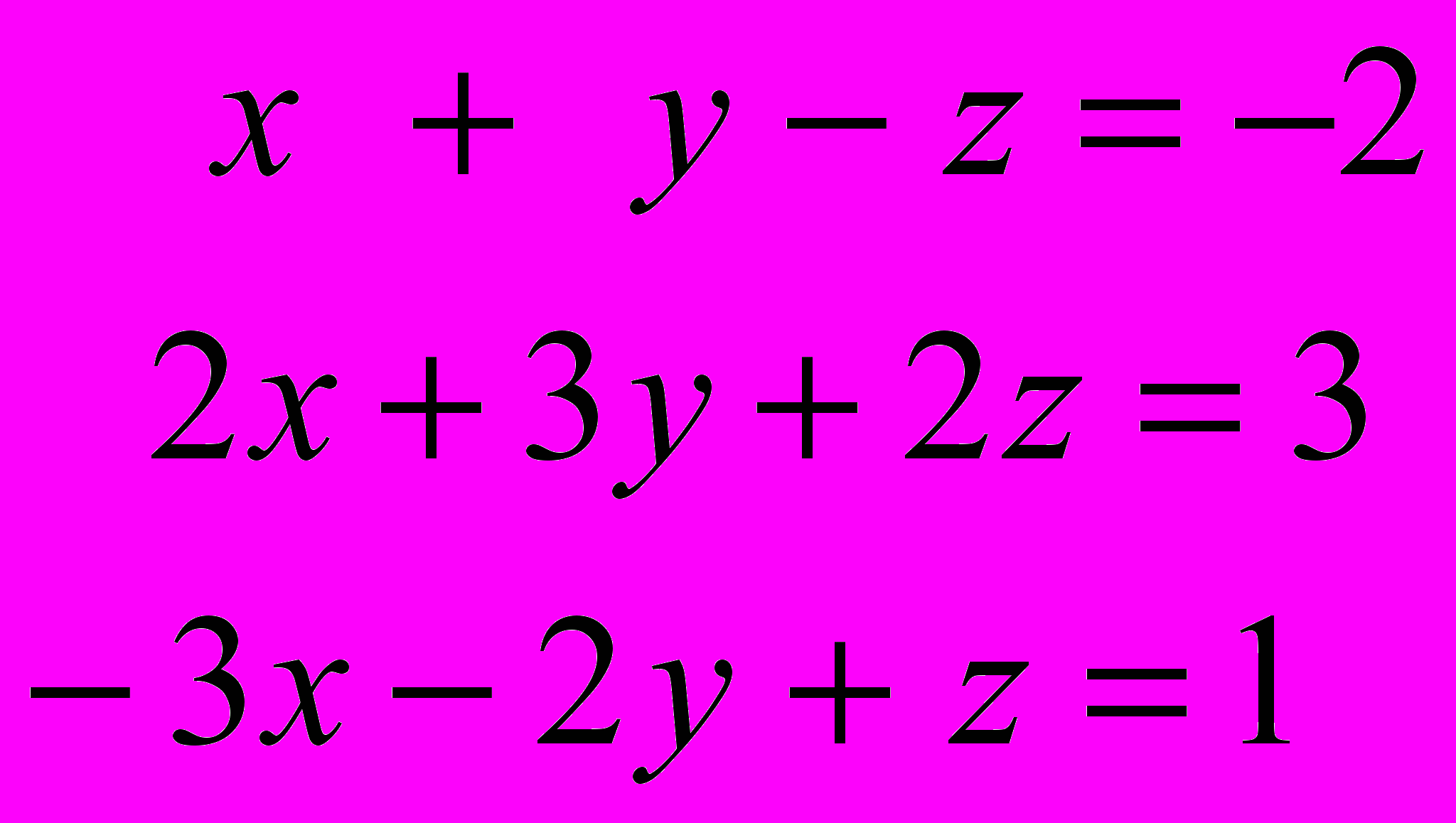
Задание 2. Найти производные и дифференциалы указанных функций


Вариант 1, 6


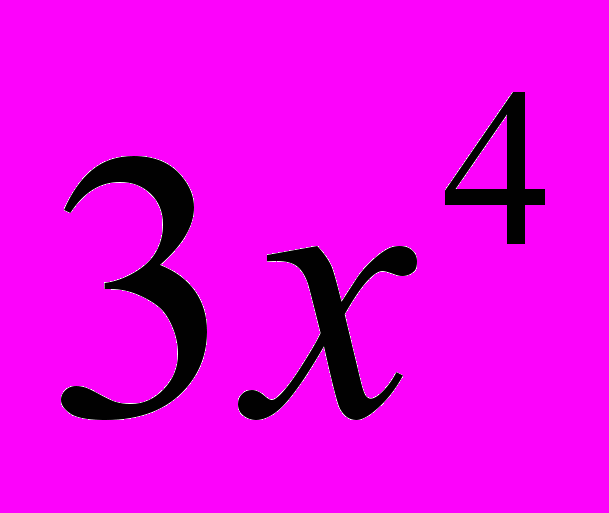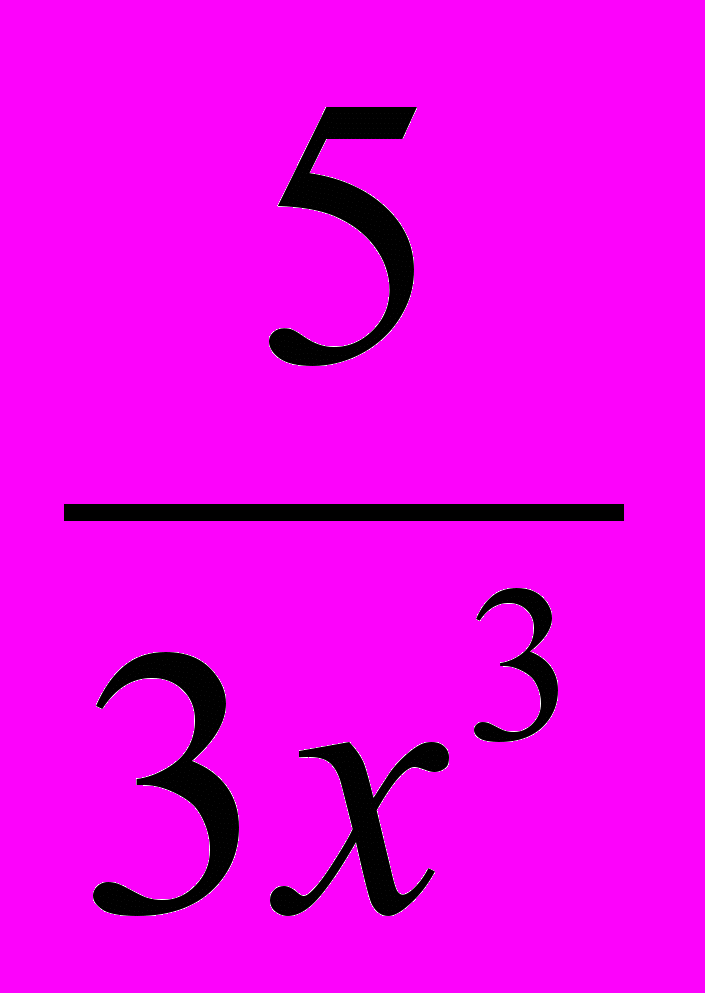
а) y = - - - 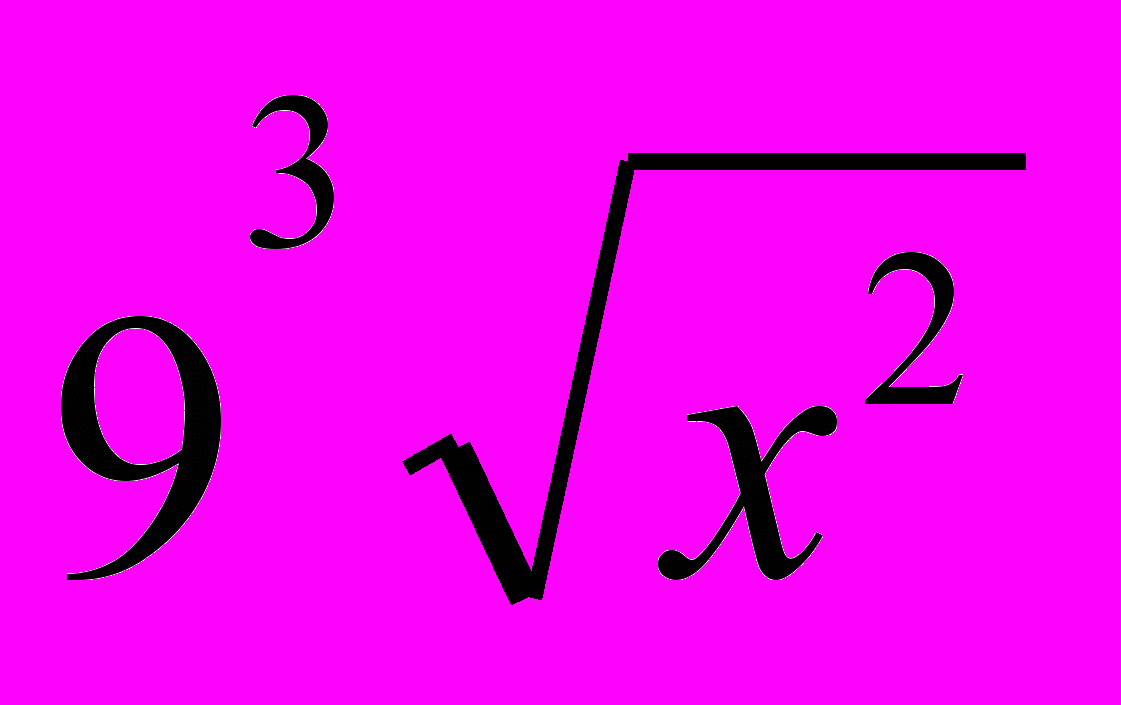1; б) y = (x³ + 1)*ln x ;


в) y = 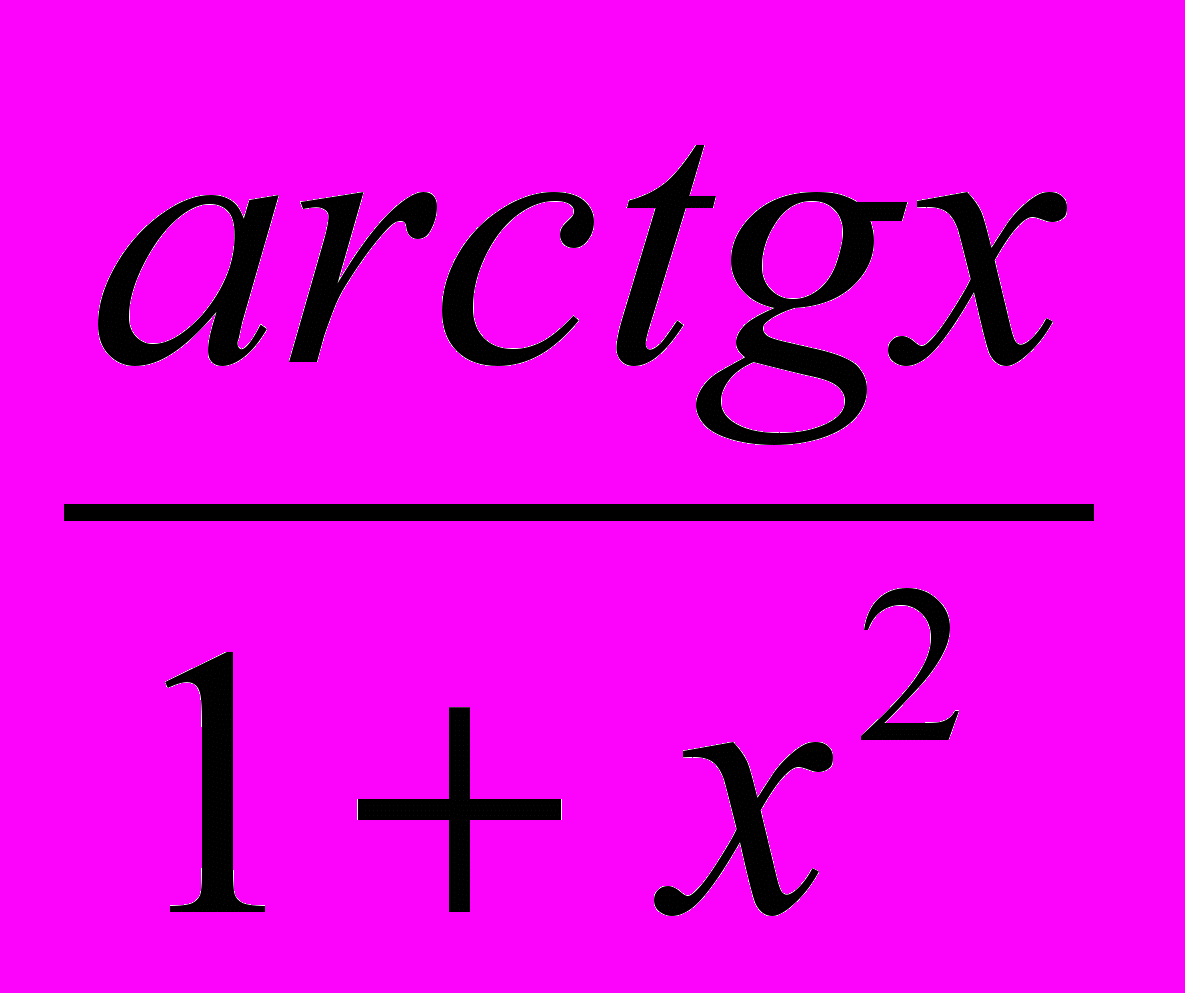; г) y = ;


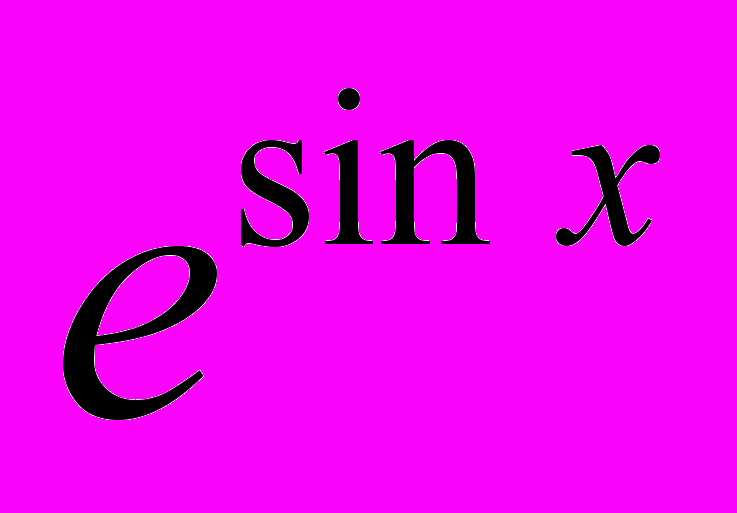Вариант 2, 7


а) y = 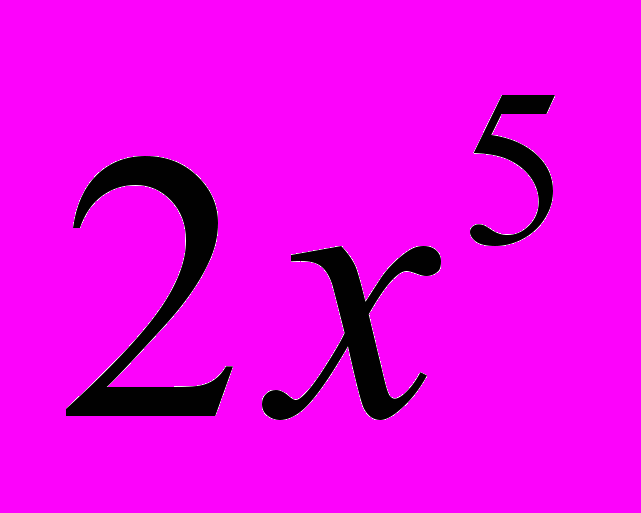- 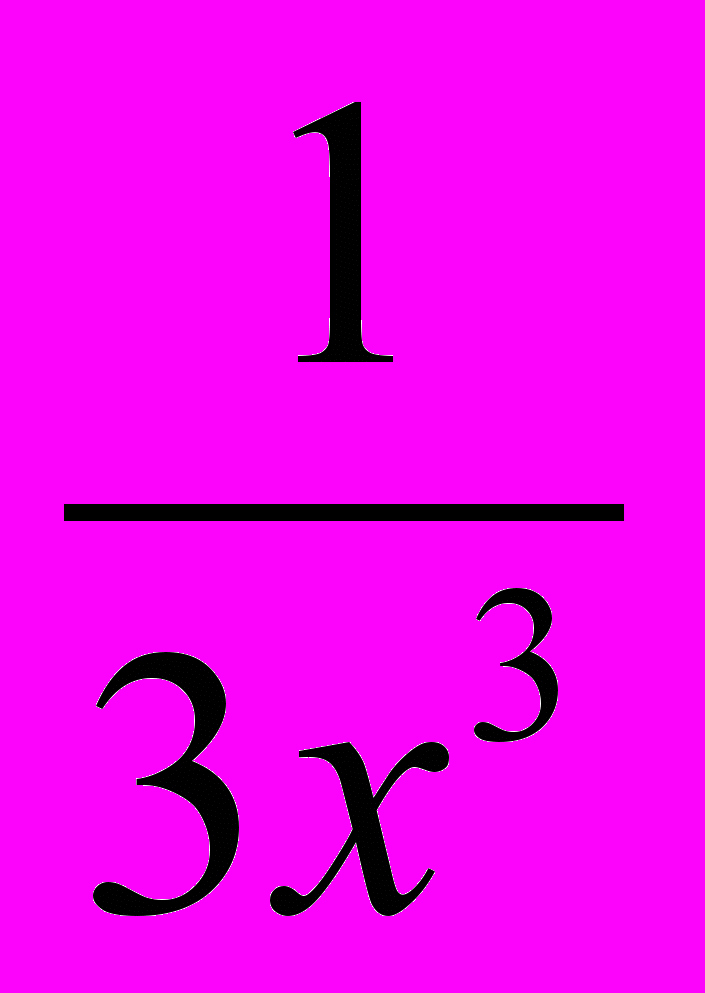+ 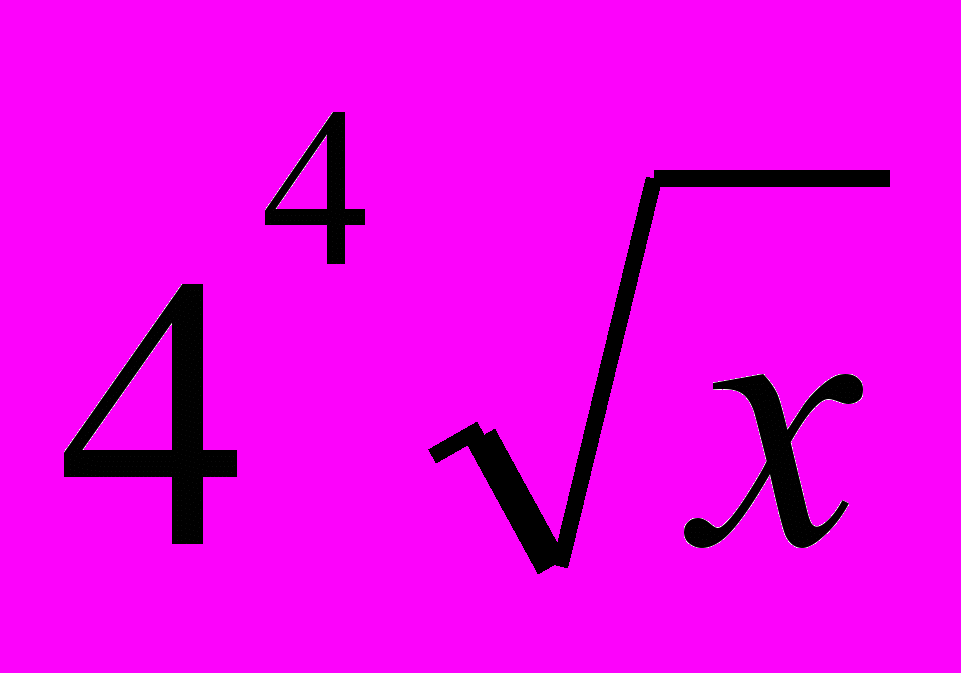; б) y = (x² – 2)*sin x;


в) y = 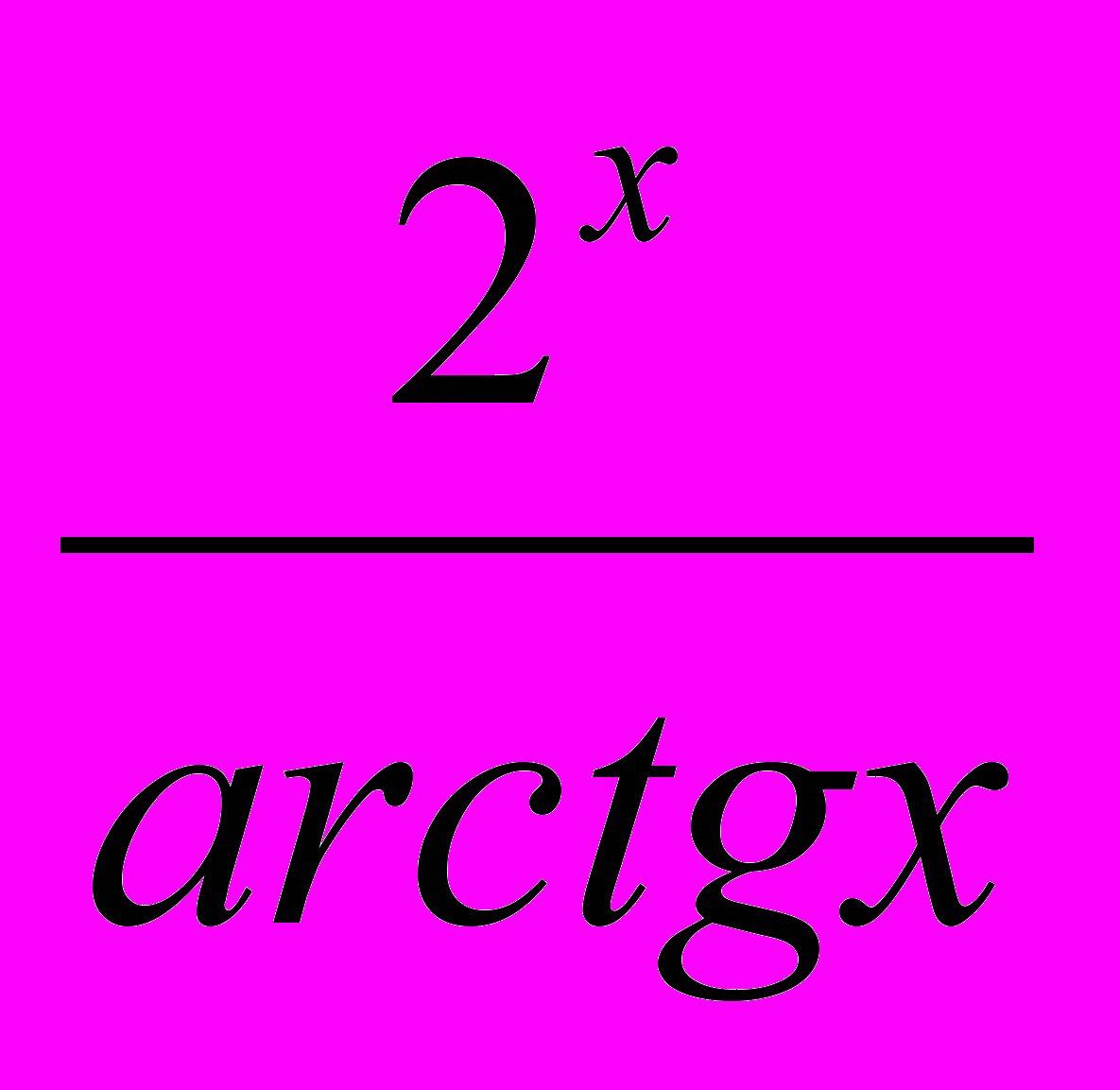; г) y = .


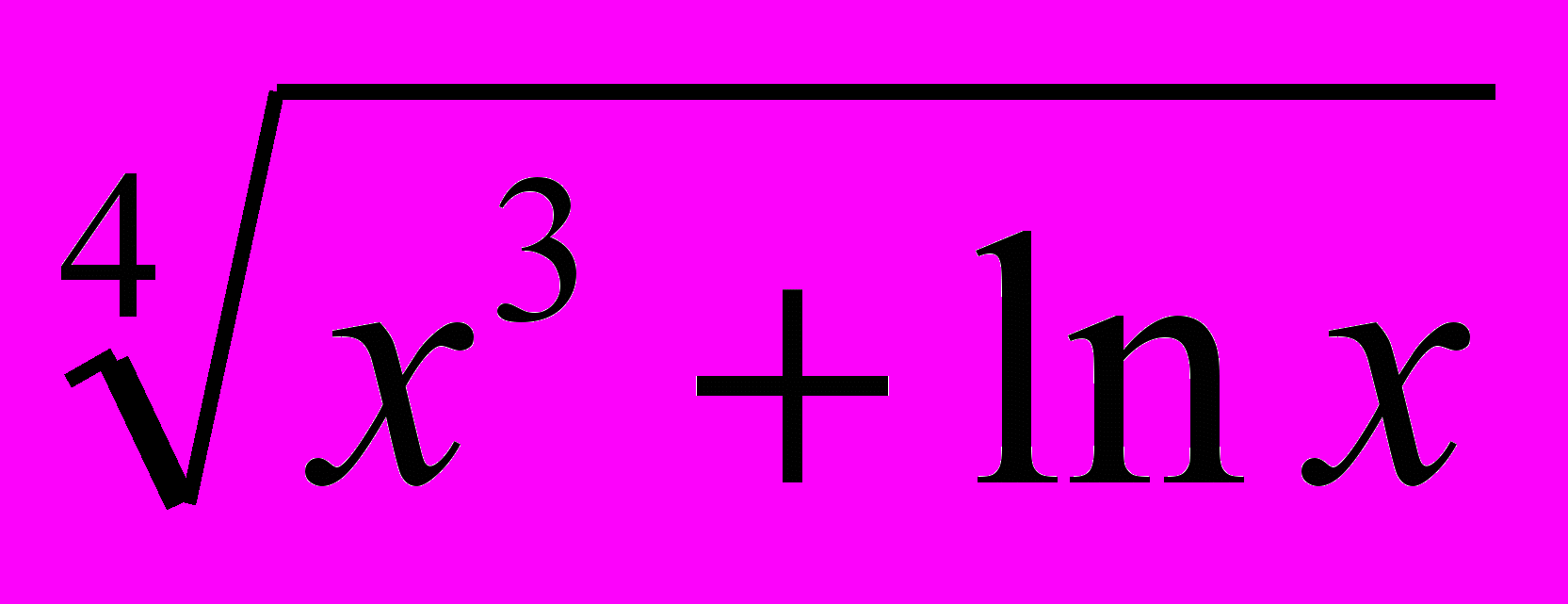Вариант 3, 8


а) y = 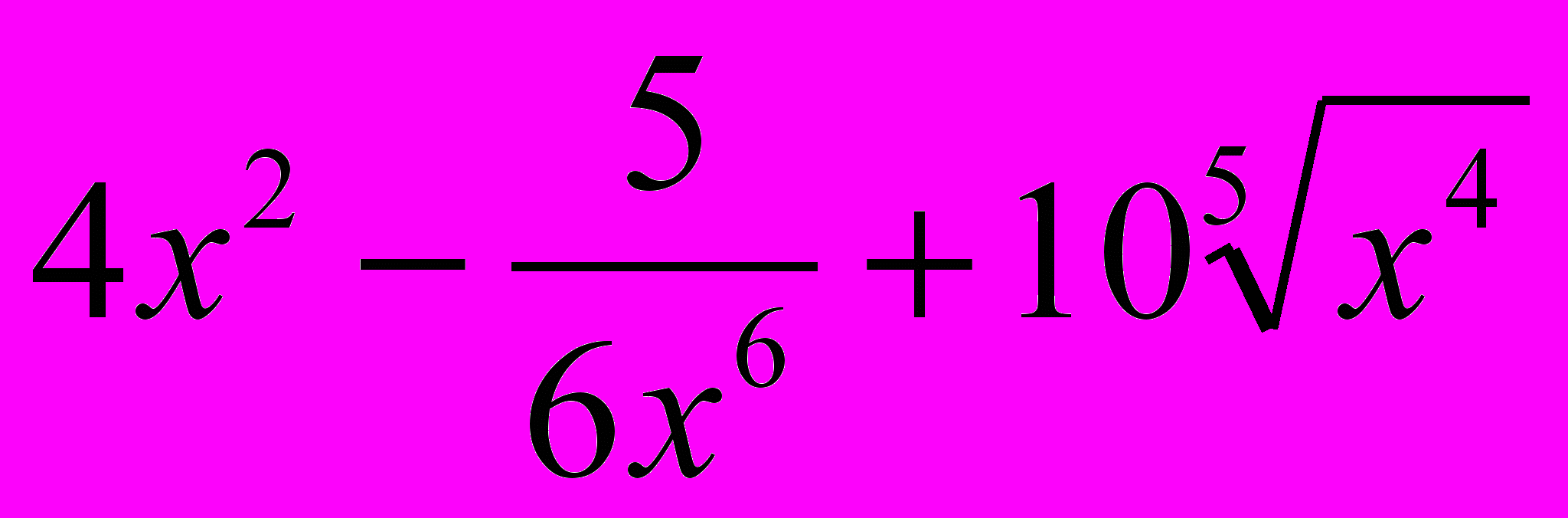; б) y = (1 – x²)*сtg x;


в) y = 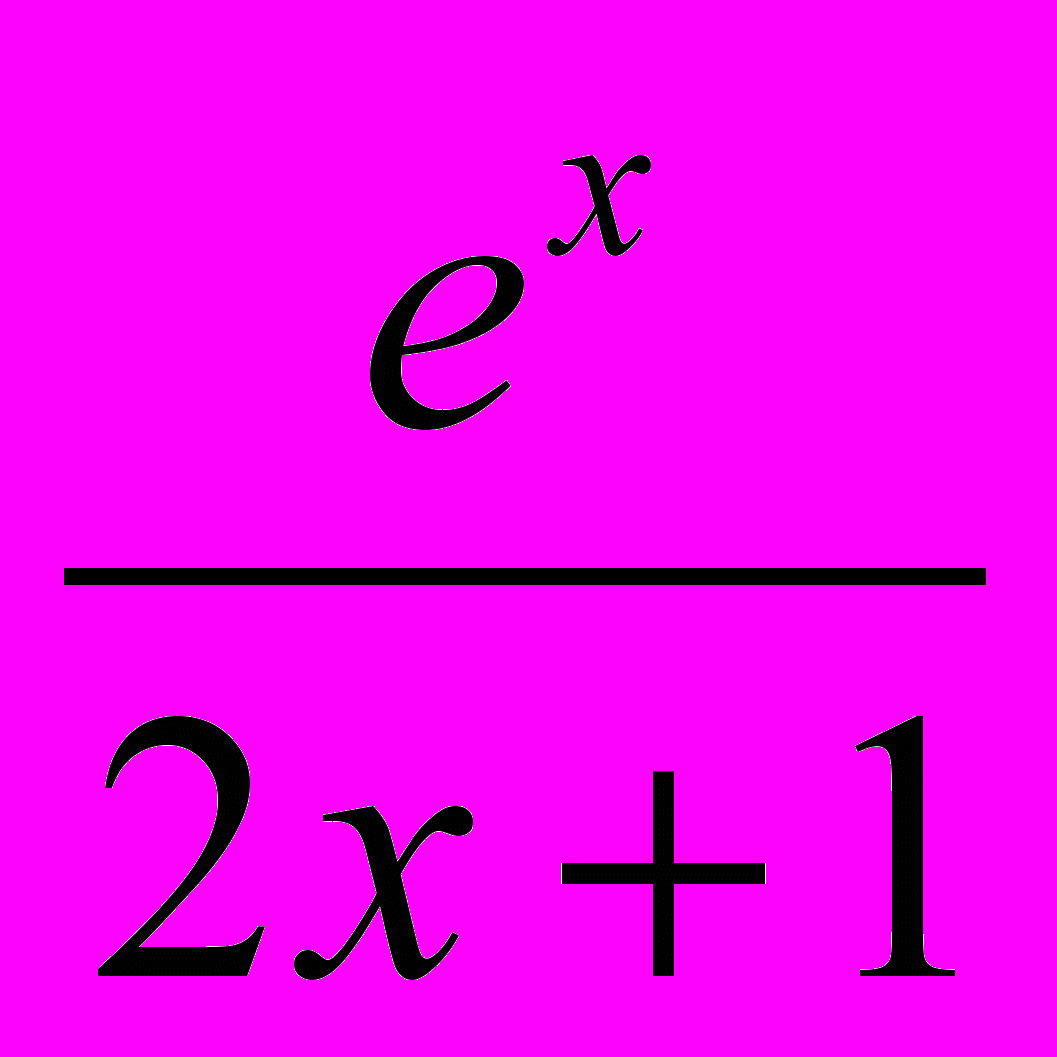; г) y = ln (x² + 5).


Вариант 4, 9


а) y = 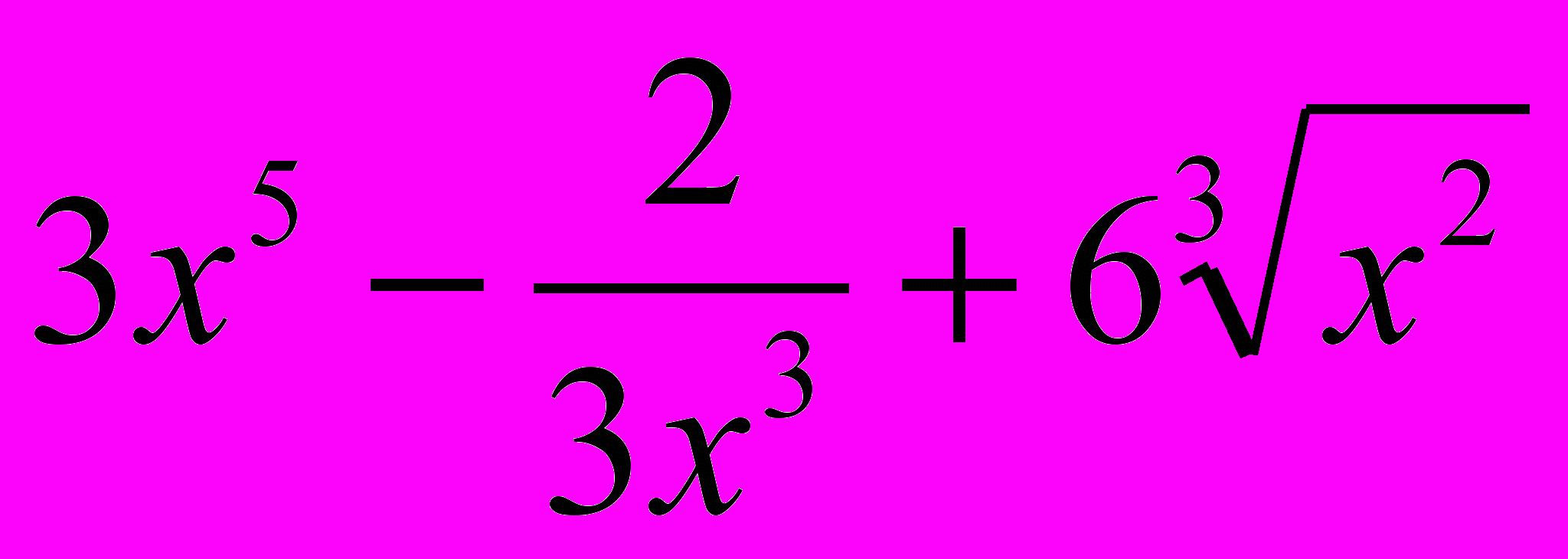; б) y = 5^x * tg x;


в) y = 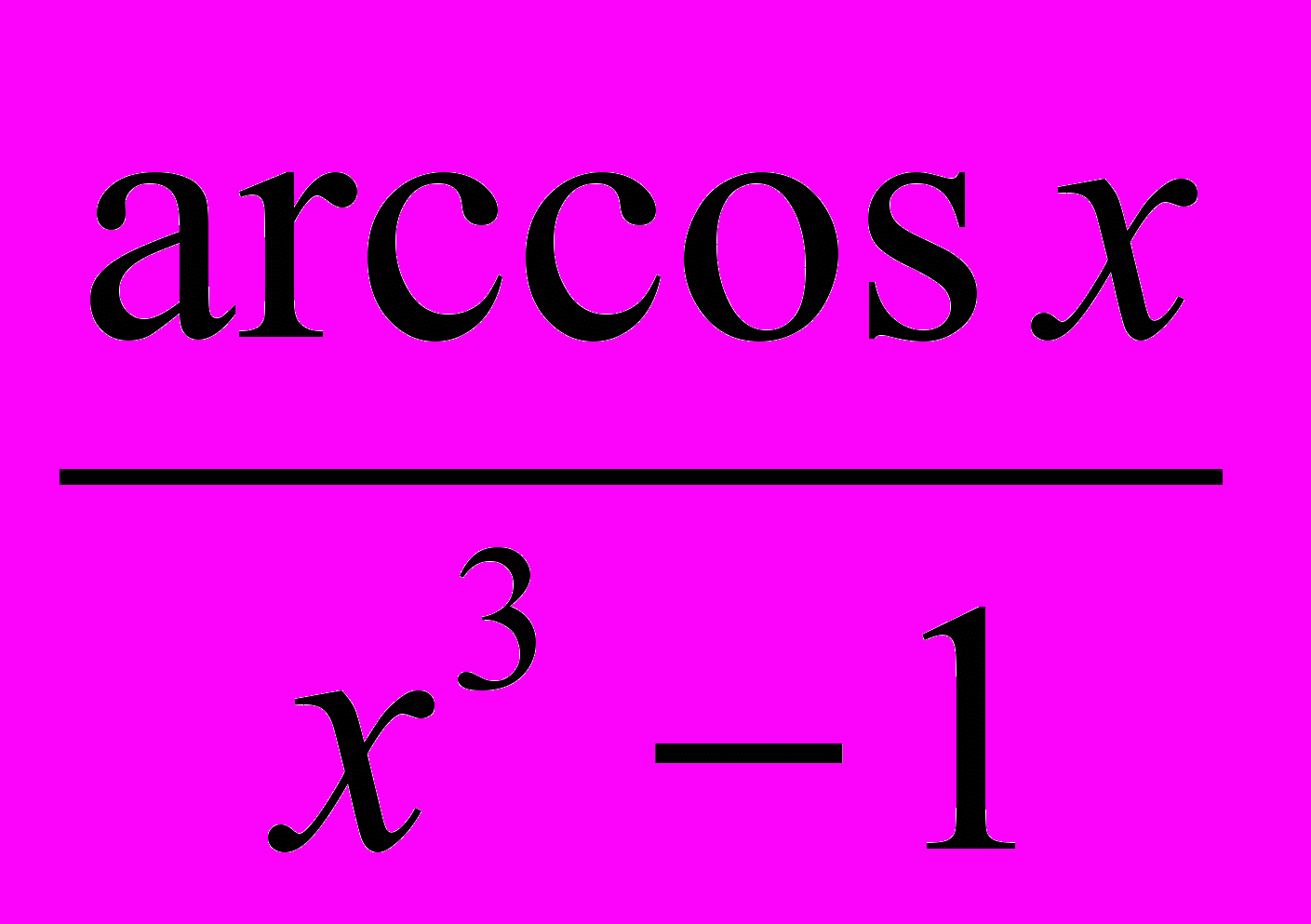; г) y = .

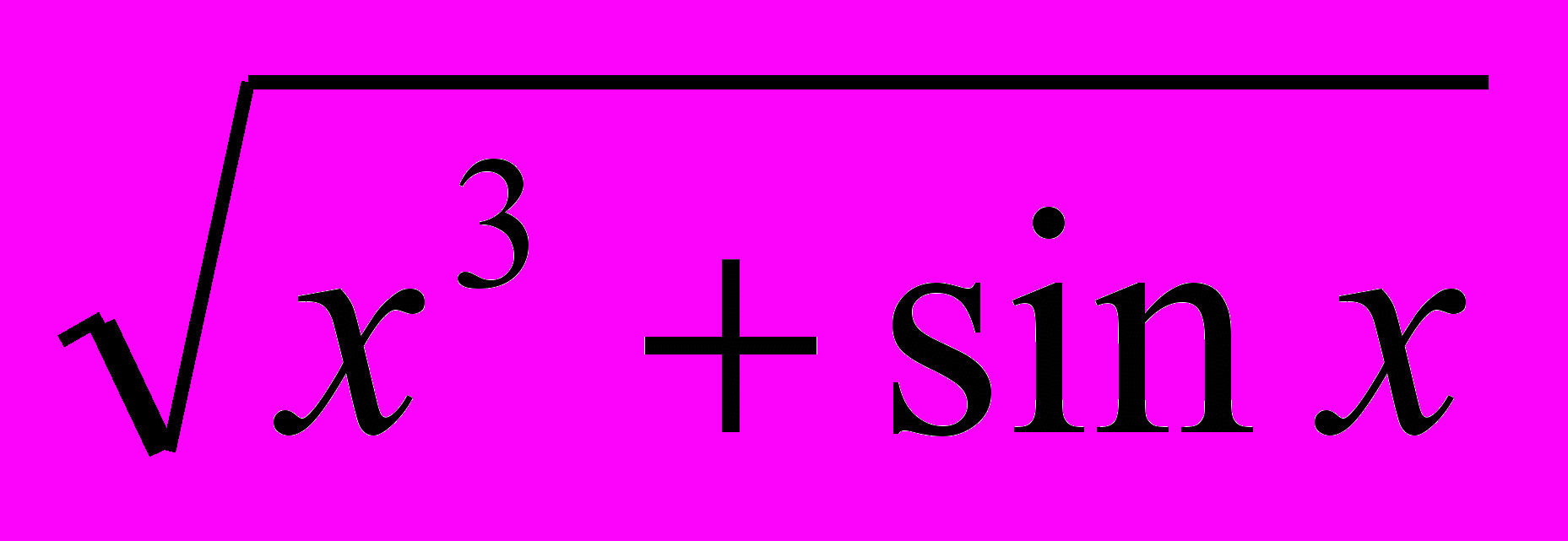Вариант 5, 0


а) y = 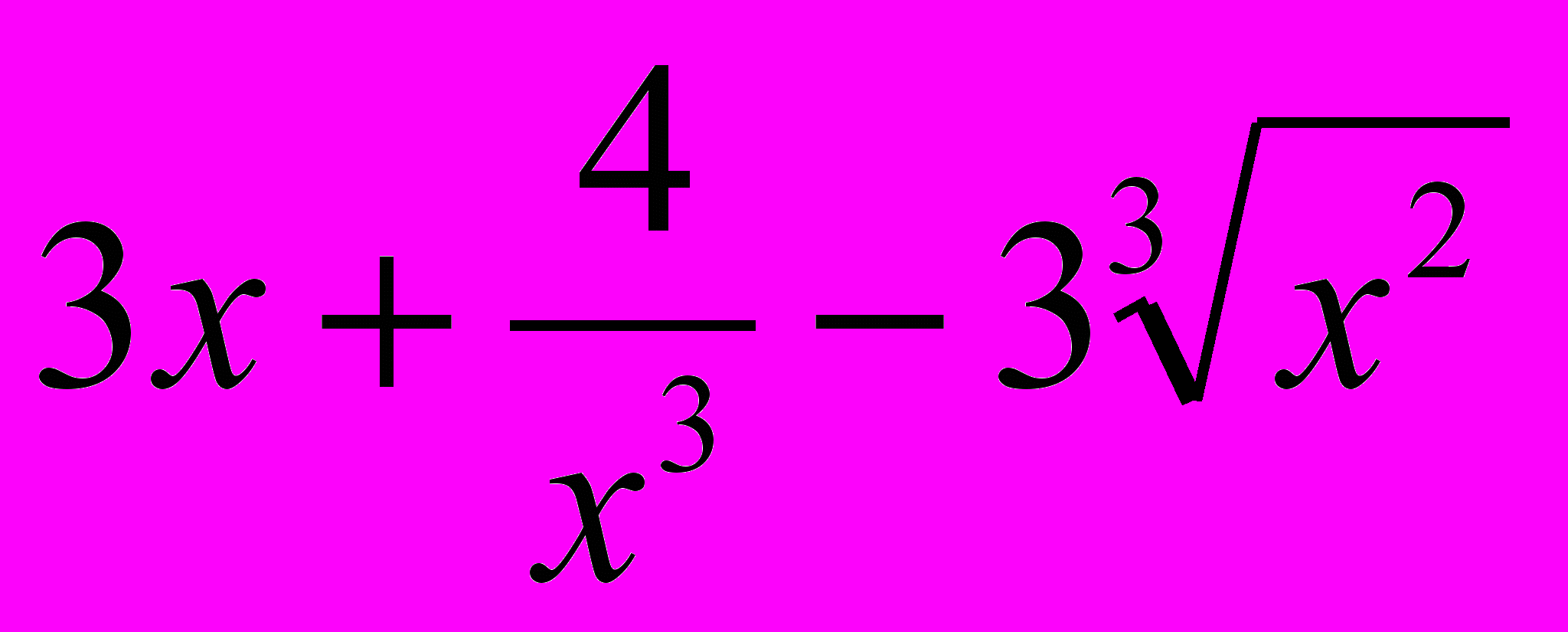; б) y = (x² + 1)*arctg x;


в) y = 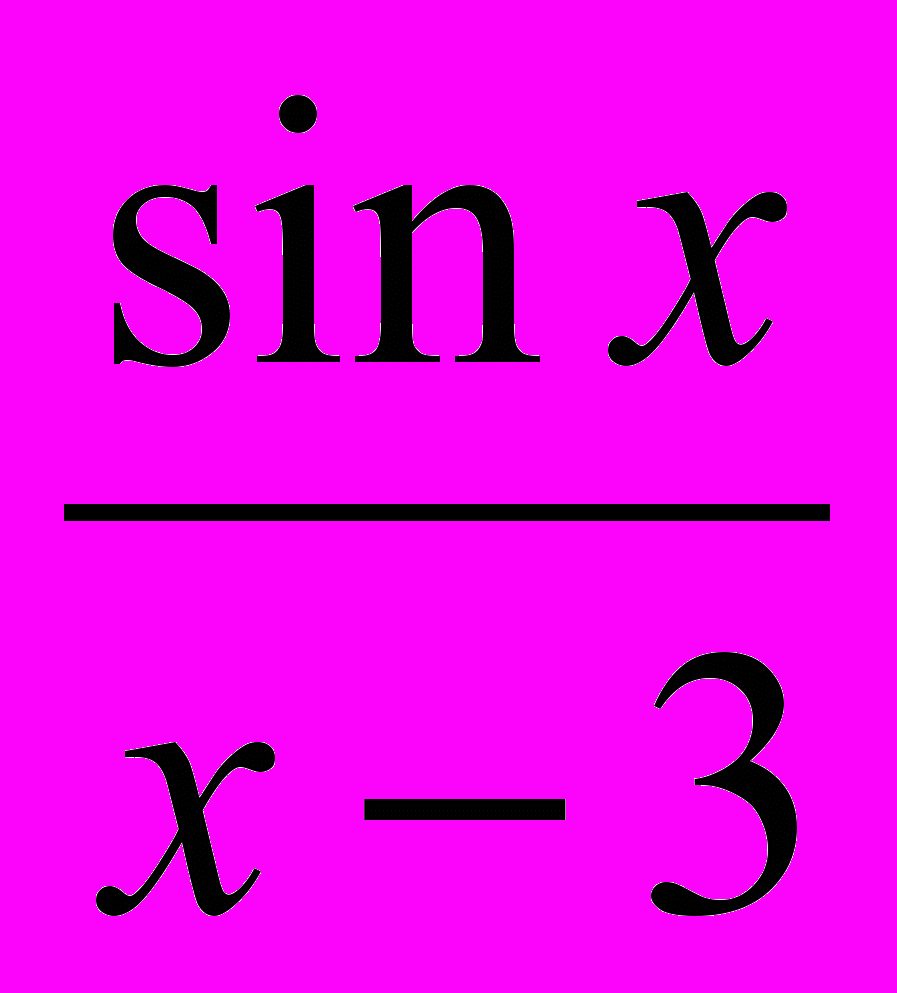; г) y = (ln x – cos x)².


Задание 3. Найти неопределенные интегралы

Вариант 1, 6 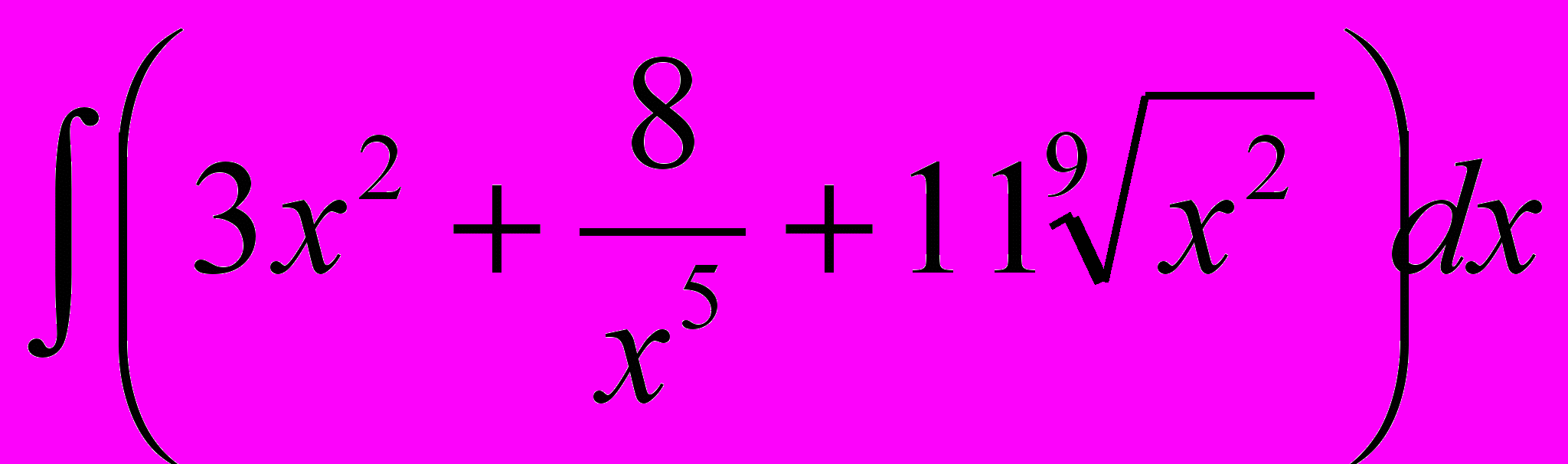. Вариант 2, 7 .

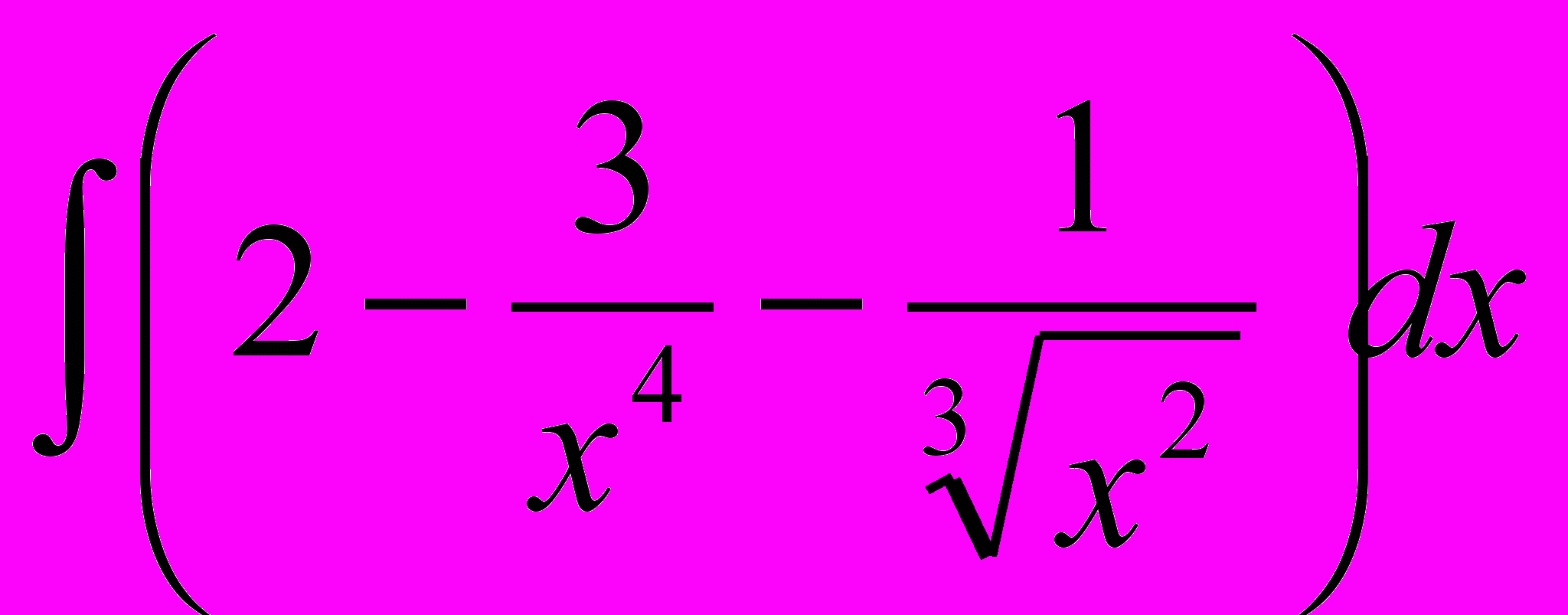Вариант 3, 8 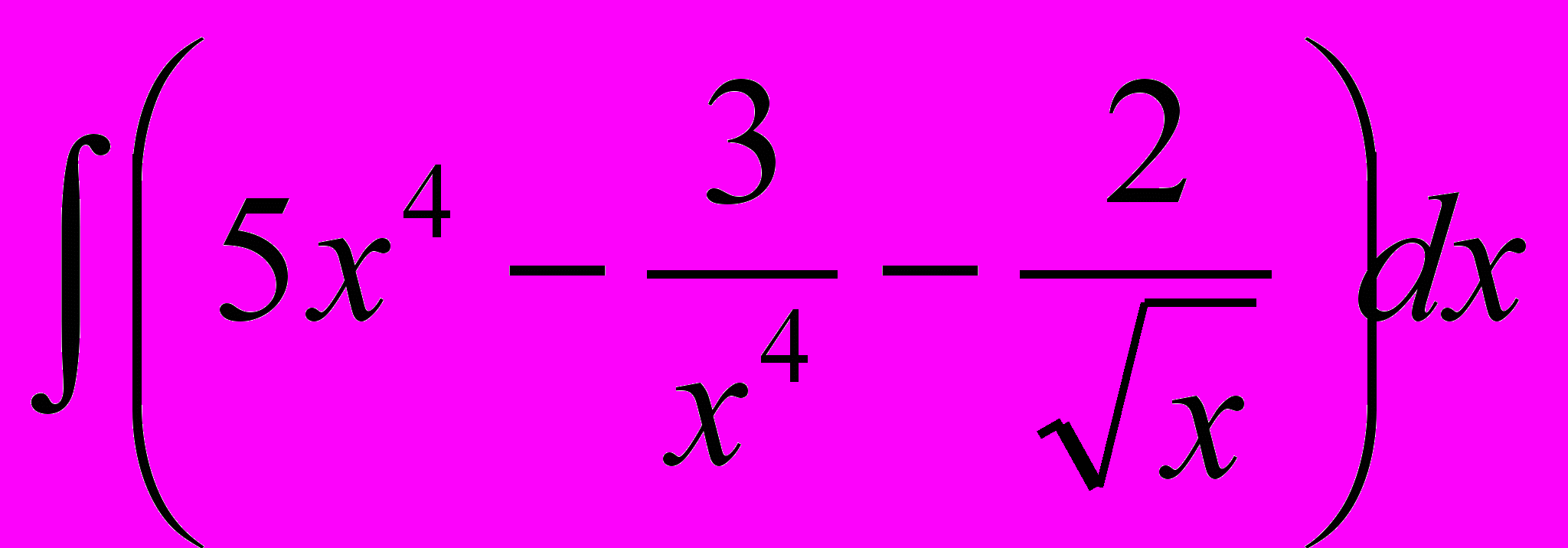. Вариант 4, 9 .


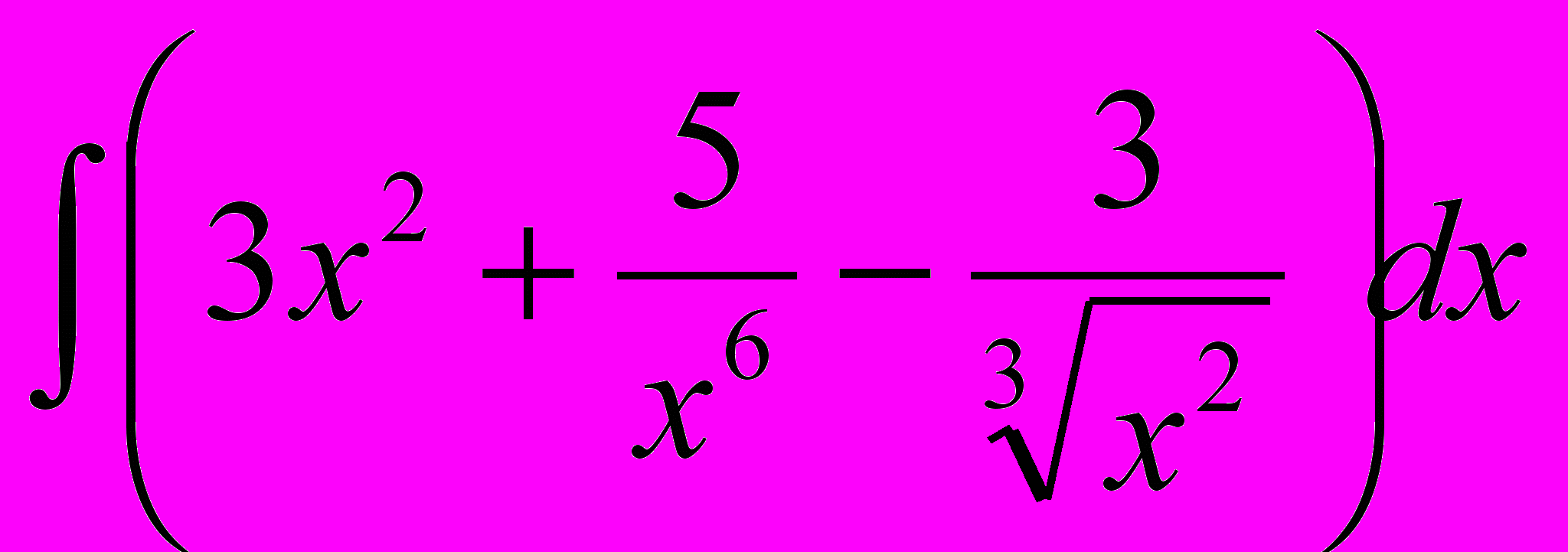Вариант 5, 0 .


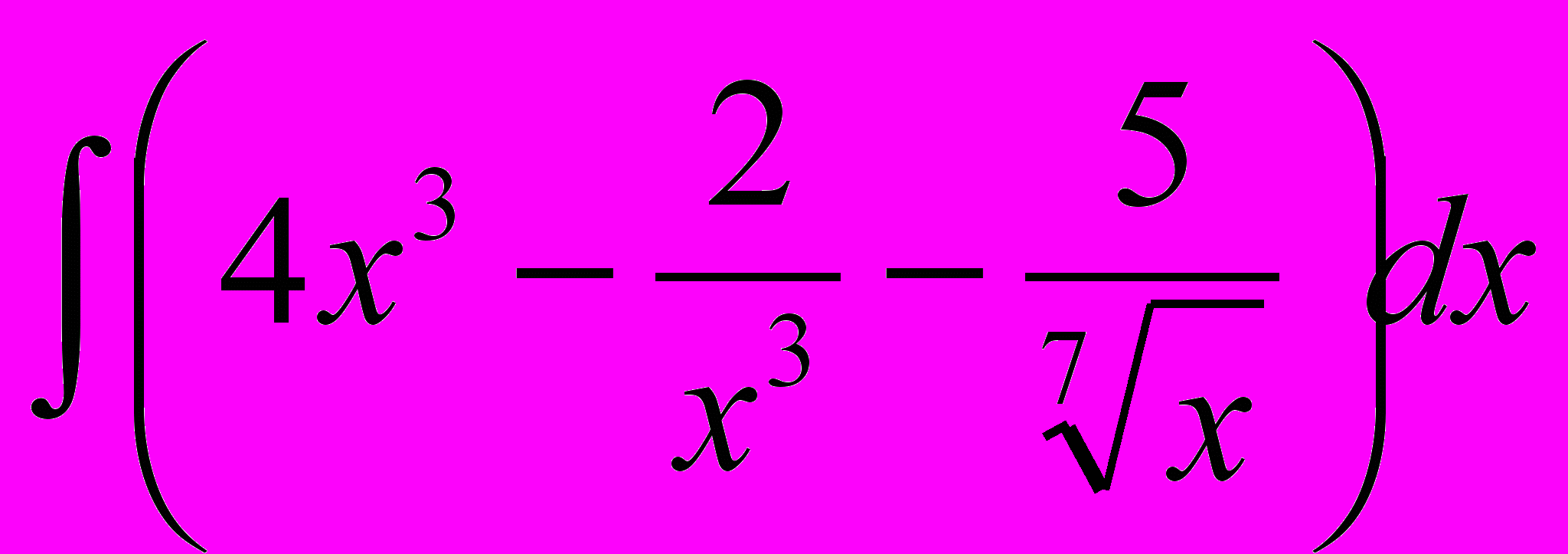Задание 4. Исследовать данную функцию на экстремум


Вариант 1, 6 y = 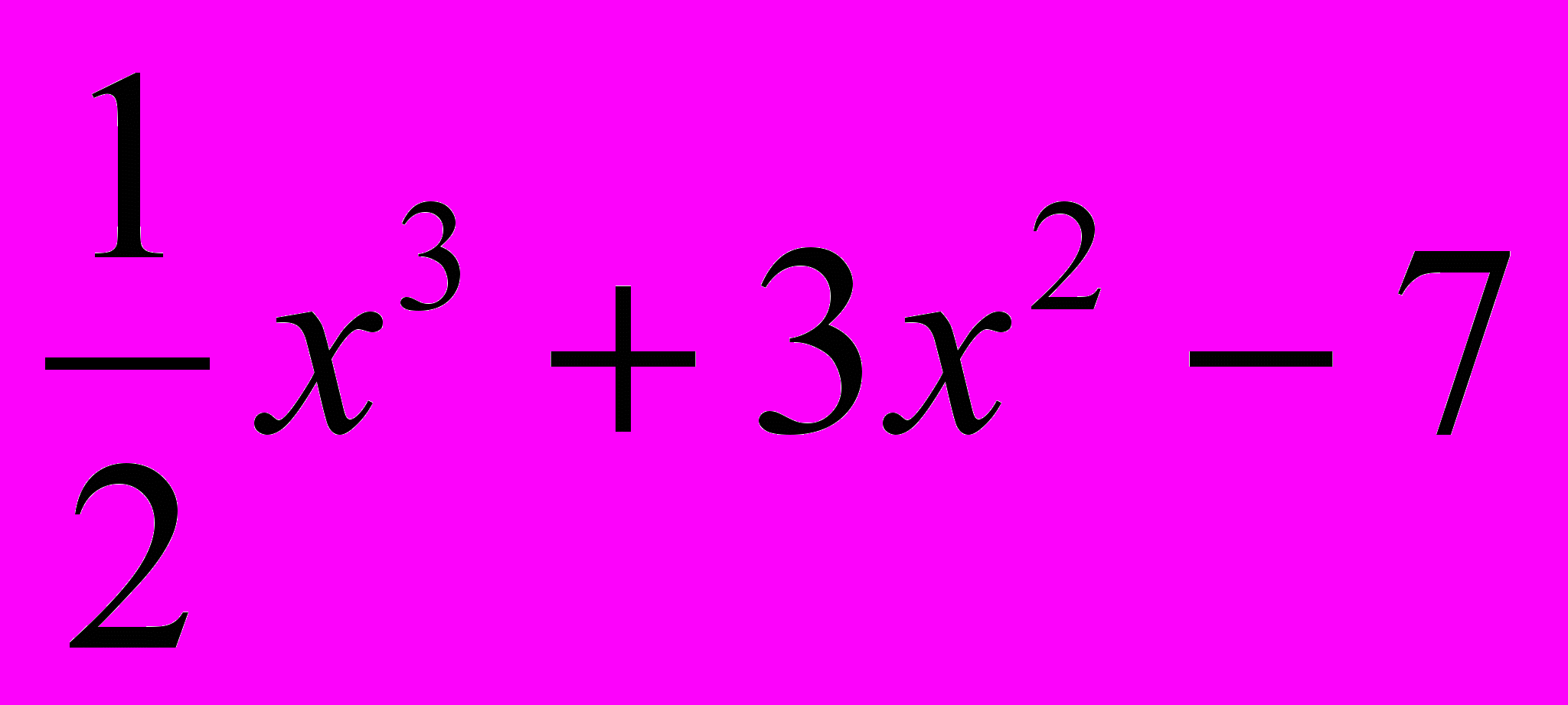. Вариант 2, 7 y = .


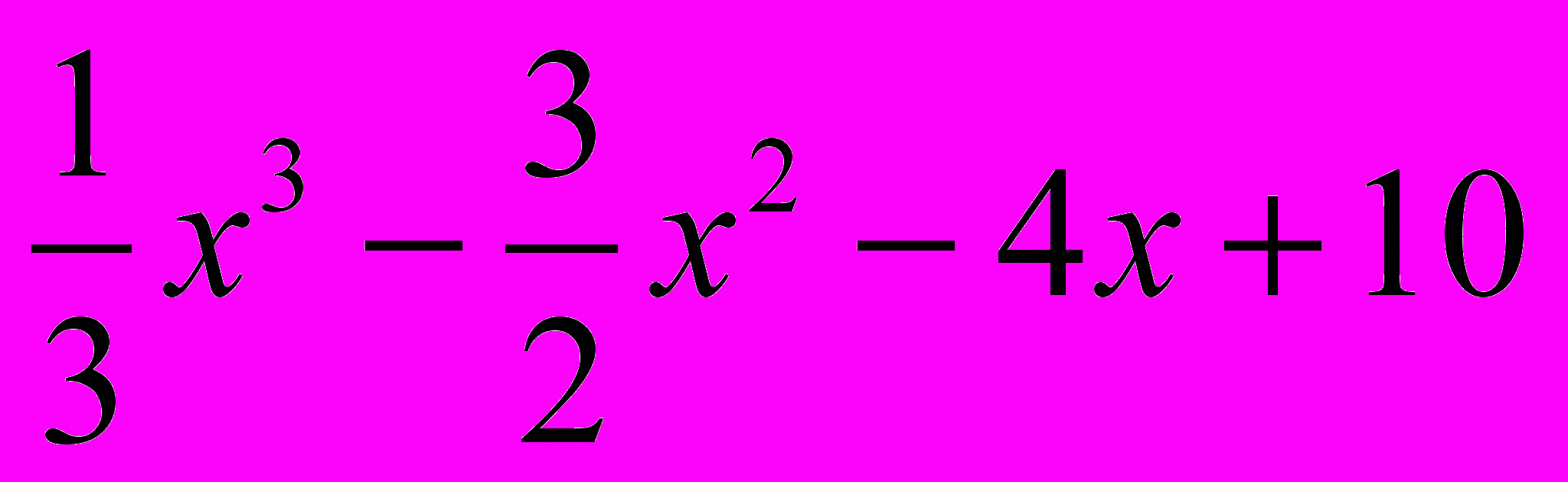Вариант 3, 8 y = 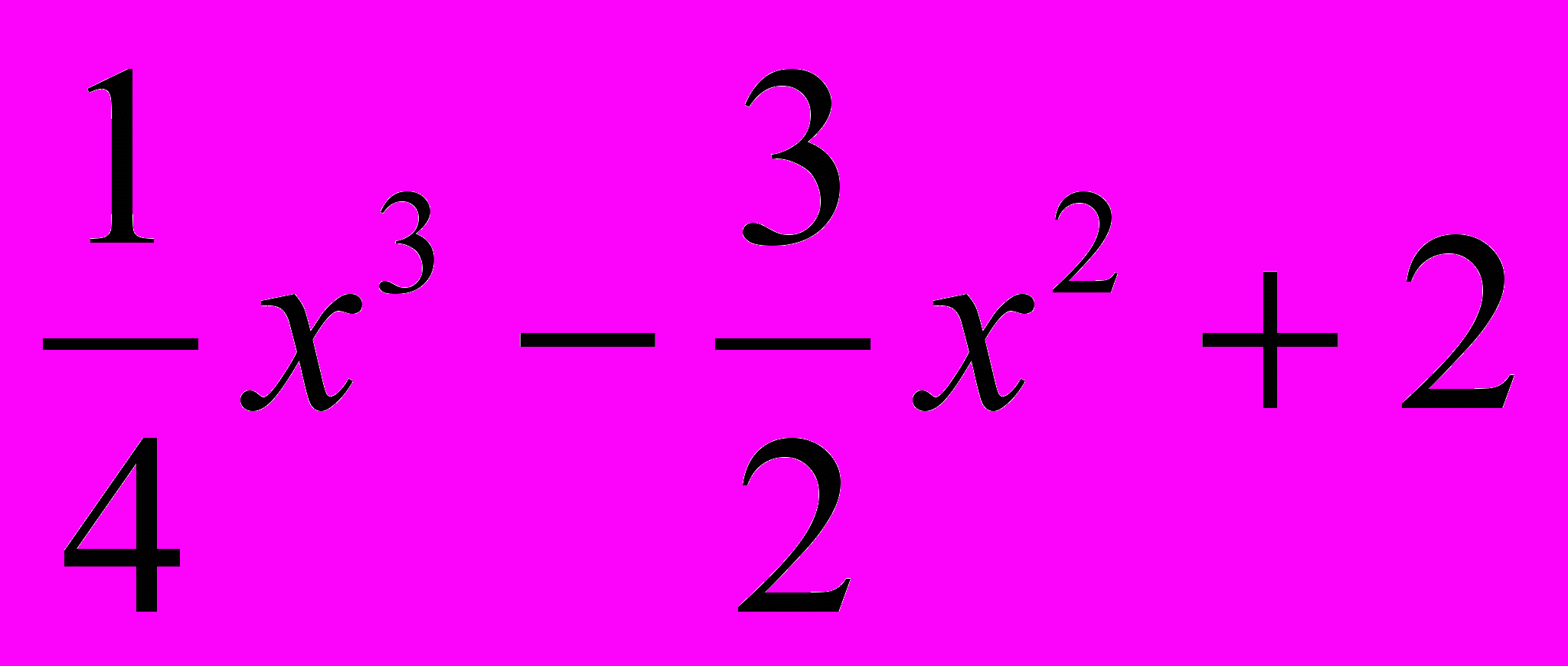. Вариант 4, 9 y = .


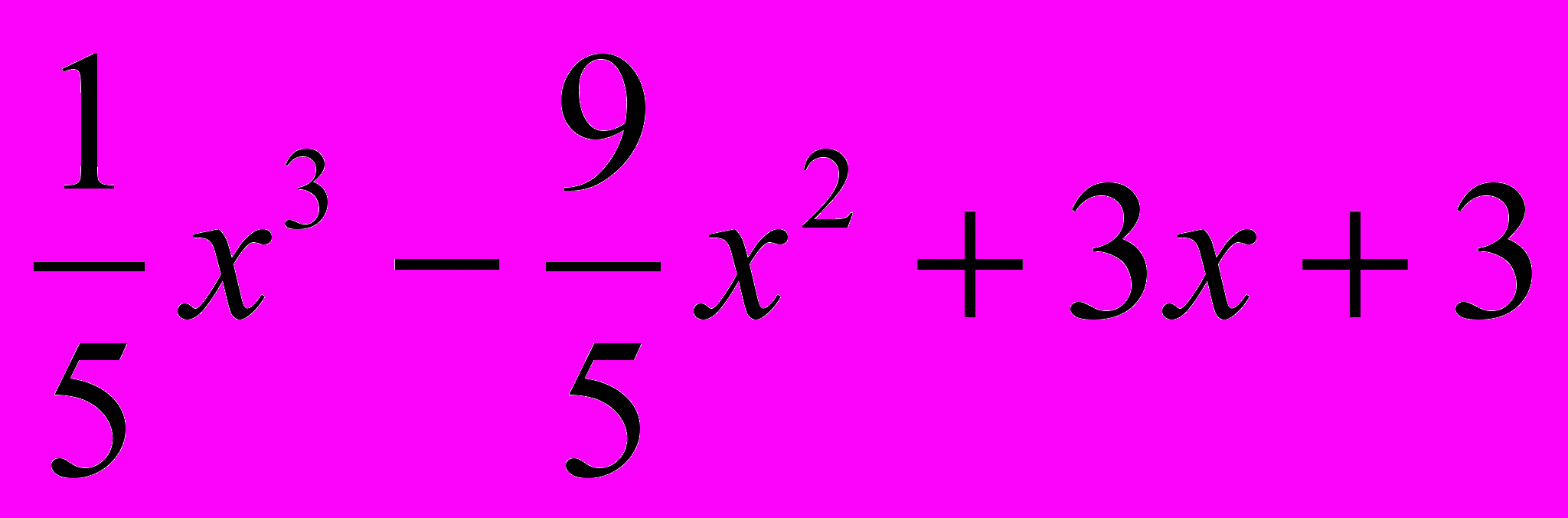Вариант 5, 0 y = .


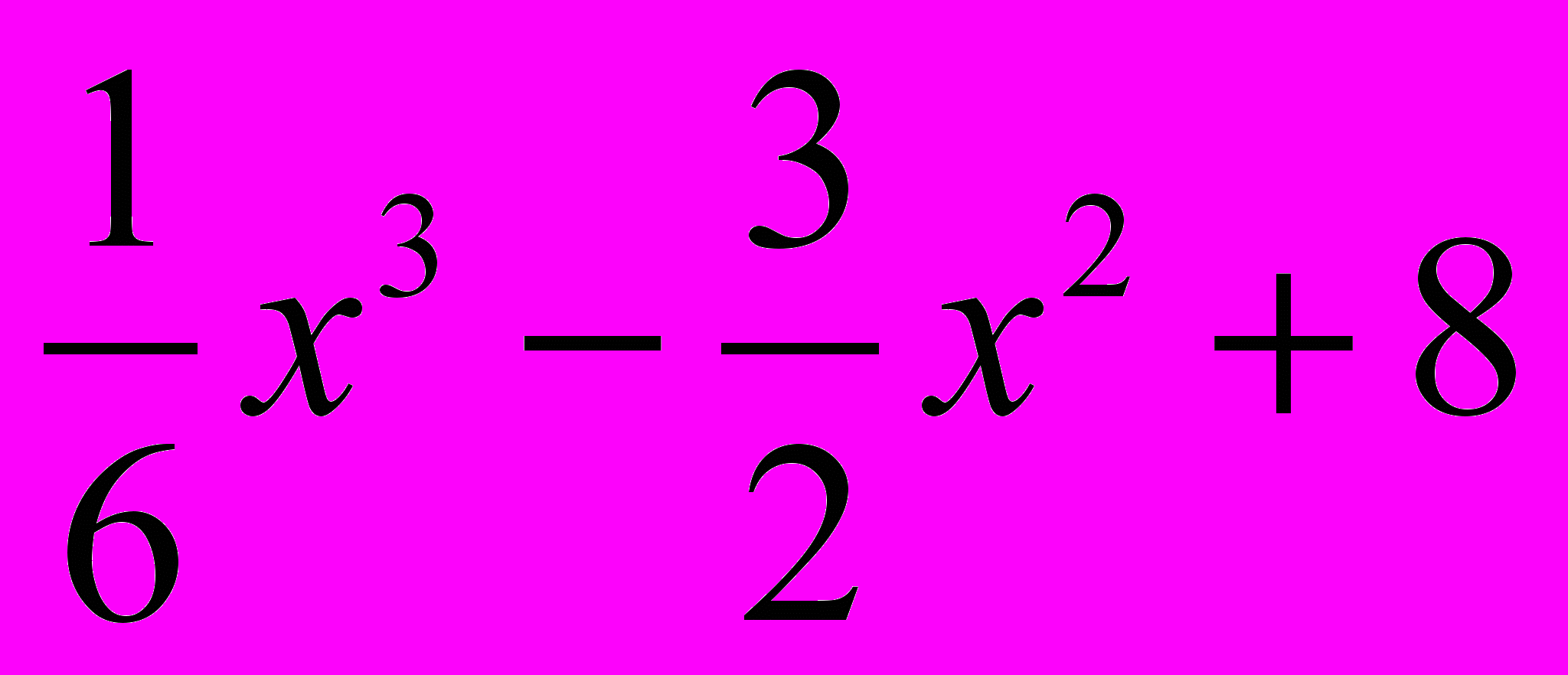Задание 5. Решить задачу


Вариант 1, 3, 5, 7, 9. Коэффициенты использования рабочего времени у двух бригад соответственно равны 0,8 0,6. Считая, что остановки в работе каждой бригады возникают случайно и независимо друг от друга, определить относительное время: 1) совместной работы бригад; 2) работы только одной бригады; 3) простоя обеих бригад.


Вариант 2, 4, 6, 8, 0. На участке две бригады. Вероятность выполнения планового задания первой бригадой равна 0,8, а вероятность выполнения планового задания второй – 0,9. Найти: 1) вероятность выполнения планового задания участком; 2) вероятность выполнения планового задания только одной бригадой участка; 3) вероятность выполнения планового задания хотя бы одной бригадой участка.


7. Контрольные вопросы

для самостоятельной проверки знаний

1. В чем заключается сущность аксиоматического метода?
   
2. Что означают слова «полнота», «непротиворечивость» системы аксиом?
   
3. Какова роль математики как языка?
   
4. Чем отличаются алгебраическая и топологическая структуры?
   
5. Что означает математическое понятие «ряд»?
   
6. Что такое пустое множество? Приведите пример.
   
7. Что такое пересечение множеств?
   
8. Какое множество называется дополнением?
   
9. Что означает термин «комбинаторика»?
   
10. Что такое перестановки, сочетания, размещения?
    
11. Что означает термин «граф»?
    
12. Что такое взвешенный граф?
    
13. Можно ли с помощью графов решать задачи комбинаторики?
    
14. Какова роль математической логики в математике и других науках?
    
15. Что такое таблица истинности?
    
16. В чем сходство теории множеств и математической логики?
    
17. В каких пределах находится вероятность случайного события?
    
18. Чему равна вероятность достоверного события?
    
19. Как определяется сумма и произведение двух событий?
    
20. Какое событие называют противоположным?
    
21. Когда следует использовать классическое определение вероятности?
    
22. В чем особенность геометрических вероятностей?
    
23. Какие события называются несовместными?
    
24. Когда следует применять теорему сложения, а когда – умножения?
    
25. Для каких событий теорема умножения имеет самый простой вид?
    
26. При каких условиях можно применить формулу Бернулли?
    
27. Чем отличаются понятия «случайное событие» и «случайная величина»?
    
28. Когда случайную величину называют дискретной?
    
29. Что такое ряд распределения?
    
30. Что подразумевает термин «числовые характеристики»?
    
31. Что показывает коэффициент корреляции?
    
32. Каковы основные задачи математической статистики?
    
33. Что называется выборкой и в чем состоит ее назначение?
    
34. Как сопоставить понятия «математическое ожидание» и «выборочная средняя»?
    
35. Что показывает выборочная дисперсия?
    
36. Для чего строят уравнение регрессии, уравнение тренда?
    
37. Что показывают в динамических рядах темп роста, темп прироста?
    
38. С помощью чего можно оценить связь между качественными признаками?
    
39. Что означает термин «исследование операций»?
    
40. Чем отличается принятие решений в условиях риска и в условиях неопределенности?
    
41. Что называется минором определителя?
    
42. Что называется алгебраическим дополнением?
    
43. Какой определитель называется главным определителем системы?
    
44. Как составить вспомогательные определители?
    
45. Когда система имеет решение? Не имеет решений?
    
46. Что показывает производная функции?
    
47. Как связаны производная и дифференциал?
    
48. В чем заключается второй достаточный признак экстремума функции?
    
49. Что такое первообразная функции?
    
50. Что называется неопределенным интегралом от данной функции?
    
51. Что называется определенным интегралом от функции на данном отрезке?
    
52. В чем заключается геометрический смысл определенного интеграла?
    

8. Примерные вопросы к зачету

1. Привести пример алгебраической структуры (с обоснованием).
   
2. Привести примеры вектора и матрицы.
   
3. Привести пример множества (назвать его элементы).
   
4. Операции над множествами.
   
5. Правила комбинаторики: правило сложения.
   
6. Правила комбинаторики: правило умножения.
   
7. Основные понятия теории графов.
   
8. Основные элементы языка математической логики.
   
9. Логическое высказывание, его значения.
   
10. «Алгебра высказываний», ее содержание.
    
11. Значения вероятностей основных видов событий.
    
12. Относительная частота события, ее связь с вероятностью.
    
13. Классическое определение вероятности.
    
14. Геометрические вероятности.
    
15. Основные операции над случайными событиями.
    
16. Теорема сложения. Несовместные события.
    
17. Теорема умножения. Независимые события.
    
18. Понятия «случайная величина», «закон распределения».
    
19. Условие нормировки, его смысл.
    
20. Непрерывные распределения: нормальный закон.
    
21. Числовые характеристики случайных величин, их смысл.
    
22. Правило трех сигм.
    
23. Понятие о законе больших чисел.
    
24. Основные понятия математической статистики.
    
25. Дискретные и интервальные ряды распределения.
    
26. Графическое изображение данных (полигон и др.), его цель.
    
27. Статистические оценки числовых характеристик (средняя, дисперсия, среднее квадратичное отклонение, коэффициент вариации).
    
28. Статистическое применение правила трех сигм.
    
29. Изучение взаимосвязей, коэффициент корреляции.
    
30. Парное линейное уравнение регрессии. МНК.
    
31. Показатели взаимосвязи качественных признаков.
    
32. Временные ряды, их классификация.
    
33. Основные показатели динамики.
    
34. Уравнение тренда: его смысл, применение.
    
35. Коэффициенты автокорреляции, коррелограмма.
    
36. Математическая модель, этапы и правила ее построения.
    
37. Игра как математическая модель, ее основные элементы.
    
38. Матричные и биматричные игры.
    
39. Игра с «природой», ее основные элементы.
    
40. Принятие решений в условиях неопределенности и риска.
    
41. Определители и их свойства.
    
42. Матрица. Обратная матрица.
    
43. Правило Крамера.
    
44. Понятие производной и дифференциала.
    
45. Правило дифференцирования суммы, разности, произведения и частного.
    
46. Правило дифференцирования сложной функции.
    
47. Неопределенный интеграл и его свойства.
    
48. Метод непосредственного интегрирования.
    
49. Определенный интеграл и его свойства.
    
50. Геометрический смысл определенного интеграла.
    

Оригинал-макет учебно-методического комплекса дисциплины

НОУ ВПО КузИЭП


Подписано в печать АКТ № « » 200 г.


Формат 60 х 90/16

Объем - п.л. Тираж экз.


Стоимость руб.


Бумага многофункциональная офисная

Отпечатано в копировально-множительном отделе.

Кузбасского института экономики и права