Методические рекомендации по использованию подготовленных учебных пособий «Алгебра и начала анализа 10-11. Ч учебник»
| Вид материала | Методические рекомендации |
- Методические рекомендации по использованию учебных пособий «Алгебра и математический, 181.08kb.
- А. н алгебра и начала анализа. Учебник, 174.46kb.
- С. М. Никольский и др. «Алгебра и начала анализа, 10», «Алгебра и начала анализа, 11», 230.35kb.
- Методические рекомендации по использованию набора цор к учебнику «Алгебра и начала, 408.2kb.
- Тематическое планирование уроков алгебры и начал анализа 10 класс, 279.38kb.
- А. Н. Колмогоров и др. «Алгебра и начала анализа, 10 11» Содержание данного учебник, 174.48kb.
- Рабочая программа учителя математики Тучиной Н. В., разработанная на основе учебных, 1602.46kb.
- Методические рекомендации по использованию комплекта печатных наглядных пособий (плакатов), 536.08kb.
- Методические рекомендации по использованию комплекта печатных наглядных пособий (плакатов), 531.02kb.
- Тема урока: «Логарифмические неравенства», 99.98kb.
Профильное обучение
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО ИСПОЛЬЗОВАНИЮ ПОДГОТОВЛЕННЫХ УЧЕБНЫХ ПОСОБИЙ «Алгебра и начала анализа 10-11. Ч.1.Учебник», автор А,Г,Мордкович и др. при изучении КУРСА «АЛГЕБРА И НАЧАЛА АНАЛИЗА, 10-11»
на базовом и профильном уровне
Допущено МО РФ
Мнемозина, 2004
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО ИСПОЛЬЗОВАНИЮ ПОДГОТОВЛЕННЫХ УЧЕБНЫХ ПОСОБИЙ ДЛЯ ПРЕПОДАВАНИЯ КУРСА «АЛГЕБРА И НАЧАЛА АНАЛИЗА, 10-11»
НА ПРОФИЛЬНОМ УРОВНЕ
(в соответствии с проектом стандарта)
Допущено МО РФ
Мнемозина, 2004
Пояснительная записка
В настоящее время в общеобразовательных школах России, наряду с другими учебниками, используется учебник «Алгебра и начала анализа,10-11», состоящий из двух частей:
А.Г.Мордкович. Алгебра и начала анализа 10-11. Часть 1. Учебник.
А.Г.Мордкович и др. Алгебра и начала анализа 10-11. Часть 2.
Задачник.
Эти две книги издательства «Мнемозина» выдержали с 2000 года несколько изданий; общий тираж каждого из двух наименований составляет свыше 300000 экз.
К учебнику имеется методическое обеспечение:
А.Г.Мордкович . Алгебра и начала анализа 10-11. Пособие для учителей.
А.Г.Мордкович, Е.Е.Тульчинская. Алгебра и начала анализа 10-11. Контрольные работы.
Л.О.Денищева, Т.А.Корешкова. Алгебра и начала анализа 10-11. Тематические тесты и зачеты (под ред. А.Г.Мордковича).
Указанные книги входят с состав комплекта, за который авторский коллек- тив под руководством А.Г.Мордковича удостоен премии Президента РФ в области образования за 2001 год.
В связи с появлением проекта стандарта математического образования возникает естественная проблема адаптации имеющихся учебников к новым условиям: как обеспечить преподавание математики на профильном уровне и как обеспечить преподавание математики на базовом уровне. Об этом и идет речь в настоящих рекомендациях.
В пояснительной записке к стандартам сказано: «В современной российской школе математика изучается на трех уровнях, которые условно обозначаются как «углубленный», общий («курс Б») и «гуманитарный» («курс А»). Эта традиция сохраняется в проекте стандарта по математике. Наряду с профильным и базовым уровнем фиксируются и требования к уровню подготовки выпускников для «общекультурного» уровня. Поэтому в данных методических рекомендациях речь идет
о том, как использовать указанные выше учебные и методические пособия на всех трех уровнях и что сделал и предполагает в дальнейшем сделать наш авторский коллектив, чтобы обеспечить полноценную реализацию стандарта на всех трех уровнях.
Структура рекомендаций
1. Выдержка из обязательного минимума содержания (профильный уровень) по разделу «Алгебра и начала анализа»; жирным шрифтом выделено то, чего нет
в изданном комплекте.
2. Комментарии по преподаванию в профильной школе выделенного материала с помощью пособий авторского коллектива под руководством А.Г.Мордко- вича, изданных или готовящихся к изданию издательством «Мнемозина».
3. Список литературы (основной, дополнительной и готовящейся к печати).
4. Примерное поурочное планирование курса алгебры и начал анализа
в 10 классах профильной школы в двух вариантах: из расчета 7 или 6 недельных часов на математику, в том числе 5 часов или, соответственно, 4 часов в неделю на курс алгебры и начал анализа.
5. Примерное поурочное планирование курса алгебры и начал анализа
в 11 классах профильной школы в двух вариантах: из расчета 7 или 6 недельных часов на математику, в том числе 5 часов или, соответственно, 4 часов в неделю на курс алгебры и начал анализа.
6. Выдержка из обязательного минимума содержания (базовый уровень)
по разделу «Алгебра и начала анализа»; жирным шрифтом выделено то, чего нет
в изданном комплекте.
7. Комментарии по преподаванию в общеобразовательной школе выделенного материала с помощью пособий авторского коллектива под руководством А.Г.Мордковича, изданных или готовящихся к изданию издательством «Мнемозина».
8.. Список литературы (основной, дополнительной и готовящейся к печати).
9. Примерное поурочное планирование курса алгебры и начал анализа
в 10 классах общеобразовательной школ: (из расчета 3 часа в неделю на этот курс).
10. Примерное поурочное планирование курса алгебры и начал анализа
в 11 классах общеобразовательной школы (из расчета 3 часа в неделю).
11. Предложения по реализации курса А.
- Обязательный минимум содержания
основных образовательных программ
(профильный уровень)
ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ
Делимость целых чисел. Деление с остатком. Сравнения. Решение задач с целочисленными неизвестными.
Комплексные числа. Геометрическая интерпретация комплексных чисел. Действительная и мнимая часть, модуль и аргумент комплексного числа. Алгебраическая и тригонометрическая формы записи комплексных чисел. Арифметические действия над комплексными числами в разных формах записи. Комплексно сопряженные числа. Возведение в натуральную степень (формула Муавра). Основная теорема алгебры.
Многочлены от одной переменной. Делимость многочленов. Деление многочленов с остатком. Рациональные корни многочленов с целыми коэффициентами. Схема Горнера. Теорема Безу. Число корней многочлена. Многочлены от двух переменных. Формулы сокращенного умножения для старших степеней. Бином Ньютона. Многочлены от нескольких переменных, симметрические многочлены.
Корень степени n>1 и его свойства. Степень с рациональным показателем
и ее свойства. Понятие о степени с действительным показателем. Свойства степени с действительным показателем.
Логарифм числа. Основное логарифмическое тождество. Логарифм произведения, частного, степени; переход к новому основанию. Десятичный и натуральный логарифмы, число е.
Преобразования выражений, включающих арифметические операции,
а также операции возведения в степень и логарифмирования.
Тригонометрия
Синус, косинус, тангенс, котангенс произвольного угла. Радианная мера угла. Синус, косинус, тангенс и котангенс числа. Основные тригонометрические тождества. Формулы приведения. Синус, косинус и тангенс суммы и разности двух углов. Синус и косинус двойного угла. Формулы половинного угла. Преобразования суммы тригонометрических функций в произведение и произведения в сумму. Выражение тригонометрических функций через тангенс половинного аргумента. Преобразования тригонометрических выражений.
Простейшие тригонометрические уравнения. Решения тригонометрических уравнений. Простейшие тригонометрические неравенства.
Арксинус, арккосинус, арктангенс, арккотангенс числа.
ФУНКЦИИ
Функции. Область определения и множество значений. График функции. Построение графиков функций, заданных различными способами. Свойства функций: монотонность, четность и нечетность, периодичность, ограниченность. Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума (локального максимума и минимума). Выпуклость функции. Графическая интерпретация. Примеры функциональных зависимостей в реальных процессах и явлениях.
Сложная функция (композиция функций). Взаимно обратные функции. Область определения и область значений обратной функции. График обратной функции. Нахождение функции, обратной данной.
Степенная функция с натуральным показателем, её свойства и график. Вертикальные и горизонтальные асимптоты графиков. Графики дробно-линейных функций.
Тригонометрические функции, их свойства и графики, периодичность, основной период. Обратные тригонометрические функции, их свойства и графики.
Показательная функция (экспонента), её свойства и график.
Логарифмическая функция, её свойства и график.
Преобразования графиков: параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой
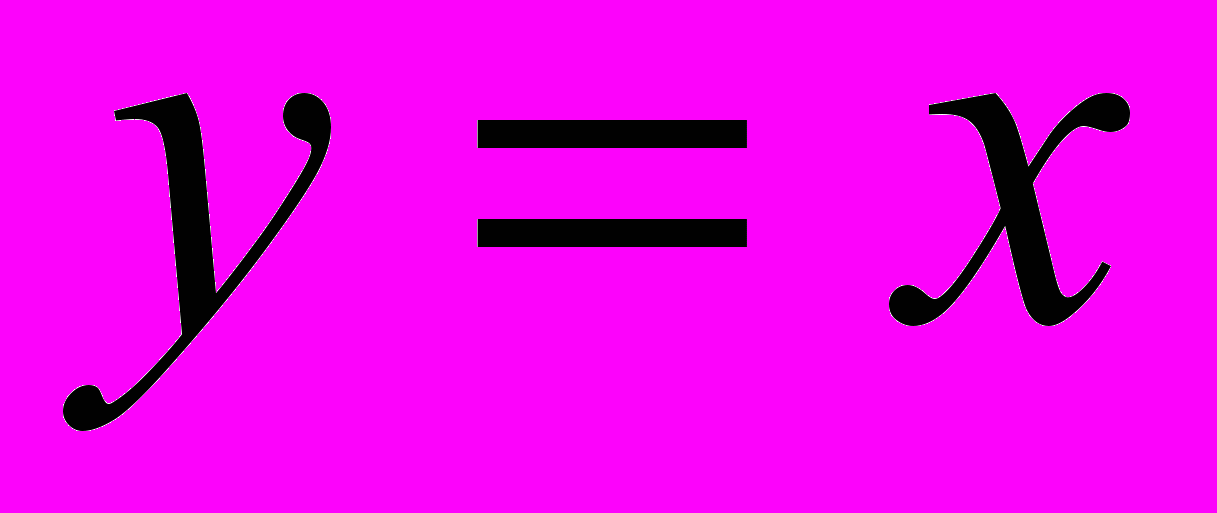, растяжение и сжатие вдоль осей координат. НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА
Понятие о пределе последовательности. Существование предела монотон- ной ограниченной последовательности. Длина окружности и площадь круга как пределы последовательностей. Бесконечно убывающая геометрическая прогрессия и ее сумма. Теоремы о пределах последовательностей. Переход к пределам в нера- венствах.
Понятие о непрерывности функции. Основные теоремы о непрерывных функциях.
Понятие о пределе функции в точке. Поведение функций на бесконечности. Асимптоты.
Понятие о производной функции, физический и геометрический смысл про- изводной. Уравнение касательной к графику функции. Производные суммы, разно- сти, произведения и частного. Производные основных элементарных функций. Производные сложной и обратной функций. Вторая производная. Применение производной к исследованию функций и построению графиков. Использование производных при решении уравнений и неравенств, при решении текстовых, физических и геометрических задач, нахождении наибольших и наименьших значений.
Площадь криволинейной трапеции. Понятие об определенном интеграле. Первообразная. Первообразные элементарных функций. Правила вычисления первообразных. Формула Ньютона-Лейбница.
Примеры использования производной для нахождения наилучшего решения в прикладных задачах. Нахождение скорости для процесса, заданного формулой или графиком. Примеры применения интеграла в физике и геометрии. Вторая производная и ее физический смысл.
УРАВНЕНИЯ И НЕРАВЕНСТВА
Решение рациональных, показательных, логарифмических и тригонометрических уравнений и неравенств. Решение иррациональных уравнений и неравенств.
Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. Равносильность уравнений, неравенств, систем. Решение систем уравнений с двумя неизвестными простейших типов. Решение систем неравенств с одной переменной.
Доказательства неравенств. Неравенство о среднем арифметическом
и среднем геометрическом двух чисел.
Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.
Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений.
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ, СТАТИСТИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ
Табличное и графическое представление данных. Числовые характеристики рядов данных.
Поочередный и одновременный выбор нескольких элементов из конечного множества. Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач. Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля.
Элементарные и сложные события. Рассмотрение случаев и вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Вероятность и статистическая частота наступления события.
2. Комментарии
Выпишем отдельно тот материал стандарта, которого нет в явном виде
в учебнике А.Г.Мордковича. В каждом пункте указано, в каких наших изданиях можно найти соответствующий материал.
1) Делимость целых чисел. Деление с остатком. Сравнения. Решение задач с целочисленными неизвестными.
Литература:
А.Г.Мордкович. Алгебра-8. Учебник для классов с углубленным изучением математики. Мнемозина, 2002.
Л.И.Звавич, А.Р.Рязановский. Алгебра-8. Задачник для классов с углублен-
ным изучением математики. Мнемозина, 2002.
А.Г.Мордкович. Алгебра и начала анализа (для поступающих в вузы). Вербум-М, 2000.
2) Комплексные числа. Геометрическая интерпретация комплексных чисел. Действительная и мнимая часть, модуль и аргумент комплексного числа. Алгебраическая и тригонометрическая формы записи комплексных чисел. Арифметические действия над комплексными числами в разных формах записи. Комплексно сопряженные числа. Возведение в натуральную степень (формула Муавра). Основная теорема алгебры.
Литература:
А.Г.Мордкович. Алгебра и начала анализа (для поступающих в вузы). Вербум-М, 2000.
А.Г.Мордкович, П.В.Семенов. Алгебра и начала анализа -10 (профильный уровень). Часть 1. Учебник (готовится к изданию издательством «Мнемозина»).
А.Г.Мордкович и др. Алгебра и начала анализа-10 (профильный уровень). Часть 2. Задачник (заканчивается работа над рукописью).
3) Многочлены от одной переменной. Делимость многочленов. Деление многочленов с остатком. Рациональные корни многочленов с целыми коэффициентами. Схема Горнера. Теорема Безу. Число корней многочлена. Многочлены от двух переменных. Формулы сокращенного умножения для старших степеней. Бином Ньютона. Многочлены от нескольких переменных, симметрические многочлены.
Литература:
А.Г.Мордкович. Алгебра-8. Учебник для классов с углубленным изучением математики. Мнемозина, 2002.
Л.И.Звавич, А.Р.Рязановский. Алгебра-8. Задачник для классов с углублен-
ным изучением математики. Мнемозина, 2002.
А.Г.Мордкович. Алгебра и начала анализа (для поступающих в вузы). Вербум-М, 2000.
4) Сложная функция (композиция функций). Взаимно обратные функции. Область определения и область значений обратной функции. График обратной функции. Нахождение функции, обратной данной. Производные сложной и обратной функций. Обратные тригонометрические функции, их свойства и графики.
Литература:
А.Г.Мордкович. Алгебра и начала анализа (для поступающих в вузы). Вербум-М, 2000.
А.Г.Мордкович, П.В.Семенов. Алгебра и начала анализа -10 (профильный уровень). Часть 1. Учебник (готовится к изданию издательством «Мнемозина»).
А.Г.Мордкович и др. Алгебра и начала анализа-10 (профильный уровень). Часть 2. Задачник (заканчивается работа над рукописью).
5) Доказательства неравенств. Неравенство о среднем арифметическом
и среднем геометрическом двух чисел.
Этот материал есть в нашем учебнике алгебры для 9 класса.
6) Раздел «Элементы комбинаторики, статистики и теории вероятностей
Литература:
А.Г.Мордкович. Алгебра и начала анализа (для поступающих в вузы). Вербум-М, 2000.
А.Г.Мордкович, П.В.Семенов. События. Вероятности. Статистическая обработка данных. Дополнительные параграфы к курсу алгебры 7-9. Мнемозина, 2003.
А.Г.Мордкович, П.В.Семенов. Алгебра и начала анализа -10 (профильный уровень). Часть 1. Учебник (готовится к изданию издательством «Мнемозина»).
А.Г.Мордкович и др. Алгебра и начала анализа-10 (профильный уровень). Часть 2. Задачник (заканчивается работа над рукописью).
3. Список литературы
Изданные книги – основные (Мнемозина)
1.. А.Г.Мордкович. Алгебра и начала анализа 10-11. Часть 1. Учебник. 2003.
Гриф – рекомендовано.
2. А.Г.Мордкович и др. Алгебра и начала анализа 10-11. Часть 2. Задачник. 2003. Гриф – рекомендовано.
3. А.Г.Мордкович . Алгебра и начала анализа 10-11. Пособие для учителей. 2003. Гриф – допущено.
4. А.Г.Мордкович, Е.Е.Тульчинская. Алгебра и начала анализа 10-11. Контрольные работы. 2003. Гриф – допущено.
5.. Л.О.Денищева, Т.А.Корешкова. Алгебра и начала анализа 10-11. Тематические тесты и зачеты (под ред. А.Г.Мордковича). 2003. Гриф – допущено.
Дополнительная литература:
6. А.Г.Мордкович, П.В.Семенов. События. Вероятности. Статистическая обработка данных. Дополнительные параграфы к курсу алгебры 7-9. Мнемозина, 2003.
7. А.Г.Мордкович. Алгебра-8. Учебник для классов с углубленным изучением математики. Мнемозина, 2002. Гриф – допущено.
- Л.И.Звавич, А.Р.Рязановский. Алгебра-8. Задачник для классов
с углубленным изучением математики. Мнемозина, 2002. Гриф – допущено.
9. А.Г.Мордкович. Алгебра и начала анализа (для поступающих в вузы). Вербум-М, 2000.
Книги, готовящиеся к изданию к началу 2004/05 уч. года (Мнемозина)
10. А.Г.Мордкович. Алгебра-9. Учебник для классов с углубленным изучением математики. Гриф – допущено.
- Л.И.Звавич, А.Р.Рязановский. Алгебра-9. Задачник для классов
с углубленным изучением математики.
12. А.Г.Мордкович, П.В.Семенов. Алгебра и начала анализа -10 (профильный уровень). Часть 1. Учебник.
13. А.Г.Мордкович и др. Алгебра и начала анализа-10 (профильный уровень). Часть 2. Задачник.
4. Примерное планирование курса алгебры и начал анализа (профильный уровень)
10 класс
5ч 4ч
в неделю
___________________________
Глава 1. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
- Натуральные и целые числа. Делимость чисел 5 3
1) Делимость натуральных чисел
2) Признаки делимости
3) Простые и составные числа
4) Деление с остатком
5) Наибольший общий делитель и наименьшее общее кратное
нескольких натуральных чисел
6) Основная теорема арифметики натуральных чисел
- Рациональные числа 2 2
- Иррациональные числа 2 1
- Множество действительных чисел 3 2
1) Действительные числа и числовая прямая
- Числовые неравенства
- Числовые промежутки
4)* Аксиоматика действительных чисел
- Модуль действительного числа 2 2
- Метод математической индукции 3 2
___________________________________________________________________
Итого: 17 12
Глава 2. ЧИСЛОВЫЕ ФУНКЦИИ
- Определение числовой функции и способы ее задания 2 2
- Свойства функций 3 3
- Периодические функции 2 1
- Обратная функция 3 2 __________________________________________________________________ Итого: 10 9
Глава 3. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
- Числовая окружность 2 2
12. Числовая окружность на координатной плоскости 3 2
13. Синус и косинус. Тангенс и котангенс 3 3
14. Тригонометрические функции числового аргумента 3 3
15. Тригонометрические функции углового аргумента 2 1
- Функции y = sin x, y = соs x, их свойства и графики 4 4
17. Построение графика функции
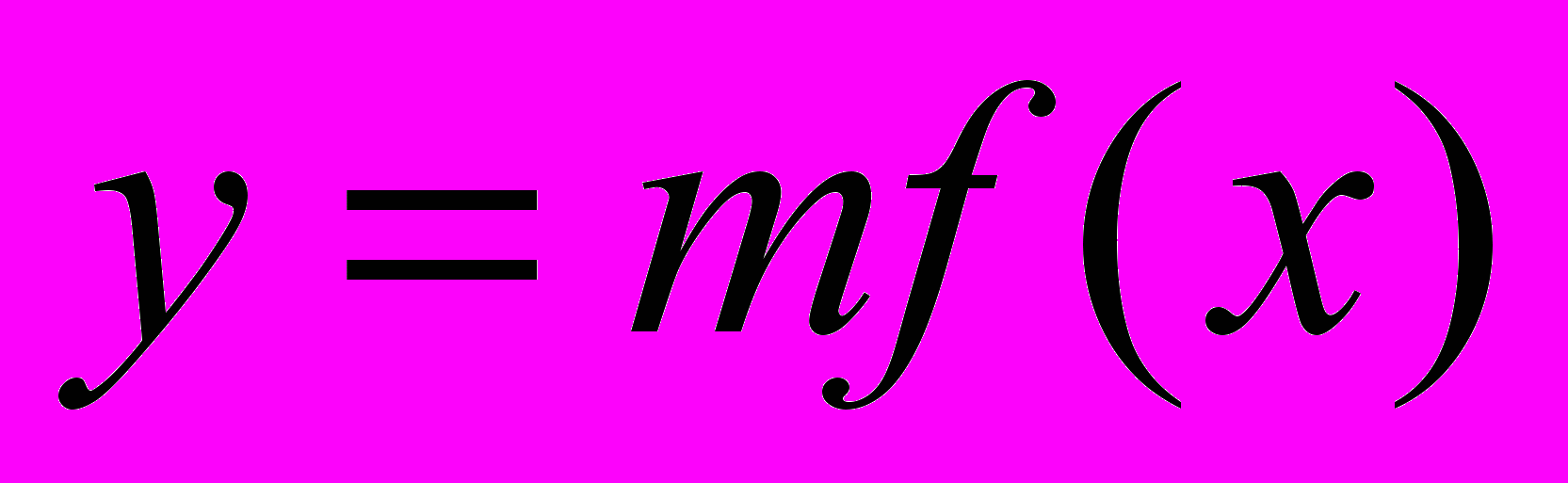2 2 18. Построение графика функции
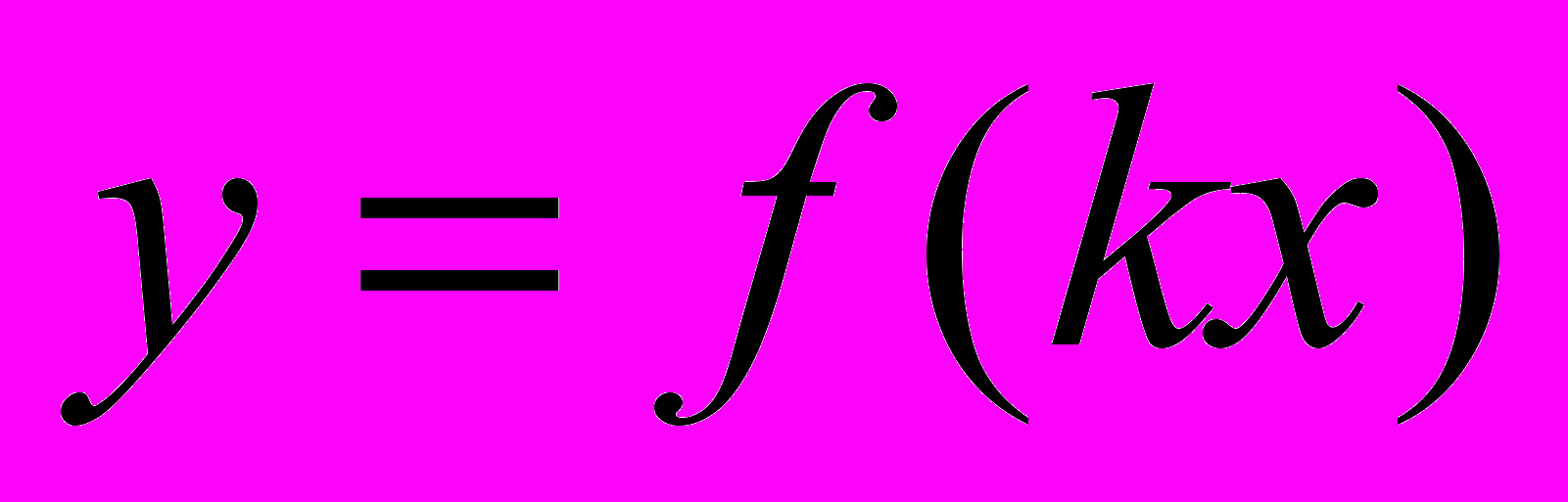2 2 19. График гармонического колебания 2 1
20. Функции y = tg x, y = ctg x, их свойства и графики 3 3
21. Обратные тригонометрические функции 5 3
1. Функция y = arcsin x
2. Функция y = arccos x
3. Функция y = arctg x
4. Функция y = arcctg x
5*. Преобразование выражений, содержащих обратные тригонометрические функции
______________________________________________________________________
Итого: 31 26
Глава 4. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
22. Простейшие тригонометрические уравнения и неравенства 5 5
23. Методы решения тригонометрических уравнений 5 5
- Метод замены переменной
- Метод разложения на множители
- Однородные тригонометрические уравнения
________________________________________________________________
Итого: 10 10
Глава 5. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
24. Синус и косинус суммы и разности аргументов 4 3
25. Тангенс суммы и разности аргументов 2 2
26. Формулы приведения 2 2
27. Формулы двойного аргумента. Формулы понижения степени 4 3
28. Преобразование сумм тригонометрических функций 3 2
в произведение
29.Преобразование произведений тригонометрических функций 2 2
в сумму
30. Преобразование выражения A sin x + B cos x к виду Csin(x + t) 2 1
31. Методы решения тригонометрических уравнений (продолжение) 5 3
____________________________________________________________________
Итого: 24 18
Глава 6. КОМПЛЕКСНЫЕ ЧИСЛА
32. Комплексные числа и арифметические операции над ними 2 2
33. Комплексные числа и координатная плоскость 2 2
34. Тригонометрическая форма записи комплексного числа 3 2
35. Комплексные числа и квадратные уравнения 2 2
36. Возведение комплексного числа в степень. Извлечение 3 2
кубического корня из комплексного числа
_____________________________________________________________________
Итого: 12 10
Глава 7. ПРОИЗВОДНАЯ
37. Числовые последовательности 3 2
- Определение числовой последовательности и способы ее задания
- Свойства числовых последовательностей
38. Предел числовой последовательности 3 2
1) Определение предела последовательности
2) Свойства сходящихся последовательностей
- Вычисление пределов последовательностей
- Сумма бесконечной геометрической прогрессии
39. Предел функции 4 3
!) Предел функции на бесконечности и в точке
- Приращение аргумента. Приращение функции
40. Определение производной 3 3
- Задачи, приводящие к понятию производной
- Определение производной
41. Вычисление производных 6 5
1) Формулы и правила дифференцирования
- Понятие и вычисление производной n-го порядка
42. Дифференцирование сложной функции. Дифференцирование 3 2
обратной функции
43. Уравнение касательной к графику функции 3 3
44. Применение производной для исследования функций: 6 4
1) Исследование функций на монотонность и экстремумы
2) Применение производной для доказательства тождеств и неравенств
45. Построение графиков функций 3 3
46. Применение производной для отыскания наибольших и наименьших
значений величин 6 4
1) Отыскание наибольших и наименьших значений непрерывной
функции на промежутке
2) Задачи на отыскание наибольших и наименьших значений величин
___________________________________________________________________
Итого: 40 31
Глава 8. КОМБИНАТОРИКА И ВЕРОЯТНОСТЬ
47. Правило умножения. Комбинаторные задачи. Перестановки
и факториалы 3 2
48. Выбор нескольких элементов. Биномиальные коэффициенты 3 2
49. Случайные события и их вероятности 3 2
50. Табличное и графическое представление данных 2 2
______________________________________________________________
Итого: 11 8
Повторение 15 12
_______________________
Всего 170 136
Использование указанной выше литературы (см. п.3)
§ 1-5 – 7, 8
§ 6-8 – 9, 10, 11
§ 9-10 – 9
§ 11-20 – 1-5
§ 21 – 9
§ 22-31 – 1-5
§ 32-36 – 9
§ 37-41 – 1-5
§ 42 – 9
§ 43-46 – 1-5
§ 47-50 – 6, 9
Примечание: Полное соответствие указанной выше программе содержится в готовящихся к изданию книгах 12 и 13.
5. Примерное планирование курса алгебры и начал анализа (профильный уровень)
11 класс
5ч 4ч
в неделю
___________________________
Глава 1. ИНТЕГРАЛ
1. Первообразная и неопределенный интеграл 3 3
2. Определенный интеграл: 6 6
1) задачи, приводящие к понятию определенного интеграла
2) определенный интеграл, его вычисление и свойства
3) вычисление площадей плоских фигур
4) примеры применения интеграла в физике
___________________________________________
Итого: 9 9
Глава 2. СТЕПЕНИ И КОРНИ. СТЕПЕННЫЕ ФУНКЦИИ
3. Понятие корня n-й степени из действительного числа 2 2
4. Функции
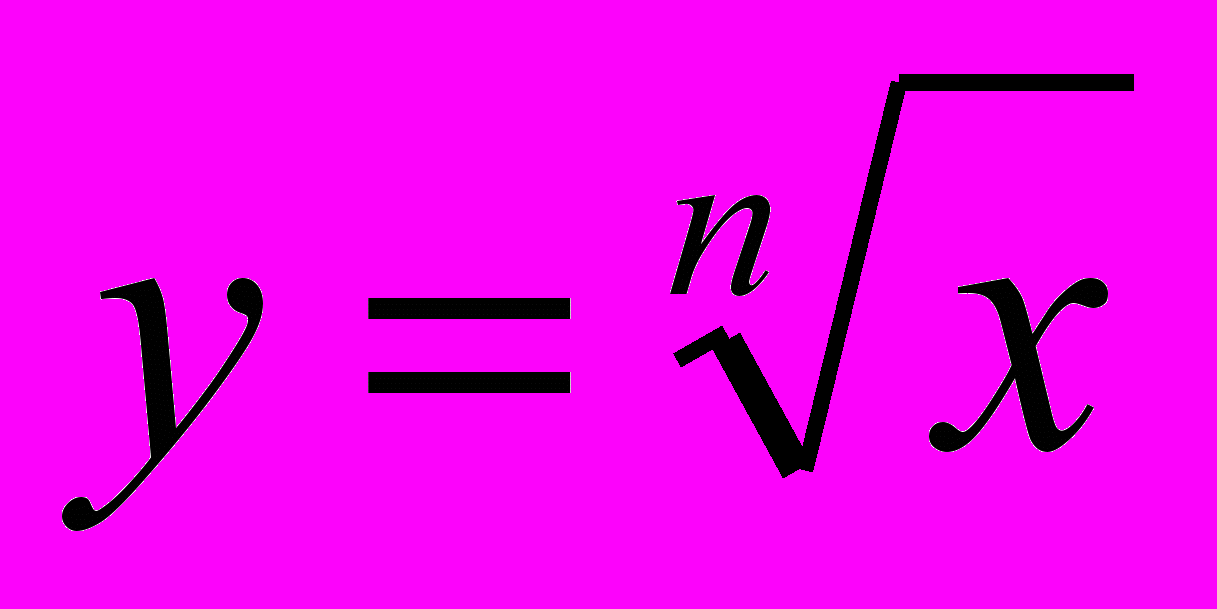, их свойства и графики 4 35. Свойства корня n-й степени 4 3
6. Преобразование выражений, содержащих радикалы 5 4
7. Обобщение понятия о показателе степени 4 4
8. Степенные функции, их свойства и графики (включая 5 4
дифференцирование и интегрирование степенной функции
с рациональным показателем)
_______________________________________
Итого: 24 20
Глава 3. ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ
9. Показательная функция, ее свойства и график 4 3
10. Показательные уравнения 4 3
11. Показательные неравенства 3 2
12. Понятие логарифма 2 2
13. Функция
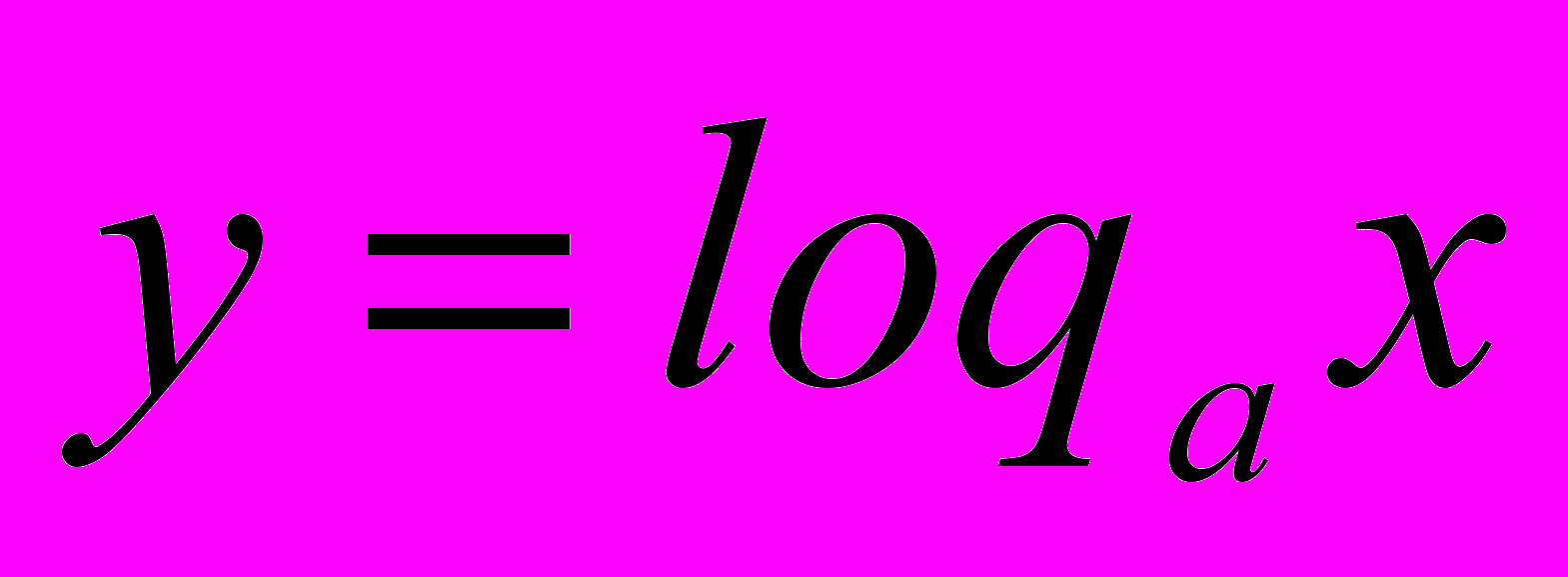, ее свойства и график 3 314. Свойства логарифмов 4 4
15. Логарифмические уравнения 5 4
16. Логарифмические неравенства 5 4
17. Переход к новому основанию логарифма 4 2
18. Дифференцирование показательной и логарифмической функций 4 3
_____________________________________________
Итого: 38 30
Глава 4. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ, СТАТИСТИКИ
И ТЕОРИИ ВЕРОЯТНОСТЕЙ
19. Числовые характеристики рядов данных. 2 2
- Решение комбинаторных задач. Формулы числа перестановок,
сочетаний, размещений. 4 3
- Формула бинома Ньютона. Свойства биномиальных
коэффициентов. Треугольник Паскаля. 3 3
22. Независимые повторения испытаний с двумя исходами.
Вероятность и статистическая частота наступления события. 5 4
_________________________________________
Итого: 14 12
Глава 5. УРАВНЕНИЯ И НЕРАВЕНСТВА. СИСТЕМЫ УРАВНЕНИЙ
И НЕРАВЕНСТВ
23. Равносильность уравнений 4 3
24. Общие методы решения уравнений 5 4
25. Многочлены от одной переменной: делимость многочленов, 4 3
деление многочленов с остатком, теорема Безу, число корней многочлена
26. Уравнения высших степеней 4 3
27. Уравнения с модулями 3 2
28. Иррациональные уравнения 4 3
29. Решение рациональных неравенств с одной переменной 5 4
30. Неравенства с модулями 3 2
31. Иррациональные неравенства 3 2
32. Многочлены от двух переменных. Формулы сокращенного 4 3
умножения для старших степеней. Бином Ньютона. Симметрические многочлены
33.Уравнения и неравенства с двумя переменными 2 2
34.Диофантовы уравнения 2 2
35.Системы уравнений 6 4
36.Уравнения и неравенства с параметрами 6 4
_____________________________________
Итого: 55 41
Повторение 30 24
_______________________
Всего 170 136
Использование указанной выше литературы (см. п.3)
§ 1-18 – 1-5
§ 19-22 – 6
§ 25-28 – 7,8
§ 29-31 – 1-5, 10-11
§ 35-36 – 1-5, 7-8, 10-11
Примечание: Полное соответствие указанной выше программе будет содержаться в готовящихся книгах:
А.Г.Мордкович, П.В.Семенов. Алгебра и начала анализа - 11 (профильный уровень). Часть 1. Учебник.
А.Г.Мордкович и др. Алгебра и начала анализа-11 (профильный уровень). Часть 2. Задачник.
6. Обязательный минимум содержания
основных образовательных программ
(базовый уровень)
АЛГЕБРА
Корни и степени. Корень степени n>1 и его свойства. Степень с рациональным показателем и ее свойства. Понятие о степени с действительным показателем. Свойства степени с действительным показателем.
Логарифм. Логарифм числа. Основное логарифмическое тождество. Логарифм произведения, частного, степени; переход к новому основанию. Десятичный
и натуральный логарифмы, число е.
Преобразования простейших выражений, включающих арифметические операции, а также операцию возведения в степень и операцию логарифмирования.
Основы тригонометрии. Синус, косинус, тангенс, котангенс произвольного угла. Радианная мера угла. Синус, косинус, тангенс и котангенс числа. Основные тригонометрические тождества. Формулы приведения. Синус, косинус и тангенс суммы и разности двух углов. Синус и косинус двойного угла. Формулы половинного угла. Преобразования суммы тригонометрических функций в произведение
и произведения в сумму. Выражение тригонометрических функций через тангенс половинного аргумента. Преобразования простейших тригонометрических выражений.
Простейшие тригонометрические уравнения. Решения тригонометрических уравнений. Простейшие тригонометрические неравенства.
Арксинус, арккосинус, арктангенс числа.
ФУНКЦИИ
Функции. Область определения и множество значений. График функции. Построение графиков функций, заданных различными способами. Свойства функций: монотонность, четность и нечетность, периодичность, ограниченность. Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума (локального максимума и минимума). Графическая интерпретация. Примеры функциональных зависимостей в реальных процессах и явлениях.
Обратная функция. Область определения и область значений обратной функции. График обратной функции.
Степенная функция с натуральным показателем, её свойства и график.
Вертикальные и горизонтальные асимптоты графиков. Графики дробно-линейных функций.
Тригонометрические функции, их свойства и графики; периодичность, основной период.
Показательная функция (экспонента), её свойства и график.
Логарифмическая функция, её свойства и график.
Преобразования графиков: параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой
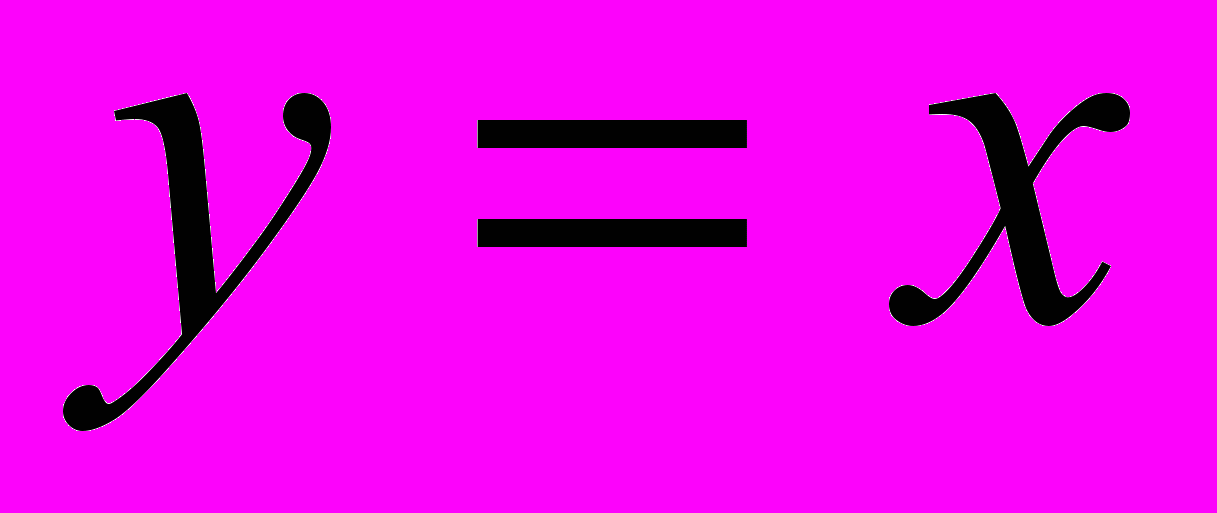, растяжение и сжатие вдоль осей координат. НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА
Понятие о пределе последовательности. Существование предела монотонной ограниченной последовательности. Длина окружности и площадь круга как пределы последовательностей. Бесконечно убывающая геометрическая прогрессия и ее сумма.
Понятие о непрерывности функции.
Понятие о производной функции, физический и геометрический смысл производной. Уравнение касательной к графику функции. Производные суммы, разности, произведения, частного. Производные основных элементарных функций. Применение производной к исследованию функций и построению графиков. Производные обратной функции и композиции данной функции с линейной.
Понятие об определенном интеграле как площади криволинейной трапеции. Первообразная. Формула Ньютона-Лейбница.
Примеры использования производной для нахождения наилучшего решения в прикладных, в том числе социально-экономических, задачах. Нахождение скорости для процесса, заданного формулой или графиком. Примеры применения интеграла в физике и геометрии. Вторая производная и ее физический смысл.
УРАВНЕНИЯ И НЕРАВЕНСТВА
Решение рациональных, показательных, логарифмических уравнений и неравенств. Решение иррациональных уравнений.
Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. Равносильность уравнений, неравенств, систем. Решение простейших систем уравнений с двумя неизвестными. Решение систем неравенств с одной переменной.
Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.
Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений.
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ, СТАТИСТИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ
Табличное и графическое представление данных. Числовые характеристики рядов данных.
Поочередный и одновременный выбор нескольких элементов из конечного множества. Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач. Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля.
Элементарные и сложные события. Рассмотрение случаев и вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Вероятность и статистическая частота наступления события. Решение практических задач с применением вероятностных методов.
7. Комментарии
Выпишем отдельно тот материал стандарта, которого нет в явном виде
в учебнике А.Г.Мордковича. В каждом пункте указано, в каких наших изданиях можно найти соответствующий материал.
1) Обратная функция. Область определения и область значений обратной функции. График обратной функции. Производные обратной функции
Литература:
А.Г.Мордкович. Алгебра и начала анализа (для поступающих в вузы). Вербум-М, 2000.
6) Раздел «Элементы комбинаторики, статистики и теории вероятностей
Литература:
А.Г.Мордкович. Алгебра и начала анализа (для поступающих в вузы). Вербум-М, 2000.
А.Г.Мордкович, П.В.Семенов. События. Вероятности. Статистическая обработка данных. Дополнительные параграфы к курсу алгебры 7-9. Мнемозина, 2003.
Примечание. Весь недостающий материал будет в новом издании имеющегося нашего учебника для общеобразовательной школы.
8. Список литературы
Изданные книги – основные (Мнемозина)
1.. А.Г.Мордкович. Алгебра и начала анализа 10-11. Часть 1. Учебник. 2003.
Гриф – рекомендовано.
2. А.Г.Мордкович и др. Алгебра и начала анализа 10-11. Часть 2. Задачник. 2003. Гриф – рекомендовано.
3. А.Г.Мордкович . Алгебра и начала анализа 10-11. Пособие для учителей. 2003. Гриф – допущено.
4. А.Г.Мордкович, Е.Е.Тульчинская. Алгебра и начала анализа 10-11. Контрольные работы. 2003. Гриф – допущено.
5.. Л.О.Денищева, Т.А.Корешкова. Алгебра и начала анализа 10-11. Тематические тесты и зачеты (под ред. А.Г.Мордковича). 2003. Гриф – допущено.
Дополнительная литература:
6. А.Г.Мордкович, П.В.Семенов. События. Вероятности. Статистическая обработка данных. Дополнительные параграфы к курсу алгебры 7-9. Мнемозина, 2003.
7. А.Г.Мордкович. Алгебра и начала анализа (для поступающих в вузы). Вербум-М, 2000.
9. Примерное планирование курса алгебры и начал анализа
(базовый уровень)
10 класс (3 ч в неделю)
Глава 1. ЧИСЛОВЫЕ ФУНКЦИИ
1. Определение числовой функции и способы ее задания 2
- Свойства функций 3
- Преобразования графиков (параллельный перенос, симметрия
относительно осей координат и относительно начала координат 3
- Периодические функции 2
- Обратная функция 2
___________________________________________________________________
Итого: 12
Глава 2. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
- Числовая окружность 2
7. Числовая окружность на координатной плоскости 2
8. Синус и косинус. Тангенс и котангенс 3
9. Тригонометрические функции числового аргумента 3
10. Тригонометрические функции углового аргумента 1
- Функции y = sin x, y = соs x, их свойства и графики 4
12. Построение графика функции
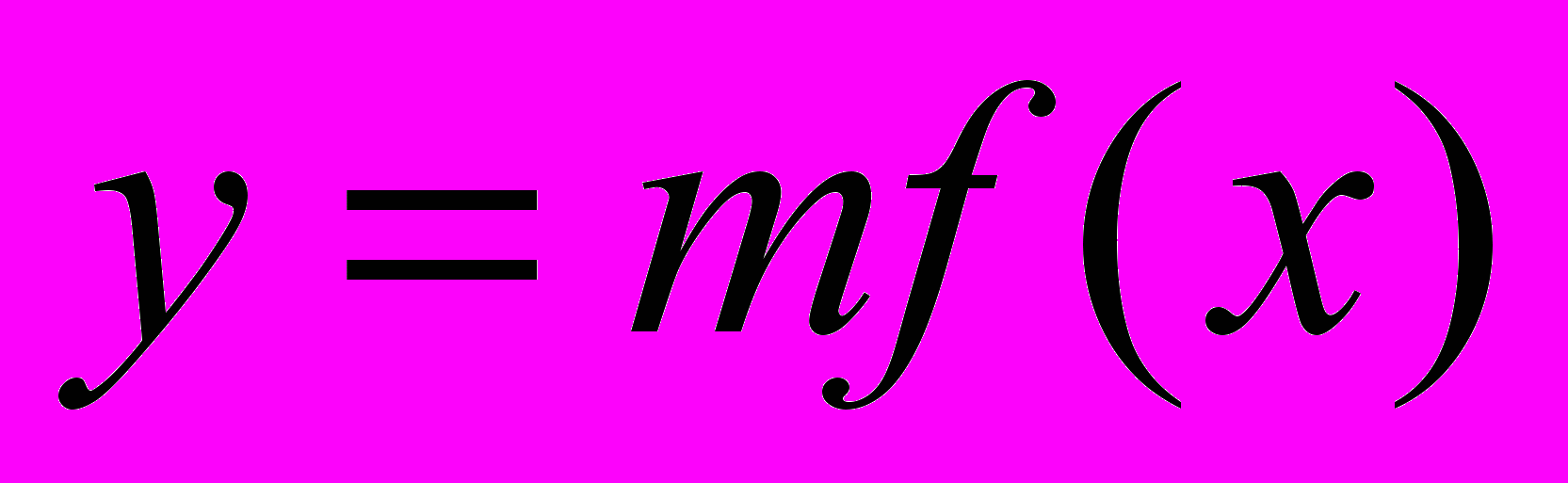2 13. Построение графика функции
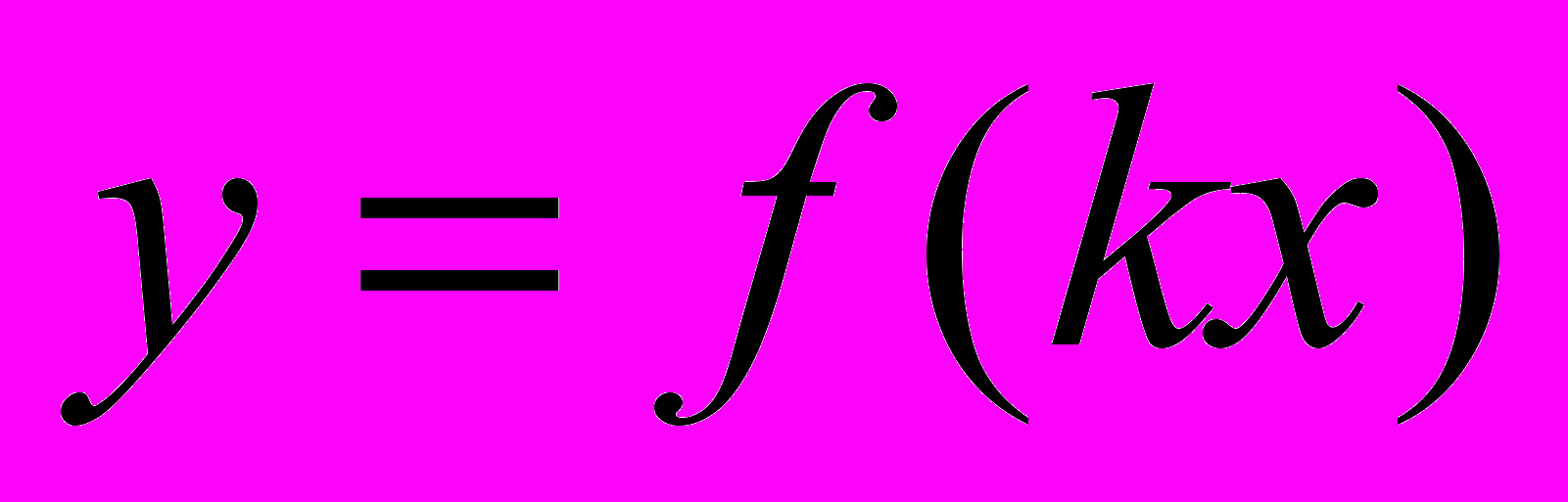2 14. График гармонического колебания 1
15. Функции y = tg x, y = ctg x, их свойства и графики 3
16. Обратные тригонометрические функции 3
______________________________________________________________________
Итого: 26
Глава 3. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
17. Простейшие тригонометрические уравнения и неравенства 5
18. Методы решения тригонометрических уравнений 5
- Метод замены переменной
- Метод разложения на множители
- Однородные тригонометрические уравнения
________________________________________________________________
Итого: 10
Глава 4. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
19. Синус и косинус суммы и разности аргументов 3
20. Тангенс суммы и разности аргументов 2
21. Формулы приведения 2
22. Формулы двойного аргумента. Формулы понижения степени 3
23. Преобразование сумм тригонометрических функций 2
в произведение
24. Преобразование произведений тригонометрических функций 2
в сумму
25. Преобразование выражения A sin x + B cos x к виду Csin(x + t) 1
____________________________________________________________________
Итого: 15
Глава 5. ПРОИЗВОДНАЯ
26. Числовые последовательности 2
- Определение числовой последовательности и способы ее задания
- Свойства числовых последовательностей
27. Предел числовой последовательности 3
1) Определение предела последовательности
2) Свойства сходящихся последовательностей
- Вычисление пределов последовательностей
- Сумма бесконечной геометрической прогрессии
28. Предел функции 3
1) Предел функции на бесконечности и в точке
- Приращение аргумента. Приращение функции
29. Определение производной 3
1) Задачи, приводящие к понятию производной
2) Определение производной
30. Вычисление производных 6
1) Формулы и правила дифференцирования
2) Вторая производная и ее физический смысл
3) Дифференцирование обратной функции
31. Уравнение касательной к графику функции 3
32. Применение производной для исследования функций 4
на монотонность и экстремумы
33. Построение графиков функций. Асимптоты. График
дробно-линейной функции 3
34. Применение производной для отыскания наибольших и наименьших
значений величин 4
1) Отыскание наибольших и наименьших значений непрерывной
функции на промежутке
2) Задачи на отыскание наибольших и наименьших значений величин
___________________________________________________________________
Итого: 31
Повторение 8
_______________________
Всего 102
Использование указанной выше литературы:
§ 1-4 – 1-5
§ 5 – 7
§ 6-15 – 1-5
§ 16 – 1-5,7
§ 17-34 – 1-5
10. Примерное планирование курса алгебры и начал анализа
(базовый уровень)
11 класс (3 ч в неделю)
Повторение курса 10 класса 6
Глава 1. ИНТЕГРАЛ
1. Первообразная 2
2. Определенный интеграл и его применения 5
__________________________
итого: 7
Глава 2. СТЕПЕНИ И КОРНИ. СТЕПЕННЫЕ ФУНКЦИИ
3. Понятие корня n-й степени из действительного числа 2
4. Функции
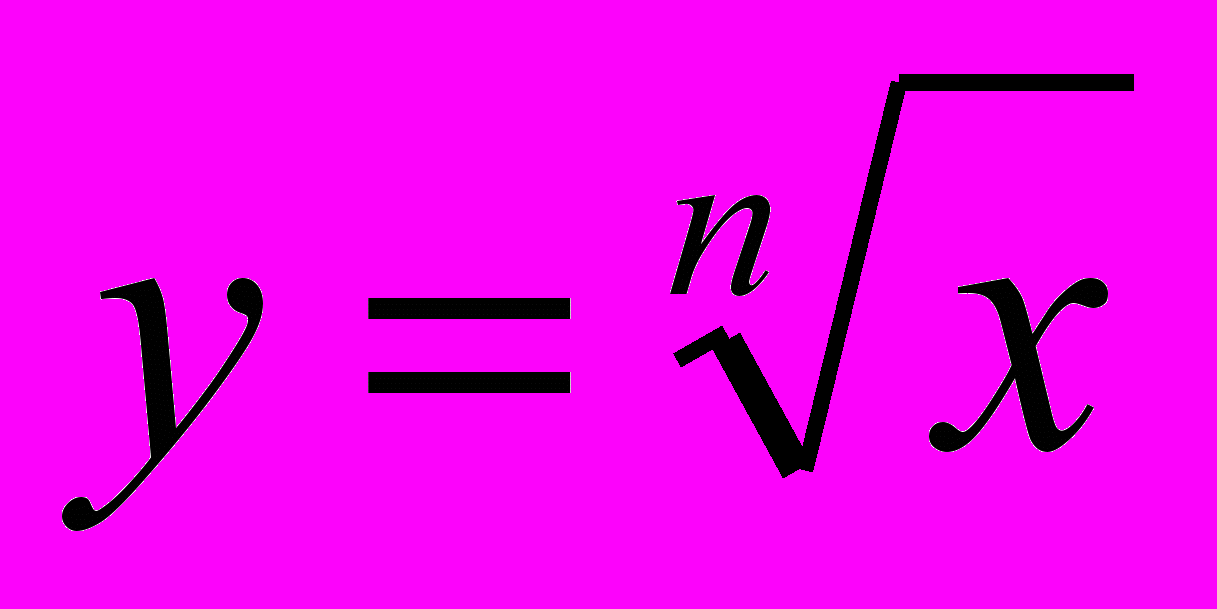, их свойства и графики 35. Свойства корня n-й степени 3
6. Преобразование выражений, содержащих радикалы 4
7. Обобщение понятия о показателе степени 3
- Степенные функции, их свойства и графики (включая 5
дифференцирование и интегрирование) _______________________
итого: 20
Глава 3. ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ
9. Показательная функция, ее свойства и график 3
10. Показательные уравнения 3
11. Показательные неравенства 2
12. Понятие логарифма 2
13. Функция
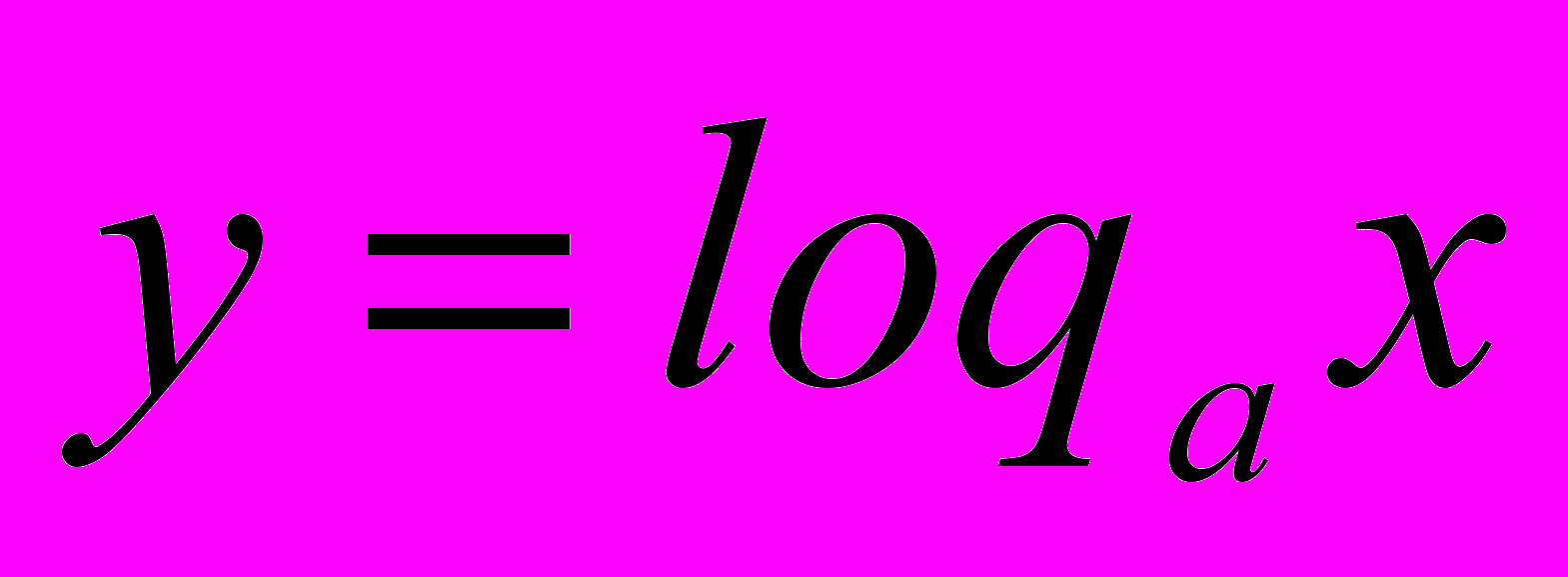, ее свойства и график 314. Свойства логарифмов 3
15. Логарифмические уравнения 3
16. Логарифмические неравенства 3
17. Переход к новому основанию логарифма 2
18. Дифференцирование показательной и логарифмической функций 3
__________________________
итого: 27
Глава 4. КОМБИНАТОРИКА И ВЕРОЯТНОСТЬ
19. Правило умножения. Перестановки и факториалы 2 20. Выбор нескольких элементов. Сочетания и размещения 2
21. Формула бинома Ньютона, свойства биномиальных коэффициентов 2
Треугольник Паскаля
22. Случайные события и их вероятности 2
23. Независимые повторения испытаний с двумя исходами 2
24. Табличное и графическое представление данных. Числовые
характеристики рядов данных. Вероятность и статистическая частота 3
наступления события ______________________________________________________________
Итого: 13
Глава 5.
УРАВНЕНИЯ И НЕРАВЕНСТВА.
СИСТЕМЫ УРАВНЕНИЙ И НЕРАВЕНСТВ
25. Равносильность уравнений 2
- Общие методы решения уравнений 4
- Решение неравенств с одной переменной 4
- Системы уравнений 4
- Уравнения и неравенства с параметрами 3
__________________________
итого: 15
Повторение 14
_______________________
Всего 102
Использование указанной выше литературы:
§ 1-18 – 1-5
§ 19-24 – 6, 7
§ 25-29 – 1-5
- Предложения по реализации курса А
Издательство «Мнемозина» готовит к изданию к началу 2004/05 уч. года новые учебные пособия:
А.Г.Мордкович, И.И.Смирнова. Математика-10.
А.Г.Мордкович, И.И.Смирнова. Математика-11.
Курс «Математика 10-11 рассчитан на 3 ч. в неделю и включает в себя два предмета – алгебру и начала анализа и геометрию. Строить изучение курса учитель может по традиционной схеме: 2 ч. в неделю на курс алгебры и начал анализа и 1 ч. в неделю на курс геометрии. Но целесообразнее подавать материал цельными блоками, завершая каждый блок контрольной работой. Тогда практически каждая контрольная работа будет содержать в себе и алгебраический, и геометрический материал. Ниже приведен вариант соответствующего поурочного планирования; номера параграфов указаны по двум упомянутым выше учебным пособия (авторы – А.Г.Мордкович и И.М.Смирнова).
Примерное поурочное планирование курса «Математика-10»
Первый блок (11 ч.)
История возникновения и развития стереометрии (§ 30) 1
Основные понятия стереометрии (§ 31) 2
Пространственные фигуры (§ 32) 1
Параллельность прямых в пространстве (§ 33) 2
Параллельность прямой и плоскости (§ 34) 2
Параллельность двух плоскостей (§ 35) 2
Контрольная работа № 1 1
Второй блок ( 13 ч.)
Числовая окружность (§ 1) 2
Числовая окружность на координатной плоскости (§ 2) 2
Синус и косинус. Тангенс и котангенс (§ 3) 3
Тригонометрические функции числового аргумента (§ 4) 2
Тригонометрические функции углового аргумента (§ 5) 1
Формулы приведения (§ 6) 2
Контрольная работа № 2 1
Третий блок (14 ч.)
Параллельное проектирование (§ 36) 1 Параллельные проекции плоских фигур (§ 37) 2 Изображение пространственных фигур на плоскости (§ 38) 2 Сечения многогранников (§ 39) 2
Функция y = sin x, ее свойства и график (§ 7) 2
Функция y = соs x, ее свойства и график (§ 8) 1
Периодичность функций y = sin x, y = соs x (§ 9) 1
Функции y = tg x, y = ctg x, их свойства и графики (§ 11) 1
Контрольная работа № 3 1
Четвертый блок (9 ч.)
Арккосинус и решение уравнения cos t = a (§ 12) 2
Арксинус и решение уравнения sin t = a (§ 13) 2
Арктангенс и арккотангенс. Решение уравнений tg x = a,
ctg x = a (§ 14) 1
Тригонометрические уравнения (§ 15) 3
Контрольная работа № 4 1
Пятый блок (9ч.)
Угол между прямыми в пространстве. Перпендикулярность
прямых (§ 40) 2 Перпендикулярность прямой и плоскости. Ортогональное
проектирование (§ 41) 2 Перпендикуляр и наклонная. Угол между прямой
и плоскостью (§ 42) 2
Двугранный угол. Перпендикулярность плоскостей (§ 43) 2
Контрольная работа № 5 1
Шестой блок (9 ч.)
Синус и косинус суммы и разности аргументов 2
Тангенс суммы и разности аргументов 1
Формулы двойного аргумента 2
Преобразование сумм тригонометрических функций в произведение 3 Контрольная работа № 6 1
Седьмой блок (13 ч.)
Предел функции (§ 21) 3.
Определение производной (§ 22) 3
Вычисление производных (§ 23) 4
Уравнение касательной к графику функции (§ 24) 2
Контрольная работа № 7 1
Восьмой блок (16 ч.)
Многогранные углы (§ 45) 2
Выпуклые многогранники (§ 46) 2
Правильные многогранники (§ 47) 2
Применение производной для исследования функций
на монотонность и экстремумы (§ 25) 3
Построение графиков функций (§ 26) 2
Применение производной для отыскания наибольших
и наименьших значений величин (§ 27) 3
Контрольная работа № 8 2
Повторение 8
___________________________________
всего: 102ч
Примерное поурочное планирование курса «Математика-11»
Первый блок (13 ч.)
Первообразная (§ 1) 3
Определенный интеграл (§ 2) 3
Цилиндр, конус (§ 23) 2
Тела вращения (§ 24) 2
Взаимное расположение сферы и плоскости (§ 25) 2
Контрольная работа № 1 1
Второй блок ( 12 ч.)
Симметрия пространственных фигур (§ 29) 2
Понятие корня n-й степени из действительного числа (§ 3) 2
Функции
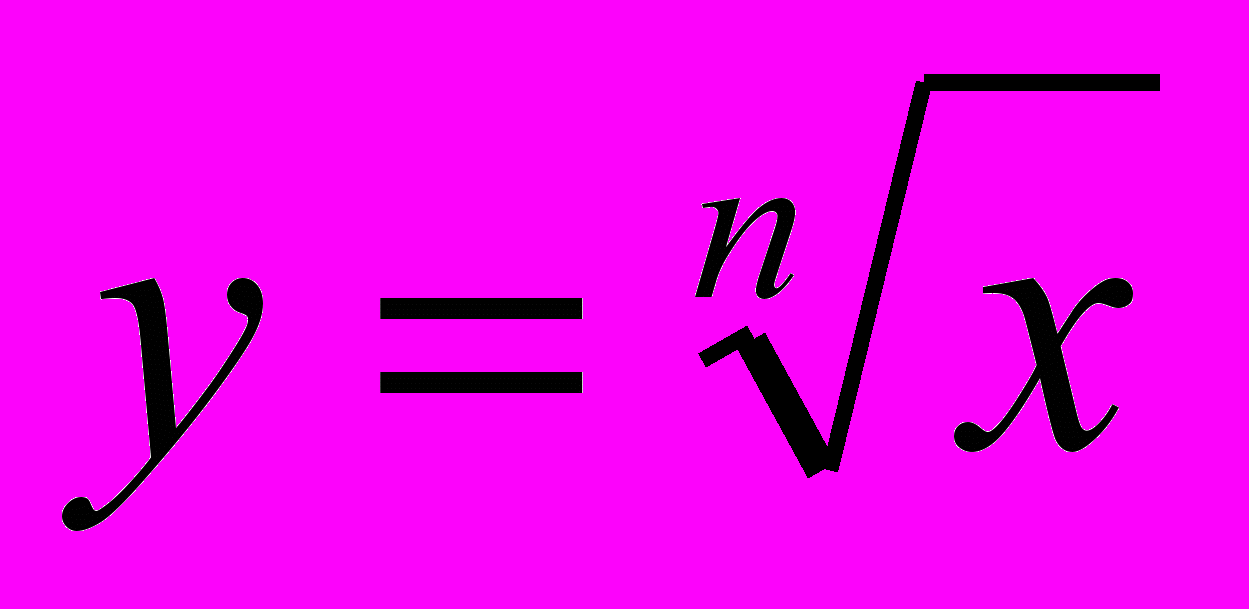, их свойства и графики (§ 4) 2 Свойства корней n-й степени (§ 5) 2
Преобразование выражений, содержащих радикалы (§ 6) 3
Контрольная работа № 2 1
Третий блок (12 ч.)
Обобщение понятия о показателе степени (§ 7) 2
Степенные функции, их свойства и графики (§ 8) 3
Объем пространственного тела. Объем цилиндра (§ 31) 1
Принцип Кавальери (§ 32) 1
Объем пирамиды (§ 33) 2
Объем конуса (§ 34) 2
Контрольная работа № 3 1
Четвертый блок (11 ч.)
Объем шара (§ 35) 2
Площадь поверхности (§ 36) 1
Площадь поверхности шара (§ 37) 2
Показательная функция, ее свойства и график (§ 9) 2
Показательные уравнения и неравенства (§ 10) 3
Контрольная работа № 4 1
Пятый блок (14 ч.)
Понятие логарифма (§ 11) 2
Функция
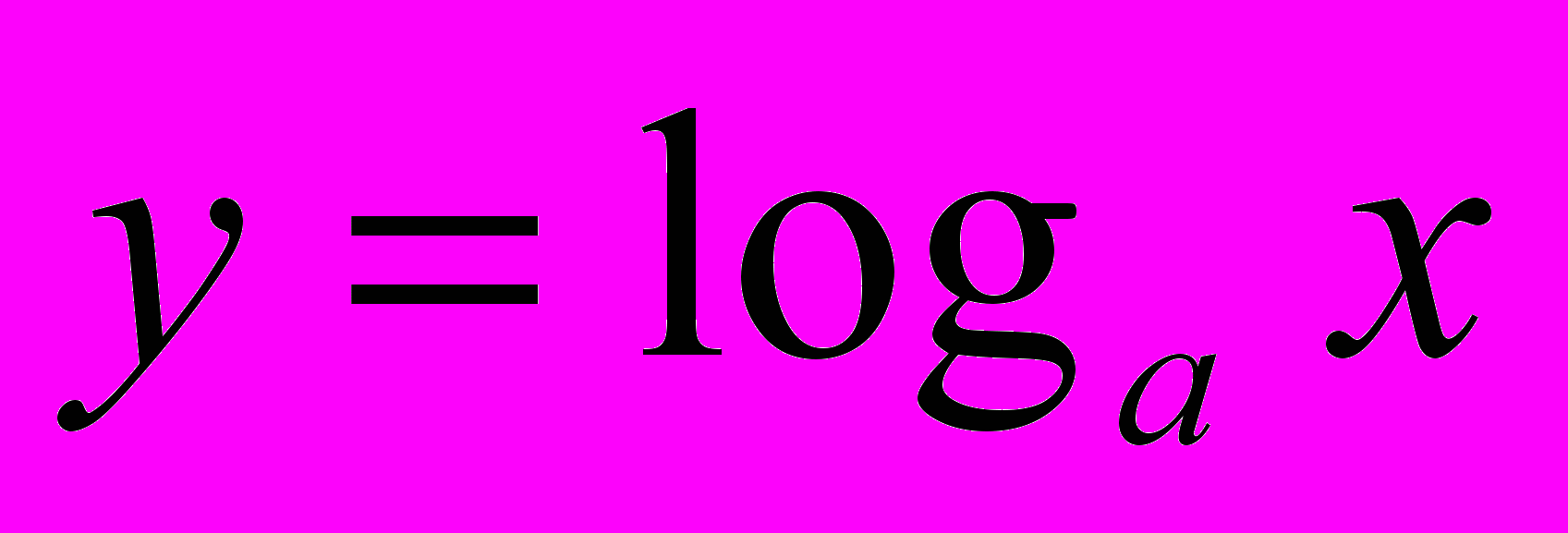, ее свойства и график (§ 12) 2 Свойства логарифмов (§ 13) 2
Логарифмические уравнения (§ 14) 3
Логарифмические неравенства (§ 15) 2
Дифференцирование показательной
и логарифмической функций (§ 17) 2
Контрольная работа № 5 1
Шестой блок (14 ч.)
Равносильность уравнений (§ 18) 2
Общие методы решения уравнений (§ 19) 3
Решение неравенств с одной переменной (§ 20) 4
Системы уравнений (§ 21) 3
Контрольная работа № 6 2
Седьмой блок (10 ч.)
Прямоугольная система координат в пространстве (§ 38) 1
Векторы в пространстве (§ 39) 2
Координаты вектора (§ 40) 2
Скалярное произведение векторов (§ 41) 2
Уравнение плоскости в пространстве (§ 42) 2
Контрольная работа № 7 1
Повторение 16
___________________________________
всего: 102ч