Задача о Кенигсбергских мостах. На рис. 1 представлен схематический план центральной части города Кенигсберг (ныне Калининград), включающий два берега реки Перголя, два острова в ней и семь соединяющих мостов.
| Вид материала | Задача |
- Екскурсія по ландшафтам о. Хортиця, 111.81kb.
- Спецкурс «Теория графов» пм 4 курс История возникновения и развития теории графов., 13.97kb.
- Этого небольшого (всего 32 тысячи жителей) города известно на весь мир, 681.25kb.
- Л. Г. Голубкова Доклад был представлен в два этапа: 11 ноября на семинар, 816.34kb.
- А. М. Горького Факультет журналистики Кафедра русского языка и стилистики морфология, 830.56kb.
- Туркомплекс в атмосфере старорусской деревни, территория которого охватывает два берега, 181.68kb.
- Доклад тема: "Травление п/п имс", 399.97kb.
- Два города: рим + неаполь, 25.53kb.
- Финист Ясный Сокол. Семь Симеонов-семь работников. Сказки народов мира: украинская, 49.92kb.
- Задача № расчет линейной электрической цепи постоянного тока по заданной обобщенной, 87.8kb.
Введение
В последнее время исследования в областях, традиционно относящихся к дискретной математике, занимают все более заметное место. Наряду с такими классическими разделами математики, как математический анализ, дифференциальные уравнения, и многих специальностях появились разделы по математической логике, алгебре, комбинаторике и теории графов. Причины этого нетрудно понять, просто обозначив круг задач, решаемых на базе этого математического аппарата. Развитие теории графов в основном обязано большому числу всевозможных приложений. По-видимому, из всех математических объектов графы занимают одно из первых мест в качестве формальных моделей реальных систем.
Графы нашли применение практически во всех отраслях научных знаний: физике, биологии, химии, математике, истории, лингвистике, социальных науках, технике и т.п. Наибольшей популярностью теоретико-графовые модели используются при исследовании коммуникационных сетей, систем информатики, химических и генетических структур, электрических цепей и других систем сетевой структуры.
История возникновения теории графов.
Родоначальником теории графов принято считать математика Леонарда Эйлера (1707-1783). Однако теория графов многократно переоткрывалась разными авторами при решении различных прикладных задач.
1. Задача о Кенигсбергских мостах. На рис. 1 представлен схематический план центральной части города Кенигсберг (ныне Калининград), включающий два берега реки Перголя, два острова в ней и семь соединяющих мостов. Задача состоит в том, чтобы обойти все четыре части суши, пройдя по каждому мосту один раз, и вернуться в исходную точку. Эта задача была решена (показано, что решение не существует (рис. 2)) Эйлером в 1736 году.
рис. 1
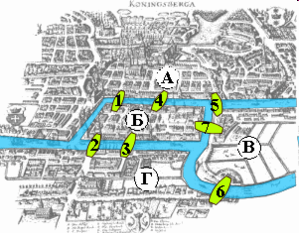
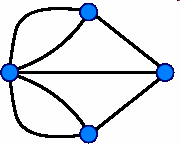
Рис. 2
1.Основные понятия
ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ
Теория графов в качестве теоретической дисциплины1 может
рассматриваться как раздел дискретной математики, исследующий свойства конечных множеств (бесконечные графы рассматривать мы не будем) с заданными отношениями между их элементами.
Как прикладная дисциплина теория графов позволяет описывать и исследовать многие технические, экономические, биологические и социальные системы.
Задача настоящего материала заключается в том, чтобы, следуя, в основном [8], изложить основные понятия и результаты теории графов, необходимые для постановки и решения задач управления организационными системами.
Изложение материала имеет следующую структуру. В первом разделе вводятся основные понятия, во втором рассматриваются задачи о максимальных путях и контурах на графах, в третьем – свойства псевдопотенциальных графов, в четвертом – задачи о
максимальном потоке, в пятом – задачи сетевого планирования и управления
Графом G=(X,U) будем называть совокупность двух конечных множеств: множества вершин Х={х1,…,хn} и множества ребер (дуг) U={u1,…,um}, состоящего из некоторых пар элементов (хi,xj) множества Х. Геометрически граф может быть представлен в виде рисунка, в котором вершинам соответствуют точки, а ребрам - линии, соединяющие все или некоторые из этих точек. Граф называется помеченным, если его вершинам приписаны некоторые метки, например, номера.
Если пары вершин(xi,xj) во множестве U являются неупорядоченными (т.е. порядок соединения вершин не существенен), то граф называется неориентированным (неографом), а пары (хi,хj) ребрами этого графа (рис.1). При этом вершины xi,xj называют концами (концевыми вершинами) ребра. В данном случае также говорят, что ребро (хi,хj) соединяет вершины хi и хj. Если пары вершин (хi,хj) во множестве U являются упорядоченными (т.е., порядок соединения вершин существенен), то граф называется ориентированным (орграфом), а пары (хi,хj) - дугами (рис.2). Дуги орграфа, в отличие от ребер неографа, будем обозначать <хi,хj > . При этом хi- начало (начальная вершина) дуги, хj - конец (конечная вершина) дуги. Говорят также, что дуга <хi,хj > исходит из вершины хi и заходит в вершину хj. Заметим, что <хi,хj > и <хj,хi > - это различные дуги в графе.
При изображении орграфа дуги обозначают стрелками, указывающими их ориентацию (направление). Графы, в которых имеются и неориентированные ребра, и дуги, называются смешанными (рис.3). Заметим, что любой неориентированный граф может быть представлен в виде орграфа путем замены каждого его ребра двумя противоположно направленными дугами.
Пара вершин хi,хj может соединяться двумя или более ребрами (дугами одного направления). Такие ребра (дуги) называют кратными. Количество одинаковых ребер (хi,хj) (дуг <хi,хj>) называется кратностью соответствующего ребра (дуги). Петлей называется дуга (ребро), с совпадающими начальной и конечной вершинами.
Граф с петлями и кратными ребрами(дугами) называется псевдографом. Граф с кратными ребрами(дугами) и без петель называется мультиграфом. Граф, не содержащий петель и кратных ребер называется простым графом. Так, граф, представленный на рисунке 1 является псевдографом, так как содержит петлю (X4,X4) и кратное ребро (X1,X2). Граф на рисунке 2 является мультиграфом, граф на рисунке 3-простым графом.
Две вершины графа называются смежными, если существует соединяющее их ребро(дуга). Два ребра (дуги) смежны, если они имеют общую вершину. Если ребро (дуга) соединяет вершины, то говорят, что ребро (дуга) инцидентно вершинам, а вершины инцидентны ребру (дуге). Так, на рисунке 1 вершина X3 инциндентна ребрам U8, U9, U10. Смежными являются вершины X1 и X5, X3 и X4; ребра U5 и U6 являются смежными.
рис.1 Неориентированный граф
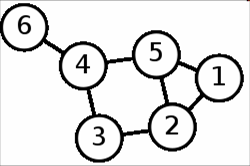
рис.2 Ориентированный граф
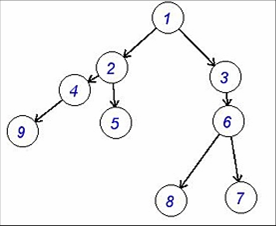
рис.3 Смешанный граф
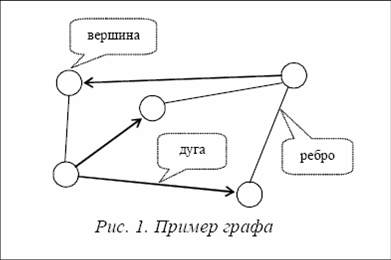
1.1 Способы задания графа
Основными способами задания графа являются геометрический, аналитический и матричный.
Основой геометрического способа задания графа является рисунок, дающий изображение графа. Изображение графа в виде рисунка наглядно раскрывает содержательный смысл представляемого объекта.
Рассмотрим аналитический способ задания графа. Говорят, что задан граф, если дано множество вершин Х, множество ребер U и инцидентор F, определяющий, какую пару вершин (хi,хj) Х соединяет ребро uk=(хi,хj).
Матричный способ с помощью матрицы смежности и матрицы инцендентности.
Матрицей смежности неориентированного графа с n вершинами называется квадратная матрица А порядка n, элементы которой определяются следующим образом:
1, если вершины хi и xj смежны;
aij=
0, в противном случае;
Для ориентированного графа:
1, если существует дуга
aij=
0, в противном случае;
Если в графе нет петель, то на главной диагонали в матрице смежности ставятся нули, в противном случае на главной диагонали – единица.
Данный способ задания графа один из наиболее удобных способов, который часто применяется при решении различных задач вручную и при составлении всевозможных программ.
2.Метрические характеристики графа
Для определения метрических характеристик графа необходимо сказать о таком понятии как расстояние d(xi,xj).
Рассмотрим граф G и 2 его несовпадающие вершины хi и хj. Длина кратчайшего маршрута соединяющего данные вершины, называется расстоянием между этими вершинами и обозначается d(xi,xj), если вершины не соединены маршрутом d(xi,xj)=∞. Необходимо заметить, что для неориентированных графов d(xi,xj)=d(xj,xi).
Расстояние d(xi,xj) удовлетворяют следующим условиям метрики:
1) d(xi,xj) = 0;
2) d(xi,xj) ≥ 0;
3) d(xi,xj)=0 тогда и только тогда, когда xi=xj;
4) d(xi,xj)=d(xj,xi) для симметрических графов;
5) d(xi,xj)+d(xj,xk) ≥d(xi,xk)(неравенство треугольника);
Расстояния для графа удобно задавать матрицей расстояний.
Матрицей расстояний графа с n вершинами называется квадратная матрица D порядка n, элементы которой определяются следующим образом:
0, если xi=xj;
dij=
d(xi,xj), если xi≠xj;
Задавая матрицу расстояний, описанным ранее способом, можно определить метрические характеристики графа. К метрическим характеристикам графа относятся:
1)Эксцентриситет.
Для фиксированной вершины xi величина:
е(xi)=max d(xi,xj), xj€ X
называется эксцентриситетом. Исходя из определения эксцентриситета, можно говорить о том, что задача нахождения е(xi) сводиться к нахождению максимального элемента из каждой строки.
2) Диаметр.
Максимальный элемент из эксцентриситетов вершин называется диаметром diam(G) :
diam(G)=max e(xi);
3) Радиус.
Минимальный элемент из эксцентриситета е(xi) называется радиусом графа r(G):
r(G)=min e(xi)
Задача нахождения радиуса и диаметра сводиться к нахождению минимального и максимального эксцентриситета.
4) Центр графа.
Вершина, имеющая минимальный эксцентриситет, называется центром графа.
5) Передаточное число.
Для фиксированной вершины хi число:
P(xi)= ∑d(xi,xj)
xiX
называется передаточным числом
Задача нахождения передаточного числа сводиться к суммированию элементов каждой строки.
6)Медиана графа
Вершина графа, которой соответствует минимальное передаточное число называется медиана графа
min P(xi)=min ∑d(xi,xj)
xiX
После всего вышесказанного остается добавить, что центров и медиан в графе может быть несколько.
3.Описание программы
3.1.Назначение
Программа предназначена для вычисления метрических характеристик графа. Обработке могут подвергаться как ориентированные, так и неориентированные графы, заданные матрицей смежности.
3.2.Выбор средств реализации
Pascal — это императивный язык программирования, разработанный Никлаусом Виртом в 1970 в качестве языка обучения структурному программированию. Название языку дано в честь выдающегося французского математика, физика, литератора и философа Блеза Паскаля. Первоначально язык компилировался в байт-код, подобно языку Java.
Особенностями языка являются строгая типизация и наличие средств структурного (процедурного) программирования. Паскаль был одним из первых таких языков. По мнению Н. Вирта, язык должен способствовать дисциплинированию программирования, поэтому, наряду со строгой типизацией, в Паскале сведены к минимуму возможные синтаксические неоднозначности, а сам синтаксис интуитивно понятен даже при первом знакомстве с языком.
Паскаль претерпел за прошедшее время довольно много изменений в лучшую сторону. Основная заслуга в этом принадлежит фирме Borland International, долгое время выпускавшей линейку Turbo Pascal. Одно из основных усовершенствований, внесенных ею, — дополнение языка разнообразными и мощными средствами ввода-вывода. Другое связано с языком Модула-2 (автором которого также стал Н. Вирт): фирма Borland отказалась от распространения компилятора этого языка, применив вместо этого модульный принцип построения в Turbo Pascal. Кроме того, в Паскаль были введены средства непосредственного доступа к портам и ячейкам памяти, а позднее — возможность включать в текст программы фрагменты, написанные на ассемблере. Все это превратило Паскаль из средства обучения в достаточно мощный универсальный язык.
3.3.Структура программы
Объявляем все переменные и массивы
Program Graf;
Const m=50;
Var a,d: array [1..m,1..m] of integer;
e,p: array [1..m] of integer;
i,j,k,max,n,summa,diam,radius,minp:integer;
Вводим количество вершин
Begin
Write ('vvedite kolichestvo vershin:');
Read (n);
Writeln;
Вводим матрицу смежности
Writeln ('vvedite matricu smezhnosti');
For i:=1 to n do
Begin
Write ('vvedite ',i, ' stroku:');
For j:=1 to n do
Если Xij=0 и присваиваем этому Эл-ту 10000, что в нашем случае эквивалентно
Begin
Read (a[i,j]);
If (a[i,j]=0)and(i<>j) then
a[i,j]:=10000;
End;
Writeln;
End;
Вычисляем кратчайшие пути между вершина-ми, считая что вес каждого ребра равен1
For k:=1 to n do
For i:=1 to n do
For j:=1 to n do
If a[i,j]>(a[k,j]+a[i,k]) then
a[i,j]:=a[k,j]+a[i,k];
Выводим матрицу расстояний
For i:=1 to n do
Begin
For j:=1 to n do
Write (a[i,j],' ');
Writeln;
End;
For i:=1 to n do
Begin
max:=0;
summa:=0;
For j:=1 to n do
Begin
If a[i,j]>max then
max:=a[i,j];
summa:=summa+a[i,j];
End;
e[i]:=max;
p[i]:=summa;
End;
diam:=0;
radius:=10000;
minp:=10000;
For i:=1 to n do
Begin
If e[i]>diam then
diam:=e[i];
If e[i]
radius:=e[i];
If p[i]
minp:=p[i];
End;
Writeln ('diametr grafa=',diam);
Writeln ('radius grafa=',radius);
Write ('cenry grafa:');
For i:=1 to n do
If e[i]=radius then
Write (i,' ');
Writeln (' vershina');
Write ('mediany grafa:');
For i:=1 to n do
If p[i]=minp then
Write (i,' ');
Writeln (' vershina');
End.
3.5.Описание входных и выходных данных
Программа написана таким образом. что количество вершин графа не должно превышать 50, следовательно максимальный размер матрицы смежности равен 50Χ50.
Теперь подробнее о том как правильно ввести величины. После появления надписи “vvedite kolichestvo vershin:” задаете количество вершин в графе и нажимаете Enter. После появления запроса “Vvedite matricu smezhnosti:”, начинаете ввод матрицы смежности. Каждый последующий символ вводите через пробел после задания последнего элемента строки матрицы нажимаете Enter, и приступаете к следующей строке. После ввода последней строки на экран выводятся метрические характеристики графа.
3.6.Контрольный пример
Для проверки программы был взят граф с 6 вершинами.
Матрица смежности
1 2 3 4 5 6 1 0 3 1 2 1 3 2 1 0 2 3 2 4 3 3 2 0 1 4 2 4 2 1 3 0 3 1 5 3 2 4 1 0 2 6 2 1 3 4 3 0
Матрица расстояний
1 2 3 4 5 6 1 0 0 1 0 1 0 2 1 0 0 0 0 0 3 0 0 0 1 0 0 4 0 1 0 0 0 1 5 0 0 0 1 0 0 6 0 1 0 0 0 0
e(x) P(x)
10 12 12 10 12 13
3 4 4 3
4 4
Диаметр равен 4
Радиус Равен 3
Центр 1 и 4 вершины
Медиана 1 и 4 вершины
4. Приведем ряд примеров приложений теории графов.
1. «Транспортные» задачи, в которых вершинами графа являются пункты, а ребрами – дороги (автомобильные, железные и др.) и/или другие транспортные (например, авиационные) маршруты.
Другой пример – сети снабжения (энергоснабжения, газоснабжения, снабжения товарами и т.д.), в которых вершинами являются пункты производства и потребления, а ребрами – возможные
маршруты перемещения (линии электропередач, газопроводы, дороги и т.д.). Соответствующий класс задач оптимизации потоков грузов, размещения пунктов производства и потребления и т.д.,
иногда называется задачами обеспечения или задачами о размещении. Их подклассом являются задачи о грузоперевозках
2. «Технологические задачи», в которых вершины отражают производственные элементы (заводы, цеха, станки и т.д.), а дуги – потоки сырья, материалов и продукции между ними, заключаются
в определении оптимальной загрузки производственных элементов и обеспечивающих эту загрузку потоков.
3. Обменные схемы, являющиеся моделями таких явлений как бартер, взаимозачеты и т.д. Вершины графа при этом описывают участников обменной схемы (цепочки), а дуги – потоки материальных и финансовых ресурсов между ними. Задача заключается в определении цепочки обменов, оптимальной с точки зрения, например, организатора обмена и согласованной с интересами участников цепочки и существующими ограничениями.
4. Управление проектами1. С точки зрения теории графов проект – совокупность операций и зависимостей между ними (сетевой график – см. ниже). Хрестоматийным примером является проект строительства некоторого объекта. Совокупность моделей и методов, использующих язык и результаты теории графов и ориентированных на решение задач управления проектами, получила название календарно-сетевого планирования и управления (КСПУ). В рамках КСПУ решаются задачи определения последовательности выполнения операций и распределения ресурсов между ими, оптимальных с точки зрения тех или иных критериев (времени выполнения проекта, затрат, риска и др.).
5. Модели коллективов и групп, используемые в социологии, сновываются на представлении людей или их групп в виде вершин, а отношений между ними (например, отношений знакомства,
доверия, симпатии и т.д.) – в виде ребер или дуг. В рамках подобного описания решаются задачи исследования структуры социальных групп, их сравнения, определения агрегированных показателей, отражающих степень напряженности, согласованности взаимодействия и др.
6. Модели организационных структур, в которых вершинами являются элементы организационной системы, а ребрами или дугами – связи (информационные, управляющие, технологические и др.) между ними
Завершив краткое описание прикладных областей, вернемся к введению основных понятий теории графов.
Подграфом называется часть графа, образованная подмножеством вершин вместе со всеми ребрами (дугами), соединяющими вершины из этого множества. Если из графа удалить часть ребер (дуг), то получим частичный граф.
Две вершины называются смежными, если они соединены ребром (дугой). Смежные вершины называются граничными вершинами соответствующего ребра (дуги), а это ребро (дуга) – инцидентным соответствующим вершинам. Путем называется последовательность дуг (в ориентированном графе), такая, что конец одной дуги является началом другой дуги. Простой путь – путь, в котором ни одна дуга не встречается дважды. Элементарный путь – путь, в котором ни одна вершина не встречается дважды. Контур – путь, у которого конечная вер-
шина совпадает с начальной вершиной. Длиной пути (контура) называется число дуг пути (или сумма длин его дуг, если послед- ние заданы).
Граф, для которого из (i, j) I V следует (j, i) I V называется симметрическим. Если из (i, j) I V следует, что (j, i) V, то соответствующий граф называется антисимметрическим.
Цепью называется множество ребер (в неориентированном графе), которые можно расположить так, что конец (в этом расположении) одного ребра является началом другого. Другое определение: цепь – последовательность смежных вершин. Замкнутая цепь называется циклом. По аналогии с простым и элементарным путем, можно определить соответственно простые и элементарные цепь и цикл. Любой элементарный цикл является простым, обратное утверждение в общем случае неверно. Элементарная цепь (цикл, путь, контур), проходящая через все вершины графа называется гамильтоновой цепью (соответственно – циклом, путем, контуром). Простая цепь (цикл, путь, контур), содержащая все ребра (дуги) графа называется эйлеровой цепью (соответственно – циклом, путем, контуром).
Если любые две вершины графа можно соединить цепью, то граф называется связным. Если граф не является связным, то его можно разбить на связные подграфы, называемые компонентами.
Связностью графа называется минимальное число ребер, после удаления которых граф становится несвязным. Для ориентированных графов, если любые две вершины графа можно соединить
путем, то граф называется сильно связным. Известно [7], что: связность графа не может быть больше, чем [2m / n], где [x] – целая часть числа x; существуют графы с n вершинами и m ребрами,
имеющие связность [2m / n]; в сильно связном графе через любые две вершины проходит контур.
Связный граф, в котором существует эйлеров цикл, называется эйлеровым графом.
В неориентированном графе степенью вершины i называется число di инцидентных ей ребер. Очевидно, di . n – 1, i I X. Граф, степени всех вершин которого равны n – 1, называется полным.
Граф, все степени вершин которого равны, называется однородным.
Вершина, для которой не существует инцидентных ей ребер (di = 0) называется изолированной. Вершина, для которой существует только одно инцидентное ей ребро (di = 1) называется висячей.
Известно [7], что:
i X
i d = 2 m (данное выражение называется «леммой о рукопожатиях» – поскольку в каждом рукопожатии участвуют две руки, то при любом числе рукопожатий общее число пожатых рук четно (при условии, что каждая рука учитывается столько раз, в скольких рукопожатиях она участвовала)); в любом графе число вершин нечетной степени четно. Связный граф является эйлеровым тогда и только тогда, когда степени всех его вершин четны (теорема Эйлера). Обозначим nk –число вершин, имеющих степень k, k = 0, 1, 2,... . Известно [7, 15],
что:
k: nk 0
k k n = 2 m.
Для ориентированных графов для каждой вершины можно ввести два числа – полустепень исхода di (число выходящих из нее вершин) и полустепень захода
di (число входящих в нее вершин). В дальнейшем, если не оговорено особо, будем рассмат-
ривать графы без петель, то есть без дуг, у которых начальная и конечная вершины совпадают. Известно [7, 15], что:
i X
i d =
i X
i d = m; для эйлерова графа имеет место:
di =
di ,
6
i = 1,n ; эйлеров граф является объединением контуров, попарно
не имеющих общих ребер.
Определим матрицу смежности графа как квадратную матрицу n . n, элемент aij которой равен единице, если (i, j) I V, и нулю, если (i, j) V, i, j I X. Для неориентированного графа
матрица смежности всегда симметрическая.
Определим матрицу инциденций для ребер графа как прямоугольную матрицу n . m, элемент rij которой равен единице, если вершина i инцидентна ребру j, и нулю в противном случае, i = 1,n ,
j = 1,m . Аналогично определяется матрица инциденций для дуг графа – как прямоугольная матрицу m . n, элемент rij которой равен плюс единице, если дуга Uj исходит из вершины i, минус
единице, если дуга Uj заходит в вершину i, и нулю в остальных случаях, i = 1,n , j = 1,m
Деревом называется связный граф без простых циклов, имеющий не менее двух вершин. Для дерева m = n – 1, а число висячих вершин равно n1 = 2 + ii i n . Легко показать, что в дереве
любые две вершины связаны единственной цепью.
Прадеревом называется ориентированное дерево, у которого одна из вершин, называемая корнем, не имеет заходящих дуг, а степени захода остальных вершин равны единице.
Плоским (планарным) называется граф, который можно изобразить на плоскости так, что различным вершинам соответствуют различные кружки и никакие два ребра не имеют общих точек, отличных от их границ (не пересекаются). Для плоского графа существует понятие грани части плоскости, ограниченной ребрами и не содержащей внутри себя ни вершин, ни ребер. Для простоты определения грани в дальнейшем в основном будем рассматривать графы без висячих вершин. Например, дерево имеет всего одну внешнюю грань – всю плоскость. Степенью грани называется число ее граничных ребер (висячие ребра считаются дважды).
Обозначим p – число граней плоского графа, pk – число его граней,
имеющих степень k, qi – степень i-ой грани. Можно показать, что
имеет место
p
i
qi
1
= 2 m,
k: pk 0
k pk = 2 m, n + p = m + 2 – формула
Эйлера [7, 15]. Данные выражения являются необходимыми условиями существования плоских графов с заданными наборами чисел {ni} и {pi}.
Любому связному плоскому графу G можно поставить в соответствие двойственный ему связный плоский граф G*, определяемый следующим образом: каждой грани графа G соответствует
вершина графа G*, каждому ребру V графа G, являющемуся граничным для граней z1 и z2, соответствует ребро V* графа G*, соединяющее соответствующие граням z1 и z2 вершины. Понятие двойственного графа тесно связано с понятием двойственности в линейном программировании [7].
