Удк 681. 3: 658. 56

Вид материала

Документы

Содержание D, таким образом, представляются интервалами («интервальными числами») [D 2. Полиинтервальные оценки исходных данных 3. Обобщенные интервальные оценки исходных данных 4. Функции распределения вероятностей для параметров, описываемых обобщенными интервальными оценками 5. Структура интеллектуальных систем поддержки экспертных решений

Подобный материал:

• Удк 340. 6+681. 327+681 015 Д. В. Ландэ, В. Н. Фурашев, 450.24kb.
• Удк 681 053: 681. 32: 007, 134.3kb.
• 01. 192. 11. 1-80, 63.6kb.
• Гост 12 005-84  , 73.15kb.
• Удк 681. 51: 303. 732+681 066 вопросы анализа проблем рыбохозяйственных комплексов:, 87.72kb.
• Удк 658. 562. 012 + 660. 2 + 006, 52.12kb.
• Удк 658. 002. 6: 006. 025, 169.96kb.
• Удк 331. 552. 4: 658. 012. 4: 502, 335.35kb.
• Гост р 12 006-2002  , 261.92kb.
• Удк 658. 87(06) оценка возможных путей оптимизации издержек обращения ритейлеровых, 267.37kb.

УДК 681.3:658.56

МЕТОД ПРЕДСТАВЛЕНИЯ ЗНАНИЙ В ИНТЕЛЛЕКТУАЛЬНЫХ СИСТЕМАХ ПОДДЕРЖКИ ЭКСПЕРТНЫХ РЕШЕНИЙ ¹

М.Ю.Стернин, Г.И.Шепелев.

Предложен новый метод представления экспертных знаний об исходных параметрах моделей интеллектуальных систем поддержки принятия решений и последующего использования таких знаний для получения результирующих показателей моделей. Метод предназначен для учета неопределенности в оценках исходной информации, задаваемой как количественные (числовые) данные. В рамках метода на базе экспертных суждений строятся обобщенные интервальные оценки (ОИО) для каждого исходного параметра, - оценки, содержащие в себе экспертные знания о прогнозируемой системе интервалов ожидаемых значений исходных данных и вероятностях их реализации в такой системе. Предложены процедуры агрегирования оценок одноименных параметров, сделанных разными экспертами.

1. Введение

Во многих областях человеческой деятельности – науке, технике, бизнесе – широко распространены проблемные ситуации, которые могут быть описаны исходными данными (параметрами), измеримыми в количественных шкалах, то есть данными, представимыми числовыми оценками. Зачастую, однако, описание таких ситуаций «точечными» величинами (оценками, задаваемыми для каждого параметра одним числом) оказывается неадекватным достижению желаемой цели – расчету значений результирующих показателей решаемой задачи в виде, способствующем принятию обоснованных решений. Недостаточно точное априорное знание исходных параметров требует тогда, чтобы для целей анализа они были представлены как некоторые связные области на шкалах, характеризующих возможные допустимые в исследуемой ситуации значения каждого параметра.

Исходные данные D, таким образом, представляются интервалами («интервальными числами») [D_l, D_r], задаваемыми их левыми D_l и правыми D_r границами. Результирующие показатели, рассчитанные на моделях, которые связывают исходные данные с показателями, также оказываются теперь интервальными числами. Подобного рода ситуации, когда исходные параметры представлены как интервалы, типичны для естественных, инженерно-технических наук и техники, где измерениям принципиально присуща некоторая погрешность, которую требуется учитывать в дальнейших расчетах, в том числе в расчетах искомых значений непосредственно неизмеримых величин. В экономических исследованиях, бизнесе в виде интервальных чисел могут быть представлены прогнозируемые параметры, при этом их значения, отвечающие прошлым моментам времени и настоящему, часто известны вполне точно.

С усложнением проблемных ситуаций, увеличением числа и значимости междисциплинарных задач существенно усилилась роль экспертов и способствующих повышению эффективности их труда интеллектуальных систем поддержки принятия экспертных решений (СППЭР). Взаимодействие квалифицированного эксперта и СППЭР позволяет всесторонне исследовать такие задачи, решение которых ранее было либо неудовлетворительно приближенным, либо требовало неприемлемо больших затрат времени и труда.

Для успешного решения подобных задач жизненно важна роль обоих взаимодействующих участников этого процесса – и эксперта, и СППЭР. СППЭР предоставляет эксперту свой вычислительный потенциал, возможность привлечения различных формальных методов и модельных схем, а также ознакомления с ранее решенными задачами близкого к анализируемой типа и разнообразными данными предметной области. Эксперт на основе своих знаний и опыта оценивает точность исходных параметров, подыскивает аналоги, выбирает модели для расчета, анализирует промежуточные результаты, разрабатывает стратегии изменения данных (сценарии), вводит поправки, связанные с учетом качественных факторов, содержательно интерпретирует окончательные результаты расчетов. Следует подчеркнуть в этой связи, что в отсутствии квалифицированного эксперта сложные задачи не могут быть надлежащим образом исследованы обычным пользователем СППЭР, даже если последняя обладает развитыми базами моделей, знаний, данных и интерфейсом.

Один из аспектов усиления роли экспертов – практическая возможность получения значений многих исходных данных требующих решения задач преимущественно в виде экспертных оценок, формируемых на базе экспертных знаний, суждений по аналогии и т.п. Однако для того, чтобы подобные неформализованные экспертные знания могли быть использованы в СППЭР, следует получить их математическое представление. Это обстоятельство стимулирует развитие различных методов анализа данных, преобразующих исходные параметры в формализованные структуры, а параметры, уже получившие формализованное представление, в интерпретируемые результаты, новые знания, содержащиеся до того в исходной информации лишь неявно [1 - 3].

Широкий класс экспертных оценок во многих прикладных задачах доставляют именно интервальные экспертные оценки. Целесообразным оказалось, например, интервальное задание экспертом значений исходных параметров в исследованных авторами ранее совместно с В.И. Пороскуном задачах подсчета запасов углеводородов и прогнозирования перспективности нефтесодержащих объектов на ранних стадиях их изученности [4 - 10]. Примеры именно из этой области будут использоваться нами ниже для иллюстрации некоторых положений настоящей статьи.

Актуальность тематики введения в практику экспертиз методов сбора и обработки интервальных экспертных оценок подчеркивалась также в работах [11, 12], где в качестве примера решенной в Институте автоматики ДвО РАН практической задачи приводилась задача с интервальным экспертным заданием ожидаемого места концентрации рыбы или других океанических биоресурсов. Другой приведенный там пример связан с оцениванием качества продукции. При формализации вербальных значений качественного признака - "отлично", "хорошо", "удовлетворительно", характеризующих достоинства продукции, каждое такое значение, наряду с другими возможностями формализации, удобно описывать интервалом. Например, оценка "отлично" описывается интервалом (0,8  1,0), оценка "удовлетворительно" - интервалом (0,4  0,6) и т.п.

Для числовых исходных данных их интервальное задание отвечает ситуации с наибольшей неопределенностью. Диапазоны допустимых изменений значений результирующих показателей моделей оказываются при этом, как правило, чрезвычайно широкими. Этот недостаток частично устраняется, а возможности количественного, математического анализа исходных данных становятся гораздо богаче, если эксперт в дополнение к интервальной оценке параметра выдвинет гипотезы о виде функций распределения вероятностей реализации значений параметра в заданном им интервале² [D_l, D_r]. Под подобного рода гипотезами нет, конечно, каких-либо строгих математико-статистических оснований. Речь здесь может идти либо о реализациях концепции субъективной вероятности, либо, что думается предпочтительнее и допустимо при анализе достаточно широкого круга задач, о трактовке одиночного суждения эксперта об анализируемом объекте как степени достоверности реализации одного события из длинной цепочки однотипных событий. Применительно к задачам оценки запасов углеводородов это означает, что эксперт сначала мысленно относит анализируемый нефте- или газосодержащий объект к объектам некоторого известного ему широкого класса (ансамблю), а затем делает вероятностные прогнозы возможных значений частных параметров объекта, исходя из общих закономерностей, присущих ансамблю. В работе [13] А.Н.Колмогоров, рассматривая сходную ситуацию, писал: «Любое определенное суждение может быть только истинным или ложным. Например, если кто-то скажет, что 23 марта 1930 г. на полях в окрестностях Москвы лежал снег, - это ошибочное утверждение. Однако это неверное суждение основано на верном общем правиле – в начале 20-х чисел марта на полях под Москвой по большей части лежит снег. Это правило отражает объективные свойства климата Подмосковья. Такого рода правила можно выражать, указывая уровень вероятности интересующего нас события, при тех или иных общих, осуществляющихся неограниченное число раз условиях. Эти оценки уже имеют объективный смысл».

Конечно, возможности анализа свойств изучаемых систем, связанных с описанием присущей им неопределенности, не ограничиваются теоретико-вероятностными методами. Вместе с тем в ряде случаев применение именно их наиболее оправдано. Так обобщение практического опыта работы с экспертами, использующими СППЭР, показало, что экспертный анализ наиболее продуктивен, если диалог с системой ведется на привычном для пользователя языке, с использованием знакомой ему терминологии [14; 15]. Не отрицая привлекательных черт таких средств анализа неопределенности как «грубые, или приближенные, множества» [16, 17], «недоопределенные множества» [18, 19], «небулярные множества» [20], нечеткие множества [21; 22; 23], следует признать, что анализ, базирующийся на теоретико-вероятностных понятиях, которые образуют часть их профессионального языка, более распространен в среде специалистов различного профиля, в частности, среди специалистов-нефтяников. Привычность теоретико-вероятностного инструментария для основного круга экспертов, занимающихся геолого-экономической оценкой, - геологов, технологов, экономистов, понимание ими математической и содержательной структуры используемого аппарата, а, в силу этого, влияния возможных изменений в описании исходных данных на результирующие показатели, оказывается существенным для продуктивности диалога «эксперт – СППЭР».

В ряде случаев преимущественное применение при моделировании того или иного математического аппарата может быть связано и с некоторыми формальными обстоятельствами. Такой формальный, но существенный аргумент в пользу использования в качестве меры достоверности различных суждений на интервалах изменения исходных параметров теоретико-вероятностных конструкций имеется, например, в задачах оценки запасов углеводородов. Речь идет о том, что международная классификация запасов, с которой неизбежно следует считаться российским нефтяникам и газодобытчикам при их вовлеченности в мировой рынок углеводородов, основывается именно на теоретико-вероятностных представлениях [24]. Они лежат также в основе так называемой «рамочной» классификации ООН, проект которой достаточно интенсивно обсуждается в последнее время. Вместе с тем следует отметить, что ряд важных работ разных авторов [25; 26, 27] посвящен исследованию вопросов построения методов оценки запасов углеводородов, базирующихся на теории нечеткости. Их результаты могут оказаться востребованными в будущем при изменениях в представлениях и «вкусах» широких кругов экспертов-нефтяников и возможных модификациях нормативных документов, регламентирующих классификационные построения.

Итак, объектом наших предыдущих исследований [4 - 10] являлись задачи, в которых оцениваемые параметры были исходными данными некоторых моделей, задавались интервально и, в дополнение, считались известными функции распределения вероятностей появления значений параметров в заданных интервалах. Предполагалось, что значительная часть исходной информации либо получена непосредственно от эксперта, либо выбрана им из списка, содержащегося в базе данных СППЭР.

В целом для этого случая методы работы с интервальными оценками и получения на их основе значений функционально связанных с ними результирующих показателей известны. В варианте, когда никакие дополнительные гипотезы о степени достоверности каких-либо высказываний о точках вложенных в «базовый» интервал [D_l^(b), D_r^(b)] подынтервалов экспертом не предъявлены, это – методы интервального анализа [28], а также метод статистических испытаний (Монте-Карло), если эксперт дополнительно к интервальным значениям может задать сопутствующие функции распределения вероятностей.

С примерами решения задач подсчета запасов углеводородов и других результирующих показателей соответствующих геолого-экономических моделей при заданных экспертом как интервальные числа исходных данных и специфицированных им соответствующих функциях распределения вероятностей можно ознакомиться в работах [4 - 10]. Для каждого из параметров задачи, рассматриваемых как случайные величины, эксперт выбирает тип распределения вероятности, отражающий его представления о возможной изменчивости значений этого параметра и шансах на возникновение тех или иных диапазонов значений применительно к анализируемому объекту.

Эксперт задает минимальное, наиболее вероятное и максимально возможное, согласно имеющейся информации, значения оцениваемого параметра на объекте, специфицируя (априорное) распределение вероятности ранее выбранного типа. Среди типов распределений наиболее широко используются экспертами равномерное, нормальное, логнормальное, треугольное и -распределение. Не следует думать, что факт такого разнообразия привлекаемых для анализа типов распределений является следствием экспертного задания данных. Так значимость теоретико-вероятностных моделей разных видов, в противоречии с распространенной точкой зрения о приоритетности нормального закона в анализе погрешностей измерений, признана и официально закреплена в ГОСТ 8.011-72. В нем устанавливается, что при сообщении размера погрешностей результата измерения целесообразно указывать вид распределения. При этом были стандартизованы модели равномерного, трапецеидального, треугольного, нормального и даже некоторых бимодальных распределений [29].

Поскольку проект освоения каждого анализируемого нефтегазового объекта во многом уникален, было признано, что при привлечении для оценки запасов и подсчета других результирующих показателей теоретико-вероятностного моделирования применение традиционных средних по распределению («математическое ожидание») величин, адекватных массовым повторяющимся явлениям, не всегда оправдано.

Более адекватным подходом в указанных условиях представляется использование дихотомических оценок, разделяющих весь интервал возможных значений результирующего показателя на две части, - одну, содержащую все исходы, классифицируемые экспертом как благоприятные, и другую, включающую все неблагоприятные случаи. Такой оценкой в теоретико-вероятностной картине является пара (R_o, P(R  R_o)), где R_o – некоторое граничное значение результирующего показателя R, анализируемое в данный момент экспертом, а P(R  R_o) - вероятность того, что в «игре с природой» реализуются лишь благоприятные возможности, то есть такие, значения результирующего показателя R для которых превосходят R_o. (Предполагается, что увеличение значений результирующего показателя увеличивают привлекательность возможных исходов для эксперта). Например, извлекаемые запасы углеводородов Q_изв, окажутся больше, чем заданное экспертом их значение Q_o, или реализуются исходы, стоимостные оценки перспективности для которых превосходят желаемую граничную, и т.д. В теории вероятностей и математической статистике такая вероятность носит название «вероятность дожития».

Применительно к задачам оценки запасов эта оценка названа [4 - 10] вероятностью гарантированного результата, имея в виду, что она показывает, какова вероятность допустимых, по имеющейся информации, исходов, реализация любого из которых приведет к результату R, значение которого, при прочих равных условиях, будет не хуже величины R_o, играющей роль эталона сравнения. Эта вероятность служит также (при наблюдаемых с неопределенностью исходных данных) мерой надежности суждений о величинах возможных запасов и перспективности освоения анализируемого нефтегазового объекта.

Интересно отметить, что к целесообразности отказа при принятии решения от критерия, основанного на математическом ожидании, и использовании оценок, аналогичных оценкам, ориентирующихся на гарантированный результат, привели исследования, посвященные формированию рационального портфеля ценных бумаг [30]. В задачах этого типа отказ от «средних» оценок, наряду с прочим, связан с существованием так называемого биржевого парадокса [31]. Он состоит в том, что если критерием оптимальности выбрано математическое ожидание дохода, то существует стратегия покупки ценных бумаг, при которой, с одной стороны, средний доход стремится к бесконечности, а с другой, вероятность разорения стремится к единице.

2. Полиинтервальные оценки исходных данных

В процессе анализа и обобщения результатов исследований, проведенных в [4 - 10], стало ясно, что не все ситуации экспертного задания исходных параметров, измеримых в количественных шкалах, могут быть описаны в рамках «моноинтервального» подхода, подхода, при котором эксперт ограничивается заданием для каждого исходного параметра единственного интервала изменчивости данных. Именно, знания эксперта о проблеме могут оказаться таковыми, что он посчитает задание значений какого-либо параметра в виде единственного интервального числа неадекватным его истинной точке зрения. Фактически его знаниям об исходном параметре может отвечать задание целой совокупности интервалов. Для спецификации такой совокупности эксперт может задать оценки нескольких характерных интервалов, входящих в совокупность. Это могут быть, например, пессимистическая, оптимистическая и наиболее вероятная оценки для интервала, описывающего, по мнению эксперта, изменчивость анализируемого исходного параметра, или какие-либо другие оценки. Тогда необходимо, исходя из предъявленных экспертом оценок, восстановить всю совокупность интервалов. Ясно, что и при фиксированном числе оценок последующий анализ зависит от того, какие именно интервалы их совокупности выбраны в качестве характерных. Рассмотрим далее более подробно простейший случай наличия экспертных оценок для двух специально выбранных характерных интервалов.

Эксперт может, например, задать оценку для наиболее ожидаемого и наименее широкого из входящих в совокупность интервалов, – «интервала-моды» - I_m = [D_l^(m), D_r^(m)] длины M = D_r^(m) - D_l^(m), и для наиболее широкого («базового») интервала совокупности I_b = [D_l^(b), D_r^(b)] длины B = D_r^(b) - D_l^(b), заведомо включающего, по мнению эксперта, «истинное», неизвестное значение параметра. Все «промежуточные» (между I_m и I_b) интервалы I_l, такие что I_m  ^…  I_l  ^…  I_b, также входят в указанную совокупность. Предполагается, что знания квалифицированного эксперта должны позволить ему даже в ситуации со столь высокой неопределенностью подойти к выбору I_m и I_b достаточно обоснованно, а не ограничиться, например, выбором I_b = (-, ). Последнее не может не означать полного незнания, и такой эксперт вряд ли компетентен в анализируемой им предметной области.

Расположим все возможные отдельные интервалы заданной таким образом экспертом их совокупности на плоскости (Y = h, X = D) друг над другом, от большего (по длине) I_b к меньшему I_m, так чтобы левые границы промежуточных интервалов лежали на левой [D_l^(b), D_l^(m)], а правые на правой [D_r^(m), D_r^(b)] боковой стороне соответствующей криволинейной трапеции. Нормируем высоту h этой трапеции на единицу, при этом базовый интервал совокупности отвечает h = 0, а интервал-мода h = 1. Полученную конструкцию назовем «полиинтервальной» экспертной оценкой возможных значений исходного параметра. При таком задании полиинтервальных оценок соответствующая система интервалов оказывается системой интервалов, вложенных друг в друга. В общем случае это не обязательно. Итак, полинтервальные оценки этого типа определяются не только заданием базового интервала и интервала-моды, но и видом левой и правой границ соответствующей криволинейной трапеции. В простейшем случае эти границы прямолинейны. Отметим, что возможность варьирования границ полинтервальных оценок и задания меры уверенности в реализации границ того или иного типа предоставляет эксперту дополнительную возможность отобразить свои знания об анализируемом исходном параметре.

3. Обобщенные интервальные оценки исходных данных

Построим теперь на базе полиинтервальной оценки такую теоретико-вероятностную модель представления экспертных знаний, которая сочетала бы в себе описание двух видов неопределенности, присущих, вообще говоря, суждениям эксперта. С одной стороны, он не знает с достоверностью, какое подмножество интервалов, включающее базовый, из всей совокупности интервалов, образующих вышеуказанную трапецию, наилучшим образом характеризует неопределенность состояния его знаний о возможном размахе изменения значений рассматриваемого параметра. Вместе с тем все множество интервалов, составляющих названную трапецию, характеризует эту неопределенность, по мнению эксперта, исчерпывающим образом. Тогда меру уверенности эксперта в адекватности описания параметра на базе имеющихся знаний каким-либо подмножеством интервалов, включающим базовый, которое в графическом представлении полиинтервальной оценки имеет высоту h, 0  h  1, можно связать с некоторой функцией от этой высоты. С другой стороны, как и в моноинтервальном случае, знаниям эксперта возможно присуща неопределенность, связанная с изменчивостью значений исходного параметра на отдельных интервалах их совокупности.

Таким образом, в нашей теоретико-вероятностной модели для каждого исходного параметра мы имеем дело с системой двух случайных величин  = h и D, заданных на его полиинтервальной оценке. Эта система обладает совместной функцией распределения вероятностей с плотностью (, D). Случайная величина  имеет плотность распределения f₁(), обычным образом связанную с вероятностью P(<_o). Эту вероятность будем считать в рамках модели вероятностью того, что при заданных боковых сторонах соответствующей криволинейной трапеции совокупность интервалов, отграниченных интервалами с h = 0 и h = _o, адекватно описывает возможную изменчивость длины интервалов, характеризующих вариабельность какого-либо исходного параметра. Отметим, что разные диапазоны изменения  могут быть снабжены разными функциями распределения вероятностей. Случайная величина D, лежащая в интервале, отвечающем h = , обладает (условной) плотностью распределения f₂(D/). Для разных  тип распределения f₂ может быть также разным. Конечно, (, D) = f₁()f₂(D/).

Полиинтервальную оценку исходного параметра, обладающую известными f₁ и f₂, назовем его обобщенной интервальной оценкой (ОИО).

Следует отметить, что известная неадекватность, для некоторых задач, моноинтервальной оценки с заданием единственной функции распределения вероятностей осознавалась и другими исследователями, предложившими свои модели представления данных.

Так в монографии [32] в рамках теоретико-вероятностной концепции при (моно) интервальном задании данных дополнительно предполагалось, что средние соответствующих распределений имеют интервальную оценку. Это эквивалентно тому, что вероятности наступления анализируемых событий также оказываются заданными интервально. В работах [33; 34] при (моно) интервальном задании данных их стохастические свойства описывались, в условиях недостатка информации, не однозначно установленной функцией распределения, а целым классом возможных таких функций. При этом степень возможности возникновения каждого из распределений класса характеризуется экспертно задаваемой функцией принадлежности (в нечетко-множественном понимании). Думается, что разнообразие возможных интервально-вероятностных моделей представления данных должно найти отражение в базах моделей СППЭР. Это позволит пользователю привлекать к исследованию те модели, которые в наибольшей степени согласуются с привычным для него языком анализа.

Наша текущая задача состоит теперь в том, чтобы, исходя из обобщенной интервальной оценки, получить функцию распределения P(D < D_s), заданную на базовом интервале ОИО. Здесь D_s – эталонное (стандартное) значение D, с которым сравниваются все другие допустимые значения анализируемого исходного параметра. Будем считать, что D_s принимают точечные значения и что D_s > 0.Соответствующие соотношения для интересующих нас функций распределения P(D < D_s) будут получены в следующем разделе. После того, как соотношения для P(D < D_s) установлены, на базе методов, описанных, например, в работах [4 - 10], можно получить вероятностные оценки гарантированного результата и некоторые другие часто интересующие пользователя показатели, такие как, например, коэффициент риска [35].

4. Функции распределения вероятностей для параметров, описываемых обобщенными интервальными оценками

Пусть D_l,r() соответственно левые (правые) границы интервалов I_, отвечающих на криволинейной трапеции ОИО значениям 0<  < 1. Тогда интересующая нас вероятность P(D < D_s) имеет вид:



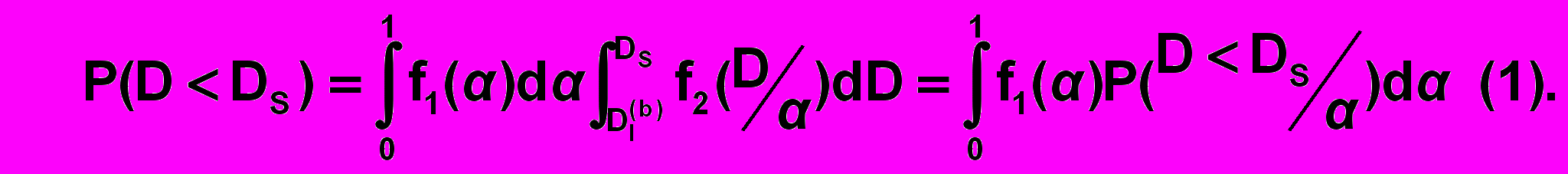
При этом



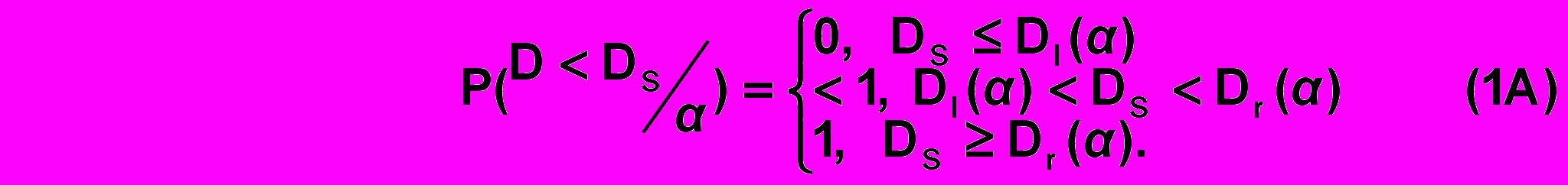
Ясно, кроме того, что P(D < D_s) = 0 при D_s  D_l^(b), P(D < D_s) = 1 при D_s  D_r^(b).

Разделив базовый интервал на три части, (D_l^(b), D_l^(m)), (D_l^(m), D_r^(m)) и (D_r^(m), D_r^(b)), соотношение (1) можно переписать в виде (2), где _l(D_s) и _r(D_s) ординаты точек пересечения соответствующих перпендикуляров D_s с боковыми сторонами криволинейной трапеции полиинтервальной оценки на плоскости (Y = , X = D).

При D_l^(b) ≤ D_s < D_l^(m):

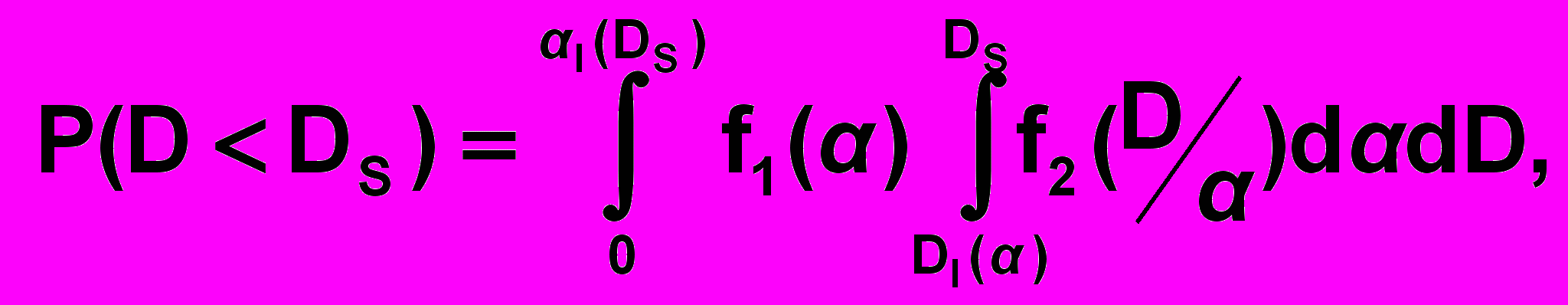
При D_l^(m) ≤ D_s ≤ D_r^(m): 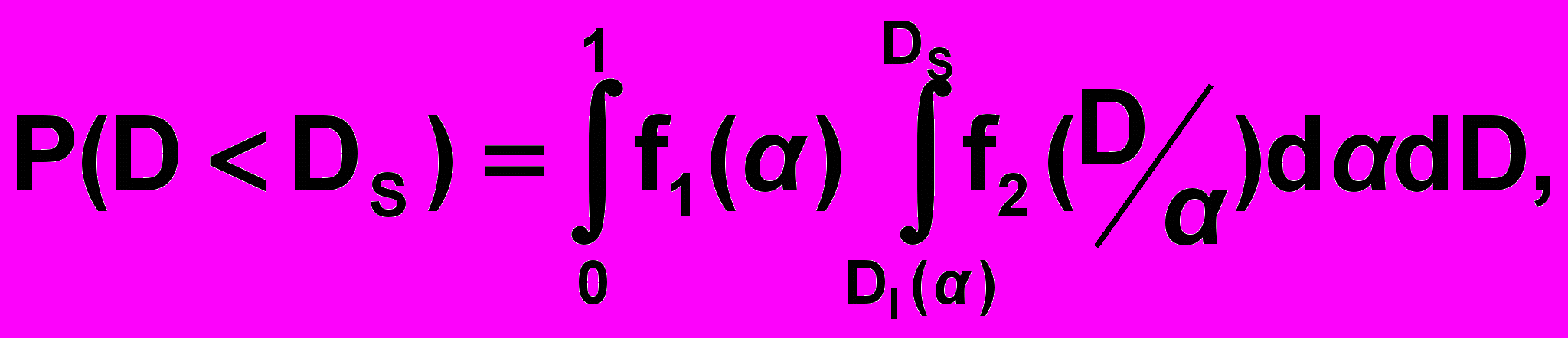(2)

При D_r^(m) < D_s ≤ D_r^(b): .

Будем в дальнейшем в этой работе для простоты предполагать, что эксперт задает для случайных величин D, определенных на разных интервалах, один и тот же тип распределения вероятностей. При этом положение наиболее вероятного значения (моды) параметра на разных интервалах будем нормировать на их длину. Это означает, что если, например, эксперт выбрал в качестве закона распределения для D треугольное распределение, то положение моды D^(m) для всех интервалов задается им коэффициентом формы 0 < K < 1. При этом D^(m)() = (1 – K)D_l() + KD_r(), где D_l,r() соответственно левая и правая границы интервала, отвечающего h = . При желании от этого ограничения, как уже отмечалось, можно отказаться.

Для частного случая прямолинейных боковых сторон трапеции ОИО, который может рассматриваться как первый шаг в экспертном анализе исходного параметра, имеем



В качестве примера применения соотношений (2) для прямолинейных боковых границ ОИО рассмотрим простейший случай равномерных распределений для случайных величин : f₁() = 1 и D: f₂(D/) = 1/[D_r() – D_l()]. Можно вычислить теперь интегралы в (2) и получить:


При D_l^(b) ≤ D_s < D_l^(m):



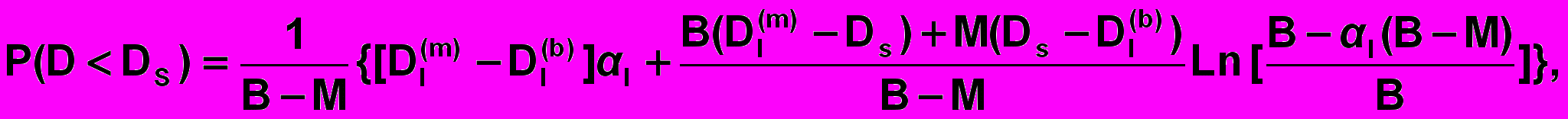
При D_l^(m) ≤ D_s ≤ D_r^(m):



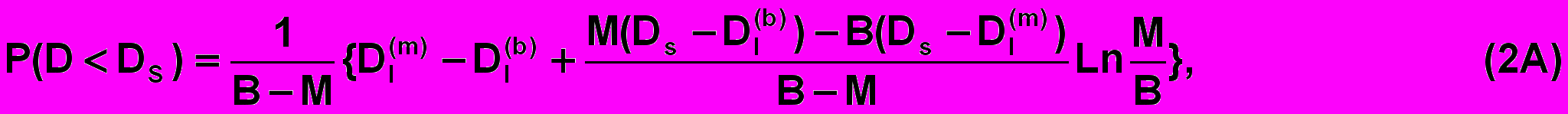
При D_r^(m) < D_s ≤ D_r^(b):



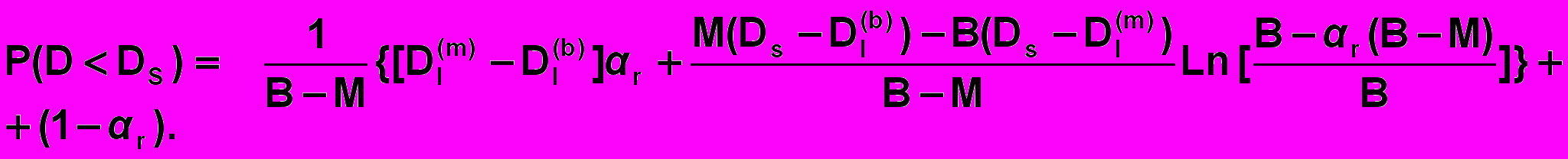
Для плотности функции распределения тогда имеем:

При D_l^(b) ≤ D < D_l^(m): .

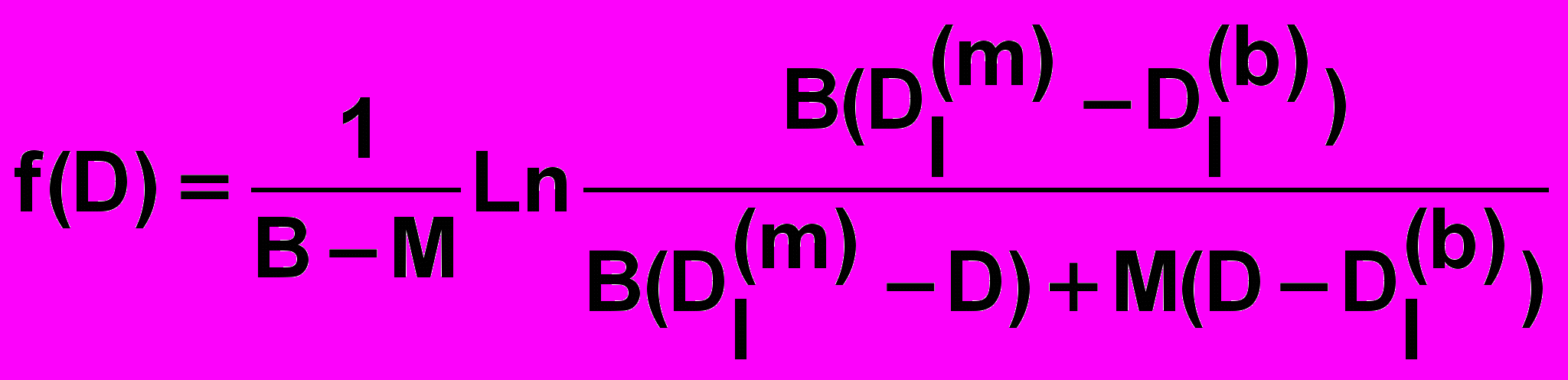При D_l^(m) ≤ D ≤ D_r^(m): .

При D_r^(m) < D ≤ D_r^(b): .

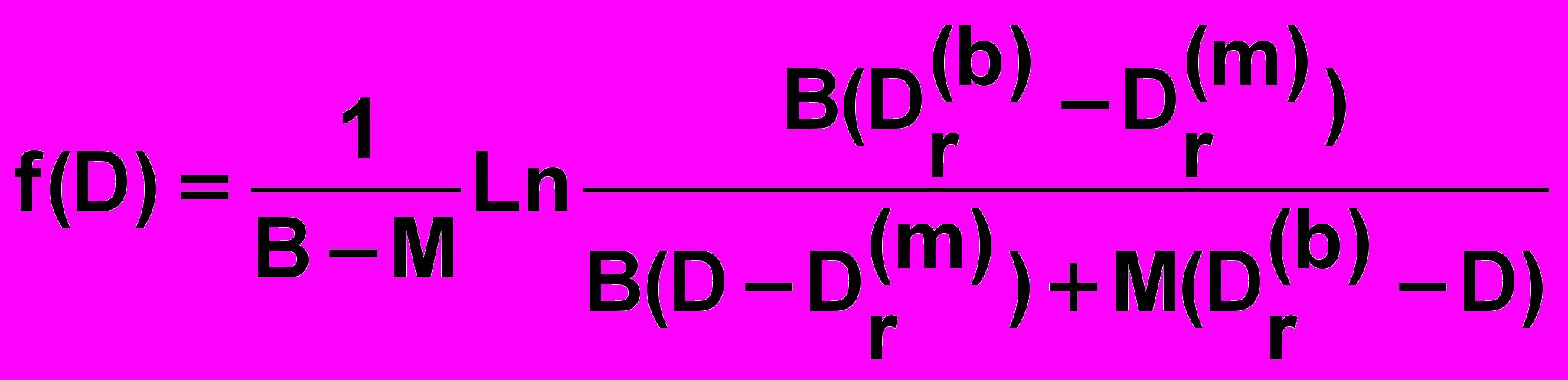Можно показать, что при MB это распределение переходит в обычное равномерное распределение: f(D)=1/M. В этом смысле полученные соотношения являются обобщением равномерной функции распределения вероятностей, заданной на моноинтервале, на случай обобщенных интервальных оценок.

Интересно сопоставить поведение функций распределения вероятностей для равномерных распределений, заданных на I_b и I_m и на обобщенной интервальной оценке (I_b, I_m). Это сравнение показано на рисунке 1 на плоскости (Y = P(D < D_s), X =D) для D_l^(b) = 10, D_r^(b) = 50, D_l^(m) = 30, D_r^(m) = 35. Все три графика имеют одну общую точку пересечения с координатами

D_i = [BD_l^(m) – MD_l^(b)]/(B – M), P_i = [D_l^(m) – D_l^(b)]/(B – M).





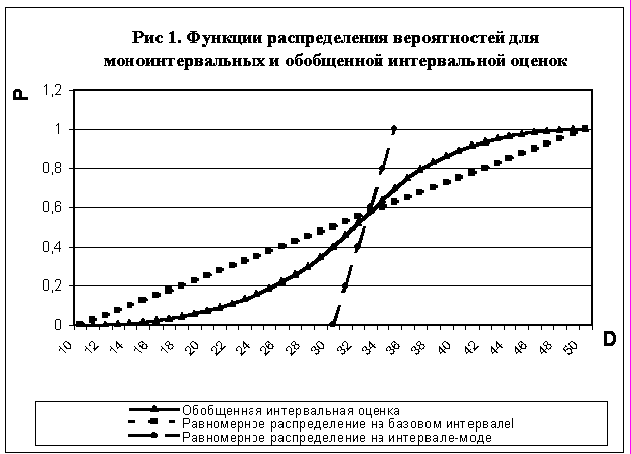
Можно видеть, что поведение функции распределения для ОИО более сбалансировано, чем для соответствующих кривых моноинтервальных оценок. Именно, ОИО увеличивает вероятность реализации гарантированных исходов для D < D_i и увеличивает эту вероятность для D > D_i. Это означает, что ОИО устраняют недооценку малых значений исходных параметров, с одной стороны, и переоценку больших значений этих параметров, с другой.

Аналитические соотношения для P(D < D_s) могут быть получены также для случаев, когда эксперт выбрал для распределения D на интервалах их системы треугольный закон, а для –распределения по-прежнему принято равномерное распределение. Аналитические формулы получаются также для различных комбинаций (по D и ) треугольного и равномерного распределений.

Для расчета P(D < D_s) в случаях, когда для распределений вероятности на D и  выбраны распределения произвольного типа, авторами разработан основанный на соотношениях (1, 1А) численный метод. При сравнении результатов, полученных с его помощью, с расчетами по точным аналитическим формулам для соответствующих случаев различия не превышают долей процента. В соответствии с (1, 1А) для расчета P(D < D_s) численным методом при каждом  на выбранной сетке надо иметь f₁() и P(D_s/).

В случае отказа от задания распределения вероятностей для D на отдельных интервалах и ограничения равномерным распределением для их совокупности получающуюся обобщенную интервальную оценку можно трактовать с позиций теории нечеткости. На факт возможности рассматривать совокупность –уровней нечеткого множества как обобщенное интервальное число указано ранее в работе [36]. Случай введения равномерного вероятностного распределения на –уровнях нечеткого числа с треугольной функцией принадлежности рассмотрен в работе [37]. Соотношения, полученные в этой работе, следуют из (2А) при M  0, D_l^(m) = D_r^(m) = D^(m). В этой работе рассмотрен также и более общий естественный в рамках нечетко-множественного подхода случай, когда стандарт сравнения D_s также нечеткое число. Нам представляется, что в рамках метода обобщенных интервальных оценок применительно к задачам получения «гарантированных» оценок для результирующих показателей достаточно ограничиться точечными значениями D_s. Вместе с тем, если пользователем СППЭР, включающей в свою базу моделей вероятностные методы, основанные на обобщенных интервальных оценках, является лицо, принимающее решение, (инвестор), ему при анализе результирующих показателей может оказаться полезным наличие возможности интервального задания D_s.

Если эксперт ограничился заданием равномерного распределения для  на системе интервалов и отказался специфицировать распределения для D по исходным параметрам, для расчета результирующих показателей моделей может быть использована арифметика нечетких чисел с получением для каждого такого показателя его функции принадлежности. Если эксперт сочтет возможным задать распределение вероятностей для результирующего показателя, определенного на совокупности –уровней соответствующего нечеткого множества, вновь могут быть использованы рассмотренные здесь вероятностные методы с расчетом вероятности наступления интересующего эксперта события P(D > D_s).

Метод ОИО может быть использован также при агрегировании мнений нескольких экспертов, предложивших различные оценки для одних и тех же исходных данных. Эта возможность будет рассмотрена в следующем разделе при обсуждении вопросов реализации интеллектуальных СППР на платформе корпоративных информационных систем.

5. Структура интеллектуальных систем поддержки экспертных решений

Реализация интеллектуальных систем поддержки решений (ИСППР) в задачах оценки перспективности объектов природопользования на ранних стадиях их изученности возможна как в локальном варианте, так и на платформе корпоративных информационных систем.

Структура ИСППР включает в себя следующие основные блоки:

• База моделей (БМ) и система управления базой моделей (СУБМ).
  
• База данных (БД) и система управления базой данных (СУБД).
  
• Генератор отчетов
  
• Интерфейс пользователя.
  

СУБМ контролирует и поддерживает взаимодействие моделей и их связи с БД. БМ содержит комплекс взаимосвязанных стохастических моделей. Это основывающаяся на объемном методе подсчета запасов модель оценки возможных уровней запасов углеводородов на объекте, феноменологическая модель оценки динамики добычи сырья, модель стоимостной оценки объекта, опирающаяся на методы проектного анализа. Отличительной чертой этих моделей является тот факт, что независимо от степени неопределенности исходных данных они имеют одинаковую алгебраическую структуру. Меняется лишь тип представления исходных параметров и методы их обработки, приводящие к результирующим показателям моделей. Например, величина запасов, оцениваемая объемным методом, является произведением исходных параметров-сомножителей. В порядке уменьшения неопределенности эти параметры задаются экспертом либо как интервальные числа, либо как случайные величины, либо как точечные (детерминистские) оценки. Методы обработки исходных параметров в модели – это методы интервального анализа [28], метод статистических испытаний и традиционные арифметические операции соответственно.

Реляционная БД состоит из таблиц фактографических описаний объектов природопользования, исходных данных моделей и промежуточных результатов моделирования величины запасов, динамики добычи, стоимостных показателей. БД содержит также итоговые результаты расчетов и таблицы, используемые при генерации отчетов.

Генератор отчетов представляет итоговые результаты и оценки в виде текстов, таблиц и графиков, необходимых эксперту для выработки заключения о перспективности освоения анализируемого объекта природопользования.

Интерфейс пользователя, как обычно, реализуется в виде, позволяющем эксперту эффективно взаимодействовать с ИСППР в диалоговом режиме.

Рассмотрим теперь некоторые особенности реализации ИСППР на платформе корпоративных информационных систем.

Оценка перспективности освоения объекта природопользования – многокритериальная проблема, требующая для своего решения привлечения экспертов, специализирующихся во многих областях деятельности.

Параметры модели подсчета запасов, в различных ее интерпретациях, оценивают эксперты-геологи.

Объемы и структуру добываемой жидкости и их изменения со временем определяют эксперты-технологи с привлечением результатов моделей динамики добычи.

Экономисты прогнозируют величину затрат на освоение и ожидаемых результатов.

Инвесторы, другие руководители и юристы анализируют стабильность налоговой базы, определяют заинтересованные активные группы и их интересы, взаимные обязательства и сопутствующие риски всех видов.

Взаимодействие перечисленных сторон, участвующих в процессе оценки перспективности, в известной мере регламентируется структурой взаимосвязей моделей ИСППР: выходы модели подсчета запасов служит частью исходных данных для модели оценки динамики добычи, а результаты обеих этих моделей используются при расчетах по модели стоимостной оценки объекта.

Рассматриваемые в ходе оценивания перспективности объекта задачи (расчеты уровней запасов, дебитов добычи, стоимостные оценки) изучаются многими экспертами, каждый из них может рассчитать с помощью ИСППР ряд вариантов. Следовательно, возникает задача агрегирования расчетов разных вариантов для каждого эксперта и задача получения общего мнения в группе экспертов, работающих над одной и той же проблемой.

Для стохастического подхода к моделированию эти задачи могут быть решены в рамках метода обобщенных интервальных оценок.

Именно, в качестве первого этапа формирования агрегированной оценки может быть рекомендована следующая процедура. Для каждого исходного параметра моделей получают от экспертов их ОИО и рассчитывают (частные) распределения вероятностей на соответствующих базовых интервалах. Агрегированное распределение задают на результирующем базовом интервале, представляющем собой (теоретико-множественное) объединение базовых интервалов всех экспертов. Значение агрегированного распределения для каждой точки результирующего базового интервала получают как нормированную на число экспертов сумму частных распределений вероятностей, отвечающих рассматриваемой точке результирующего базового интервала. Отметим, что эта процедура не зависит от того, полиинтервальной оценкой какого вида пользуется каждый эксперт.

Ясно, что при этом предполагается равная компетентность всех экспертов. Можно, однако, проводить вышеописанное агрегирование частных оценок с учетом «веса» каждого эксперта. Веса устанавливаются либо «суперэкспертом», либо формируются автоматически, если существуют соответствующие решающие правила.

Итак, в рамках Интернет или Интранет ИСППР может быть реализована следующем образом.

Серверная часть системы содержит БМ, БД и генератор отчетов. Пользователь (руководитель или эксперт по проблеме или ее составной части) имеет доступ к соответствующим разделам интерфейса, позволяющим ему взаимодействовать с требуемыми для работы моделями и базами данных. Помимо этого пользователь может использовать отдельные компоненты ИСППР и работать в автономном режиме, загружая необходимые для этого модули на своем компьютере.

Руководитель инициирует начало анализа проблемы после чего эксперты формируют необходимую исходную информацию. Если исходные данные для какого-либо варианта получены, производятся расчеты по выбранным моделям. Найденные таким образом промежуточные результаты предъявляются эксперту, который может продолжить расчеты, изменить исходные данные или отвергнуть текущий вариант.

После получения достаточного числа вариантов система предлагает эксперту отобрать варианты, которые будут участвовать в формировании агрегированной оценки. Окончательные результаты моделирования и агрегированные оценки предъявляются эксперту системой как отчет в виде текстов, таблиц и графиков.

Процедура взаимодействия группы экспертов с ИСППР регламентируется правилом, согласно которому эксперты могут перейти к работе с последующей моделью их комплекса только после получения итоговых результатов коллективного обсуждения расчетов по предыдущим моделям. При этом эксперты могут проводит анализ также и самостоятельно, в автономном режиме, основываясь лишь на частично доступной информации и собственных соображениях.

Итоговые результаты включают в себя отчеты, содержащие результаты расчетов по всем моделям, и предварительное заключение о перспективности анализируемого объекта, сформированное системой.

Укрупненная структура распределенной ИСППР представлена на рис. 2.




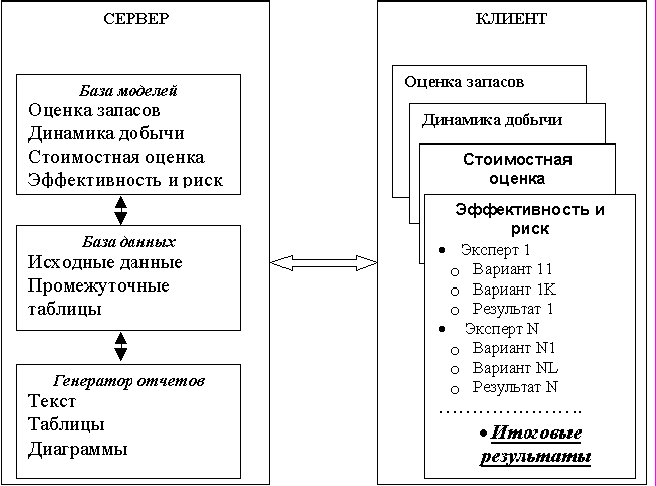
Рис.2. Структура распределенной интеллектуальной системы поддержки принятия решений

6. Заключение

Метод обобщенных интервальных оценок, предложенный в настоящей статье, является новым методом представления экспертных знаний в задачах, исходные данные которых могут быть описаны количественными оценками. Он может быть также использован при агрегировании интервальных оценок, заданных разными экспертами.

Метод предназначен для учета неопределенности в оценках исходной информации, задаваемой как количественные (числовые) данные. В рамках метода на базе экспертных суждений для каждого исходного параметра строятся их обобщенные интервальные оценки (ОИО), - оценки, содержащие в себе экспертные знания о прогнозируемой системе интервалов ожидаемых значений исходных данных и вероятностях их реализации в такой системе. Разработаны интегральное представление и численный метод получения агрегированного результирующего распределения вероятностей реализации значений исходных данных, заданного на базовом интервале системы интервалов, образующих ОИО исходного параметра. Предложены процедуры агрегирования оценок одноименных параметров, сделанных разными экспертами Получены отправляющиеся от агрегированных ОИО процедуры расчета результирующих показателей моделей.

Литература

1. Финн В.К. Интеллектуальные информационные системы. //Итоги науки и техники. Сер. Информатика. Т. 15. М.: ВИНИТИ. 1991.
   
2. Финн В.К. Об особенностях ДСМ-метода как средства интеллектуального анализа данных. //Научно-техническая информация, сер. 2. № 5. 2001, с. 1 – 4.
   
3. Чечкин А.В. Математическая информатика. М.: Наука. 1991.
   
4. Пороскун В.И., Стернин М.Ю., Шепелев Г.И. Принятие решений в условиях неопределенности и риска в задачах оценки нефтегазовых месторождений. //Экономика и управление нефтегазовой промышленности. № 8. 1995, с. 17- 20.
   
5. Пороскун В.И., Стернин М.Ю., Шепелев Г.И., Аракелян В.А. Система поддержки принятия решений в задачах стоимостной оценки нефтегазовых месторождений СППР OIL. М.: Геоинформмарк. 1996.
   
6. Пороскун В.И., Стернин М.Ю., Шепелев Г.И. СППР для стоимостной оценки нефтегазовых объектов на ранней стадии их изученности. //Научно-техническая информация, сер. 2. № 3. 1998, с. 46 – 51.
   
7. Пороскун В.И., Стернин М.Ю., Шепелев Г.И. Вероятностная оценка запасов на начальных стадиях изучения залежей нефти и газа. //Геология нефти и газа. Вып. 5 – 6. 1999, с. 59 – 63.
   
8. Пороскун В.И., Стернин М.Ю., Шепелев Г.И. База моделей системы поддержки экспертных решений для прогноза перспективности нефтегазовых объектов на ранних стадиях изученности. //Искусственный интеллект. № 2. 2000, с. 432 – 436-.
   
9. Пороскун В.И., Стернин М.Ю., Шепелев Г.И. Экспертные модели прогнозных оценок подготовки и освоения запасов нефти. //Тезисы международной научной конференции «Интеллектуализация обработки информации». Симферополь. Таврический национальный университет. 2002, с. 143.
   
10. Пороскун В.И., Стернин М.Ю., Шепелев Г.И. Экспертные модели прогнозных оценок подготовки и освоения запасов нефти. //Искусственный интеллект. № 2. 2002, с. 540 – 546-.
    
11. Орлов А.И. Доклад на семинаре «Многомерный статистический анализ и вероятностное моделирование реальных процессов. //Заводская лаборатория. Т. 56, № 7. 1990, с. 86 - 88.
    
12. Орлов А.И. Экспертные оценки. //Заводская лаборатория. Т.62, № 1. 1996, с. 541- 60.
    
13. Колмогоров А.Н. «Вероятность». //Математическая энциклопедия. Т.1. М.: Советская энциклопедия. 1977.
    
14. Ларичев О.И., Петровский А.Б. Системы поддержки принятия решений: современное состояние и перспективы развития. //Итоги науки и техники. Сер. «Техническая кибернетика». Т.21, с. 131 – 164. М.: ВИНИТИ. 1987.
    
15. Петровский А.Б. Компьютерная поддержка принятия решений: современное состояние и перспективы развития. //Системные исследования. Методологические проблемы. Ежегодник 1996, с. 146 – 178. М.: Эдиториал УРСС. 1996.
    
16. Pawlak Z. Some remarks about rough sets. //ICS PAS Rep. No 456. Warszawa. 1982.
    
17. Pawlak Z. Rough Sets and Fuzzy Sets. Warsaw: Pol. Acad. of Sciences. 1984.
    
18. Нариньяни А.С. Недоопределенность в системе представления и обработки знаний. //Известия АН СССР. Техническая кибернетика. № 5. 1986, с. 3 - 28.
    
19. Нариньяни А.С. Не-факторы и естественный прагматизм: что представляют интервалы. //Интервальные вычисления. № 4(6). 1992, с. 42 – 46.
    
20. Кулик В.Т. Небулярные множества. //Промышленная кибернетика. № 1. 1971, с. 3 - 14.
    
21. Аверкин А.Н., Батыршин И.З., Блишун А.Ф., Силов В.Б., Тарасов В.Б. Нечеткие множества в моделях управления и искусственного интеллекта. М.: Наука. 1986.
    
22. Кофман А., Хил Алуха Х. Введение теории нечетких множеств в управлении предприятиями. Минск: Вышэйшая школа. 1992.
    
23. Рыжов А.П. Элементы теории нечетких множеств и измерения нечеткости. М.: Диалог-МГУ. 1998.
    
24. Золотухин А.Б. Начальные и извлекаемые запасы нефти и газа. //Процесс принятия управленческих решений на основе экономического анализа работ по поискам и разведке нефти и газа. М.: ВНИИОЭНГ. 2001.
    
25. Алтунин А.Е., Семухин М.В. Модели и алгоритмы принятия решений в нечетких условиях. Тюмень: Изд-во ТГУ. 2000.
    
26. Алтунин А.Е., Чуклеев С.Н., Семухин М.В. Применение теории нечеткости для идентификации параметров в АСУ ВПО “Тюменгазпром”. //Проблемы нефти и газа Тюмени. Вып.58. 1983, с. 57 - 59.
    
27. Кирсанов А.И., Семухин М.В., Адлер В.В. Подсчет запасов газа с использованием теории нечетких множеств. //В сб. «Петрофизическое обеспечение подсчета запасов нефти и газа». Тюмень: 1989, с. 96 - 105.
    
28. Калмыков С.А., Шокин Ю.И., Юлдашев З.Х. Методы интервального анализа. Новосибирск: Наука. 1986.
    
29. Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений. Л.: Энергоатомиздат. 1991.
    
30. Кибзун А.И., Кузнецов Е.А. Оптимальное управление портфелем ценных бумаг. //Автоматика и телемеханика. Вып. 9. 2001, с. 101 – 113.
    
31. Секей Г. Парадоксы в теории вероятностей и математической статистике. М.: Мир. 1990.
    
32. Кузнецов В.П. Интервальные статистические модели. М.: Радио и связь. 1991.
    
33. Аркин В.И., Смоляк С.А. О структуре критериев оптимальности в условиях неопределенности. //Вероятностные проблемы управления и математическая экономика. М.: ЦЭМИ РАН. 1985, с. 3 – 28.
    
34. Смоляк С.А. Оценка эффективности проектов в условиях нечеткой вероятностной неопределенности. //Экономика и математические методы. Т. 37, № 1. 2001, с. 3 – 17.
    
35. Бачкаи Т., Месена Д., Мико Д., Сеп Е., Хусти Э. Хозяйственный риск и методы его измерения. М.: Экономика. 1979.
    
36. Бессарабов Н.В. Множества уровня как обобщенные интервальные числа. //Управление при наличии расплывчатых категорий. Тезисы VI научного семинара. Пермь: НИИУМС. 1983, с. 21 – 25.
    
37. Недосекин А.О. Применение теории нечетких множеств к задачам управления финансами. //Аудит и финансовый анализ. № 2. 2000, с. 137 – 160.
    
38. Кендалл М., Моран П. Геометрические вероятности. М.: Наука. 1972.