Geum.ru

Фгуп снииггиМС, г. Новосибирск Россия,630091, Новосибирск,Красный пр

Вид материалаДокументы

Содержание


Сколько параметров необходимо использовать?
Как смоделировать динамику системы, если прямое наблюдение временных рядов невозможно?
Первая проблема
Вторая проблема
Подобный материал:
В.В.Филатов, доктор физ.-мат. наук

ФГУП СНИИГГиМС, г. Новосибирск

(Россия,630091, Новосибирск,Красный пр., 67

Тел. 2224722, E-mail filatov@sniiggims.ru )


ДИНАМИЧЕСКИЕ СИСТЕМЫ И ЗАДАЧИ ПРОГНОЗА


В работе рассмотрены вопросы оптимизации комплекса геолого-геофизических данных при решении прогнозных задач на основе использования методов реконструкции аттракторов динамических систем и факторного анализа. Предложенный подход позволяет оптимизировать набор геолого-геофизических параметров требуемый для прогнозных оценок при поисках полезных ископаемых (оценить количество параметров и их состав). При определенных условиях этот подход позволяет прогнозировать поведение и самой динамической системы.


Одна из главных особенностей задач, связанных с геолого-геофизическим прогнозом – это то, что в таких задачах мы в той или иной форме имеем дело с результатом действия некоторых динамических систем. Под динамической системой будем понимать в соответствии с одним из определений наиболее близким к задачам [1], «систему любой природы, состояние которой изменяется (дискретно или непрерывно) во времени». Для полноты картины к этому определению можно добавить замечание из работы [2]: «Динамическая система – система, поведение которой задается некоторым набором правил (алгоритмом). При этом динамическая система представляет собой лишь модель какой-либо реальной системы. Любая реальная система подвержена флуктуациям и потому не может быть динамической».

С точки зрения математики, любая динамическая система, что бы она ни моделировала, описывает движение точки в фазовом пространстве. Важнейшая характеристика этого пространства - его размерность, или, попросту говоря, число величин, которые необходимо задать для определения состояния системы.

В процессе эволюции изображающая точка с течением времени, смещается вдоль некоторой линии – фазовой траектории. Совокупность характерных фазовых траекторий называют фазовым портретом системы. При определенном навыке по фазовому портрету можно многое сказать о возможных движениях системы.

В типичной фазовой траектории можно выделить начальный участок (переходный процесс) и более поздний этап движений, которые отличаются большей степенью повторяемости – установившиеся движения. Установившимся движениям, которые менее разнообразны, чем переходные процессы, в фазовом пространстве диссипативных систем соответствуют объекты, названные аттракторами. Во фрактальной среде динамический хаос, то есть непериодическое движение в детерминированных системах, приводит к специальному виду аттрактора, который называется странным аттрактором.

Одним из путей решения задачи эффективного комплексирования различных методов при решении прогнозных задач является выявление элементов внутренней упорядоченности систем (как правило, довольно однородных и слабоконтрастных). Часто это сводится к выявлению латентной макроскопической организации сложных многокомпонентных геохимических и других аномалий, сопровождающих месторождения, что представляет исключительную важность на поисковой стадии.

Можно указать два пути для выделения подобного рода связей.

1-фрактальный и вейвлет-анализ внешне хаотических систем аномалий в пространстве параметров, позволяющий выделить объекты одного масштаба для их адекватно сопоставления при комплексировании;

2-анализ совокупности данных как реализации некоторой динамической системы, дающей возможность оценить состояние такой системы и, в зависимости от этого пытаться дать прогнозные оценки.

При подобном анализе возникает ряд вопросов.

Сколько параметров необходимо использовать?

Какие параметры наиболее целесообразно использовать для выделения латентных связей и последующей интерпретации?

Как смоделировать динамику системы, если прямое наблюдение временных рядов невозможно?

Рассмотрим, как можно ответить на поставленные вопросы на примере двух участков из Восточной Сибири, содержащих известные месторождения

Как уже отмечалось, один из путей использования фазовых портретов динамической системы, в которой в качестве параметров выступают различные геолого-геофизические данные, заключается в применении их при комплексировании геолого-геофизической информации. В частности, нас будет интересовать задача прогноза залежей углеводорода по комплексу данных. При этом мы ограничимся методами, не имеющими четко выраженной динамики: потенциальные поля и радиогеохимия. Необходимо отметить, что данные были получены с помощью аэрометодов.

В такой задаче построение интегральных «фазовых» характеристик системы по фиксированному набору площадных наблюдений связано с целым рядом проблем. Рассмотриим две такие проблемы.

Первая проблема - выбор последовательности точек, в которой анализируются параметры. Другими словами мы должны построить по площадной системе измерений некоторый «псевдовременной» ряд. Если это удается и если предположить, что мы имеем дело с установившимся режимом колебаний диссипативной системы, то мы можем перейти в фазовое пространство с реконструированным «псевдовременем» и получить реконструированный портрет аттрактора.

Это построение позволяет связать с анализируемой реализацией наглядный образ, что само по себе заслуживает внимания [5]. Уже рассматривая реконструированный портрет при небольших размерностях, именно, т = 2, 3, можно сделать полезные качественные заключения. Картинку можно интерпретировать как проекцию изображения аттрактора из «естественного» фазового пространства системы в «реконструированное» пространство размерности т.

Чтобы задать «псевдовременной» параметр необходимо исходить из геологических особенностей формирования объектов поиска. В нашем случае приуроченность залежей к зоне выклинивания материнских пород и их последующих смещений в результате различных подвижек позволила остановиться на варианте «псевдовременного» ряда, приведшего к реконструкции аттрактора, показанного на рис.1

Анализировать полученный аттрактор можно по схеме, разработанной для аттракторов, восстановленных на основе теоремы Таккенса [3].




Рисунок 1 Пример аттрактора, реконструированного по реальным данным на, на одном из рассматриваемых участков


То есть, если изображение выглядит как бесструктурная область, заполненная точками, то это означает, что размерность системы N велика по сравнению с т, либо анализируемый сигнал имеет природу случайного шума (рис.2a). Если же сигнал генерируется динамической системой с невысокой размерностью фазового пространства, то наблюдается картинка с характерной выраженной внутренней структурой (рис.2b).



a b

Рисунок 2 Аттракторы, реконструированные по различным наборам данных на одном из исследуемых участков


Можно указать и количественный критерий динамической природы обрабатываемой реализации. В начале 80-х годов было предложено использовать для этой пели корреляционную размерность, адаптируя соответствующим образом алгоритм Грассбергера-Прокаччиа ([4], [6] которая сводится к последовательному определения фрактальной размерности восстановленного аттрактора D(m) в m-мерном пространстве (для m =1,2,3,…). Асимптота полученной кривой и дает величину D, которая принимается в качестве оценки корреляционной размерности аттрактора динамической системы, породившей наблюдаемый сигнал Основываясь на оценке D и так называемой теореме о вложении, можно заключить, что размерность фазового пространства этой динамической системы не превышает 2D +1 (рис. 3).



Рисунок 3 Оценка корреляционной размерности пространства параметров.

Таким образом, использование корреляционных интегралов позволяет оценить размерность фазового пространства и, тем самым, количество параметров, от которых зависит динамическая система. Это, в свою очередь позволяет оценить необходимое количество измеряемых величин – размерность комплекса.

Вторая проблема -какие именно параметры из имеющегося набора целесообразно использовать. Ответить на этот вопрос можно с помощью с помощью метода главных компонент, сущность которого заключается в преобразовании многомерного пространства переменных и в поиске оптимального подпространства, позволяющего выделить небольшое число основных факторов (главных компонент), описывающих изучаемое явление.

Так, из рисунка 4 видно, что совокупность 9 параметров разделилась фактически на три группы, формирующие основные факторы. Таким образом, для задач прогноза целесообразно выбирать всего три параметра из различных групп.





Рисунок 4. Распределение параметров, по факторам

Другим немаловажным фактором выбора параметра является его характеристика с точки зрения реконструированного аттрактора, то есть, отражает ли данный параметр динамику системы. Установление латентных связей между тремя параметрами из различных групп позволило четко выделить зоны месторождений на первом из рассматриваемых участков (рис.5)

На основе этих связей сделан прогноз на втором участке. Было локализовано наиболее крупное из имеющихся там месторождений (рис.6) и выделены дополнительные аномальные зоны.




Рисунок 5. Выделение аномальных зон на основе установление латентных связей между параметрами входящими в разные факторы на первом участке.



Рисунок 6. Прогнозная карта второго участка, построенная на основе связей, установленных на первом участке.


Оценка количества фазовых параметров позволяет строить модели поведения системы в пространстве гипотетических параметров, с помощью реконструкции системы уравнений, которым подчиняется система [4]. Пример такой реконструкции, построенной по реальным данным, измеренным на втором участке, показан yа рисунке 7. Безусловно, такая реконструкция дает идеальную систему, развитие которой может существенно отличаться от реального. Но при определенных условиях она позволят предсказать поведение реальной системы на некотором небольшом промежутке времени.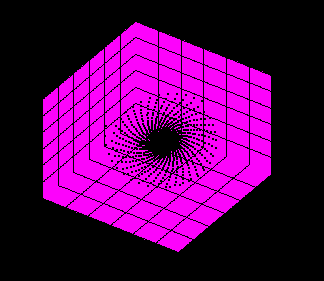




Рисунок 7. Аттрактор реконструированной системы в пространстве гипотетических параметров P1,P2,P3.


Список литературы


1.Берже П. Порядок в хаосе.[Текст]. Берже П., Помо И., Видаль К. М.:Мир, 1991.366 с.

2. Бутенин Н.В. Введение в теорию нелинейных колебаний. [Текст]. Бутенин Н.В., Неймарк Ю.И., Фуфаев Н.А. М.: Наука, 1987. 207 с.

3.Takens F. Detecting strange attractors in turbulence.| [Text]. In: Dynamical Systems and Turbulence. Lecture Notes in Mathematics / Eds D. A. Rand, L.-S. Young.| Berlin: Springer-Verlag, 1980. V. 898. P. 366-381.

4.Кузнецов С. П. Динамический хаос (курс лекций). [Текст]. М: Издательство физико-математической литературы, 2001.—296 с

5.Geometry from a Time Serirs [Text]. Packard N.H.,Crutchfild J.P.,Farmer J.D., Shaw R.S. // Phys. Rev. Lett. 1980. V.45. P. 712-715

6.Malraison B. Dimension of strange attractors. An experimental determination for the chaotic regime of two convective systems [Text]. Malraison B., Atten P., Berge P., Dubois M. // J. Phys. Lett. 1983. V. 44. P. 897-902.


© В.В.Филатов, 2008