Лабораторная работа №2 Приближенное вычисление интеграла

Вид материала

Лабораторная работа

Содержание Относительная погрешность

Подобный материал:

• Лекция 16. Приближенное вычисление определенного интеграла, 52.97kb.
• Курсовая работа тема: «Вычисление определённого интеграла с помощью метода трапеций, 164.04kb.
• Инструкция пользователя 18 Подготовьте модуль функций согласно образцу в приложении, 259.63kb.
• Вычисление определённого интеграла с помощью метода трапеций на компьютере, 165.39kb.
• Методические указания к лабораторным работам Лабораторная работа, 357.24kb.
• Лабораторная работа №3 кпк лабораторная работа №3 Тема: карманный персональный компьютер, 173.34kb.
• Методические возможности стенда Особенности работы на стендах уилс-1 Ознакомительное, 1487.3kb.
• Лабораторная работа по курсу «Физические основы микроэлектроники», 136.21kb.
• Курсовой проект расчет определенного интеграла, 190.12kb.
• Лабораторная работа №11 «Вычисление интегралов методом Монте-Карло», 43.39kb.

Лабораторная работа № 2

Приближенное вычисление интеграла

Вариант 11


Цель данной работы:

изучение различных методов вычисления определенных интегралов, практическое интегрирование функций на ЭВМ.

Для выполнения данной лабораторной работы необходимо разработать схемы интегрирования по формулам прямоугольников, трапеций и Симпсона и реализовать на ЭВМ, организовать необходимые вычисления и сделать вывод по результатам сделанной работы.

Для написания программы была выбрана формула Симпсона, которая относится к приемам численного интегрирования. Суть приема заключается в приближении функции на отрезке [a,b] интерполяционным многочленном второй степени p₂(x), т.е. приближение графика функции на отрезке параболой. Метод Симпсона имеет порядок погрешности 4 и алгебраический порядок точности 3.

Формулой Симпсона называется интеграл от интерполяционного многочлена второй степени на отрезке [a,b]:

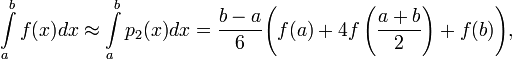где f(a), f((a + b) / 2) и f(b) — значения функции в соответствующих точках (на концах отрезка и в его середине).

При условии, что у функции f(x) на отрезке [a,b] существует четвёртая производная, погрешность E(f), согласно найденной Джузеппе Пеано формуле равна:



В связи с тем, что значение ζ зачастую неизвестно, для оценки погрешности используется следующее неравенство:



Для более точного вычисления интеграла, интервал [a,b] разбивают на N отрезков одинаковой длины и применяют формулу Симпсона на каждый из них. Значение исходного интеграла является суммой результатов всех отрезков.

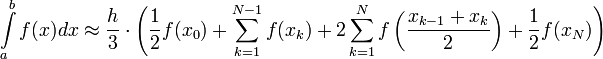, где величина шага, а 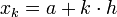границы отрезков.

Общая погрешность E(f) при интегрировании по отрезку [a,b] с шагом x_i − x_{i − 1} = h определяется по формуле:

.

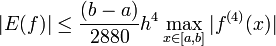Так же, при невозможности оценить погрешность с помощью максимума четвёртой производной (например, на заданном отрезке она не существует, либо стремится к бесконечности), можно использовать более грубую оценку:

.

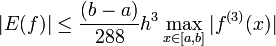Для определения величины шага, обеспечивающего требуемую точность, необходимо найти с помощью двойного пересчета.


Относительная погрешность

После проведенных действий необходимо определить только относительную погрешность:



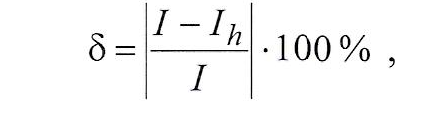
где I – точное значение интеграла, вычисленное через первообразную функцию; I_h – значение интеграла, полученное в результате применения конкретной формулы интегрирования.


Блок-схема





Вывод: для реализации метода Симпсона на практике были даны следующие данные:

• подынтегральная функция f(x) = x ln x
  
• первообразная функция F(x) =x*x/2*lnx-x*x/4 заданная точность 0.00001
  
• интервал [a,b] [2,6]
  

Реализовав данный метод на практике, выявились следующие результаты:

• значение интеграла по методу Симпсона, равно 22,8653760852764
  
• значение интеграла по первообразной, равно 22,8653760849851
  
• погрешность вычислений (%), равно 0.000000001274108